1 Introduction

Nano and microstructure research has seen an increasing interest recently [1]. At such a small scale, mechanical devices exhibit exotic mechanical properties related to atomic-scale interactions, called length scale mechanical properties [2,3,4,5,6] . These effects can be computationally captured using molecular dynamics (MD) simulations. This approach though accurate is very computationally intensive; thus, higher-order continuum mechanics is usually used as a more practical alternative. The strain gradient theory (SGT) is a higher-order continuum theory that is extensively used in small-scale mechanics. This theory introduces different forms of strain energy gradients that can be included in the expression of strain energy. The choice of the strain gradient form yields a different version of SGT [1, 7,8,9,10,11,12] commonly named as SGT family, a detailed list of which can be found in [1, 13]. Most SGTs generate additional high-order derivative degrees of freedom (DOFs) at the boundaries.

To model key nanostructures like carbon nanotubes and graphene sheets [14,15,16,17,18,19,20,21], researchers couple SGT constitutive equations with common beam and plate theories such as Euler–Bernoulli beam theories (EBT), Timoshenko beam (TBT), Reddy beam (RBT), and other beam and plate theories. With the addition of high-order DOFs, deriving shape functions for a finite element method (FEM) has generated a lot of interest in the literature [1, 21,22,23,24,25,26,27,28,29,30,31,32]. In fact, either utilizing a higher-order SGT or raising the order of the element significantly complicates the process of computing the shape functions [22, 25, 31]. Hence, developing high-order elements for nano-mechanics applications is challenging and difficult. However, this type of element provides several advantages including faster convergence and reducing potential numerical problems. To derive high-order solutions, differential quadrature method (DQM) and locally adaptive differential quadrature method (LaDQM) [33, 34] constitute attractive alternatives to FEM. However, these methods lack the geometric flexibility of FEM and suffer from few limitations related to concentrated loads, implementation of boundary conditions (BCs), in addition to spurious eigenvalues [35]. The introduction of the strong form quadrature-element method (SQEM) [36] helps alleviate a few of the conventional DQM deficiencies. However, unlike FEM, both DQM and SQEM do not solve the weak form formulation. Lately, higher-order FEMs [37] and weak quadrature element method (WQEM) [38] were proposed as weak form high-order alternatives to FEM. These methods still offer the same advantages as the regular FEM while providing a high-order convergence rate. WQEM is a weak-form method that uses DQM differentiation matrices and quadrature integral to compute the mass and stiffness matrices without the need to compute explicitly the shape functions [39].

Unlike DQM and LaDQM, SQEM and WQEM explicitly require the presence of derivative degrees of freedom at the boundaries. This limits the number of methods used to derive the DQM differentiation matrices for the latter methods. In fact, to the best of the authors’ knowledge, there is no available method to implement WQEM formulation for more than two extra derivative DOFs at the boundaries [36, 39,40,41]. Besides, computing these matrices is both challenging and complicated. In fact, Hermite-based DQM matrices used for the second strain gradient (SSG) EBT are totally different from the ones used for SSG TBT which complicates its implementation. Moreover, few SSG beam and plate models may require more than two extra derivative DOFs at the boundaries which is still not supported by the current DQM matrix implementations. This makes implementing WQEM difficult for SGT EBT, TBT, and other third-order beams [42]. To cover this gap in the literature, a new WQEM formulation is proposed in this paper referred to as the locally adaptive weak quadrature element method (LaWQEM). The proposed formulation uses a transfer matrix-based technique to build DQM matrices with derivative degrees of freedom at the boundaries. Hermite polynomial shape functions are also developed using the same technique. This formulation is employed to develop high-order elements for nonlinear SSG TBT and SSG EBT. The proposed elements are designed to ensure full integration capability and account for the nonlinear von Kármán strain.

This manuscript is organized as follows. Following the Introduction, variational statements for a nonlinear SSG TBT and a nonlinear SSG EBT are developed in Sect. 2. Then, the implementation of standard WQEM is presented for both SSG beam models in Sect. 3. The proposed LaWQEM, as well as the proposed LaWQEM SSG TBT and SSG EBT element formulations, are detailed in Sect. 4. Section 5 reports the performance of the proposed formulation based on data from the literature and results from well-established methods. Finally, concluding remarks are provided in Sect. 6.

2 Weak integral for SSG EBT and TBT beam theory

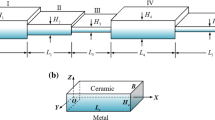
A graded nanobeam of rectangular cross section with a width b, a height h and a length l, shown in Fig. 1, is considered in this study. For a beam graded in the depth direction, the elastic and shear moduli, E and G, and the density \(\rho \) are assumed to vary following a power-law function of the transverse coordinate as follows:

$$\begin{aligned} E(z_{G})= & {} (E_{U}-E_{L})\left( \frac{z_{G}}{h}+\frac{1}{2}\right) ^{n}+E_{L},\,G(z_{G})=(G_{U}-G_{L})\left( \frac{z_{G}}{h}+\frac{1}{2}\right) ^{n}+G_{L}, \end{aligned}$$
(1.1)
$$\begin{aligned} \rho (z_{G})= & {} (\rho _{U}-\rho _{L})\left( \frac{z_{G}}{h}+\frac{1}{2}\right) ^{n}+\rho _{L}, \end{aligned}$$
(1.2)
Fig. 1
figure 1

Schematics of FGM beam reference frames

Full size image

where U and L represent, respectively, the upper and lower layers of the functionally graded material, and \(z_{G}\) is measured from the mid-plane of the beam. Here, n is the material gradation index, and h is the height of the beam. For a homogeneous beam, the neutral axis is located at the mid-plane of the beam. However, due to the uneven distribution of stiffness in the FGM, the position of the neutral axis is located based on the following equation [43, 44]:

$$\begin{aligned} x_{G}&=x,&z_{G}&=z+h_{0}, \end{aligned}$$
(2)
$$\begin{aligned} h_{0}&=\frac{\int _{-\frac{h}{2}}^{\frac{h}{2}}E(z_{G})z_{G}\,dz_{G}}{\int _{-\frac{h}{2}}^{\frac{h}{2}}E(z_{G})\,dz_{G}}= & {} \frac{n\left( E_{U}-E_{L}\right) h}{2\left( E_{U}-nE_{L}\right) \left( n+2\right) } \end{aligned}$$
(3)

where \((x_{G},z_{G})\) and (x, z) are the coordinates at the mid-plane and the neutral axis, respectively. Such a choice should remove stretching and bending couplings caused by the FG material variation and reduce the number of nonlinear terms in the equation of motion. Accounting for the von Kármán strain, the Green–Lagrange strain tensor for the nanobeam can be written as

$$\begin{aligned} \text {For a TBT} \varepsilon _{xx}=\;&\underset{\varepsilon _{xx}^{(0)}}{ \underbrace{\frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}}}+\underset{\varepsilon _{xx}^{(1)}}{z\underbrace{\frac{\partial \phi }{\partial x}}},&\gamma _{xz}=\;&\underset{\gamma _{xz}^{(0)}}{ \underbrace{\phi +\frac{\partial w}{\partial x}}}, \end{aligned}$$
(4.1)
$$\begin{aligned} \text {For an EBT }&\phi = -\frac{\partial w}{\partial x},\nonumber \\ \varepsilon _{xx}=\;&\underset{\varepsilon _{xx}^{(0)}}{ \underbrace{\frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}}}-\underset{\varepsilon _{xx}^{(1)}}{z\underbrace{\frac{\partial ^{2}w}{\partial x^{2}}}},&\gamma _{xz}=\;&0, \end{aligned}$$
(4.2)

where u and w are, respectively, the axial and the transverse displacement at the beam’s neutral axis and \(\phi \) is the angle of rotation of the normal to the neutral axis of the beam. SGT is selected to account for the length scale effect in the nanobeam. According to Jafari and Azzati [31], the different SGTs can generally fall into two different categories, namely the first strain gradient (FSG) and the second strain gradient (SSG). The deformation energy for SSG is given by [31]

$$\begin{aligned} {\displaystyle U_{ssc=}\frac{1}{2}\int \{\sigma _{ij}\varepsilon _{ij}+\sigma _{ijm}^{\left\langle s\right\rangle }\varepsilon _{ij,k}\}dV} \end{aligned}$$
(5)

where

$$\begin{aligned} \sigma _{ij}&=\lambda \varepsilon _{kk}\delta _{ij}+2\mu \varepsilon _{ij}, \end{aligned}$$
(6.1)
$$\begin{aligned} \sigma _{ijm}^{\left\langle s\right\rangle }&=l_{s}^{2}(\lambda \varepsilon _{kk,m}\delta _{ij}+2\mu \varepsilon _{ij,m})=l_{s}^{2}\sigma _{ij,m}, \end{aligned}$$
(6.2)
$$\begin{aligned} {\displaystyle \varepsilon _{ij}}&=\frac{1}{2}(u_{i,j}+u_{j,i}) \end{aligned}$$
(6.3)

in which \(l_{s}\) is the first non-classical constant and \(\varepsilon _{ij}\) is the strain tensor. The notation of the derivative convention used in this paper is given by

$$\begin{aligned} \begin{array}{ccc} \frac{\partial ^{2}u}{\partial t^{2}}=\partial _{t}^{2}u=\ddot{u}=u_{,tt},&\,&\frac{\partial u}{\partial x}=\partial _{x}u=u'=u_{,x}.\end{array} \end{aligned}$$
(7)

The weak integral form for the nonlinear nanobeam can be derived using Hamilton’s principle,

$$\begin{aligned} \int \limits _{t_{1}}^{t_{2}}\left( \delta K-\delta U\right) dt=0, \end{aligned}$$
(8)

where \(\delta K\)and \(\delta U\) denote, respectively, the variation of the kinetic and strain energy and which can be written as

$$\begin{aligned} \text {For a TBT} \delta K= & {} \int _{0}^{l}\Biggl \{m_{0}(\dot{u}\delta \dot{u}+\dot{w}\delta \dot{w})+m_{2}\dot{\phi }\delta \dot{\phi }\Biggr \} dx, \end{aligned}$$
(9.1)
$$\begin{aligned} \delta U= & {} \int _{0}^{l}\left\{ \int _{A}\left[ \sigma _{xx}\delta \varepsilon _{xx}+\sigma _{xz}\delta \gamma _{xz}\right] +\left[ \sigma _{xxx}^{\left\langle s\right\rangle }\delta \varepsilon _{xx,x}+\sigma _{xzx}^{\left\langle s\right\rangle }\delta \gamma _{xz,x}\right] dA\right\} dx\nonumber \\= & {} \int _{0}^{l}\left\{ \int _{A}\left[ \sigma _{xx}\delta \varepsilon _{xx}+\sigma _{xz}\delta \gamma _{xz}\right] +l_{s}^{2}\left[ \sigma _{xx,x}\delta \varepsilon _{xx,x}+\sigma _{xz,x}\delta \gamma _{xz,x}\right] dA\right\} dx\nonumber \\= & {} \int _{0}^{l}\Biggl \{\left[ M_{xx}^{(0)}\left( \delta u'+w'\delta w'\right) +M_{xx}^{(1)}\delta \phi '+M_{xz}^{(0)}\left( \delta \phi +\delta w'\right) \right] \nonumber \\&+l_{s}^{2}\left[ \partial _{x}M_{xx}^{(0)}\left( \delta u''+\partial _{x}\left( w'\delta w'\right) \right) +\partial _{x}M_{xx}^{(1)}\delta \phi ''+\partial _{x}M_{xz}^{(0)}\left( \delta \phi '+\partial _{x}^{2}\delta w\right) \right] \Biggr \} dx, \end{aligned}$$
(9.2)
$$\begin{aligned} \text {For an EBT}\nonumber \\ \delta K= & {} \int _{0}^{l}\Biggl \{m_{0}(\dot{u}\delta \dot{u}+\dot{w}\delta \dot{w})+m_{2}\dot{w}'\delta \dot{w}'\Biggr \} dx, \end{aligned}$$
(9.3)
$$\begin{aligned} \delta U= & {} \int _{0}^{l}\Biggl \{\left[ M_{xx}^{(0)}\left( \delta u'+w'\delta w'\right) -M_{xx}^{(1)}\delta w''\right] \nonumber \\&+l_{s}^{2}\left[ \partial _{x}M_{xx}^{(0)}\left( \delta u''+\partial _{x}\left( w'\delta w'\right) \right) -\partial _{x}M_{xx}^{(1)}\delta w'''\right] \Biggr \} dx \end{aligned}$$
(9.4)

where \(m_{0}=\int _{A}\rho dA\), \(m_{2}=\int _{A}z^{2}\rho dA\), and the stress resultants appearing in the above equations are defined as

$$\begin{aligned} M_{ij}^{(m)}&=\int _{A}z^{m}\sigma _{ij}(x,z)dA=b\int _{-\frac{h}{2}-h_{0}}^{\frac{h}{2}-h_{0}}z^{m}\sigma _{ij}(x,z)dz\nonumber \\&=b\int _{-\frac{h}{2}}^{\frac{h}{2}}\left( z_{G}-h_{0}\right) ^{m}\sigma _{ij}(x_{G},z_{G})dz_{G}. \end{aligned}$$
(10)

The axial stress can be removed following the same process used in [44, 45] based on the following assumptions [45, 46]:

  1. 1.

    \(m_{0}\ddot{u}\) is very small and can be neglected.

  2. 2.

    The beam is supported at \(x=0\) and \(x=l\) such that \(u(0)=u(l)=0\).

  3. 3.

    \(\partial _{x}M_{xx}^{(0)}|_{x=0}=\partial _{x}M_{xx}^{(0)}|_{x=l}=0\).

Then, the following nonlinear term appearing in the expression of \(\delta U\) can be simplified:

$$\begin{aligned}&\int _{0}^{l}\Biggl \{ M_{xx}^{(0)}w'\delta w'+l_{s}^{2}\partial _{x}M_{xx}^{(0)}\partial _{x}\left( w'\delta w'\right) \Biggr \} dx \end{aligned}$$
(11)
$$\begin{aligned} =&\int _{0}^{l}\Biggl \{\left( M_{xx}^{(0)}-l_{s}^{2}\partial _{x}^{2}M_{xx}^{(0)}\right) w'\delta w'\Biggr \} dx+l_{s}^{2}\left[ \partial _{x}M_{xx}^{(0)}\left( w'\delta w'\right) \right] _{l}^{0} \end{aligned}$$
(12)
$$\begin{aligned} =&\int _{0}^{l}\Biggl \{\left( \frac{\tilde{E}_{0}}{2l}\int _{0}^{l}w'^{2}dx\right) w'\delta w'\Biggr \} dx. \end{aligned}$$
(13)

The process of determining the expression of \(M_{xx}^{(0)}-l_{s}^{2}\partial _{x}^{2}M_{xx}^{(0)}\) as a function of the displacement is derived in [47], and the stress resultants (10) can be expressed in terms of displacements as follows:

(14.1)
(14.2)

in which

(15)

The following non-dimensional parameters are introduced:

$$\begin{aligned} \xi =\frac{x}{l},\,\underline{w}=\frac{w}{r},\,\underline{\phi }=\frac{l}{r}\phi ,\,s^{2}=\frac{\tilde{E}_{2}}{l^{2}\tilde{G_{0}}},\,\kappa _{0}=\frac{r^{2}\tilde{E}_{0}}{2\tilde{E}_{2}}, \end{aligned}$$
(16.1)
$$\begin{aligned} \tau =t\frac{1}{l^{2}}\sqrt{\frac{\tilde{E}_{2}}{m_{0}}},r=\sqrt{\frac{I}{A}},\,\underline{l}_{s}=\frac{l_{s}}{l},\,\underline{m}_{2}=\frac{m_{2}}{l^{2}m_{0}}. \end{aligned}$$
(16.2)

WQEM requires the expression of the variational statement as a function of the displacement. Thus, utilizing the normalized variables in (16), applying Hamilton’s principle (8) whose components are given by (9.1), then writing the stress resultants as a function of displacements (14.2) yields the following normalized variational statement:

$$\begin{aligned} \text {For a TBT}: 0=\!&\int _{0}^{1}\Biggl \{\left( \!\begin{array}{c} \ddot{\underline{w}}\\ \left[ \kappa _{0}\left[ \int _{0}^{1}\underline{w}'^{2}d\xi \right] +\frac{1}{s^{2}}\right] \underline{w}'+\frac{1}{s^{2}}\underline{\phi }\\ \frac{\underline{l}_{s}^{2}}{s^{2}}\left( \underline{w}''+\underline{\phi }'\right) \end{array}\!\right) .\left( \!\begin{array}{c} \delta \underline{w}\\ \delta \underline{w}'\\ \delta \underline{w}'' \end{array}\!\right) \!+\!\left( \!\begin{array}{c} \underline{m}_{2}\ddot{\underline{\phi }}+\frac{1}{s^{2}}\left( \underline{w}'+\underline{\phi }\right) \\ \frac{\underline{l}_{s}^{2}}{s^{2}}\underline{w}''+\left[ \frac{\underline{l}_{s}^{2}}{s^{2}}+1\right] \underline{\phi }'\\ \underline{l}_{s}^{2}\underline{\phi }'' \end{array}\!\right) .\left( \begin{array}{c} \delta \underline{\phi }\\ \delta \underline{\phi }'\\ \delta \underline{\phi }'' \end{array}\right) \Biggr \} d\xi . \end{aligned}$$
(17)
$$\begin{aligned} \text {For an EBT}:\nonumber \\ 0=&\int _{0}^{1}\Biggl \{\left( \begin{array}{c} \ddot{\underline{w}}\\ \kappa _{0}\left[ \int _{0}^{1}\underline{w}'^{2}d\xi \right] \underline{w}' + \underline{m}_{2}\ddot{\underline{w}}'\\ \underline{w}''\\ \underline{l}_{s}^{2}\underline{w}^{'''} \end{array}\right) \cdot \left( \begin{array}{c} \delta \underline{w}\\ \delta \underline{w}'\\ \delta \underline{w}''\\ \delta \underline{w}^{'''} \end{array}\right) \Biggr \} d\xi . \end{aligned}$$
(18)

Integrating by parts, the variational statement yields the boundary conditions of the problem [47]. For a hinged–hinged beam (HH) and a clamped–clamped beam (CC), the classical boundary conditions are, respectively, given by

$$\begin{aligned}&\underline{w} |_{\xi =\xi _{b}}=0 \quad \text {HH nanobeam},\end{aligned}$$
(19.1)
$$\begin{aligned}&\underline{w} |_{\xi =\xi _{b}}=0\quad \mathrm {and}\quad {\left\{ \begin{array}{ll} \underline{\phi }|_{\xi =\xi _{b}}=0 \qquad \mathrm {TBT\ nanobeam} \\ \underline{w}'|_{\xi =\xi _{b}}=0 \qquad \mathrm {EBT\ nanobeam} \end{array}\right. \quad \text {CC nanobeam} }. \end{aligned}$$
(19.2)

These conditions should be coupled with the following non-classical boundary conditions:

(20.1)
(20.2)
(21)

3 Proposed LaWQEM formulation

This Section aims to describe the newly proposed WQEM formulation for SSG beams, which can be employed to develop WQEM elements for any other theory requiring several degrees of freedom at the boundary such as non-local strain gradient theory [13, 47, 48] or other versions of SGT [13, 31]. First, generalities about the WQEM are described including the required degrees of freedom for each beam theory, the matrix form of the integration quadrature, and the derivation of the matrix form of the variational statement. Then LaWQEM transfer matrix-based formulation is presented to facilitate the mapping between the LaWQEM degrees of freedom and LaDQM degrees of freedom. Such mapping ensures the compatibility of the required degrees of freedom with the order of the polynomial shape functions. Furthermore, this mapping allows the use of regular WQEM tools with Hermite-type SSG beams’ degrees of freedom and enables the development of various types of Hermite polynomials using linear combinations of Lagrange polynomials.

3.1 Standard weak form Quadrature Element Method

The goal of this Section is to discretize the variational integral statements (17) and (18). To this end, the following mesh distribution with n grid points is generally used with DQM and WQEM:

$$\begin{aligned} \xi _{i}=\frac{1}{2}\left\{ 1-\cos \left( \frac{\pi (i-1)}{n-1}\right) \right\} \quad (i=1,\ldots n). \end{aligned}$$
(22)

Let \(Y_{1}\) and \(Y_{2}\) be the discretized displacement vectors relative to \(\underline{w}(x,t)\) and \(\underline{\phi }(x,t)\) and Y be the general displacement vector such as \(Y=\left[ \begin{array}{c} Y_{1}\\ Y_{2} \end{array}\right] \) for the TBT problem. For the EBT case, \(Y=Y_{1}\) is the nodal displacement vector for \(\underline{w}\) which can be written as

$$\begin{aligned} Y_{1}= & {} \left[ \begin{array}{ccc} \underset{\text {Derivative degrees of freedom}}{\underbrace{\begin{array}{c} \underline{w}_{1}'\end{array}}}&\quad \underset{\text {Internal degrees of freedom}}{\underbrace{\begin{array}{ccc} \underline{w}_{1}&\cdots&\underline{w}_{n}\end{array}}}&\quad \underset{\text {Derivative degrees of freedom}}{\underbrace{\begin{array}{c} \underline{w}_{n}'\end{array}}}\end{array}\right] ^{T},\nonumber \\ Y_{2}= & {} \left[ \begin{array}{ccc} \underset{\text {Derivative degrees of freedom}}{\underbrace{\begin{array}{c} \underline{\phi }_{1}'\end{array}}}&\quad \underset{\text {Internal degrees of freedom}}{\underbrace{\begin{array}{ccc} \underline{\phi }_{1}&\cdots&\underline{\phi }_{n}\end{array}}}&\quad \underset{\text {Derivative degrees of freedom}}{\underbrace{\begin{array}{c} \underline{\phi }_{n}'\end{array}}}\end{array}\right] ^{T}, \end{aligned}$$
(23.1)
$$\begin{aligned}&\text {for the TBT problem},\nonumber \\ Y_{1}= & {} \left[ \begin{array}{ccc} \underset{\text {Derivative degrees of freedom}}{\underbrace{\begin{array}{cc} \underline{w}_{1}''&\quad \underline{w}_{1}'\end{array}}}&\quad \underset{\text {Internal degrees of freedom}}{\underbrace{\begin{array}{ccc} \underline{w}_{1}&\cdots&\underline{w}_{n}\end{array}}}&\quad \underset{\text {Derivative degrees of freedom}}{\underbrace{\begin{array}{cc} \underline{w}_{n}'&\underline{w}_{n}''\end{array}}}\end{array}\right] ^{T}.\nonumber \\&\text {for the EBT problem}. \end{aligned}$$
(23.2)

and the velocity and acceleration vectors are, respectively, designated by \(\dot{Y}\) and \(\ddot{Y}\). It is worth noting that, similar to FEM, SSG EBT WQEM requires continuity to the second derivatives across elements boundaries. This is due to the fact that the weak form of the SSG EBT has third-order derivatives. Such requirement cannot be satisfied with Lagrange-based WQEM elements. The proposed LaWQEM formulation can generate derivative DOFs at the boundaries to any prescribed derivative order. It is, therefore, capable of ensuring continuity for the SSG EBT system. LaDQM, however, is not designed to handle such a task despite possessing the same number of DOFs. To simplify the implementation of WQEM, the discretized system can be written in a matrix form. The discretization of the normalized variational statement (17) yields the WQEM matrix form for an SSG TBT which can be written as

$$\begin{aligned}&\left( \left[ \omega _{\xi }\right] \left[ M_{0}\right] \right) ^{T}.\left( \left[ M_{0}\right] .\ddot{Y}_{1}\right) +\left( \left[ \omega _{\xi }\right] \left[ M_{2}\right] \right) ^{T}..\left( \frac{\underline{l}_{s}^{2}}{s^{2}}\left( \left[ M_{1}\right] .Y_{2}+\left[ M_{2}\right] .Y_{1}\right) \right) \nonumber \\&\quad + \left( \left[ \omega _{\xi }\right] \left[ M_{1}\right] \right) ^{T}.\left( \kappa _{0}i{\mathcal {W}}\left( Y_{1}\right) \left[ M_{1}\right] .Y_{1}+\frac{1}{s^{2}}\left( \left[ M_{0}\right] .Y_{2}+\left[ M_{1}\right] .Y_{1}\right) \right) = 0, \end{aligned}$$
(24.1)
$$\begin{aligned}&\left( \left[ \omega _{\xi }\right] \left[ M_{0}\right] \right) ^{T}.\left( \underline{m}_{2}\left[ M_{0}\right] .\ddot{Y}_{2}+\frac{1}{s^{2}}\left( \left[ M_{0}\right] .Y_{2}+\left[ M_{1}\right] .Y_{1}\right) \right) +\left( \left[ \omega _{\xi }\right] \left[ M_{2}\right] \right) ^{T}.\left( \underline{l}_{s}^{2}\left[ M_{2}\right] .Y_{2}\right) \nonumber \\&\quad + \left( \left[ \omega _{\xi }\right] \left[ M_{1}\right] \right) ^{T}.\left( \left[ M_{1}\right] .Y_{2}+\frac{\underline{l}_{s}^{2}}{s^{2}}\left( \left[ M_{1}\right] .Y_{2}+\left[ M_{2}\right] .Y_{1}\right) \right) = 0. \end{aligned}$$
(24.2)

On the other hand, the WQEM matrix form of the normalized variational statement (18) of an SSG EBT can be expressed as follows:

$$\begin{aligned} \left( \left[ \omega _{\xi }\right] \left[ M_{0}\right] \right) ^{T}.\left( \left[ M_{0}\right] .\ddot{Y}-\underline{m}_{2}\left[ M_{2}\right] .\ddot{Y}\right) +\left( \left[ \omega _{\xi }\right] \left[ M_{3}\right] \right) ^{T}.\left( \underline{l}_{s}^{2}\left[ M_{3}\right] .Y\right)&+\nonumber \\ \left( \left[ \omega _{\xi }\right] \left[ M_{1}\right] \right) ^{T}.\left( \kappa _{0}i{\mathcal {W}}\left( Y\right) \left[ M_{1}\right] .Y\right) +\left( \left[ \omega _{\xi }\right] \left[ M_{2}\right] \right) ^{T}.\left( \left[ M_{2}\right] .Y\right)= & {} 0 \end{aligned}$$
(25)

where \(\left[ \omega _{\xi }\right] \) is the integral quadrature weight vector, \(\left[ M_{k}\right] \) is the DQM \(k^{th}\) derivative matrix whose expression can be found in [39, 42, 49], and \(\left[ M_{0}\right] \) is the identity matrix. The term \(\left[ \omega _{\xi }\right] \left[ M_{1}\right] \) is an element by element multiplication. If \([X]_{i,j}\) denotes the elements of the matrix [X], the term \(\left[ \omega _{\xi }\right] \left[ M_{1}\right] \) is equivalent to the following matrix product:

$$\begin{aligned}{}[\omega _{\xi }][M_1] = \left[ \begin{array}{ccc} [\omega _{\xi }]_{1} &{} 0\cdots &{} 0 \\ 0&{} \ddots &{} 0\\ {} 0 &{} \cdots 0 &{} [\omega _{\xi }]_{n} \end{array}\right] \cdot [M_{1}]. \end{aligned}$$
(26)

It is important to note that the following relation is employed to obtain the WQEM matrix form of both normalized variational statements:

$$\begin{aligned}&\int _{a}^{b}f^{[k]}(x)g^{[l]}(x)dx= & {} \overset{n}{\underset{i=1}{\sum }}[\omega _{\xi }]_{i}f(\xi _{i})g(\xi _{i})= & {} \left[ \begin{array}{c} [\omega _{\xi }]_{1}f^{[k]}(\xi _{1})\\ \vdots \\ {} [\omega _{\xi }]_{n}f^{[k]}(\xi _{n}) \end{array}\right] ^{T}.\left[ \begin{array}{c} g^{[l]}(\xi _{1})\\ \vdots \\ g^{[l]}(\xi _{n}) \end{array}\right] \nonumber \\&= & {} \left( [\omega _{\xi }]\underset{\left[ f^{[k]}\left( \xi \right) \right] }{\underbrace{\left[ \begin{array}{c} f^{[k]}(\xi _{1})\\ \vdots \\ f^{[k]}(\xi _{n}) \end{array}\right] }}\right) ^{T}.\underset{\left[ g^{[l]}\left( \xi \right) \right] }{\underbrace{\left[ \begin{array}{c } g^{[l]}(\xi _{1})\\ \vdots \\ g^{[l]}(\xi _{n}) \end{array}\right] }}\nonumber \\&= & {} \left( \left[ \omega _{\xi }\right] \left[ M_{k}\right] \cdot \left[ f\left( \xi \right) \right] \right) ^{T}.\left[ M_{l}\right] . \left[ g\left( \xi \right) \right] \nonumber \\&= & {} \left[ f\left( \xi \right) \right] ^{T}\cdot \left( \left[ \omega _{\xi }\right] \left[ M_{k}\right] \right) ^{T}.\left[ M_{l}\right] . \left[ g\left( \xi \right) \right] \end{aligned}$$
(27.1)

where in this particular context \(\xi _{i},(i=1,...,n),\) are the quadrature points coordinates. Note that \(\omega _{\xi }\), the integral quadrature weight coefficient vector, should be compatible with the selected grid. For example, a Gauss–Lobatto–Legendre (GLL) grid can be used in conjunction with compatible integral quadrature weight coefficients. However, in the current cases, the presence of derivative degrees of freedom raises the order of the interpolation polynomial. Thus, the accurate evaluation of the discretized variational statement requires a far higher accuracy than offered by GLL. In fact, using GLL, the accuracy of the integration is limited to an order of \(2n-3\), which is enough to achieve reduced integration accuracy for a problem without derivative degrees of freedom. However, unlike non-local TBT [39, 46], neither the mass nor the stiffness matrices are fully integrated. To improve the accuracy of the solution, another transfer matrix is required [39].

To obtain a fully integrated system, a higher number of integration points and a high-order integration scheme must be used such as Gauss quadrature integration. Let, for example, f(x) be an arbitrary function discretized in the SSG EBT Hermite grid. Using Hermite interpolation, the \(k^{th}\) derivative of f(x) can be interpolated as follows:

$$\begin{aligned} f^{[k]}(x)&\thickapprox&{\mathcal {H}}_{-1}^{[k]}(x)f''(\xi _{1})+{\mathcal {H}}_{n+2}^{[k]}(x)f''(\xi _{n})+{\mathcal {H}}_{0}^{[k]}(x)f'(\xi _{1})+{\mathcal {H}}_{n+1}^{[k]}(x)f'(\xi _{n})+\overset{n}{\underset{i=1}{\sum }}{\mathcal {H}}_{i}^{[k]}(x)f(\xi _{i}),\nonumber \\ \end{aligned}$$
(27.2)
$$\begin{aligned}&\thickapprox&\left[ \begin{array}{ccc} {\mathcal {H}}_{-1}^{[k]}(x)&\ldots&{\mathcal {H}}_{n+2}^{[k]}(x)\end{array}\right] .\underset{\left[ f_{\xi }\right] }{\underbrace{\left[ \begin{array}{c} f''(\xi _{1})\\ f'(\xi _{1})\\ f(\xi _{1})\\ \vdots \\ f(\xi _{n})\\ f'(\xi _{n})\\ f''(\xi _{n}) \end{array}\right] }} \end{aligned}$$
(27.3)

where \({\mathcal {H}}_{i}(x)\) are the Hermite interpolation functions based on grid coordinates \(\xi _{i}\) and \(\left[ f_{\xi }\right] \) is f(x) DOFs vector. Applying the Gauss quadrature rule [38, 39] gives

$$\begin{aligned} \int _{a}^{b}f^{(k)}(x)dx&\thickapprox \overset{n+2}{\underset{i=-1}{\sum }}[\omega _{\varsigma }]_{i} f^{(k)}(\varsigma _{i})=\left[ \begin{array}{c} [\omega _{\varsigma }]_{-1}\\ \vdots \\ {} [\omega _{\varsigma }]_{n+2} \end{array}\right] ^{T}.\left[ \begin{array}{ccc} {\mathcal {H}}_{-1}^{\left[ k\right] }(\varsigma _{1}) &{} \ldots &{} {\mathcal {H}}_{n+2}^{\left[ k\right] }(\varsigma _{1})\\ \vdots &{} {\mathcal {H}}_{i}^{\left[ k\right] }(\varsigma _{j}) &{} \vdots \\ {\mathcal {H}}_{-1}^{\left[ k\right] }(\varsigma _{n}) &{} \ldots &{} {\mathcal {H}}_{n+2}^{\left[ k\right] }(\varsigma _{n}) \end{array}\right] \cdot \left[ f_{\xi }\right] \nonumber \\&=\left[ \begin{array}{c} [\omega _{\varsigma }]_{0}\\ \vdots \\ {} [\omega _{\varsigma }]_{n+1} \end{array}\right] ^{T}\cdot \underset{{{[iT_{{\mathcal {H}}}]}}}{\left[ \varsigma M_{k}\right] \cdot \underbrace{\left[ \begin{array}{ccc} {\mathcal {H}}_{-1}(\varsigma _{1}) &{} \ldots &{} {\mathcal {H}}_{n+2}(\varsigma _{1})\\ \vdots &{} {\mathcal {H}}_{i}(\varsigma _{j}) &{} \vdots \\ {\mathcal {H}}_{-1}(\varsigma _{n}) &{} \ldots &{} {\mathcal {H}}_{n+2}(\varsigma _{n}) \end{array}\right] }}\cdot \left[ f_{\xi }\right] =[\omega _{\varsigma }]^{T}\underset{[\varsigma M_{{\mathcal {H}},k}]}{\underbrace{\left[ \varsigma M_{k}\right] .[iT_{{\mathcal {H}}}]}}.\left[ f_{\xi }\right] \end{aligned}$$
(28)

where \(\varsigma _{i}\) and \([\omega _{\varsigma }]_{i}\) are, respectively, the Gauss quadrature points and weights, \([iT_{{\mathcal {H}}}]\) is the Hermite integral transfer matrix, \(\left[ {\varsigma M_{k}}\right] \) is the DQM differentiation matrix relative to \({\varsigma _{i}}\), and \([\varsigma M_{{\mathcal {H}},k}]\) is the WQEM Hermite differentiation matrix relative to \({\varsigma _{i}}\) and \({\xi _{i}}\). Combining Eqs. (27.1) and (28) yields

$$\begin{aligned} \int _{a}^{b}f^{(k)}(x)g^{(m)}(x)dx&=\overset{n}{\underset{i=1}{\sum }}[\omega _{\varsigma }]_{i}f^{(k)}(\varsigma _{i})g^{(m)}(\varsigma _{i})\nonumber \\&=\left( [\omega _{\varsigma }]\underset{[\varsigma M_{{\mathcal {H}},k}]}{\underbrace{\left[ \varsigma M_{k}\right] .\left[ iT_{{\mathcal {H}}}\right] }}.\left[ f_{\xi }\right] \right) ^{T}.\underset{[\varsigma M_{{\mathcal {H}},m}]}{\underbrace{\left[ \varsigma M_{m}\right] .\left[ iT_{{\mathcal {H}}}\right] }}.\left[ g_{\xi }\right] \nonumber \\&=\left[ f_{\xi }\right] ^T .\left( [\omega _{\varsigma }]\left[ \varsigma M_{{\mathcal {H}},k}\right] \right) ^{T}.\left[ \varsigma M_{{\mathcal {H}},m}\right] .\left[ g_{\xi }\right] . \end{aligned}$$
(29)

Thus, all DQM derivative matrices \(\left[ M_k\right] \) and quadrature weights \(\left[ \omega _{\xi }\right] \) in the discretized variational statement should be now replaced by \([\varsigma M_{{\mathcal {H}},k}]\) and \({\left[ \omega _{\varsigma }\right] }\), respectively. Further details about this formulation can be found in [46].

3.2 Derivation of the proposed LaWQEM formulation

The proposed LaWQEM transfer matrix-based formulation is presented in this Section to facilitate the mapping between the LaWQEM degrees of freedom and LaDQM degrees of freedom, thereby ensuring the compatibility of the required degrees of freedom with the order of the polynomial shape functions. As a result, it is possible to employ regular WQEM tools with Hermite-type SSG beams’ degrees of freedom and build various types of Hermite polynomials using linear combinations of Lagrange polynomials.

3.2.1 Development of LaWQEM DOFs

The proposed LaWQEM formulation relies on an LaDQM compatible mesh. The coordinates of the LaDQM mesh adopted in this paper are given by [39]

$$\begin{aligned} \xi _{i}={\left\{ \begin{array}{ll} \xi _{1}-\delta \left( \xi _{1}-\xi _{2-i}\right) &{} 1-n_{L}\le i<1\\ \\ \xi _{n}+\delta \left( \xi _{n}-\xi _{2n-i}\right) &{} n+n_{R}\ge i>n\\ \\ \frac{1}{2}\left( 1-\cos \left( \frac{\pi (i-1)}{n-1}\right) \right) &{} 1\le {{i\le n}} \end{array}\right. } \end{aligned}$$
(30)

where \(\delta \) is a scaling factor, n is the number of internal nodes, and \(n_{R}\) and \(n_{L}\) denote, respectively, the number of external nodes at the right and the left sides. Based on this mesh, a vector of \(n+n_{R}+n_{L}\) degrees of freedom is required for each dependent variable.

Unlike the Hermite-based DQM matrices, the basic LaWQEM matrices do not provide a direct interpolation polynomial basis. The only known interpolation polynomials are the Lagrange polynomial associated with the LaDQM grid. Thus, applying a similar approach as in Sect. (3.1) is not straightforward.

Assuming that the normalized displacement \(\underline{w}\) is discretized on an LaDQM grid, then \(Y_{1}\) (i.e., the vector of nodal displacements for \(\underline{w}\)) can be written as

$$\begin{aligned} Y_{1}=\left\{ \begin{array}{ccc} \underset{\text {External degrees of freedom}}{\underbrace{\begin{array}{cc} \underline{w}_{1n_{L}}&\cdots \end{array}}}&\quad \underset{\text {Internal degrees of freedom}}{\underbrace{\begin{array}{ccc} \underline{w}_{1}&\cdots&\underline{w}_{n}\end{array}}}&\quad \underset{\text {External degrees of freedom}}{\underbrace{\begin{array}{cc} \cdots&\underline{w}_{n+n_{R}}\end{array}}}\end{array}\right\} ^{T}. \end{aligned}$$
(31)

For the EBT case, \(Y=Y_{1}\) is the displacement vector such as \(n_{R}=n_{L}=2\),

$$\begin{aligned} Y=\left\{ \begin{array}{ccc} \underset{\text {External degree of freedom}}{\underbrace{\begin{array}{cc} \underline{w}_{-1}&\underline{w}_{0}\end{array}}}&\quad \underset{\text {Internal degrees of freedom}}{\underbrace{\begin{array}{ccc} \underline{w}_{1}&\cdots&\underline{w}_{n}\end{array}}}&\quad \underset{\text {External degree of freedom}}{\underbrace{\begin{array}{cc} \underline{w}_{n+1}&\underline{w}_{n+2}\end{array}}}\end{array}\right\} ^{T}. \end{aligned}$$
(32)

The DOFs of the LaDQM displacement vector in (32) are related to the DOFs of the standard WQEM displacement vector in (23.2) using the following relationship:

$$\begin{aligned} \left[ \begin{array}{c} \underline{w}_{1}''\\ \underline{w}_{1}'\\ \underline{w}_{1}\\ \vdots \\ \underline{w}_{n}\\ \underline{w}_{n}'\\ \underline{w}_{n}'' \end{array}\right]= & {} \underset{[T]}{\underbrace{\left[ \begin{array}{ccccccc} [{\mathcal {M}}_{2}]_{1,{-1}} &{} &{} &{} \cdots &{} &{} &{} [{\mathcal {M}}_{2}]_{1,n+2}\\ {} [{\mathcal {M}}_{1}]_{1,{-1}} &{} &{} &{} \cdots &{} &{} &{} [{\mathcal {M}}_{1}]_{1,n+2}\\ 0 &{} 0 &{} 1 &{} 0 &{} \cdots &{} 0 &{} 0\\ \vdots &{} \vdots &{} &{} \ddots &{} &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} 0 &{} 1 &{} 0 &{} 0\\ {} [{\mathcal {M}}_{1}]_{n,-1} &{} &{} &{} \cdots &{} &{} &{} [{\mathcal {M}}_{1}]_{n,n+2}\\ {} [{\mathcal {M}}_{2}]_{n,-1} &{} &{} &{} \cdots &{} &{} &{} [{\mathcal {M}}_{2}]_{n,n+2} \end{array}\right] }}.\left[ \begin{array}{c} \underline{w}_{-1}\\ \vdots \\ \\ \vdots \\ \\ \vdots \\ \underline{w}_{n+2} \end{array}\right] \end{aligned}$$
(33)

where \({\mathcal {M}}_{i}\) is the DQM \(i^{th}\)derivative matrix relative to the LaDQM mesh and \(\left[ T\right] \) is the LaWQEM mapping matrix. Further details about the derivation of [T] can be found in Appendix A.

3.2.2 LaWQEM transfer matrix-based formulation

Equation (33) establishes a relation between the LaWQEM and the LaDQM DOFs. However, it does not allow to generate a direct interpolation polynomial basis associated with LaWQEM matrices. The closest useful interpolation polynomials are the Lagrange polynomial basis relative to the original LaDQM grid. This means that using the relation established in Eqs. (28) and (29) is difficult since building \([iT_{{\mathcal {H}}}]\) is not possible without the explicit expression of the Hermite basis. To get around this problem, consider the integration of a function f(x), discretized in the LaDQM grid, using the Gauss quadrature rule [38, 39],

$$\begin{aligned} \int _{a}^{b}f^{\left( k\right) }(x)dx&\thickapprox \overset{n+2}{\underset{i=-1}{\sum }}[\omega _{\varsigma }]_{i} f^{\left( k\right) }(\varsigma _{i})=\left[ \begin{array}{c} [\omega _{\varsigma }]_{-1}\\ \vdots \\ {} [\omega _{\varsigma }]_{n+2} \end{array}\right] ^{T}.\left[ \begin{array}{ccc} {\mathcal {L}}_{-1}^{\left[ k\right] }(\varsigma _{-1}) &{} \ldots &{} {\mathcal {L}}_{n+2}^{\left[ k\right] }(\varsigma _{-1})\\ \vdots &{} {\mathcal {L}}_{i}^{\left[ k\right] }(\varsigma _{j}) &{} \vdots \\ {\mathcal {L}}_{-1}^{\left[ k\right] }(\varsigma _{n+2}) &{} \ldots &{} {\mathcal {L}}_{n+2}^{\left[ k\right] }(\varsigma _{n+2}) \end{array}\right] .\left[ \begin{array}{c} f(\xi _{-1})\\ f(\xi _{0})\\ \vdots \\ f(\xi _{n+1})\\ f(\xi _{n+2}) \end{array}\right] \end{aligned}$$
(34.1)
$$\begin{aligned}&=\left[ \begin{array}{c} [\omega _{\varsigma }]_{-1}\\ \vdots \\ {} [\omega _{\varsigma }]_{n+2} \end{array}\right] ^{T}.\left[ \varsigma {M_{k}}\right] . \underset{{{[iT_{{\mathcal {L}}}]}}}{\underbrace{\left[ \begin{array}{ccc} {\mathcal {L}}_{-1}(\varsigma _{-1}) &{} \ldots &{} {\mathcal {L}}_{n+2}(\varsigma _{-1})\\ \vdots &{} {\mathcal {L}}_{i}(\varsigma _{j}) &{} \vdots \\ {\mathcal {L}}_{-1}(\varsigma _{n+2}) &{} \ldots &{} {\mathcal {L}}_{n+2}(\varsigma _{n+2}) \end{array}\right] }}.\left[ \begin{array}{c} f(\xi _{-1})\\ f(\xi _{0})\\ \vdots \\ f(\xi _{n+1})\\ f(\xi _{n+2}) \end{array}\right] \end{aligned}$$
(34.2)
$$\begin{aligned}&=[\omega _{\varsigma }]^{T}.\underset{[\varsigma M_{{\mathcal {I}},k}]}{\underbrace{[\varsigma M_{k}].\left[ {iT_{{\mathcal {L}}}}\right] }}.\left[ \begin{array}{c} f(\xi _{-1})\\ f(\xi _{0})\\ \vdots \\ f(\xi _{n+1})\\ f(\xi _{n+2}) \end{array}\right] \end{aligned}$$
(34.3)

where

$$\begin{aligned} \xi _{i}:&\text {Mesh coordinates }\\ \varsigma _{i}:&\text {Gauss quadrature points }\\{} [\omega _{\varsigma }]_{i}:&\text {Gauss quadrature weights }\\ {\mathcal {L}}_{i}(x):&\text {Lagrange interpolation function based on }\xi _{i}\\{} [iT_{{\mathcal {L}}}]:&\text {The Lagrange integral transfer matrix}\\{} [\varsigma M_{k}]:&\text {The DQM differentiation matrix relative to }{\varsigma _{i}}\\{} [\varsigma M_{{\mathcal {I}},k}]:&\text {The transfered LaDQM differentiation matrix relative to }{\varsigma _{i}}and {\xi _{i}}. \end{aligned}$$

Switching to the LaWQEM coordinate requires the use of the transfer matrix \([T]^{-1}\) as stated in Eq. (33),

$$\begin{aligned} \int _{a}^{b}f^{\left[ k\right] }(x)dx\thickapprox \left[ \begin{array}{c} [\omega _{\varsigma }]_{0}\\ \vdots \\ {} [\omega _{\varsigma }]_{n+1} \end{array}\right] ^{T}\underset{[\varsigma M_{{\mathcal {L}},k}]}{\underbrace{\left[ {\varsigma M_{k}}\right] \left[ {iT_{{\mathcal {L}}}}\right] .\left[ T\right] ^{-1}}}.\left[ \begin{array}{c} f''(\xi _{1})\\ f'(\xi _{1}\\ f(\xi _{1})\\ \vdots \\ f(\xi _{n})\\ f'(\xi _{n})\\ f''(\xi _{n}) \end{array}\right] , \end{aligned}$$
(35)

where \(\left[ \varsigma M_{{\mathcal {L}},k}\right] \) is the LaWQEM differentiation matrix relative to \({\varsigma _{i}} \) and \({\xi _{i}}\). Comparing (28) and (35) shows that \([\varsigma M_{{\mathcal {L}},k}]\) can be used to replace \([\varsigma M_{{\mathcal {H}},k}]\) in (29) if the Hermite basis is unacceptable. Thus, all DQM derivative matrices and quadrature weights in the discretized variational statement in (24) and (25) should be now substituted, respectively, with \([\varsigma M_{{\mathcal {L}},i}]=\left[ {\varsigma M_{k}}\right] \left[ {iT_{{\mathcal {L}}}}\right] .\left[ T\right] ^{-1}\text { and } {\left[ \omega _{\varsigma }\right] }\).

3.2.3 LaWQEM polynomial-based new formulation

It was stated previously that the proposed formulation does not come with an explicit polynomial basis. However, it is possible to obtain a suitable basis using the same transfer matrix method. Consider a function expressed in the current LaDQM mesh using the following scalar product:

$$\begin{aligned} f(x)\thickapprox \left[ \begin{array}{ccc} {\mathcal {L}}_{-1}(x)&\ldots&{\mathcal {L}}_{n+2}(x)\end{array}\right] .\left[ \begin{array}{c} f(\xi _{-1})\\ f(\xi _{0})\\ \vdots \\ f(\xi _{n+1})\\ f(\xi _{n+2}) \end{array}\right] . \end{aligned}$$
(36)

Transitioning to LaWQEM coordinates can be obtained using Eq. (37),

$$\begin{aligned} f(x)\thickapprox \underset{\left[ \mathcal{HL}\mathcal{}(x)\right] }{\underbrace{\left[ \begin{array}{ccc} {\mathcal {L}}_{-1}(x)&\ldots&{\mathcal {L}}_{n+2}(x)\end{array}\right] .\left[ T\right] ^{-1}}}.\left[ \begin{array}{c} f''(x_{1})\\ f'(x_{1})\\ f(x_{1})\\ \vdots \\ f(x_{n})\\ f'(x_{n})\\ f''(x_{n}) \end{array}\right] , \end{aligned}$$
(37)

for the current SSG EBT formulation. Technically, the product of the LaDQM Lagrange base with \([T]^{- 1}\), that is \(\left[ \begin{array}{ccc} {\mathcal {L}}_{-1}(x)&\ldots&{\mathcal {L}}_{n+2}(x)\end{array}\right] .\left[ T\right] ^{-1}\) appearing in (37) produces a Hermite basis with two derivative DOFs at the boundaries. Hence, \(\left[ \mathcal{HL}\mathcal{}(x)\right] \) is considered to be the analytical basis associated with LaWQEM coordinates, and it is, therefore, possible to create any Hermite basis using a combination of Lagrange polynomial and a DQ rule. Figure 2 shows a plot of these polynomials for a mesh of 7 internal nodes and 11 DOFs. It is clear from the plots that the \(\left[ \mathcal{HL}\mathcal{}(x)\right] \) verifies a number of required properties at the mesh points. The mesh along with the nodal location is plotted using short vertical lines along the horizontal axis of all the plots illustrated in Fig. 2. It is also worth mentioning that it is possible to perform the same procedure for Hermite basis with single derivative DOFs at the boundaries. Using the new \(\left[ \mathcal{HL}\mathcal{}(x)\right] \) basis, it is possible to calculate \(\int _{a}^{b}f^{\left( k\right) }(x)dx\) similar to the Hermite interpolation case in Eq. (28),

$$\begin{aligned} \int _{a}^{b}f^{\left[ k\right] }(x)dx&\thickapprox \overset{n+2}{\underset{i=-1}{\sum }}[\omega _{\varsigma }]_{i}f^{\left[ k\right] }(\varsigma _{i}) =\left[ \begin{array}{c} [\omega _{\varsigma }]_{-1}\\ \vdots \\ {} [\omega _{\varsigma }]_{n+2} \end{array}\right] ^{T}.\left[ \begin{array}{ccc} \mathcal{HL}\mathcal{}_{-1}^{\left[ k\right] }(\varsigma _{-1}) &{} \ldots &{} \mathcal{HL}\mathcal{}_{n+2}^{\left[ k\right] }(\varsigma _{-1})\\ \vdots &{} \mathcal{HL}\mathcal{}_{i}^{\left[ k\right] }(\varsigma _{j}) &{} \vdots \\ \mathcal{HL}\mathcal{}_{-1}^{\left[ k\right] }(\varsigma _{n+2}) &{} \ldots &{} \mathcal{HL}\mathcal{}_{n+2}^{\left[ k\right] }(\varsigma _{n+2}) \end{array}\right] .\left[ \begin{array}{c} f''(\xi _{1})\\ f'(\xi _{1}\\ f(\xi _{1})\\ \vdots \\ f(\xi _{n})\\ f'(\xi _{n})\\ f''(\xi _{n}) \end{array}\right] \end{aligned}$$
(38.1)
$$\begin{aligned}&=\left[ \begin{array}{c} [\omega _{\varsigma }]_{-1}\\ \vdots \\ {} [\omega _{\varsigma }]_{n+2} \end{array}\right] ^{T}.\left[ \varsigma {M_{k}}\right] . \underset{{{[iT_{\mathcal{HL}\mathcal{}}]}}}{\underbrace{\left[ \begin{array}{ccc} \mathcal{HL}\mathcal{}_{-1}(\varsigma _{-1}) &{} \ldots &{} \mathcal{HL}\mathcal{}_{n+2}(\varsigma _{-1})\\ \vdots &{} \mathcal{HL}\mathcal{}_{i}(\varsigma _{j}) &{} \vdots \\ \mathcal{HL}\mathcal{}_{-1}(\varsigma _{n+2}) &{} \ldots &{} \mathcal{HL}\mathcal{}_{n+2}(\varsigma _{n+2}) \end{array}\right] }}.\left[ \begin{array}{c} f''(\xi _{1})\\ f'(\xi _{1}\\ f(\xi _{1})\\ \vdots \\ f(\xi _{n})\\ f'(\xi _{n})\\ f''(\xi _{n}) \end{array}\right] \end{aligned}$$
(38.2)
$$\begin{aligned}&=[\omega _{\varsigma }]^{T}.[\varsigma M_{k}].\left[ {iT_{\mathcal{HL}\mathcal{}}}\right] .\left[ \begin{array}{c} f''(\xi _{1})\\ f'(\xi _{1}\\ f(\xi _{1})\\ \vdots \\ f(\xi _{n})\\ f'(\xi _{n})\\ f''(\xi _{n}) \end{array}\right] \end{aligned}$$
(38.3)
Fig. 2
figure 2

Plots of half the analytical basis associated with an LaWQEM SSG EBT DOFs for a mesh of 7 nodes and 11 DOFs

Full size image

where

$$\begin{aligned} \xi _{i}:&\text {Mesh coordinates }\\ \varsigma _{i}:&\text {Gauss quadrature points }\\ {}[\omega _{\varsigma }]_{i}:&\text {Gauss quadrature weights }\\ \mathcal{HL}\mathcal{}_{i}(x):&\text {The new Hermite interpolation function based on }\xi _{i}\\{} [iT_{\mathcal{HL}\mathcal{}}]:&\text {The new Hermite integral transfer matrix}\\{} [\varsigma M_{k}]:&\text {The DQM differentiation matrix relative to } {\varsigma _{i}}. \end{aligned}$$

Details about applying the boundary conditions for an LaWQEM system can be found in [46].

4 Validation of the proposed LaWQEM formulation

The aim of this Section is to validate the proposed LaWQEM approach using data from the literature in addition to analytical results and well-established numerical methods. As detailed in Section 3.2, LaWQEM relies on modified LaDQM matrices obtained using the transfer matrix approach. The solutions of free vibration of SSG TBT and SSG EBT were developed using LaWQEM. SSG usually results in a large number of possible boundary conditions. In this study, only a symmetric set of boundary conditions is selected, a list of which is presented in Table 1. Each boundary condition will be referred to by a reference number as stated in Table 1. However, to assess the validity of the proposed formulation, an analytical solution to a simple vibration problem is treated beforehand. High-order methods rely generally on raising the order of the elements to achieve numerical convergence. The number of element is, thus, kept to a minimum [39, 41, 46]. Elements are introduced at discontinuities such as an abrupt loading, geometric or material property variation. Therefore, one single element discretization is used though this study unless indicated otherwise.

Table 1 Set of imposed Dirichlet boundary conditions for SSG TBT and SSG EBT
Full size table

4.1 Analytical free vibration of classical EBT validation

EBT beam vibration is one of the most common classical mechanics problems that requires imposing two BCs at each boundary. This problem is certainly one major contributor that led to the development of several methods based on DQM. Since an analytical solution to this problem is available, it can be used to assess the validity of the proposed LaWQEM formulation. This problem was used before in the literature for a similar purpose [35]. The normalized version of the equation of motion of the free vibration of an EBT beam is given by [35]

$$\begin{aligned} w^{(4)}(x)&=\omega ^{2}w(x)&0\le x\le 1 \end{aligned}$$
(39)

where w(x) is the transverse displacement. The weak integral form is given by

$$\begin{aligned} \int _{0}^{1}\delta w^{(2)}(x)w^{(2)}(x)dx+[w^{(3)}(x)\delta w(x)-w^{(2)}(x)\delta w^{(1)}(x)]_{0}^{1}=\omega ^{2}\int _{0}^{1}\delta w(x)w(x)dx\quad 0\le x\le 1. \end{aligned}$$
(40)

For a weak form solution, only the following boundary conditions are required:

$$\begin{aligned}&w(0)=0&&w(1)=0&&\text {Simply supported (SS)} \end{aligned}$$
(41.1)
$$\begin{aligned}&w(0)=0&&w(1)=0&w^{[1]}(1)=0&\text {Simply supported--clamped (SC)} \end{aligned}$$
(41.2)
$$\begin{aligned}&w(0)=0&&&&\text {Simply supported-Free (SF)} \end{aligned}$$
(41.3)
$$\begin{aligned}&w(0)=0&w^{[1]}(0)=0&w(1)=0&w^{[1]}(1)=0&\text {Camped--Clamped (CC)} \end{aligned}$$
(41.4)
$$\begin{aligned}&w(0)=0&w^{[1]}(0)=0&&&\text {Camped--Free (CF)} \end{aligned}$$
(41.5)
$$\begin{aligned}&\text {none}&&&&\text {Free--Free (FF)}. \end{aligned}$$
(41.6)

The convergence error with respect to the analytical solution of the first five nonzero linear natural frequencies of a classical EBT is reported in Fig. 3. The data are plotted for LaWQEM EBT using six different mesh densities. Similar data are also reported using LaDQM to help assess and compare the convergence speed. The results indicate that LaWQEM rapidly converges to the analytical solution faster than LaDQM which proves the validity of the proposed approach to deriving DQM matrices. It is well known that variational methods like LaWQEM generally converge faster than collocation methods like LaDQM. A similar observation was also made by Trabelssi et al. [46] when comparing DQM and QEM convergence speed. The modeshapes generated using LaWQEM are also plotted in Fig. 4. It can be seen that the generated modeshapes are similar to the conventional EBT modeshapes

Fig. 3
figure 3

Mesh convergence error for LaWQEM EBT first 5 linear natural frequencies (i.e., modes)

Full size image
Fig. 4
figure 4

LaWQEM EBT first 5 linear modeshapes

Full size image

4.2 Hermite-based WQEM SSG EBT validation

The free vibration of a simply supported linear SSG EBT study by Ishaquddin and Gopalakrishnan [41] is used as the second validation benchmark for the proposed LaWQEM formulation. Both analytical and numerical solutions of this problem are available in the literature. The numerical solution was obtained using Hermite-based WQEM with the GLL grid for numerical integration. Assuming the rotary inertia to be negligible, the following parameters are selected in consistent units for this validation: \(L=1,\) Young’s modulus \(E=3\times 10^{{6}}\), Poisson’s ratio \(\nu =0.3\), density \(\rho =1\). The simply supported boundary conditions for the linear SSG EBT used in this study are given by

$$\begin{aligned} w={\mathbb {M}}_{xx}^{(1)}=&0,&w''&=0 \end{aligned}$$
(42)

at both boundaries of the beam. The results of this study are presented in Table 2. It can be seen that LaWQEM gives an accuracy similar to the Hermite-based WQEM and to the analytical results. However, the use of full integration in the LaWQEM formulation provided, in general, a faster convergence rate compared to Hermite-based WQEM.

Table 2 LaWQEM simply supported SSG EBT: first six linear natural frequencies for a set of mesh densities
Full size table

5 Results and discussion

The goal of this Section is to study the accuracy of the proposed LaWQEM formulation for linear and nonlinear vibration problems based on SSG nanobeams. First, the proposed method is applied to a linear vibration problem. Then, the general procedure for obtaining the nonlinear fundamental vibration mode is detailed. Finally, a study of the accuracy of the proposed method in comparison with the regular LaDQM approach is performed.

5.1 Linear natural frequency results and mesh convergence study

In this Section, the beam is set to the following configuration \(\underline{l}_{s}=0.2,\frac{L}{h}=10,{\mathbf {n}}=3\) while the remaining material properties are provided in Table 3. The first set of data is shown in Figure 5. It summarizes a convergence study of the first three linear natural frequencies using different mesh densities. To limit the amount of data, only four boundary conditions among the ones listed in Table 1 are considered for each beam theory. It is generally known that variational methods converge faster than their collocation counterparts [39, 41, 46]. Examining the LaWQEM natural frequencies in Fig. 5 seems to confirm this statement for both SSG TBT and SSG EBT systems. In fact, for the TBT case, the first mode can be obtained accurately within a mesh of only 9 nodes. A mesh of 9 nodes is also required to obtain the same accuracy for the EBT problem. Given that the EBT case requires two more derivative DOFs at the boundaries, it can be concluded that for both systems LaWQEM converges at a comparable mesh density. To better assess the convergence error, the percentage difference between the current mesh and the highest mesh density is presented in Fig. 5. It is clear that the rest of the eigenvalues data converges within 9 to 11 nodes for the TBT problem, while 11 nodes are required to deliver sufficient accuracy for the EBT problem. In general, the accuracy of LaWQEM with 11 nodes is comparable to LaDQM with 15 nodes. Therefore, it can be concluded that the proposed method was successfully employed to calculate the first three linear frequencies of both SSG TBT and SSG EBT problems.

Table 3 Material properties of the constituent materials of the graded nanobeam [45]
Full size table
Fig. 5
figure 5

Mesh convergence of the first three linear frequencies: \(l_{s}=0.2,\frac{L}{h}=10,{\mathbf {n}}=3\)

Full size image

5.2 Nonlinear natural frequency and mesh convergence study

To solve for the eigenvalues, Y is set as \(Y=\widetilde{Y}e^{i\omega t}\). The discretized variational statement, given by (24) and (25) for the TBT and EBT beams, respectively, can be written in a unified manner as follows:

$$\begin{aligned} \left( \left[ K_{Sys}(Y)\right] -\omega ^{2}\left[ M_{Sys}\right] \right) .\widetilde{Y}=0. \end{aligned}$$
(43)

The linear natural frequencies can be obtained by replacing \(\left[ K_{Sys}(Y)\right] \) with \(\left[ K_{Sys}(\{0\})\right] \) in (43). The nonlinear frequency is, however, generally obtained by an iterative process [45, 46, 51,52,53] or using the harmonic balance method for highly nonlinear problems [54].

In this Section, a study of the mesh convergence of the fundamental nonlinear mode is performed. To this end, the following parameters are selected: \(\underline{l}_{s}=0.3,A=1,\frac{L}{h}=10,{\mathbf {n}}=3\). The same boundary conditions employed in Section 5.1 are applied for each beam theory. The results of this study are provided in Fig. 6. Examination of this Figure reveals few interesting observations. Despite possible rounding errors due to the presence of the transfer matrix given by (35) and (37), the LaWQEM data show rapid convergence compared to LaDQM. In fact, even for a mesh of 9 nodes the results are below 0.01% error for most cases for both SSG TBT and SSG EBT systems. As far as mesh convergence is concerned, the data in Fig. 6 indicate that LaDQM converges at about 13 to 15 nodes. In addition, a mesh of 9 nodes is sufficient to have an error less than 0.001% for both SSG TBT and SSG EBT beams. Therefore, a mesh of 11 nodes is selected for LaWQEM subsequently.

5.3 Nonlinear natural frequencies: results and discussion

To further demonstrate the accuracy of the proposed method, an extensive parametric study is performed based on the selected mesh configuration for each beam theory. In this Section, a combination of different material properties such as \({\mathbf {n}}\) and \(\hat{l}_{s}\) is used while the same set BCs kept. The vibration amplitude A ranges from 0 to 1, which basically covers the linear and most nonlinear cases. The aspect ratio \(\frac{L}{h}\) of the beam ranges between 10 and 100 for the SSG EBT and between 5 to 100 for the SSG TBT. The choice of adding a lower aspect ratio for the SSG TBT is to ensure that the proposed formulation still provides accurate results for low aspect ratios and does not experience shear locking [46]. The data are presented in Tables 4, 5, 6, 7, 8, 9, 10, 11, each of which covers one single boundary condition configuration. Similar to the previous Section, LaDQM results are included for assessing the accuracy of each method.

Fig. 6
figure 6

Mesh convergence study error for \(\underline{l}_{s}=0.3,A=1,\frac{L}{h}=10,{\mathbf {n}} =3\)

Full size image
Table 4 Fundamental nonlinear eigenvalues for a BC1 TBT nanobeam
Full size table
Table 5 Fundamental nonlinear eigenvalues for a BC4 TBT nanobeam
Full size table
Table 6 Fundamental nonlinear eigenvalues for a BC5 TBT nanobeam
Full size table
Table 7 Fundamental nonlinear eigenvalues for a BC8 TBT nanobeam
Full size table
Table 8 Fundamental nonlinear exigent values for a BC1 EBT nanobeam
Full size table
Table 9 Fundamental nonlinear exigent values for a BC2 EBT nanobeam
Full size table
Table 10 Fundamental nonlinear exigent values for a BC3 EBT nanobeam
Full size table
Table 11 Fundamental nonlinear exigent values for a BC4 EBT nanobeam
Full size table

The results show similar trends as those mentioned in the mesh convergence Section (Sect. 5.2). The LaWQEM results seem to be unaffected by the presence of a transfer matrix. In fact, using only a mesh of 11 nodes, the results are as accurate as the LaDQM results obtained with a 15-node mesh. This should offset the complexity of developing a discretized variational statement including the integration procedure. Besides, despite the low aspect ratio used in the TBT results, comparing both LaDQM and LaWQEM shows that the proposed method provides the same results as LaDQM even when the vibration amplitude is set to 1. Since LaDQM does not experience shear locking, these results show that the proposed LaWQEM SSG TBT element does not experience shear locking either [46]. It can be concluded that the proposed LaWQEM formulation offers similar performance for both nonlinear SSG TBT and EBT systems, despite the differences in the DQM matrix formulation.

6 Conclusions

A novel formulation of the weak form quadrature element method referred to as the locally adaptive weak quadrature element method was proposed to develop elements for nonlinear graded strain gradient Timoshenko and Euler–Bernoulli nanobeams. The proposed formulation develops a Hermite-based polynomial basis using the Lagrange-based differential quadrature method. These matrices can be customized to accommodate any number of extra derivative degrees of freedom encountered in higher-order strain gradient beam problems without requiring an entirely new formulation. The proposed DQM matrix formulation combines the implementation simplicity of the regular DQM and the flexibility of LaDQM. The proposed strain gradient Timoshenko beam element covers the classical and non-classical degrees of freedom while accounting for the von Kármán strain. This required accounting for an extra derivative degree of freedom at each boundary. Similarly, the proposed strain gradient Euler–Bernoulli beam element formulation accounts for the von Kármán strain and covers the classical and non-classical EBT degrees of freedom. In the latter case, two extra derivative degrees of freedom at each boundary are required. Unlike the Hermite-based DQM, these elements were developed using similar transfer matrices with minimal coding effort while providing support for both full quadrature integration and GLL reduced quadrature integration.

The variational statements were derived using Hamilton’s principle while accounting for the von Kármán strain and the position of the beam neutral axis. The validation first task was performed based on the analytical results of the free vibration problem of a classical beam. A second validation was performed using numerical data from an SSG EBT Hermite-based WQEM element formulation whose natural frequencies are available in the literature. The results showed a good agreement with the analytical solution of the classical beam and the numerical solution of the SSG EBT Hermite-based WQEM element. The use of Gauss quadrature in the proposed formulation yields faster convergence than the SSG EBT Hermite-based WQEM element which utilizes reduced GLL quadrature.

The mesh convergence study was carried out for both linear and nonlinear free vibration versions of the strain gradient Timoshenko and Euler–Bernoulli beams. LaDQM results were also computed to compare the accuracy and the convergence rate with the proposed method. The proposed LaWQEM results converged consistently faster than the LaDQM results for the same mesh density. These results were consistent for both linear and nonlinear tests.

Finally, several nonlinear natural frequencies were computed for a large number of material properties combinations, vibration amplitudes, and boundary conditions. A low-aspect-ratio case was also included in SSG TBT results. Based on the obtained results, it was concluded that the proposed LaWQEM method can produce accurate solutions of strain gradient Timoshenko and Euler–Bernoulli beams for various boundary conditions and material properties. The formulation may eventually be extended to third-order nanobeams and higher-order strain gradient beams that may require more than two derivative degrees of freedom at each boundary.