A high-order FEM formulation for free and forced vibration analysis of a nonlocal nonlinear graded Timoshenko nanobeam based on the weak form quadrature element method

Abstract

The purpose of this paper is to provide a high-order finite element method (FEM) formulation of nonlocal nonlinear nonlocal graded Timoshenko based on the weak form quadrature element method (WQEM). This formulation offers the advantages and flexibility of the FEM without its limiting low-order accuracy. The nanobeam theory accounts for the von Kármán geometric nonlinearity in addition to Eringen’s nonlocal constitutive models. For the sake of generality, a nonlinear foundation is included in the formulation. The proposed formulation generates high-order derivative terms that cannot be accounted for using regular first- or second-order interpolation functions. Hamilton’s principle is used to derive the variational statement which is discretized using WQEM. The results of a WQEM free vibration study are assessed using data obtained from a similar problem solved by the differential quadrature method (DQM). The study shows that WQEM can offer the same accuracy as DQM with a reduced computational cost. Currently the literature describes a small number of high-order numerical forced vibration problems, the majority of which are limited to DQM. To obtain forced vibration solutions using WQEM, the authors propose two different methods to obtain frequency response curves. The obtained results indicate that the frequency response curves generated by either method closely match their DQM counterparts obtained from the literature, and this is despite the low mesh density used for the WQEM systems.

1 Introduction

Nanobeams, nanoplates, nanoshells and other small-scale structural elements constitute the building blocks of micro- and nanoelectromechanical systems (MEMS and NEMS), actuators, sensors and atomic force microscopes [1,2,3]. The choice of integrating small-scale components is related to exotic mechanical properties and size effects experimentally observed [4,5,6,7,8] at the nanoscale. While these size effects can be accurately captured and studied using molecular dynamics (MD) simulations, the computational cost of MD is generally prohibitive. Hence, higher-order continuum mechanics approaches have been widely adopted as an alternative in the modeling of small-scale structures. Several higher-order continuum theories have been developed, each of which was based on a different perspective of small-scale behavior. However, in general, most of these theories can be classified into three different categories, namely micro-continuum, strain gradient family and nonlocal elasticity theories.

The nonlocal elasticity theory postulates that the stress in a continuum at a given location depends not only on the strain at that location but also on the strains in a finite neighborhood of such point. This dependency on the nonlocal strain is captured by a size effect parameter called the nonlocal parameter. The nonlocal elasticity theory was first proposed by Kroner [9] and then later improved by Eringen and co-workers [10,11,12]. To simplify the implementation of the theory in practical problems, a differential form was developed [13] based on a specific kernel function. Lately, researchers have explored the possibility of combining nonlocal strain effects with strain gradient theory in a single higher-order theory [14,15,16] referred to as nonlocal strain gradient theory. These size-dependent theories were exploited to model nanorods [2], nanobeams [1, 17, 18] and nanoplates [19,20,21,22]. These simple structures are conventionally modeled based on Euler–Bernoulli beam theory (EBT) and classical plate theory (CPT), respectively. Other models like Timoshenko beam theory (TBT) and first-order shear deformation theory (FSDT) account for shear to model thick beams and plates, respectively, accurately [23, 24].

To overcome the limitations of analytical solutions [24], methods like the finite element method (FEM), the differential quadrature method (DQM), the mesh-free method, the Ritz method, the Galerkin method, etc. were employed to solve small-scale problems and have become the most suitable methods for such problems. In general, numerical techniques are used to solve either the equation of motion or the variational statement. Although developing a solution to the former is generally simpler using collocation methods, solving the variational statement offers several advantages. For example, FEM has weaker regularity requirements (i.e., existence of high-order derivatives) and can easily handle complicated geometries and boundary conditions [25]. These advantages have made FEM the most commonly used method in the analysis of small-scale structures [24].

A few selected studies that use FEM in size-dependent beam problems are summarized in this paragraph, and a more comprehensive review can be found in [24]. Demir and Civalek used a linear nonlocal EBT element in two separate studies [1, 18] . The EBT element is based on Hermite cubic interpolation with two nodes and two degrees of freedom per node. The effect of an elastic matrix was accounted for in both studies. Eltaher and his colleagues developed [26,27,28,29,30] nonlocal EBT elements for both functionally graded (FG) nanobeams [26,27,28] and homogeneous nanobeams [29, 30]. The EBT element is a two-node element with three degrees of freedom per node: axial and transverse displacements in addition to rotation. The axial displacement is based on a Lagrange linear interpolation, while the transverse displacement is based on Hermite cubic interpolation. Eltaher et al. investigated free vibration problems of FG nanobeams on two separate occasions [26, 28]. In the second paper, the authors reexamined the location of the nanobeam’s neutral axis based on the physical neutral surface of FG beams [28]. In addition, Eltaher et al. [27] studied the buckling and bending response of graded nanobeams. Like their FG counterparts, homogeneous nanobeams have received considerable attention in the literature. The free vibration problem of homogeneous nanobeams was also examined by Eltaher et al. [29], while static bending of homogeneous nanobeams was considered by Alshorbagy et al. [30]. Nguyen et al. [31] proposed a mixed formulation consisting of developing a nonlocal mixed beam element to examine the static bending response of homogeneous nanobeams. This two-node element uses Lagrange interpolation for both deflection and bending. The literature also shows fewer nonlocal TBT elements. Reddy and El-Borgi [32] developed a finite element formulation for both nonlocal homogeneous EBT and TBT beams. Their models accounted for moderate rotations using the von Kármán strain nonlinearity. Hence, a nonlinear factor was added to the model. Similarly, the nonlinear EBT element relies on a mix of Lagrange and Hermite cubic interpolation for its axial and transverse displacements, while the nonlinear TBT element uses Lagrange interpolation for all its dependent variables. Later this work was extended to graded nanobeams [33]. Eltaher et al. [34] investigated the buckling and bending behavior of nonlocal graded Timoshenko nanobeams.

According to the literature, there have been several nonlocal beam element formulations. Each was tailored or designed to treat a specific problem. Though some elements were developed for TBT, EBT elements dominates the literature [24]. Technically, linear shape functions are sufficient to design an element model for nonlocal TBT. However, when nonlinear behaviors such as von Kármán strain nonlinearity and nonlinear elastic foundations are considered, even second-order elements may fall short of addressing all the high-order derivative continuity requirements in the variational statement. This problem was noted by Reddy and El-Borgi [32, 33] where the authors chose to neglect high-order derivatives in the variational statement to be able to solve using FEM. Moreover, the literature shows that none of the cited FEM studies have been used to investigate force vibration response and generate frequency response curves (FRC). The lack of forced vibration response prediction in numerical studies can be traced to difficulties in obtaining steady-state responses for a system with a high number of degrees of freedom.

To address the shortcoming related to estimating higher-order derivatives, the problem was generally solved using high-order collocation methods like DQM [35, 36] or the quadrature element method (QEM). This method is a high-order method used to solve FEM problems using a single or few high-order elements without the need to explicitly identify shape functions [37]. It relies on DQM matrices and a clever choice of the grid to simplify its implementation and hence may eliminate the need of an assembly subroutine [37]. QEM can be classified into two major families, namely the strong form quadrature element method (SQEM) [38, 39] and the weak form quadrature element method (WQEM) [37, 40,41,42,43,44,45,46,47]. SQEM is also referred in the literature as the differential quadrature element method [37, 48] or the strong formulation finite element method [49]. This approach is formulated similar to the regular DQM [37,38,39, 48, 49] with the additional freedom to subdivide the domain into few elements connected by their respective boundary conditions. This allows more flexibility and mitigates the weakness of DQM for discontinuous loading and geometries. On the other hand, WQEM can be formulated in a similar manner as FEM based on the minimum energy principle or the weak form of the integral or the variational statement. It has also been concluded that WQEM converges faster than FEM [50] and it is also more flexible than SQEM since it is essentially a higher-order FEM [37, 40, 43]. On another note, the applications to two-dimensional thin-plate problems by either DQM or SQEM have been mostly limited to simple domain shapes. Handling more complicated geometries, though theoretically possible [51], may come at the cost of accuracy and efficiency [52]. On the other hand, WQEM, and similar to FEM, can be employed to solve problems with any irregular shapes without any loss of accurately [40, 43]. Furthermore, WQEM stiffness matrix is symmetrical, unlike that of SQEM which may have unstable complex eigenvalues.

WQEM is present in several studies in the literature [46, 50, 52,53,54,55,56,57,58,59,60,61,62,63]. Wang et al. [53] performed a comprehensive state-of-the-art review of WQEM and its applications in various engineering applications, including crack propagation [57], 3D domains [55, 58], graded media [46, 58], beam and plate problems [46, 50, 52, 54, 59, 63]. Such studies helped extend the range of applications of WQEM. Other studies focused on the accuracy and high convergence rate of WQEM to solve challenging problems which are inaccurately solved using DQM and FEM such as the case of vibration of skewed thin plates [52]. Finally, few other studies focused on solving mathematical challenges such as integration accuracy [46, 53], complex form system and system requiring derivative degrees of freedom at the boundary such as the case of slender beams and thin plates [45, 46, 53].

In spite of the fact that WQEM is useful in estimating higher-order derivatives, few investigators have realized, however, its importance in solving size-dependent continuum mechanics problems [64] and most notably in the case of forced vibration. To fill this gap in the literature, the authors propose to develop a new FEM formulation based on WQEM to model the free and forced vibration response of a nonlocal TBT resting on a nonlinear elastic foundation accounting for moderate rotation through von Kármán strain. The foundation models the interaction between the beam and the medium in which the beam is embedded such as a protein microtubule embedded in a matrix [1] or a carbon nanotube (CNT) embedded in a foundation [3]. To model [65] the forced vibration response, the authors propose two new numerical methods to estimate the frequency response curves of the nanobeam which are validated based on results obtained by the main authors using the differential quadrature method [36]. The closest study to this work is the paper published recently by Jin and Wang [16] who investigated the free vibration response of a linear and classical Timoshenko graded beam using WQEM. As an extension of this paper, the authors added nonlocal and nonlinear effects in addition to forced vibration response.

Following this introduction, the size-dependent equations of motion and the corresponding variational statement for a nonlocal nonlinear graded TBT are established. The following section outlines how the variational statement is discretized using WQEM to obtain the free vibration response of the nanobeam. Section 4 summarizes the WQEM-based forced vibration solution using two different strategies to obtain the frequency response curves. Free and forced vibration results obtained by WQEM are presented and compared with DQM results in Sect. 5. Finally, a summary of this study and concluding remarks are given in Sect. 6.

2 Equations of motion and variational statement for a nonlocal TBT

2.1 Hamilton’s principle

According to Eringen’s nonlocal theory [10, 13], the nonlocal stress is given by

$$\begin{aligned} \bar{\varvec{\sigma }}=\int _{\Omega }K(\vert \mathbf{x}'-\mathbf{x}\vert ,\tau _0)\,\varvec{\sigma }(\mathbf{x}')\,d\mathbf{x}' \end{aligned}$$

(1)

where $\varvec{\sigma }(\mathbf{x}')$ is the classical macroscopic Cauchy stress tensor at point $\mathbf{x}'$ and $K(\vert \mathbf{x}'-\mathbf{x}\vert ,\tau )$ is the kernel function of the nonlocal modulus, $\vert \mathbf{x}'-\mathbf{x}\vert$ being the distance and $\tau _0$ being a material parameter that depends on internal and external characteristic lengths. Unlike classical mechanics, this relation stipulates that the stress at a given point in an elastic continuum depends on strains all over the body. An equivalent differential model, based on the exponential kernel, was proposed [13] as

$$\begin{aligned} \bigl (1-\mu _{0}^{2}\nabla ^{2}\bigr )\bar{\varvec{\sigma }}=\mathbf{C}:\varvec{\varepsilon },\quad \mu _{0}=\tau _0\ell =e_{0}a \end{aligned}$$

(2)

where $e_{0}$ is a material constant, $\nabla ^{2}$ is the Laplacian operator, and a and $\ell$ are the internal and external characteristic lengths, respectively. It is usually assumed that the nonlocal size effect is only significant along the x-axis of the nanobeam which its along its longitudinal direction. In light of this assumption, Eq. (2) is reduced to the following:

$$\begin{aligned} \left( 1-\mu _{0}^{2}\frac{\partial ^{2}}{\partial x^{2}}\right) {\bar{\sigma }}_{xx}=&E\varepsilon _{xx} \end{aligned}$$

(3a)

$$\begin{aligned} \left( 1-\mu _{0}^{2}\frac{\partial ^{2}}{\partial x^{2}}\right) {\bar{\sigma }}_{xz}=&G\gamma _{xz} \end{aligned}$$

(3b)

where $\nabla ^{2}$ is reduced to $\partial ^{2}/\partial x^{2}$, E is the elastic modulus of the beam and G is its shear modulus.

It is worth noting at this point that the transformation from the integral to the differential form of the nonlocal model comes with a paradox for beam bending problems with an exponential nonlocal kernel. In fact, Fernandez-Saez et al. [66] and Romano et al. [67] reported that this transformation yields a relationship that must be satisfied between the bending moment and the spatial derivative of the bending moment at the boundaries. The bending moment obtained from the solution of the differential equation should be checked to ensure the obtained solution is also a solution to the integral form of the model. This is easily done for problems with displacement-type boundary conditions, since the bending moment will be the solution of a second-order differential equation, and the constants of integration can be used to satisfy the bending moment boundary conditions. However, it should be noted that the integral form is incapable to model local effects at boundaries, which may result in some discrepancies between the actual and simulated bending moment at the boundary. Knowing that neither the integral form nor the differential form can solve all possible discrepancies at the boundaries, the differential form is selected in this study. These arguments were also used by the last two authors in a previous paper for choosing the nonlocal differential model [68].

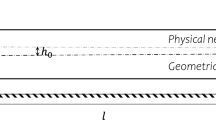
A Timoshenko beam resting on a nonlinear foundation shown in Fig. 1 is considered in this study. Within the context of the small displacement and small deformation theory and only accounting for bending in the x-z plane, the components of the displacement field in a TBT model are assumed to be written as

$$\begin{aligned} u_{x}\left( x,z,t\right) =&u\left( x,t\right) +z\phi _{x}\left( x,t\right) \end{aligned}$$

(4a)

$$\begin{aligned} u_{z}\left( x,z,t\right) =&w\left( x,t\right) \end{aligned}$$

(4b)

Accounting for von Kármán strain, the Green–Lagrange strain components can be expressed as

$$\begin{aligned} \varepsilon _{xx}=\varepsilon _{xx}^{(0)} +z\varepsilon _{xx}^{(1)},\quad \gamma _{xz}=\gamma _{xz}^{(0)} \end{aligned}$$

(5)

where

$$\begin{aligned} \varepsilon _{xx}^{(0)}=\frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2},\quad \varepsilon _{xx}^{(1)}=\frac{\partial \phi _{x}}{\partial x},\quad \gamma _{xz}^{(0)}=\phi _{x}+\frac{\partial w}{\partial x} \end{aligned}$$

(6)

Hamilton’s principle for the current nonlinear Timoshenko nanobeam can be written as

$$\begin{aligned} \int \limits _{t_{1}}^{t_{2}}\left( \delta K-\delta U+\delta W\right) dt=0 \end{aligned}$$

(7)

where $\delta K$ is the variation of the kinetic energy, $\delta U$ is the variation of strain energy and $\delta W$ is the variation of the external work. These terms can be expressed as

$$\begin{aligned} \delta K&=\int _{0}^{l}\left( m_{0}{\dot{u}}\delta {\dot{u}}+m_{2}\dot{\phi _{x}}\delta \dot{\phi _{x}}+m_{0}{\dot{w}}\delta {\dot{w}}\right) dx \end{aligned}$$

(8a)

$$\begin{aligned} \delta U&=\int _{0}^{l}\int _{A}\left( \sigma _{xx}\delta \varepsilon _{xx}+\sigma _{xz}\delta \gamma _{xz}\right) dAdx+\int _{0}^{l}F_{v}\delta wdx\nonumber \\&=\int _{0}^{l}\Biggl \{ M_{xx}^{(0)}\left( \frac{\partial \delta u}{\partial x}+\frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x}\right) +M_{xx}^{(1)}\frac{\partial \delta \phi _{x}}{\partial x}+M_{xz}^{(0)}\left( \delta \phi _{x}+\frac{\partial \delta w}{\partial x}\right) +F_{v}\delta w\Biggr \} dx \end{aligned}$$

(8b)

$$\begin{aligned} \delta W&=-\int _{0}^{l}\left( q\delta w\right) dx \end{aligned}$$

(8c)

where q is the distributed transverse load and $F_{v}=\mu _{f}{\dot{w}}$ represents the damping force assumed to be proportional to the velocity ${\dot{w}}$ wherein $\mu _{f}$ is the damping coefficient. It is worth noting that there is no damping associated with rotation since the beam is considered elastic and not viscoelastic [69]. Finally, $M_{ij}^{(k)}$ is a stress resultant defined as

$$\begin{aligned} M_{ij}^{(k)}=\int _{A}z^{k}\sigma _{ij}dA \end{aligned}$$

(9)

2.2 Equations of motion

Substituting Eqs. (8a), (8b) and (8c) into Hamilton’s principle (7), and then integrating by parts, yields the motion equations of the nanobeam which can be written as

$$\begin{aligned} -\frac{\partial M_{xx}^{(0)}}{\partial x}+m_{0}\frac{\partial ^{2}u}{\partial t^{2}}=&0 \end{aligned}$$

(10a)

$$\begin{aligned} -\frac{\partial }{\partial x}\left( M_{xz}^{(0)}+M_{xx}^{(0)}\frac{\partial w}{\partial x}\right) +\mu _{f}\frac{\partial w}{\partial t}+m_{0}\frac{\partial ^{2}w}{\partial t^{2}}=&q \end{aligned}$$

(10b)

$$\begin{aligned} M_{xz}^{(0)}-\frac{\partial }{\partial x}M_{xx}^{(1)}+m_{2}\frac{\partial ^{2}\phi _{x}}{\partial t^{2}}=&0 \end{aligned}$$

(10c)

For a beam graded in the z direction, the elastic and shear moduli, appearing in Eqs. (3a) and (3b), are assumed to follow the power-law function below [27, 46]

$$\begin{aligned} E(z)=(E_{U}-E_{L})\left( \frac{z}{h}+\frac{1}{2}\right) ^{n_k}+E_{L}, \qquad G(z)=K_{s}E(z) \end{aligned}$$

(11)

where the subscripts U and L designate the upper and lower faces of the beam. Here, h is the thickness of the beam and $n_k$ is the material gradation index. In light of the above equations, the nanobeam is considered to be nonhomogeneous with an isotropic stress–strain law. Combining (3a) and (3b) with Eq. (9) yields:

$$\begin{aligned} M_{xx}^{(0)}-\mu _{0}^2 \frac{\partial ^{2}M_{xx}^{(0)}}{\partial x^{2}}&= {\tilde{A}}\varepsilon _{xx}^{(0)} ={\tilde{A}}\left[ \frac{\partial u}{\partial x}+\frac{1}{2}\left( \frac{\partial w}{\partial x}\right) ^{2}\right] \end{aligned}$$

(12a)

$$\begin{aligned} M_{xx}^{(1)}-\mu _{0}^2 \frac{\partial ^{2}M_{xx}^{(1)}}{\partial x^{2}}&= {\tilde{B}}\varepsilon _{xx}^{(1)} ={\tilde{B}}\frac{\partial \phi _{x}}{\partial x} \end{aligned}$$

(12b)

$$\begin{aligned} M_{xz}^{(0)}-\mu _{0}^2 \frac{\partial ^{2}M_{xz}^{(0)}}{\partial x^{2}}&= {\tilde{G}}\gamma _{xz}^{(0)} ={\tilde{G}}\left[ \phi _{x}+\frac{\partial w}{\partial x}\right] \end{aligned}$$

(12c)

in which

$$\begin{aligned} {\tilde{A}}=\int _{A}E(z)dA,\quad {\tilde{B}}=\int _{A}z^{2}E(z)dA, \quad {\tilde{G}}=\int _{A}G(z)dA \end{aligned}$$

(13)

Next, using the technique developed by Nayfeh and Pai [70], the axial displacement u is eliminated from the equations of motion. To apply this technique, the following assumptions are adopted: (i) The beam is supported at its both boundary points such that $u(0)=u(l)=0$ and (ii) the longitudinal acceleration $m_{0}\partial ^{2}u/\partial t^{2}$ and the corresponding velocity are assumed to be very small and hence can be neglected. Applying these assumptions yields the following expression of $M_{xx}^{(0)}$ which can be written as:

$$\begin{aligned} M_{xx}^{(0)}={\tilde{A}}\varepsilon _{xx}^{(0)}=C_{2}(t) =\frac{1}{2S}\Biggl \{\int _{0}^{l}\left( \frac{\partial w}{\partial x}\right) ^{2}dx\Biggr \} \end{aligned}$$

(14)

where $S=\int _{0}^{l}\frac{1}{{\tilde{A}}}dx\,=\frac{l}{{\tilde{A}}}$. Further details about this simplification can be found in [36]. With further manipulations, it can be shown that the nonlocal stress resultants can be written entirely in terms of displacements

$$\begin{aligned} M_{xx}^{(0)}=&{\tilde{A}}\varepsilon _{xx}^{(0)}=C_{2} \end{aligned}$$

(15a)

$$\begin{aligned} M_{xz}^{(0)}=&\mu _{0}^2 \Biggl \{-\frac{\partial ^{2}}{\partial x^{2}}\left[ \frac{\partial w}{\partial x}C_{2}\right] -\frac{\partial q}{\partial x}+\mu _{f}\frac{\partial ^{2}w}{\partial x\partial t}+m_{0}\frac{\partial ^{3}w}{\partial x\partial t^{2}}\Biggr \}+{\tilde{G}}\left( \phi _{x}+\frac{\partial w}{\partial x}\right) \end{aligned}$$

(15b)

$$\begin{aligned} M_{xx}^{(1)}=&\mu _{0}^2 \Biggl \{-\frac{\partial }{\partial x}\left[ \frac{\partial w}{\partial x}C_{2}\right] -q+\mu _{f}\frac{\partial w}{\partial t}+m_{0}\frac{\partial ^{2}w}{\partial t^{2}}+m_{2}\frac{\partial ^{3}\phi _{x}}{\partial x\partial t^{2}}\Biggr \}+{\tilde{B}}\frac{\partial \phi _{x}}{\partial x} \end{aligned}$$

(15c)

Finally, substituting the above equations into (10b) and (10c) yields the following reduced equations of motion:

$$\begin{aligned} \left[ 1-\mu _{0}^2 \frac{\partial ^{2}}{\partial x^{2}}\right] \left\{ m_{0}\frac{\partial ^{2}w}{\partial t^{2}}+\mu _{f} \frac{\partial w}{\partial t}-\frac{\partial ^{2}w}{\partial x^{2}} \Biggl \{\frac{1}{2S}\int _{0}^{l}\left( \frac{\partial w}{\partial x}\right) ^{2} dx\Biggr \}-q\right\} -{\tilde{G}}\frac{\partial }{\partial x} \left( \phi _{x}+\frac{\partial w}{\partial x}\right)&=0 \end{aligned}$$

(16a)

$$\begin{aligned} \left[ 1-\mu _{0}^2 \frac{\partial ^{2}}{\partial x^{2}}\right] \left\{ m_{2} \frac{\partial ^{2}\phi _{x}}{\partial t^{2}}\right\} +{\tilde{G}}\left( \phi _{x}+\frac{\partial w}{\partial x}\right) -{\tilde{B}}\frac{\partial ^{2}\phi _{x}}{\partial x^{2}}&=0 \end{aligned}$$

(16b)

The nonlinear elastic foundation is assumed to be a transversely acting stiffness. Hence, in the case of a forced vibration load, q(x, t) is given by

$$\begin{aligned} q(x,t)=-k_{L}w-k_{NL}w^{3}+k_{s}\frac{\partial ^{2}w}{\partial x^{2}}+F(x)\cos (\omega t) \end{aligned}$$

(17)

where $k_{L}$, $k_{NL}$ and $k_{s}$ are, respectively, the linear, nonlinear and shear coefficients of the nonlinear medium in which the beam is embedded and therefore represent the effect of the surrounding medium. It is also worth noting that this model is a generalization of the linear models known as Winkler [71] and Pasternak [72] foundations, although a more complex model could be a viscoelastic foundation [73]. Previous papers published by the main authors [35, 36] confirm that the effect of the surrounding material is crucial and the nonlinear stiffness parameter $k_{NL}$ appearing in Eq. (17) plays a dominant role in the response of the nanobeam. Therefore, it was decided to adopt the current nonlinear foundation in this study rather than the linear classical Winkler-type and Pasternak-type foundations. Finally, F(x) and $\omega$, appearing in the above equation, designate, respectively, the forcing function amplitude and frequency. Finally, the amplitude is set to zero for free vibration case.

For scaling purposes, the following normalization is utilized:

$$\begin{aligned} \xi =&\frac{x}{l},\,\, {\hat{w}}=\frac{w}{r},\,\, {\hat{\phi }}=\frac{l}{r}\phi _{x},\,\, s^{2}=\frac{{\tilde{B}}}{l^{2}{\tilde{G}}},\,\, \kappa _{0}=\frac{r^{2}{\tilde{A}}}{2{\tilde{B}}} \end{aligned}$$

(18a)

$$\begin{aligned} \tau =&t\frac{1}{l^{2}}\sqrt{\frac{{\tilde{B}}}{m_{0}}},\,\, r=\sqrt{\frac{I}{A}},\,\, {\hat{\mu }}_{0}=\frac{\mu _{0}}{l},\,\, m=\frac{m_{2}}{l^{2}m_{0}},\,\, {\hat{\mu }}_{f}=\frac{\mu _{f}l^{2}}{\sqrt{m_{0}{\tilde{B}}}} \end{aligned}$$

(18b)

$$\begin{aligned} {\hat{k}}_{L} =&k_{L}\frac{l^{4}}{{\tilde{B}}},\,\, {\hat{k}}_{NL}=k_{NL}\frac{r^{2}l^{4}}{{\tilde{B}}},\,\, {\hat{k}}_{s}=k_{s}\frac{l^{2}}{{\tilde{B}}},\,\, {\hat{F}}(\xi )=F(x)\frac{l^{4}}{{\tilde{B}}},\,\, {\hat{\omega }}=\omega l^{2}\sqrt{\frac{m_{0}}{{\tilde{B}}}} \end{aligned}$$

(18c)

This yields the following nondimensional equations of motion:

$$\begin{aligned} \left[ 1-{\hat{\mu }}_{0}^2\frac{\partial ^{2}}{\partial \xi ^{2}}\right] \left( \frac{\partial ^{2}{\hat{w}}}{\partial \tau ^{2}}+{\hat{\mu }}_{f} \frac{\partial {\hat{w}}}{\partial \tau }-\kappa _{0}\frac{\partial ^{2}{\hat{w}}}{\partial \xi ^{2}}\int _{0}^{1}\left( \frac{\partial {\hat{w}}}{\partial \xi }\right) ^{2} d\xi -{\hat{q}}\right) -\frac{1}{s^{2}}\frac{\partial }{\partial \xi } \left( {\hat{\phi }}+\frac{\partial {\hat{w}}}{\partial \xi }\right)&= 0 \end{aligned}$$

(19a)

$$\begin{aligned} \left[ 1-{\hat{\mu }}_{0}^2\frac{\partial ^{2}}{\partial \xi ^{2}}\right] \left( m\frac{\partial ^{2}{\hat{\phi }}}{\partial \tau ^{2}}\right) +\frac{1}{s^{2}}\left( {\hat{\phi }}+\frac{\partial {\hat{w}}}{\partial \xi }\right) -\frac{\partial ^{2}{\hat{\phi }}}{\partial \xi ^{2}}&= 0 \end{aligned}$$

(19b)

where ${\hat{q}}={\hat{k}}_{s}\frac{\partial ^{2}{\hat{w}}}{\partial \xi ^{2}} -{\hat{k}}_{L}{\hat{w}}-{\hat{k}}_{NL}{\hat{w}}^{3}+{\hat{F}}(\xi ) \cos ({\hat{\omega }}\tau )$ and

$$\begin{aligned} \left( {\hat{q}}-{\hat{\mu }}_{0}^2\frac{\partial ^{2}{\hat{q}}}{\partial \xi ^{2}}\right)&={\hat{k}}_{s}\left( \frac{\partial ^{2}{\hat{w}}}{\partial \xi ^{2}}-{\hat{\mu }}_{0}^2 \frac{\partial ^{4}{\hat{w}}}{\partial \xi ^{4}}\right) -{\hat{k}}_{L}\left( {\hat{w}} -{\hat{\mu }}_{0}^2\frac{\partial ^{2}{\hat{w}}}{\partial \xi ^{2}}\right) -{\hat{k}}_{NL} \Bigg [{\hat{w}}^{3}-3{\hat{\mu }}_{0}^2\left( 2{\hat{w}}\left( \frac{\partial {\hat{w}}}{\partial \xi }\right) ^{2}+{\hat{w}}^{2}\frac{\partial ^{2}{\hat{w}}}{\partial \xi ^{2}}\right) \Bigg ]\\&+\left( {\hat{F}}(\xi )-{\hat{\mu }}_{0}^2\frac{\partial ^{2}}{\partial \xi ^{2}}{\hat{F}}\right) \cos ({\hat{\omega }}\tau ) \end{aligned}$$

For the hinged–hinged (HH) case, the following boundary conditions must be satisfied at the ends of the beam, i.e., at both $\xi =0$ and $\xi =1$:

$$\begin{aligned} {\hat{w}}=0,\quad {\hat{M}}_{xx}^{(1)}=0 \end{aligned}$$

(20)

which is equivalent to

$$\begin{aligned} {\hat{w}}= & {} 0 \end{aligned}$$

(21a)

$$\begin{aligned} \frac{\partial {\hat{\phi }}}{\partial \xi }-\kappa _0{\hat{\mu }}_{0}^2\left( \int _{0}^{1}\left( \frac{\partial {\hat{w}}}{\partial \xi }\right) ^{2}d\xi \right) \frac{\partial ^{2}{\hat{w}}}{\partial \xi ^{2}} +{\hat{\mu }}_{0}^2\left[ \frac{\partial ^{2}{\hat{w}}}{\partial \tau ^{2}}+m\frac{\partial ^{3}{\hat{\phi }}}{\partial \xi \partial \tau ^{2}}+{\hat{\mu }}_{f}\frac{\partial {\hat{w}}}{\partial \tau }-{\hat{q}}\right]= & {} 0 \end{aligned}$$

(21b)

A clamped–clamped (CC) nanobeam must satisfy the following boundary conditions at $\xi =0$ and at $\xi =1$:

$$\begin{aligned} {\hat{w}}=0,\quad {\hat{\phi }}=0 \end{aligned}$$

(22)

2.3 Variational statement

The aim of this study is to formulate a high-order variational method. To this end, Eq. (15) is substituted into Eqs. (8a), (8b) and (8c). The resulting expressions are then substituted into the expression of Hamilton’s principle (7). Finally, integrating (8a) by parts, the variational formulation can be written as a function of displacements as follows:

$$\begin{aligned}&\int _{0}^{l}\left[ m_{0}\ddot{w}+\mu _{f}{\dot{w}}-q\right] \delta w \nonumber \\&+\left[ \mu _{0}^{2}m_{0}\ddot{w}'+\mu _{f}\mu _{0}^{2}{\dot{w}}'-\mu _{0}^{2}q'+{\tilde{G}}\left( w'+\phi _{x}\right) +\left( w'-\mu _{0}^{2}w'''\right) \frac{1}{2S}\int _{0}^{l}w'^{2}dx\right] \delta w'\nonumber \\&+\left[ \mu _{0}^{2}m_{0}\ddot{w}'+m_{2}\ddot{\phi }_{x}+\mu _{f}\mu _{0}^{2}{\dot{w}}'+{\tilde{G}}\left( w'+\phi _{x}\right) -\mu _{0}^{2}\left( q'+w'''\left( \frac{1}{2S}\int _{0}^{l}w'^{2}dx\right) \right) \right] \delta \phi _{x}\nonumber \\&+\left[ \mu _{0}^{2}m_{0}\ddot{w}+\mu _{0}^{2}m_{2}\ddot{\phi }_{x}+\mu _{f}\mu _{0}^{2}{\dot{w}}+{\tilde{B}}\phi _{x}^{'}-\mu _{0}^{2}\left( q+w''\left( \frac{1}{2S}\int _{0}^{l}w'^{2}dx\right) \right) \right] \delta \phi _{x}'dx \end{aligned}$$

(23)

which can be rewritten in scalar product form as follows:

$$\begin{aligned} \int _{0}^{l}\left( \begin{array}{c} \delta w\\ \delta w'\\ \delta \phi _{x}\\ \delta \phi _{x}' \end{array}\right) ^{T}\centerdot \left( \frac{\partial ^{2}}{\partial t^{2}}\left( \begin{array}{c} m_{0}w\\ \mu _{0}^{2}m_{0}w'\\ \mu _{0}^{2}m_{0}w'+m_{2}\phi _{x}\\ \mu _{0}^{2}m_{0}w+\mu _{0}^{2}m_{2}\phi _{x}^{'} \end{array}\right) +\mu _{f}\frac{\partial }{\partial t}\left( \begin{array}{c} w\\ \mu _{0}^{2}w'\\ \mu _{0}^{2}w'\\ \mu _{0}^{2}w \end{array}\right) +\left( \begin{array}{c} -q\\ -\mu _{0}^{2}q'+{\tilde{G}}\left( w'+\phi _{x}\right) +\left( w'-\mu _{0}^{2}w'''\right) \frac{1}{2S}\int _{0}^{l}w'^{2}dx\\ {\tilde{G}}\left( w'+\phi _{x}\right) -\mu _{0}^{2}\left( q'+w'''\left( \frac{1}{2S}\int _{0}^{l}w'^{2}dx\right) \right) \\ {\tilde{B}}\phi _{x}^{'}-\mu _{0}^{2}\left( q+w''\left( \frac{1}{2S}\int _{0}^{l}w'^{2}dx\right) \right) \end{array}\right) \right) dx\nonumber \\ \end{aligned}$$

(24)

Since only one element will be used to model the nanobeam, the external forces at the boundaries of the beam element are basically reaction forces. Hence, the work of external forces at the boundaries of the nanobeam is zero and does not need to be added to the variational statement [32].

Examining the above variational statement reveals that w is raised to the third derivative in several terms. One alternative used by Reddy et al. [33] is to neglect these terms and adopt a quadratic finite element model that does not account for all mechanical aspects of the system. A better alternative is to raise the order of the finite element model and one viable approach is the p-version of the finite element method. However, a simpler alternative adopted in this paper is to deploy WQEM to discretize the system, which in addition brings high-order accuracy.

Finally, utilizing the normalized variables in (18), the normalized variational statement can then be expressed as follows:

$$\begin{aligned} \int _{0}^{1}\left( \begin{array}{c} \delta {\hat{w}}\\ \delta {\hat{w}}'\\ \delta {\hat{\phi }}\\ \delta {\hat{\phi }}' \end{array}\right) ^{T}\centerdot \left( \frac{\partial ^{2}}{\partial \tau ^{2}}\left( \begin{array}{c} {\hat{w}}\\ {\hat{\mu }}_{0}^{2}{\hat{w}}'\\ {\hat{\mu }}_{0}^{2}{\hat{w}}'+m{\hat{\phi }}\\ {\hat{\mu }}_{0}^{2}{\hat{w}}+\mu _{0}^{2}m\hat{\phi '} \end{array}\right) +{\hat{\mu }}_{f}\frac{\partial }{\partial \tau }\left( \begin{array}{c} {\hat{w}}\\ {\hat{\mu }}_{0}^{2}{\hat{w}}'\\ {\hat{\mu }}_{0}^{2}{\hat{w}}'\\ {\hat{\mu }}_{0}^{2}{\hat{w}} \end{array}\right) +\left( \begin{array}{c} -{\hat{q}}\\ -{\hat{\mu }}_{0}^{2}{\hat{q}}'+\frac{1}{s^{2}}\left( {\hat{w}}'+{\hat{\phi }}\right) +\kappa _{0}\left( {\hat{w}}'-{\hat{\mu }}_{0}^{2}{\hat{w}}'''\right) \int _{0}^{l}{\hat{w}}'^{2}d\xi \\ \frac{1}{s^{2}}\left( {\hat{w}}'+{\hat{\phi }}\right) -{\hat{\mu }}_{0}^{2}\left( {\hat{q}}'+\kappa _{0}{\hat{w}}'''\int _{0}^{l}{\hat{w}}'^{2}d\xi \right) \\ {\hat{\phi }}'-{\hat{\mu }}_{0}^{2}\left( {\hat{q}}+\kappa _{0}{\hat{w}}''\int _{0}^{l}{\hat{w}}'^{2}d\xi \right) \end{array}\right) \right) d\xi \nonumber \\ \end{aligned}$$

(25)

The above nondimensional variational statement is the one subsequently solved in the free and forced vibration studies (Sects. 4 and 5). Furthermore, it is obvious that the highest derivative ${\hat{w}}'''$ appearing in Eqs. (24) and (25) cannot be accounted for based on a regular FEM formulation even with second-order elements. The formulation of classical FEM requires the definition of shape functions whose order defines the element’s order. Modifying the element order to accommodate higher derivatives (or to increase elements precision) requires the development of a brand new formulation. This locks the order FEM element at the formulation stage. WQEM, however, does not require an explicit computation of shape functions or their derivatives [37]. This allows the use of adaptive order of precision and hence can avoid any unnecessary approximations.

3 Free vibration WQEM formulation

To simplify the computation of the discretized system and later write the variational statement in matrix form, the following integral is first approximated $\int _{a}^{b}f(\xi )^{(m)}g(\xi )^{(k)}d\xi$. Here, $f(\xi )$ and $g(\xi )$ are arbitrary functions that can be interpolated using a Lagrange polynomial basis of order n and $f(\xi )^{(m)}$ and $g(\xi )^{(k)}$ are, respectively, the mth-order and kth-order derivatives of $f(\xi )$ and $g(\xi )$ with respect to $\xi$. To this end, an n-node mesh has to be selected and the integral can be evaluated as

$$\begin{aligned} \int _{a}^{b}f(\xi )^{(m)}g(\xi )^{(k)}d\xi\approx & {} \overset{n}{\underset{i=1}{\sum }}[\omega _{\xi }]_{i}f^{(m)} (\xi _{i})g^{(k)}(\xi _{i})\nonumber \\= & {} \left[ \begin{array}{c} [\omega _{\xi }]_{1}f^{(m)}(\xi _{1})\\ \vdots \\ {} [\omega _{\xi }]_{n}f^{(m)}(\xi _{n}) \end{array}\right] ^{T}.\left[ \begin{array}{c} g^{(k)}(\xi _{1})\\ \vdots \\ g^{(k)}(\xi _{n}) \end{array}\right] \nonumber \\= & {} \left( [\omega _{\xi }]\underset{\left[ f^{(m)}\left( \{\xi \}\right) \right] }{\underbrace{\left[ \begin{array}{c} f^{(m)}(\xi _{1})\\ \vdots \\ f^{(m)}(\xi _{n}) \end{array}\right] }}\right) ^{T}.\underset{\left[ g^{(k)}\left( \{\xi \}\right) \right] }{\underbrace{\left[ \begin{array}{c} g^{(k)}(\xi _{1})\\ \vdots \\ g^{(k)}(\xi _{n}) \end{array}\right] }} \end{aligned}$$

(26)

where $\xi _{i}(1\le i\le n)$ are the mesh coordinates, $\{\xi \}$ is the mesh coordinate vector and $[\omega _{\xi }]{}_{i}$ are the integral quadrature weights relative to $\xi _{i},(1\le i\le n)$. In the above equation, the term $[\omega _{\xi }][f\left( \xi \right) ]$ is an element by element multiplication and $\left[ f^{(m)}\left( \{\xi \}\right) \right] ^T . \left[ g^{(k)}\left( \{\xi \}\right) \right]$ is a regular matrix (or vector) multiplication. Using DQM matrices, Eq. (26) can be further simplified as follows:

$$\begin{aligned} \int _{a}^{b}f(\xi )^{(m)}g(\xi )^{(k)}d\xi\approx & {} \left( [\omega _{\xi }]\underset{\left[ f^{(m)}\left( \{\xi \}\right) \right] }{\underbrace{[M_{m}].\left[ \begin{array}{c} f(\xi _{1})\\ \vdots \\ f(\xi _{n}) \end{array}\right] }}\right) ^{T}.\underset{\left[ g^{(k)}\left( \{\xi \}\right) \right] }{\underbrace{[M_{k}].\left[ \begin{array}{c} g(\xi _{1})\\ \vdots \\ g(\xi _{n}) \end{array}\right] }}\nonumber \\= & {} \underset{\left[ f\left( \{\xi \}\right) \right] }{\left[ \begin{array}{c} f(\xi _{1})\\ \vdots \\ f(\xi _{n}) \end{array}\right] }\left( [\omega _{\xi }][M_{m}]\right) ^{T}.[M_{k}]. \underset{\left[ g\left( \{\xi \}\right) \right] }{\underbrace{\left[ \begin{array}{c} g(\xi _{1})\\ \vdots \\ g(\xi _{n}) \end{array}\right] }} \end{aligned}$$

(27)

where $[M_{m}]$ is the mth-order differentiation DQM matrix whose expression is given in “Appendix” 7. $M_{0}$ designates the identity matrix which has the same order as the DQM matrices. Here, the notation $[\omega _{\xi }][M_{m}]$ indicates that the elements of $[\omega _{\xi }]$ multiply the rows of $[M_{m}]$. It will be referred to later simply as $[\omega _{\xi }M_{m}]$. Using (27), the integrals in (25) can be discretized and written in a matrix form. Technically, $Y_{1}$ and $Y_{2}$ are defined as vectors of nodal displacements such as $[Y_{1}]_{i}={\hat{w}}_{i}(\tau )$ and $[Y_{2}]_{i}={\hat{\phi }}_{i}(\tau )$ where $(1\le i\le n)$. In addition, $\delta Y_{1}$ and $\delta Y_{2}$ are vectors of virtual displacements such as $[\delta Y_{1}]_{i}=\delta {\hat{w}}_{i}(\tau )$ and $[\delta Y_{2}]_{i}=\delta {\hat{\phi }}_{i}(\tau )$. Finally, the general displacement vector Y is defined as $Y=\left[ \begin{array}{c} Y_{1}\\ Y_{2} \end{array}\right]$, while the velocity and acceleration vectors are denoted by ${\dot{Y}}$ and ${\ddot{Y}}$, respectively.

A WQEM discretization is utilized to obtain the free vibration solution of the nanobeam. The mesh coordinates $\xi _{i}(i=1,\ldots ,n)$ for n nodes are chosen based on the Gauss–Lobatto–Legendre (GLL) quadrature grid which yields an integration accuracy up to a polynomial of degree (2n – 3) [37, 45]. For a general linear TBT, this should result in a fully integrated stiffness matrix and reduced integrated mass matrix [37, 45]. Applying the spatial discretization in (27) to the variational statement (25) yields the following:

$$\begin{aligned}&\left[ \omega _{\xi }M_{0}\right] ^{T}.\left( M_{0}.{\ddot{Y}}_{1}-{\hat{q}}\right) +{\hat{\mu }}_{0}^2\left[ \omega _{\xi }M_{1}\right] ^{T}.\left( M_{1}.{\ddot{Y}}_{1}-{\hat{q}}'\right) +\nonumber \\&\quad \left[ \omega _{\xi }M_{1}\right] ^{T}.\left( i{\mathcal {C}}\left( M_{1}.Y_{1}-{\hat{\mu }}_{0}^2M_{3}.Y_{1}\right) +\frac{1}{s^{2}}\left( M_{0}.Y_{2}+M_{1}.Y_{1}\right) \right) = 0 \end{aligned}$$

(28a)

$$\begin{aligned}&- \quad - \quad - \quad - \nonumber \\&\quad \left[ \omega _{\xi }M_{0}\right] ^{T}.\left( \frac{1}{s^{2}}\left( M_{0}.Y_{2}+M_{1}.Y_{1}\right) +mM_{0}.{\ddot{Y}}_{2}+{\hat{\mu }}_{0}^2M_{1}.{\ddot{Y}}_{1}-{\hat{\mu }}_{0}^2i{\mathcal {C}}M_{3}.Y_{1}-{\hat{q}}'\right) + \nonumber \\&\quad \left[ \omega _{\xi }M_{1}\right] ^{T}.\left( M_{1}.Y_{2}+{\hat{\mu }}_{0}^2\left( mM_{1}.{\ddot{Y}}_{2}+M_{0}.{\ddot{Y}}_{1}-i{\mathcal {C}}M_{2}.Y_{1}-{\hat{q}}\right) \right) = 0 \end{aligned}$$

(28b)

where

$$\begin{aligned} i{\mathcal {C}}&=\kappa _{0}\left( \left\{ \omega _{\xi }\right\} .\left\{ \left( M_{1}.Y_{1}\right) {}^{2}\right\} \right) \\ {\hat{q}}&={\hat{k}}_{s}M_{2}.Y_{1}-{\hat{k}}_{L}M_{0}.Y_{1}-{\hat{k}}_{NL}\left( M_{0}.Y_{1}\right) ^{3}\\ {\hat{q}}'&={\hat{k}}_{s}M_{3}.Y_{1}-{\hat{k}}_{L}M_{1}.Y_{1}-3{\hat{k}}_{NL}\left( M_{0.}Y_{1}\right) ^{2}M_{1}.Y_{1} \end{aligned}$$

and $\omega _{\xi }$ is an integral quadrature weight coefficient vector compatible with the GLL grid. $M_{2}M_{1}$ or $M_{1}^{2}$ is an element by element product (i.e., the Hadamard product) of either two vectors or two matrices. The matrix form in Eqs. (28a) and (28b) produces a system of 2n coupled differential equations, n for each degree of freedom. Hinged–hinged (HH) and clamped–clamped (CC) beams are the only boundary conditions considered herein. Since all boundary conditions present in this study are homogeneous, only essential boundary conditions need to be explicitly stated for variational methods. These boundary conditions are given by

$$\begin{aligned} \left[ Y_{1}\right] _{k_{b}} =0&\nonumber \\ - \quad - \quad -&\nonumber \\ \left[ Y_{1}\right] _{k_{b}} =0&\nonumber \\ \left[ Y_{2}\right] _{k_{b}} =0&\end{aligned}$$

(29)

where $k_{b}$ is either 1 or n. The system of Eqs. (28a) and (28b) is then reduced to its basic degrees of freedom using the procedure outlined in [35, 64, 65, 74]

$$\begin{aligned} \begin{array}{c} \left[ M_{Sys}^{\{R\}}\right] .\left[ \begin{array}{c} {\ddot{Y}}^{\{R\}}\end{array}\right] +\left[ K_{Sys}^{\{R\}} \left( Y^{\{R\}}\right) \right] .\left[ \begin{array}{c} Y^{\{R\}}\end{array}\right] =\left\{ 0\right\} \end{array} \end{aligned}$$

(30)

Here, the superscript $\{R\}$ denotes the reduced formulation of the system, $M_{Sys}$ is the mass matrix and $K_{Sys}(Y)$ is the nonlinear stiffness matrix. To obtain the eigenvalues, Y is assumed to have the following form $Y={\widetilde{Y}}e^{i\omega t}$. Then, Eq. (30) is rewritten in the following form:

$$\begin{aligned} \left( \left[ K_{Sys}^{\{R\}}\left( Y^{\{R\}}\right) \right] -\omega ^{2}\left[ M_{Sys}^{\{R\}}\right] \right) . {\widetilde{Y}}^{\{R\}}=0 \end{aligned}$$

(31)

To obtain the linear natural eigen-system, $Y^{\{R\}}$ is set to $\{0\}$ in $\left[ K_{Sys}^{\{R\}}(Y^{\{R\}})\right]$ in (31). The i th nonlinear natural frequency is obtained through an iterative process which starts with the i th linear eigenvector to evaluate $\left[ K_{Sys}^{\{R\}}(Y^{\{R\}})\right]$. The newly estimated eigenvector is used to update $\left[ K_{Sys}^{\{R\}}(Y^{\{R\}})\right]$ until reaching convergence. Since the nonlinear frequency is amplitude dependent, the i th eigenvector must always be scaled relative to the mode shape of $w\left( x,t\right)$ in order to keep the mode shape’s amplitude constant.

4 Forced vibration WQEM formulation

The free vibration studies related to the problems similar to the one under investigation largely outnumbered their force vibration counterparts in the literature. In fact, there are limited number studies of forced vibration involving DQM [36, 65, 74, 75], especially in size-dependent mechanics. A number of nonclassical mechanics WQEM studies are extremely rare and are focused on the free vibration response [64]. To the best of the authors knowledge, there have been no forced vibration WQEM studies in the literature similar to the one present with DQM. To fill this gap, two force vibration methods are proposed in this section. Each of the proposed methods aims at finding the periodic steady-state solution of the system for different excitation frequencies. For this aim, the time is discretized using a periodic grid and periodic derivation matrices. However, adding a time discretization is equivalent to adding another dimension to the problem with consequential important computational cost. Hence, knowing that the forcing term should only excite a few modes, it is necessary to reduce the spatial degrees of freedom. In this section, each proposed method introduces a different approach to perform this task.

Adding the forcing and the damping terms to (28a) and (28b) yields the following WQEM formulation of the variational statement for the forced vibration case:

$$\begin{aligned}&\left[ \omega _{\xi }M_{0}\right] ^{T}.\left( M_{0}.{\ddot{Y}}_{1}+{\hat{\mu }}_{f}M_{0}.{\dot{Y}}_{1}-{\hat{q}}\right) +{\hat{\mu }}_{0}^{2}\left[ \omega _{\xi }M_{1}\right] ^{T}.\left( M_{1}.{\ddot{Y}}_{1}+{\hat{\mu }}_{f}M_{1}.{\dot{Y}}_{1}-{\hat{q}}'\right) +\nonumber \\&\quad \left[ \omega _{\xi }M_{1}\right] ^{T}.\left( i{\mathcal {C}}\left( M_{1}.Y_{1}-{\hat{\mu }}_{0}^{2}M_{3}.Y_{1}\right) +\frac{1}{s^{2}}\left( M_{0}.Y_{2}+M_{1}.Y_{1}\right) \right) =0 \end{aligned}$$

(32a)

$$\begin{aligned}&-\quad -\quad -\quad -\nonumber \\&\quad \left[ \omega _{\xi }M_{0}\right] ^{T}.\left( \frac{1}{s^{2}}\left( M_{0}.Y_{2}+M_{1}.Y_{1}\right) +mM_{0}.{\ddot{Y}}_{2}+{\hat{\mu }}_{0}^{2}\left( M_{1}.{\ddot{Y}}_{1}+{\hat{\mu }}_{f}M_{1}.{\dot{Y}}_{1}-i{\mathcal {C}}M_{3}.Y_{1}\right) -{\hat{q}}'\right) +\nonumber \\&\quad \left[ \omega _{\xi }M_{1}\right] ^{T}.\left( M_{1}.Y_{2}+{\hat{\mu }}_{0}^{2}\left( mM_{1}.{\ddot{Y}}_{2}+M_{0}.{\ddot{Y}}_{1}+{\hat{\mu }}_{f}M_{0}.{\dot{Y}}_{1}-i{\mathcal {C}}M_{2}.Y_{1}-{\hat{q}}\right) \right) =0 \end{aligned}$$

(32b)

where

$$\begin{aligned} i{\mathcal {C}}&=\kappa _{0}\left( \left\{ \omega _{\xi }\right\} .\left\{ \left( M_{1}.Y_{1}\right) {}^{2}\right\} \right) \\ {\hat{q}}&={\hat{k}}_{s}M_{2}.Y_{1}-{\hat{k}}_{L}M_{0}.Y_{1}-{\hat{k}}_{NL}\left( M_{0}.Y_{1}\right) ^{3}+{\hat{F}}\cos ({\hat{\omega }}\tau )\\ {\hat{q}}'&={\hat{k}}_{s}M_{3}.Y_{1}-{\hat{k}}_{L}M_{1}.Y_{1}-3{\hat{k}}_{NL}\left( M_{0.}Y_{1}\right) ^{2}M_{1}.Y_{1}+M_{1}.{\hat{F}}\cos ({\hat{\omega }}\tau ) \end{aligned}$$

in which ${\hat{\mu }}_{f}$ is the normalized damping coefficient and ${\hat{F}}$ denotes the normalized discretized force distribution.

4.1 WQEM formulation using a mode shape interpolation basis

The mode shape-based forced vibration approach follows three main steps [35, 74]:

• 1. switching the interpolation basis from a Lagrange basis to a modal basis to reduce the number of degrees of freedom;

• 2. discretizing time using a periodic method, such as the spectral method (SM) or the harmonic quadrature method (HQM);

• 3. solving the discretized system for a different forcing frequency at the vicinity of its first eigen-frequency and plotting the frequency response curve.

4.1.1 Switching the interpolation basis

As explained earlier, WQEM is a high-order FEM that relies on DQM to express the derivatives of the shape functions at the integration points [64]. This is technically, equivalent to making the following assumptions:

$$\begin{aligned} \begin{array}{c} {\hat{w}}\left( \xi ,\tau \right) =\underset{{\mathcal {L}}(\xi )}{\underbrace{\left[ \begin{array}{c} {\mathcal {L}}_{1}(\xi )\\ \vdots \\ {\mathcal {L}}_{n}(\xi ) \end{array}\right] }}_{(n\times 1)}^{T}.\underset{Y_{1}\left( \tau \right) }{\underbrace{\left[ \begin{array}{c} {\hat{w}}_{1}\left( \tau \right) \\ \vdots \\ {\hat{w}}_{n}\left( \tau \right) \end{array}\right] }}_{(n\times 1)}\\ \\ {\hat{\phi }}\left( \xi ,\tau \right) ={\mathcal {L}}(\xi ).Y_{2}\left( \tau \right) \end{array} \end{aligned}$$

(33)

where ${\mathcal {L}}(\xi )$ is a vector of the Lagrange basis relative to $\{\xi \}$ and the dimensions of each term are specified as a subscript in parentheses. Note that this discretization applies for both the displacements ${\hat{w}}\left( \xi ,\tau \right)$ and ${\hat{\phi }}\left( \xi ,\tau \right)$, and virtual displacements $\delta {\hat{w}}\left( \xi ,\tau \right)$ and $\delta {\hat{\phi }}\left( \xi ,\tau \right)$. To reduce the size of the problem, ${\hat{w}}\left( \xi ,\tau \right)$ and ${\hat{\phi }}\left( \xi ,\tau \right)$, as well as $\delta {\hat{w}}\left( \xi ,\tau \right)$ and $\delta {\hat{\phi }}\left( \xi ,\tau \right)$, are expressed using a reduced number of mode shapes m. Terms related to the reduced coordinates will use a double script font or will be underlined as indicated below

$$\begin{aligned} \begin{array}{c} {\hat{w}}\left( \xi ,\tau \right) \end{array}&=\underset{{\mathcal {L}}(\xi )}{\underbrace{\left[ \begin{array}{c} {\mathcal {L}}_{1}(\xi )\\ \vdots \\ {\mathcal {L}}_{n}(\xi ) \end{array}\right] ^{T}}}.\left[ \begin{array}{c} \Phi _{1}\end{array}\right] _{(n\times m)}.\underset{{\mathbb {Y}}_{1}(\tau )}{\underbrace{\left[ \begin{array}{c} {\underline{w}}_{1}\left( \tau \right) \\ \vdots \\ {\underline{w}}_{m}\left( \tau \right) \end{array}\right] }}_{(m\times 1)} \end{aligned}$$

(34a)

$$\begin{aligned} \begin{array}{c} {\hat{\phi }}\left( \xi ,\tau \right) \end{array}&=[{\mathcal {L}}(\xi )]^{T}.\left[ \begin{array}{c} \Phi _{2}\end{array}\right] _{(n\times m)}.[{\mathbb {Y}}_{2}(\tau )] \end{aligned}$$

(34b)

$$\begin{aligned} _{(n\times m)}&=\underset{\text {The mode shape approximation basis for } {{\hat{w}}\left( \xi ,\tau \right) }}{\underbrace{[\begin{array}{ccc} \{{\widetilde{Y}}_{w,1}\}&\ldots&\{{\widetilde{Y}}_{w,m}\}\end{array}]}}\end{aligned}$$

(34c)

$$\begin{aligned} _{(n\times m)}&=\underset{\text {The mode shape approximation basis for } {\hat{\phi }}\left( \xi ,\tau \right) }{\underbrace{[\begin{array}{ccc} \{{\widetilde{Y}}_{\phi ,1}\}&\ldots&\{{\widetilde{Y}}_{\phi ,m}\}\end{array}]}} \end{aligned}$$

(34d)

in which ${\mathbb {Y}}_{1}(\tau )$ and ${\mathbb {Y}}_{2}(\tau )$ denote, respectively, the reduced generalized coordinate vectors for ${\hat{w}}\left( \xi ,\tau \right)$ and ${\hat{\phi }}\left( \xi ,\tau \right)$. The virtual displacements $\delta {\hat{w}}\left( \xi ,\tau \right)$ and $\delta {\hat{\phi }}\left( \xi ,\tau \right)$ are also interpolated in a similar manner. $[\Phi _{1}]$ and $[\Phi _{2}]$ are a collection of m columns representing linear eigenvectors relative to ${\hat{w}}$ and ${\hat{\phi }}$, respectively, such that $\{{\widetilde{Y}}_{w,i}\}$ and $\{{\widetilde{Y}}_{\phi ,i}\}$ are the i th linear eigenvectors with respect to ${\hat{w}}$ and ${\hat{\phi }}$, respectively. The basic concept here is to interpolate the dependent variables and the virtual displacements using the limited number of dominant linear mode shapes. Hence, the reduced generalized coordinates in ${\mathbb {Y}}_{1}(\tau )$ and ${\mathbb {Y}}_{2}(\tau )$ are simply the amplitudes of each dominant linear mode.

Substituting into (25) gives a system of equations similar to Eqs. (32a) and (32b) as

$$\begin{aligned}&\left[ \omega _{\xi }{\mathbb {M}}_{1,0}\right] ^{T}.\left( {\mathbb {M}}_{1,0}.\ddot{{\mathbb {Y}}}_{1}+{\hat{\mu }}_{f}{\mathbb {M}}_{1,0}.\dot{{\mathbb {Y}}}_{1}-{\hat{q}}\right) +{\hat{\mu }}_{0}^{2}\left[ \omega _{\xi }{\mathbb {M}}_{1,1}\right] ^{T}.\left( {\mathbb {M}}_{1,1}.\ddot{{\mathbb {Y}}}_{1}+{\hat{\mu }}_{f}{\mathbb {M}}_{1,0}.\dot{{\mathbb {Y}}}_{1}-{\hat{q}}'\right) +\nonumber \\&\quad \left[ \omega _{\xi }{\mathbb {M}}_{1,1}\right] ^{T}.\left( i{\mathcal {C}}\left( {\mathbb {M}}_{1,1}.{\mathbb {Y}}_{1}-{\hat{\mu }}_{0}^{2}{\mathbb {M}}_{1,3}.{\mathbb {Y}}_{1}\right) +\frac{1}{s^{2}}\left( {\mathbb {M}}_{2,0}.{\mathbb {Y}}_{2}+{\mathbb {M}}_{1,1}.{\mathbb {Y}}_{1}\right) \right) =0 \end{aligned}$$

(35a)

$$\begin{aligned}&-\quad -\quad -\quad -\nonumber \\&\quad \left[ \omega _{\xi }{\mathbb {M}}_{2,0}\right] ^{T}.\left( \frac{1}{s^{2}}\left( {\mathbb {M}}_{2,0}.{\mathbb {Y}}_{2}+{\mathbb {M}}_{1,1}.{\mathbb {Y}}_{1}\right) +m{\mathbb {M}}_{2,0}.\ddot{{\mathbb {Y}}}_{2}+{\hat{\mu }}_{0}^{2}\left( {\mathbb {M}}_{1,1}.\ddot{{\mathbb {Y}}}_{1}+{\hat{\mu }}_{f}{\mathbb {M}}_{1,0}.\dot{{\mathbb {Y}}}_{1}-i{\mathcal {C}}{\mathbb {M}}_{1,3}.{\mathbb {Y}}_{1}\right) -{\hat{q}}'\right) +\nonumber \\&\quad \left[ \omega _{\xi }{\mathbb {M}}_{2,1}\right] ^{T}.\left( {\mathbb {M}}_{2,1}.{\mathbb {Y}}_{2}+{\hat{\mu }}_{0}^{2}\left( m{\mathbb {M}}_{2,1}.\ddot{{\mathbb {Y}}}_{2}+{\mathbb {M}}_{1,0}.\ddot{{\mathbb {Y}}}_{1}+{\hat{\mu }}_{f}{\mathbb {M}}_{1,0}.\dot{{\mathbb {Y}}}_{1}-i{\mathcal {C}}{\mathbb {M}}_{1,2}.{\mathbb {Y}}_{1}-{\hat{q}}\right) \right) =0 \end{aligned}$$

(35b)

where

$$\begin{aligned} {\mathbb {M}}_{k,i}&=M_{i}.\left[ \Phi _{k}\right] \\ i{\mathcal {C}}&=\kappa _{0}\left( \left\{ \omega _{\xi }\right\} .\left\{ \left( {\mathbb {M}}_{1,1}.{\mathbb {Y}}_{1}\right) {}^{2}\right\} \right) \\ {\hat{q}}&={\hat{k}}_{s}{\mathbb {M}}_{1,2}.{\mathbb {Y}}_{1}-{\hat{k}}_{L}{\mathbb {M}}_{1,0}.{\mathbb {Y}}_{1}-{\hat{k}}_{NL}\left( {\mathbb {M}}_{1,0}.{\mathbb {Y}}_{1}\right) ^{3}+\hat{{\mathbb {F}}}\cos ({\hat{\omega }}\tau )\\ {\hat{q}}'&={\hat{k}}_{s}{\mathbb {M}}_{1,3}.{\mathbb {Y}}_{1}-{\hat{k}}_{L}{\mathbb {M}}_{1,1}.{\mathbb {Y}}_{1}-3{\hat{k}}_{NL}\left( {\mathbb {M}}_{1,0}.{\mathbb {Y}}_{1}\right) ^{2}{\mathbb {M}}_{1,1}.{\mathbb {Y}}_{1}+{\mathbb {M}}_{1,0}.\hat{{\mathbb {F}}}\cos ({\hat{\omega }}\tau ) \end{aligned}$$

Switching to a mode shape interpolation basis reduces the problem size from 2n equations (n is number of nodes in the mesh) to 2m. This step is driven by the fact that a limited number of first mode shapes generally dominate the dynamic behavior of the nanobeam. In addition, the forcing term is focused to mostly excite the first w modes. Thus, ${\hat{F}}$ or $\hat{{\mathbb {F}}}$ is selected such that

$$\begin{aligned} {\hat{F}}&=\mu _{F}{\bar{F}}_{1}\{{\widetilde{Y}}_{w,1}\} \end{aligned}$$

(36a)

$$\begin{aligned} \hat{{\mathbb {F}}}&=\mu _{F}{\bar{F}}_{1}\left\{ \begin{array}{cccc} 1&0&\cdots&0\end{array}\right\} _{(m\times 1)}^{T} \end{aligned}$$

(36b)

$$\begin{aligned}&\mu _{F}=\left\{ \int _{0}^{1}\psi ^{2}d\xi \right\} ^{-1/2}= \left\| \psi \right\| _{2}^{-1} \thickapprox \left\{ \{\omega _{\xi }\}.\{{\widetilde{Y}}_{w,1}^{2}\}\right\} ^{-1/2} \end{aligned}$$

(36c)

where ${\bar{F}}_{1}$ denotes the amplitude of the forcing term and $\mu _{F}$ represents a scaling factor.Finally, let us define ${\mathbb {Y}}=\left[ \begin{array}{c} {\mathbb {Y}}_{1}\\ {\mathbb {Y}}_{2} \end{array}\right]$, so that Eqs. (35a) and (35b) can be expressed in the following form:

$$\begin{aligned} {[}M_{Sys}].\ddot{{\mathbb {Y}}}+[C_{Sys}].\dot{{\mathbb {Y}}} +[K_{Sys}({\mathbb {Y}})].{\mathbb {Y}}-[F_{Sys}]\cos ({\hat{\omega }}\tau ) =0 \end{aligned}$$

(37)

4.1.2 Time discretization

Introducing a new timescale ${\hat{\tau }}$ such that ${\hat{\tau }}=\frac{\tau }{T}=\frac{\tau }{2\pi }{\hat{\omega }}$, Eq. (37) becomes

$$\begin{aligned} \left( \frac{{\hat{\omega }}}{2\pi }\right) ^{2}[M_{Sys}]. \ddot{{\mathbb {Y}}}+\left( \frac{{\hat{\omega }}}{2\pi }\right) [C_{Sys}].\dot{{\mathbb {Y}}}+[K_{Sys}({\mathbb {Y}})]. {\mathbb {Y}}-\left[ F_{Sys}\right] \cos (2\pi {\hat{\tau }})=0 \end{aligned}$$

(38)

The choice of this timescale eliminates the need to update the forcing term for various values of ${\hat{\omega }}$. A periodic steady-state solution must be reached to compute the frequency response of the system. This can be expressed with the following periodic initial conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {Y}}|_{{\hat{\tau }}=0}={\mathbb {Y}}|_{{\hat{\tau }}=1}\\ \dot{{\mathbb {Y}}}|_{{\hat{\tau }}=0}=\dot{{\mathbb {Y}}}|_{{\hat{\tau }}=1} \end{array}\right. } \end{aligned}$$

(39)

A numerical solution for the forced vibration problem requires an adequate discretization of the time dimension. Both spectral method (SM) and harmonic differential quadrature method (HQM) can be utilized for this aim since both methods implicitly implement periodic initial conditions with additional accuracy of high-order methods. Hence, the corresponding compatible mesh is adopted

$$\begin{aligned} {\hat{\tau }}_{i}&=\frac{i}{n_{\tau }},\;0<{\hat{\tau }}_{i}\le 1,\;1\le i\le n_{\tau } \, n_{\tau }\text { is even} \text { for SM} \end{aligned}$$

(40)

$$\begin{aligned} {\hat{\tau }}_{i}&=\frac{i}{n_{\tau }},\;0\le {\hat{\tau }}_{i}<1,\;0\le i\le n_{\tau }-1 \, n_{\tau }\text { is odd} \text { for HQM} \end{aligned}$$

(41)

where $n_{\tau }$ designates the time increment number. Here, the SM and HQM differentiation matrices are, respectively, provided in Appendices B and C and the discretized time space coordinate matrix is defined as

$$\begin{aligned}{}[Q]=\left[ \begin{array}{c} [Q_{w}]\\ ---\\ {} [Q_{\phi }] \end{array}\right] =\left[ \begin{array}{c} \begin{array}{ccc} {\mathbb {Y}}_{1}({\hat{\tau }}_{1}) &{} \cdots &{} {\mathbb {Y}}_{1} ({\hat{\tau }}_{n_{\tau }})\end{array}\\ ---\\ \begin{array}{ccc} {\mathbb {Y}}_{2}({\hat{\tau }}_{1}) &{} \cdots &{} {\mathbb {Y}}_{2}({\hat{\tau }}_{n_{\tau }})\end{array} \end{array}\right] =\left[ \begin{array}{ccc} {\underline{w}}_{1}({\hat{\tau }}_{1}) &{} \cdots &{} {\underline{w}}_{1}({\hat{\tau }}_{n_{\tau }})\\ \vdots &{} &{} \vdots \\ {\underline{w}}_{m}({\hat{\tau }}_{1}) &{} \cdots &{} {\underline{w}}_{m}({\hat{\tau }}_{n_{\tau }})\\ \_\_ &{} \_\_ &{} \_\_\\ {\underline{\phi }}{}_{1}({\hat{\tau }}_{1}) &{} \cdots &{} {\underline{\phi }}_{n}({\hat{\tau }}_{n_{\tau }})\\ \vdots &{} &{} \vdots \\ {\underline{\phi }}_{m}({\hat{\tau }}_{1}) &{} \cdots &{} {\underline{\phi }}_{m}({\hat{\tau }}_{n_{\tau }}) \end{array}\right] _{(2m\times n_{\tau })} \end{aligned}$$

(42)

Here, the columns and lines of [Q] correspond to the discretized space and time, respectively. This approach yields the following discretized equation of motion:

$$\begin{aligned} \left( \frac{{\hat{\omega }}}{2\pi }\right) ^{2}[M_{Sys}].[Q]. [D_{\tau }^{(2)}]^{T}+\left( \frac{{\hat{\omega }}}{2\pi }\right) [C_{Sys}].[Q].[D_{\tau }^{(1)}]^{T}+[K_{Sys}(Q)].[Q]-[F_{Sys}].[A]=0 \end{aligned}$$

(43)

im which $[D_{\tau }^{(k)}]$ is the kth-order time derivative matrix and [A] is a $(1\times n_{\tau })$ line matrix such as $[A]_{i}=\cos (2\pi {\hat{\tau }}_{i})$. Finally, solving (43) for different values of ${\hat{\omega }}$ in the neighborhood of the first linear frequency is required to obtain the frequency response curve.

4.1.3 Frequency response curve

A frequency response curve can be generated in the neighborhood of each resonance. This applies to both system’s dependent variables, namely ${\hat{w}}$ and ${\hat{\phi }}$. The amplitudes of ${\hat{w}}$’s mode shapes as a function of time are obtained through the following transformation:

$$\begin{aligned} \begin{array}{c} \underset{\{{\mathbb {Y}}_{1}({\hat{\tau }})\}}{\underbrace{\left[ \begin{array}{c} {\underline{w}}_{1}({\hat{\tau }})\\ \vdots \\ {\underline{w}}_{m}({\hat{\tau }}) \end{array}\right] }}_{(m\times 1)}=\underset{[Q_{w}]}{\underbrace{\left[ \begin{array}{ccc} {\underline{w}}_{1}({\hat{\tau }}_{1}) &{} \cdots &{} {\underline{w}}_{1}({\hat{\tau }}_{n_{\tau }})\\ \vdots &{} &{} \vdots \\ {\underline{w}}_{m}({\hat{\tau }}_{1}) &{} \cdots &{} {\underline{w}}_{m}({\hat{\tau }}_{n_{\tau }}) \end{array}\right] }}_{(m\times n_{\tau })}.\underset{\{{\mathcal {L}} ({\hat{\tau }})\}}{\underbrace{\left[ \begin{array}{c} {\mathcal {L}}_{1}({\hat{\tau }})\\ \vdots \\ {\mathcal {L}}_{n_{\tau }}({\hat{\tau }}) \end{array}\right] }}_{(n_{\tau }\times 1)}\end{array} \end{aligned}$$

(44)

where $[Q_{w}]$ is defined in (42). Finally, $[{\mathcal {L}}(\tau )]$, the time discretization basis is given by [76,77,78]

$$\begin{aligned} {\mathcal {L}}_{i}(\tau )= & {} \frac{1}{n_{\tau }}\cot \left( \pi \left( t-\frac{i}{n_{\tau }}\right) \right) \sin \left( \pi n_{\tau }\left( t-\frac{i}{n_{\tau }}\right) \right) \quad \text {for spectral method}\nonumber \\ {\mathcal {L}}_{i}(\tau )= & {} {\displaystyle \prod _{j=1,j\ne i}^{n_{\tau }}\frac{\sin (\pi (\tau -\tau _{j}))}{\sin (\pi (\tau _{i}-\tau _{j}))}} \quad \text {for HQM} \end{aligned}$$

(45)

The frequency response curve was established such that the forcing term excited only the fundamental natural frequency. This corresponds to finding $\max ({\underline{w}}_{1}(\tau ))$ of the QEM system (32) at several values of ${\hat{\omega }}$ in the neighborhood of the first natural frequency.

4.2 WQEM formulation using Galerkin technique

It is also possible to write (32a) and (32b) as

$$\begin{aligned}{}[M_{Sys}].{\ddot{Y}}+[C_{Sys}].{\dot{Y}}+[K_{Sys}(Y)]. Y-[F_{Sys}]\cos ({\hat{\omega }}\tau )=0 \end{aligned}$$

(46)

Based on this form, the forced vibration problem can be treated similarly to the DQM case in [74, 75, 79, 80]. Despite the similarity, there are few differences to be noted

• 1. In this case, a Galerkin projection is applied to discretize the variational statement.

• 2. Two nested integrals have to be calculated: the WQEM integral and the Galerkin integral.

• 3. Thanks to the careful mesh choice, it is possible to use the same high-order integration scheme for the WQEM and Galerkin integrals.

• 4. This method is computationally more intensive than the method presented in the previous section.

• 5. The main difference between this approach and the one presented in the previous section is the procedure of reducing the number of the degrees of freedom.

Going back to (46), all matrices present in this equation along with $[F_{Sys}]$ are established using WQEM, i.e., the high-order variational statement. Now that the system looks like a time-dependent differential equation, the Galerkin technique is adopted to limit the size of the WQEM system to 2m equations. As stated in the previous section, only a limited number of mode shapes dominate the nanobeam’s vibrational response. Hence, the 2m first linear nonlocal mode shapes are selected as the basis in applying the Galerkin technique [74, 75, 79, 80]. Consequently, the following change of variables has to be made:

$$\begin{aligned} \begin{array}{c} \underset{Y}{\underbrace{\left[ \begin{array}{c} Y_{1}\\ Y_{2} \end{array}\right] }}_{(2n\times 1)}=\underset{[\Phi ]}{\underbrace{\left[ \begin{array}{cc} [\Phi _{w}] &{} 0\\ 0 &{} [\Phi _{\phi }] \end{array}\right] }}_{(2n\times 2m)}.\underset{{\mathcal {Y}}(\tau )}{\underbrace{\left[ \begin{array}{c} \{{\mathcal {Y}}_{1}(\tau )\}_{(m\times 1)}\\ \{{\mathcal {Y}}_{2}(\tau )\}_{(m\times 1)} \end{array}\right] }}_{(2m\times 1)}\end{array} \end{aligned}$$

(47)

where ${\mathcal {Y}}(\tau )$ and $[\Phi ]$ are, respectively, the reduced generalized coordinates and the Galerkin approximation basis. The idea is similar to the one presented in the previous section except here the change of variable is performed after the evaluation of the variational statement. $\{{\mathcal {Y}}_{1}(\tau )\}$ and $\{{\mathcal {Y}}_{2}(\tau )\}$ denote, respectively, the reduced generalized coordinates relative to ${\hat{w}}$ and ${\hat{\phi }}$. $[\Phi ]$ is composed of two blocks $[\Phi _{w}]$ and $[\Phi _{\phi }]$, which are identical to the ones presented in the previous section. The Galerkin approximation consists of premultiplying Eq. (46) by a numerical Galerkin projection operator denoted by [G] to yield the following:

$$\begin{aligned} \underset{[G]_{(2m\times 2n)}}{\underbrace{[[S][\Phi ]]^{T}}}. \left( [M_{Sys}].[\Phi ].\ddot{{\mathcal {Y}}}+[C_{Sys}].[\Phi ]. \dot{{\mathcal {Y}}}+[K_{Sys}([\Phi ].{\mathcal {Y}})].[\Phi ]. {\mathcal {Y}}-[F_{Sys}]\cos ({\hat{\omega }}\tau )\right) =0 \end{aligned}$$

(48)

in which [S] is the integral quadrature weight coefficient matrix and $[\Phi ]$ is given by (47). In the literature, [S] is usually computed using the trapezoidal rule [36, 65, 75]. However, since a GLL grid is used, a more accurate result can be obtained by setting $[S]=[\omega _{\xi }]$. The final system is given by

$$\begin{aligned} \overline{[M}_{Sys}].\ddot{{\mathcal {Y}}}+\left[ {\overline{C}}_{Sys}\right] .\dot{{\mathcal {Y}}}+\left[ {\overline{K}}_{Sys}({\mathcal {Y}})\right] . {\mathcal {Y}}-[{\overline{F}}_{Sys}]\cos ({\hat{\omega }}\tau )=0 \end{aligned}$$

(49)

where

$$\begin{aligned}&\overline{[M}_{Sys}]_{(2m\times 2m)}= & {} [G]_{(2m\times 2n)}.[M_{Sys}]_{(2n\times 2n)}.[\Phi ]_{(2n\times 2m)}\\&\overline{[K}_{Sys}({\mathcal {Y}}(\tau ))]_{(2m\times 2m)}= & {} [G]_{(2m\times 2n)}.[K_{Sys}([\Phi ].{\mathcal {Y}}(\tau ))]_{(2n\times 2n)}.[\Phi ]_{(2n\times 2m)}\\&\overline{[C}_{Sys}]_{(2m\times 2m)}= & {} [G]_{(2m\times 2n)}.[C_{Sys}]_{(2n\times 2n)}.[\Phi ]_{(2n\times 2m)}\\&\overline{[F}_{Sys}]_{(2m\times 1)}= & {} [G]_{(2m\times 2n)}.[F_{Sys}]_{(2n\times 1)} \end{aligned}$$

This system looks similar to (37), although the resulting matrices are not the same. Nevertheless, the solution procedure is exactly the same from this point onward.

5 Numerical results and discussion

Various aspects of the graded nanobeam vibration are presented herein including nonlocal linear and nonlinear frequencies in addition to force vibration frequency response curves. A schematic of the beam is presented in Fig. 1. It is assumed that the beam has a square cross section such that $b=h=\frac{1}{10}L$. It is further assumed that its material distribution is graded in the z-direction according to Eq. (11) where $-\frac{h}{2}\le z\le \frac{h}{2}$ and $P_{L}$ and $P_{U}$ designate aluminum and silicon properties, respectively. In this study, the utilized material properties are reported in Table 1 and the considered boundary conditions include hinged–hinged $(\mathrm {HH})$ and clamped–clamped $(\mathrm {CC})$.

Fig. 1

A hinged–hinged nanobeam resting on a nonlinear elastic foundation

Table 1 Material properties of the constituent materials of the graded nanobeam [81]

5.1 Performance of WQEM

A mesh convergence study is the first step. To give a better assessment of the convergence performance of WQEM, it was decided to conduct a mesh convergence study on all cases treated later in Table 5. Generally, the CC case is the slowest to converge. A selection of these difficult CC cases are presented in Table 2 along with their HH analogs. Table 2 shows that the errors for the CC cases fall below 0.5% for as few as 7 nodes. A choice of 7 nodes is totally acceptable, although an 11-node grid is selected for better accuracy. In fact, the error for the HH cases drops below 0.05% using just 7 nodes. This rapid convergence is one of the major advantages for using a high-order variational statement. A similar system would have required 15 nodes to converge using DQM [36]. It is important to note that these results are obtained despite the fact that the nanobeam is highly nonlinear. In this study, a choice of 11 nodes is adopted. The DQM results in this paper were provided from a study by Trabelssi et al. [36] which used a 15-node grid.

Table 2 WQEM convergence performance ($\frac{L}{h}=10$,${\hat{\mu }}_{0}^2=5$,${n_k}=0.5$,$A=1)$: slowest converging cases selected from the study performed in Table 5

5.2 Free vibration response

The aim of this section is to replicate the results obtained by Trabelssi et al. [36] for a similar problem using WQEM. The results obtained herein can be divided into two tables. First, the effect of different parameters including the material inhomogeneity index $n_k$, the amplitude of the free vibration A and the stiffness parameters of the elastic foundation, on the free vibration of the nanobeam is investigated in Table 3 for HH and CC nanobeams. The results reported in Table 3 were generated based on the WQEM discretization. For the sake of comparison, Table 3 contains DQM data obtained by Tarbelssi et al. [36], which helps to assess the performance of the proposed approach. The present data utilize a range of values of the amplitude and the nonlocal parameter A and ${\hat{\mu }}_{0}$, while the inhomogeneity index $n_k$ varies from 1 to 4. Both HH and CC configurations are included in this study, while L/h varies between 10 to 100. The foundation stiffness configuration is described with the following parameters ${\hat{k}}_{s}=5$, ${\hat{k}}_{L}=50$ and ${\hat{k}}_{NL}=50$. Table 3 shows that the frequencies obtained using WQEM match their DQM counterparts up to the fourth digit regardless of the configuration of the nanobeam, the vibration amplitude or the boundary conditions. Knowing that WQEM results were obtained with a significantly lower mesh density, this truly assesses the accuracy of the WQEM data.

To assess the sensitivity of the proposed formulation to shear locking, the same configuration used to generate the data in Table 3 is used to recompute the nonlocal nonlinear frequencies for thick nanobeams where the aspect ratio $\frac{L}{h}$ is kept below 10. To the best of the authors’ knowledge, there has been no study that confirmed the presence of shear locking in DQM. In light of this, DQM data were also generated to assess the accuracy of the WQEM results. According to Table 4, the data generated using WQEM are in good agreement with DQM data, indicating the absence of shear locking. This is in agreement with Jin and Wang [82] who also found no shear locking in their linear classical WQEM TBT model.

The effect of the nonlinear foundation is investigated in Table 5. Using the same set of boundary conditions, the nonlinear nonlocal frequencies were computed using WQEM along with DQM data [36]. The values of the different parameters are chosen to underline the effect of the nonlinear elastic foundation which is the highest nonlinear element in the system. It is also the only controllable nonlinearity in the system. The foundation’s linear and nonlinear coefficients ${\hat{k}}_{L}$ and ${\hat{k}}_{NL}$ are set to vary between 0 and 100 for the former and between 10 and 100 for the latter. The shear coefficient ${\hat{k}}_{s}$ varies between 0 and 50, while the inhomogeneity index $n_k$ and the amplitude A are set to a fixed value of 0.5 and 1, respectively. Both ${\hat{k}}_{S}$ and ${\hat{k}}_{NL}$ are known to affect considerably the behavior of the nanobeam [36]. Despite the wide range of the selected variables, Table 5 shows that the WQEM and DQM results still show great consistency regardless of the selected configuration. In fact, the WQEM low density mesh still performs as good as DQM’s higher-density mesh. Technically, variational methods converge faster than their collocation counterparts indicating that these results were expected. The use of the GLL grid helped improve the integration accuracy although the mass matrix is still not fully integrated. It is still possible to improve the accuracy of WQEM with a higher-order integration technique, although this may increase the complexity of the implementation [37].

Table 3 Effect of the material inhomogeneity index $n_k$ on the nonlinear nonlocal frequencies of a FG TBT nanobeam (${\hat{k}}_{s}=5$; ${\hat{k}}_{L}=50$ and ${\hat{k}}_{NL}=50$)

Table 4 Effect of the material inhomogeneity index $n_{k}$ on the nonlinear nonlocal frequencies of a FG TBT thick nanobeam (${\hat{k}}_{s}=5$; ${\hat{k}}_{L}=50$ and ${\hat{k}}_{NL}=50$)

Table 5 Effect of the nonlinear elastic foundation ($A=1$; $n_k=0.5)$

5.3 Forced vibration response

The forced vibration of the nanobeam is examined in this section. This investigation covers both WQEM force vibration approaches detailed in Sects. 4.1 and 4.2 in addition to the previously validated DQM [36]. For each method, the FRC is plotted individually for various values of ${\hat{k}}_{s}$ and for ${n_k}=2, {\hat{\mu }}_{0}^2=2, {\hat{k}}_{NL}=50, {\hat{k}}_{L}=10, {\bar{F}}_{1}=0.75$ and $\frac{L}{h}=10$. This configuration is chosen due to its highly nonlinear behavior and its high dependency on ${\hat{k}}_{s}$. All WQEM FRCs were generated using only 9 nodes, while the DQM FRCs were generated based on a 15-node grid. Figure 2 shows all of the FRC plots for each method as well as a plot of all methods together. These plots are generated for the HH nanobeam. These results show that, despite the lower mesh density, both WQEM methods were able to achieve the same level of convergence as the 15-node DQM results. In fact, Fig. 2 shows that the FRCs totally overlap. The same FRCs are plotted for the CC case in Fig. 3. For this configuration, ${\bar{F}}_{1}$ had to be raised to ${\bar{F}}_{1}=1.5$ in order to obtain a comparable deformation to the HH case. The mesh density is left unchanged and the FRCs are plotted in a similar manner. Figure 3 shows similar convergence of all methods since again all of the FRCs overlap. Based on the reported results, it is clear that WQEM offers a significant computational advantage over DQM. The method requires fewer nodes than DQM, and WQEM solves this FEM problem using a single high-order element without the need to explicitly identify the shape functions. This simplifies its implementation and eliminates the need of element assembly. It is important to note that the first approach requires less computational effort than the second one since only one integration is required, while the second approach requires two integrations.

Fig. 2

Frequency response curves for the HH TBT: effect of ${\hat{k}}_{s}$$\left[ {n_k}=2,{\hat{\mu }}_{0}^2=2,{\hat{k}}_{NL}=50, {\hat{k}}_{L}=10,{\bar{F}}_{1}=0.75\right]$

Fig. 3

Frequency response curves for the CC beam: effect of ${\hat{k}}_{s}$$\left[ {n_k}=2,{\hat{\mu }}_{0}^2=2,{\hat{k}}_{NL}=50, {\hat{k}}_{L}=10,{\bar{F}}_{1}=1.5\right]$

6 Conclusion

A general formulation of the WQEM with arbitrary element order is presented for an FG nonlocal nonlinear nanobeam based on Timoshenko beam theory. Eringen’s nonlocal elasticity was employed to capture size effects of the nanobeam, and a power-law function was utilized to model the material property distribution in the nanobeam. The use of DQ rule simplifies the implementation of the proposed WQEM elements and easily allows an increase in the element order, while the GLL mesh guarantees a significant integration accuracy. For the sake of generality, the formulation accounts for the nonlinear von Kármán strain as well as the contribution of the nonlinear elastic foundation.

The suitability and computational efficiency of the proposed quadrature elements for the vibration analysis of FG beams are demonstrated. A free vibration study was carried out for several mesh densities as well as a set of nonlinear configurations. The study shows an improved convergence rate compared to DQM. The free vibration results indicate that the proposed quadrature FG Timoshenko nonlinear nanobeam element is highly accurate and efficient. A study of the nonlinear free vibration of thick nanobeams revealed that the proposed element is shear locking free and can yield accurate solutions with a small number of nodes for both thin and moderately thick nanobeams. This approach offers the precision of high-order methods such as DQM without sacrificing the flexibility of variational methods such as FEM. In addition, due to the presence of von Kármán strain and the nonlinear foundation, high-order derivatives are required to evaluate accurately the system response. Such behavior is hard to capture using conventional low-order methods and high-order collocation methods can be used to overcome this problem. WQEM solves this by offering high-order accuracy in a variational method.

The study also aims to establish a standard procedure to solve forced vibration WQEM problems. In general, plotting FRCs using numerical methods is challenging due to limitations related to time integration and transient response. Various types of periodic time discretization are generally used which allows time to be treated similarly to a space dimension. However, it consequently adds an extra dimension to the computational problem. Generally DQM force vibration systems resort to Galerkin techniques to reduce the computational cost. To achieve a similar goal for WQEM problems, the authors proposed two different methods to reduce the number degrees of freedom of the WQEM system. The first approach replaces the Lagrange interpolation shape functions generally used in WQEM with mode shape-based functions. The second method utilizes a similar approach to the one used in DQM. Both methods were validated based on a previous DQM study performed by the authors. Despite the lower WQEM mesh density, the FRCs generated using either of these methods overlapped with the DQM FRCs. Obtaining FRCs generally requires that time is discretized like a space dimension which relatively adds a considerable computational cost. The fact that regardless of the approach, WQEM offers comparable results to DQM using a much smaller mesh and this highlights the accuracy and efficiency of WQEM.

Appendices

A DQM differentiation matrices appearing in Eq. (27)

$$\begin{aligned}{}[M_{m}]_{i,j}= & {} {\left\{ \begin{array}{ll} {{\Pi }\xi _{i}}/{\left( {\Pi }\xi _{j}\left[ \Delta \xi \right] {}_{i,j}\right) } &{} m=1,\;i {{\ne }}j\\ m\left( [M_{1}]_{i,j}[M_{m-1}]_{i,i}-\frac{[M_{m-1}]_{i,j}}{\left[ \Delta \xi \right] {}_{i,j}}\right) &{} m>1,\;i\ne j\\ -\sum _{k=1,k\ne i}^{n}[M_{m}]_{i,k} &{} m>0,\;i=j \end{array}\right. } \end{aligned}$$

(A.1)

where m is the order of the derivative and

$$\begin{aligned} \left[ \Delta \xi \right] {}_{i,j}= & {} \xi {}_{i}-\xi {}_{j},\;1\le i,j\le n\\ \Pi \xi _{i}= & {} \prod _{k=1,k{{\ne i}}}^{n}[\Delta \xi ]_{i,k},\;1\le i\le n \end{aligned}$$

B spectral method time differentiation matrices appearing in Eq. (43)

$$\begin{aligned} \left[ D_{\tau }^{(1)}\right] _{i,j} \quad =&{\left\{ \begin{array}{ll} 0 &{} i=j\\ 2\pi \left\{ \frac{1}{2}(-1)^{i-1}\cot \left( \frac{\pi }{n}(i-1)\right) \right\} &{} j=1\\ 2\pi \left\{ \frac{1}{2}(-1)^{n-j+1}\cot \left( \frac{\pi }{n}(n-j+1)\right) \right\} &{} i=1\\ {} [D_{\tau }^{(1)}]_{i+1,j+1}=[D_{\tau }^{(1)}]_{i,j} &{} i,j>1 \end{array}\right. } \end{aligned}$$

(B.1a)

$$\begin{aligned} \left[ D_{\tau }^{(2)}\right] _{i,j} \quad =&{\left\{ \begin{array}{ll} (2\pi )^{2}\left( -\frac{n^{2}}{12}-\frac{1}{6}\right) &{} i=j\\ (2\pi )^{2}\left\{ \frac{1}{2}(-1)^{i-1}\csc \left( \frac{\pi }{n}(i-1)\right) ^{2}\right\} &{} j=1\\ (2\pi )^{2}\left\{ \frac{1}{2}(-1)^{n-j+1}\csc \left( \frac{\pi }{n}(n-j+1)\right) ^{2}\right\} &{} i=1\\ {} [D_{\tau }^{(2)}]_{i+1,j+1}=[D_{\tau }^{(2)}]_{i,j} &{} i,j>1 \end{array}\right. } \end{aligned}$$

(B.1b)

C HQM time differentiation matrices appearing in Eq. (43)

$$\begin{aligned} \left[ H_{m}\right] _{i,j}&={\left\{ \begin{array}{ll} {{\Pi _{S}}\xi _{i}} / {\left( 2\left[ \Delta _{S}\xi \right] {}_{i,j} {{\Pi _{S}}}\xi _{j}\right) } &{} m=1,\; i{{\ne }}j\\ {[}H_{1}]_{i,j} \left( 2[H_{1}]_{i,i}-\left[ \Delta _{Ct}\xi \right] _{i,j}\right) &{} m{=}2,\; i {{\ne }}j \\ -\sum _{k=1,k\ne i}^{n}[H_{m}]_{i,k} &{} m>0,\; i=j \end{array}\right. } \end{aligned}$$

(C.1)

where

$$\begin{aligned} \left[ \Delta _{S}\xi \right] {}_{i,j}&=\sin \left( \frac{\xi {}_{i}-\xi {}_{j}}{2}\right) ,\;1\le i,j\le n\\ \left[ \Delta _{Ct}\xi \right] {}_{i,j}&=\cot \left( \frac{\xi {}_{i}-\xi {}_{j}}{2}\right) ,\;1\le i,j\le n\\ \Pi _{S}\xi _{i}&=\prod _{k=1,k{{\ne }}i}^{n}[\Delta _{S}\xi ]_{i,k},\;1\le i\le n \end{aligned}$$

These formulas are valid for a $2\pi$ periodic case. The derivative matrices $D_{\tau }^{(m)}$ for $x\in [0,1[$ are given by [76, 78]

$$\begin{aligned} D_{\tau }^{(m)}=(2\pi )^{m}H_{m} \end{aligned}$$

(C.2)