Abstract
A balance law for material momentum in shells and plates is proposed. The implications of this balance law for the propagation of defects, phase transformations, and shocks are explored. The developments are presented using a purely mechanical theory of a Cosserat (or directed) shell and specialized to the cases of a Kirchhoff–Love shell theory and a linearly elastic plate theory. To explore connections to the literature on delamination and adhesion, the balance law is applied to the problem of blistering.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Formulating the governing equations for elastic shells undergoing phase transformations, adhesion of a thin-walled structure to a substrate, blistering of an elastic sheet from a surface, and delamination of elastic shells are challenging problems with a wide range of applications. In these problems not only must the governing equations be solved in different regions of the elastic body, the complex conditions at the interface between the phases or adhered portions of the shell must also be formulated. When variational formulations of the governing equations are employed, then, following Eshelby’s [12, 13] celebrated practice, the first variation of the interface is used to establish jump conditions at the interface. For the problem of an elastic rod or shell adhering to a rigid substrate, the jump conditions produce an equation relating the interfacial work of adhesion \(w_\text {ad}\) to the jump in a complementary strain energy function (see, e.g., [25, 26, 36]). As emphasized in the aforementioned papers, this equation is also needed either to determine the adhered region or, if the region is known a priori, the conditions under which the bond can be broken.
In recent years, studies on related problems in the context of three-dimensional continuum mechanics [14, 20, 30, 41] and elastic rods [36] have found the use of a configurational (or material) force balance as a supplement to the traditional balance laws to be an attractive alternative to variational methods.Footnote 1 In these studies, the balance of material momentum is used to establish the interface conditions. Recent applications of this balance include a wide range of falling chain problems [36], the elastica arm scale [6, 35], sliding rods [4, 5], and adhered rods [16, 27, 28].
There is a large literature that employs a variational principle to establish interface conditions between phases of elastic shells and plates. We mention in particular Adams and Majidi’s works [25, 26] on adhesion and delamination of elastic shells, Pietraszkiewicz and coworker’s papers [10, 11, 29, 38] on phase transformations, Gioia and Ortiz’s work [15] on blistering of elastic plates from substrates, and Storåkers and Andersson’s work [43] on delamination. In some of these works, an expression for the energy–momentum tensor \(\mathbf{C}\) is presented. While some of these works contain tantalizing glimpses of a local balance law for material momentum balanceFootnote 2 or a jump condition for material momentumFootnote 3, a comprehensive treatment of a balance law for elastic shells and plates has not been presented in the literature. The present paper addresses this gap in the literature. In particular, a balance law for material (or configurational) momentum for elastic shells is proposed. The balance law reduces to a local form (cf. (6.6)) and a jump condition (cf. (6.7)) that holds at a point  , respectively:
, respectively:

As discussed in further detail in Sect. 6, \(\mathbf{p}\) is a material momentum, \(\mathbf{c}\) and \(\mathbf{C}^\beta \) are contact material forces that are related to an energy–momentum tensor \(\mathbf{C}\), \(\rho _0 \mathbf{b}\) is an assigned material force,  is a singular supply of material momentum, and \((\cdot )_{|,\beta }\) denotes a covariant derivative. In contrast to earlier works, we postulate expressions for \(\mathbf{C}\) and the associated material momentum \(\mathbf{p}\) that encompass situations where dynamic propagation occurs.
is a singular supply of material momentum, and \((\cdot )_{|,\beta }\) denotes a covariant derivative. In contrast to earlier works, we postulate expressions for \(\mathbf{C}\) and the associated material momentum \(\mathbf{p}\) that encompass situations where dynamic propagation occurs.
We commence our developments of a balance law in the context of a Cosserat theory of shells with a single director. This theory was developed by Naghdi and his coworkers [19, 31, 32] starting in the 1960s and continuing through the 1990s. In this theory, which we refer to as Green–Naghdi shell theory, the three-dimensional shell-like body is modeled as a material surface to which at each point a deformable vector, known as a director, \(\mathbf{d}_3\), is attached. The material surface, which is embedded in \({\mathbb {E}}^3\), and its associated director together comprise a directed surface \(\mathcal {S}\). The director in this theory is free to change its magnitude and its orientation relative to the tangent plane of the material surface. In the present paper, we supplement the balance laws for this theory with a balance of material momentum. Following standard practice, the local form of this balance law is assumed to be identically satisfied but the jump condition associated with the balance law provides an additional pair of equations that are often required to help form a determinate system of equations to solve for the motion of the shell. To accommodate a wide range of problems, we also incorporate singular supplies of angular momentum  , linear momentum
, linear momentum  , material momentum
, material momentum  , and energy
, and energy  into the Green–Naghdi shell theory. A point load acting at a point on a shell is a common example of a situation where linear and director momenta supplies are present. Paralleling the situation in other theories of deformable media [33, 34], the supplies are not independent and can be shown to satisfy a pair of identities (cf. (5.9) and (8.1)).
into the Green–Naghdi shell theory. A point load acting at a point on a shell is a common example of a situation where linear and director momenta supplies are present. Paralleling the situation in other theories of deformable media [33, 34], the supplies are not independent and can be shown to satisfy a pair of identities (cf. (5.9) and (8.1)).
There are several works on shell theory, including [18, 31, 32], that discuss specialized theories of shells as special cases of Green–Naghdi shell theory and their relation to other shell theories including the popular theory proposed by Simmonds and Danielson [40]. The classic Kirchhoff–Love shell theory can be obtained from Green and Naghdi’s theory by imposing constraints and introducing corresponding constraint responses or as a restricted theory (cf. [31, Section 10]). For the Kirchhoff–Love shell theory, the director is assumed to have a unit magnitude and to remain normal to the material surface in its present configuration. A recent paper by Steigmann [42] is the first to present a development of how the governing equations for Kirchhoff–Love shell theory can be obtained from the Green–Naghdi theory by imposing constraints and introducing constraint forces. Steigmann’s arguments are detailed and delicate. We follow his developments, albeit with one significant difference, in the present paper when we formulate a balance of material momentum for a Kirchhoff–Love shell theory. The treatment is then simplified to the case of a linearly elastic plate in Sect. 10 of the paper.
The present paper complements earlier work by Makowski et al. [29] who discussed jump conditions for linear and angular momentum in the context of Kirchhoff–Love shells. We can also extend our developments to the shell theory developed by Simmonds and Danielson [40] and used by Pietraszkiewicz and coworkers [11, 38]. In Simmonds and Danielson’s theory, the deformation of the shell is characterized by the displacement of a point on the material surface and a rotation tensor that is associated with this point. It is straightforward to apply our work to theories of elastic plates that are often used to explore problems of the blistering of elastic sheets on rigid substrates [15, 17, 26, 43]. Indeed, in the closing Section of the paper, Sect. 11, we explore how the jump condition (9.30) from the material momentum balance law and an identity (9.20) relating the supplies of energy can be used to characterize problems where shells and plate-like structures are adhered to rigid surfaces. Our developments in this respect are related to work on the adhesion of rods [24, 27, 34, 36].
2 Preliminary developments
We consider a material surface for which a deformable vector field, or director, is associated with each material point P. The surface, which is embedded in \({\mathbb {E}}^3\), and the associated director field are known as a directed or Cosserat surface \(\mathcal {S}\). The material points of \(\mathcal {S}\) are uniquely identified by a pair of convected coordinates: \(\left( \theta ^1, \theta ^2\right) \). We assume that \(\mathcal {S}\) occupies the region \(\mathcal {R}_0 \in {\mathbb {E}}^3\) in its fixed reference configuration and \(\mathcal {R}\in {\mathbb {E}}^3\) in its current configuration. As illustrated in Fig. 1, the configurations are bounded by closed curves: \(\partial \mathcal {R}_0\) and \(\partial \mathcal {R}\), respectively.
Schematic of the reference and present configurations of a directed surface \(\mathcal {S}\) that is embedded in \({\mathbb {E}}^3\). The covariant basis vectors \(\mathbf{a}_1 = \mathbf{r}_{,1}\) and \(\mathbf{a}_2 = \mathbf{r}_{,2}\), the director \(\mathbf{d}_3\) at a point P of \(\mathcal {S}\) in the present configuration, and the Cartesian basis vectors \(\left\{ \mathbf{E}_1, \mathbf{E}_2, \mathbf{E}_3\right\} \) are also shown
The position vector of a material point in the present configuration relative to a fixed origin O is denoted by \(\mathbf{r}\), and the director is denoted by \(\mathbf{d}_3\). Both of these quantities are vector-valued functions of time t and the convected coordinates. The vector \(\mathbf{d}_3\) is free to change its orientation relative to the material surface and its length. The associated velocity vectors are
where the superposed dot denotes the material time derivative. The corresponding position vector relative to a fixed origin O and director in the fixed reference configuration are denoted by \(\mathbf{R}\) and \(\mathbf{D}_3\) and are functions of the convected coordinates only.
Covariant \(\left\{ \mathbf{d}_i\right\} \) and contravariant \(\left\{ \mathbf{d}^k\right\} \) bases can be defined where
Here, and in the sequel, lower-case Latin indices range from 1 to 3, lower-case Greek indices range from 1 to 2, and \(\mathbf{r}_{,\alpha }\) denotes the partial derivative of the function \(\mathbf{r}\) with respect to \(\theta ^\alpha \): \(\mathbf{r}_{,\alpha } = \frac{\partial \mathbf{r}}{\partial \theta ^\alpha }\). The following triple product is assumed to be strictly positive:
The summation convention on repeated indices will be used in the sequel. We note that \(\mathbf{d}^i\cdot \mathbf{d}_k = \delta ^i_k\), where \(\delta ^i_k\) is the Kronecker delta. Companion sets of vectors \(\left\{ \mathbf{D}_i\right\} \) and \(\left\{ \mathbf{D}^i\right\} \) can be defined for the reference configuration.
The tangent space to a point P of the material surface in the present configuration is spanned by the vectors \(\mathbf{d}_\alpha \). The unit normal vector \(\mathbf{n}\) can be defined by the identity
For future reference we define the basis \(\left\{ \mathbf{a}_i\right\} \) and its dual \(\left\{ \mathbf{a}^k\right\} \):
where \(\sqrt{a} = \left( \mathbf{a}_1\times \mathbf{a}_2\right) \cdot \mathbf{n}\). The bases \(\left\{ \mathbf{A}_1, \mathbf{A}_2, \mathbf{A}_3= \mathbf{n}_0\right\} \) and \(\left\{ \mathbf{A}^1, \mathbf{A}^2, \mathbf{A}^3 = \mathbf{n}_0\right\} \) associated with the material point P in the reference configuration of the material surface can be defined in an identical manner. We note that \(\mathbf{A}^i\cdot \mathbf{A}_k = \delta ^i_k\).
Consider a curve \(\mathcal {C}\) on the directed surface \(\mathcal {S}\) (cf. Fig. 2). The unit tangent vector  and unit normals
and unit normals  and \(\mathbf{n}_0\) to the curve in the reference configuration have the following representations:
and \(\mathbf{n}_0\) to the curve in the reference configuration have the following representations:

It is important to note that  lies in the tangent plane:
lies in the tangent plane:  . The unit tangent vector and unit normal vectors to a curve \(\mathcal {C}\) on \(\mathcal {S}\) in the present configurations have the representations
. The unit tangent vector and unit normal vectors to a curve \(\mathcal {C}\) on \(\mathcal {S}\) in the present configurations have the representations

For the shell theory being considered at this stage in the paper, neither \(\mathbf{n}_0\) and \(\mathbf{D}_3\) nor \(\mathbf{n}\) and \(\mathbf{d}_3\) are necessarily assumed to be equal. In particular, situations where \(\mathbf{d}_3\cdot \mathbf{a}^\alpha \ne 0\) and \(\mathbf{D}_3\cdot \mathbf{A}^\alpha \ne 0\) are accommodated.
For future reference, a trio of tensors \(\mathbf{F}_a\), \(\mathbf{F}\), and \(\mathbf{G}\) can be defined as follows [7, 11, 32]:
We note that \(\mathbf{F}_{a}{} \mathbf{D}_\beta = \mathbf{d}_\beta \) and \(\mathbf{F}_a\mathbf{A}_3 = \mathbf{0}\) while \(\mathbf{F}{} \mathbf{D}_i = \mathbf{d}_i\). In addition, \(\mathbf{G}{} \mathbf{A}_\beta = \frac{\partial \mathbf{d}_3}{\partial \theta ^\beta }\) and \(\mathbf{G}{} \mathbf{A}_3 = \mathbf{0}\).
The linear momentum \(\mathbf{g}_l\), director momentum \(\mathbf{g}_d\), angular momentum relative to a point O \(\mathbf{H}_O\), and kinetic energy T of the directed surface per unit area in the reference configuration are
Here, \(\rho _0 = \rho _0\left( \theta ^\beta \right) \) is the mass density per unit area, \(y^\beta = y^\beta \left( \theta ^\alpha \right) \) are inertia coefficients. Prescriptions for \(\rho _0\) and \(y^\beta \) in terms of quantities associated with the three-dimensional body the directed surface is modeling can be found in [31, 32].
3 The interface
Our developments will encompass situations where there will be singular supplies of momenta and energy at sets of discrete locations on the material surface. These sources will induce discontinuities in contact forces and momenta. To establish the framework needed to accommodate these situations, we consider a directed material curve on \(\mathcal {S}\). This curve is defined by the pair of functions
and is denoted by \(\Gamma _0\) in the reference configuration and \(\Gamma \) in the present configuration. In the sequel, we shall use the notation  to denote the material point \(\left( \theta ^1, \theta ^2\right) = \left( \gamma ^1, \gamma ^2\right) \). The position vectors of material points and their associated directors on \(\Gamma _0\) and \(\Gamma \), respectively, are defined by
to denote the material point \(\left( \theta ^1, \theta ^2\right) = \left( \gamma ^1, \gamma ^2\right) \). The position vectors of material points and their associated directors on \(\Gamma _0\) and \(\Gamma \), respectively, are defined by

We are assuming that \(\mathbf{r}\) and \(\mathbf{d}_3\) are continuous across the interface. Thus, \(\Gamma \) and \(\Gamma _0\) are coherent interfaces.
The curves \(\Gamma _0\) (and by extension \(\Gamma \)) are allowed to propagate along the directed material surface (see Fig. 3). Associated with \(\Gamma _0\), we define the velocity vectors

In the present configuration, we need to allow for the possibility of discontinuities. Thus,

We have used the standard notation for a function \(f = f\left( \theta ^\alpha ,t\right) \) in the previous relations:
where \(\sigma _1 > 0\) and \(\sigma _2 > 0\). For future reference,

denotes the jump in f at the material point  .
.
Two well-known compatibility conditions follow from (3.4):

4 Balance laws: general considerations
We recall from Naghdi (cf.[31, Eq. (8.58), Section 8] or [32, Eqs. (3.16)–(3.17)]) the canonical form for a balance law for a directed (or Cosserat) surface whose material surface occupies a region \(\mathcal {P}_0\) with a boundary \(\partial \mathcal {P}_0\) and an interface \(\Gamma _0\) in the reference configuration:
In this equation, \(\mathsf {a}\), \(\mathsf {b}\), \(\mathsf {c}\), \(\mathsf {d}\), and  are vector-valued functions of \(\theta ^\beta \) and t, \(\mathrm{d}S\) is the line-element, \(d\Sigma \) is the area element,
are vector-valued functions of \(\theta ^\beta \) and t, \(\mathrm{d}S\) is the line-element, \(d\Sigma \) is the area element,
and \(\hat{\delta }\) denotes the product of two Dirac delta functions:
The balance law is described in terms of quantities measured in a reference configuration.Footnote 4
We assume that the balance laws hold for all possible \(\mathcal {P}_0\) of \(\mathcal {S}\). A standard argument (see, e.g., [3, Chapter 17], [21], or [31, Section 9]) can then be used to show that
where the components of the unit normal vector to the curve \(\partial \mathcal {P}_0\) have the representations  . Assuming that the region \(\mathcal {P}_0\) is free of discontinuities and singular supplies (i.e.,
. Assuming that the region \(\mathcal {P}_0\) is free of discontinuities and singular supplies (i.e.,  ), application of Stokes’ theorem to (4.1) can be used to show that
), application of Stokes’ theorem to (4.1) can be used to show that
where the surface divergence operator \(\text{ Div}_s\) can also be identified with the covariant derivative:
In the sequel, we denote the covariant derivative of a vector-valued function \(\mathbf{x}\) using a |:
To establish the conditions that hold at a discontinuity or defect, we consider a region \(\mathcal {P}_0\) that contains an interface \(\Gamma \). We divide \(\mathcal {P}_0\) into two regions and \(\partial \mathcal {P}_0\) into two curves:
The boundaries of the regions \(\Omega ^-\) and \(\Omega ^+\) are
Reynolds’ transport theorem can be used to show that the material time derivative of the integral of \(\mathsf {a}\) over \(\mathcal {P}_0\) has the representation

where  is the normal component of the velocity of \(\Gamma _0\):
is the normal component of the velocity of \(\Gamma _0\):

Application of Stokes’ theorem and Reynolds’ transport theorem (4.10) to the balance law (4.1) for each of \(\Omega ^{+}\) and \(\Omega ^{-}\), followed by an application of (4.5), and the representation (4.4) produce the jump conditionFootnote 5

that holds at every point \(\gamma \in \Gamma _0\).
5 Balance laws for an elastic shell
For a theory of an elastic Cosserat shell, the strain energy function \(\rho _0 \psi \) is assumed to be a function of the surface geometry and the director:
The standard assumption that \(\rho _0\psi \) is invariant under superposed rigid body motions of the directed surface is adopted in the sequel. For the directed surface, seven balance laws are postulated: balances of mass and two inertias, a balance of linear momentum, a balance of director momentum, a balance of angular momentum, and a balance of energy.
The local form of the balances of mass and inertia implies that the mass density \(\rho _0\) and inertia coefficients \(y^\beta \) are independent of time:
where \(\rho \) is the mass density per unit area of \(\mathcal {S}\) in the present configuration. The local forms of the remaining four balance laws are
In these equations, \(\rho _0 \psi \) is the strain-energy density function, \({}_0\mathbf{N}^\beta \) are contact forces, \( {}_0 \mathbf{M}^\beta \) are contact director forces, \({}_0 \mathbf{k}\) is an intrinsic director force, \(\rho _0 \mathbf{f}\) is an assigned force, and \(\rho _0 \mathbf{l}\) is an assigned director force. We have expressed the local form of the balance of angular momentum (i.e., (5.3.1)) as a statement that the tensor \(\mathbf{T}\) is symmetric:
where
and
The local form of the balance of energy (5.3.4) is an identity that provides constitutive relations for the contact force  , intrinsic director force \({}_0\mathbf{k}\), and contact director force
, intrinsic director force \({}_0\mathbf{k}\), and contact director force  :
:
It can be shown that if \(\rho _0 \psi \) is properly invariant under superposed rigid body motions, then the local form of the balance of angular momentum (5.3.3) is identically satisfied. The local forms of the balances of linear (5.3.1) and director momentum (5.3.2) then provide a set of six scalar partial differential equations for \(\mathbf{r}\) and \(\mathbf{d}_3\).
The discontinuities we are considering include ones that are induced by possible singular supplies of linear momentum  , director momentum
, director momentum  , moment of momentum
, moment of momentum  , and energy
, and energy  at a material point
at a material point  . In the presence of these supplies, by paralleling the arguments presented in Sect. 4, the jump conditions associated with the balances of mass, inertia, linear momentum, director momentum, moment of momentum, and energy can be established:
. In the presence of these supplies, by paralleling the arguments presented in Sect. 4, the jump conditions associated with the balances of mass, inertia, linear momentum, director momentum, moment of momentum, and energy can be established:





As we are assuming that \(\mathbf{r}\) and \(\mathbf{d}_3\) are continuous across the discontinuity (and have the respective values  and
and  ), the jump condition associated with the balance of moment of momentum (5.8.6) reduces to an identity with the help of (5.8.4, 5.8.5):
), the jump condition associated with the balance of moment of momentum (5.8.6) reduces to an identity with the help of (5.8.4, 5.8.5):

where the moment relative to  ,
,  , is identified with the moment due to the singular supply of director momentum
, is identified with the moment due to the singular supply of director momentum  :
:

The reduction to the identity (5.9) parallels the situation in theories of rods [36] and 3-dimensional continua [33]. The jump conditions from the balances of mass and inertia (5.8.1-3) are identically satisfied either if \(\rho _0\) and \(\rho _0y^\beta \) are continuous or the jump is stationary, i.e.,  .
.
6 Balance of material momentum
In postulating a balance law for material momentum in shells, we are guided by developments in 3-dimensional continua [20, 30], elastic rods [34, 36], and works on the energy–momentum tensor in shells [10, 11] and plates [15, 43]. We define a contact material force \(\mathbf{c}\), an assigned contact force \(\rho _0\mathbf{b}\), a singular supply of material momentum  , and a material momentum \(\mathbf{p}\). The balance of material momentum is
, and a material momentum \(\mathbf{p}\). The balance of material momentum is

Here,
A standard argument (cf., (4.4)) can be used to show that
Concomitant with this result, the energy momentum tensor \(\mathbf{C}\), where  , is prescribed as
, is prescribed as
Thus,
For static problems in continuum mechanics, the prescription for the contact material force \(\mathbf{c}\) or, equivalently, the energy momentum tensor \(\mathbf{C}\) is motivated by a variational principle. Often as a result, the tensor will include a contribution from the potential energy of the assigned forces.Footnote 6 Here, we have chosen not to include this potential energy in our prescription for \(\mathbf{C}\).
The balance law (6.1) can be shown to be equivalent to the following local form:
and a jump condition

It follows from this condition that  has the representation
has the representation

As discussed in [33, 34], the singular supply of material momentum  can be identified with Abeyaratne and Knowles’ driving traction [1, 2].
can be identified with Abeyaratne and Knowles’ driving traction [1, 2].
If we were to employ a variational principle in an attempt to establish (6.7), then, following the methods used in [11] in the context of a different shell theory, we would arrive at the jump conditionFootnote 7

This jump condition is equivalent to (6.7), if  , T, and \(\mathbf{p}\) are all set to zero.Footnote 8
, T, and \(\mathbf{p}\) are all set to zero.Footnote 8
7 Additional comments on the local form of the balance of material momentum
The local forms of the energy and moment of momentum balance laws (cf. (5.3.3, 5.3.4)) are identically satisfied by the constitutive relations for \({}_0\mathbf{n}\), \({}_0\mathbf{k}\), and \({}_0\mathbf{m}\). In a similar manner, we follow [20, 30, 34], assume that the local form of the balance of material momentum (6.6) is identically satisfied and prescribe the assigned material force \(\rho _0 \mathbf{b}\) accordingly.
To arrive at the prescription for \(\rho _0 \mathbf{b}\), we substitute for \(\dot{\mathbf{p}}\) and \(\mathbf{C}^\beta \) using (6.2) and (6.4) in (6.6) and solve for
After some manipulations, we arrive at the following prescription for \(\rho _0 \mathbf{b}\):
Observe that if there are no assigned forces and assigned director forces, and the reference configuration is homogeneous, then the assigned material force will vanish: \(\rho _0 \mathbf{b} = \mathbf{0}\). In addition, for static situations, \(\dot{\mathbf{p}} = \mathbf{0}\), and the local form of the material momentum balance yields a conservation law for the energy momentum tensor: \(\text{ Div}_s\left( \mathbf{c}\right) = \mathbf{C}^\beta _{|\beta } = \mathbf{0}\). That is, the contact material force in this case is a divergence-free vector field throughout \(\mathcal {S}\).
If the prescription (6.4) for \(\mathbf{C}\) were to contain a contribution \(U \mathbf{A}^\beta \otimes \mathbf{A}_\beta \) where \(U = U\left( \mathbf{r}, \mathbf{d}_3, \theta ^\beta \right) \) is the potential energy of the conservative assigned forces and assigned director forces, then the prescription (7.2) for \(\rho _0 \mathbf{b}\) would change in a manner that is straightforward to compute. If  and
and  both vanish, then we anticipate that
both vanish, then we anticipate that  , and thus the jump condition (6.7) would be unaffected by the addition of the term \(U \mathbf{A}^\beta \) to \(\mathbf{C}^\beta \).
, and thus the jump condition (6.7) would be unaffected by the addition of the term \(U \mathbf{A}^\beta \) to \(\mathbf{C}^\beta \).
8 An identity for the supply of energy
In addition to the identity (5.9) for the source of moment of momentum  , it can be proven that the source terms
, it can be proven that the source terms  ,
,  ,
,  , and
, and  also satisfy an identity:
also satisfy an identity:

The shock speeds  ,
,  , and
, and  were defined previously in (3.3) and (3.4).
were defined previously in (3.3) and (3.4).
The identity (8.1) has counterparts in a theory of a thermomechanical continuum [33] and in theories of rods and strings [34]. For all of these cases, the identity clearly identifies the conjugate velocity associated with the singular supply. Thus, the singular supply \(\mathbf{B}_\gamma \) of material momentum is work conjugate to the referential speed of the discontinuity \(\mathbf{V}_\gamma \). For applications to blister formation or delamination, the identity can also be used to classify the energy release rate associated with propagation of a singularity. Thus, a discontinuity is dissipative if \(\Phi _{E_\gamma } < 0\) and energy conserving if \(\Phi _{E_\gamma } = 0\).
To establish (8.1), we start by computing  :
:

Substituting for \(\mathbf{p}\) and \(\mathbf{C}\) using (6.2) and (6.4), the identitiesFootnote 9

and invoking the jump conditions for linear momentum and director momentum (cf. (5.8.4, 5.8.5)), we find that

Thus, the identity is established. We observe that we invoked the jump condition for energy (5.8.7) in the penultimate step.
9 Application to Kirchhoff–Love shell theory
For the Kirchhoff–Love shell theory, the director \(\mathbf{d}_3\) is constrained to be the unit normal vector to the directed material surface: \(\mathbf{d}_3 = \mathbf{n}\). The balance laws and constitutive relations for this popular theory can be postulated as an independent theory (also known as a restricted theory in [31, Sects. 10 and 15] or as a constrained version of the shell theory discussed previously). In this Section of the paper, we follow the treatment presented in Steigmann [42] and pursue the latter approach. Our discussion will focus on the role played by the balance of material momentum for Kirchhoff–Love shell theory. It will also become apparent from our developments that the balance law for material momentum can also be postulated rather than derived by imposing constraints on a more general theory.
As the director \(\mathbf{d}_3 = \mathbf{n}\) in the Kirchhoff–Love shell theory: \(\mathbf{n}\cdot \mathbf{a}_\alpha = 0\). We find the Weingarten relations by differentiating this pair of identities:
As \(\mathbf{a}_{\beta ,\alpha } = \mathbf{r}_{, \beta \alpha } = \mathbf{r}_{, \alpha \beta } = \mathbf{a}_{\alpha ,\beta }\), these relations imply that
These identities will be helpful in the sequel when bending strains are introduced.
Several simplifications in the kinematics of the more general theory follow from the constraints \(\mathbf{d}_3 = \mathbf{n}\). A rotation tensor \(\mathbf{Q}\) can be defined where
As a result, the derivatives of the director can be represented using axial vectors:

Here,

where, for any skew-symmetric tensor \(\mathbf{B}\), the axial vector \(\text{ ax }\left( \mathbf{B}\right) \) is a unique vector \(\mathbf{B}{} \mathbf{a} = \text{ ax }\left( \mathbf{B}\right) \times \mathbf{a}\) where \(\mathbf{a}\) is any vector.
At a point of discontinuity where  vanishes, the angular speed
vanishes, the angular speed  can be defined by differentiating \(\mathbf{Q}\left( \gamma ^1,\gamma ^2, t\right) \):
can be defined by differentiating \(\mathbf{Q}\left( \gamma ^1,\gamma ^2, t\right) \):

The expressions for  enable us to show that the compatibility condition (3.7.2) is equivalent to
enable us to show that the compatibility condition (3.7.2) is equivalent to

The kinetic energy and material momentum for the Kirchhoff–Love shell have representations that can be found from the more general theory by substituting for \(\mathbf{w}\) and \(\mathbf{d}_{3,\beta }\) in (2.9.4) and (6.2), respectively:

where the inertia tensor
To avoid any confusion where it may occur, we ornament quantities with the subscript \(\text {KL}\) to distinguish a quantity from its counterpart in the more general theory. The assigned force acting on the shell is \(\rho _0 \mathbf{f}\). For the Kirchhoff–Love theory, it is convenient to define an assigned moment \(\mathbf{m}_a\) using the assigned director force \(\rho _0 \mathbf{l}\):
9.1 Constraints and constitutive relations
For the Kirchhoff–Love theory, the director \(\mathbf{d}_3\) is identified with the unit normal vector \(\mathbf{n}\). Thus, the director is subject to three constraints:
where
By taking the partial derivatives of these constraints, it can be shown that Eqs. (9.12) imply that
The strain energy function of the shell \(\rho _0 \psi _\text {KL}\) is a function of 6 strains:
where the strains
The strains \(C_{\alpha \beta }\) are synonymous with stretching of \(\mathcal {S}\) and are known as the membrane strains. The strain measures \(K_{\alpha \beta }\) are associated with bending of \(\mathcal {S}\).
While we are closely following Steigmann’s developments in [42], we only impose three constraints on the directed shell in contrast to the six constraints imposed in his work.Footnote 10 In this respect, we are paralleling work by O’Reilly and Turcotte [37] who showed how Kirchhoff–Love rod theory can be obtained as a constrained theory from a rod theory developed by Green and Naghdi.
9.2 The balance of energy and constitutive relations
The local form of the balance of energy (5.3.4) is assumed to be identically satisfied for all motions of the shell that satisfy the constraints (9.12). Referring to Steigmann [42], the constitutive relations for \({}_0\mathbf{N}^\alpha \), \({}_0\mathbf{M}^\beta \), and \({}_0\mathbf{k}\) can be additively decomposed into constraint responses (involving Lagrange multipliers \(\lambda ^1\), \(\lambda ^2\), and \(\lambda ^3\)) that are needed to enforce the constraints (9.12) and a piece involving the derivatives of the strain energy function \(\rho _0 \psi _\text {KL}\):
where \(\sqrt{A} \varepsilon ^{\beta \alpha } = e^{\beta \alpha }\),
and
We shall see in the sequel that the Lagrange multipliers \(\lambda ^\alpha \) are ultimately responsible for the contact director force \({}_0\mathbf{M}^\alpha \nu _{0_\alpha }\) (and the bending strains) appearing in the governing partial differential equation for Kirchhoff–Love shells and plates (cf. (9.25) and (10.11), respectively).
In most treatments of Kirchhoff–Love shell theory, the contact director force \({}_0\mathbf{M}^\alpha \nu _{0_\alpha }\) is rarely discussed. Instead, the contact moment \({}_0\hat{\mathbf{M}}^\alpha = \mathbf{n}\times {}_0\mathbf{M}^\alpha \) is used:
where we used the cross products (2.5) to simplify the final expression.
The jump condition (5.8.7) that is found from the balance of energy is identically satisfied by the identity (8.1) for the power of the supplies. Using the definition of the singular supply  where
where  is the unit normal vector at the material point
is the unit normal vector at the material point  , and the speed
, and the speed  (cf. (9.6)), the identity can be expressed in the form
(cf. (9.6)), the identity can be expressed in the form

As an application of this identity, consider a moving load problem where a point load \(\mathbf{R}_a\) is applied to a time-varying sequence of points  on a shell. In the absence of a phase transformation, then
on a shell. In the absence of a phase transformation, then  is the mechanical power supplied to the shell by the moving load.
is the mechanical power supplied to the shell by the moving load.
9.3 The balance of director momentum
As discussed in [42], and paralleling [37], the local form of the balance of director momentum (5.3.2) can be used to solve for the Lagrange multipliers:
where  .
.
From the constitutive relations (9.16.2) for \({}_0 \mathbf{M}^\alpha \) we note that this pair of vectors has no components in the normal direction. Thus, with the help of (9.19) the jump condition for director momentum (cf. (5.8.5) can be expressed as a pair of equations,


These jump conditions can be used for a variety of purposes. For instance, consider a static problem and suppose that a couple is applied at a point  on the boundary of a shell. Then, (9.22.1) can be used to show that
on the boundary of a shell. Then, (9.22.1) can be used to show that  .
.
9.4 The balance of moment of momentum
Paralleling related developments in theories of constrained rods [37] and three-dimensional continua [8], the invariance under superposed rigid body motions of the constraints \(\varphi _{1} = 0\), \(\varphi _2 = 0\), and \(\varphi _3 = 0\) and the strain energy function \(\rho _0 \psi _\text {KL}\) implies that the local form of the balance of angular momentum (5.3.3) is identically satisfied. To verify this result, we substitute (9.16.1-3) for \({}_0\mathbf{N}^\alpha \), \({}_0\mathbf{M}^\alpha \), and \({}_0\mathbf{k}\) into the left-hand side of (5.3.3),
and then impose the constraints \(\varphi _{1} = 0\), \(\varphi _{2} = 0\), and \(\varphi _3 = 0\). The vanishing of (9.23), which implies the identical satisfaction of (5.3.3), then follows. The jump condition associated with the balance of moment of momentum was shown earlier to reduce to (5.9). As with the more general theory, the jump condition (5.9) for Kirchhoff–Love shell theory is an identity relating the resultant supply of angular momentum relative to O as a linear combination of the moment of supply of linear momentum  and the supply of angular momentum relative to the material point
and the supply of angular momentum relative to the material point  .
.
9.5 The balance of linear momentum
To explore the local form of the balance of linear momentum (5.3.1), we first note that the contact forces \({}_0\mathbf{N}^\beta \) contain constraint responses (cf. (9.16.1-3)):
With the help of (9.21), the underbraced terms are equal to \(\left( {}_0\bar{\mathbf{M}}^\beta _{| \beta } + \rho _0 \mathbf{l} - \dot{\mathbf{g}}_d \right) \cdot \mathbf{a}^\alpha \). Whence, the local form of the balance of linear momentum reduces to the following set of partial differential equations for \(\mathbf{r}\):
This form of the balance of linear momentum is reassuringly free from Lagrange multipliers. Given that the Kirchhoff–Love shell theory can also be postulated as a restricted theory, this result is anticipated.Footnote 11
The jump condition for linear momentum (5.8.4) can be expressed in the form:

where \(\lambda _\alpha = \left( {}_0\bar{\mathbf{M}}^\beta _{| \beta } + \rho _0 \mathbf{l} - \dot{\mathbf{g}}_d \right) \cdot \mathbf{a}^\alpha \). As anticipated, this jump condition is free of Lagrange multipliers. The condition can be used for a variety of purposes including the determination of the speed of propagation of shock waves and boundary conditions associated with points on the boundary of the shell where point loads are applied.
9.6 The balance of material momentum
The expressions for the material momentum \(\mathbf{p}_\text {KL}\) and kinetic energy \(T_\text {KL}\) for the Kirchhoff–Love shell were described previously (cf. (9.8)). The expression for the contact material force \(\mathbf{C}\) can be obtained from the general representation (6.4) by substituting for the kinetic energy \(T_\text {KL}\) and the constitutive relations for \({}_0\mathbf{N}^\alpha \), \({}_0\mathbf{M}^\alpha \), and \({}_0\mathbf{k}\) that are presented in (9.16.1-3). After some work, we find that
where
We used the definitions of \(C_{\alpha \beta }\) and \(K_{\alpha \beta }\) to arrive at the final expression for the contact material force component. It is interesting to note that the Lagrange multipliers are absent from the final representation for \(\mathbf{C}^\beta _\text {KL}\).
The local form of the balance of material momentum is assumed to be identically satisfied with the help of the prescription for the applied material force \(\rho _0 \mathbf{b}\). With the help of (9.10) and (9.16.1-3), it can be shown that the prescription (7.2) simplifies to

As anticipated from our discussion of the contact material force, the Lagrange multipliers are absent from the prescription for the applied material force \(\rho _0 \mathbf{b}_\text {KL}\). As a result, if we were to consider Kirchhoff–Love shell theory as a restricted theory (in the sense used in [31]), then a balance law for material momentum can be postulated without reference to the more general theory.
The jump condition for material momentum for the Kirchhoff–Love shell theory can be inferred from (6.7):

As in the general case, this jump condition can be used to determine \(\dot{\gamma }^1\) and \(\dot{\gamma }^2\) or, in the event that  , the change in the material contact force
, the change in the material contact force  due to a supply of material momentum
due to a supply of material momentum  . This jump condition can also provide the adhesion boundary conditions in the event that the shell is adhering to a rigid surface using a dry adhesive force. As discussed in [11] in the context of a different shell theory, the projection of (9.30) with
. This jump condition can also provide the adhesion boundary conditions in the event that the shell is adhering to a rigid surface using a dry adhesive force. As discussed in [11] in the context of a different shell theory, the projection of (9.30) with  onto
onto  can be used to determine the static location of the axisymmetric interface between two phases of a circular plate containing a hole and of infinite extent. Without this jump condition, determining the location of the interface would not be possible.
can be used to determine the static location of the axisymmetric interface between two phases of a circular plate containing a hole and of infinite extent. Without this jump condition, determining the location of the interface would not be possible.
10 Application to Kirchhoff–Love plate theory
In the simplest version of Kirchhoff–Love plate theory, the material surface is assumed to be inextensible, and transverse shearing is constrained to vanish. Here, we consider a circular plate of thickness h that is flat in its reference configuration. We employ a set of convected coordinates to parameterize the material points of the plate. Because the displacement of the plate is assumed to be \(O\left( \epsilon \right) \), the convected coordinates are identified with a set of cylindrical polar coordinates \(\left( r, \vartheta , z\right) \) for \({\mathbb {E}}^3\).
The sole displacement \(u = O\left( \epsilon \right) \) of the material points of the directed surface that is used to model the plate is assumed to be in the \(\mathbf{E}_3\) direction:
where \(u = u\left( r, \vartheta , t\right) \),
For future reference,
For the reference configuration, we find that
It follows that \(\sqrt{A} = r\) and \(\sqrt{a} = r + O\left( \epsilon \right) \). In the sequel we expand all expressions to first order in \(\epsilon \) unless stated otherwise.
For this theory, the strains \(C_{\alpha \beta }\) all vanish, and the strains \(K_{\alpha \beta }\) are the components of the following symmetric tensor \(\mathbf{K}\):
We observe that the trace of \(\mathbf{K}\) is related to the Laplacian of u: \(\nabla ^2 u = - \text{ tr }\left( \mathbf{K}\right) = - K_{11} - K_{22}/r^2\).
The strain energy function and kinetic energy functions of the plate are
where D is the flexural rigidity. Thus, for the plate we are assuming that \(y^1 = y^2 = 0\). As with the Kirchhoff–Love shell theory, to avoid any confusion where it may occur, we ornament quantities with the subscript \(\text {P}\) to distinguish a quantity from its counterpart in more general theories.
To obtain the constitutive relations for \({}_0\mathbf{N}^\beta \), \({}_0\mathbf{M}^\alpha \), and \({}_0\mathbf{k}\), we can start with the constitutive relations (9.16.1-3) for a Kirchhoff–Love shell and then impose three additional constraints:
These constraints will introduce Lagrange multipliers \(\lambda ^7\), \(\lambda ^8\), and \(\lambda ^9\) into the constitutive relations. Paralleling our earlier developments, we find with the help of (10.6) that
and
where
For the plate theory of interest, the plate is assumed to be sufficiently thin that the assigned director force \(\rho _0 \mathbf{l}\) and momentum \(\dot{\mathbf{g}}_d\) vanish to second order in \(\epsilon \).
To establish the well-known governing equation for the plate, we consider the local form of the balance of linear momentum for the shell (cf. (9.25)), introduce the aforementioned approximations for the forces and momenta, and compute the normal component of
After some lengthy, but straightforward calculations, we find the following well-known equation for u:
where \(\nabla ^4\) is the biharmonic operator.
The expression for the material momentum of the plate can be computed with the help of (9.8). To first order we find that
The expression for the contact material forces \(\mathbf{C} = \mathbf{C}^\beta _\text {P}\otimes \mathbf{A}_\beta \) can be found with the help of (9.27). In the interests of brevity, we simply state the final results:
This completes the development of this classic plate theory as a constrained Kirchhoff–Love shell.
It is a straightforward exercise to use the expressions for \(\mathbf{C}^\beta \) in conjunction with (9.29) to arrive at a prescription for the assigned contact force \(\rho _0 \mathbf{b}_\text {P}\) that will identically satisfy the local form of the balance of material momentum. The jump condition for material momentum for the plate is simpler than that for a shell because the material momentum can be ignored:

As we shall demonstrate with the help of an application in Sect. 11, a restricted form of this jump condition can be obtained from a variational principle.
11 Insights from studies on the propagation of blisters
While the presentation of an explicit balance law for material momentum for shells has not appeared previously in the literature, several earlier works on delamination in composite plates and the formation of blisters [15, 43] use an energy–momentum tensor to determine energy release rates. Other works, such as [25, 26], have discussed the presence of a singular moment at the adhesion interface of a shell-like structure with a substrate. We now explore how these earlier works are precursors to the balance law presented in the current paper. Referring to Fig. 4, we commence with a blister test proposed by Williams [45, 46].
Schematic of a directed surface \(\mathcal {S}\) a portion of which is attached to a fixed rigid substrate using an adhesive. A pressure field \(\mathbf{f}_p\) acts on the free lateral surface of \(\mathcal {S}\) to test the strength of the bond. The free and adhered portions of \(\mathcal {S}\) are separated by an interface \(\Gamma \). The source of material momentum  and the source (or singular) couple
and the source (or singular) couple  at the interface are also shown
at the interface are also shown
As shown in Fig. 4, consider a directed surface \(\mathcal {S}\). A portion of the surface is adhered to a rigid substrate, and the lower surface of the free portion of the surface is subject to a force field \(\mathbf{f}_p\). We divide the material surface into three sets \(\Omega _1\), \(\Gamma \) and \(\Omega _2\). The portion \(\Omega _1\) is the set of material points that are adhered to the substrate while the portion \(\Omega _2\) is free. The curve \(\Gamma \) is the continuous set of material points at the interface between \(\Omega _1\) and \(\Omega _2\).
Given \(\mathbf{f}_p\), we can compute representations for the assigned forces \(\rho _0\mathbf{f}\) and \(\rho _0\mathbf{l}\) and the assigned moment \(\mathbf{m}_a = \mathbf{d}_3\times \rho _0\mathbf{l}\). Solving for the configuration of the directed surface then involves solving for the balance of linear momentum and director momentum for \(\mathbf{r}\) and \(\mathbf{d}_3\) for material points in \(\Omega _1\) and \(\Omega _2\). However, the interface \(\Gamma \) is an unknown in this problem. The jump condition for material momentum provides a pair of equations to determine \(\Gamma \).
Several treatments (e.g., [15, 43]) of the blister problem model the directed surface using von Kármán’s plate theory. Following Eshelby [12, 13], most authors use variational formulations to establish an expression for the energy–momentum tensor and a conservation law for this tensor. The variation involves examining the change in the total potential energy of the plate and the loading on the plate due to movement of an interface. That is, the variation is distinct from the variations used to establish the Euler–Lagrange equations for the plate. Because these treatments do not consider the kinetic energy or material momentum, we are faced with the unsatisfactory situation that a correspondence to the treatment presented in this paper can only be made in the strictest sense if the material momentum is ignored.
To elaborate, we consider the problem shown in Fig. 4 and assume that a Kirchhoff–Love plate theory is being used to model the directed surface. On the adhered portion \(\Omega _1\) of the plate, u is identically zero and (10.11) is identically satisfied. With the help of (10.12), we find that the following boundary value problem needs to be solved on the unadhered portion \(\Omega _2\) of the plate:

At the interface \(\Gamma \),  vanishes because contact between the plate and substrate is lost; however, there are supplies of material momentum and angular momentum. With the help of (9.22.1), (9.26), (10.15), and the constitutive relations (10.8), (10.9), and (10.14):
vanishes because contact between the plate and substrate is lost; however, there are supplies of material momentum and angular momentum. With the help of (9.22.1), (9.26), (10.15), and the constitutive relations (10.8), (10.9), and (10.14):

Let us assume that the interface is axisymmetric and has a radius R. In this instance,  . The jump conditions for this case imply that \(\mathbf{N}^1\) is continuous across the interface:
. The jump conditions for this case imply that \(\mathbf{N}^1\) is continuous across the interface:

The jump condition (11.2) demonstrates that \(\mathbf{M}_\gamma \) is nonzero:

That is, as the interface is traversed the bending strains suffer a discontinuity, and a bending moment must be supplied for equilibrium. Our results here are in complete agreement with Majidi and Adams [25, 26]. A similar phenomenon occurs in adhesion of elastic rods (see, e.g., [36, 39] and references therein).Footnote 12
Turning to the jump condition (10.15) for material momentum, we use the continuity of \({}_0\mathbf{N}^1\), to simplify this condition to
As \(M = - D \text{ tr }\left( \mathbf{K}\right) \), this condition can be expressed as
Prescribing
we find that (11.6) is equivalent to a pair of conditions:
The second of these equations is satisfied by \(K^{-}_{12} = 0\). As \(K_{12} = r \frac{\partial }{\partial r}\left( \frac{1}{r} \frac{\partial u}{\partial \vartheta }\right) \), this is consistent with an axisymmetric solution to the boundary-value problem on \(\Omega _2\). The first equation is an example of an adhesion boundary condition. If we impose the boundary condition at \(\Gamma ^{-}\) and assume an axisymmetric solution, then \(K^{-}_{22} = 0\), and (11.8.1) simplifies to
This is the adhesion boundary condition that can be found in several works in the literature (see, e.g., [25, 26]) where it is derived from a variational principle and not as a consequence of a balance law for material momentum.
For this problem,  vanishes. Thus, the supply of energy at the interface \(\Gamma \) can be computed using the identity (9.20), the jump condition (9.30) and (11.4):
vanishes. Thus, the supply of energy at the interface \(\Gamma \) can be computed using the identity (9.20), the jump condition (9.30) and (11.4):

Comparison of (11.10) with [15, Eqs (94)-(95)] and [43], we can identify  as the driving force \(\mathcal {G}\) and
as the driving force \(\mathcal {G}\) and  as the rate at which energy is released as
as the rate at which energy is released as  evolves. However, neither of the works [15, 43] considered the effects of the moment
evolves. However, neither of the works [15, 43] considered the effects of the moment  .
.
12 Concluding remarks
A balance law for material (or configurational) momentum in shells is presented in this paper. The balance laws are used to establish a local form (cf. (6.6)) and a jump condition (cf. (6.7)) that holds at a point  , respectively:
, respectively:

Following standard procedures, the local form (12.1.1) is identically satisfied by the assigned material force \(\rho _0\mathbf{b}\). The jump condition (12.1.1,2) enables us to provide closed systems of equations for boundary-value problems particularly when energy loss or adhesion is present at a point of discontinuity. Thus, our developments parallel those found in applications of rod theories to problems involving adhesion.
The balance of material momentum is first presented in the context of a general shell theory and then, with the assistance of [42], specialized to the cases of elastic Kirchhoff–Love shells and plates. The developments for a Kirchhoff–Love plate are then applied to examine the classic problem of the propagation of a blister. Our discussion of this problem serves to provide additional motivation for the singular supply of material momentum  and the singular moment
and the singular moment  at an interface. We note in closing that the developments in Sect. 11 can be used to extend the formulation of a liquid blister on a rigid plate studied in [44] to a liquid blister on a flexible plate.
at an interface. We note in closing that the developments in Sect. 11 can be used to extend the formulation of a liquid blister on a rigid plate studied in [44] to a liquid blister on a flexible plate.
Notes
Cf. [43, Eq. (3.8)].
In the interests of a compact notation, we refrain from ornamenting \(\mathsf {d}\) and \(\mathsf {c}\) with a subscript 0. This subscript is equivalent to the subscript \(\text {R}\) used in [31, Section 9, \(\delta \)].
The procedure we are employing here is identical to the one described in Chadwick [9, Chapter 3].
For quasi-static problems in the absence of sources of momenta and energy, the jump condition (6.9) along with the jump conditions
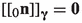 and
and 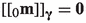 , is known as the Weierstrass–Erdmann corner condition in the calculus of variations.
, is known as the Weierstrass–Erdmann corner condition in the calculus of variations.The jump condition is similar to a related jump condition for a different shell theory that can be found in [11, Eq. (40)].
The additional three constraints imposed in [42] are \(\varphi _4 = 0\), \(\varphi _5 = 0\) and \(\varphi _6 = 0\), where \(\varphi _4 = \mathbf{d}_{3,1}\cdot \mathbf{d}_3\), \(\varphi _5 = \mathbf{d}_{3,2}\cdot \mathbf{d}_3\), and \(\varphi _6 = \mathbf{d}_{3,2}\cdot \mathbf{a}_1 - \mathbf{d}_{3,1}\cdot \mathbf{a}_2\).
We note that related results can be found in [31, 42]. However, these authors imposed the constraint \(\mathbf{d}_{3,2}\cdot \mathbf{a}_1 - \mathbf{d}_{3,1}\cdot \mathbf{a}_2 = 0\). The enforcement of this constraint introduces a contribution \(\lambda ^6 \varepsilon ^{\alpha \beta } \mathbf{n}_{,\beta }\) to \({}_0 \mathbf{N}^\alpha \), where \(\lambda ^6\) is a Lagrange multiplier. As a result, these authors needed to demonstrate that the divergence of this term vanishes. That is, \(\left( \lambda ^6 \varepsilon ^{\alpha \beta } \mathbf{n}_{,\beta }\right) _{|,\alpha } = \mathbf{0}\).
An explanation for the singular moment as a limiting case of dry adhesion can be found in [39].
References
Abeyaratne, R., Knowles, J.K.: On the driving traction acting on a surface of strain discontinuity in a continuum. J. Mech. Phys. Solids 38(3), 345–360 (1990). https://doi.org/10.1016/0022-5096(90)90003-M
Abeyaratne, R., Knowles, J.K.: Nucleation, kinetics and admissibility criteria for propagating phase boundaries. In: Fosdick, R., Dunn, E., Slemrod, H. (eds.) Shock induced transitions and phase structures in general media, IMA Volumes in Mathematics and its Applications, 52:1–33. Springer-Verlag, New York (1993). https://doi.org/10.1007/978-1-4613-8348-2_1
Antman, S.S.: Nonlinear Problems of Elasticity. Applied Mathematical Sciences, vol. 107, second edn. Springer-Verlag, New York (2005)
Bigoni, D., Bosi, F., Misseroni, D., Dal Corso, F., Noselli, G.: New phenomena in nonlinear elastic structures: from tensile buckling to configurational forces. In: Bigoni, D. (ed.) Extremely Deformable Structures, pp. 55–135. Springer-Verlag, Vienna (2015). https://doi.org/10.1007/978-3-7091-1877-1_2
Bigoni, D., Corso, F.D., Bosi, F., Misseroni, D.: Eshelby-like forces acting on elastic structures: theoretical and experimental proof. Mech. Mater. 80, 368–374 (2015). https://doi.org/10.1016/j.mechmat.2013.10.009
Bosi, F., Misseroni, D., Dal Corso, F., Bigoni, D.: An elastica arm scale. Proc. R. Soc. A Math. Phys. Eng. Sci. 470(2169), 20140232 (2014). https://doi.org/10.1098/rspa.2014.0232
Carroll, M.M., Naghdi, P.M.: The influence of the reference geometry on the response of elastic shells. Arch. Ration. Mech. Anal. 48(4), 302–318 (1972). https://doi.org/10.1007/BF00250856
Casey, J., Carroll, M.M.: Discussion of “A treatment of internally constrained materials” by. J. Casey. ASME J. Appl. Mech. 63(1), 240 (1996). https://doi.org/10.1115/1.2787205
Chadwick, P.: Continuum Mechanics. Dover Publications, New York (1999)
Eremeyev, V.A., Konopińska-Zmysłowska, V.: On the correspondence between two- and three-dimensional Eshelby tensors. Continuum Mech. Thermodyn. 31(6), 1615–1625 (2019). https://doi.org/10.1007/s00161-019-00754-6
Eremeyev, V.A., Pietraszkiewicz, W.: The nonlinear theory of elastic shells with phase transitions. J. Elast. 74, 67–86 (2004). https://doi.org/10.1023/B:ELAS.0000026106.09385.8c
Eshelby, J.D.: The force on an elastic singularity. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 244, 84–112 (1951). https://doi.org/10.1098/rsta.1951.0016
Eshelby, J.D.: Energy relations and the energy-momentum tensor in continuum mechanics. In: Ball, J.M., Kinderlehrer, D., Podio-Guidugli, P. (eds.) Fundamental Contributions to the Continuum Theory of Evolving Phase Interfaces in Solids, pp. 82–119. Springer-Verlag, Berlin (1999). https://doi.org/10.1007/978-3-642-59938-5_5
Fried, E., Gurtin, M.E.: The role of the configurational force balance in the nonequilibrium epitaxy of films. J. Mech. Phys. Solids 51(3), 487–517 (2003). https://doi.org/10.1016/S0022-5096(02)00077-7
Gioia, G., Ortiz, M.: Delamination of compressed thin films. In: Hutchinson, J. W., Wu, T.Y. (eds.) Advances in Applied Mechanics, 33, 119–192. Elsevier (1997). https://doi.org/10.1016/S0065-2156(08)70386-7
Goldberg, N.N., O’Reilly, O.M.: On contact point motion in the vibration analysis of elastic rods. J. Sound Vib. 487, 115579 (2020). https://doi.org/10.1016/j.jsv.2020.115579
Goldberg, N.N., O’Reilly, O.M.: Electrostatically actuated MEMS in the post-touchdown regime: the thin-dielectric limit and a novel reduced-order model for release dynamics. Int. J. Solids. Struct. 252, 111812 (2022). https://doi.org/10.1016/j.ijsolstr.2022.111812
Green, A.E., Naghdi, P.M.: On the derivation of shell theories by direct approach. ASME J. Appl. Mech. 41(1), 173–176 (1974). https://doi.org/10.1115/1.3423218
Green, A.E., Naghdi, P.M.: A unified procedure for construction of theories of deformable media. II. Generalized continua. Proc. R. Soc. Lond. Ser. A. Math. Phys. Eng. Sci. 448(1934), 357–377 (1995). https://doi.org/10.1098/rspa.1995.0021
Gurtin, M.E.: Configurational Forces as Basic Concepts of Continuum Physics, Applied Mathematical Sciences, vol. 137. Springer-Verlag, New York (2000)
Irschik, H.: On the necessity of surface growth terms for the consistency of jump relations at a singular surface. Acta Mech. 162, 195–211 (2003). https://doi.org/10.1007/s00707-002-0995-9
Irschik, H.: On rational treatments of the general laws of balance and jump, with emphasis on configurational formulations. Acta Mech. 194, 11–32 (2007). https://doi.org/10.1007/s00707-007-0485-1
Irschik, H.: On configurational formulations in the director theory of rods. In: Steinmann, P. (ed.) Proceedings of the IUTAM Symposium on the Progress in the Theory and Numerics of Configurational Mechanics, Erlangen 2008, pp. 131–138. Springer, Dordrecht, NL (2009). https://doi.org/10.1007/978-90-481-3447-2_12
Majidi, C.: Remarks on formulating an adhesion problem using Euler’s elastica. Mech. Res. Commun. 34(1), 85–90 (2007). https://doi.org/10.1016/j.mechrescom.2006.06.007
Majidi, C., Adams, G.G.: A simplified formulation of adhesion problems with elastic plates. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 465(2107), 2217–2230 (2009). https://doi.org/10.1098/rspa.2009.0060
Majidi, C., Adams, G.G.: Adhesion and delamination boundary conditions for elastic plates with arbitrary contact shape. Mech. Res. Commun. 37(2), 214–218 (2010). https://doi.org/10.1016/j.mechrescom.2010.01.002
Majidi, C., O’Reilly, O.M., Williams, J.A.: On the stability of a rod adhering to a rigid surface: Shear-induced stable adhesion and the instability of peeling. J. Mech. Phys. Solids 60(5), 827–843 (2012). https://doi.org/10.1016/j.jmps.2012.01.015
Majidi, C., O’Reilly, O.M., Williams, J.A.: Bifurcations and instability in the adhesion of intrinsically curved rods. Mech. Res. Commun. 49, 13–16 (2013). https://doi.org/10.1016/j.mechrescom.2013.01.004
Makowski, J., Pietraszkiewicz, W., Stumpf, H.: Jump conditions in the non-linear theory of thin irregular shells. J. Elast. 54, 1–26 (1999). https://doi.org/10.1023/A:1007645414077
Maugin, G.A.: Material forces: concepts and applications. ASME Appl. Mech. Rev. 48(5), 213–245 (1995). https://doi.org/10.1115/1.3005101
Naghdi, P.M.: The theory of shells and plates. In: Truesdell, C. (ed.) Linear Theories of Elasticity and Thermoelasticity: Linear and Nonlinear Theories of Rods, Plates, and Shells, pp. 425–640. Springer-Verlag, Berlin, Heidelberg (1973). https://doi.org/10.1007/978-3-662-39776-3_5
Naghdi, P.M.: Finite deformation of elastic rods and shells. In: Carlson, D.E., Shield, R.T. (eds.) Proceedings of the IUTAM Symposium on Finite Elasticity, Bethlehem PA 1980, pp. 47–104. Martinus Nijhoff, The Hague (1982). https://doi.org/10.1007/978-94-009-7538-5_4
O’Reilly, O.M.: The energy jump condition for thermomechanical media in the presence of configurational forces. Continuum Mech. Thermodyn. 18(6), 361–365 (2007). https://doi.org/10.1007/s00161-006-0036-3
O’Reilly, O.M.: A material momentum balance law for rods. J. Elast. 86(2), 155–172 (2007). https://doi.org/10.1007/s10659-006-9089-6
O’Reilly, O.M.: Some perspectives on Eshelby-like forces in the elastica arm scale. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 471(2174), 20140785 (2015). https://doi.org/10.1098/rspa.2014.0785
O’Reilly, O.M.: Modeling nonlinear problems in the mechanics of strings and rods: the role of the balance laws. Interact. Mech. Math. (2017). https://doi.org/10.1007/978-3-319-50598-5
O’Reilly, O.M., Turcotte, J.S.: Some remarks on invariance requirements for constrained rods. Math. Mech. Solids 1(3), 343–348 (1996). https://doi.org/10.1177/108128659600100306
Pietraszkiewicz, W., Eremeyev, V., Konopińska, V.: Extended non-linear relations of elastic shells undergoing phase transitions. Z. Angew. Math. Mech. 87(2), 150–159 (2007). https://doi.org/10.1002/zamm.200610309
Roy, A., Chatterjee, A.: Vibrations of a beam in variable contact with a flat surface. ASME J. Vib. Acoust. 131(4) (2009). https://doi.org/10.1115/1.3086930
Simmonds, J.G., Danielson, D.A.: Nonlinear shell theory with finite rotation and stress function vectors. ASME J. Appl. Mech. 39(4), 1085–1090 (1972). https://doi.org/10.1115/1.3422833
Singh, H., Hanna, J.A.: Pseudomomentum: origins and consequences. Z. Angew. Math. Phys. 72(3), 122 (2021). https://doi.org/10.1007/s00033-021-01507-9
Steigmann, D.J.: On the relationship between the Cosserat and Kirchhoff–Love theories of elastic shells. Math. Mech. Solids 4(3), 275–288 (1999). https://doi.org/10.1177/108128659900400301
Storåkers, B., Andersson, B.: Nonlinear plate theory applied to delamination in composites. J. Mech. Phys. Solids 36(6), 689–718 (1988). https://doi.org/10.1016/0022-5096(88)90004-X
Wang, Z.Q., Detournay, E.: Eshelbian force on a steadily moving liquid blister. Int. J. Eng. Sci. 170, 103591 (2022). https://doi.org/10.1016/j.ijengsci.2021.103591
Williams, M.L.: The continuum interpretation for fracture and adhesion. J. Appl. Polym. Sci.13(1), 29–40 (1969)
Williams, M.L.: The fracture threshold for an adhesive interlayer. J. Appl. Polym. Sci. 14(5), 1121–1126 (1970). https://doi.org/10.1002/app.1970.070140501
Acknowledgements
This work was supported by the National Defense Science and Engineering Graduate Fellowship (United States Department of Defense) and the Berkeley Fellowship for Graduate Study (University of California, Berkeley) awarded to N. N. Goldberg.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Goldberg, N.N., O’Reilly, O.M. A material momentum balance law for shells and plates with application to phase transformations and adhesion. Acta Mech 233, 3535–3555 (2022). https://doi.org/10.1007/s00707-022-03287-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-022-03287-3






 and
and  are displayed. The unit vector
are displayed. The unit vector 

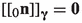 and
and 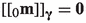 , is known as the Weierstrass–Erdmann corner condition in the calculus of variations.
, is known as the Weierstrass–Erdmann corner condition in the calculus of variations.