Abstract
This work presents a thermomechanical finite strain shape memory alloy model that utilizes a projection method to deal with the incompressibility constraint on inelastic strains. Due to its finite strain formulation, it is able to accurately predict the behavior of shape memory alloys with high transformation strains. The key feature of this model is the thermomechanical modeling of the shape memory effect and superelastic behavior by optimizing a global, incremental mixed thermomechanical potential, the variation of which yields the linear momentum balance, the energy balance, the evolution equations of the internal variables as well as boundary conditions of Neumann- and Robin-type. The proposed thermal strain model allows to properly capture transformation induced volume changes, which occur in some shape memory alloys. A finite strain dissipation potential is formulated, which incorporates the disappearance of inelastic strains upon austenite transformation. This important property is consistently transferred to the time-discrete potential using a logarithmic strain formulation. Yield and transformation criteria are derived from the dual dissipation potential. The implementation based on an active set search and the algorithmically consistent linearization are discussed in detail. The model is applied in three-dimensional simulations of a bistable actuator design to explore its capabilities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the discovery of their unique properties, shape memory alloys are used in many medical and engineering fields in various applications. Their frequent appearance stems from their unique features, like the shape memory effect and superelasticity. Both effects emerge from the characteristic first-order phase transition from the austenite to the martensite state and vice versa. While the occurring crystallographic effects involving the detwinning of the martensite phase, which enables the shape memory effect, are well understood, the thermomechanical modeling of the occurring effects is not straightforward. In recent times, there has been a high effort to improve shape memory alloy models and to obtain fitting models for specific use cases (see, for reviews, Section 4 of Lester et al. [27] or Cisse et al. [8]). They can be roughly categorized into three classes: models based on statistical thermodynamics, models founded in micromechanics and phenomenological models.
The models based on statistical thermodynamics rely on finding the phase equilibrium through a minimization of a three well potential energy (e.g., Seelecke and Müller [43] or Govindjee et al. [16]). Since these models yield results that also consider the microstructure of the materials, they come mostly with a computational cost which is too high for large, structural simulations. Additionally, gathering required micromechanical material parameters is sometimes an elaborate task.
On the other hand, models based on micromechanics usually consider the mechanics of shape memory alloy (SMA) single-crystals. Many models are then extended into the regime of polycrystal modeling by usage of homogenization techniques (e.g., see Patoor et al. [35] and Lagoudas et al. [25] or the more recent models by Mirzaeifar et al. [29] and Yu et al. [55]). While these models consider the deep, underlying phenomena of shape memory alloys, this advantage again comes with a high computational cost. This makes it really challenging to use these models in large structural simulations of shape memory alloy actuators.
The third group of models is the class of phenomenological models.
Usually, they come with the advantage of only having macroscopic material parameters, which mostly are obtained through tensile tests at different temperatures. In recent years, due to the plethora of shape memory alloys effects and applications, many new shape memory alloy models were published, which try to include more and more physical phenomenons. They can be divided into two subgroups: models which include a geometrically linear theory (see, e.g., Auricchio et al. [3], Auricchio et al. [4] and Sedlak et al. [42]), and models which include a geometrically nonlinear theory.
The two main ways to include a geometric nonlinearity in the shape memory alloy model is to either employ a multiplicative split of the deformation gradient going back to [10, 24, 26] or to make use of an additive split (see Nemat-Nasser [32]) of the rate of deformation, which are both well known from plasticity. While models based on the additive split are computationally enticing, they only allow for small strains, while still capturing large rotations well (see, e.g., Qidwai and Lagoudas [37], Müller and Bruhns [31] or Zhang and Baxevanis [57]). On the other hand, models employing a multiplicative split are computationally more elaborate, but can represent finite stretches well (see, e.g., Reese and Christ [38], Arghavani et al. [1] or Wang et al. [49]). Additionally, there exist many new models considering geometric nonlinearities, which are limited to superelasticity (see, e.g., Bellini et al. [5], Wang et al. [48] and Rezaee-Hajidehi et al. [39]). Furthermore, some models also consider transformation induced plasticity (see, e.g., Hartl et al. [19], Xu et al. [53] and it’s extension to partial phase transformations by Scalet et al. [41]).
Many of these models capture thermomechanics, martensite reorientation and detwinning as well as superelasticity at different temperatures or allow for different elastic properties of the materials while being numerically efficient and robust. However, when trying to model bistable shape memory actuators (see the actuator design in Arivanandhan [2]), one needs a numerically robust, fully thermomechanically coupled finite strain model that also models thermal expansion and volumetric effects during phase transition (see, e.g., Potapov et al. [36]). To our knowledge, there is no model in the literature fulfilling all of the aforementioned requirements, which led to the model described in this paper. For example, the model of Wang et al. [49] considers a thermomechanically coupled finite strain theory which is capable of modeling the shape memory effect as well as superelasticity, neglecting volumetric effects due to transformation as well as different expansion coefficients of the SMA phases. The model at hand falls into the aforementioned category of phenomenological models. It is embedded into the generalized standard materials framework developed by Halphen and Nguyen [17], which was extended to thermomechanics by Yang et al. [54] and which allows to ensure thermodynamic consistency. The energies as well as the dissipation potential can be seen as an extension of Sedlak et al. [42] to the finite strain case. Because the satisfaction of the incompressibility of inelastic strains for finite strains is not as straightforward as for the small strain case, a projection method developed for plasticity is incorporated into the model (see Hurtado et al. [21] and Sielenkämper et al. [44]). Further, due to the character of the energies used in this model, special numerical treatment is necessary to solve the model equations using a Newton scheme. Since our aim is to model microactuators in which the R-Phase is not present, it is not incorporated into the model. Additionally, tension-compression anisotropy, which is an important effect in many shape memory alloys (for experimental publications see, e.g., Gall et al. [15] or Wang and Zhu [47], and for modeling approaches see, e.g., Zaki et al. [56] or Sedlak et al. [42]), is not included in the model.
In the past, numerous advancements to current microelectromechanical systems (MEMS) based on electrostatics, magnetism and electrothermal principals have been made. For example, Hoffmann et al. [20] proposed a microactuator based on electrothermal activation making use of bimetal effects. This, however, comes with the downside of low actuation frequencies and a high power consumption. Han et al. [18] proposed an electrostatic actuator-based micro-switch for photonics. Devices based on electrostatics usually can be actuated with high frequencies and are adaptable to many applications. Devices using optomechanics were developed by, e.g., Eichenfield et al. [11], which come with a rather small tuning range, but allow for a very high operation speed [9]. Despite their unique advantages, current MEMS devices are challenging to use in downsized applications, where a high work output combined with a high power efficiency and bistability is crucial. The microactuator modeled in this paper is based on a concept published by Winzek et al. [50], which utilizes a high temperature shape memory alloy with a large thermal hysteresis. This concept may overcome the aforementioned weaknesses of other actuation principles, as shape memory alloys usually have a large work output density and favorable downscaling capabilities (see, e.g., Kohl [22]). Additionally, downscaling this design is expected to drastically increase the possible actuation frequency in comparison to other, electrothermally activated actuators due to the decreasing masses and increasing thermal gradients. One further key aspect is, that the proposed actuator design requires no power in the stable states.
The paper is structured as follows: First, the energies as well as the dissipation potential is derived. Then, in Sect. 3, numerical strategies necessary to solve the model equations are discussed. The numerical results are subsequently shown in Sect. 4 before a summary and outlook concludes the paper in Sect. 5.
Notation
Throughout this paper, a direct tensor notation is preferred. Scalars and scalar valued functions are typeset using light-face italic characters, e.g., a or A. First and second-order tensors and tensor-valued functions are represented by bold-face italic letters, e.g., \(\varvec{a}\) or \(\varvec{A}\). Further, blackboard bold-faced letters are used to denote fourth-order tensors, e.g.,  or
or  .
.
Additionally, the transpose of a second-order tensor is designated by  , while the major transpose of a fourth-order tensor is given by
, while the major transpose of a fourth-order tensor is given by  . The symmetric and deviatoric part of a second-order tensor \(\varvec{A}\) are denoted by \(\text {sym}( \varvec{A} ) = \frac{1}{2}( \varvec{A}+ {\varvec{A}}^\mathsf{T})\) and \(\varvec{A}^\prime = \varvec{A}- \frac{1}{3}\text {tr}( \varvec{A} )\varvec{I}\), respectively. Here, \(\varvec{I}\) is the second-order identity tensor and \(\text {tr}( \varvec{A} )\) denotes the trace of \(\varvec{A}\). A double contraction of two tensors \(\varvec{A}\) and \(\varvec{B}\) is denoted by \(\varvec{A}:\varvec{B}\), while the dyadic product is denoted by \(\varvec{a}\otimes \varvec{b}\). A determinant of a tensor \(\varvec{A}\) is either designated by \(\text {det}( \varvec{A} )\) or by \(\varvec{A}\)’s third invariant
. The symmetric and deviatoric part of a second-order tensor \(\varvec{A}\) are denoted by \(\text {sym}( \varvec{A} ) = \frac{1}{2}( \varvec{A}+ {\varvec{A}}^\mathsf{T})\) and \(\varvec{A}^\prime = \varvec{A}- \frac{1}{3}\text {tr}( \varvec{A} )\varvec{I}\), respectively. Here, \(\varvec{I}\) is the second-order identity tensor and \(\text {tr}( \varvec{A} )\) denotes the trace of \(\varvec{A}\). A double contraction of two tensors \(\varvec{A}\) and \(\varvec{B}\) is denoted by \(\varvec{A}:\varvec{B}\), while the dyadic product is denoted by \(\varvec{a}\otimes \varvec{b}\). A determinant of a tensor \(\varvec{A}\) is either designated by \(\text {det}( \varvec{A} )\) or by \(\varvec{A}\)’s third invariant  .
.
2 Modeling of shape memory alloys
2.1 Kinematics
The deformation gradient \(\varvec{F}\) maps a line element from the reference configuration of a body with Volume \(V_0\) into the current configuration of a body with Volume V and is defined as
where \(\text {Grad\!}\left( \bullet \right) \) refers to the gradient with respect to the reference configuration while \(\varvec{X}\) and \(\varvec{x}\) are the position vectors of a material point in the reference and current configuration, respectively. We consider a multiplicative split of the deformation gradient in the form
(see Wang et al. [49]), where \(\varvec{F}^{\text {e}}\) is the elastic, \(\varvec{F}^{\text {i}}\) the isochoric part of the deformation due to transformationFootnote 1 and \(\varvec{F}^{\theta }\) the part which describes the volume change due to thermal expansion and transformationFootnote 2 of the deformation gradient. This is fairly similar to the multiplicative split in plasticity going back to the works of Eckart [10], Kröner [24] and Lee [26]. Further, we define the determinant \(J^{\theta }= J^{\theta }(\theta ,\xi ) = \text {det}( \varvec{F}^{\theta } )\) to be a function of the absolute temperature \(\theta \) and the martensite volume fraction \(\xi \in [0,1]\). Since the thermal deformation is assumed to be volumetric, we can express \(\varvec{F}^{\theta }\) in terms of \(J^{\theta }\) as
As is commonly done and will be useful later, we define the elastic and inelastic left Cauchy-Green tensors as
Likewise, we define the inelastic right Cauchy-Green tensor and the inelastic Green-Lagrange strain
Motivated by the observation that the shape-memory effect is caused by an almostFootnote 3 volume preserving transformation of the crystal lattice, we assume \(\varvec{C}^{\text {i}}\) to be volume preserving. Therefore, because \(\text {det}( \varvec{F}^{\text {i}} )= 1\) has to hold, the determinant of the deformation gradient is given by

with \(J^{\text {e}}=\text {det}( \varvec{F}^{\text {e}} )\). Additionally, we define the velocity gradient \(\varvec{l}\) and its symmetric part \(\varvec{d}\) as
Finally, we define the inelastic ’velocity gradient’ \(\varvec{L}^{\text {i}}\) and its symmetric part \(\varvec{D}^{\text {i}}\) in analogy to \(\varvec{l}\) and \(\varvec{d}\) by

2.2 (Im-)Balance equations
2.2.1 Momentum balances
The quasistatic linear momentum balance for a body with volume V in the current configuration is given by
where \(\varvec{b}\) is the body force and \(\rho \) is the mass density. Further, Cauchy’s lemma \(\varvec{t}= {\varvec{\sigma }}\varvec{n}\) as well as the angular momentum balance \({\varvec{\sigma }}= {{\varvec{\sigma }}}^\mathsf{T}\) are assumed to hold.
2.2.2 Energy balance
Next, the balance of the energies is given by
where u is the internal energy density per unit reference volume, \({\varvec{\tau }}\) denotes the Kirchhoff stress tensor, \(\varvec{q}\) is the heat flux vector in the current configuration and w represents the energy source term. Further, the divergence of the heat flux vector \(\varvec{Q}= J \varvec{F}^{\text {-1}}\varvec{q}\) with respect to the reference configuration is then given by \(J \text {div}\!\left( \varvec{q} \right) = \text {Div\!}\left( \varvec{Q} \right) \).
2.2.3 Clausius–Planck inequality
To be thermodynamically consistent, the Clausius–Planck inequality

where  is the mechanical dissipation density per unit reference volume and s is the entropy density per unit reference volume, has to be fulfilled at any time. Further, the Helmholtz free energy, which is defined by \(\psi = u - \theta s\), is introduced. We assume \(\psi \) to be a function of the deformation gradient \(\varvec{F}\), the absolute temperature \(\theta \) and the internal variables \(\xi \) and \(\varvec{C}^{\text {i}}\), i.e., \(\psi = \psi (\varvec{F},\varvec{C}^{\text {i}},\xi ,\theta )\). Furthermore, we make the common assumption that
is the mechanical dissipation density per unit reference volume and s is the entropy density per unit reference volume, has to be fulfilled at any time. Further, the Helmholtz free energy, which is defined by \(\psi = u - \theta s\), is introduced. We assume \(\psi \) to be a function of the deformation gradient \(\varvec{F}\), the absolute temperature \(\theta \) and the internal variables \(\xi \) and \(\varvec{C}^{\text {i}}\), i.e., \(\psi = \psi (\varvec{F},\varvec{C}^{\text {i}},\xi ,\theta )\). Furthermore, we make the common assumption that

i.e., there is no energy dissipation when the internal variables are virtually fixed. As Eq. (12) must hold for arbitrary processes, one can show the following standard results:
Now, it is easy to show that

with shorthand notations for the effective Mandel stress with respect to the intermediate configuration \({\varvec{\Sigma }}^{\text {i}}= -2\varvec{F}^{\text {i}}\left( \partial \psi / \partial \varvec{C}^{\text {i}}\right) \varvec{F}^{\text {i} \mathsf T}\) and the thermodynamic force \(q = -\partial \psi /\partial \xi \) associated with the martensite volume fraction \(\xi \).
2.3 Helmholtz free energy
The Helmholtz free energy density \(\psi \) for this model is assumed to be a sum of elastic, chemical and hardening-like contributions in the form
2.3.1 Elastic energy
The elastic energy \(\psi _\text {e}\) is assumed to be isotropic and to follow a modified Neo-Hookean formulation:
Here, \(\lambda (\xi )\) and \(\mu (\xi )\) are the Lamé parameters in dependence of the martensite volume fraction \(\xi \). Further, we use a Reuss-like mixture rule to estimate the elastic constants, i.e.,
Here, and subsequently, the indices \(\bullet _\text {A}\) and \(\bullet _\text {M}\) refer to the austenite and martensite phase, respectively. Manipulating Eq. (13), one can show that the ordinary form
holds for elastic isotropy. Using Eqs. (14) and (18), one can show that
where \({\varvec{\Sigma }}^{\text {e}}= \varvec{C}^{\text {e}}\varvec{F}^{\text {e} -1}{\varvec{\tau }}\varvec{F}^{\text {e} -\mathsf{T}}\) is the Mandel stress with respect to the intermediate, elastically unloaded configuration, which is symmetric due to the assumption of elastic isotropy.
2.3.2 Chemical energy
For the chemical energy, we assume a standard relationship (see, e.g., Lexcellent et al. [28] or Panico and Brinson [34]):
where c is the specific heat capacity and \(\Delta s^{\text {AM}}\) is the difference in specific entropy of the austenite and martensite phase: \(\Delta s^{\text {AM}}= s_0^\text { A} - s_0^\text { M}\). Here, c is assumed constant (compare [42]). In Eq. (20), we made use of the definition of the equilibrium temperature of austenite and martensite, which is \(\theta _0 = \Delta u^{\text {A}\text {M}}/\Delta s^{\text {A}\text {M}}\). Further, we assume for the equilibrium temperature \(A_\text {s}>\theta _0>M_\text {s}\), where \(A_\text {s}\) is the temperature where the reverse transformation starts and \(M_\text {s}\) is the starting temperature of the forward transformation.
2.3.3 Hardening energy
Since the inelastic strains vanish as \(\xi \rightarrow 0\), the inelastic strains \(\varvec{E}^{\text {i}}\) are assumed to satisfy the relation \(\varvec{E}^{\text {i}}= \xi \varvec{E}^{\text {t}}\) (see Otsuka and Ren [33]), where \(\varvec{E}^{\text {t}}\) is a measure for the effective transformation strain. Now, the hardening-like energy adapted from Sedlak et al. [42] for finite strains is assumed to be given by
Here, k is the maximum transformation strain, \(E^{\text {int}}\) is a hardening related parameter and \(\big \langle \varvec{E}^{\text {t}}\big \rangle \) is a modified von Mises equivalent strain. Obviously, \(\psi _\text {h}\rightarrow \infty \) for \(\big \langle \varvec{E}^{\text {t}}\big \rangle \rightarrow 1\). This is desired, since it captures the martensite becoming fully detwinned, which is assumed to cost additional energy.
2.3.4 Thermal strains
Modeling thermal strains of multi-phase materials requires attention and special treatment. In this work, the determinant of the thermal part of the deformation gradient is connected to the coefficients of thermal expansion (CTEs) by

Here, \(\varepsilon ^\theta (\xi ,\theta )\) is the thermal strain. Additionally, \(\alpha _\text {M}\) and \(\alpha _\text {A}\) are the CTEs of the martensite and austenite phase, respectively. Further, \(\theta _{\text { refM}}\) and \(\theta _{\text { refA}}\) are the reference temperatures for austenite and martensite. Here, we want to note that it is necessary to distinguish the two in order to properly represent the transformation-induced volume change which is present in some shape memory alloys (see below).
Example
We assume a one-dimensional SMA rod with only one reference temperature. Further, we simplify the SMA model by assuming that martensite and austenite transformation occur at the distinct temperatures \(\theta _\text {M}\) and \(\theta _\text {A}\), and not at temperature ranges (see Fig. 1). The thermal strains are then given by \(\varepsilon ^\theta = \alpha _{\text {A}\text {M}} (\theta - \theta _\text { ref})\), with \(\alpha _{\text {A}\text {M}}=\xi \alpha _\text {M}+ (1-\xi )\alpha _\text {A}\). Furthermore, we assume that we know the shape of our rod at the thermal annealing temperature \(\theta _\text { ref}\) (see Fig. 1).
During forward transformation, the jump of \(\varepsilon ^\theta \) at \(\theta _\text {M}\) can be analytically calculated and is given by
Here, we can not only see that this jump is dependent on the reference temperature, but that it can be positive or negative, depending on the reference temperature \(\theta _\text { ref}\) being larger or smaller than the forward transformation temperature \(\theta _\text {M}\).
Using two reference temperatures \(\theta _{\text {ref M}}\) and \(\theta _{\text {ref A}}\), we can not only circumvent this problem, but also model the magnitude of this jump in compliance with, e.g., the experimental results of Potapov et al. [36], where they calculated the jump \(\Delta V\) in volume from the lattice parameters for \({\hbox {Ni}_{49.8}\hbox {Ti}_{35.2}\hbox {Hf}_{15}}\) to be \({0.47\%}\). However, we want to emphasize that this effect does not play a significant role in many other shape memory alloys.
2.4 Dissipation potential
The dissipative behavior of the shape memory alloy is assumed to be governed by the dissipation potential
Here, depending on the direction of transformation, either \(\phi _\text {M}\) or \(\phi _\text {A}\) are used as the active dissipation potential. As is commonly done for plasticity, the dissipation is assumed to be infinite if \(\text {tr}( \varvec{D}^{\text {i}} ) \ne 0 \), which guarantees volume-preserving inelastic deformations (compare Rockafellar [40]). Additionally, we define the dissipation potential for an increasing martensite volume fraction as
where \(M_{\text {f}}\) is the finish temperature of forward transformation and \(\sigma ^{\text {reo}}\) is the reorientation stress. Likewise, the dissipation potential when going to a higher austenite volume fraction is defined as
Here, \(A_{\text {f}}\) is the finish temperature of reverse transformation and \({\varvec{\varepsilon }}^{\text {i}}= \frac{1}{2}\ln {\varvec{b}^{\text {i}}}\). The significance of using the logarithmic inelastic strain \({\varvec{\varepsilon }}^{\text {i}}\) as a strain measure for the dissipation is explained below. The dissipation potential represents a geometrically nonlinear generalization of the small strain potential proposed in Sedlak et al. [42], which is based on the works of Bernardini and Pence [6], Panico and Brinson [34] and Moumni et al. [30].
2.5 Transformation/yield criteria and inelastic evolution equations
It is assumed that the evolution of \(\varvec{C}^{\text {i}}\) and \(\xi \) follows from the minimization problem
which is equivalent to the Legendre–Fenchel transformed problem (compare Eqs. (14), (19))
where \(\phi ^{*}\) is the dual dissipation potential of \(\phi \):
Due to the minimization in Eq. (27), there is a tendency that for \(\dot{\xi }<0\) we get \(\varvec{D}^{\text {i}}-(\dot{\xi }/\xi ){\varvec{\varepsilon }}^{\text {i}}= \varvec{0}\) as a result of the last term in Eq. (26). In that case \(\varvec{b}^{\text {i}}\rightarrow \varvec{I}\) as \(\xi \rightarrow 0\) in time (for a proof, see Appendix A), i.e., for vanishing martensite content, the inelastic strain vanishes, which is a physical necessity. With the reparametrization \(\varvec{D}^{\text {t}}= \varvec{D}^{\text {i}}- ({\dot{\xi }}/{\xi }) {\varvec{\varepsilon }}^{\text {i}}\) (compare Eq. (26)) we find
where \(Q_\text {M}\) and \(Q_\text {A}\) are defined in Eqs. (25) and (26) and capture the transformation hysteresis due to temperature change. Further reparametrizing \(\varvec{D}^\text { i / t} = \lambda \varvec{N}\) with \(\lambda \ge 0\) and the obvious solution
it follows that
Thus, we find the following transformation and yield criteria in the classical Karush-Kuhn-Tucker form as well as evolution equations:
with the Macaulay bracket \(\langle \bullet \rangle = ( \bullet + |\bullet |)/2\) and its modified form \(\langle \bullet \rangle \_ = ( \bullet - |\bullet |)/2\). It is then straightforward to prove thermodynamic consistency (see Eq. (14)). The ’0’-branch in Eq. (32) implies that (see Eq. (28))

Thus, we find with Eqs. (4) and (10) the following alternative form of the energy balance:
2.6 Rate potential
To simplify the discussion, we start by the isothermal case, i.e., in a first step, the temperature \(\theta \) is considered to be a given parameter. The rate potential and its time discretized form read
Here, \(\psi _n\) refers to the Helmholtz free energy at the previous time, \(\Delta t\) is the time step from \(t_n\) to \(t_{n+1}\)Footnote 4 and \(\phi _{\Delta }\) is the time discretized version of the dissipation potential multiplied by \(\Delta t\), defined by

with \(\text {sg}\left( \bullet \right) \) referring to the sign function and \(\Delta \xi = \xi - \xi _n\). Additionally,  is the third invariant of \(\varvec{C}^{\text {i}}\), i.e.,
is the third invariant of \(\varvec{C}^{\text {i}}\), i.e.,

The constraint  in Eq. (37) is consistent with the requirement \(\text {tr}( \varvec{D}^{\text {i}} ) = 0\) (see Eq. (24)). Additionally, we compute the effective inelastic strain increment \(\Delta \alpha \) as
in Eq. (37) is consistent with the requirement \(\text {tr}( \varvec{D}^{\text {i}} ) = 0\) (see Eq. (24)). Additionally, we compute the effective inelastic strain increment \(\Delta \alpha \) as
where the inelastic right stretch is \(\varvec{U}^{\text {i}}= \sqrt{\varvec{C}^{\text {i}}}\), \(\Delta _\text {r}\varvec{C}^{\text {i}}= \varvec{C}^{\text {i}}- \varvec{C}^{\text {i}}_\text {r}\) and the shorthand notation \(\left\| \bullet \right\| _{{{\varvec{U}}^{\text {i}- 1}_n}}=\left\| \varvec{U}^{\text {i}- 1}_n\bullet \varvec{U}^{\text {i}- 1}_n \right\| \) is used. Further, we define \(\varvec{C}^{\text {i}}_\text {r}\) as
Now, for \(\xi \) going to zero in any given step, i.e., \(\xi = \xi _n+ \Delta \xi = 0 \Leftrightarrow \Delta \xi = -\xi _n\rightarrow \varvec{C}^{\text {i}}_\text {r}= \left( \varvec{C}_n^{\text {i}}\right) ^0=\varvec{I}\), \(\varvec{C}^{\text {i}}_\text {r}\) goes back to unity again. Thus, the time discrete potential (37) based on definition (40) of \(\varvec{C}^{\text {i}}_\text {r}\) is the key to ensure that the inelastic strain consistently disappears during the transformation from martensite to austenite. Further, the function \(Q(\varvec{C}_n^{\text {i}},\xi _{n+\frac{1}{2}},\text {sg}\left( \Delta \xi \right) )\) is given by
where \(\xi _{n+\frac{1}{2}} = (\xi +\xi _n)/2\) is the midpoint evaluation of \(\xi \), which is employed to obtain a reasonable transformation when the material is not stressed (see Frost et al. [14] for a similar concept). Moreover, we used \(\varvec{C}_n^{\text {i}}\) and \(\xi _n\) for the reverse transformation in Eq. (41) to circumvent the eigenvalue problem as well as its linearization in every local Newton iteration. In this way, it suffices to solve the eigenvalue problem once per time step.
Using some further shorthand notations for constant terms in Q, we obtain
where H and Q summarize \(H^\text {M}\), \(H^\text {A}\), \(Q^{\text {M}0}\) and \(Q^{\text {A}0}\), respectively. Further, \(\text {det}( \varvec{C}^{\text {i}}_\text {r} ) = \text {det}( \varvec{C}_n^{\text {i}} ) = 1\) clearly holds when looking at the definition of \(\varvec{C}^{\text {i}}_\text {r}\) in Eq. (40). Additionally, the consistency of \(\phi _\Delta \) with the time-continuous theory is trivially proven except for \(\Delta \alpha \). Therefore, we have a look at the approximation of \(a^{1+x}\) at \(x\ll 1\):
as \(\ln {a^x} \approx a^x-1\). Hence, we can approximate \(\varvec{C}^{\text {i}}_\text {r}\) as
We can use this result for computation of the time-discrete derivative of \(\alpha \):
Therefore, with the time step width going to zero, we obtain
which is consistent with the time-continuous Eq. (26). Furthermore, since  , we get for the time derivative of
, we get for the time derivative of  :
:

Hence, since \(\phi _{\Delta }\) is time-continuous, we can use the discretized potential to solve for \(\varvec{C}^{\text {i}}\) and \(\xi \):
3 Numerical strategies
The potential \(\pi _{\Delta }\), as we formulated it in Eq. (48) carries two major numerical difficulties. First, \(\varvec{C}^{\text {i}}\) is constrained to be volume preserving, i.e., \(\text {det}( \varvec{C}^{\text {i}} ) = 1\), which is very important to be exactly satisfied to comply with physics and not accumulate errors. Second, \(\pi _{\Delta }\) is not differentiable at \(\Delta _\text {r}\varvec{C}^{\text {i}}= 0\). The strategies employed to overcome these and other numerical difficulties as well as general numerical approaches are presented in this section.
3.1 Inelastic volume preservation
To deal with the constraint in \(\varvec{C}^{\text {i}}\), we employ a strategy using a projection of \(\varvec{C}^{\text {i}}\) into the space of unimodular tensors, which was introduced by Hurtado et al. [21] for crystal plasticity. Our approach here closely follows the approach presented in Sielenkämper et al. [44].
First, we express \(\varvec{C}^{\text {i}}\) in terms of the unconstrained inelastic auxiliary right Cauchy-Green tensor  :
:

Thus, \(\text {det}( \varvec{C}^{\text {i}} ) = 1\) is automatically satisfied. This idea is borrowed from various formulations in hyperelasticity, where similar approaches are used to decouple volumetric and deviatoric deformations (see, e.g., Flory and Volkenstein [13] or Simo et al. [45]). Now, we replace \(\varvec{C}^{\text {i}}\) by  in the minimization problem in Eq. (48):
in the minimization problem in Eq. (48):

However, while this removes the constraint from the minimization problem, \(\pi _{\Delta }\) is now invariant with respect to changes of  , and is therefore not uniquely solvable. For this reason, we add the regularization energy
, and is therefore not uniquely solvable. For this reason, we add the regularization energy

to \(\pi _{\Delta }\). We want to emphasize that this has no effect on the solution. This is due to the fact that  is exactly satisfied after converging to a solution, since \(\psi _\text {r}\) is the only term in \(\pi _{\Delta }\) that is dependent on
is exactly satisfied after converging to a solution, since \(\psi _\text {r}\) is the only term in \(\pi _{\Delta }\) that is dependent on  . Therefore, \(\psi _\text {r}\) is zero at any solution of the minimization problem. Further, the constants A and B can be chosen arbitrarily. They do not have to be chosen particularly large. In this paper, we chose \(B = 1\), but any other positive value could be chosen and would lead to the exact same results. In this special case,
. Therefore, \(\psi _\text {r}\) is zero at any solution of the minimization problem. Further, the constants A and B can be chosen arbitrarily. They do not have to be chosen particularly large. In this paper, we chose \(B = 1\), but any other positive value could be chosen and would lead to the exact same results. In this special case,  is exactly satisfied once the solution algorithm is converged. However, we want to note that this equality does not hold in the not yet converged state.
is exactly satisfied once the solution algorithm is converged. However, we want to note that this equality does not hold in the not yet converged state.
The following tensor, which is used in the residuals and stiffness terms later, is also known from hyperelastic models:

where  is the fourth-order identity on symmetric second-order tensors.
is the fourth-order identity on symmetric second-order tensors.
3.2 Differentiability at \(\Delta _\text {r}\varvec{C}^{\text {i}}= 0\)
The ansatz  renders the solution \(\varvec{C}^{\text {i}}\) a priori volume preserving, but it does not solve the lack of differentiability of \(\phi _{\Delta }\) for \(\varvec{C}^{\text {i}}= \varvec{C}^{\text {i}}_\text {r}\). However, this is achieved by the following reparametrization:
renders the solution \(\varvec{C}^{\text {i}}\) a priori volume preserving, but it does not solve the lack of differentiability of \(\phi _{\Delta }\) for \(\varvec{C}^{\text {i}}= \varvec{C}^{\text {i}}_\text {r}\). However, this is achieved by the following reparametrization:

where  is an unconstrained, symmetric 2nd-order tensor. The final unconstrained minimization problem now reads
is an unconstrained, symmetric 2nd-order tensor. The final unconstrained minimization problem now reads

It is easy to show that \(\pi _{\Delta }\) is invariant with respect to  . In order to render the solution unique, we further modify \(\psi _\text {r}\):
. In order to render the solution unique, we further modify \(\psi _\text {r}\):

where the choice of A, with the same argument as in Sect. 3.1, still has no effect on the solution. Additionally, the last term with a very small and constant \(\epsilon \) is explained in Sect. 3.5. Now, the minimization problem from Eq. (54) is computed by solving the stationary conditions:
where in general only a subset of these three equations is involved, depending on the ’active’ variables. The active set of variables is determined by the activation or yield criteria presented in the sequel (see Sects. 3.3 and 3.10).
3.3 Algorithmic yield criterion
In a given time step, \(\varvec{C}^{\text {i}}\) will only change (i.e., \(\varvec{C}^{\text {i}}\ne \varvec{C}_n^{\text {i}}\Leftrightarrow \Delta \gamma > 0\)), if this decreases (minimizes) the potential. In order to decide whether the couple  is activated for a given state \((\varvec{F},\varvec{C}^{\text {i}}_\text {r},\xi ,\theta )\), we evaluate the algorithmic yield condition
is activated for a given state \((\varvec{F},\varvec{C}^{\text {i}}_\text {r},\xi ,\theta )\), we evaluate the algorithmic yield condition

If \(f>0\), \(\Delta \gamma \) is activated, i.e.,  are put into the active set. Otherwise, \(\Delta \gamma = 0\) minimizes \(\pi _{\Delta }\), which corresponds to the case where
are put into the active set. Otherwise, \(\Delta \gamma = 0\) minimizes \(\pi _{\Delta }\), which corresponds to the case where  are part of the active set, the related equations and concerning residuals are: \(\partial \pi _{\Delta }/ \partial \Delta \gamma {\mathop {=}\limits ^{!}}0\) and
are part of the active set, the related equations and concerning residuals are: \(\partial \pi _{\Delta }/ \partial \Delta \gamma {\mathop {=}\limits ^{!}}0\) and  . For a given \(\varvec{F},\xi \) and \(\theta \), we obtain the explicit form of f by variation of \(\pi \): \(\Delta \gamma = 0\) if \(\pi _{\Delta }(\varvec{F},\varvec{C}^{\text {i}},\xi ,\theta )\) is minimized by \(\varvec{C}^{\text {i}}= \varvec{C}^{\text {i}}_\text {r}\). In other words, \(\Delta \gamma = 0\) is minimizer of \(\pi _{\Delta }\) if
. For a given \(\varvec{F},\xi \) and \(\theta \), we obtain the explicit form of f by variation of \(\pi \): \(\Delta \gamma = 0\) if \(\pi _{\Delta }(\varvec{F},\varvec{C}^{\text {i}},\xi ,\theta )\) is minimized by \(\varvec{C}^{\text {i}}= \varvec{C}^{\text {i}}_\text {r}\). In other words, \(\Delta \gamma = 0\) is minimizer of \(\pi _{\Delta }\) if

with the shorthand notation

for an arbitrary  and \(\delta \gamma \ge 0\). Further, taking a closer look at the variation of \(\pi _{\Delta }\), we obtain (compare Appendix B)
and \(\delta \gamma \ge 0\). Further, taking a closer look at the variation of \(\pi _{\Delta }\), we obtain (compare Appendix B)

Using the definition of the unimodular projector in Eq. (52), we obtain
With the definitions of \({\varvec{N}^{\text {s}}}\) in Eq. (59) and \({\text {DEV}}_{{\varvec{C}}^\text {i}_\text {r}}(\bullet )\) in Eq. (61) as well as making use of the fact that \(\varvec{U}^{\text {i}- 1}_n\) and \(\varvec{C}^{\text {i}- 1}_\text {r}\) are coaxial, we can simplify Eq. (60) to

Now, since inequality (58) must hold for arbitrary symmetric  , we get
, we get
Thus, the algorithmic yield criterion reads
However, note that for \(\xi =0\), and thus \(\varvec{C}^{\text {i}}_\text {r}= \varvec{C}_n^{\text {i}}\), we have a simplified yield criterion
where the superscript ’\({\text {tr}}\)’ denotes the trial state and \(\varvec{R}^{\text {i}}= \varvec{F}^{\text {i}}\varvec{U}^{\text {i}- 1}\). This result again shows the consistency with the time-continuous theory (see Eq. (33)).
3.4 Algorithmic transformation criteria
In analogy to Sect. 3.3, the activation criteria for forward (’\(\text {M}\)’, \(\Delta \xi \ge 0\)) and reverse (’\(\text {A}\)’, \(\Delta \xi <0\)) transformations read
where \(0^+\) and \(0^-\) denote the right- and left-hand limit (recall that \(\text {sg}\left( \xi \right) \) is an argument of Q in Eq. (41)).
3.5 Initial guess for 
In general, the direction of inelastic flow  is determined by the minimization of \(\pi _{\Delta }\) through a Newton scheme, which requires a reasonable initial guess when \(\Delta \gamma \) is activated. Coincidentally, an analytical solution for \(\Delta \gamma \rightarrow 0\) exists for
is determined by the minimization of \(\pi _{\Delta }\) through a Newton scheme, which requires a reasonable initial guess when \(\Delta \gamma \) is activated. Coincidentally, an analytical solution for \(\Delta \gamma \rightarrow 0\) exists for  :
:

The proof is given in Appendix B.
It is noted that for \(\Delta \gamma = 0\), it follows that \(\varvec{C}^{\text {i}}= \varvec{C}^{\text {i}}_\text {r}\), which is independent of  . That means that any choice of
. That means that any choice of  minimizes \(\pi _{\Delta }\), i.e., there is no unique solution. For very small \(\Delta \gamma \), the sensitivity of \(\pi _{\Delta }\) with respect to
minimizes \(\pi _{\Delta }\), i.e., there is no unique solution. For very small \(\Delta \gamma \), the sensitivity of \(\pi _{\Delta }\) with respect to  is also small, which can lead to a bad condition of the nonlinear equation system, which needs to be solved to minimize \(\pi _{\Delta }\). To stabilize the solution process, the last term in Eq. (55) is added to \(\pi \), since for \(\Delta \gamma \rightarrow 0\) it is known that
is also small, which can lead to a bad condition of the nonlinear equation system, which needs to be solved to minimize \(\pi _{\Delta }\). To stabilize the solution process, the last term in Eq. (55) is added to \(\pi \), since for \(\Delta \gamma \rightarrow 0\) it is known that  minimizes \(\pi _{\Delta }\). In theory, \(\epsilon \) can be chosen arbitrarily small, in practice a finite value is necessary due to the limited numerical accuracy. Thus, the last term in Eq. (55) is used to ’guide’ the algorithm toward the right solution when it is no longer able to find it by itself.
minimizes \(\pi _{\Delta }\). In theory, \(\epsilon \) can be chosen arbitrarily small, in practice a finite value is necessary due to the limited numerical accuracy. Thus, the last term in Eq. (55) is used to ’guide’ the algorithm toward the right solution when it is no longer able to find it by itself.
3.6 Computing derivatives of \(\Delta \alpha \) for \(\Delta \gamma \rightarrow 0\)
The derivatives of \(\Delta \alpha \) are numerically tough to obtain for \(\Delta \gamma \rightarrow 0\), due to an almost zero denominator of \(\tilde{\varvec{M}}_{{\varvec{C}}^{\text {i}}}\) (see Eq. (112) and preceding equations). To overcome this issue, we derived the derivatives of \(\Delta \gamma \) with respect to \(\xi \),  and \(\Delta \gamma \) separately for \(\Delta \gamma \rightarrow 0\), which are then numerically feasible to obtain. However, this seems to be a rather theoretical as we never observed the case that \(\Delta \gamma \) was too close to zero to obtain the derivatives using the usual way shown in Appendix C. Therefore, and for brevity, we do not discuss them here.
and \(\Delta \gamma \) separately for \(\Delta \gamma \rightarrow 0\), which are then numerically feasible to obtain. However, this seems to be a rather theoretical as we never observed the case that \(\Delta \gamma \) was too close to zero to obtain the derivatives using the usual way shown in Appendix C. Therefore, and for brevity, we do not discuss them here.
3.7 Regularization of \(\psi _\text {h}\)
Numerically, \(\psi _\text {h}\) is challenging, since with \(\big \langle \varvec{E}^{\text {t}}\big \rangle \rightarrow 1\), \(\psi _\text {h}\) and \(\partial \psi _\text {h}/ \partial \big \langle \varvec{E}^{\text {t}}\big \rangle \) go to infinity. This is very demanding, because values of \(\big \langle \varvec{E}^{\text {t}}\big \rangle \ge 1\) can occur during the iterative solution process of the Newton scheme, leading to a loss of convergence. The term (compare to Eq. (21))
is illustrated in Fig. 2 in black.
To stabilize the solution process, we partially replace the function \(\varphi \) by a linear approximation in the region where \(\big \langle \varvec{E}^{\text {t}}\big \rangle >c\), where c is close to 1 (see Fig. 2 in green). This regularization approach is adopted from crystal plasticity, where it successfully improved the numerical treatment of the power law in Wulfinghoff and Böhlke [52]. In order to prevent the solution \(\big \langle \varvec{E}^{\text {t}}\big \rangle \) from taking nonphysical solutions beyond 1, we add a penalty-type energy as illustrated in Fig. 3. We penalize all states \((\big \langle \varvec{E}^{\text {i}}\big \rangle ,\xi )\) (see Fig. 3) below the dashed half-line starting at \(\xi _0\) by the energy
where \(l_\text {F}\) is the minimum distance of the point \((\big \langle \varvec{E}^{\text {i}}\big \rangle ,\xi )\) from the half-line and \(H_\text {p}\) is a large penalty parameter.
3.8 Viscosity of the martensite volume fraction \(\xi \)
To further improve the numerical robustness, we added an artificial viscosity-like term for the martensite volume fraction. Since it is a dissipative term, we add this term to the discretized dissipation potential:
where \(\eta _\xi \) is a small, positive constant.
3.9 Thermomechanical coupling
Like the displacements, the temperature is an unknown for our model. Both fields are coupled through the thermomechanical energy and through the dissipative terms, which lead to a heating of the material. Additionally, the temperature changes the material behavior and leads to thermal strains. Both fields are coupled using a potential-based monolithic approach similar to the one presented in Yang et al. [54]. Further, we assume Fourier’s heat conduction law with heat conductivity \(\kappa \). The thermomechanic quasistatic time-discrete potential then reads
where we neglect the influence of body forces. The integral form \(\Pi _{\Delta }\) of the local potential \(\pi _{\Delta }\) is then given by
where w denotes the heat source and \(\bar{\hat{\varvec{t}}}\) as well as \(\bar{Q}\) denote prescribed tractions and normal heat flux at the Neumann-type boundaries \(\partial V_{{0\text {t}}}\) and \(\partial V_{0\text {Q}}\), respectively. Now, the classical weak form of the linear momentum balance is obtained by variation of Eq. (71) with respect to \(\varvec{u}\):
with \(\varvec{d}_\delta = \text {sym}( \text {Grad\!}\left( \delta \varvec{u} \right) \varvec{F}^{\text {-1}} )\). Likewise, we obtain the weak form of the energy balance by variation of Eq. (71) with respect to \(\theta \):

Subsequently, we find \(\varvec{u}, \theta , \xi , \varvec{C}^{\text {i}}\) by finding the solution to the saddle point problem
where \(\kappa _{{\varvec{u}}} = \{\varvec{u}: \varvec{u}= {\bar{\varvec{u}}}\ on\ \partial V_{0\text {u}}\}\) is the set of admissible displacements satisfying the Dirichlet boundary conditions imposed on the boundary \(\partial V_{0\text {u}}\) and \(\kappa _\theta = \{\theta : \theta = {\bar{\theta }}\ on\ \partial V_{0\theta }\}\) is the set of admissible temperatures satisfying the Dirichlet boundary conditions imposed on the boundary \(\partial V_{0\theta }\). Additionally, \(\varvec{z}\) is the vector of internal variables, i.e., \(\varvec{z}= (\xi ,\varvec{C}^{\text {i}})\).
Manipulating Eq. (74) using the definition \(s = -\partial \psi / \partial \theta \) as well as applying Gauss theorem, we obtain
where \(\varvec{N}\) is the external normal on the boundary \(\partial V_0\) in the reference configuration. To show consistency with the time-continuous theory, we take a look at the integrand over the volume integral in Eq. (76). By multiplying with \(\theta _n/\Delta t\), we get
Here, we want to note that this requires \(\kappa \) to be independent of the temperature \(\theta \). However, one possibility is to consider \(\kappa =\kappa (\theta _n)\), which could circumvent this limitation.
Now, for \(\Delta t\rightarrow 0\), we get (also see Eq. (35))
Hence, we arrived at the energy balance (Eq. (35)) with Fourier’s law \(\varvec{Q}= - \kappa \text {Grad\!}\left( \theta \right) \), which proves the consistency with the time-continuous theory. Further, the surface integrals in Eq. (76) imply the Neumann boundary condition \(\bar{Q} = -\kappa \text {Grad\!}\left( \theta \right) \cdot \varvec{N}\) on \(\partial V_{0\text {Q}}\). Alternatively, one can include Robin-type boundary conditions into the model by replacing the integrand \(\Delta t \bar{Q} \theta /\theta _n\) in Eq. (72) by \(1/2 \Delta t h(\theta -\theta _\text {s})^2/\theta _n\), where h is the heat convection coefficient and \(\theta _\text {s}\) is the temperature of the surrounding medium. In that case, the variation of \(\Pi _{\Delta }\) yields the boundary condition \(-\kappa \text {Grad\!}\left( \theta \right) \cdot \varvec{N}= h (\theta - \theta _\text {s})\) on \(\partial V_{0\text {Q}}\).
3.10 Active set search
When solving the set of Eq. (56), one has to decide which variables will evolve using the activation criteria given in Eqs. (64) and (66). They will then be put into the active array of variables  . If then, at a later state, an activation criterion is inactive, the variable is taken from
. If then, at a later state, an activation criterion is inactive, the variable is taken from  again. This is done using the active set search algorithm outlined in Algorithm 1.
again. This is done using the active set search algorithm outlined in Algorithm 1.


The algorithm is structured as follows: First, if  or no variable from
or no variable from  was rescaled (see the end of this subsection for an explanation of rescaling) during the last iteration, we need to evaluate the activation criteria. With them at hand, we determine our new set
was rescaled (see the end of this subsection for an explanation of rescaling) during the last iteration, we need to evaluate the activation criteria. With them at hand, we determine our new set  . The details for determining which variable to activate are given in Algorithm 2. Subsequently, we check if the active set changed from the last iteration. If this is not the case, the solution from the last iteration is confirmed as solution of the equation system. In that case, we compute the algorithmic tangent (see Appendix E for details), save the history variables and exit the material routine. Otherwise, we solve the minimization problem for the current active set
. The details for determining which variable to activate are given in Algorithm 2. Subsequently, we check if the active set changed from the last iteration. If this is not the case, the solution from the last iteration is confirmed as solution of the equation system. In that case, we compute the algorithmic tangent (see Appendix E for details), save the history variables and exit the material routine. Otherwise, we solve the minimization problem for the current active set  . This is done using a Newton scheme. First, we compute our residual and stiffness concerning active set
. This is done using a Newton scheme. First, we compute our residual and stiffness concerning active set  , i.e., only derivatives with respect to the active set are computed. If the maximum iterations are exceeded or the norm of the residual is lower than the tolerance, we exit the loop. Otherwise, we check if updating \(\xi ^{j+1}\) would result in a negative \(\xi \) when applying the Newton step. If this is the case, we rescale, i.e., multiply the increments by a scalar such that \(\xi ^\star _{k+1}\) is set to \(\xi ^\text { hard}_\text { min}\), which is \({5\times 10^{-5}}\) in this work. Subsequently, we compute \(\Delta \xi \star _{k+1}\), \(\Delta \Delta \gamma ^\star _{j+1}\) and
, i.e., only derivatives with respect to the active set are computed. If the maximum iterations are exceeded or the norm of the residual is lower than the tolerance, we exit the loop. Otherwise, we check if updating \(\xi ^{j+1}\) would result in a negative \(\xi \) when applying the Newton step. If this is the case, we rescale, i.e., multiply the increments by a scalar such that \(\xi ^\star _{k+1}\) is set to \(\xi ^\text { hard}_\text { min}\), which is \({5\times 10^{-5}}\) in this work. Subsequently, we compute \(\Delta \xi \star _{k+1}\), \(\Delta \Delta \gamma ^\star _{j+1}\) and  . In fact, we do not update \(\xi ^{j+1}\), \(\Delta \gamma ^{j+1}\) or
. In fact, we do not update \(\xi ^{j+1}\), \(\Delta \gamma ^{j+1}\) or  yet. We update them only after exiting the Newton scheme and being sure that \(\xi \) incremented in a direction matching \(g_\text {A}\) and \(g_\text {M}\), which were calculated before the Newton loop. If, due to a bad starting solution, this is not the case, we rescale the Newton step such that \(\xi ^{j+1}=\xi _n\). If this happens, we make sure that in the next iteration of the active set algorithm, we won’t activate \(\xi \) again.
yet. We update them only after exiting the Newton scheme and being sure that \(\xi \) incremented in a direction matching \(g_\text {A}\) and \(g_\text {M}\), which were calculated before the Newton loop. If, due to a bad starting solution, this is not the case, we rescale the Newton step such that \(\xi ^{j+1}=\xi _n\). If this happens, we make sure that in the next iteration of the active set algorithm, we won’t activate \(\xi \) again.
4 Numerical results
In this section, the previously presented model is tested for different examples. First, to test the model’s time convergence behavior and to show the superelastic as well as martensite reorientation behavior at high and low temperatures, respectively, thermomechanical Gauss point evaluations are conducted. Finally, a full actuator model is simulated. To cope with the thin structures occurring in the actuator, the SMA model at hand is embedded into a hexahedral element formulation with reduced integration and hourglass stabilization for the displacement, while the heat conduction terms are fully integrated.
4.1 Gauss point evaluations
For the Gauss point evaluations, thermal expansion as well as the transformation induced volume change, which is discussed in Sect. 2.3.4, are neglected for simplicity. The simulations are conducted using a reduced integration hexahedral element with hourglass stabilization, which is embedded into the finite element program FEAP [46]. The material constants used in the Gauss-point are given in Table 1.
Here, it is noted that \(\theta _{\text { refA}}\) and \(\theta _{\text { refA} }\) are chosen such that \(\Delta V = 0.47\%\) (see Eq. (23)), matching the findings reported in Potapov et al. [36]. The numerical parameters are summarized in Table 2.
Figure 4 shows a tensile test at a temperature of \({270}\,^{\circ }{\hbox {C}}\) for 49 and 40,000 time steps.
Clearly, convergence with regard to time step width is not an issue, as both time step widths yield accurate results.
To demonstrate that the model results indeed do not depend on the numerical parameters, we compare results for two different sets of numerical parameters in a tensile test. The first set of numerical parameters is the one given in Table 2, which is used in the remainder of this paper. The second set is defined in Table 3 just for this comparison. The results are shown in Fig. 5. Clearly, the numerical parameters do not have a noticeable effect on the results.
Next, we modeled tensile tests at \({50}\,^{\circ }{\hbox {C}}\), \({100}\,^{\circ }{\hbox {C}}\), \({160}\,^{\circ }{\hbox {C}}\) and \({200}\,^{\circ }{\hbox {C}}\). The resulting stress–strain curves are shown in Fig. 6.
For low temperatures, i.e. \({50}\,^{\circ }{\hbox {C}}\) and \({100}\,^{\circ }{\hbox {C}}\), the model predicts a remaining martensite reorientation. On the other hand, for rather high temperatures, the model captures superelastic material behavior when unloading. However, we want to emphasize that these results do not consider any damage or plastic deformations which might already occur.
Finally, the model captures the shape memory effect well. This is shown in Fig. 7, where we applied different stresses (160 MPa, 300 MPa, 400 MPa and 500 MPa) and then started a thermal cycle.
For \({160}\,{\hbox {MPa}}\), one obtains only twinned martensite, i.e., \(\varvec{E}^{\text {t}}= \varvec{0}\) in the context of this work. Therefore, one only gets a small hysteresis due to the different elastic constants of austenite and martensite. For the larger prestresses, the austenite is transformed into detwinned martensite, i.e., \(\big \langle \varvec{E}^{\text {t}}\big \rangle \ne 0\). This leads to the typical shape memory effect.
4.2 Plate with a hole
In this example, we simulate a plate with a cylindrical hole (see Fig. 8), which is at first loaded by a traction \(\bar{\hat{\varvec{t}}}\), then unloaded and subsequently heated, which lets it recover the initial shape.
The material and numerical parameters are unchanged from Sect. 4.1, except the reference temperatures are now \(\theta _{\text {refA}}={80}\,^{\circ }{\hbox {C}}\) and \(\theta _{\text {refM}} = {87.66}\,^{\circ }{\hbox {C}}\). Due to the symmetry, using appropriate symmetry conditions, only one-eighth of the entire plate is simulated.
During the loading by the traction, the temperature at the upper and lower end is held constant at the initial temperature of \(\bar{\theta }= {80}\,^{\circ }\hbox {C}\) (\(M_{\text {s}}<\bar{\theta }<A_{\text {s}}\)). Additionally, in the initial state, the plate is fully austenite. First, the traction \(\bar{\hat{\varvec{t}}}\) is increased linearly to a maximum of \({330}\,\hbox {MPa}\) in longitudinal direction over the duration of \({50}{\text {s}}\). Subsequently, the traction \(\bar{\hat{\varvec{t}}}\) is decreased to zero over the duration of \({50}{\text {s}}\). Finally, the temperature at both ends of the plate is increased to \({200}\,^{\circ }\hbox {C}\) over the course of \({20}{\text {s}}\).
The mesh used in the eighth of the plate consists of 2907 uniformly distributed elements and is shown in Fig. 9.
For the entire simulation, 293 time steps were required, taking a total CPU-time of \({2524}{\text {s}}\).
At first, during the loading, almost the entire plate is transformed to martensite. The plate at maximum traction is shown in Fig. 10a. Here, the \(E_{xx}\) strain at the edge of the hole reaches roughly up to 18% (see Fig. 11).
Additionally, the plate heats up slightly due to the latent heat and mechanical dissipation (Fig. 10a). However, most of the heat is conducted out of the plate at the temperature Dirichlet boundaries due to the small size of the plate and the long simulated timeFootnote 5. Subsequently, after unloading, the plate does not transform back, which is shown in Fig 10b. Finally, when increasing the temperature at both ends, the martensite is transformed back to austenite, leading to a recovery of the initial shape (see Fig. 10c). Further, Fig. 12 shows the temperature and displacement of point A (see Fig. 8) over time. Here, the increase in slope of the displacement at roughly \({15}{\text {s}}\) is the point where we have a forward transformation in the vicinity of the hole. Then, the second change in slope of the displacement at roughly \({36}{\text {s}}\) is the rest of the plate starting to undergo forward transformation. At \({50}{\text {s}}\), when releasing the traction, the displacements decrease. Then again, due to thermal expansion, the displacement increases slightly after increasing the temperature at the ends at \({100}{\text {s}}\). However, when the temperature reaches the backward transformation temperatures, the material almost recovers the initial shape. The nonzero displacement at \(t={120}{\text {s}}\) stems from thermal expansion and the \(\Delta V\) effect.
Overall, the examples have been chosen such that the stresses in the vicinity of the hole reach unphysical values, at which a real material is expected to show irrecoverable strains or even fracture. Thus, this simulation rather serves as an example showing that the implementation is able to find a solution, even under severe loads.
4.3 Finite element actuator model
In this section, we model a bistable shape memory microactuator using in the finite element program FEAP [46]. The actuator concept was published by Winzek et al. [50] for large structures and is built with three layers: a bottom layer of molybdenum, a middle layer of NiTiHf and a top layer of polymethyl methacrylate (PMMA) (Winzek et al. [50] used PMMA layers on both sides). For simplicity, a hexahedral element formulation with reduced integration and hourglass stabilization for the displacements is used for all materials. The material and numerical parameters for the shape memory alloy remain unchanged (see Tables 1 and 2).
4.3.1 Actuating principle
The actuator works through interlacing of the large hysteresis of NiTiHf with the polymers hysteresis. This is shown in Fig. 13.
Temperature and displacement at point A (see Fig. 8) over time
It is actuated by joule heating to specific temperatures and cooling back to room temperature. Depending on the heat cycle, the martensite state or austenite state is held in place by the polymer. This is understood best when looking at the following example, which is depicted in Fig. 14, where we neglected the CTE of PMMA for simplicity. Here, we compare a bimorph of SMA and molybdenum on the left to the proposed actuator on the right. When heating from ambient temperature (blue, Fig. 14a) to a temperature above \(A_{\text {f}}\) (red), the glass transition temperature is reached, which drastically decreases the stiffness of the PMMA. Subsequently, the SMA in the bimorph as well as the bistable actuator reach reverse transformation temperatures, which makes them bend up (Fig. 14b). Now, upon cooling, the actuator reaches \(\theta _\text {g}\), which ’freezes’ it’s current shape. Thus, when subsequently reaching forward transformation temperatures, unlike the bimorph, it will not revert into the original shape at room temperature (Fig. 14c). Now, we can heat the actuator to a temperature above \(\theta _\text {g}\) but below \(A_{\text {s}}\) (orange in Fig. 14d) to soften the polymer, which makes the actuator adopt the deformation of the bimorph. When now cooling back to room temperature again, the actuator is in it’s initial stable state again and the actuation cycle could be started again. The two stable states at room temperature are given by Figs. 14c, e.
For the actuation behavior, it is important to have a homogeneous temperature profile in the actuator. Therefore, a wing-shape actuator developed in Arivanandhan et al. [2] is used to obtain rather homogeneous temperatures in the double beam cantilever.
To rapidly optimize the actuators properties, it turned out that building and modeling only the beam section of the actuator is advantageous. Therefore, we simulated just the beam part with suitable boundary conditions instead of simulating the entire wing structure including the attached wafer material. This thin film actuator with a zoom into the layers is shown in Fig. 15, where the Dirichlet boundary condition for the displacements and the Robin boundary condition for the temperature are indicated as well.
4.3.2 Polymer and molybdenum model
Since the interest in modeling the actuator lies rather in the states at \(\theta _1\) , \(\theta _2\) and \(\theta _3\), and less in the states between them, we chose a very simple polymer model. It is governed by a thermally coupled viscoelastic Maxwell model for finite strains (Young’s modulus and Poisson’s ratio are \({500} \hbox { MPa}\) and 0.4, respectively), where the viscosity is high (\(10^{7} \hbox { MPas}\)) at low temperatures and low (\({1} \hbox { MPas})\) at high temperatures. Therefore, it has almost no stiffness at high temperatures while it behaves almost elastically at low ones. Additionally, the glass transition temperature is given by \(\theta _\text {g}= {77}^{\circ } \hbox {C}\). The molybdenum is modeled with a thermally coupled Neo-Hookean elastic model. For the molybdenum, Young’s modulus, Poisson’s ratio, the thermal expansion coefficient as well as the reference temperature are \(E={65\times 10^{3}} {\hbox { MPa}}\), \(\nu = 0.31\), \(\alpha =5 \times 10^{-6}{\hbox {K}^{-1}}\) and \(\theta _{\text {ref}} = {500}\,^{\circ }{\hbox {C}}\), respectively.
4.3.3 Mesh convergence
The actuator considered is shown in Fig. 15. It is clamped on the left side. It has a length of 10 mm, a width of 5 mm. The layer thicknesses of the molybdenum and TiNiHf are for this work  and
and  , respectively. The polymer layer thickness is
, respectively. The polymer layer thickness is  for now, before different layer thicknesses are compared in Sect. 4.3.4. For the initial conditions, we assume zero displacements as well as a temperature of \({500}\,^{\circ }{\hbox {C}}\), i.e., the temperature at which the actuator is thermally annealed in a flat state. Furthermore, we assume the material to be in its austenite state at \(t=0\), which directly implies that initially \(\varvec{C}^{\text {i}}=\varvec{I}\). Subsequently, it is cooled down to room temperature at \({20}\,^{\circ }{\hbox {C}}\), which bends the actuator due to the mismatch in the coefficients of thermal expansions and difference in cell volume between the austenite and martensite phase.
for now, before different layer thicknesses are compared in Sect. 4.3.4. For the initial conditions, we assume zero displacements as well as a temperature of \({500}\,^{\circ }{\hbox {C}}\), i.e., the temperature at which the actuator is thermally annealed in a flat state. Furthermore, we assume the material to be in its austenite state at \(t=0\), which directly implies that initially \(\varvec{C}^{\text {i}}=\varvec{I}\). Subsequently, it is cooled down to room temperature at \({20}\,^{\circ }{\hbox {C}}\), which bends the actuator due to the mismatch in the coefficients of thermal expansions and difference in cell volume between the austenite and martensite phase.
The heating cycle is realized through applying a heat source in the Mo and NiTiHf material. The heat source magnitude is modeled by a sine function, which is cut off when below 0. It is given by
for the higher and lower heat cycles, respectively.
At the top and at the bottom face of the actuator a Robin boundary condition is applied, which cools the thin film to room temperature over time. Due to their small areas, the heat transfer at the lateral faces is neglected. The surrounding air’s temperature is \({20}\,^{\circ }{\hbox {C}}\) while the convective heat transfer coefficient is assumed to be \({70}\hbox { W m}^{-2}\,\hbox { K}^{-1}\) in accordance with Kohl et al. [23].
For these thin structures, a sufficiently fine mesh is crucial to obtain converged results. Therefore, we conducted convergence studies with regard to the necessary elements in each layer and the amount of elements needed over the length and width of the actuator. First, it turned out that due to the bending deformation of the thin film, it is sufficient to only use one element over the width of the actuator. Then, the convergence with respect to the amount of elements over the length is tested using four elements over the thickness for each material layer. The results are shown in Fig. 16, where the stroke and temperature of the SMA at the tip is plotted over time. Here, only the temperature for 20 elements over the length is shown, since there was virtually no difference in temperature for the different discretizations. Further, we concluded that using 20 elements over the length leads to an acceptable error in stroke while the main features of the actuator are conveyed well. Additionally, roughly 160 time steps were used for one actuation cycle, e.g., from \({0}~\hbox {s}\) to \({180}~{\hbox {s}}\) in Fig. 16.
Next, the convergence with regards to the elements used over the depth for each material was studied. The results are depicted in Fig. 17.
Here, for the number of elements over the SMA thickness, one element is already enough to obtain results with an acceptable error. For the molybdenum and polymer layer, one needs at least two elements to obtain converged results.
To illustrate the importance of modeling the \(\Delta V\) effect, Fig. 18 shows the stroke and temperature over time for \(\Delta V\) being 0 and \(0.49\%\). Here, one can see that the volume change contributes to large parts of the achieved stroke between the two stable states at room temperature.
4.3.4 Influence of the polymer thickness
The polymer layer thickness plays a key role for this actuator design—if it is too thin, the high temperature shape cannot be held at room temperature by the polymer layer. On the other hand, it should not be too thick, since body forces and manufacturing problems come up in that case. Further, since the polymer insulates the actuator thermally to one side, thinner polymer layers lead to the possibility of faster actuation cycles. Therefore, we tested several polymer layer thicknesses, the results are shown in Fig. 19.
First, at  (see Fig. 19), the actuator is heated. At first, the larger CTE of the polymer makes the actuator bend down. Then, when reaching \(\theta _\text {g}\), the polymer softens up and the actuator relaxes. Subsequently, at
(see Fig. 19), the actuator is heated. At first, the larger CTE of the polymer makes the actuator bend down. Then, when reaching \(\theta _\text {g}\), the polymer softens up and the actuator relaxes. Subsequently, at  , the actuator is cooled down to room temperature by the surrounding air. The polymer hardens again and the device reaches stable configuration
, the actuator is cooled down to room temperature by the surrounding air. The polymer hardens again and the device reaches stable configuration  at room temperature. Now, when heating again, the actuator bends down due to the large CTE of the PMMA at
at room temperature. Now, when heating again, the actuator bends down due to the large CTE of the PMMA at  . As soon as the temperature reaches \(\theta _\text {g}\), the polymer softens up. Afterward, at
. As soon as the temperature reaches \(\theta _\text {g}\), the polymer softens up. Afterward, at  the shape memory alloy reaches \(A_{\text {f}}\) and the martensite is transformed back to austenite, which makes the actuator deflect up. Finally, when we remove the source at
the shape memory alloy reaches \(A_{\text {f}}\) and the martensite is transformed back to austenite, which makes the actuator deflect up. Finally, when we remove the source at  , the polymer hardens before \(M_{\text {f}}\) is reached. Thus, depending on the polymer thickness, the polymer may hold the actuators shape or release some of it’s stroke. Finally, the actuator reaches it’s second stable state
, the polymer hardens before \(M_{\text {f}}\) is reached. Thus, depending on the polymer thickness, the polymer may hold the actuators shape or release some of it’s stroke. Finally, the actuator reaches it’s second stable state  at room temperature, which is also it’s initial state.
at room temperature, which is also it’s initial state.
For many actuator designs, one wants to maximize the achievable stroke while keeping the device as small and power efficient as possible. Therefore, we try to maximize the difference in stroke between states  and
and  . In turn, one must choose a sufficient polymer thickness, such that the actuator does not release too much stroke at
. In turn, one must choose a sufficient polymer thickness, such that the actuator does not release too much stroke at  . For example, 0.1mm of PMMA is not thick enough to hold the shape, while 0.3 mm holds the shape perfectly (see Fig. 19 at
. For example, 0.1mm of PMMA is not thick enough to hold the shape, while 0.3 mm holds the shape perfectly (see Fig. 19 at  ). Depending on the actuation frequency in mind and necessary achievable stroke, either value in between might be a suitable choice.
). Depending on the actuation frequency in mind and necessary achievable stroke, either value in between might be a suitable choice.
5 Summary and outlook
In this paper, a new thermomechanical shape memory alloy model for finite strains is presented. It uses a projection method to fulfill the incompressibility constraint for the inelastic stretches. Further, the model is realized in the generalized standard material formulation being extended to thermomechanics. The optimization of the global, incremental mixed thermomechanical potential by variation yields the mechanical balance principles as well as the evolution equations of the internal variables and boundary condition integrals. The presented model employs a thermal strain formulation for the shape memory alloy which allows to describe the transformation induced volume changes found in some shape memory alloys. Using a logarithmic strain formulation, a finite strain dissipation potential incorporates vanishing inelastic strains upon austenite transformation in a manner consistent with the time-continuous case. Additionally, yield and transformation criteria as well as the algorithmically consistent tangent for the coupled problem are given and discussed. Due to numerical difficulties, a regularization of the hardening energy term is implemented.
The numerical results show, that the model is capable of producing reasonable results in tensile tests. The dependency on the temperature at which the tensile tests are carried out is captured accurately. Furthermore, it enables the solution of thin film problems.
Using the model, we are now able to estimate viable layer thicknesses and device sizes as well as fitting joule heating parameters. Additionally, it turned out that only applying polymer to one side increases the maximum actuation frequency while also introducing more deflection between the stable states and requiring more power. Moreover, we found that the \(\Delta V\) effect as well as the thermal expansion of the SMA, due to the design being very sensitive to volume changes, is fairly important for the actuators stroke and therefore needs to be modeled accurately as well. Furthermore, the model results show that the bistability at room temperature, which is enabled by the polymer locking in the deformation, is achievable for the shown actuator concept.
In the future, it remains interesting to find ways of solving the model problem without any penalty terms, which are not reasoned physically and are numerically challenging to deal with. A possible solution to this problem could be to make use of the Fischer-Burmeister [12] complementary function. In fact, this has been done in Auricchio et al. [4] for shape memory alloys and in Brepols et al. [7] for damage-plasticity with great success. Furthermore, there is still space for improvements to the algorithms convergence behavior which could increase the speed of the proposed material model, especially under severe loading conditions. Additionally, an inclusion of functional fatigue properties, e.g., a shifting of the TiNiHf transformation temperatures over several transformation cycles into the model would enable to predict the long-term behavior of the actuators.
Notes
For brevity, \(\varvec{F}^{\text {i}}\) is called the inelastic part of the deformation gradient throughout this paper.
For brevity, \(\varvec{F}^{\theta }\) is called the thermal part of the deformation gradient throughout this paper.
Actually, for some shape memory alloys, there exists a difference in density between the martensite and austenite phase. For NiTiHf, see the article by Potapov et al. [36] and for modeling approaches for this effect in NiTi the work of Qidwai and Lagoudas [37]. We also model this phenomenon in Sect. 2.3.4.
For brevity and simplicity, we dropped the index \(n+1\) whenever we deemed it to be not helpful for the presentation.
A separate simulation with “zero heat flux” boundary conditions led to a temperature increase in approximately \({50}\,^{\circ }\hbox {C}\).
References
Arghavani, J., Auricchio, F., Naghdabadi, R.: A finite strain kinematic hardening constitutive model based on Hencky strain: general framework, solution algorithm and application to shape memory alloys. Int. J. Plast. 27(6), 940–961 (2011). https://doi.org/10.1016/j.ijplas.2010.10.006
Arivanandhan, G., Li, Z., Curtis, S., Velvaluri, P., Quandt, E., Kohl, M.: Temperature homogenization of co-integrated shape memory-silicon bimorph actuators. Proceedings (2020). https://doi.org/10.3390/IeCAT2020-08501
Auricchio, F., Reali, A., Stefanelli, U.: A three-dimensional model describing stress-induced solid phase transformation with permanent inelasticity. Int. J. Plast. 23(2), 207–226 (2007). https://doi.org/10.1016/j.ijplas.2006.02.012
Auricchio, F., Bonetti, E., Scalet, G., Ubertini, F.: Theoretical and numerical modeling of shape memory alloys accounting for multiple phase transformations and martensite reorientation. Int. J. Plast. 59, 30–54 (2014). https://doi.org/10.1016/j.ijplas.2014.03.008
Bellini, C., Berto, F., Di Cocco, V., Iacoviello, F.: A cyclic integrated microstructural-mechanical model for a shape memory alloy. Int. J. Fatigue 153, 106473 (2021). https://doi.org/10.1016/j.ijfatigue.2021.106473
Bernardini, D., Pence, T.J.: Models for one-variant shape memory materials based on dissipation functions. Int. J. Non-Linear Mech. 37(8), 1299–1317 (2002). https://doi.org/10.1016/S0020-7462(02)00020-3
Brepols, T., Wulfinghoff, S., Reese, S.: Gradient-extended two-surface damage-plasticity: micromorphic formulation and numerical aspects. Int. J. Plast. 97, 64–106 (2017). https://doi.org/10.1016/j.ijplas.2017.05.010
Cisse, C., Zaki, W., Ben Zineb, T.: A review of constitutive models and modeling techniques for shape memory alloys. Int. J. Plast. 76, 244–284 (2016). https://doi.org/10.1016/j.ijplas.2015.08.006
Du, H., Chau, F.S., Zhou, G.: Mechanically-tunable photonic devices with on-chip integrated mems/nems actuators. Micromachines 7(4), 69 (2016). https://doi.org/10.3390/mi7040069
Eckart, C.: The thermodynamics of irreversible processes. IV. The theory of elasticity and anelasticity. Phys. Rev. 73(4), 373 (1948). https://doi.org/10.1103/PhysRev.73.373
Eichenfield, M., Camacho, R., Chan, J., Vahala, K.J., Painter, O.: A picogram-and nanometre-scale photonic-crystal optomechanical cavity. Nature 459(7246), 550–555 (2009). https://doi.org/10.1038/nature08061
Fischer, A.: A special newton-type optimization method. Optimization 24(3–4), 269–284 (1992). https://doi.org/10.1080/02331939208843795
Flory, P.J., Volkenstein, M.: Statistical mechanics of chain molecules. Biopolymers 8(5), 699–700 (1969). https://doi.org/10.1002/bip.1969.360080514
Frost, M., Benešová, B., Sedlák, P.: A microscopically motivated constitutive model for shape memory alloys: formulation, analysis and computations. Math. Mech. Solids 21(3), 358–382 (2016). https://doi.org/10.1177/1081286514522474
Gall, K., Sehitoglu, H., Chumlyakov, Y.I., Kireeva, I.V.: Tension-compression asymmetry of the stress-strain response in aged single crystal and polycrystalline niti. Acta Mater. 47(4), 3 (1999). https://doi.org/10.1016/S1359-6454(98)00432-7
Govindjee, S., Mielke, A., Hall, G.J.: The free energy of mixing for n-variant martensitic phase transformations using quasi-convex analysis. J. Mech. Phys. Solids 51(4), I–XXVI (2003). https://doi.org/10.1016/S0022-5096(03)00015-2
Halphen, B., Nguyen, Q.S.: Sur les matériaux standard généralisés. (1975)
Han, S., Seok, T.J., Quack, N., Yoo, B.-W., Wu, M.C.: Large-scale silicon photonic switches with movable directional couplers. Optica 2(4), 370–375 (2015). https://doi.org/10.1364/OPTICA.2.000370
Hartl, D.J., Chatzigeorgiou, G., Lagoudas, D.C.: Three-dimensional modeling and numerical analysis of rate-dependent irrecoverable deformation in shape memory alloys. Int. J. Plast. 26(10), 1485–1507 (2010). https://doi.org/10.1016/j.ijplas.2010.01.002
Hoffmann, M., Bezzaoui, H., Voges, E.: Micromechanical cantilever resonators with integrated optical interrogation. Sens. Actuators A 44(1), 71–75 (1994). https://doi.org/10.1016/0924-4247(94)00776-4
Hurtado, D., Stainier, L., Ortiz, M.: The special-linear update: an application of differential manifold theory to the update of isochoric plasticity flow rules. Int. J. Numer. Methods Eng. 97(4), 298–312 (2014). https://doi.org/10.1002/nme.4600
Kohl, M.: Shape Memory Microactuators. Springer, Berlin (2004)
Kohl, M., Krevet, B., Just, E., Sma microgripper system. Sens. Actuators A Phys. 97–98, 646–652. https://doi.org/10.1016/S0924-4247(01)00803-2
Kröner, E.: Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Arch. Ration. Mech. Anal. 4(1), 273 (1959). https://doi.org/10.1007/BF00281393
Lagoudas, D.C., Entchev, P.B., Popov, P., Patoor, E., Brinson, L.C., Gao, X.: Shape memory alloys, part II: modeling of polycrystals. Mech. Mater. 38(5), 430–462 (2006). https://doi.org/10.1016/j.mechmat.2005.08.003
Lee, E.H.: Elastic-plastic deformation at finite strains. J. Appl. Mech. 36(1), 1–6 (1969). https://doi.org/10.1115/1.3564580
Lester, B.T., Baxevanis, T., Chemisky, Y., Lagoudas, D.C.: Review and perspectives: shape memory alloy composite systems. Acta Mech. 226(12), 3907–3960 (2015). https://doi.org/10.1007/s00707-015-1433-0
Lexcellent, C., Boubakar, M., Bouvet, C., Calloch, S.: About modelling the shape memory alloy behaviour based on the phase transformation surface identification under proportional loading and anisothermal conditions. Int. J. Solids Struct. 43(3), 613–626 (2006). https://doi.org/10.1016/j.ijsolstr.2005.07.004
Mirzaeifar, R., DesRoches, R., Yavari, A., Gall, K.: A micromechanical analysis of the coupled thermomechanical superelastic response of textured and untextured polycrystalline niti shape memory alloys. Acta Mater. 61(12), 4542–4558 (2013). https://doi.org/10.1016/j.actamat.2013.04.023
Moumni, Z., Zaki, W., Nguyen, Q.S.: Theoretical and numerical modeling of solid-solid phase change: application to the description of the thermomechanical behavior of shape memory alloys. Int. J. Plast. 24(4), 614–645 (2008). https://doi.org/10.1016/j.ijplas.2007.07.007
Müller, C., Bruhns, O.: A thermodynamic finite-strain model for pseudoelastic shape memory alloys. Int. J. Plast. 22(9), 1658–1682 (2006). https://doi.org/10.1016/j.ijplas.2006.02.010
Nemat-Nasser, S.: On finite deformation elasto-plasticity. Int. J. Solids Struct. 18(10), 857–872 (1982). https://doi.org/10.1016/0020-7683(82)90070-1
Otsuka, K., Ren, X.: Physical metallurgy of ti-ni-based shape memory alloys. Prog. Mater Sci. 50(5), 511–678 (2005). https://doi.org/10.1016/j.pmatsci.2004.10.001
Panico, M., Brinson, L.: A three-dimensional phenomenological model for martensite reorientation in shape memory alloys. J. Mech. Phys. Solids 55(11), 2491–2511 (2007). https://doi.org/10.1016/j.jmps.2007.03.010
Patoor, E., Lagoudas, D.C., Entchev, P.B., Brinson, L.C., Gao, X.: Shape memory alloys, part I: general properties and modeling of single crystals. Mech. Mater. 38(5), 391–429 (2006). https://doi.org/10.1016/j.mechmat.2005.05.027
Potapov, P., Shelyakov, A., Gulyaev, A., Svistunov, E., Matveeva, N., Hodgson, D.: Effect of hf on the structure of ni-ti martensitic alloys. Mater. Lett. 32(4), 247–250 (1997). https://doi.org/10.1016/S0167-577X(97)00037-2
Qidwai, M., Lagoudas, D.: On thermomechanics and transformation surfaces of polycrystalline niti shape memory alloy material. Int. J. Plast. 16(10), 1309–1343 (2000). https://doi.org/10.1016/S0749-6419(00)00012-7
Reese, S., Christ, D.: Finite deformation pseudo-elasticity of shape memory alloys—constitutive modelling and finite element implementation. Int. J. Plast. 24(3), 455–482 (2008). https://doi.org/10.1016/j.ijplas.2007.05.005
Rezaee-Hajidehi, M., Tůma, K., Stupkiewicz, S.: Gradient-enhanced thermomechanical 3d model for simulation of transformation patterns in pseudoelastic shape memory alloys. Int. J. Plast. 128, 102589 (2020). https://doi.org/10.1016/j.ijplas.2019.08.014
Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton, 2015. ISBN 9781400873173. https://doi.org/10.1515/9781400873173
Scalet, G., Karakalas, A., Xu, L., Lagoudas, D.: Finite strain constitutive modelling of shape memory alloys considering partial phase transformation with transformation-induced plasticity. Shape Memory Superelast. 7(2), 206–221 (2021). https://doi.org/10.1007/s40830-021-00330-5
Sedlák, P., Frost, M., Benešová, B., Ben Zineb, T., Šittner, P.: Thermomechanical model for niti-based shape memory alloys including r-phase and material anisotropy under multi-axial loadings. Int. J. Plast. 39, 132–151 (2012). https://doi.org/10.1016/j.ijplas.2012.06.008
Seelecke, S., Müller, I.: Shape memory alloy actuators in smart structures: modeling and simulation. Appl. Mech. Rev. 57(1), 23–46 (2004). https://doi.org/10.1115/1.1584064
Sielenkämper, M., Dittmann, J., Wulfinghoff, S.: Numerical strategies for variational updates in large strain inelasticity with incompressibility constraint. Int. J. Numer. Methods Eng. https://doi.org/10.1002/nme.6855
Simo, J., Taylor, R., Pister, K.: Variational and projection methods for the volume constraint in finite deformation elasto-plasticity. Comput. Methods Appl. Mech. Eng. 51(1), 177–208 (1985). https://doi.org/10.1016/0045-7825(85)90033-7
Taylor, R.L.: FEAP—finite element analysis program. http://projects.ce.berkeley.edu/feap/ (2017)
Wang, B., Zhu, S.: Cyclic tension-compression behavior of superelastic shape memory alloy bars with buckling-restrained devices. Constr. Build. Mater. 186, 103–113 (2018). https://doi.org/10.1016/j.conbuildmat.2018.07.047
Wang, J., Moumni, Z., Zhang, W.: A thermomechanically coupled finite-strain constitutive model for cyclic pseudoelasticity of polycrystalline shape memory alloys. Int. J. Plast. 97, 194–221 (2017). https://doi.org/10.1016/j.ijplas.2017.06.003
Wang, J., Moumni, Z., Zhang, W., Xu, Y., Zaki, W.: A 3d finite-strain-based constitutive model for shape memory alloys accounting for thermomechanical coupling and martensite reorientation. Smart Mater. Struct. 26(6), 065006 (2017). https://doi.org/10.1088/1361-665x/aa6c17
Winzek, B., Schmitz, S., Rumpf, H., Sterzl, T., Hassdorf, R., Thienhaus, S., Feydt, J., Moske, M., Quandt, E.: Recent developments in shape memory thin film technology. Mater. Sci. Eng. A 378(1), 40–46 (2004). https://doi.org/10.1016/j.msea.2003.09.105
Wriggers, P.: Nonlinear Finite Element Methods. Springer, Berlin (2008)
Wulfinghoff, S., Böhlke, T.: Equivalent plastic strain gradient crystal plasticity—enhanced power law subroutine. GAMM-Mitteilungen 36(2), 134–148 (2013). https://doi.org/10.1002/gamm.201310008
Xu, L., Solomou, A., Baxevanis, T., Lagoudas, D.: Finite strain constitutive modeling for shape memory alloys considering transformation-induced plasticity and two-way shape memory effect. Int. J. Solids Struct. 221, 42–59 (2021). https://doi.org/10.1016/j.ijsolstr.2020.03.009
Yang, Q., Stainier, L., Ortiz, M.: A variational formulation of the coupled thermo-mechanical boundary-value problem for general dissipative solids. J. Mech. Phys. Solids 54(2), 401–424 (2006). https://doi.org/10.1016/j.jmps.2005.08.010
Yu, C., Kang, G., Sun, Q., Fang, D.: Modeling the martensite reorientation and resulting zero/negative thermal expansion of shape memory alloys. J. Mech. Phys. Solids 127, 295–331 (2019). https://doi.org/10.1016/j.jmps.2019.03.015
Zaki, W., Moumni, Z., Morin, C.: Modeling tensile-compressive asymmetry for superelastic shape memory alloys. Mech. Adv. Mater. Struct. 18(7), 559–564 (2011). https://doi.org/10.1080/15376494.2011.605016
Zhang, M., Baxevanis, T.: An extended three-dimensional finite strain constitutive model for shape memory alloys. J. Appl. Mech. 88(11), 08 (2021). https://doi.org/10.1115/1.4051833.111010
Acknowledgements
Financial support of subproject A3 Cooperative Actuator Systems for Nanomechanics and Nanophotonics: Coupled Simulation of the Priority Programme SPP 2206 by the German Research Foundation (DFG) (Grant WU847/3-1) is gratefully acknowledged by the authors.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
A Discussion of the dissipation potential \(\phi _{\Delta }\)
In this section, we have a close look at the term
from Eq. (26). If this term is zero, then \(\varvec{b}^{\text {i}}\rightarrow \varvec{I}\) for \(\xi \rightarrow 0\).
Proof
Consider \(\xi (t) = \xi _0 \left( 1-\frac{t}{T}\right) \) and \(\varvec{D}^{\text {i}}= \frac{\dot{\xi }}{\xi _0}{\varvec{\varepsilon }}^\text {i}_0 = -\frac{1}{2T}\ln {(\varvec{b}^\text {i}_0)}\). Then
While this only shows that \(\varvec{b}^{\text {i}}\) goes to \(\varvec{I}\) for one special \(\xi (t)\), one could easily rescale the time to obtain arbitrary \(\xi (t)\), for which \(\varvec{b}^{\text {i}}\rightarrow \varvec{I}\) with \(\xi \rightarrow 0\).
B Proof of  minimizing \(\pi _{\Delta }\) for \(\Delta \gamma \rightarrow 0\)
minimizing \(\pi _{\Delta }\) for \(\Delta \gamma \rightarrow 0\)
Proof
We are looking for  minimizing \(\pi _\Delta \) for \(\Delta \gamma \rightarrow 0\):
minimizing \(\pi _\Delta \) for \(\Delta \gamma \rightarrow 0\):
where the variation is done exclusively with respect to  . Here, the dissipation potential \(\phi _{\Delta }\) is neglected because
. Here, the dissipation potential \(\phi _{\Delta }\) is neglected because

Since \(\pi _\Delta \) is constructed such that it is minimized by  , we constrain
, we constrain  to be in the subspace of symmetric 2nd-order tensors satisfying
to be in the subspace of symmetric 2nd-order tensors satisfying  (i.e., we only search this subspace for the minimizer). Hence,
(i.e., we only search this subspace for the minimizer). Hence,  and
and
which is independent of  .
.
With the definition of the tensor

Eq. (81) becomes

Since \({\varvec{N}^{\text {i}}}\) is normalized (i.e., its norm is one), the solution reads
which leads to  in Eq. (67).
in Eq. (67).
C First derivatives of \(\pi _\Delta \)
To minimize the potential using the active set algorithm including the Newton scheme, we need to obtain first and second-order derivatives of the potential with respect to the set of internal variables and temperature. The differential of the discretized potential with respect to the internal variables (\(\varvec{u}\) and \(\theta \) are fixed) is given by

where, for simplicity, the factor \(\theta /\theta _n\) is neglected in front of \(\sigma ^{\text {reo}}\), Q and H. Here, the tensor  is given by (see Eq. (59))
is given by (see Eq. (59))

Further, the derivative of \(\varvec{C}^{\text {i}}_\text {r}\) with respect to \(\Delta \xi \) is (see Eq. (40))
where \(H_-(\Delta \xi )\) is the double negative Heaviside function: \(H_-(\Delta \xi ) = -H(-\Delta \xi )\). The remaining occurring derivatives are given by





Here, \(a_1\) is the slope of the linear approximation in Fig. 2 at \(\big \langle \varvec{E}^{\text {t}}\big \rangle = ck\) and \(a_0\) is the value of the function \(\varphi \) at that same point. Further, the terms related to \(\psi _\text {p}\) are set to zero if \(\xi > \big \langle \varvec{E}^{\text {i}}\big \rangle /c+\xi _0\).
D Second derivatives of \(\pi _{\Delta }\)
The second derivatives of the potential \(\pi _{\Delta }\) are necessary to compute the algorithmic tangent. They are briefly given in this appendix. First, we define the symmetrizing box product as
where \(\varvec{A}\) and \(\varvec{B}\) are arbitrary second-order tensors. Now, we compute the differential of the operator  :
:

where \(\varvec{B}\) is an arbitrary symmetric second-order tensor and

Here, \(\varvec{B}\) is defined as

Similarly, we define the derivative of \(\mathbb {P}_{\text {i}}\) via

with

Subsequently, we find for the derivatives of \(\pi _{\Delta }\):






Here, for the occurring derivatives we find:
















E Consistent tangent
When using the finite element method to solve boundary value problems, we make use of the consistent tangent operator. To derive it with respect to \(\varvec{d}_\text {d}\) from the potential, we start with the virtual work of the internal forces
Here, \(\varvec{d}_\delta \) is defined as
Now, we need to calculate the differential of virtual work of the internal forces:
where through using the symmetry of \({\varvec{\tau }}\) we can simplify to
Now, the differential reads

where the first term, i.e., \(\varvec{l}_\text {d}{\varvec{\tau }}\varvec{l}_\delta ^\mathsf{T}\) is related to the so-called geometric tangent and the second term arises from the incremental material stiffness. Further, \(\varvec{l}_\text {d}\) and \(\varvec{d}_\text {d}\) are defined in analogy to \(\varvec{l}_\delta \) and \(\varvec{d}_\delta \). Here, we neglected, in a first step, the influence of perturbations \(\text {d}\theta \) of the temperature (for the full linearization, see below). Now, we can split  into the elastic and inelastic parts:
into the elastic and inelastic parts:

where (with a small abuse of notation)  denotes the vector of active variables and may contain \(\xi \), \(\Delta \gamma \) and
denotes the vector of active variables and may contain \(\xi \), \(\Delta \gamma \) and  . Additionally, the elastic tangent
. Additionally, the elastic tangent  is given by
is given by

Next, we need to obtain  . Therefore, we take a look at the local Newton scheme, where
. Therefore, we take a look at the local Newton scheme, where

holds in the converged state. Now, calculating the differential of Eq. (162), we obtain

Rearranging the result from Eq. (163) we obtain

which we can insert into Eq. (160) to finally obtain the algorithmic tangent:

In here, the term  is computed as
is computed as

with the additional derivatives




Additionally, the algorithmic consistent tangent with respect to \(\theta \) as well as the mixed contributions can be computed through linearizing the weak form in Eq. (74):

Here, the derivative \(\partial \tau / \partial \theta \) is given by

with

Now, using standard formulations for the element ansatz functions \(\varvec{N}\) and its gradients \(\varvec{B}\), one can assemble the element stiffness matrix (see, e.g., Wriggers [51]).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sielenkämper, M., Wulfinghoff, S. A thermomechanical finite strain shape memory alloy model and its application to bistable actuators. Acta Mech 233, 3059–3094 (2022). https://doi.org/10.1007/s00707-022-03236-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-022-03236-0



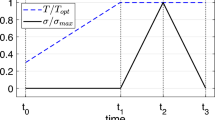




















 minimizing
minimizing