1 Introduction

One of the main drawbacks of structural composites is—apart from the numerous and obvious advantages—that these materials are susceptible to delamination failure. The delamination or interlaminar fracture alters significantly the dynamic properties of such structural elements. The free vibration analysis of delaminated structures has been investigated since several decades in the literature. The earliest solutions were based on the application of Euler–Bernoulli and Timoshenko beam theories [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16].

For the free vibration characterization of delaminated beams, the free and constrained mode models were introduced originally in [2]. The free mode model is based on the assumption of independent deflections of the top and bottom subbeams of the delaminated part. This model was found to be physically inconsistent providing interpenetration of the top and bottom subbeams into each other. The constrained mode model, on the other hand, does not make any delamination opening possible during free vibration and leads to a certain stiffening effect compared to the free mode model. In other words, higher stiffness leads to higher frequencies provided that the mass is the same [17].

In the related field, Shen and Grady published an important paper performing vibration measurements and numerical analysis on delaminated beams [18]. They also displayed the mode shapes and showed that the vibration shape is asymmetric during one vibration period. This was obviously an important experimental observation. Later, some more papers were published and the delamination opening was captured by different approximations [8, 9, 19]. In [20], nonlinear springs were placed between the crack faces of the top and bottom subbeams. The delamination opening was controlled by the spring stiffness, although only some limit cases were investigated effectively.

The current and recent literature offers large number of works carried out on delaminated composite and sandwich beams under different circumstances. Many authors investigated the problem of multiple delaminated clamped and clamped–clamped beams [16, 21,22,23]. In these papers, the first and second eigenshapes were determined. In a series or articles [24,25,26], the contact between the delamination faces was modeled and it was concluded that the frequencies decrease with the increase in delamination length. Other authors applied higher-order model analysis [6, 27]) and finite element models [28, 29] assuming that the delamination opening takes place because of the inertia forces. In [30], experimental results on natural frequency were presented for cross-ply laminated beams using traditional models. In [31], the free vibration of delaminated beams was analyzed considering fluid-structure interaction. The so-called dynamic stiffness method was applied in [32, 33] to delaminated composite beams. Moreover, in [34] a delaminated beam subjected to a follower force was analyzed leading to an interesting engineering problem and results. Finally, but not least papers for delamination detection are available as well, e.g.: [35, 36]. For sandwich beams with partial delaminations and debonding effect, some recent articles are available, too [37,38,39,40]. Models developed for delaminated beams were also extended to plates and shells for the linear and nonlinear vibration analysis by the finite element [41,42,43,44] and meshfree [45] methods.

Another important effect is the bending-stretching coupling on the natural frequencies of delaminated beams. Shu and Fan [4] found that the flexural and longitudinal frequencies of Euler–Bernoulli beams are far from each other; therefore, the coupling effect is negligible. Actually, in [20, 28] the agreement with the experimental results of Shen and Grady was found to be better by leaving the coupling effect out of consideration. However, in [46] it was elaborated that the former agreement was likely just a fortune: the Euler–Bernoulli theory is inaccurate for the description of the mentioned problem, and the longitudinal wave is influenced by the cross-sectional rotations at the delamination tips. For an accurate model, both the transverse shear effect and longitudinal wave motion are required to be accounted for and if so, then the agreement of the model with the experimental results will be significantly better [46].

To the best of the authors’ knowledge, refs. [46, 47] were the first publications discovering the existence of parametric excitation during the free vibration of delaminated composite beams. The problem was treated by the method of harmonic balance and the critical forces as well as critical amplitudes were determined numerically and the latter experimentally. The critical force is the value of normal force in the delaminated subbeams which is required to initiate the dynamic buckling during vibration. On the other hand, the critical amplitude is the value of the vibration amplitude at the end of the built-in-free beam that is required to initiate the buckling during the free vibration. These works were followed by a similar analysis of delaminated plates performing free vibration [48]. Since then, several other papers were published; however, in these works the parametric instability was investigated in the traditional way using the harmonic balance [49,50,51] and the so-called multi-frequency method [17]. In this current work, the main aspect and more specifically the scientific novelty is the application of Winkler elastic foundation, the built-in length is resting on. A general model is developed based on the first-order shear deformable beam theory taking the bending-extension coupling into account. Moreover, the parametric excitation the delaminated part is subjected to is analyzed more deeply than before [47] and it is shown how sensitive the critical buckling force is to the natural frequency.

2 The boundary value problem—strong form

Fig. 1
figure 1

Mechanical model of a delaminated beam with possible boundary conditions

Full size image

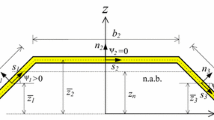
Figure 1 shows the model of a delaminated beam. The beam consists of five parts: (1) and (5) mean the intact part, (3) represents the delaminated part based on the so-called free mode model [2]. Finally, (2) and (4) capture the transition between the intact and delaminated parts of the beam, respectively. The latter is distinctly interpreted from the analytical and finite element modeling points of view. From the analytical viewpoint, regions (2) and (4) mean the continuity conditions between the (1)-(3) and (3)-(5) transitions. From the viewpoint of FE modeling, the continuity between regions (1)-(3) and (3)-(5) is achieved by transition elements (2) and (4), see later. The possible boundary conditions are also shown in Figure 1 and these are: pinned end, built-in (or rigidly fixed) end, intact part resting on elastic (Winkler) foundation and the free end. Any of these can be imposed at both ends of the beam. The related equations will be given later on. Region (0) represents the built-in intact part resting on Winkler-type elastic foundation. It is noteworthy that continuity conditions are required between regions (0)-(1) if the built-in length resting elastic foundation is involved; however, these are straightforward conditions (see later).

Each part (1, 2, 3, 4, 5) is further sliced by the plane of the delamination meaning that there are two subbeams in each region: a top (t) and a bottom (b) one, respectively. The kinematic continuity between the top and bottom parts is discussed in the sequel. Each part of the beam is captured by the laminated first-order shear deformable, or simply the Timoshenko beam theory [52]. The assumed displacement field of the model can be written as

$$\begin{aligned} u_\delta (x, y^{(\delta )}, t) = u_0 + u_\delta ^0 (x,t) + \theta _\delta (x,t)y^{(\delta )} , \end{aligned}$$
(1)

where \(\delta \) can take t or b for the top and bottom subbeams, respectively. Moreover, \(u_0\) is the global membrane displacement, \(u_{\delta }^0\) is the local (through-thickness) constant axial or membrane displacement, \(\theta _{\delta }\) is the rotation of the cross section about axis z, as it is shown in Fig. 1. In the sequel, the different regions are discussed separately. Figure 2 shows how the transition between regions (1, 2, 3) is established. In Fig. 2a, the two oblique lines separate the intact (1) and delaminated (3) parts, these lines represent the longitudinal displacement distributions and mean that the (1) and (3) portions are described by different mechanical models. These models are connected through the transition(2) by imposing the required continuity conditions. The horizontal lines of the delaminated part (3) are the delamination faces of the top and bottom subbeams. The separation gap between the top and bottom delamination faces is zero. Figure 2b depicts the same transition; however, the top and bottom parts are shown in exploded form. The top and bottom subbeams work perfectly together along the intact part (1) (continuous in-plane displacement), in contrast the delaminated part (3) is discontinuous, meaning that the displacement field of the top and bottom subbeams is independent of each other. The transition between regions (3, , 5) is based on the same concept.

Fig. 2
figure 2

Reference planes and displacement parameters of the top and bottom subbeams of the intact (1) and delaminated (3) parts, (a). Displacement continuity at transition (2) between the intact (1) and delaminated (3) parts, (b).

Full size image

2.1 Intact part

Along the intact part, the deflection of the top and bottom beams is the same, i.e.: \(v_t(x,t)\)=\(v_b(x,t)\)=v(x, t). The in-plane displacements of the top and bottom subbeams at the interface (delamination plane) are identical, i.e., [47]:

$$\begin{aligned} \left. {u_t } \right| _{y^{(t)} = - y_R^{(t)} } = \left. {u_b } \right| _{y^{(b)} = t_b - y_R^{(b)} }. \end{aligned}$$
(2)

The second condition against the in-plane displacements is the assignment of global membrane displacement, \(u_0\) to the reference plane [47]:

$$\begin{aligned} y_R \left\{ \begin{aligned}&\leqslant t_b :\left. {\quad u_b } \right| _{y^{(b)} = y_R - y_R^{(b)} } = u_0 ,\\&\geqslant t_b :\left. {\quad u_t } \right| _{y^{(t)} = - (y_R^{(t)} - y_R + t_b )} = u_0. \\ \end{aligned} \right. \end{aligned}$$
(3)

As it can be seen, two cases are included by Eq.(3): the first case is when the top beam is thinner than the bottom one and obviously the global reference plane is within the bottom subbeam. The second case means that the bottom beam is thinner than the top one and the reference plane is within the top subbeam. Using Eqs.(2, 3), it is possible to assign the relationship between the constant parts of in-plane displacements and the rotations of the intact part in Eq. (1):

$$\begin{aligned} u_t^0 = y_R^{(t)} \theta _t + (t_b - y_R )\theta _b , \quad u_b^0 = - (y_R - y_R^{(b)} )\theta _b . \end{aligned}$$
(4)

Combining Eqs. (1, 2, 3, 4), the displacement functions of the intact part become:

$$\begin{aligned} u_t = u_0 + y_R^{(t)} \theta _t + (t_b - y_R )\theta _b + \theta _t (x,t)y^{(t)} ,\quad u_b = u_0 - (y_R - y_R^{(b)} )\theta _b + \theta _b y^{(b)} . \end{aligned}$$
(5)

In accordance with the basic equations of linear elasticity [53], the normal strain and shear strain of the top subbeam become:

$$\begin{aligned} \varepsilon _{xt} = \frac{{d u_0 }}{{dx}} +y_R^{(t)} \frac{{d\theta _t }}{{dx}} + (t_b - y_R )\frac{{d\theta _b }}{{dx}} + \frac{{d\theta _t }}{{dx}}y^{(t)} , \quad \gamma _{xyt} = \frac{{dv}}{{dx}} + \theta _t . \end{aligned}$$
(6)

Likewise, the strains for the bottom subbeam are:

$$\begin{aligned} \varepsilon _{xb} = \frac{{d u_0 }}{{dx}} - (y_R - y_R^{(b)} )\frac{{d\theta _b }}{{dx}} + \frac{{d\theta _b }}{{dx}}y^{(b)} , \quad \gamma _{xyb} = \frac{{dv}}{{dx}} + \theta _b . \end{aligned}$$
(7)

To derive the governing equations, we apply Hamilton’s principle [52, 53]. Thus, we need the potential energy and the kinetic energy of the system. The former is determined by the following equation:

$$\begin{aligned} {\mathcal {U}} = \frac{1}{2}\sum _{\delta =t,b}\bigg ( \int _{(V)} \sigma _{ij(\delta )} \varepsilon _{ij(\delta )} dV \bigg ) = \frac{1}{2}\sum _{\delta =t,b}\bigg ( \int _{(V)} \big ( \sigma _{x(\delta )}\varepsilon _{x(\delta )} + \tau _{xy(\delta )} \gamma _{xy(\delta )} \big )dV \bigg ), \end{aligned}$$
(8)

which is the sum of volumetric integrals for the top and bottom subbeams. Calculating the stresses using the constitutive equation and carrying out the surface integral to the beam cross section, we have

$$\begin{aligned} {\mathcal {U}} = \frac{1}{2} \sum _{\delta =t,b}\bigg ( \int _{(L)} \big ( N_{x(\delta )}\varepsilon _{x(\delta )}^0 + M_{x(\delta )}\varepsilon _{x(\delta )}^1 + Q_{x(\delta )} \gamma _{xy(\delta )} \big )dx \bigg ), \end{aligned}$$
(9)

where L is the length, \(N_x\) is the normal force, \(M_x\) is the bending moment, \(Q_x\) is the shear force, i.e., the stress resultants, that are determined by [52, 54]:

$$\begin{aligned} \left( {\begin{array}{*{20}c} N_x \\ M_x \\ \end{array} } \right) _\delta = \left( {\begin{array}{*{20}c} A_{11} &{} B_{11} \\ B_{11} &{} D_{11} \\ \end{array} } \right) _\delta \left( {\begin{array}{*{20}c} \varepsilon _{x\delta }^0 \\ \varepsilon _{x\delta }^1 \\ \end{array} } \right) _\delta , \quad Q_{x\delta } = k A_{55\delta } \gamma _{xy\delta }, \end{aligned}$$
(10)

where \(A_{11}\), \(B_{11}\), \(D_{11}\) and \(A_{55}\) are the extensional, coupling, bending and shear stiffnesses computed based on the lay-up of the beam and each is determined with respect to the local midplane of the actual subbeam:

$$\begin{aligned} (A_{11}, B_{11}, D_{11})_{\delta } =\sum \limits _{k=1..N} \int \limits _{y^{(\delta )}_k}^{y^{(\delta )}_{k+1}} b E_{11}^{(k)} (1,y,y^2) dy^{(\delta )}, \quad A_{55\delta } = k \sum \limits _{l=1..N} \int \limits _{y^{(\delta )}_l}^{y^{(\delta )}_{l+1}} b G_{12}^{(l)} dy^{(\delta )}, \end{aligned}$$
(11)

where \(E_{11}\) is the flexural, \(G_{12}\) is the shear modulus, b is the width and \(k=5/6\) is the shear correction factor for rectangular cross section, respectively.

We continue with the determination of the kinetic energy of the beam. Similarly to the potential one, the kinetic energy is calculated by summing the relevant expressions to the top and bottom subbeams:

$$\begin{aligned} {\mathcal {T}} = \frac{1}{2} \sum _{\delta =t,b}\bigg ( \int _{(V)} \rho _{(\delta )} \dot{u}_{i(\delta )} \dot{u}_{i(\delta )} dV \bigg ) = \frac{1}{2} \sum _{\delta =t,b}\bigg (\int _{(V)} \rho \big ( \dot{u_{(\delta )}^0} ^2 +2 \dot{u}_{(\delta )}^0 {\dot{\theta }}_{\delta } y^{\delta } + ({\dot{\theta }}_{\delta } y^{\delta })^2 \big )dV \bigg ). \end{aligned}$$
(12)

Considering the fact that the density, \(\rho \), may vary from layer-by-layer, after integrating Eq. (12) with respect to the cross-sectional surface we can write the following:

$$\begin{aligned} {\mathcal {T}} = \frac{1}{2} \int _{(L)} \big ( I_{0\delta } (\dot{u}_{(\delta )}^0) ^2 + 2I_{1\delta } \dot{u}_{(\delta )}^0 {\dot{\theta }}_{\delta } + I_{2\delta } {\dot{\theta }}_{\delta }^2 \big )dx, \end{aligned}$$
(13)

where the so-called inertia parameters [52] are defined by:

$$\begin{aligned} I_{0}, I_{1}, I_{2} =\sum \limits _{k=1..N} \int \limits _{y_k^{(\delta )}}^{y_{k+1}^{(\delta )}} b \rho ^{(k)} (1,y,y^2) dy^{(\delta )}. \end{aligned}$$
(14)

The variational calculus is performed to obtain the governing equations of the system. The variation of the total potential energy, \(\Pi = {\mathcal {U}} - {\mathcal {T}}\), with respect to the global membrane displacement provides the following equation:

$$\begin{aligned} \begin{aligned} \delta u_0: \; N_{xt,x} + N_{xb,x}&= (I_{0t} + I_{0b}) \ddot{u}_0 + I_{0t} ( y_{Rt} \ddot{\theta }_t + (t_b-y_{R}) \ddot{\theta }_b ) \\&\quad -I_{0b}(y_R-y_{Rb}) \ddot{\theta }_b + I_{1t} \ddot{\theta }_t + I_{1b} \ddot{\theta }_b. \end{aligned} \end{aligned}$$
(15)

The variation with respect to the rotations leads to further two equations:

$$\begin{aligned}&\begin{aligned} \delta \theta _t:&\; M_{xt,x} + y_{Rt} N_{xt,x} - Q_{xt} \\&= (I_{0t}y_{Rt} + I_{1t}) \ddot{u}_0 + (I_{0t}y_{Rt}^2 + I_{1t}2 y_{Rt} + I_{2t}) \ddot{\theta }_t \\&+ (I_{0t} y_{Rt} + I_{1t} )(t_b-y_{R}) \ddot{\theta }_b , \end{aligned} \end{aligned}$$
(16)
$$\begin{aligned}&\begin{aligned} \delta \theta _b:&\; M_{xb,x} -(y_{R}-y_{Rb}) N_{xb,x} + (t_b-y_{R}) N_{xt,x} - Q_{xb} \\&= (I_{0t}(t_b-y_{R}) - I_{0b}(y_R-y_{Rb}) + I_{1b}) \ddot{u}_0 \\&+ (I_{0t}y_{Rt}(t_b-y_{R}) + I_{1t}(t_b-y_{R}) ) \ddot{\theta }_t \\&+ (I_{2b} + I_{0t} (t_b-y_{R})^2 + I_{0b} (y_R-y_{Rb})^2 ) \ddot{\theta }_b \\&+ -2 I_{1b}(y_R-y_{Rb}) \ddot{\theta }_b. \end{aligned} \end{aligned}$$
(17)

Finally, the equation with respect to the transverse deflection (or vibration) becomes:

$$\begin{aligned} \delta v: Q_{xt,x} + Q_{xb,x} = (I_{0t} + I_{0b}) \ddot{v} . \end{aligned}$$
(18)

2.2 Delaminated part—free mode model

The delaminated part is modeled by traditional laminated first-order shear deformable (Timoshenko) beams; both the top and bottom subbeams are based on Eq.(1); however, \(u_0\) is ignored. The procedure to obtain the governing equations is exactly the same as it was in the case of the intact part. The most important aspect is that independent membrane displacements, rotations and deflections are implied. The latter means that a free mode model is applied. The governing equations obtained based on variational calculus are:

$$\begin{aligned}&\delta u_{0\delta }: N_{x(\delta ),x} = I_{0\delta } \ddot{u}_{0\delta } + I_{1\delta } \ddot{\theta }_{x\delta }, \end{aligned}$$
(19)
$$\begin{aligned}&\delta \theta _{\delta }: M_{x(\delta ),x} - Q_{x(\delta )} = I_{1\delta } \ddot{u}_{0\delta } + I_{2\delta } \ddot{\theta }_{x\delta }, \end{aligned}$$
(20)
$$\begin{aligned}&\delta v_{\delta }: Q_{x(\delta ),x} = I_{0\delta } \ddot{v}_{\delta }. \end{aligned}$$
(21)

where Eqs.(19, 20, 21) are related to the longitudinal, rotational and transverse wave motion including the coupling effect.

2.3 Elastic foundation part

If any of the beam ends is extended by a built-in length resting on Winkler-type foundation, then the first step is that we determine the foundation stiffness (\(k_w\)). This stiffness should be determined in terms of the through-thickness modulus based on Fig. 3 and the following equations [55]:

$$\begin{aligned} k_w = \frac{b \sigma _y(x)}{v(x)}, \quad \sigma _y(x) = E_{22} \varepsilon _y(x), \quad \varepsilon _y(x) = \frac{v(x)}{(t_t+t_b)/2}. \end{aligned}$$
(22)

where \(\sigma _y\) is the average transverse normal stress in the beam and determined by the simple Hooke’s law by the second equation. Moreover, \(\varepsilon _y\) is the through-thickness strain. In accordance with Fig. 3, the strain is calculated by the ratio of change of original length over the original length in the transverse direction. The combination of the equations above leads to the following result:

$$\begin{aligned} k_w = \frac{b}{t_t+t_b}E_{22}. \end{aligned}$$
(23)
Fig. 3
figure 3

Elastic foundation part (0) with parameters required to determine the \(k_w\) foundation stiffness

Full size image

The basic concept of the built-in part resting on Winkler foundation (refer to Fig. 1) is that is far enough from the delamination tip, and thus, there is no need to imply two independent rotations of the top and bottom subbeams. Thus, the potential and kinetic energies of the system can be derived in the standard way. The only difference is that the springs should be considered. The elastic energy stored in the foundation springs is given by:

$$\begin{aligned} {\mathcal {U}}_w = \frac{1}{2} \int _{(c)} k_w v_b^2 dx, \end{aligned}$$
(24)

The governing equations based on variational calculus become:

$$\begin{aligned}&\delta u_{0}: N_{x,x} = I_{0} \ddot{u}_{0} + I_{1} \ddot{\theta }_{x}, \end{aligned}$$
(25)
$$\begin{aligned}&\delta \theta _{x}: M_{x,x} - Q_{x} = I_{1} \ddot{u}_{0} + I_{2} \ddot{\theta }_{x}, \end{aligned}$$
(26)
$$\begin{aligned}&\delta v: Q_{x,x} - k_w v = I_{0} \ddot{v}, \end{aligned}$$
(27)

describing again the longitudinal, rotational and transverse wave motions together with the coupling effect.

2.4 Frequency and mode shape analysis

The system of governing equations (15, 16, 17, 18), (19, 20, 21) and (25, 26, 27) can be solved easily for each region of the beam for example based on the previous works of the author [46, 47]. For any regions of the beam, the deflection and the rotations can be obtained by assuming harmonic motion in time:

$$\begin{aligned} \left( {\begin{array}{*{20}c} {v _{\delta }(x,t)} \\ {\theta _{\delta }{ (x,t)} } \\ {u _{0\delta }{ (x,t)}} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {V _{\delta }(x)} \\ {X_{\delta } (x)} \\ {U_{0\delta } (x)} \\ \end{array} } \right) \sin (\alpha t), \quad \left( {\begin{array}{*{20}c} {V _{\delta }(x)} \\ {X_{\delta } (x)} \\ {U_{0\delta } (x)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} K_{\delta } \\ L_{\delta } \\ M_{\delta } \\ \end{array} } \right) e^{\lambda x} , \end{aligned}$$
(28)

where \(\alpha \) is the natural frequency of the system and \(\lambda \) is the characteristic root. Moreover, \(V_{\delta }(x)\), \(U_{\delta }(x)\) and \(\theta _{\delta }(x)\) are the eigenshape functions of the corresponding parameters representing the standing wave solution of the free vibration problem.

Table 1 Continuity conditions of the delaminated composite beam in Fig. 1
Full size table

The required continuity conditions are listed in Table 1. The set of conditions includes the continuity of displacement parameters and the sum of stress resultants at the transitions. The conditions against the longitudinal displacements are derived based on Eq.(5). An important detail is that between (1)-(3) and (3)-(5) the equivalent bending moments should be used to ensure the continuity [46], these are derived based on Eqs.(16, 17):

$$\begin{aligned} \hat{M}_{xt} = M_{xt} + y_{Rt} N_{xt}, \quad \hat{M}_{xb} = M_{xb} -(y_{R}-y_{Rb}) N_{xb} + (t_b-y_{R}) N_{xt}. \end{aligned}$$
(29)
Table 2 Boundary conditions of the delaminated composite beam depending on the constraints in Fig. 1
Full size table

The possible boundary conditions shown in Fig. 1 are formulated by equations in Table 2. If the ends are resting on elastic foundation, then further continuity conditions are required between regions (0) and (1).

Based on the solution functions, boundary and continuity conditions, a system of linear algebraic equations is created and the determinant of the matrix term provides the frequency equation. The latter can be solved by, e.g., a bisection method [17, 50] to find the natural frequencies of the system. In the knowledge of the frequencies, the eigenshapes in Eq.(28) can be determined by using the system of algebraic equations and determining the constant coefficients (K, L and M).

3 Finite element discretization—weak form

The finite element discretization is carried out based on the weak formulation of the problem [52, 56]. The FE model is developed based on Fig. 4 indicating the stress resultants (a) and the nodal parameters (b). Essentially, for each region—shown by Fig. 4b—there are three independent displacement parameters: the membrane displacement, the rotation and the deflection. The interpolation scheme of these parameters is the following:

$$\begin{aligned} u_0 = {\mathbf {N}}^T_u {\mathbf {u}}_e, \, \theta = {\mathbf {N}}^T_{\theta } {\mathbf {u}}_e, \, v = {\mathbf {N}}^T_v {\mathbf {u}}_e, \end{aligned}$$
(30)
Fig. 4
figure 4

Stress resultants at the transition cross sections of a delaminated composite beam (a). Finite element discretization and nodal DoFs of a composite beam with delamination (b).

Full size image

where \({\mathbf {N}}_u\), \({\mathbf {N}}_\theta \) and \({\mathbf {N}}_v\) are the vectors of interpolation functions and contain the linear, quadratic and cubic interpolation functions, respectively [57].

3.1 Elastic foundation part

We get started with the elastic foundation part (region (0) in Fig. 4) and based on Eq. (9) it is possible to give the potential energy of the system by:

$$\begin{aligned} {\mathcal {U}} = \frac{1}{2} {\mathbf {u}}_e^T \big ( {\mathbf {K}}_{eu} + {\mathbf {K}}_{eu\theta } + {\mathbf {K}}_{e\theta } + {\mathbf {K}}_{esh} + {\mathbf {K}}_{ew} \big ) {\mathbf {u}}_e, \end{aligned}$$
(31)

where the stiffness matrices are defined as:

$$\begin{aligned} {\mathbf {K}}_{eu} = \int \limits _{0}^{1} \frac{\beta _1}{l_e} {\mathbf {N}}'_u {\mathbf {N}}'^T_u d\xi , \quad {\mathbf {K}}_{eu\theta } = \int \limits _{0}^{1} \frac{\beta _2}{l_e} \big ( {\mathbf {N}}'_u {\mathbf {N}}'^T_{\theta } \big )_\text {sym} d\xi , \quad {\mathbf {K}}_{e\theta } = \int \limits _{0}^{1} \frac{\beta _3}{l_e} {\mathbf {N}}'_{\theta } {\mathbf {N}}'^T_{\theta } d\xi , \end{aligned}$$
(32)

where \(\xi \) is the dimensionless coordinate and \(l_e\) is the element length. Note that in the middle of Eq. (32) the symmetric part of the product should be determined. Moreover:

$$\begin{aligned} {\mathbf {K}}_{esh} = \int \limits _{0}^{1} \beta _4 {\mathbf {B}}_{sh} {\mathbf {B}}^T_{sh} l_e d\xi , \quad {\mathbf {K}}_{ew} = \int \limits _{0}^{1} k_w {\mathbf {N}}_v {\mathbf {N}}^T_v l_e d\xi , \end{aligned}$$
(33)

where \(\beta \) denotes coefficients related to the stiffness parameters, \({\mathbf {B}}\) is the strain-displacement vector:

$$\begin{aligned} \beta _1&= A_{11t}+A_{11b}, \quad {\mathbf {B}}_{sh} = {\mathbf {N}}_{\theta } + \frac{1}{l_e}{\mathbf {N}}'_v, \end{aligned}$$
(34)
$$\begin{aligned} \beta _2&= 2 A_{11t} (y_{Rt} + t_b - y_R) - 2 A_{11b}(y_R-y_{Rb}) + 2(B_{11t}+B_{11b}), \end{aligned}$$
(35)
$$\begin{aligned} \beta _3&= A_{11t} (y_{Rt}^2 + (t_b - y_R)^2) - A_{11b}(y_R-y_{Rb})^2 + \nonumber \\&2B_{11t}(y_{Rt} + t_b - y_R) - 2B_{11b}(y_R - y_{rB}) + D_{11t} + D_{11b}, \end{aligned}$$
(36)
$$\begin{aligned} \beta _4&= k(A_{55t}+A_{55b}). \end{aligned}$$
(37)

The kinetic energy of the system can be formulated based on Eqs. (13)–(14). The following can be obtained:

$$\begin{aligned} {\mathcal {T}} = \frac{1}{2} \dot{{\mathbf {u}}}_e^T \big ({\mathbf {M}}_{eu} + {\mathbf {M}}_{eu\theta } + {\mathbf {M}}_{e\theta } + {\mathbf {M}}_{ev}\big ) \dot{{\mathbf {u}}}_e, \end{aligned}$$
(38)

where the mass matrices are given below:

$$\begin{aligned} {\mathbf {M}}_{eu}&= \int \limits _{0}^{1} \kappa _1 {\mathbf {N}}_u {\mathbf {N}}^T_u l_e d\xi , \quad {\mathbf {M}}_{eu\theta } = \int \limits _{0}^{1} \kappa _2 \big ( {\mathbf {N}}'_u {\mathbf {N}}'^T_{\theta } \big )_\text {sym} l_e d\xi , \quad \end{aligned}$$
(39)
$$\begin{aligned} {\mathbf {M}}_{e\theta }&= \int \limits _{0}^{1} \kappa _3 {\mathbf {N}}_{\theta } {\mathbf {N}}^T_{\theta } l_e d\xi , \quad {\mathbf {M}}_{ev} = \int \limits _{0}^{1} \kappa _1 {\mathbf {N}}_{v} {\mathbf {N}}^T_{v} l_e d\xi . \end{aligned}$$
(40)

The coefficients, denoted by \(\kappa \), are related to the inertia parameters according to the following:

$$\begin{aligned} \kappa _1&= I_{0t} + I_{0b}, \end{aligned}$$
(41)
$$\begin{aligned} \kappa _2&= 2 I_{0t} (y_{Rt} + t_b - y_R) - 2 I_{0b}(y_R-y_{Rb}) + 2(I_{1t}+I_{1b}), \end{aligned}$$
(42)
$$\begin{aligned} \kappa _3&= I_{0t} (y_{Rt}^2 + (t_b - y_R)^2) + I_{0b}(y_R-y_{Rb})^2 + \nonumber \\&2I_{1t}(y_{Rt} + t_b - y_R) - 2I_{1b}(y_R - y_{Rb}) + I_{2t} + I_{2b}. \end{aligned}$$
(43)

To calculate the vectors of interpolation functions, we assign the function approximation as follows:

$$\begin{aligned} v_e = \sum \limits _{i=0}^3 a_i \xi _i, \quad \theta _e= \gamma _{0e} - \frac{1}{l_e}v_e', \quad u_e = \sum \limits _{i=0}^1 b_i \xi _i \end{aligned}$$
(44)

where \(\gamma _{0e}\) is the shear strain. The literature offers different variants of the interpolation of Timoshenko beams [58], in this work an element with constant elementwise shear strain is chosen [52, 56]. The shear strain can be determined based on the static equilibrium equation of the intact part, i.e., by Eqs. (16, 17) and assuming identical rotations (\(\theta _b=\theta _t\)):

$$\begin{aligned} \gamma _{0e}= \frac{6 a_3 \beta _3 }{l_e^3 (A_{55t} + A_{55b})}. \end{aligned}$$
(45)

The \(a_i\) and \(b_i\) coefficients in Eq. (44) can be determined based on the nodal conditions. Since this is a standard FE step [47, 52, 56], it is not detailed in this paper. The vector of nodal displacements of the intact part with elastic foundation becomes (refer to Fig. 4b):

$$\begin{aligned} {\mathbf {u}}_e^T = \left( {\begin{array}{*{20}c} {u_1 } &{} {v_1 } &{} {\theta _1 } &{} {u_{2} } &{} {v_{2} } &{} {\theta _{2} } \\ \end{array} } \right) . \end{aligned}$$
(46)

Using the above and the interpolated forms by Eq. (30), it is possible to seek the interpolation functions and the corresponding vectors. Afterward, the stiffness and mass matrices can be determined as well.

3.2 The intact part

Out of the stiffness matrices in Eq. (31), \({\mathbf {K}}_{ew}\) should be ignored to have the total stiffness matrix of the intact part denoted by (1) in Fig. 1. The mass matrices are the same as given by Eqs. (39, 40). It is important to note that in the FE model the rotations are the same in the top and bottom subbeams of the intact part, in contrast with the analytical model (refer to Eq. (15)). The comparison of the analytical and FE models indicated that the two different cases lead to essentially the same natural frequencies and mode shapes.

3.3 Transition elements

The left transition element denoted by (2) can be seen in Fig. 4b and provides the kinematic relationship (continuity) between the intact (1) and delaminated (3) parts. In other words, the transition element represents the delamination tip. As it can be recognized, there is one node at the left side and two nodes are on the right-hand side. Thus, the nine related DoFs and the vector of nodal displacements can be written as:

$$\begin{aligned} {\mathbf {u}}_e^T = \left( {\begin{array}{*{20}c} {u_1 } &{} {v_1 } &{} {\theta _1 } &{} {u_{t2} } &{} {v_{t2} } &{} {\theta _{t2} } &{} {u_{b2} } &{} {v_{b2} } &{} {\theta _{b2} } \\ \end{array} } \right) . \end{aligned}$$
(47)

The displacement parameters are interpolated by the following scheme:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {u_t (\xi )} \\ {v_t (\xi )} \\ {\theta _t (\xi )} \\ {u_b (\xi )} \\ {v_b (\xi )} \\ {\theta _b (\xi )} \\ \end{array} } \right\} = \sum \limits _{i = 1}^9 {\left\{ {\begin{array}{*{20}c} {N_{ui}^t } \\ {N_{vi}^t } \\ {N_{\theta i}^t } \\ {N_{ui}^b } \\ {N_{vi}^b } \\ {N_{\theta i}^b } \\ \end{array} } \right\} u_{ei} } , \end{aligned}$$
(48)

where the displacement parameters are captured by:

$$\begin{aligned} u_\delta (\xi ) =&\sum \limits _{i=0}^1 b_{i\delta } \xi ^i = \sum \limits _{i = 1}^9 {N_{ui}^\delta } u_i = (\mathbf{N }_u^\delta )^T \mathbf{u }_e , \end{aligned}$$
(49)
$$\begin{aligned} v_\delta (\xi )&= \sum \limits _{i=0}^3 a_{i\delta } \xi ^i = \sum \limits _{i = 1}^9 {N_{vi}^\delta } u_i = (\mathbf{N }_v^\delta )^T \mathbf{u }_e , \end{aligned}$$
(50)
$$\begin{aligned} \theta _{\delta e}(\xi )&= \gamma _{0\delta e} - \frac{1}{l_e} \frac{d v_{\delta e}}{d \xi }= (\mathbf{N }_{\theta }^\delta )^T \mathbf{u }_e , \quad \gamma _{0\delta e} = \frac{6 D_{11\delta }a_{3\delta }}{l_e^2 A_{55\delta }}, \end{aligned}$$
(51)

where \(\gamma _0\) is determined again based on the static equilibrium equation (set the right hand side of Eq. (20) to zero) and the elementwise constant shear strain assumption for the static case. The deflection and the angle of rotation is formulated quite similarly; however, the deflection is approximated by cubic, the rotation is interpolated by quadratic functions, and the latter two are not independent of each other (refer to Eq. (34)). The equations above mean twelve unknown coefficients altogether. The required nodal conditions in accordance with Fig. 4b and Eq. (5) are:

$$\begin{aligned} v_t (0)&= v_1 , \quad v_t (1) = v_{t2} , \quad \theta _t (0) = \theta _1 , \quad \theta _t (1) = \theta _{t2}, \nonumber \\ v_b (0)&= v_1 , \quad v_b (1) = v_{b2} , \quad \theta _b (0) = \theta _1 , \quad \theta _b (1) = \theta _{b2}, \nonumber \\ \end{aligned}$$
(52)
$$\begin{aligned} u_t (0)&= u_1 + (y_R^{(t)} + t_b - y_R )\theta _1 , \quad u_t (1) = u_{t2} , \nonumber \\ u_b (0)&= u_1 - (y_R - y_R^{(b)} )\theta _1 , \quad u_b (1) = u_{b2}. \nonumber \\ \end{aligned}$$
(53)

With the aid of the conditions above, the vectors of interpolation functions and the stiffness matrices can be determined exactly in the same way as it was performed for the intact part, i.e., using Eqs. (31, 32, 33, 34, 35, 36, 37). Thus, the stiffness matrices of the left transition element are:

$$\begin{aligned} {\mathbf {K}}_{eu} = \sum \limits _{\delta =t}^b \int \limits _{0}^{1} \frac{A_{11\delta }}{l_e} {\mathbf {N}}'_{u\delta } {\mathbf {N}}'^T_{u\delta } d\xi , \quad {\mathbf {K}}_{eu\theta } = \sum \limits _{\delta =t}^b \int \limits _{0}^{1} \frac{2B_{11\delta }}{l_e} \big ( {\mathbf {N}}'_{u\delta } {\mathbf {N}}'^T_{\theta \delta } \big )_\text {sym} d\xi , \end{aligned}$$
(54)

and:

$$\begin{aligned} {\mathbf {K}}_{esh} = \sum \limits _{\delta =t}^b \int \limits _{0}^{1} A_{55\delta } l_e {\mathbf {B}}_{sh\delta } {\mathbf {B}}^T_{sh\delta } d\xi , \quad {\mathbf {K}}_{e\theta } = \sum \limits _{\delta =t}^b \int \limits _{0}^{1} \frac{D_{11\delta }}{l_e} {\mathbf {N}}'_{\theta \delta } {\mathbf {N}}'^T_{\theta \delta } d\xi , \end{aligned}$$
(55)

where:

$$\begin{aligned} {\mathbf {B}}_{sh\delta } = {\mathbf {N}}_{\theta \delta } + \frac{1}{l_e}{\mathbf {N}}'_{v\delta }, \end{aligned}$$
(56)

Using the kinetic energy expression by Eq. (13) and the vectors of interpolation functions in Eq. (49, 50, 51), the mass matrices are calculated as:

$$\begin{aligned} {\mathbf {M}}_{eu}&= \sum \limits _{\delta =t}^b \int \limits _{0}^{1} I_{0\delta } {\mathbf {N}}_{u\delta } {\mathbf {N}}^T_{u\delta } l_e d\xi , \quad {\mathbf {M}}_{eu\theta } = \sum \limits _{\delta =t}^b \int \limits _{0}^{1} 2I_{1\delta } \big ( {\mathbf {N}}_{u\delta } {\mathbf {N}}^T_{\theta \delta } \big )_\text {sym} l_e d\xi , \quad \end{aligned}$$
(57)
$$\begin{aligned} {\mathbf {M}}_{e\theta }&= \sum \limits _{\delta =t}^b \int \limits _{0}^{1} I_{1\delta } {\mathbf {N}}_{\theta \delta } {\mathbf {N}}^T_{\theta \delta } l_e d\xi , \quad {\mathbf {M}}_{ev} = \sum \limits _{\delta =t}^b \int \limits _{0}^{1} I_{0\delta } {\mathbf {N}}_{v\delta } {\mathbf {N}}^T_{v\delta } l_e d\xi . \end{aligned}$$
(58)

The right transition element is also visible in Fig. 4b and by means of the previous procedure the stiffness and mass matrices can be derived similarly.

3.4 Delaminated part

The FE matrices of the delaminated part can be obtained quite simply in the knowledge of the previous computations. The laminated Timoshenko beam element with elementwise constant shear strain is applied to both the top and bottom subbeams [59]. Moreover, in Eqs. (32, 33) and in Eqs. (39, 40) the following parameters should be altered (obviously, there is no elastic foundation):

$$\begin{aligned} \beta _1&= A_{11\delta }, \quad \beta _2 = 2B_{11\delta }, \quad \beta _3 = D_{11\delta }, \quad \beta _4 = kA_{55\delta }, \end{aligned}$$
(59)
$$\begin{aligned} \kappa _1&= I_{0\delta }, \quad \kappa _2 = 2I_{1\delta }, \quad \kappa _3 = I_{2\delta }, \end{aligned}$$
(60)

where the matrices should be determined equally for the top and bottom subbeams. The interpolation scheme is quite similar to that by Eq. (44).

3.5 Boundary conditions

The possible boundary conditions of the FE model are discussed based on Fig. 1. If the boundary is pinned, then the end section is constrained by fixing the deflection and the longitudinal displacement at that node. For a built-in end the deflection, membrane displacement and the rotation are equally zero. If the end is free, then there is nothing to do with that since only the kinematic conditions are treated by the FE method [56].

3.6 Free mode model with no delamination opening

In a recent paper [47], it was shown that for beams made out of unidirectional layers, i.e., when the material is transversely isotropic, then the free mode model can be modified in order to prevent the delamination opening during vibration. Let \(\eta = t_t /t_b\) be the ratio of thicknesses, then the modified densities satisfying the conservation law of mass become [47]:

$$\begin{aligned} \rho _{eq}^{(t)} = \rho \frac{{(1 + \eta )\eta ^2 }}{{1 + \eta ^3 }}, \quad \rho _{eq}^{(b)} = \rho (1 + \eta ) - \rho _{eq}^{(t)} \eta . \end{aligned}$$
(61)

In accordance with the equations above, the densities and so the inertia parameters in the top and bottom subbeams of the delaminated part (3) should be modified. In some recent papers [46, 47], it has been shown that these equations work perfectly in transversely isotropic beams including the Euler–Bernoulli and Timoshenko beam theories as well. However, if the system is discretized by the FE method, then the equations above work correctly only for the Euler–Bernoulli beam theory, but not for the Timoshenko beam element. The reason is the elementwise constant strain approximation. In spite of that, by introducing a further power parameter in the equations of the inertia parameters the delamination opening can be prevented:

$$\begin{aligned} I_{0t} = \rho _{eq}^{(t)} b t_t (1+ (t_t/t_b))^{p_0}, \quad I_{0b} = \rho b (t_t + t_b) - I_{0t}, \end{aligned}$$
(62)

where \(p_0\) is the power parameter and its value depends on the position and the length of delamination. In other words, it should be determined by a trial or iterative technique calculating the mode shapes and observing the delamination opening relatively to the vibration amplitude. The natural frequencies are not influenced by the power parameter, because the vibrating mass is always the same. The power parameters will be given later (refer to Table 5).

3.7 Free vibration analysis

The free vibration analysis of the system was carried out in the usual way by solving the \({\mathbf {M}} \ddot{{\mathbf {U}}} + {\mathbf {K}} {\mathbf {U}}={\mathbf {0}}\) equation of motion by assuming harmonic motion in time: \({\mathbf {U}}={\mathbf {A}} \sin \alpha t\), where \(\alpha \) is the natural frequency of the system. The fist step is to determine the natural frequencies through the \(\det (- \alpha ^2 \mathbf{M } + \mathbf{K })=0\) equation, then by using the frequencies the second step involves the calculation of the eigenshape vectors by means of the \((- \alpha ^2 \mathbf{M } + \mathbf{K }) \mathbf{U }={\mathbf {0}}\) equation. Note that damping is not considered in the analysis; however, a recent publication [50] revealed that the effect of damping on the natural frequencies is negligible from engineering point of view.

4 Geometry, material properties and ANSYS plane FE model

Table 3 Reference plane coordinates for unidirectional isotropic beams with symmetric lay-up
Full size table
Table 4 Geometry of the tested delaminated composite beams
Full size table

The analysis is carried out on delaminated composite beams made out of unidirectional glass-polyester layers. The left end is resting on elastic foundation, the right end is free in accordance with Fig. 1. This model is referred to as “elastic.” For comparison purposes, the left end is built-in and the analysis is carried out again, the model is referred to as“rigid.” The properties required for the analysis are: \(E_{11}\)=33 GPa, \(E_{22}\)=7.2 GPa, \(G_{12}\)=3 GPa, \(\rho \)=1330 kg/m\(^3\), L=180 mm (total length), c=50 mm (built-in length), b=20 mm (width). The thickness of the beams is always 6.2 mm (=\(t_t + t_b\)). The reference plane coordinates in this special case are listed in Table 3. The length of delamination, a as well as \(L_1\) and \(L_3\) are given in Table 4. Each beam is built-up using 14 unidirectional layers. The primal assembly of the system is performed based on Fig. 4b. In the sequel, a user-defined beam code number will be assigned to refer to the delamination length and the thicknesswise position of the delamination: as matter of fact, the 60/0 code means that the length of delamination is 60 mm (first number) and the position of the delamination is exactly the global midplane of the beam (second number), i.e.: \(t_t=t_b =6.2 \cdot 7/14 = 3.1\)mm. Some other code numbers are: 60/2 meaning that the thicknesses are: \(t_t = 6.2 \cdot 5/14\) mm and\(t_b = 6.2 \cdot 9/14\)mm, 60/4 means that\(t_t = 6.2 \cdot 3/14\)mm and \(t_b = 6.2 \cdot 11/14\)mm, finally 60/6 means that\(t_t = 6.2 \cdot 1/14\)mm and \(t_b = 6.2 \cdot 13/14\)mm. The number of elements is chosen to achieve the convergence of the first four natural frequencies. For the 60/... and 80/... beams, \( N_{e0} = N_{e1} = N_{e3} = N_{e5} = 30\) elements are applied. In the case of the 100/... and 120/... beams, \(N_{e0} = 30\), \(N_{e1} = N_{e5} = 20\) and \(N_{e3} = 40\) elements are used. The lengths of the transition elements are\(L_2 = L_4\)=0.5 mm. The power parameters for the specified geometries are given in Table 5.

Table 5 Power parameter for the Timoshenko beam finite element for Eq.(62)
Full size table

To validate the results of the analytical and the own-developed FE models, the delaminated beams with c=50 mm long built-in length and free end are created in ANSYS, too, using isoparametric QUAD elements under plane stress assumption. The element size is 1 mm \(\times \) 1 mm in each case, and the convergence of the frequencies is checked. Mode shapes are also determined, and the delamination opening is prevented by imposing identical transverse displacements along the nodes of the two delamination faces. The mode shapes are physically consistent with those obtained by the analytical and own-developed FE solutions.

5 Experiments—natural frequencies

Two different tests are performed on the delaminated unidirectional specimens: the modal hammer (or impact hammer) test and the sweep excitation test. Further details of the experiments can be found in [46, 47]. The experiments are repeated in this paper for the sake of completeness. For unidirectional composite beams, the reference plane coordinates are given in Table 3. The further geometrical data are listed in Table 4.

6 Results and discussion

In this section, the first four natural frequencies by the analytical and finite element models are presented and compared to experimentally measured frequencies and also to those by the ANSYS plane FE model. Moreover, the displacement parameters and stress resultants are discussed. In the final subsection, the dynamic buckling phenomenon and the related stability diagrams as well as the critical forces and amplitudes are determined and commented.

6.1 Natural frequencies by models and experiments

The natural frequencies for sixteen different beam configurations are presented by the following models:

  • Euler–Bernoulli beam theory, rigidly fixed end, analytical model [46] and FE solution [47] (note that this model can be obtained by using the Timoshenko beam model with \(G_{12}\)=\(\infty \)),

  • Euler–Bernoulli beam theory, elastic foundation effect, analytical model and FE solution (using the Timoshenko beam model with \(G_{12}\)=\(\infty \)),

  • Timoshenko beam theory, rigidly fixed end, analytical model developed in Sect. 2 and solved by Eq. (28) and FE solution detailed in section 3,

  • Timoshenko beam theory, elastic foundation effect, analytical model developed in Sect. 2 and solved in accordance with Eq. (28) and FE solution developed in Sect. 3.

Table 6 Free vibration frequencies of the (60/0) and (60/2) composite beams with built-in+free ends in [Hz]
Full size table

Table 6 presents the natural frequencies for the 60/0 and the 60/2 beams. It is observable right away that as the model is refined the values of frequencies get closer and closer to the measured values. As a matter of fact, the first effect is transverse shear, which is not considered by the Euler–Bernoulli beam theory. Comparing the results of the two theories from this point of view, it can be recognized that the effect of transverse shear is very small on the first frequency and moderate on higher frequencies. The second effect is the Winkler foundation that the built-in length is resting on. A significant decrease in frequencies is clearly observable considering the Euler–Bernoulli beam models. This tendency further goes on by taking the results of the Timoshenko beam model into account. The explanation of the decrease in first frequency from 151 to 138 Hz in the latter case is the interaction between the transverse shear and elastic foundation effects. The elastic foundation represents the transverse elasticity of the built-in length, and thus, the stiffness of the system decreases compared to the rigidly fixed models. The degree of decrease results in the fact that the agreement between the first two and the last before rows in Table 6 becomes very good for all of the frequencies.

It was recognized that the sweep excitation test provides always a lower value for the first frequency than the modal hammer test. Considering the other frequencies, no clear tendencies were observed regarding the relationship (which one is higher or smaller); however, the values by the two methods are very close to each other.

The plane stress ANSYS FE model including the built-in length of the beams seems to agree very well with the Euler–Bernoulli model with elastic foundation effect if the first two frequencies are investigated. The third and fourth frequencies by the ANSYS model agree rather with the Timoshenko model dealing with the elastic foundation effect. Nevertheless, the definite agreement between the frequencies by the developed beam models and those by the ANSYS plane FE ones validates the former. This holds for any of the forthcoming tables.

Table 7 Free vibration frequencies of the (60/4) and (60/6) composite beams with built-in+free ends in [Hz]
Full size table

The results of the 60/4 and 60/6 beams are summarized in Table 7. The tendencies and the relations of the analytical models and the experiments are likewise in the case of Table 6. For both Tables 6 and 7, the agreement between the analytical models and the corresponding FE models is excellent: there are only slight mismatches and essentially only the fourth frequency involves larger absolute differences. These small mismatches are dedicated to the different solution algorithms (bisection root finding vs. eigenvalue calculation).

The results of the 80/0, 80/2 and 80/4, 80/6 beams are collected in Tables 8 and 9. These results support the previous conclusions and observations; however, the agreement between the last before line and the first two ones is even better than in Tables 6 and 7. The difference between the analytical (or FE) models and the experiments is associated with the possible manufacturing defects. The final conclusion is that it is very important to apply an appropriate model to capture the reality and get consistent result. Some more tables are presented for the 100/0-100/6 and 120/0-120/6 beams, these are placed in Appendix A. The same conclusions are maintained as those for Tables 6, 7, 8, 9.

Table 8 Free vibration frequencies of the (80/0) and (80/2) composite beams with built-in+free ends in [Hz]
Full size table
Table 9 Free vibration frequencies of the (80/4) and (80/6) composite beams with built-in+free ends in [Hz]
Full size table

6.2 Displacement parameters and stress resultants

In the subsequent part of this article, the results of the Timoshenko beam finite element model are presented if otherwise not stated. Each figure is created with a 1 mm vibration amplitude at the end of the beam. Fig. 5 presents the deflection and the angle of rotation along the beam length for the first two natural frequencies of the 100/4 beam. The main aspect highlighted that is the influence of elastic foundation. Although the deflections are almost the same, the mismatch between the angle of rotations by rigidly fixed and Winkler foundation models is more pronounced. The effect of elastic foundation is the most significant at the built-in cross section (i.e., at \(x=0\)) and decreases subsequently till the free end. It can be seen that the artificial power parameter (\(p_0\)) works well and prevents any delamination opening during vibration.

Fig. 5
figure 5

Deflection and rotation along the length of the 100/4 beam for the first two vibration modes by rigid and elastic clamping

Full size image

The longitudinal displacement and the normal force are plotted in Fig. 6 again for the 100/4 beam including the first two natural frequencies. An immediate observation is that the longitudinal displacement of the rigidly fixed model has a relatively higher slope than that of the elastic foundation model. The normal force is determined by the derivative of the longitudinal displacement (refer to Eq.(10)). The first and most important outcome of this analysis is that the normal force along the delaminated region is constantly distributed. Another important finding of this study is that the normal force by elastic foundation model is higher by around 10 percent than the one by the rigidly fixed model at the same vibration amplitude if the system performs harmonic vibration by the first natural frequency. In the case of the second natural frequency, the two models predict almost the same normal force. For higher modes, the effect of elastic foundation on the normal force distribution is more and more negligible.

Fig. 6
figure 6

Longitudinal displacement and normal force along the length of the 100/4 beam for the first two vibration modes

Full size image

The stress resultants (total bending moment and total shear force) are displayed in Fig. 7 for the first two vibration frequencies, again for the 100/4 beam. Note, that the sum of bending moments (\(M_{xt} + M_{xb}\)) is shown and not sum of the equivalent bending moments [46], that is the reason for the discontinuity between the delaminated and intact beam parts. For the first two frequencies, it is clearly recognized that the moment by elastic foundation model is smaller by approximately 18 and 27 % at \(x=0\) than those by the rigidly fixed formulation. From the standpoint of shear force, Fig. 7 indicates that it goes up suddenly and reaches a maximum value close to \(x=0\). First, the shear force is the higher at a specified cross section along the built-in length. Second, the shear force by the FE solution is piecewise constant. Thus, even the analytical solution is plotted in Fig. 7 for the elastic foundation providing excellent agreement with the FE solution. The difference between the shear forces by the two formulations is significant even along the effective beam length.

Fig. 7
figure 7

The sum of bending moments and shear forces along the length for the first two vibration modes of the 100/4 beam

Full size image

The most important role out of the stress resultants is attributed to the normal force, because this is the one governing the dynamic buckling phenomenon during free vibration.

6.3 Dynamic buckling analysis

Figure 8 indicates how the parametric excitation takes place as the beam performs harmonic vibration. If the upward motion occurs, then the top beam is always compressed, the bottom is extended. If the downward motion is considered, then the top beam is extended and the bottom one is compressed. In other words, the tensile and compressive forces interchange each other with respect to the vibration frequency. It is important to recognize that the top beam can buckle only in the outward direction.

Fig. 8
figure 8

The harmonically changing normal force in a delaminated beam under free vibration. Upward motion—compressive force (a), downward motion—tensile force (b). Local model of the parametrically excited top subbeam (c)

Full size image

6.3.1 The geometric stiffness matrix

The buckling analysis requires the determination of the geometric stiffness matrix of the delaminated part for Euler-buckling. The strain energy from the nonlinear strain is [57]:

$$\begin{aligned} {\mathcal {U}}^{NL} = \int \limits _{V} \sigma _x^0 \varepsilon ^{NL} dV = \frac{1}{2} {\mathbf {u}}_e^T {\mathbf {K}}_{Ge} {\mathbf {u}}_e, \end{aligned}$$
(63)

where the geometric stiffness matrix can be defined as:

$$\begin{aligned} {\mathbf {K}}_{Ge}=\int \limits _{(V)} {\mathbf {G}}^T {\mathbf {S}} {\mathbf {G}} dV = \int \limits _{0}^{1} \frac{N}{l_e}{\mathbf {N}}_v'{\mathbf {N}}_v'^T d\xi , \end{aligned}$$
(64)

where everything is determined for the top subbeam of the delaminated part using the Timoshenko beam model and N is the normal force distributed uniformly over the delamination length in accordance with Fig. 6. It has already been shown that the buckling takes place locally; thus, it is only investigated within the delaminated region.

6.3.2 The equation of motion and the solution

Let us consider only the top beam, the equation of motion has the following form [47]:

$$\begin{aligned} \mathbf{M }_t \ddot{\mathbf{U }}_t + \mathbf{K }_t \mathbf{U }_t + \left( {F_d \mathbf{K }_{Gt}^0 \cos \left( {\Theta t} \right) } \right) \mathbf{U }_t = \mathbf{0 }, \end{aligned}$$
(65)

where \({\mathbf {U}}_t\) is the increment of the nodal displacement vector due to delamination buckling of the top subbeam, \(\Theta \) is the frequency of parametric excitation; however, in this work, it will be one of the natural frequencies of the whole beam: \(\Theta = \alpha \). The solution can be developed in accordance with [47]:

$$\begin{aligned} \mathbf{U }_t = \varvec{\varPhi }{\hat{T}}(t), \end{aligned}$$
(66)

where \({\hat{T}}(t)\) is the time function of the local delamination buckling having only a positive amplitude. This function can be expanded into a Fourier series and taken back into Eq. (65) [47]:

$$\begin{aligned} {\mathbf{U }_t} = \mathbf{a }_0 + \sum \limits _{k = 1,2,3...}^\infty {\mathbf{a }_k \cos } \left( {k\alpha t} \right) , \quad \mathbf{a }_0 = a_0 \varvec{\varPhi }, \quad \mathbf{a }_k = a_k \varvec{\varPhi }, \quad k = 1,2,3,... \end{aligned}$$
(67)

where \(\varvec{\varPhi }\) is the first mode static buckling eigenshape vector of the top subbeam of the delaminated region under clamped-clamped conditions. The acceleration vector is determined by:

$$\begin{aligned} \ddot{\mathbf{U }}_t = - \alpha ^2 \sum \limits _{k = 1,2,3...}^\infty {\mathbf{a }_k k^2 \cos } \left( {k\alpha t} \right) , \quad k = 1,2,3,... \end{aligned}$$
(68)

Using the series solution by Eqs. (67, 68) and taking it back into the equation of motion an infinite equation can be obtained. This equation can be sorted in accordance with the wavelengths of the \(\cos \) functions and can be arranged into a matrix equation with infinite dimension. The limit curves of stability can be determined by calculating the finite determinant of the coefficient matrix [60]:

$$\begin{aligned} \begin{aligned} \left| {\begin{array}{*{20}c} {\mathbf{K }_t } &{} {\frac{1}{2}F_d \mathbf{K }_{Gt}^0 } &{} \mathbf{0 } &{} \mathbf{0 } &{} \mathbf{0 } &{} \cdots \\ {F_d \mathbf{K }_{Gt}^0 } &{} {\mathbf{K }_t - \alpha ^2 \mathbf{M }_t } &{} {\frac{1}{2}F_d \mathbf{K }_{Gt}^0 } &{} \mathbf{0 } &{} \mathbf{0 } &{} \cdots \\ \mathbf{0 } &{} {\frac{1}{2}F_d \mathbf{K }_{Gt}^0 } &{} {\mathbf{K }_t - 4\alpha ^2 \mathbf{M }_t } &{} {\frac{1}{2}F_d \mathbf{K }_{Gt}^0 } &{} \mathbf{0 } &{} \cdots \\ \mathbf{0 } &{} \mathbf{0 } &{} {\frac{1}{2}F_d \mathbf{K }_{Gt}^0 } &{} {\mathbf{K }_t - 9\alpha ^2 \mathbf{M }_t } &{} {\frac{1}{2}F_d \mathbf{K }_{Gt}^0 } &{} \cdots \\ \mathbf{0 } &{} \mathbf{0 } &{} \mathbf{0 } &{} {\frac{1}{2}F_d \mathbf{K }_{Gt}^0 } &{} {\mathbf{K }_t - 16\alpha ^2 \mathbf{M }_t } &{} \cdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ \end{array} } \right| =0 . \end{aligned} \end{aligned}$$
(69)

The determinant above leads to a lengthy two-variable function including the frequency and the force amplitude. Eq.(69) is called the general solution of the dynamic stability problem.

The second solution is based on the modal decomposition of the equation of motion. By multiplying the equation of motion by \(\varvec{\varPhi }\) (eigenmode vector of static buckling) from the left and right hand sides, the following scalar equation is obtained:

$$\begin{aligned} \ddot{{\hat{T}}}(t) + \text{\O}mega ^2 (1 + 2 \mu \cos \alpha t) \hat{T}(t) = 0, \end{aligned}$$
(70)

where:

$$\begin{aligned} \text{\O}mega = \frac{ \varvec{\varPhi }^T {\mathbf {K}}_t \varvec{\varPhi }}{ \varvec{\varPhi }^T {\mathbf {M}}_t \varvec{\varPhi }}, \quad \mu = \frac{1}{2} \frac{1}{\text{\O}mega ^2} \frac{ \varvec{\varPhi }^T {\mathbf {K}}_{Gt} \varvec{\varPhi }}{ \varvec{\varPhi }^T {\mathbf {M}}_t \varvec{\varPhi }}. \end{aligned}$$
(71)

The same procedure [47] as we have seen before to obtain Eq.(69) leads to the determinant below:

$$\begin{aligned} \begin{aligned} \left| {\begin{array}{*{20}c} \text{\O}mega ^2 &{} \text{\O}mega ^2 \mu &{} 0 &{} 0 &{} 0 &{} \cdots \\ 2\text{\O}mega ^2 \mu &{} \text{\O}mega ^2 - \alpha ^2 &{} \text{\O}mega ^2 \mu &{} 0 &{} 0 &{} \cdots \\ 0 &{} \text{\O}mega ^2 \mu &{} \text{\O}mega ^2 - 4\alpha ^2 &{} \text{\O}mega ^2 \mu &{} 0 &{} \cdots \\ 0 &{} 0 &{} \text{\O}mega ^2 \mu &{} \text{\O}mega ^2 - 9\alpha ^2 &{} \text{\O}mega ^2 \mu &{} \cdots \\ 0 &{} 0 &{} 0 &{} \text{\O}mega ^2 \mu &{} \text{\O}mega ^2 - 16\alpha ^2 &{} \cdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ \end{array} } \right| =0 . \end{aligned} \end{aligned}$$
(72)

As it can be seen in this case, the elements within the determinant are scalar parameters. However, the vector \(\varvec{\varPhi }\) should be determined for each delamination length and \(t_t\) thickness separately. In the sequel, we present the results of the dynamic stability analysis using both models (Eq. (69) and Eq. (72)). In each case, the matrices are determined by the Timoshenko beam finite element model Table 11.

6.4 Dynamic stability analysis results

This subsection is divided into two parts: one related to the determination of the critical value of the force and another dedicated to the critical amplitude of the free vibration.

6.4.1 Determination of the critical value of dynamic force

Figure 9 provides the stability diagram plots of the 100/6 and the 120/6 beams using the modal decomposition technique. Twenty (\(N_e\)) elements are applied along the length, and the twentieth-order determinant (\(N_{det}\)) is calculated. The convergence of the solution was investigated as well, and these parameters were found to be appropriate. The critical values of the dynamic force amplitude, \(F_d\) are shown against the natural frequency, the curves are determined by Eq. (72). The values of the first natural frequency by Timoshenko and Euler–Bernoulli beam theories including the Winkler foundation together with the modal hammer and sweep excitation tests are also shown with the corresponding force values. The enlarged subfigures on the right top corner show how the intersection and projection is performed in order to obtain the critical dynamic force amplitude. A detailed description of this procedure is given below:

Fig. 9
figure 9

Stability diagrams for local dynamic buckling of the 100/6 (a) and 120/6 (b) beams using the modal decomposition technique, \(N_e\)=20, \(N_{det}\)=20

Full size image

  • The first step is that we choose the theory or method the frequency is determined by. Let it be the Timoshenko beam theory. In Table 12, the first free vibration frequency of the 100/6 beam is 138 Hz by the Timoshenko beam theory including the elastic foundation effect (Tables 13, 14).

  • Convert the former frequency to rad/s, this provides 867 rad/s.

  • In order to find the critical value of the force, \(F_d\) indicated in Fig. 8 we consider Fig. 9. We find the first intersection between the solution curve and the vertical line going across the frequency value of 867 rad/s.

  • The critical value of the force is determined by a horizontal line going across the intersection point, leading to 189.5 N as it can be seen in Fig. 9 as well.

  • The same procedure can be applied to any other frequency in order to determine the corresponding critical force. A consequence is that the critical value of the dynamic force is frequency dependent.

For both Figs. 9a, b, it can be recognized that the critical force amplitude is quite sensitive to the frequency. For the 100/6 beam, the first natural frequency by the Timoshenko, Euler–Bernoulli beam models and modal hammer test and the sweep excitation test intersects the same limit curve. However, it is possible that any of the former four frequencies—being a slightly smaller or greater than the other three—intersects with another limit curve resulting in a significantly smaller or larger critical force amplitude. The picture is quite similar to this if we take a look at Fig. 9b for the 120/6 beam.

Fig. 10
figure 10

Stability diagrams for local dynamic buckling of the 100/6 (a) and 120/6 (b) beams using the general solution, \(N_e\)=12, \(N_{det}\)=10

Full size image

Figure 10 presents the diagrams using the general description of the dynamic stability problem (Eq. (69)). In this case, both \(N_e\) and \(N_{det}\) are reduced (\(N_e\)=12, \(N_{det}\)=10) because of the significantly higher matrix size; however, convergence was again achieved in each investigated case. The first observance is that the picture by this general solution is quite different compared to that obtained by the modal decomposition technique related to Fig. 9. Nevertheless, the technique to determine the critical force amplitude is exactly the same. The frequencies for the 100/6 beam are given in the figure in rad/s and can be found in Table 12 in Hz. Based on the frequencies, the critical forces are easy to locate using the diagram. For both beam configurations, the limit curves in Figure 10 are again quite different than those in Fig. 9. In Fig. 10a, the critical force values are relatively close to each other; however, there is a huge mismatch with the forces in Fig. 9a (100/6 beam). For the 120/6 beam, the mismatch between Figs. 9b and 10b is again significant from the standpoint of critical forces; however, the solution is definitely more sensitive to the frequency by the general solution because of the relatively large slope of the curves.

In order to elaborate how the thicknesswise position of the delamination influences the stability diagrams, we provide Figs. 11 and 12. In Fig. 11, the results by the modal decomposition technique are plotted for the 100/0, 100/2 and 100/4 beams, respectively. Obviously, relatively huge values are obtained for the dynamic force amplitude in each case. This can be explained by the fact that the slope of the curves becomes higher and higher. The general solution provides the curves in Figs. 12a–c; the sensitivity of the critical dynamic force to the frequency is still brought to the stage by these results.

Here, an alternative utilization of the results in Figs. 9, 10, 11, 12 is explained. The dynamic stability analysis is carried out by taking only the top beam of the delaminated part into consideration (local model, refer to Figure 8). Therefore, the surrounding structure of this top beam is no longer required to obtain the critical force values. The conclusion is that if in any (fictitious) structure the delaminated part has the same geometry and material as that Figs. 9, 10, 11, 12 are determined based on, then the presented figures remain true even for this structure. Once the frequencies of this fictitious structure are determined, we know the frequency of parametric excitation and we can determine the critical force, too.

Fig. 11
figure 11

Stability diagrams for local dynamic buckling of the 100/0 (a), 100/2 (b) and 100/4 (c) beams using the modal decomposition technique, \(N_e\)=20, \(N_{det}\)=20

Full size image
Fig. 12
figure 12

Stability diagrams for local dynamic buckling of the 100/0 (a), 100/2 (b) and 100/4 (c) beams using the general solution, \(N_e\)=12, \(N_{det}\)=10

Full size image

6.4.2 Determination of the critical vibration amplitude

In this work, the Timoshenko beam model without and with built-in length resting on Winkler elastic foundation is chosen to determine the critical amplitudes required to initiate dynamic buckling. The modal decomposition technique as well as the general solution are applied to both models. The structure of Table 10 is the following. The results of the continuum model, i.e., the numerical FE model (they give the same results) are collected in the third and fourth columns for the .../6 beams. These results are the first natural frequency and the normal force at the left crack tip (which is uniform along the delaminated part). The subsequent columns contain the critical values of the \(F_d\) force amplitude (detailed in the previous subsection) and the critical vibration amplitude. The latter is always the ratio of \(F_d\) over \(N_{xt}\). The critical amplitudes were also determined experimentally in a previous work [47]; these values are listed in the last column of Table 10. The comparison of the critical vibration amplitudes from the models and by experiments shows that the agreement is bad. The biggest discrepancy takes place for the 100/6 beam by the elastic foundation model combined with the modal decomposition technique providing a critical vibration amplitude of 6.33 mm against the 0.12 mm value by experiment. Overall, it seems that in spite of the fact that the modal decomposition technique seems to be justified, the general solution is free of extreme discrepancies compared to the experiments. We highlight again the sensitivity of the force amplitude to the frequency, which is the main reason for the mismatches between model prediction and experiments. Also, in a previous work the agreement between the critical vibration amplitudes by the Euler–Bernoulli model without elastic foundation and by experiments was better. The reason for this is that based on Fig. 9 lower dynamic force amplitudes are associated with the higher frequencies, and based on Tables 6, 7, 8, 9 the Euler–Bernoulli model without the elastic foundation results in the highest natural frequencies.

Table 10 Critical dynamic force values and critical vibration amplitudes by Timoshenko beam theory and experiment
Full size table

7 Conclusions

In this paper, the dynamics of delaminated composite beams was investigated using the Timoshenko and Euler–Bernoulli beam theories. The work was done essentially in two different aspects. In the first phase, the free vibration of the clamped beams was investigated using two different models. The built-in length of the model was captured by the Winkler type elastic foundation providing an additional transverse displacement and rotation compared to the rigidly fixed case. The analysis was carried out by developing the governing differential equations for every regions of the beam and by solving the equations analytically. Also, the numerical solution was provided by the finite element method. The natural frequencies, mode shapes and the stress resultants were determined in the first phase of the work. The natural frequencies were determined also by experiments using modal hammer and sweep excitation tests. The comparison of analytical and experimental results showed that the Timoshenko beam theory with elastic foundation along the built-in length provides the best agreement with the measured frequencies. Note, that the first four natural frequencies were compared to each other.

In the second phase, the dynamic buckling phenomenon was investigated using the harmonic balance method. Two different approximations were applied. The general description is based on a determinant of a matrix with matrix elements. This approximation was also applied in a previous paper [47]. The second solution is based on the modal decomposition technique providing a quite similar determinant of a matrix; however, the latter contained scalar terms only. The stability limit curves of dynamic buckling in the plane of the free vibration frequency and the dynamic force amplitude were determined by both approximations. The critical dynamic forces were determined for the frequencies by Timoshenko beam theory, Euler–Bernoulli beam theory (both involved the effect of elastic foundation), moreover, for the frequencies by modal hammer and sweep excitation tests, respectively. The results indicated that the critical dynamic force is quite sensitive to the frequency. Thus, the agreement between the theoretical and experimental critical vibration amplitudes at which the buckling initiates was bad. However, the models developed in this work made it clear that the phenomenon itself is more complex than it was thought before and neither of the previous works revealed this feature of the free vibration problem of delaminated composite beams in the past.

The next step should be to elaborate how the damping affects the stability curves. Apparently, damping has a negligible effect on the natural frequencies but has a substantial effect on the stability curves of parametrically excited systems [50]. Nevertheless, being a special case investigated in this paper it is still an unsolved problem.