On the sensitivity of bifurcation-based electrostatic MEMS sensors: cantilever with tip plate

Abstract

An electrostatic bifurcation-based microcantilever sensor equipped with a tip plate is investigated for sensitivity. A closed-form expression for sensitivity of this type of sensors is approximated using the frequency-response equation of the cantilever. The expression relates the sensor sensitivity due to the added mass with its geometric and material properties. The formula shows that the sensitivity of the sensor is quadratically proportional to the quality factor. Further, the sensitivity is inversely proportional to the third power of the beam stiffness and the ninth power of the gap distance. This formulation unveils the factors influencing the sensitivity of this sensor class configuration and could serve as a guideline in optimizing the design of this type of sensors for enhanced performance.

Appendix

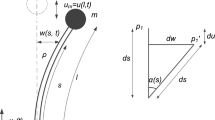
In this appendix, the parameters given in the above analysis are introduced. For a sensor made of polysilicon as structural material with $\rho =2300$ kg/m$^3$ and $E=160$ GPa, the following data are used: $L=100\,\upmu$m, $b=10\,\upmu$m, $L_p=30\,\upmu$m, $b_p=60\,\upmu$m, $h=h_p=1.5\,\upmu$m [14]. Implementing Eq. (7) using one mode shape for the system, the numerical form of the ordinary differential equation describing the motion of the beam-plate system can be obtained as

$$\begin{aligned}&\left( 8.69 M+27.47 M L_c +28.39 M L_c^2 + 2 \right) {\ddot{q}(t)}+\frac{1}{Q} \, {\dot{q}(t)} \nonumber \\&\qquad +\, \left( 26.31 - \left( 34.78 \, L_c \alpha + 109.88 \, L_c^2 \alpha + 115.72 \, L_c^3 \alpha \right) \left( V_{\text {AC}}+V_{\text {DC}}\right) ^2 \right) q(t) \nonumber \\&\qquad -\, \left( 108.77 \, L_c \alpha + 515.49 \, L_c^2 \alpha + 1089.79 \, L_c^3 \alpha + 857.64 \, \alpha L_c^4 \right) \left( V_{\text {AC}}+V_{\text {DC}}\right) ^2 \, q(t)^2 \nonumber \\&\qquad -\, \left( 302.39 \, L_c \alpha + 1910.78 \, L_c^2 \alpha + 6037.08 \, L_c^3 \alpha + 9537.03 \, \alpha L_c^4 \right) \left( V_{\text {AC}}+V_{\text {DC}}\right) ^2 \, q(t)^3 \nonumber \\&\quad = \left( 8.34 \, L_c \alpha + 13.18 \, L_c^2 \alpha \right) \left( V_{\text {AC}}+V_{\text {DC}}\right) ^2. \end{aligned}$$

(27)

where the actuating electrostatic force is expanded in a Taylor series to the third order. It is worth noting that the electrostatic force causes softening in the beam stiffness which explains the negative signs of the coefficients of $q(t)^2$ and $q(t)^3$.

To have an estimate of the weight of each term of the equation of motion, a small bookkeeping parameter $\epsilon \ll 1$ is used as a gauge parameter to signify how small the nondimensional system’s states and parameters are compared to 1. In this regard, q(t) is ordered at $O(\epsilon )$, $L_c$ at $O(\epsilon )$, $\alpha$ at $O(\epsilon ^2)$, $V_\mathrm{DC}$ at $O(1/\epsilon )$, and $V_\mathrm{AC}$ at $O(\epsilon )$. Carrying out the scaling analysis and retaining terms up to order $O(\epsilon ^4)$, a consistently expanded equation of motion is obtained in the form

$$\begin{aligned}&\left( 8.69 \, M + 2 + 27.47 \, \epsilon M L_c + 28.39 \, \epsilon ^2 M L_c^2 \right) {\ddot{q}(t)} +\frac{1}{Q} \, {\dot{q}(t)} \nonumber \\&\qquad +\, \left( 26.31 \epsilon - 34.78 \, \epsilon ^2 L_c \alpha V_{\text {DC}}^2 - 109.88 \, \epsilon ^3 L_c^2 \alpha V_{\text {DC}}^2 - 69.56 \, \epsilon ^4 L_c \alpha V_{\text {DC}} V_{\text {AC}} - 115.72 \, \epsilon ^4 L_c^3 \alpha V_{\text {DC}}^2 \right) \, q(t) \nonumber \\&\qquad -\, \left( 108.77 \, \epsilon ^3 L_c \alpha V_{\text {DC}}^2 +515.49 \, \epsilon ^4 L_c^2 \alpha V_{\text {DC}}^2 \right) \, q^2(t)-\, 302.39 \, \epsilon ^4 L_c \alpha V_{\text {DC}}^2 \, q(t)^3 \nonumber \\&\quad =8.34 \, \epsilon L_c \alpha V_{\text {DC}}^2 + 13.17 \, \epsilon ^2 L_c^2 \alpha V_{\text {DC}} V_{\text {AC}} + 16.68 \, \epsilon ^3 L_c \alpha V_{\text {DC}} V_{\text {AC}} + 26.35 \, \epsilon ^4 L_c^2 \alpha V_{\text {DC}} V_{\text {AC}}. \end{aligned}$$

(28)

Once the scaling analysis is carried out and very small terms are removed, the bookkeeping parameter $\epsilon$ is removed and the expanded equation of motion reduces to

$$\begin{aligned}&\left( 8.69 \, M + 2 + 27.47 \, M L_c + 28.39 \, M L_c^2 \right) {\ddot{q}(t)} +\frac{1}{Q} \, {\dot{q}(t)} \nonumber \\&\qquad +\, \left( 26.31 - 34.78 \, L_c \alpha V_{\text {DC}}^2 - 109.88 \, L_c^2 \alpha V_{\text {DC}}^2 - 69.56 \, L_c \alpha V_{\text {DC}} V_{\text {AC}} - 115.72 \, L_c^3 \alpha V_{\text {DC}}^2 \right) \, q(t) \nonumber \\&\qquad -\left( 108.77 \, L_c \alpha V_{\text {DC}}^2 +515.49 \, L_c^2 \alpha V_{\text {DC}}^2 \right) \, q^2(t)-\, 302.39 \, L_c \alpha V_{\text {DC}}^2 \, q(t)^3 \nonumber \\&\quad =8.34 \, L_c \alpha V_{\text {DC}}^2 + 13.17 \, L_c^2 \alpha V_{\text {DC}} V_{\text {AC}} + 16.68 \, L_c \alpha V_{\text {DC}} V_{\text {AC}} + 26.35 \, L_c^2 \alpha V_{\text {DC}} V_{\text {AC}}. \end{aligned}$$

(29)

The modal coordinate q(t) is rewritten as summation of a static component $q_s$ due to DC forcing and a dynamic component $q_d(t)$ due to AC forcing:

$$\begin{aligned} q(t) = q_s + q_d(t). \end{aligned}$$

(30)

The equation under static DC forcing is obtained by setting $q(t)=q_s$, $\dot{q}(t)=0$, $\ddot{q}(t)=0$, $V_\mathrm{{AC}}=0$ in Eq. (29), which yields

$$\begin{aligned}&\left( 26.31 - 34.78 \, L_c \alpha V_{\text {DC}}^2 -115.72 \, L_c^3 \alpha V_{\text {DC}}^2 -109.88 \, L_c^2 \alpha V_{\text {DC}}^2 \right) q_s \nonumber \\&\qquad -\, \left( 515.49 L_c^2 \alpha V_{\text {DC}}^2 +108.77 L_c \alpha V_{\text {DC}}^2 \right) q_s^2 -302.39 \, L_c \alpha V_{\text {DC}}^2 q_s^3 \nonumber \\&\quad = 8.34 \, L_c \alpha V_{\text {DC}}^2 +13.17 \, L_c^2 \alpha V_{\text {DC}}^2. \end{aligned}$$

(31)

Substituting for q(t) with Eq. (30) and using Eq. (31) in Eq. (29), to eliminate the static deflection $q_s$ terms, an equation representing the motion of the sense-plate around the equilibrium position $q_s$ is obtained in the form

$$\begin{aligned} M_e \, {\ddot{q}}_d (t)+ C \, {\dot{q}}_d (t)+ K_1 \, q_d (t)+ K_2 \, q_d^2 (t)+ K_3 \, q_d^3 (t)= K_e \, \mathrm{cos}(\varOmega t), \end{aligned}$$

where

$$\begin{aligned} M_e = \,&8.69 M + 2 + 27.47 M L_c + 28.93 M L_c^2, \\ C = \,&1/Q, \\ K_1 = \,&26.31 - 34.78 \, L_c \alpha V_\mathrm{{DC}}^2 -69.56 \,L_c \alpha V_\mathrm{{DC}} V_\mathrm{{AC}}- 109.88 \, L_c^2 \alpha V_\mathrm{{DC}}^2, \\&- 115.72 \, L_c^3 \alpha V_\mathrm{{DC}}^2 - 217.54 \, L_c \alpha V_\mathrm{{DC}}^2 q_s - 907.16 \, L_c \alpha V_\mathrm{{DC}}^2 q_s^2 - 1031 \, L_c^2 \alpha V_\mathrm{{DC}}^2 q_s, \\ K_2 =\,&-108.77 \, L_c \alpha V_\mathrm{{DC}}^2 - 515.49 \, L_c^2 \alpha V_\mathrm{{DC}}^2 - 907.16 \, L_c \alpha V_\mathrm{{DC}}^2 q_s, \\ \nonumber K_3 =\,&- 302.39 \, L_c \alpha V_\mathrm{{DC}}^2, \\ K_e =\,&16.68 \, L_c \alpha V_\mathrm{{DC}} V_\mathrm{{AC}} + 26.35 \, L_c^2 \alpha V_\mathrm{{DC}} V_\mathrm{{AC}} + 69.56 \, L_c \alpha V_\mathrm{{DC}} V_\mathrm{{AC}} \, q_s. \end{aligned}$$

It is noted that for a sensor with geometric specifications similar to the present class of sensors, the first term in each of the above expressions is the dominant term of the expression leading to the approximations in Eqs. (17) and (22).