1 Introduction

‘A rotor with variable mass’ is a mass variable body rotating around its axis. This type of rotor is the fundamental working element of many machines and devices in the textile, cable, or paper industry, but also in process industry and machining. The efficiency of these machines is directly connected to the rotation speed of rotors: for higher velocity, the productivity of machines is higher. However, in rotors rotating with high speed and having mass variation, vibration occurs, as a side effect. It is found that vibrations are harmful, shorten the working life of machines and tools and have a negative influence on the quality of products. Therefore, investigation on vibration of rotors with variable mass is of special interest.

Usually, the rotor with variable mass is assumed as a two-degree-of freedom system and vibration of the rotor is described by a system of two coupled differential equations. In general, there is not a closed form solution for the system of equations with time variable parameters and only an approximate solution is calculated. Based on approximate analytic methods (see [1–8]) developed for one-degree-of freedom oscillators with time varying mass, various methods for solving the equations of motion for rotors with time variable parameters are developed [9–12]. Utilizing these methods the approximate analytic solutions are obtained. Comparing the analytical solutions with numerical ones and experimentally measured values it is observed that a difference exists.

The aim of the paper is to improve the mathematical model of the rotor and also to give a procedure for obtaining a more appropriate solution. In the model the gyroscopic force [13, 14] is included. The suggested solution method is an extended version of the Krylov-Bogolubov procedure modified for equations with complex numbers [15]. In this paper, the analytically developed method is applied for vibration analysis of the work piece during the turning operation.

It is known that due to dynamic interaction between the cutter and the work piece, during the turning operation vibrations occur. A vast number of research works is devoted to the study of causes of vibrations and its minimization. Most of the investigations are done experimentally by measuring and recording vibration data and cutting force for various cutting parameters. It is concluded that during machining the forced vibrations, excited by unbalance, misalignment, etc., and also self-excited vibration, like chatter due to instabilities in the cutting process, occur. Investigation done by Ganguli [16] and Das and Hazarika [17] shows that the main cause of vibration and chattering instability is the lack of dynamic stiffness of the whole machine tool system. In the most of publication it is assumed that work piece is rigid and the cutting tool is elastic [18] and [19]. This model is suitable for analysis of the chatter vibration which is believed to be the cause of the roughness of the cutting surface [20–22]. The correlation between vibration of the cutting tool and the surface roughness is investigated [23–27]. Piotrowska et al [28] improved the turning operation model. The elastic properties of the cutting tool, but also of the work piece are introduced into consideration ([29–31]). Turning operation is described with a system of two coupled differential equations. Simulation of certain numerical examples is done. It is obtained that there is the difference between numerically calculated and experimentally measured vibration properties. To overcome the problem, further improvement of the model is necessary.

The aim of this paper is to improve the dynamic model of turning operation by taking into account the fact that the mass of the working piece is decreasing in time. Vibration of the working piece due to a single point radial cutting force and the reactive force, caused by mass decrease, is investigated. Vibration model of the work piece has two-degrees-of freedom and is described with two coupled equations with time variable parameters. Using the aforementioned method developed in this paper, the vibration properties of the work piece are calculated. Analytically obtained results are compared with those obtained experimentally by measuring on a real work piece. On the work piece the roughness is measured. Connection between analytically obtained vibration and experimentally measured surface roughness is determined.

2 Motion of the rotor with time variable mass

In general, the model of the rotor is considered as a Jeffcott two-degrees-of-freedom shaft-disk system with time variable mass [14]. The disk with mass m(t) is settled in the middle of the massless elastic shaft with rigidity k(t) supported in two layers. The mathematical model of the rotor center is

$$\begin{aligned} m(t)\ddot{z}+k(t)z-ig(t)\Omega {\dot{z}}=Z(z,{\dot{z}})-{\dot{m}}(t){\dot{z}}, \end{aligned}$$
(1)

where \(z=x+iy\) is the complex deflection, x and y are coordinates of the mass center, \(i=\sqrt{-1}\) is imaginary unit, g(t) is the gyroscopic coefficient [13], \(\Omega \) is the angular velocity of the rotor, \( Z(z,{\dot{z}})=X+iY\) is a function which depends on z and \({\dot{z}}\) (X and Y are projections in the x and y direction) due to physical and geometric nonlinearity of the rotor. The last term on the right hand side represents the reactive force which is caused by mass variation in time. For the case when the parameter variation is slow in time, i.e., the parameters are functions of the ‘slow time’ \(\tau =\varepsilon t,\) where \(\varepsilon<<1\) is a small parameter, Eq. (1) is

$$\begin{aligned} m(\tau )\ddot{z}+k(\tau )z-ig(\tau )\Omega {\dot{z}}=\varepsilon Z(z,{\dot{z}} )-\varepsilon m^{\prime }(\tau ){\dot{z}}, \end{aligned}$$
(2)

where \(m^{\prime }(\tau )=dm/d\tau \) and \(\varepsilon Z(z,{\dot{z}})\) is a small function. After some modification of (2) we have

$$\begin{aligned} \ddot{z}+K(\tau )z-iG(\tau )\Omega {\dot{z}}=\frac{\varepsilon }{m(\tau )}Z(z, {\dot{z}})-\varepsilon \frac{m^{\prime }(\tau )}{m(\tau )}{\dot{z}}, \end{aligned}$$
(3)

where \(K(\tau )=k(\tau )/m(\tau )\) and \(G(\tau )=g(\tau )/m(\tau )\). Equation (3) is a differential equation with complex function and slow time variable parameters. There is not a closed form solution for (3). An analytic procedure for solving Eq. (3) is developed in the following.

3 Analytical solution method

Separating the real and imaginary parts in (3), we obtain

$$\begin{aligned} \overset{\cdot \cdot }{x}+K(\tau )x+G(\tau )\Omega \overset{\cdot }{y}= & {} \frac{\varepsilon }{m(\tau )}X-\varepsilon \frac{m^{\prime }(\tau )}{m(\tau ) }\overset{\cdot }{x}, \end{aligned}$$
(4)
$$\begin{aligned} \overset{\cdot \cdot }{y}+K(\tau )y-G(\tau )\Omega \overset{\cdot }{x}= & {} \frac{\varepsilon }{m(\tau )}Y-\varepsilon \frac{m^{\prime }(\tau )}{m(\tau ) }\overset{\cdot }{y}. \end{aligned}$$
(5)

It is obvious that the right hand side terms are small (multiplied with \( \varepsilon )\). The parameters in the equation are functions of the slow time \(\tau \) . Equations (4) and (5) are the perturbed version of the linear equations with constant parameters

$$\begin{aligned} \overset{\cdot \cdot }{x}+Kx+G\Omega \overset{\cdot }{y}= &\, {} 0, \end{aligned}$$
(6)
$$\begin{aligned} \overset{\cdot \cdot }{y}+Ky-G\Omega \overset{\cdot }{x}= & {}\, 0, \end{aligned}$$
(7)

where for \(\varepsilon =0\) the parameters K and G are constant values. The assumption is that the solution of (4) and (5) has to be the perturbed version of the solution for (6) and (7).

The assumed solutions for the coupled second-order differential equations (6) and (7) are

$$\begin{aligned} x=A\cos \omega t,\qquad y=B\sin \omega t, \end{aligned}$$
(8)

where A, B and \(\omega \) are unknown constant values. Substituting (8) into (6) and (7), the frequency equation follows as

$$\begin{aligned} (K-\omega ^{2})^{2}-G^{2}\Omega ^{2}\omega ^{2}=0. \end{aligned}$$
(9)

Solving (9), two frequencies of vibration of the system are obtained

$$\begin{aligned} \omega _{1}=\frac{G\Omega }{2}+\sqrt{(\frac{G\Omega }{2})^{2}+K},\qquad \omega _{2}=-\frac{G\Omega }{2}+\sqrt{(\frac{G\Omega }{2})^{2}+K}. \end{aligned}$$
(10)

The corresponding shape coefficients are

$$\begin{aligned} \kappa _{1}=\frac{B_{1}}{A_{1}}=\frac{\omega _{1}^{2}-K}{G\Omega \omega _{1}} =1,\qquad \kappa _{2}=\frac{B_{2}}{A_{2}}=\frac{\omega _{2}^{2}-K}{G\Omega \omega _{2}}=-1. \end{aligned}$$
(11)

Using (8), (10) and (11), the closed form solution of (4) and (5) with its derivative follows as

$$\begin{aligned} x= & {} A_{1}\cos \psi _{1}+A_{2}\cos \psi _{2}, \end{aligned}$$
(12)
$$\begin{aligned} y= & {} A_{1}\sin \psi _{1}-A_{2}\sin \psi _{2}, \end{aligned}$$
(13)

and

$$\begin{aligned} {\dot{x}}= & {} -A_{1}\omega _{1}\sin \psi _{1}-A_{2}\omega _{2}\sin \psi _{2}, \end{aligned}$$
(14)
$$\begin{aligned} {\dot{y}}= & {} A_{1}\omega _{1}\cos \psi _{1}-A_{2}\omega _{2}\cos \psi _{2}, \end{aligned}$$
(15)

with

$$\begin{aligned} \psi _{1}=\omega _{1}t+\theta _{1},\qquad \psi _{2}=\omega _{2}t+\theta _{2}, \end{aligned}$$
(16)

where \(A_{1},\) \(A_{2},\) \(\theta _{1}\) and \(\theta _{2}\) are arbitrary constants.

Due to the method suggested in the paper, the solution and the first derivative of the solution (4) and (5) are assumed in the form (12)–(15), but with time variable amplitudes \(A_{1}(t)\) and \(A_{2}(t)\)and phases \(\theta _{1}(t)\) and \(\theta _{2}(t),\) i.e.,

$$\begin{aligned} x= & {} A_{1}(t)\cos \psi _{1}(t)+A_{2}(t)\cos \psi _{2}(t), \end{aligned}$$
(17)
$$\begin{aligned} y= & {} A_{1}(t)\sin \psi _{1}(t)-A_{2}(t)\sin \psi _{2}(t), \end{aligned}$$
(18)

and

$$\begin{aligned} {\dot{x}}= & {} -A_{1}(t)\omega _{1}(\tau )\sin \psi _{1}(t)-A_{2}(t)\omega _{2}(\tau )\sin \psi _{2}(t), \end{aligned}$$
(19)
$$\begin{aligned} {\dot{y}}= & {} A_{1}(t)\omega _{1}(\tau )\cos \psi _{1}(t)+A_{2}(t)\omega _{2}(\tau )\cos \psi _{2}(t), \end{aligned}$$
(20)

with

$$\begin{aligned} {\dot{\psi }}_{1}(t)=\omega _{1}(\tau )+{\dot{\theta }}_{1}(t),\qquad {\dot{\psi }} _{2}(t)=\omega _{2}(\tau )+{\dot{\theta }}_{2}(t), \end{aligned}$$
(21)

and

$$\begin{aligned} \omega _{1}(\tau )=\frac{G(\tau )\Omega }{2}+\sqrt{(\frac{G(\tau )\Omega }{2} )^{2}+K(\tau )},\qquad \omega _{2}=-\frac{G(\tau )\Omega }{2}+\sqrt{(\frac{ G(\tau )\Omega }{2})^{2}+K(\tau )}. \end{aligned}$$
(22)

Comparing the first time derivative of (17) and (18) with ( 19) and (20) two constraints are obtained

$$\begin{aligned} ({\dot{A}}_{1}\cos \psi _{1}-A_{1}{\dot{\theta }}_{1}\sin \psi _{1})+({\dot{A}} _{2}\cos \psi _{2}-A_{2}{\dot{\theta }}_{2}\sin \psi _{2})= & {}\, 0, \end{aligned}$$
(23)
$$\begin{aligned} ({\dot{A}}_{1}\sin \psi _{1}+A_{1}{\dot{\theta }}_{1}\cos \psi _{1})-({\dot{A}} _{2}\sin \psi _{2}+A_{2}{\dot{\theta }}_{2}\cos \psi _{2})= & {} \,0, \end{aligned}$$
(24)

where \((^{\prime })=d/d\tau \), \(A_{1}=A_{1}(t),\) \(A_{2}=A_{2}(t),\) \(\theta _{1}(\tau ),\) \(\theta _{2}(\tau ),\) \(\psi _{1}(\tau )\) and \(\psi _{2}(\tau ). \) Using the first derivative of (19) and (20) and relations (17) and (18), Eqs. (4) and (5 ) are transformed into

$$ \begin{array}{cccc} & {\omega _1}({{\dot A}_1}\sin {\psi _1} + {A_1}{{\dot \theta }_1}\cos {\psi _1}) + {\omega _2}({{\dot A}_2}\sin {\psi _2} + {A_2}{{\dot \theta }_2}\cos {\psi _2})\\ & \quad = - \varepsilon \left[ {\frac{X}{m} + \frac{{{m^\prime }}}{m}({A_1}{\omega _1}\sin {\psi _1} + {A_2}{\omega _2}\sin {\psi _2})} \right.\\ & \quad \quad \left. {+ ({A_1}\omega _1^\prime \sin {\psi _1} + {A_2}\omega _2^\prime \sin {\psi _2})} \vphantom{\frac{x}{m}}\right],\end{array} $$
(25)
$$\begin{aligned} & {\omega _1}({{\dot A}_1}\cos {\psi _1} - {A_1}{{\dot \theta }_1}\sin {\psi _1}) - {\omega _2}({{\dot A}_2}\cos {\psi _2} - {A_2}{{\dot \theta }_2}\sin {\psi _2}) \\ & \quad = \varepsilon \left[ {\frac{Y}{m} - \frac{{{m^\prime }}}{m}({A_1}{\omega _1}\cos {\psi _1} - {A_2}{\omega _2}\cos {\psi _2})} \right. \\ & \quad \quad - \left. {({A_1}\omega _1^\prime \cos {\psi _1} - {A_2}\omega _2^\prime \cos {\psi _2})} \vphantom{\frac{X}{m}}\right], \\ \end{aligned} $$
(26)

where \(X=X(x,y,{\dot{x}},{\dot{y}})\) and \(Y=Y(x,y,{\dot{x}},{\dot{y}})\) with (17)-(20). Equations (23)–(26) are four first-order differential equations which correspond to (4) and (5). Introducing the notation

$$\begin{aligned} P_{1}= & {} \,A_{1}\omega _{1}^{\prime }\sin \psi _{1}+A_{2}\omega _{2}^{\prime }\sin \psi _{2}, \nonumber \\ P_{2}= &\, {} A_{1}\omega _{1}\sin \psi _{1}+A_{2}\omega _{2}\sin \psi _{2}, \nonumber \\ Q_{1}= & {}\, A_{1}\omega _{1}^{\prime }\cos \psi _{1}-A_{2}\omega _{2}^{\prime }\cos \psi _{2}, \nonumber \\ Q_{2}= &\, {} A_{1}\omega _{1}\cos \psi _{1}-A_{2}\omega _{2}\cos \psi _{2}, \end{aligned}$$
(27)

into (23)–(26) and after some modification it is

$$\begin{aligned} {\dot{A}}_{2}\sin \psi _{2}+A_{2}{\dot{\theta }}_{2}\cos \psi _{2}= & {} -\frac{ \varepsilon }{\omega _{1}+\omega _{2}}(\frac{X}{m}+\frac{m^{\prime }}{m} P_{2}+P_{1}), \nonumber \\ {\dot{A}}_{1}\sin \psi _{1}+A_{1}{\dot{\theta }}_{1}\cos \psi _{1}= & {} -\frac{ \varepsilon }{\omega _{1}+\omega _{2}}(\frac{X}{m}+\frac{m^{\prime }}{m} P_{2}+P_{1}), \nonumber \\ {\dot{A}}_{2}\cos \psi _{2}-A_{2}{\dot{\theta }}_{2}\sin \psi _{2}= & {} -\frac{ \varepsilon }{\omega _{1}+\omega _{2}}(\frac{Y}{m}-\frac{m^{\prime }}{m} Q_{2}-Q_{1}), \nonumber \\ {\dot{A}}_{1}\cos \psi _{1}-A_{1}{\dot{\theta }}_{1}\sin \psi _{1}= & {} \frac{ \varepsilon }{\omega _{1}+\omega _{2}}(\frac{Y}{m}-\frac{m^{\prime }}{m} Q_{2}-Q_{1}). \end{aligned}$$
(28)

Finally, after separation of variables we have

$$\begin{aligned} {\dot{A}}_{1}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}}[(\frac{X}{m}+ \frac{m^{\prime }}{m}P_{2}+P_{1})\sin \psi _{1}-(\frac{Y}{m}-\frac{m^{\prime }}{m}Q_{2}-Q_{1})\cos \psi _{1}], \nonumber \\ A_{1}{\dot{\theta }}_{1}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}}[( \frac{X}{m}+\frac{m^{\prime }}{m}P_{2}+P_{1})\cos \psi _{1}+(\frac{Y}{m}- \frac{m^{\prime }}{m}Q_{2}-Q_{1})\sin \psi _{1}], \nonumber \\ {\dot{A}}_{2}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}}[(\frac{X}{m}+ \frac{m^{\prime }}{m}P_{2}+P_{1})\sin \psi _{2}+(\frac{Y}{m}-\frac{m^{\prime }}{m}Q_{2}-Q_{1})\cos \psi _{2}], \nonumber \\ A_{2}{\dot{\theta }}_{2}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}}[( \frac{X}{m}+\frac{m^{\prime }}{m}P_{2}+P_{1})\cos \psi _{2}-(\frac{Y}{m}- \frac{m^{\prime }}{m}Q_{2}-Q_{1})\sin \psi _{2}]. \end{aligned}$$
(29)

To solve the system of coupled nonlinear differential equations is not an easy task. It is the reason that the averaging procedure over the period of the periodic functions with argument \(\psi _{1}\) and \(\psi _{2}\) are introduced. The averaged equations of motion are

$$\begin{aligned} {\dot{A}}_{1}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}}[A_{1}(\omega _{1}^{\prime }+\omega _{1}\frac{m^{\prime }}{m})+\left\langle \frac{X}{m} \sin \psi _{1}\right\rangle -\left\langle \frac{Y}{m}\cos \psi _{1}\right\rangle \nonumber \\&-A_{2}(\omega _{2}^{\prime }+\omega _{2}\frac{m^{\prime }}{m})\left\langle \cos (\psi _{1}+\psi _{2})\right\rangle ], \nonumber \\ A_{1}{\dot{\theta }}_{1}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}} [\left\langle \frac{X}{m}\cos \psi _{1}\right\rangle +\left\langle \frac{Y}{m }\sin \psi _{1}\right\rangle +A_{2}(\omega _{2}^{\prime }+\omega _{2}\frac{ m^{\prime }}{m})\left\langle \sin (\psi _{1}+\psi _{2})\right\rangle ], \nonumber \\ {\dot{A}}_{2}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}}[A_{2}(\omega _{2}^{\prime }+\omega _{2}\frac{m^{\prime }}{m})+\left\langle \frac{X}{m} \sin \psi _{2}\right\rangle +\left\langle \frac{Y}{m}\cos \psi _{2}\right\rangle \nonumber \\&-A_{1}(\omega _{1}^{\prime }+\omega _{1}\frac{m^{\prime }}{m})\left\langle \cos (\psi _{1}+\psi _{2})\right\rangle ], \nonumber \\ A_{2}{\dot{\theta }}_{2}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}} [\left\langle \frac{X}{m}\cos \psi _{2}\right\rangle -\left\langle \frac{Y}{m }\sin \psi _{2}\right\rangle \nonumber \\&+A_{1}(\omega _{1}^{\prime }+\omega _{1}\frac{m^{\prime }}{m})\left\langle \sin (\psi _{1}+\psi _{2})\right\rangle ], \end{aligned}$$
(30)

where \(\left\langle \cdot \right\rangle \) is the notation for averaging. For \(\left\langle \cos (\psi _{1}+\psi _{2})\right\rangle =0\) and \(\left\langle \sin (\psi _{1}+\psi _{2})\right\rangle =0\) the averaged equations are

$$\begin{aligned} {\dot{A}}_{1}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}}[A_{1}(\omega _{1}^{\prime }+\omega _{1}\frac{m^{\prime }}{m})+\left\langle \frac{X}{m} \sin \psi _{1}\right\rangle -\left\langle \frac{Y}{m}\cos \psi _{1}\right\rangle ], \nonumber \\ A_{1}{\dot{\theta }}_{1}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}} [\left\langle \frac{X}{m}\cos \psi _{1}\right\rangle +\left\langle \frac{Y}{m }\sin \psi _{1}\right\rangle ], \nonumber \\ {\dot{A}}_{2}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}}[A_{2}(\omega _{2}^{\prime }+\omega _{2}\frac{m^{\prime }}{m})+\left\langle \frac{X}{m} \sin \psi _{2}\right\rangle +\left\langle \frac{Y}{m}\cos \psi _{2}\right\rangle ], \nonumber \\ A_{2}{\dot{\theta }}_{2}= & {} -\frac{\varepsilon }{\omega _{1}+\omega _{2}} [\left\langle \frac{X}{m}\cos \psi _{2}\right\rangle -\left\langle \frac{Y}{m }\sin \psi _{2}\right\rangle ]. \end{aligned}$$
(31)

Integrating Eqs. (31) for \(A_{1}\), \(A_{2}\), \(\theta _{1}\) and \( \theta _{2},\) and substituting into (17) and (18) the averaged solution of (4) and (5), i.e., (3) is obtained.

3.1 Discussion for the linear rotor

For the linear rotor (nonlinearity is zero) the averaged differential equations are

$$\begin{aligned} {\dot{A}}_{1}= & {} \,-\frac{\varepsilon A_{1}}{\omega _{1}+\omega _{2}}(\omega _{1}^{\prime }+\omega _{1}\frac{m^{\prime }}{m}), \nonumber \\ A_{1}{\dot{\theta }}_{1}= & {}\, 0, \nonumber \\ {\dot{A}}_{2}= & {} -\frac{\varepsilon A_{2}}{\omega _{1}+\omega _{2}}(\omega _{2}^{\prime }+\omega _{2}\frac{m^{\prime }}{m}), \nonumber \\ A_{2}{\dot{\theta }}_{2}= & {} \,0. \end{aligned}$$
(32)

For initial conditions \(A_{1}(0)=A_{10},\) \(A_{2}(0)=A_{20},\) \(\theta _{1}(0)=\theta _{10},\) \(\theta _{2}(0)=\theta _{20}\) the solution of (32) is

$$\begin{aligned} A_{1}= & {} A_{10}\exp \left(-\int \limits _{0}^{\tau }\frac{1}{\omega _{1}+\omega _{2}}(\omega _{1}^{\prime }+\omega _{1}\frac{m^{\prime }}{m})d\tau \right),\qquad \theta _{1}=\theta _{10}, \nonumber \\ A_{2}= & {} A_{20}\exp \left(-\int \limits _{0}^{\tau }\frac{1}{\omega _{1}+\omega _{2}}(\omega _{2}^{\prime }+\omega _{2}\frac{m^{\prime }}{m})d\tau \right),\qquad \theta _{2}=\theta _{20}. \end{aligned}$$
(33)

Substituting (22) into (33), it follows that

$$\begin{aligned} A_{1}= & {} A_{10}\exp\left(-\int \limits _{0}^{\tau }\frac{2K}{4K+\Omega ^{2}G^{2}} \frac{dm}{m}\right),\qquad \psi _{1}=\theta _{10}+\int \limits _{0}^{t}\omega _{1}(\tau)dt, \\ A_{2}= & {} A_{20}\exp\left (-\int \limits _{0}^{\tau }\frac{2K}{4K+\Omega ^{2}G^{2}} \frac{dm}{m}\right),\qquad \psi _{2}=\theta _{20}+\int \limits _{0}^{t}\omega _{2}(\tau)dt. \end{aligned}$$
(34)

Finally, the vibration of the rotor is according to (17) and (18)

$$\begin{aligned} x= &{} \exp \left(-\int \limits _{0}^{\tau }\frac{2K}{4K+\Omega ^{2}G^{2}}\frac{dm}{m }\right)(A_{10}\cos \psi _{1}+A_{20}\cos \psi _{2}), \\ y= & {} \exp\left (-\int \limits _{0}^{\tau }\frac{2K}{4K+\Omega ^{2}G^{2}}\frac{dm}{m }\right)(A_{10}\sin \psi _{1}-A_{20}\sin \psi _{2}), \end{aligned}$$
(35)

i.e.,

$$\begin{aligned} z=\exp\left (-\int \limits _{0}^{\tau }\frac{2K}{4K+\Omega ^{2}G^{2}}\frac{dm}{m}\right )(A_{10}\exp (i\psi _{1})+A_{20}\exp (-i\psi _{2})). \end{aligned}$$
(36)

3.1.1 Special cases

a) If the gyroscopic effect is neglected (\(g=0\)), the frequency \(\omega _{1}=\omega _{2}=\sqrt{K}\) and the relations (35) simplify into

$$\begin{aligned} x= & {} \sqrt{\frac{m_{0}}{m}}(A_{1c}\cos (\omega t)-A_{1s}\sin (\omega t)), \nonumber \\ y= & {} \sqrt{\frac{m_{0}}{m}}(A_{2s}\cos (\omega t)+A_{2c}\sin (\omega t)), \end{aligned}$$
(37)

where

$$\begin{aligned} A_{1c}= & {}\, A_{10}\cos \theta _{10}+A_{20}\cos \theta _{20},\qquad A_{1s}=A_{10}\sin \theta _{10}+A_{20}\sin \theta _{20}, \nonumber \\ A_{2c}= & {} \,A_{10}\cos \theta _{10}-A_{20}\cos \theta _{20},\qquad A_{2s}=A_{10}\sin \theta _{10}-A_{20}\sin \theta _{20}. \end{aligned}$$
(38)

The trajectory of the rotor center is an ellipse with slow time varying parameters

$$\begin{aligned} (A_{2c}x+A_{1s}y)^{2}+(A_{2s}x-A_{1c}y)^{2}=\frac{m_{0}}{m} (A_{1s}A_{2s}+A_{1c}A_{2c})^{2}. \end{aligned}$$
(39)

b) For \(g=0\) and initial conditions \(\theta _{10}=\theta _{20}=0\) solutions ( 37) modify into

$$\begin{aligned} z=\sqrt{\frac{m_{0}}{m}}(A_{10}\exp (i\omega t)+A_{20}\exp (-i\omega t)) \end{aligned}$$
(40)

and the trajectory of the rotor center is a central ellipse with variable parameters:

$$\begin{aligned} \frac{x^{2}}{(A_{10}+A_{20})^{2}}+\frac{y^{2}}{(A_{10}^{{}}-A_{20}^{{}})^{2}} =\frac{m_{0}}{m(\tau )}. \end{aligned}$$
(41)

c) For \(g=0\) and initial conditions \(\theta _{10}=\theta _{20}=0\) and \( A_{20}=0\) the solution (40) simplifies into

$$\begin{aligned} z=\sqrt{\frac{m_{0}}{m}}A_{10}\exp (i\psi _{1}), \end{aligned}$$
(42)

and the trajectory is a circle with time variable radius:

$$\begin{aligned} x^{2}+y^{2}=\frac{m_{0}}{m}A_{10}^{2}. \end{aligned}$$
(43)

d) For \(g=0\) and initial conditions \(\theta _{10}=\theta _{20}=\theta \) and \( A_{10}=A_{20}=A\) the rotor center is vibrating along a line with time variable amplitude, i.e.,

$$\begin{aligned} x=2A\sqrt{\frac{m_{0}}{m}}\cos (\omega t+\theta ). \end{aligned}$$
(44)

The aforementioned cases were previously discussed for the rotor with constant mass [32]. Comparing the results for obtained for the rotor with variable mass and those for the rotor with constant mass, it is seen that there is a difference between trajectories due to the fact that for the first ones the parameters are dependent on slow time.

4 Vibration of the work piece during turning operation

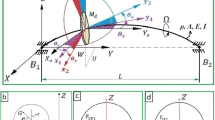
In Fig. 1a the model of the work piece and the cutting tool for turning operation is shown. On the work piece, which is fixed to the spindle and pin mounted at the tailstock, a cutter tool acts. The cutting force acts radially on the work piece [17]. The cutting force is proportional to the frontal area of the cutted chip, which is the product of the chip thickness h (equal to the cutting depth) and the width of the cut a,

$$\begin{aligned} F=k_{C}ah(t), \end{aligned}$$
(45)

where \(k_{c}\) is the cutting coefficient. The work piece is rotating with the constant angular velocity \(\Omega \), while the cutting tool is translatory moving along the work piece with constant velocity v. During turning the geometric and mass properties of the work piece are varying. Mass and moment of inertia of the work piece are changing in time. It causes the change of the rigidity of the work piece. Due to mass variation the reactive force acts, which in addition to the cutting force causes the working piece to vibrate.

For further analysis it is necessary to define the mass and the rigidity of the work piece.

4.1 Mass variation of the work piece

The work piece is modeled with two coaxial cylinders: one with radius \( R_{0} \), which corresponds to the case before cutting, and the other with radius \(R_{1}\), after cutting (Figs. 1a, b).

Fig. 1
figure 1

a Workpiece-cutting tool model, b Geometry of the work piece

Full size image

The total mass m of the work piece is the sum of masses \(m_{1}\) and \(m_{0}\) of the already cut and of the unmachined piece, respectively, i.e.,

$$\begin{aligned} m=m_{0}+m_{1}, \end{aligned}$$
(46)

where

$$\begin{aligned} m_{0}=A_{0}(l-vt)\rho ,\qquad m_{1}=A_{1}(vt)\rho , \end{aligned}$$
(47)

\(\rho \) is material density, \(S_{0}\) is the surface of work piece before turning, \(S_{1}\) is the surface after turning and l is the length of the work piece. If the initial radius of the work piece is \(R_{0}\) and the cutting depth is h,  the surfaces before and after cutting are

$$\begin{aligned} S_{0}=R_{0}^{2}\pi ,\qquad S_{1}=R_{1}^{2}\pi =(R_{0}-h)^{2}\pi =S_{0}(1-2 \frac{h}{R_{0}}+\frac{h^{2}}{R_{0}^{2}}). \end{aligned}$$
(48)

Substituting (47) with (48) into (46), the mass of the work piece is obtained as a function of time:

$$\begin{aligned} m=m_{0}(1-2\frac{v}{l}\frac{h}{R_{0}}t+\frac{v}{l}\frac{h^{2}}{R_{0}^{2}}t). \end{aligned}$$
(49)

4.2 Variable rigidity of the work piece

During cutting the rigidity of the work piece varies due to variation of its geometry. Namely, the rigidity of the part obtained by cutting and the rigidity of the remaining part of the work piece are different. Due to Hook’s law, the elastic stress \(\sigma \) and strain e relations in the parts of the work piece before and after cutting are, respectively,

$$\begin{aligned} \sigma _{0}=Ee_{0},\qquad \sigma _{1}=Ee_{1}, \end{aligned}$$
(50)

where E is the modulus of elasticity and for the deformations \(s_{0}\) and \( s_{1}\) along the work piece the strains \(e_{0}\) and \(e_{1}\) are

$$\begin{aligned} e_{0}=\frac{s_{0}}{l-vt},\qquad e_{1}=\frac{s_{1}}{vt}. \end{aligned}$$
(51)

In addition, for an axial force P the axial stresses in the unmachined and machined work piece are

$$\begin{aligned} \sigma _{0}=\frac{P}{S_{0}},\qquad \sigma _{1}=\frac{P}{S_{1}}. \end{aligned}$$
(52)

According to relations (52) and (50) it follows that

$$\begin{aligned} P=k_{0}s_{0},\qquad P=k_{1}s_{1}, \end{aligned}$$
(53)

where rigidities of the working piece parts are

$$\begin{aligned} k_{0}=\frac{S_{0}E}{l-vt},\qquad k_{1}=\frac{S_{1}E}{vt}. \end{aligned}$$
(54)

Let us introduce the equivalent rigidity k which satisfies the relation

$$\begin{aligned} P=ks, \end{aligned}$$
(55)

where s is the total displacement

$$\begin{aligned} s=s_{0}+s_{1}. \end{aligned}$$
(56)

Substituting (53)–(55) into (56) the equivalent rigidity is

$$\begin{aligned} \frac{1}{k}=\frac{1}{k_{0}}+\frac{1}{k_{1}}, \end{aligned}$$
(57)

i.e.,

$$\begin{aligned} k=\frac{S_{0}S_{1}E}{S_{0}vt+S_{1}(l-vt)}. \end{aligned}$$
(58)

Finally, due to (48) and (58) we have

$$\begin{aligned} k=\frac{S_{0}E}{l}\frac{1-2\frac{h}{R_{0}}+\frac{h^{2}}{R_{0}^{2}}}{(1-2 \frac{h}{R_{0}}+\frac{h^{2}}{R_{0}^{2}})+\frac{h}{R_{0}}(2-\frac{h}{R_{0}}) \frac{v}{l}t}. \end{aligned}$$
(59)

Analyzing relations for mass (49) and rigidity variation (59) it is seen that they depend on the relation \(h/R_{0}\). It is known that during tuning the parameter ratio \(h/R_{0}\) is small. Introducing the notation of the small parameter \(\varepsilon<<1\) and the slow time, respectively,

$$\begin{aligned} \varepsilon =\frac{h}{R_{0}},\qquad \tau =\varepsilon t, \end{aligned}$$
(60)

mass and rigidity variation are

$$\begin{aligned} m(\tau )=m_{0}-\frac{m_{0}v}{l}(2-\varepsilon )\tau ,\qquad k(\tau )=\frac{ A_{0}E}{l}\frac{1}{1+\frac{2-\varepsilon }{1-2\varepsilon +\varepsilon ^{2}} \frac{v}{l}\tau }. \end{aligned}$$
(61)

Neglecting the terms with higher order of small parameter \(\varepsilon \) the approximate mass and rigidity values are as follow

$$\begin{aligned} m(\tau )=m_{0}(1-2\frac{v}{l}\tau ),\qquad k(\tau )=\frac{S_{0}E}{l}(1-2 \frac{v}{l}\tau ). \end{aligned}$$
(62)

The time derivative of mass variation (62) is

$$\begin{aligned} {\dot{m}}(\tau )=-2\varepsilon \frac{m_{0}v}{l}. \end{aligned}$$
(63)

It is a constant which depends on the velocity of the cutting tool v.

4.3 Mathematical model

The model of the work piece is assumed as a rotating mass—spring system with concentrated mass \(m(\tau )\) the spring with equivalent rigidity \( k(\tau ).\) Motion of the mass is in plane (Fig. 2). The system is rotating with constant angular velocity \(\Omega .\)

Fig. 2
figure 2

Model of the work piece

Full size image

If the coordinates of rotor center are X and y and if the angular velocity of the work piece is \(\Omega ,\) the kinetic energy is

$$\begin{aligned} T=\frac{1}{2}m(\tau )(({\dot{X}}-y\Omega )^{2}+({\dot{y}}+X\Omega )^{2}), \end{aligned}$$
(64)

and the potential energy

$$\begin{aligned} V=\frac{1}{2}k(\tau )(X^{2}+y^{2}). \end{aligned}$$
(65)

The Lagrange differential equations of motion in x and y direction are

$$\begin{aligned} m(\tau ){\ddot{X}}-2m(\tau )\Omega {\dot{y}}+k(\tau )X= & {} -F-{\dot{m}}(\tau )(\dot{ X}-\Omega y), \nonumber \\ m(\tau )\ddot{y}+2m(\tau )\Omega {\dot{X}}+k(\tau )y= & {} -{\dot{m}}(\tau )({\dot{y}} +\Omega X), \end{aligned}$$
(66)

i.e.,

$$\begin{aligned} {\ddot{X}}-2\Omega {\dot{y}}+\frac{k(\tau )}{m(\tau )}X= & {} -\frac{F}{m(\tau )} -\varepsilon \frac{m^{\prime }}{m(\tau )}({\dot{X}}-\Omega y), \nonumber \\ \ddot{y}+2\Omega {\dot{X}}+\frac{k(\tau )}{m(\tau )}y= & {} -\varepsilon \frac{ m^{\prime }}{m(\tau )}({\dot{y}}+\Omega X). \end{aligned}$$
(67)

For simplification let us introduce the new variable

$$\begin{aligned} x=X+\frac{F}{k(\tau )}. \end{aligned}$$
(68)

Substituting (68) and its derivative into (67) and assuming the terms up to the first-order of small value \(\varepsilon ,\) we obtain

$$\begin{aligned} \ddot{x}-2\Omega {\dot{y}}+Kx= & {} -\varepsilon \frac{m^{\prime }}{m(\tau )}( {\dot{x}}-\Omega y), \nonumber \\ \ddot{y}+2\Omega {\dot{x}}+Ky= & {} -\varepsilon \frac{m^{\prime }}{m(\tau )}( {\dot{y}}+\Omega x+\frac{\Omega F}{k(\tau )}), \end{aligned}$$
(69)

where

$$\begin{aligned} K=\frac{S_{0}E}{m_{0}l}=\text{const.} \end{aligned}$$
(70)

Utilizing the previously mentioned solving procedure Eqs. (69) are rewritten into four first-order equations with new variables \(A_{1}\), \( A_{2}\), \(\theta _{1}\), \(\theta _{2}\):

$$\begin{aligned} 0= &\, {} ({\dot{A}}_{1}\cos \psi _{1}-A_{1}{\dot{\theta }}_{1}\sin \psi _{1})+({\dot{A}} _{2}\cos \psi _{2}-A_{2}{\dot{\theta }}_{2}\sin \psi _{2}), \nonumber \\ 0= & \,{} ({\dot{A}}_{1}\sin \psi _{1}+A_{1}{\dot{\theta }}_{1}\cos \psi _{1})-({\dot{A}} _{2}\sin \psi _{2}+A_{2}{\dot{\theta }}_{2}\cos \psi _{2}), \nonumber \\&\omega _{1}({\dot{A}}_{1}\sin \psi _{1}+A_{1}{\dot{\theta }}_{1}\cos \psi _{1})+\omega _{2}({\dot{A}}_{2}\sin \psi _{2}+A_{2}{\dot{\theta }}_{2}\cos \psi _{2}) \nonumber \\= & {}\, -\varepsilon \frac{m^{\prime }}{m}(A_{1}(\omega _{1}+\Omega )\sin \psi _{1}+A_{2}(\omega _{2}-\Omega )\sin \psi _{2}) \nonumber \\&-\varepsilon (A_{1}\omega _{1}^{\prime }\sin \psi _{1}+A_{2}\omega _{2}^{\prime }\sin \psi _{2}), \nonumber \\&\omega _{1}({\dot{A}}_{1}\cos \psi _{1}-A_{1}{\dot{\theta }}_{1}\sin \psi _{1})-\omega _{2}({\dot{A}}_{2}\cos \psi _{2}-A_{2}{\dot{\theta }}_{2}\sin \psi _{2}) \nonumber \\= & {} -\varepsilon \frac{m^{\prime }}{m}(A_{1}(\omega _{1}+\Omega )\cos \psi _{1}-A_{2}(\omega _{2}-\Omega )\cos \psi _{2}+\frac{\Omega F}{k(\tau )}) \nonumber \\&-\varepsilon (A_{1}\omega _{1}^{\prime }\cos \psi _{1}-A_{2}\omega _{2}^{\prime }\cos \psi _{2})), \end{aligned}$$
(71)

where

$$\begin{aligned} \omega _{1}=-\Omega +\sqrt{\Omega ^{2}-K},\qquad \omega _{2}=\Omega +\sqrt{ \Omega ^{2}+K}. \end{aligned}$$
(72)

After some modification of (71) we obtain

$$\begin{aligned} (\omega _{1}+\omega _{2}){\dot{A}}_{1}= & {} P_{1}\sin \psi _{1}+P_{2}\cos \psi _{1}, \nonumber \\ (\omega _{1}+\omega _{2})A_{1}{\dot{\theta }}_{1}= & {} P_{1}\cos \psi _{1}-P_{2}\sin \psi _{1}, \nonumber \\ (\omega _{1}+\omega _{2}){\dot{A}}_{2}= & {} P_{1}\sin \psi _{2}-P_{2}\cos \psi _{2}, \nonumber \\ (\omega _{1}+\omega _{2})A_{2}{\dot{\theta }}_{2}= & {} P_{1}\cos \psi _{2}+P_{2}\sin \psi _{2}, \end{aligned}$$
(73)

where

$$\begin{aligned} P_{1}=-\varepsilon (A_{1}p\sin \psi _{1}+A_{2}q\sin \psi _{2}), \end{aligned}$$
$$\begin{aligned} P_{2}=-\varepsilon (A_{1}p\cos \psi _{1}-A_{2}q\cos \psi _{2}+\frac{ m^{\prime }\Omega F}{m(\tau )k(\tau )}), \end{aligned}$$
(74)
$$\begin{aligned} p=\frac{m^{\prime }}{m}(\omega _{1}+\Omega )+\omega _{1}^{\prime },\qquad q= \frac{m^{\prime }}{m}(\omega _{2}-\Omega )+\omega _{2}^{\prime }. \end{aligned}$$
(75)

Averaging the equations over the period of the trigonometric functions \(\psi _{1}\) and \(\psi _{2}\), the averaged equations follow as

$$\begin{aligned} {\dot{A}}_{1}= & {} -\frac{\varepsilon A_{1}p}{\omega _{1}+\omega _{2}},\qquad A_{1}{\dot{\theta }}_{1}=0, \nonumber \\ {\dot{A}}_{2}= & {} -\frac{\varepsilon A_{2}q}{\omega _{1}+\omega _{2}},\qquad A_{1}{\dot{\theta }}_{1}=0. \end{aligned}$$
(76)

Substituting (72) and (75) into (76) it is obtained

$$\begin{aligned} {\dot{A}}_{1}= & {} -\varepsilon A_{1}\frac{m^{\prime }}{2m},\qquad {\dot{\theta }} _{1}=0, \nonumber \\ {\dot{A}}_{2}= & {} -\varepsilon A_{2}\frac{m^{\prime }}{2m},\qquad {\dot{\theta }} _{1}=0. \end{aligned}$$
(77)

Integrating (77) and using the initial conditions \(A_{1}(0)=A_{10},\) \(A_{2}(0)=A_{20},\) \(\theta _{1}(0)=\theta _{10},\) \(\theta _{2}(0)=\theta _{20},\) we have

$$\begin{aligned} A_{1}=A_{10}\sqrt{\frac{m_{0}}{m(\tau )}},\qquad A_{2}=A_{20}\sqrt{\frac{ m_{0}}{m(\tau )}},\qquad \theta _{1}=\theta _{10},\qquad \theta _{2}=\theta _{20}. \end{aligned}$$
(78)

For (78) the averaged solution of Eq. (69) is

$$\begin{aligned} x= & {} \sqrt{\frac{m_{0}}{m(\tau )}}(A_{10}\cos ((\sqrt{\Omega ^{2}+K}-\Omega )t+\theta _{10}) \nonumber \\&+A_{20}\cos ((\sqrt{\Omega ^{2}+K}+\Omega )t+\theta _{20})), \end{aligned}$$
(79)
$$\begin{aligned} y= & {} \sqrt{\frac{m_{0}}{m(\tau )}}(A_{10}\sin ((\sqrt{\Omega ^{2}+K}-\Omega )t+\theta _{10}) \nonumber \\&-A_{20}\sin ((\sqrt{\Omega ^{2}+K}+\Omega )t+\theta _{20})). \end{aligned}$$
(80)

Finally, the approximate solution of (67) is

$$\begin{aligned} X= & {} \frac{F}{k(\tau )}+\sqrt{\frac{m_{0}}{m(\tau )}}(A_{10}\cos ((\sqrt{ \Omega ^{2}+K}-\Omega )t+\theta _{10}) \nonumber \\&+A_{20}\cos ((\sqrt{\Omega ^{2}+K}+\Omega )t+\theta _{20})), \end{aligned}$$
(81)
$$\begin{aligned} y= & {} \sqrt{\frac{m_{0}}{m(\tau )}}(A_{10}\sin ((\sqrt{\Omega ^{2}+K}-\Omega )t+\theta _{10}) \nonumber \\&-A_{20}\sin ((\sqrt{\Omega ^{2}+K}+\Omega )t+\theta _{20})), \end{aligned}$$
(82)

i.e.,

$$\begin{aligned} z= & {} \frac{F}{\frac{S_{0}E}{l}(1-2\frac{v}{l}\tau )}+\sqrt{\frac{1}{1-2\frac{ v}{l}\tau }}(A_{10}(\exp i((\sqrt{\Omega ^{2}+\frac{S_{0}E}{m_{0}l}}-\Omega )t+\theta _{10})) \nonumber \\&+A_{20}\exp (-i((\sqrt{\Omega ^{2}+\frac{S_{0}E}{m_{0}l}}+\Omega )t+\theta _{20}))). \end{aligned}$$
(83)

For the initial conditions which satisfy the relation

$$\begin{aligned} A_{10}\exp (i\theta _{10})=A_{20}\exp (i\theta _{10})=A_{0}\exp (i\theta _{0}), \end{aligned}$$
(84)

the motion of the work piece center is

$$\begin{aligned} z=\frac{F}{\frac{S_{0}E}{l}(1-2\frac{v}{l}\frac{h}{R_{0}}t)}+2\sqrt{\frac{1}{ 1-2\frac{v}{l}\frac{h}{R_{0}}t}}A_{0}\exp (i\theta _{0})\exp (i\Omega t)\cos (t\sqrt{\Omega ^{2}+\frac{S_{0}E}{m_{0}l}}). \end{aligned}$$
(85)

If the mass variation of the work piece is neglected the vibration reduces to

$$\begin{aligned} z_{S}=\frac{F}{\frac{S_{0}E}{l}}+2A_{0}\exp (i\theta _{0})\exp (i\Omega t)\cos (t\sqrt{\Omega ^{2}+\frac{S_{0}E}{m_{0}l}}). \end{aligned}$$
(86)

Comparing (85) and (86) it is obvious that the deflection of the work piece due to the cutting force and the amplitude of vibration is smaller if it is calculated without taking into account the mass variation.

4.4 Discussion of the result

The expression (85) has two parts: one is the relation between the cutting force and the parameters of the work piece with variable mass, and the other shows the effect of the reactive force which occurs due to mass variation of the working piece during turning. The first term gives the deflection of the working piece center and the second the oscillation of the system.

If the initial amplitude of the work piece is zero, i.e., \(A_{0}=0,\) there is only the deflection which depends on the cutting force, velocity of the cutting tool and depth of cutting:

$$\begin{aligned} z=\frac{F}{\frac{S_{0}E}{l}(1-2\frac{v}{l}\frac{h}{R_{0}}t)}. \end{aligned}$$
(87)

An increase in the cutting force causes an increase in the deflection of the work piece. If the length of the machined part is longer in comparison to the length of the unworked piece, the deflection is higher. For the work piece with larger radius before machining, the deflection of the work piece is smaller. However, the deflection is larger for higher cutting velocity and higher cutting depth. According to (87) it is evident that the deflection depends also on the rigidity of the working piece: for a higher value of \(S_{0}E,\) the deflection is smaller.

For one rotation of the working piece, when the width of the cut is \(a=2\pi v/\Omega ,\) and using the definition of the cutting force, the vibration of the working piece is

$$\begin{aligned} z_{F}=\frac{k_{c}ah}{\frac{S_{0}E}{l}(1-2\frac{ah}{lR_{0}})}. \end{aligned}$$
(88)

The relation (88) shows that for higher width of the chip the deflection of the working piece is higher and tends to the limit value (\( k_{c}l^{2}R_{0}/2S_{0}E)\) which depends on the rigidity, length and radius of the working piece.

The vibration of the work piece center has the amplitude

$$\begin{aligned} A_{\rho }=2A_{0}\sqrt{\frac{1}{1-2\frac{v}{l}\frac{h}{R_{0}}t}}\cos (t\sqrt{ \Omega ^{2}+\frac{S_{0}E}{m_{0}l}}). \end{aligned} $$
(89)

The amplitude of vibration has the tendency to increase over time. The higher the amount of mass eliminated from the work piece, the higher is the amplitude of vibration. Compared with the case when the mass variation is neglected, it is seen that the amplitude of vibration is higher than for the unmachined work piece. The amplitude of vibration is higher for a higher value of the chip width, higher cutting velocity and higher cutting depth. The longer the machined part of the work piece in comparison to the total length of the work piece is the higher is the amplitude of vibration. The frequency of vibration depends on the angular speed and rigidity of the working piece. For higher angular velocity and rigidity of the working piece, the period of vibration is shorter.

4.5 Comparison of the analytic and experimental data

Fig. 3
figure 3

Experimetnal rig for measuring of the surface roughness

Full size image

At the University of Obuda the surface roughness of the work piece after tuning was measured (Fig. 3). The surface roughness tester positioned in the radial direction of the machined work piece and the roughness was measured and recorded. The parameters of cutting operation and the geometric and physical characteristics of the work piece were as follows: \( R_{0}=0.05\text{m}\), \(l=1\text{m}\), \(F=824.67\text{N}\), \(E=2.110^{11}\text{Pa}\), \(a=2.5\text{mm}\), \(h=1.2\text{mm}.\) In Fig. 4 the recorded diagram is shown. It is obvious that the diagram is a periodic function with almost constant amplitude and short period.

Fig. 4
figure 4

Roughness distribution obtained experimentally

Full size image
Fig. 5
figure 5

\(X-t\) (full line) and \(A\rho -t\) (dotted line) diagrams obtained analytically

Full size image

Using the analytically obtained relations (87) and (89) and the aforementioned numerical data, the vibration properties of the work piece are calculated. It is obtained that the displacement (87) of the work piece center has the value \(z_{F}=0.5\) \(\upmu\text{m}.\) For the initial amplitude \(A_{0}=1\) \(\upmu\text{m}.\) the magnitude of amplitude variation (89 ) is

$$\begin{aligned} A_{\rho }=2.0001\cos (5188.7t), \end{aligned}$$

while the period is \(T=1.210\,9\times 10^{-3}\) s. In Fig. 5 the amplitude-time diagram is shown.

Comparing diagrams in Figs. 4 and 5 it is shown that there is a direct correlation between vibration and the surface roughness. Prediction of the surface roughness is possible to be done by using the vibration of the working piece.

5 Conclusion

In the paper a method for solving a system of two coupled second-order differential equations with slow time variable parameters which describes the motion of the one-mass body with two degrees of freedom is developed. It is a perturbation procedure, where amplitude and phase of vibration are assumed to be time variable. The approximate solution based on averaging is determined and discussed. Trajectories of the rotor center for various initial conditions are determined. It is concluded that the trajectory of the rotor with slow time variable parameters is the perturbed version of the trajectory of the rotor with constant parameters. In general, the trajectory of the rotor center is of elliptic type with time variable parameters.

The analytical consideration given in the paper is applied for obtaining the vibration of the working piece during turning operation. Assuming that the working piece is elastic, the motion of the mass center of the body is determined. Using the analytical and experimentally obtained results it is concluded that mass variation in turning operation has a significant influence on the vibration properties of the working piece and is necessary to be included into consideration. By increasing the cutting time, when the mass of the working piece is decreasing, the amplitude of vibration is increasing. The faster the mass decrease is, the faster is the increase in the amplitude of vibration. For higher cutting velocity, mass decrease is faster and the vibration amplitude increase is greater. The depth of cut and the width of the chip have a more prominent effect on vibration. A higher cut depth produces greater vibration magnitude. However, the influence of mass variation in turning operation on the frequency of vibration is quite small and can be omitted. In addition, comparison of the analytically obtained vibration results and experimentally obtained measured results have shown good correlation between the work piece vibration and surface roughness. It is concluded that the vibration measure can be used as a control of the finish surface of the work piece and for prediction of the surface roughness during turning operation.