Coupled simulation of flow-induced viscous and elastic anisotropy of short-fiber reinforced composites

Abstract

The present work discusses the impact of the back coupling of the fiber orientation distribution on the base flow and on the fiber orientation itself during mold filling simulations. Flows through a channel and over a backward-facing step are investigated. Different closure approximations are considered for modeling the flow-induced evolution of anisotropy. The results corresponding to the decoupled approach, in which the effect of fibers on local fluid properties is neglected, build the basis of comparison. The modeling is limited to a laminar, incompressible, and isothermal flow of a fiber suspension consisting of rigid short fibers suspended in an isotropic Newtonian matrix fluid. A linear, anisotropic constitutive law is used in combination with a uniform fiber volume fraction of 10% and an aspect ratio of 10. To evaluate the impact of back coupling and of different closure methods in view of the manufactured solid composite the resulting anisotropic elastic properties are investigated based on the Mori–Tanaka method combined with an orientation average scheme. Relative to the range [0, 1] the pointwise difference in fiber orientation between the decoupled and the coupled approach is found to be $\pm 5{\%}$ in the channel and $\pm 30{\%}$ in the backward-facing step, respectively. The viscosity and the elasticity tensor show both significant flow-induced anisotropies as well as a strong dependence on closure and coupling.

1 Introduction

1.1 Motivation

The addition of rigid short fibers into a polymer matrix is an established method in lightweight design [32]. When used instead of conventional metals or polymers without reinforcement, such materials help to meet environmental requirements by reducing the mass of components and simultaneously ensuring high stiffness and good formability [32]. One challenge of dealing with short-fiber reinforced polymers is the reliable prediction of fiber orientation distribution induced by the strongly heterogeneous flow process, which determines the final effective mechanical properties of the product [6, 43, 67]. In this context, it is necessary to consider the anisotropic viscous properties of the fiber suspension already during the mold filling simulations. This aspect is often absent in numerical simulations of the processing of fiber-reinforced composites, in which only the effect of the flow on fiber orientation is considered while the local modification of the suspension properties due to fiber orientation is neglected [67]. The present study addresses the influence of these coupling levels with direct reference to the related solid properties.

1.2 State of the art

Based on Jeffery’s equation [22, 35, 36] describing the motion of a single rigid fiber in an incompressible Newtonian fluid without body forces, fiber–fiber interaction and Brownian motion, Folgar and Tucker [25] introduced an additional term considering interaction phenomena in concentrated suspensions. Instead of calculating the direction of every fiber included in the flow process, Advani and Tucker [1] suggested using so-called orientation tensors (or fabric tensors [37]) in order to describe the local orientation state within fiber suspensions. This method goes along with decreased computational effort [6], albeit at the cost of a loss of information in relation to a complete description of the microstructure in the context of mean field modeling [1, 37, 51], due to the practical choice of limiting to low-order orientation tensors. As known from turbulence modeling, averaged equations lead to a loss of information, and this always results in an endless closure problem. In case of fiber orientation, the evolution equation of the even $n^\mathsf{{th}}$-order orientation tensor always includes the unknown orientation tensor of $(n+2)^\mathsf{{th}}$-order [1, 6]. Various closure methods have been published which range from simple [1, 2, 20, 30] to complex [14,15,16, 45, 46, 62, 63] and thus leading to different results. The Folgar–Tucker equation [1, 25] is known to underpredict the characteristic time for the orientation of fibers subject to flow stresses [5]. Furthermore, the interaction between the fibers is modeled with a single parameter, which can only take isotropic fiber–fiber interaction into account [5]. To overcome these disadvantages, new models have been developed [54, 65].

The back coupling of the fiber orientation to the base flow is realized with constitutive laws affecting the diffusion term in the balance of linear momentum. In Advani and Tucker [1, 2], a general form of the viscosity tensor in the context of Newtonian matrix fluids is given. Based on a single fiber defining the transversely isotropic material symmetry, five scalar constants have to be determined to express the stress tensor in terms of the fiber orientation state [1]. After applying an orientation average scheme [1], the stress tensor can be expressed in terms of the second- and fourth-order orientation tensor, while the material symmetry remains unchanged. Further details are given in Sect. 2. Various models of different complexity and areas of validity exist determining the scalar coefficients of the anisotropic viscosity tensor [19, 42, 53, 55, 56]. Moreover, constitutive laws considering non-Newtonian matrix fluids can be used [26, 43, 57].

In the context of decoupled simulations in which the stress tensor is only determined by the matrix fluid, analytical solutions can be used for validation [4, 45]. The behavior of different closure methods compared to such exact solutions is discussed by Verleye and Dupret [62] and Montgomery-Smith et al. [45]. For a developing channel flow, a flow around a cylinder and a contraction flow Latz et al. [41] show the effect of coupling the fiber orientation to the base flow. The study is limited to isothermal flows of a Newtonian matrix fluid and to the use of orientation tensors. Two different models calculating the orientation tensor are considered in combination with the constitutive model of Dinh and Armstrong [19]. The study of Mezi et al. [43] also considers a simple channel flow and a planar contraction flow. Furthermore, the constitutive model of Dinh and Armstrong [19] is used. In contrast to Latz et al. [41], both Newtonian and non-Newtonian matrix fluids are investigated. Moreover, a simulation method involving the solution of the Fokker–Planck equation for the fiber orientation distribution function is adopted by Mezi et al. [43] to overcome the disadvantage of closure methods of tensorial approaches. The results of both studies show a flattening of the velocity profile leading to a significant change of the shear rate and thus to recognizable differences in the fiber orientation compared to the decoupled simulations. Altan et al. [3] and Altan and Tang [59] study channel flows of fiber suspensions with different inlet conditions and also show the impact of back coupling as flattening the velocity profile. The constitutive law has the structure of Dinh and Armstrong [19] with different coupling strengths. Furthermore, simplified equations are considered by Altan and Tang [59], who observe that a parabolic velocity profile is recovered as asymptotic state in the coupled case. A comprehensive modeling including temperature effects, shear thinning matrix behavior, curing kinetics, and two-phase flow is given in Wittemann et al. [66] for the decoupled and in Wittemann et al. [67] for the coupled simulation approach. These studies deal with realistic plate geometries and with the backward-facing step geometry of Chiba and Nakamura [13]. Based on the description of Heinen [31], the open source software OpenFOAM is used and adapted in the context of fiber orientation description by the use of tensors.

1.3 Goals and scope of the study

The manufacturing process of short-fiber reinforced polymers is characterized by a complex interaction between the fibers and the flow. The goal of the present study is to compare the decoupled and coupled approaches and assess their influence on both the anisotropic viscous behavior and the anisotropic elastic properties of the final part. The following points constitute the framework of the present study:

• The flow of fiber suspension is described at the simplest modeling level possible, i.e., without considering temperature, shear-thinning, and curing effects (see Sect. 2.2).

• A channel flow and a backward-facing step flow are considered as simple models of the mold filling process (see Sect. 3).

• The quadratic closure (QC) and the invariant-based optimal fitting closure (IBOF) are adopted and compared (see Sect. 2.2).

• The velocity field is discussed in terms of the impact of coupling (see Sects. 4.1 and 4.2).

• The direction-dependent viscosity and Young’s modulus are assessed by quantifying both the effect of coupling and the choice of different, commonly used closures (see Sects. 4.2 and 4.3).

Fig. 1

Example of the processing of fiber-reinforced composites (own sketch based on Grote and Feldhusen [28])

Within the framework outlined above, this study contributes to the understanding and quantification of the impact of the coupling from both the fluid mechanics and the solid mechanics standpoints. The content of the present work is limited to simple internal flows sketched in Fig. 1. The paper is structured as follows. The motivation of the problem, a literature review, and the explanation of the used notation are described in Sect. 1. Section 2 contains the modeling, the basic assumptions and the system of equations. The flow cases, geometries and parameter settings are listed in Sect. 3. Section 4 contains both the results and the discussion of the results. Section 5 summarizes the proceeding and the results of the study. At the end of the paper, a list of frequently used symbols and abbreviations is given.

1.4 Notation

In this Section, the symbolic tensor notation used in this paper is introduced (see, for instance, Bertram [7] and Gurtin et al. [29]). Scalar quantities are written as follows: $a,A,\alpha ,\ldots \in \mathcal{R}$. Vectors are considered objects of a vector space $\mathcal{V}\subset \mathcal{R}^{3}$ and are denoted by lower case bold letters $\varvec{ a},\varvec{ b},\ldots \in \mathcal{V}$. Second-order tensors describe linear mappings between two vector spaces, and they are written as follows: $\varvec{ A},\varvec{ B},\varvec{\sigma },\ldots \in \mathrm {Lin}:\mathcal{V}\rightarrow \mathcal{V}$. Fourth-order tensors represent linear mappings between the space of second-order tensors, and they are denoted by upper case blackboard bold letters, ${\mathbb { A}},{\mathbb { B}},\ldots : \mathrm {Lin} \rightarrow \mathrm {Lin}$. In the following, the index notation refers to Cartesian coordinate systems. The scalar product between tensors of equal order is written as follows: $\varvec{ a}\cdot \varvec{ b}=a_i b_i$ and $\varvec{ A}\cdot \varvec{ B}= A_{ij}B_{ij}$. Furthermore, $\varvec{ A}\varvec{ b}=A_{ij}b_j\varvec{ e}_i$ represents the linear mapping of a vector and the composition of two tensors. The linear mapping of second-order tensors is denoted by . The dyadic product is denoted symbolically by and the box-product by . The Rayleigh product with the proper orthogonal tensor $\varvec{ Q}\in \mathrm {Orth^+}$ is defined as follows: . The summation convention applies. Throughout this work symbolic expressions for differential operators are preferred, e.g., $\mathrm {grad}(\cdot )$ for the gradient operator and $\mathrm {div}(\cdot )$ for the divergence operator, respectively. The material time derivative of Eulerian quantities $(\cdot )$ is abbreviated as follows with the operator $\circ$ depending on the tensor order:

$$\begin{aligned} \dot{(\cdot )} = \displaystyle \frac{\partial (\cdot )}{\partial t} + \mathrm {grad}(\cdot )\circ \varvec{ v}. \end{aligned}$$

(1)

The operator $(\cdot )^{\otimes n}$ denotes the application of the dyadic product to generate a tensor of order n. Thus, the number of operations depends on the tensor order of the basis $(\cdot )$.

2 Theory and model assumptions

2.1 Orientation tensors

The probability density function $f(\varvec{ x},t,\varvec{ n})$ describes the probability of a fiber being oriented with the direction $\varvec{ n}$ at the time t at the spatial location $\varvec{ x}$. It is nonnegative $f \ge 0$ and has the following properties $\forall \varvec{ x},t,\varvec{ n}$ [1]:

$$\begin{aligned} f(\cdot ,\varvec{ n}) = f(\cdot ,-\varvec{ n}), \qquad \int _{\mathcal{S}}f\mathrm {d}S = 1. \end{aligned}$$

(2)

The surface of the unit sphere $\mathcal{S}$ is defined by $\mathcal{S}= \{\varvec{ n}\in \mathcal{R}^3: \Vert \varvec{ n} \Vert _2=1 \}$ with the corresponding surface element $\mathrm {d}S$ ensuring invariant integration. Using the directional data f, three kinds of orientation tensors can be derived [37]. The present work follows the suggestion of describing the fiber orientation state with tensors of the first kind [1, 37]. In general, the $n^\mathsf{{th}}$-order orientation tensor ${\mathbb { N}}_{\langle n \rangle }(\varvec{ x},t)$ of the first kind can be written as follows [1, 37, 44]:

$$\begin{aligned} {\mathbb { N}}_{\langle n \rangle } = \int _{\mathcal{S}} f \varvec{ n}^{\otimes n}\mathrm {d}S. \end{aligned}$$

(3)

In the following, the expressions $\varvec{ N}={\mathbb { N}}_{\langle 2 \rangle }$ and ${\mathbb { N}}={\mathbb { N}}_{\langle 4 \rangle }$ are used for simplicity.

2.2 System of equations

The flow of the fiber suspension is modeled as incompressible, isothermal, with rigid fibers in a Newtonian matrix fluid and without phase transition. The flow problem is laminar both on the micro- and macroscale levels. The system of equations which governs the coarse-grained pressure field $p(\varvec{ x},t)$, the velocity field $\varvec{ v}(\varvec{ x},t)$, and the orientation tensor $\varvec{ N}(\varvec{ x},t)$ based on the Folgar–Tucker equation for a stable, neutrally buoyant fiber suspension is as follows [1, 29, 43]:

$$\begin{aligned} 0&=\mathrm {div}(\varvec{ v}) \Leftrightarrow \mathrm {tr}(\varvec{ D})=0, \end{aligned}$$

(4)

$$\begin{aligned} \rho \dot{\varvec{ v}}&= \mathrm {div}(\varvec{\sigma }), \end{aligned}$$

(5)

$$\begin{aligned} \varvec{\sigma }&= {\varvec{\sigma }}^\mathsf{T}, \end{aligned}$$

(6)

$$\begin{aligned} \dot{\varvec{ N}}&= \varvec{ W}\varvec{ N}- \varvec{ N}\varvec{ W}+ \xi \big (\varvec{ D}\varvec{ N}+ \varvec{ N}\varvec{ D}- 2 {\mathbb { N}}[\varvec{ D}]\big ) + 2C_\mathsf{{I}}\dot{\gamma }(\varvec{ I}-3\varvec{ N}), \end{aligned}$$

(7)

$$\begin{aligned} {\mathbb { N}}&\approx {\mathbb { N}}_\mathsf{{closure}}(\varvec{ N}). \end{aligned}$$

(8)

In (5), volume forces are not considered. In (4)–(8) the Cauchy stress tensor for Boltzmann continua is described by $\varvec{\sigma }(\varvec{ x},t)$, the mass density by $\rho =\mathrm {const.}$, the strain rate tensor by $\varvec{ D}(\varvec{ x},t)$, and the spin tensor by $\varvec{ W}(\varvec{ x},t)$. The identity tensor is indicated by $\varvec{ I}$, while the shape factor of the fibers is $\xi =(\alpha ^2-1)/(\alpha ^2+1)$ depending on the fiber aspect ratio $\alpha$. The interaction coefficient is denoted by $C_\mathsf{{I}}$, while the scalar shear rate is defined by $\dot{\gamma }= \sqrt{\varvec{ D}\cdot \varvec{ D}/2}$. It is noted that different definitions of $\dot{\gamma }$ can be utilized by changing the value of $C_\mathsf{{I}}$ accordingly. In the framework of the present paper, ${\mathbb { N}}$ is approximated by the quadratic closure ${\mathbb { N}}_\mathsf{{QC}}$ and the invariant-based optimal fitting closure ${\mathbb { N}}_\mathsf{{IBOF}}$ as follows [1, 15, 20]:

(9)

(10)

The operator $\mathrm {sym}(\cdot )$ describes the symmetrization in terms of every index [21], while the coefficients $\beta _i$ are given functions of the invariants of $\varvec{ N}$ [15]. The QC is chosen for its simplicity, while the IBOF closure is chosen as an example of complex closure, albeit without the need of both calculating eigenvalues and coordinate system transformations. In addition, the large differences between the closures illustrate their effect. In Sect. 2.3, the constitutive modeling is presented for the coupled approach connecting p, $\varvec{ v}$, $\varvec{ N}$, and ${\mathbb { N}}$ with $\varvec{\sigma }$ to obtain a closed system of governing Eqs. (4)–(8). The constitutive modeling is limited to the macroscale in the context of coarse graining.

2.3 Constitutive modeling

In the present work, it is assumed that the general form of the Cauchy stress tensor reads $\varvec{\sigma }= \varvec{ G}(\varvec{ D},\varvec{ N},{\mathbb { N}})$. This means that the anisotropy information is completely described by the tensors $\varvec{ N}$ and ${\mathbb { N}}$ in the argument list of the material function $\varvec{ G}$. Based on the principle of material objectivity $\forall \varvec{ Q}\in \mathrm {Orth^+}$ [29] with the objective tensors $\varvec{ D}$, $\varvec{ N}$, and ${\mathbb { N}}$,

(11)

the general structure of an isotropic tensor function $\varvec{ G}$ [40] can be concluded. In addition, the generalized constitutive law $\varvec{\sigma }= \varvec{ G}(\varvec{ D},\varvec{ N},{\mathbb { N}})$ is assumed to have the following linear structure with the viscosity tensor ${\mathbb { V}}(\varvec{ N},{\mathbb { N}})$ describing the anisotropy of the fiber suspension [2, 6]:

$$\begin{aligned} \varvec{\sigma }= -p\varvec{ I}+ {\mathbb { V}}[\varvec{ D}]. \end{aligned}$$

(12)

One can interpret (12) as a Newtonian fluid with the set of state variables $\{\varvec{ N},{\mathbb { N}}\}$. Further assumptions are made modeling ${\mathbb { V}}$ linear in $\varvec{ N}$ and ${\mathbb { N}}$ [2]. Please note that nonlinear terms of $\varvec{ N}\hbox { and }{\mathbb { N}}$ are not considered. The general form of ${\mathbb { V}}$ simplified for incompressible flows reads [2]

(13)

In (13), $\mu$ describes the Newtonian matrix viscosity and $\mu _i$ additional viscosities depending on the material model [19, 42, 53, 55, 56]. Furthermore, ${\mathbb { P}}_2$ stands for the projector on symmetric traceless second-order tensors determined by ${\mathbb { P}}_2 = {\mathbb { I}}^\mathsf{{S}}-{\mathbb { P}}_1$ with the projector on spherical second-order tensors and the identity of symmetric second-order tensors [6, 29].

In the following, the properties of ${\mathbb { V}}$ are discussed. Based on the dissipation principle , the main symmetry ${\mathbb { V}}= {{\mathbb { V}}}^{\mathsf{T}_\mathsf{H}}\Leftrightarrow V_{ijkl}=V_{klij}$ can be derived without loss of generality. The balance of angular momentum for Boltzmann continua $\varvec{\sigma }= {\varvec{\sigma }}^\mathsf{T}$ justifies the left minor symmetry ${\mathbb { V}}= {{\mathbb { V}}}^{\mathsf{T}_\mathsf{L}}\Leftrightarrow V_{ijkl}=V_{jikl}$. As a consequence, the right minor symmetry ${\mathbb { V}}= {{\mathbb { V}}}^{\mathsf{T}_\mathsf{R}}\Leftrightarrow V_{ijkl}=V_{ijlk}$ follows, directly. Considering the viscous stress tensor $\varvec{\sigma }_\mathsf{{V}}={\mathbb { V}}[\varvec{ D}]$ in combination with $\mathrm {tr}(\varvec{ D})=\varvec{ D}\cdot \varvec{ I}=0$ for incompressible flows,

$$\begin{aligned} \varvec{\sigma }_\mathsf{{V}} = 2(\mu +\mu _4)\varvec{ D}+ \mu _1{\mathbb { N}}[\varvec{ D}] + \mu _2(\varvec{ N}\cdot \varvec{ D})\varvec{ I}+ 2\mu _3(\varvec{ D}\varvec{ N}+\varvec{ N}\varvec{ D}), \end{aligned}$$

(14)

the trace $\mathrm {tr}(\varvec{\sigma }_\mathsf{{V}})$ can be derived with $\varvec{ D}\cdot \varvec{ I}=0$ and with the property of the orientation tensors ${\mathbb { N}}[\varvec{ I}]=\varvec{ N}$:

$$\begin{aligned} \mathrm {tr}(\varvec{\sigma }_\mathsf{{V}}) = (\mu _1+3\mu _2)\varvec{ N}\cdot \varvec{ D}+ 2\mu _3(\varvec{ D}\varvec{ N}+\varvec{ N}\varvec{ D})\cdot \varvec{ I}. \end{aligned}$$

(15)

Based on (14) and (15) the following statements can be made. In case of isotropic fiber orientation states $\varvec{ N}_\mathsf{{iso}}=\varvec{ I}/3$ and ${\mathbb { N}}_\mathsf{{iso}}={\mathbb { P}}_1/3+2{\mathbb { P}}_2/15$ [6, 44], the trace of $\varvec{\sigma }_\mathsf{{V}}$ is equal to $\mathrm {tr}(\varvec{\sigma }_\mathsf{{V}})=0$, and p describes the hydrostatic stress state completely. Conversely, anisotropic fiber orientation states yield $\mathrm {tr}(\varvec{\sigma }_\mathsf{{V}}) \ne 0$, meaning that traceless tensors $\varvec{ D}$ (incompressible flows) induce hydrostatic stresses. As a consequence, p does not describe the hydrostatic stress state completely in case of back coupling. It is possible to force ${\mathbb { V}}[\varvec{ D}]$ to be traceless defining a new viscosity tensor $\tilde{{\mathbb { V}}}$ with the property $\varvec{ I}\cdot \tilde{{\mathbb { V}}}[\varvec{ D}]=0$, $\forall \varvec{ D}$. This procedure goes along with the definition of an effective pressure $p_\mathsf{{eff}}$ completely describing the hydrostatic stress in a fiber suspension,

$$\begin{aligned} \mathrm {tr}(\varvec{\sigma }) = -3p_\mathsf{{eff}}, \qquad p_\mathsf{{eff}} = p - \frac{1}{3}\mathrm {tr}(\varvec{\sigma }_\mathsf{{V}}). \end{aligned}$$

(16)

The previous considerations lead to the last property of ${\mathbb { V}}$ discussed in this Section. Rewriting (15) and using the index notation leads to $\sigma _{ii}^\mathsf{{V}} = V_{iikl} D_{kl}$. This equation is equal to the property $V_{iikl} \ne 0_{kl}$. Using the symmetries mentioned above, also $V_{klii} \ne 0_{kl}$ is valid. In other words, ${\mathbb { V}}$ is not deviatoric in the left and right index pair in terms of anisotropic fiber orientation. It is noted that inserting the splittings $\varvec{ N}=\varvec{ N}_\mathsf{{iso}}+\varvec{ N}_\mathsf{{aniso}}$ and ${\mathbb { N}}={\mathbb { N}}_\mathsf{{iso}}+{\mathbb { N}}_\mathsf{{aniso}}$ into (13) shows that the fibers both increase the viscosity isotropically and induce a direction-dependent effect. In the present paper, the constitutive model of Dinh–Armstrong is used with the volume fraction $\phi$ of the fibers [19, 43, 61],

$$\begin{aligned} {\mathbb { V}}= 2\mu {\mathbb { P}}_2 + \mu _1 {\mathbb { N}}, \qquad \mu _1 = \frac{2\mu \phi \alpha ^2}{3\mathrm {ln}(\sqrt{\pi /\phi })}. \end{aligned}$$

(17)

Note that (17) implies $\mathrm {tr}(\varvec{\sigma }_\mathsf{{V}}) \ne 0$ for anisotropic fiber orientation. This leads to the use of the common equilibrium pressure p keeping in mind that additional contributions to p can be included in $\varvec{\sigma }_\mathsf{{V}}$.

2.4 Thermodynamic consistency

During the numerical procedure of solving for p, $\varvec{ v}$, and $\varvec{ N}$ the thermodynamic consistency is checked. The Clausius–Duhem inequality for constant mass density and constant temperature $\varvec{\sigma }\cdot \varvec{ D}-\rho \dot{\psi }\ge 0$ [17] is rewritten under the assumption that the specific free energy $\psi$ does only depend on $\varvec{ D}$ [29, 48],

$$\begin{aligned} -p\varvec{ I}\cdot \varvec{ D}+ 2\mu \varvec{ D}\cdot \varvec{ D}+ \mu _1{\mathbb { N}}[\varvec{ D}]\cdot \varvec{ D}-\rho \displaystyle \frac{\partial \psi }{\partial \varvec{ D}}\cdot \dot{\varvec{ D}}\ge 0. \end{aligned}$$

(18)

Additionally, $\varvec{ I}\cdot \varvec{ D}=0$ holds for incompressible flows. Moreover, (18) is linear in $\dot{\varvec{ D}}$ leading to $\psi \ne \psi (\varvec{ D})$ ensuring the thermodynamic consistency for arbitrary processes [29]. As a consequence, only the following inequality has to be fulfilled:

$$\begin{aligned} 2\mu \varvec{ D}\cdot \varvec{ D}+ \mu _1{\mathbb { N}}[\varvec{ D}]\cdot \varvec{ D}\ge 0. \end{aligned}$$

(19)

In the framework of this paper, a splitting method concerning the dissipation $\delta =\delta _\mathsf{{M}}+\delta _\mathsf{{F}}$ is used as follows leading to stricter conditions:

$$\begin{aligned} \delta _\mathsf{{M}} = 2\mu \varvec{ D}\cdot \varvec{ D}\ge 0, \qquad \delta _\mathsf{{F}} = \mu _1{\mathbb { N}}[\varvec{ D}]\cdot \varvec{ D}\ge 0. \end{aligned}$$

(20)

From $\delta _\mathsf{{M}} \ge 0$ the requirement $\mu \ge 0$ follows trivially. In contrast, $\delta _\mathsf{{F}} \ge 0$ depends on the choice of the closure method [48] and is checked for every mesh cell in all time steps during the numerical procedure.

2.5 Effective elastic properties

In the following, the assumptions employed in the present work for estimating the effective elastic properties are briefly described. Further details can be found in the literature [27, 49, 50, 60]. It is assumed that the composite consists of two phases without cracks or voids. Furthermore, the matrix and the fibers are assumed to be isotropic, linear elastic, and homogeneous. The effective elastic behavior of the composite also is described with a linear elastic law. The fibers are modeled with a constant aspect ratio and a circular cross section (prolate inclusions). The validity of the Hill condition is assumed [33]. With the elasticity tensor ${\mathbb { C}}$ of the matrix (M) and fiber material (F) defined with the compression modulus K and the shear modulus G as [6]

$$\begin{aligned} {\mathbb { C}}_\mathsf{{(F,M)}} = 3K_\mathsf{{(F,M)}}{\mathbb { P}}_1 + 2G_\mathsf{{(F,M)}}{\mathbb { P}}_2, \end{aligned}$$

(21)

the following relation describes the effective elasticity tensor $\bar{{\mathbb { C}}}$ of the composite material [27]:

$$\begin{aligned} \bar{{\mathbb { C}}} = {\mathbb { C}}_\mathsf{{M}} + \phi ({\mathbb { C}}_\mathsf{{F}}-{\mathbb { C}}_\mathsf{{M}})\langle {\mathbb { A}}\rangle _\mathsf{{F}}. \end{aligned}$$

(22)

The operation $\langle \cdot \rangle _\mathsf{{F}}$ describes the volume average over the fiber phase with the strain concentration tensor ${\mathbb { A}}(\varvec{ x})$ defining $\bar{\varvec{\varepsilon }}_\mathsf{{F}} = \langle {\mathbb { A}}\rangle _\mathsf{{F}}[\bar{\varvec{\varepsilon }}]$ with the strain tensor $\varvec{\varepsilon }(\varvec{ x})$ [27]. Equation (22) is exact in the context of the mentioned assumptions. However, the tensor $\langle {\mathbb { A}}\rangle _\mathsf{{F}}$ is unknown and has to be modeled [27]. In the present work, this is accomplished via the Mori–Tanaka method (MT), which leads to the explicit formula [12, 47]

$$\begin{aligned} \bar{{\mathbb { C}}}^\mathsf{{MT}} = {\mathbb { C}}_\mathsf{{M}} + \phi \big [(1-\phi )\big \langle \big ({\mathbb { P}}_0 + ({\mathbb { C}}_\mathsf{{F}}-{\mathbb { C}}_\mathsf{{M}})^{-1}\big )^{-1} \big \rangle _\mathsf{{F}}^{-1} + \phi ({\mathbb { C}}_\mathsf{{F}}-{\mathbb { C}}_\mathsf{{M}})^{-1} \big ]^{-1}. \end{aligned}$$

(23)

The tensor ${\mathbb { P}}_0$ is called polarization tensor and depends on the shape of the inclusions and the elastic properties of the matrix material [27]. The identity ${\mathbb { P}}_0={\mathbb { E}}{\mathbb { C}}_\mathsf{{M}}^{-1}$ holds with ${\mathbb { E}}$ called Eshelby tensor [27]. For prolate inclusions, ${\mathbb { P}}_0$ is given analytically [23, 24, 27, 58] leading to a transversely isotropic material symmetry. The effect of the local fiber orientation state can be considered by using the following orientation average scheme for the expression $\langle \cdot \rangle _\mathsf{{F}}$ in (23). Thus, the equation $\langle \cdot \rangle _\mathsf{{F}}=(\cdot )_\mathsf{{oa}}$ applies. The five coefficients $b_i$ depend on the transversely isotropic tensor ${\mathbb { T}}$ within the operator $\langle {\mathbb { T}}\rangle _\mathsf{{F}}$ referring to a single prolate inclusion and whose definition can be obtained from (23) [1, 39],

(24)

It is assumed that the stationary fiber orientation state received from the mold filling simulation describes the fiber orientation in the manufactured part. The local Young’s modulus $\bar{E}(\varvec{ d},\varvec{ x})$ depending on the direction $\varvec{ d}$ can be determined using the following relationship [11]:

(25)

The vector $\varvec{ d}(\varphi ,\theta )$ is parameterized in spherical coordinates with $\varphi \in [0,2\pi )$ and $\theta \in [0,\pi ]$. In the following, the special case $\bar{E}(\varvec{ d},\varvec{ x}) = \bar{E}(\varphi ,\theta =\pi /2,\varvec{ x})$ is considered [39] defining a polar plot in the $\varvec{ e}_1$–$\varvec{ e}_2$-plane. For $\varphi =0$ the equality $\varvec{ d}=\varvec{ e}_1$ holds. The quantity $\bar{E}$ is based on the normalized Voigt notation of $\bar{{\mathbb { C}}}^\mathsf{{MT}}$ [11, 64].

3 Numerical procedure and settings

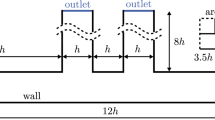
Figure 2 shows the geometrical details of the studied flow cases. The flow through a channel (CF) [43] and above a backward-facing step (BFS) [13, 67] are sketched in the top and bottom panel, respectively. The velocity profile at the inlet is parabolic in both cases. The initial velocity field corresponds to the steady-state uncoupled solution determined by the parabolic profile at the inlet, the no-slip condition at the channel walls and the fully developed state at the outlet. The initial and the inlet fiber orientation is assumed to be isotropic, while at the channel walls and at the outlet the fully developed state is forced. The Reynolds number is defined as

$$\begin{aligned} \mathrm{Re}=\frac{2v_\mathsf{{b}}h}{\nu } = \frac{\dot{V}}{\nu }, \end{aligned}$$

(26)

with the characteristic length h (see Fig. 2), the characteristic velocity $2v_\mathsf{{b}}$, both of which define the volume flow rate per unit depth $\dot{V}=2v_\mathsf{{b}} h$, and the kinematic viscosity of the matrix $\nu =\mu /\rho$. A second dimensionless quantity governs the problem, namely the ratio $\mu _1 / \mu$ (see Eq. (17)), which equals zero in the decoupled case. With $(\cdot )^*$ labeling dimensionless quantities, the velocity profiles at the inlet are defined as follows:

$$\begin{aligned} v_{1,\mathsf {CF}}^* = \frac{3}{4}x_2^*(2-x_2^*), \qquad v_{1,\mathsf {BFS}}^* = \frac{12}{5}x_2^*(1-2x_2^*). \end{aligned}$$

(27)

Fig. 2

Geometrical and fluid mechanical details of the investigated flow cases together with the initial and boundary conditions of the fiber orientation (colored red, color figure online)

The fiber aspect ratio is set to $\alpha =10$, the fiber–fiber interaction is modeled with $C_\mathsf{{I}}=0.01$, and the volume fraction of the fibers is $\phi =0.1$ in the coupled simulation. A non-uniform mesh with $2000\times 150$ cells is used for the lower half CF case, while $798 \times 400$ cells are used for the BFS case, referred to the area downstream of the step. Note that the simulation domains are twice as long as shown in Fig. 2 to ensure that the outlet boundary condition has no effect on the analyzed results. The dimensionless time step is set to in the CF and in the BFS. The spatial discretization schemes are of second order for both CF and BFS cases. The Folgar–Tucker equation for $\varvec{ N}$ is solved with the Crank–Nicolson time scheme [18]. The temporal discretization of the linear momentum equation employs a second-order implicit method for both flow cases. The open source finite-volume solver OpenFOAM (icoFOAM) is used to solve the system of equations described in Sect. 2.2 [31, 52, 67]. Please note that the IBOF closure terms given in Heinen [31] are provided correctly in the “Appendix”. For calculating p, an extended PISO algorithm [34] is used to take into account the flow-fiber coupling. The numerical procedure is described in detail elsewhere [38]. The analysis of the anisotropic elastic properties is based on UPPH as matrix material and glass as fiber material with the following material parameters [39]:

$$\begin{aligned} K_\mathsf{{M}}&= 4.93\,\mathrm {GPa}, \qquad K_\mathsf{{F}} = 43.45\,\mathrm {GPa}, \nonumber \\ G_\mathsf{{M}}&= 1.23\,\mathrm {GPa}, \qquad G_\mathsf{{F}} = 29.92\,\mathrm {GPa}. \end{aligned}$$

(28)

4 Results and discussion

4.1 Channel flow

In Fig. 3, the velocity profile $v_1^*$ is shown at various positions $x_1^*$ in the channel. The decoupled profile refers to the fully developed state given in Sect. 3 and remains unchanged at all streamwise locations. In the coupled case, a flattening of $v_1^*$ is observed in agreement with the results of previous studies [41, 43]. Depending on the overall channel length, the flattening of $v_1^*$ reverts for increasing $x_1^*$ to the fully developed profile. This coincides with the considerations that the steady flow behavior is characterized by a parabolic profile $v_1^*$ describing the fully developed state [59], owing to continuity. The impact of the chosen closure method can be studied by comparing both diagrams in Fig. 3. While the qualitative behavior of flattening remains present, the use of the QC leads to a faster recovery of the analytical profile. According to Mezi et al. [43], the change of $v_1^*$ depends on the shear viscosity of the fiber suspension. It is clear that using different closure approximations leads to different fiber orientation states. Hence, the local shear viscosity is influenced by the closure method leading to different behaviors of the fluid velocity.

Fig. 3

Velocity profiles $v_1^*$ over the channel height $x_2^*$ at different positions $x_1^*$ in the channel for different closures (QC, IBOF), both for the decoupled and the coupled approach

In the following, the spatial evolution of $v_1^*$ observed in Fig. 3 is explained by considering the balance of linear momentum in the main flow direction $\varvec{ e}_1$ for two-dimensional flows,

$$\begin{aligned} \rho \dot{v}_1 = -\displaystyle \frac{\partial p}{\partial x_1} + \mu \left( \displaystyle \frac{\partial ^2v_1}{\partial x_1\partial x_1} + \displaystyle \frac{\partial ^2v_1}{\partial x_2\partial x_2} \right) + \mu _1 \left( \displaystyle \frac{\partial N_{11kl}D_{kl}}{\partial x_1} + \displaystyle \frac{\partial N_{12kl}D_{kl}}{\partial x_2} \right) . \end{aligned}$$

(29)

The fiber-related contribution to the resultant of the viscous stress in Eq. (29) is simplified by assuming that the coupling-induced deviation from the fully developed state is negligible for the velocity field, i.e.,

$$\begin{aligned} D_{11}^* \approx D_{22}^* \approx 0, \qquad \displaystyle \frac{\partial D_{12}^*}{\partial x_1^*}\approx 0, \qquad \displaystyle \frac{\partial D_{12}^*}{\partial x_2^*}\approx \frac{1}{2}\displaystyle \frac{\partial ^2v_1^*}{\partial x_2^{*2}} = -\frac{3}{4}. \end{aligned}$$

(30)

Inserting the assumptions (30) into (29), one can derive the following dimensionless term $r_\mathsf{{F}}^*$ realizing the back coupling via $2\mu _1r_\mathsf{{F}}$ in (29), which is exact in the fully developed state and approximate elsewhere:

$$\begin{aligned} r_\mathsf{{F}}^* = \displaystyle \frac{\partial N_{1112}}{\partial x_1^*}D_{12}^* + \displaystyle \frac{\partial N_{1122}}{\partial x_2^*}D_{12}^* -\frac{3}{4}N_{1122}. \end{aligned}$$

(31)

In Fig. 4a, the dimensionless term $r_\mathsf{{F}}^*$ is shown at two different positions $x_1^*$ over the half channel height $x_2^*$. Similarly, the difference of the decoupled and coupled velocity is given in Fig. 4b. Note that throughout the present work the difference operator is defined generally as follows:

(32)

Fig. 4

Profiles of $r_\mathsf{{F}}^*$ describing the impact of back coupling on the evolution of $v_1^*$, profiles of at different positions $x_1^*$ in the channel over the half channel height $x_2^*$ and the field in the lower channel half (limited to the IBOF closure method)

In Fig. 4c, the field of is given for the lower channel half along with marking the positions of the profiles shown in the diagrams above. Figure 4 shows data limited to the IBOF closure method. Observing the plot of $r_\mathsf{{F}}^*$, three characteristic extremes can be identified. The two peaks with negative contribution to the balance of linear momentum are marked with blue color and the positive peak with red color, respectively. Negative means that the fiber-induced stresses are locally decelerating the flow, while positive means the opposite. With increasing $x_1^*$, both the position and the magnitude of the extremes change in the following way. On the one hand, the position of the peaks shifts toward the center of the channel, and on the other hand, the magnitudes decrease. This process is accompanied by a spreading of the asymptotic state $r_\mathsf{{F}}^{*\infty }$ from the lower channel wall, where it is achieved first. Keeping this in mind, the behavior of in Fig. 4b can be explained. Near the channel inlet, the positive peak of $r_\mathsf{{F}}^*$ starts in the lower wall region leading to an acceleration close to the wall. Based on the continuity equation, the negative peak near the center of the channel leads to a deceleration ensuring a constant volume flow rate. Both aforementioned effects are responsible for the flattening of $v_1^*$. With increasing $x_1^*$, the positive peak of $r_\mathsf{{F}}^*$ shifts toward the channel center diminishing the flattening of $v_1^*$. Due to the coupling via the continuity equation, the second negative peak near the channel wall reduces the acceleration close to the channel wall. Both effects are leading to a decrease of which can be seen in Fig. 4c at the outlet region. It is noted that the mentioned effects should be interpreted in an integral sense over the distance covered by the fiber suspension in the channel. Figure 4a gives an indication that the asymptotic state is characterized by a constant value $r_\mathsf{{F}}^{*\infty }$ over the channel height which can be derived based on (31) knowing that $N_{1112}$ and $N_{1122}$ are characterized by a constant asymptotic state as well,

$$\begin{aligned} r_\mathsf{{F}}^{*\infty }=-\frac{3}{4} N_{1122}^{\infty }, \end{aligned}$$

(33)

which has the same structure as derived by Altan and Tang [59]. The value and the distribution of $r_\mathsf{{F}}^{*\infty }$ can be interpreted as a contribution that increases the pressure gradient required to drive the flow compared to the decoupled simulation. Motivated by splitting the orientation tensors in an isotropic and in an anisotropic part, the fibers increase the shear viscosity isotropically, and an increased pressure gradient is necessary to ensure the same volume flow rate. Furthermore, the splitting shows that the fibers lead to an anisotropic material behavior. It is noted that the volume flow rate is defined by the integral value of the inlet velocity profile over the channel height. The new effective dimensionless pressure gradient,

$$\begin{aligned} \left( \displaystyle \frac{\partial p^*}{\partial x_1^*}\right) _\mathsf{{eff}} = \displaystyle \frac{\partial p^*}{\partial x_1^*} - 2\frac{r_\mathsf{{F}}^{*\infty }}{\mathrm {Re}}\frac{\mu _1}{\mu }, \end{aligned}$$

(34)

ensures that the general solution of (29) describing the fully developed state is of parabolic nature. This statement agrees with Altan and Tang [59]. In the same work, it is shown that the smaller $\mathrm {Re}$, the smaller the channel length to reach the fully developed velocity profile.

Based on Fig. 5, the impact of back coupling on the fiber orientation is discussed. The field plots in Fig. 5a, c show the components $N_{11}$ and $N_{12}$ in case of the decoupled approach. The local value of $N_{11}$ represents the probability to find a fiber aligned in the longitudinal direction $\varvec{ e}_1$. The only non-vanishing off-diagonal component $N_{12}$ describes how much the principal directions of $\varvec{ N}$ deviate from the base coordinate system $\varvec{ e}_i$. In Fig. 5b, d, the corresponding local difference is shown according to (32) and can be seen as an extension of previous studies [41, 43]. As before, Fig. 5 is limited to the IBOF closure method. It is known by analyzing (7) and from the literature [41, 43] that the shear component $D_{12}$ is decisive for the evolution of a high level of $N_{11}$ in the CF. Furthermore, the consideration of fiber–fiber interaction leads to an asymptotic orientation state which depends on the value of $C_\mathsf{{I}}$, $\alpha$, and the chosen closure method. It is emphasized that the asymptotic orientation state is not influenced by the back coupling. The asymptotic value of the components $N_{ij}$ is reached if the total shear of a fiber reaches a critical value which can be determined by simulating a simple Couette flow. By looking at the plots in Fig. 5a, c it can be seen that the asymptotic fiber orientation state is reached instantaneously at the channel wall. At the center of the channel, the fiber orientation stays isotropic due to the absence of $\mathrm {grad}(\varvec{ v})$. In between the walls and the center, the necessary flow length leading to the critical total shear increases toward the center of the channel. These statements coincide with the investigation of previous studies [41, 43]. Analyzing the difference between the coupled and decoupled approaches in Fig. 5b, d, the component $N_{11}$ is decreased near the center while no significant differences are observed near the channel walls. This result has many reasons. First of all, due to the continuity equation the flattening of the profile $v_1^*$ goes hand in hand with a relocation of the mass flow toward the channel walls. Compared to the decoupled case, the shear components of $\mathrm {grad}(\varvec{ v})$ favor the evolution of $N_{22}$ leading to a decreased $N_{11}$ near the center line. On the other hand, the flattening decreases $D_{12}$ in the center region [43] leading to a slower alignment in the direction $\varvec{ e}_1$. As mentioned before, the asymptotic state is not influenced by the back coupling. As a consequence, the difference is zero in the wall region and also in the limit case of an infinitely long channel. Compared to the decoupled approach, the fiber orientation at the center line changes with $x_1^*$ due to the coupling-induced streamwise gradients of the velocity at the center line. The difference in fiber orientation due to coupling varies between $\pm 5{\%}$ related to the range [0, 1]. Finally, it is remarked that the QC predicts more extreme fiber orientation states than the IBOF closure [62]. This detail will impact the resulting elastic properties obtained via different closure methods, which will be discussed later on in Fig. 13 for the BFS case.

Fig. 5

Fields of the components $N_{11}$ and $N_{12}$ in the CF on the left-hand side for the decoupled approach and the associated difference on the right- hand side (limited to the IBOF closure method)

4.2 Backward-facing step flow

In the following, the more complex BFS case is discussed, aided by the observation made in the previous Sect. 4.1 for the simpler CF case. In Fig. 6, the velocity profile $v_1^*$ is shown at various positions $x_1^*$ in the BFS. Note that the presentation is limited to the region after the step $x_1^*\in [2,10]$. For more details, see Fig. 2. As done before, the QC and the IBOF closure method are considered. Compared to the CF, the decoupled results of $v_1^*$ represented by the dotted lines show a spatial development with increasing $x_1^*$ toward a parabolic profile. Owing to the present low value of $\mathrm {Re}$, the flow follows the step, and no significant separation occurs at the top corner. Higher values of $\mathrm {Re}$ lead to a completely different flow pattern characterized by a growing corner vortex [13, 67]. Thus, increasing $\mathrm {Re}$ leads to a larger channel length to achieve the fully developed velocity profile. The coupled results of $v_1^*$ represented by solid lines in Fig. 6 confirm the flattening of the profiles already discussed for the CF case. Furthermore, a slight delay of the downward motion after the step is observed. It is pointed out that the differences between the velocities calculated with the QC and with the IBOF closure method can be neglected. Therefore, and without loss of generality, it can be said that in complex flows performing coupled simulations is more important than selecting a specific closure method. It should be noted, however, that this statement refers to the velocity field and not to the fiber orientation state, which shows a strong dependence on the selected closure method.

Fig. 6

Velocity profiles $v_1^*$ over the channel height $x_2^*$ at different positions $x_1^*$ in the BFS for different closures (QC, IBOF), both for the decoupled and the coupled approach

The behavior of the difference fields , shown in Fig. 7, can be easily explained in light of the observations made in the previous Sect. 4.1 for the CF case. In Fig. 7a showing the flattening in the center region and the acceleration near the upper wall can be observed. Near the lower wall, a region characterized by a deceleration in the coupled approach can be observed. The deceleration is due to the growing corner vortex, which induces a back flow near the lower wall. In between the center and the wall region, the well-known area of acceleration generated by the back coupling can be seen. In Fig. 7b, the field is shown. Near the vertical wall at $x_1^*=2$ a region of larger (marked with $\circledast$) and a region with smaller (marked with $\circledast \circledast$) downstream velocity are observed. These regions of near the vertical wall are the counterparts to the flattening of $v_1^*$ along the $x_1^*$-direction observed at the horizontal walls. It is noted that decrease downstream as the velocity field reaches a fully-developed state.

Fig. 7

Fields of the difference in the BFS (limited to the IBOF closure method)

Fig. 8

Fields of the components $N_{11}$ and $N_{12}$ in the BFS on the left-hand side for the decoupled approach and the associated difference on the right-hand side (limited to the IBOF closure method)

The impact of back coupling on the fiber orientation is discussed based on Fig. 8. In Fig. 8a, c, the fields of $N_{11}$ and $N_{12}$ are shown for the decoupled approach utilizing the IBOF closure. In Fig. 8b, d, the pointwise difference between the coupled and the decoupled fiber orientation field is given in the sense of (32). The mechanisms contributing to the evolution of the fiber orientation state described in Sect. 4.1 can be transferred to the more complex BFS case. Keeping in mind that shear effects tend to align the fibers in the corresponding direction, two particular areas can be identified. The first area lies close to the vertical wall at $x_1^*=2$ where the fluid shear ensures a fiber alignment parallel to the vertical wall. This means that $N_{22}$ is close to unity, which is visualized by small values of $N_{11}$ shown in Fig. 8a. The second area is defined by the downstream region, which is directly comparable with the CF case in Sect. 4.1. The local shear results here in a preferential streamwise alignment of the fibers, which is expressed by high values of $N_{11}$ close to the horizontal walls. Toward the channel centerline, where $N_{11}$ is low, the complex flow kinematics caused by the shift of the flow toward the lower channel half favors the development of $N_{22}$. The shear $D_{12}$ becomes dominant with increasing $x_1^*$, thus leading to a decrease of $N_{22}$ in favor of $N_{11}$. The pointwise difference due to the modified flow kinematics caused by back coupling varies between $\pm 30{\%}$ related to the range [0, 1].

As a supplement to Fig. 8, selected profile data of the fiber orientation state are shown in Fig. 9. The positions $x_1^*$ in the BFS are marked with vertical dotted lines in Fig. 8. In addition, the component $N_{33}$ is not shown and can be calculated with $\mathrm {tr}(\varvec{ N})=1$. First of all, the development from a non-symmetric to a symmetric orientation state with increasing $x_1^*$ is clarified by the profiles in Fig. 9. The results show that in the coupled case the non-symmetric state is more distinct. This observation depends directly on the vertical flow after the step, which is shifted downstream in the coupled case, thus delaying the recovery of centerline symmetry. Furthermore, the asymptotic fiber orientation state, which does not depend on the coupling, can be identified close to the channel walls. Near the center of the BFS, the flattening of $v_1^*$ is represented by lower values of $N_{11}$ in favor of the dominant orientation component $N_{22}$.

Fig. 9

Profiles $N_{ij}$ over the channel height $x_2^*$ at different positions $x_1^*$ in the BFS (limited to the IBOF closure method)

To conclude the fluid mechanical investigation of the BFS, the anisotropic viscosity tensor defined in (17) is considered in the following non-dimensionalized form based on the matrix viscosity $\mu$:

$$\begin{aligned} {\mathbb { V}}^* = 2{\mathbb { P}}_2 + \mu _1^* {\mathbb { N}}, \qquad \mu _1^* = \frac{2\phi \alpha ^2}{3\mathrm {ln}(\sqrt{\pi /\phi })}. \end{aligned}$$

(35)

The following relationships are used to determine the local dimensionless anisotropic viscosity $\mu ^*(\varvec{ p},\varvec{ d},\varvec{ x})$ [6, 11]:

(36)

where $\varvec{ M}$ is an auxiliary variable defining the shear plane. The interpretation of $\varvec{ p}$ and $\varvec{ d}$ is shown in Fig. 10. The normal vector of the shear plane is described by $\varvec{ p}$, and $\varvec{ d}$ represents the shear direction lying in the plane. In the present work, $\varvec{ p}=\varvec{ e}_2$ holds, and the remaining variable $\varvec{ d}$ is replaced by $\varphi$ defining a polar plot in the $\varvec{ e}_1$–$\varvec{ e}_3$-plane. For $\varphi =0$ the equality $\varvec{ d}=\varvec{ e}_1$ holds. The dimensionless viscosity tensor ${\mathbb { V}}^*$ in (36) is used in normalized Voigt notation.

Fig. 10

Interpretation of $\varvec{ p}$, $\varvec{ d}$, $\varvec{ x}$, and $\varphi$ in the context of the direction-dependent shear viscosity $\mu ^*(\varvec{ p},\varvec{ d},\varvec{ x})=\mu ^*(\varphi ,\varvec{ x})$ of the fiber suspension

In Fig. 11 the direction-dependent shear viscosity $\mu ^*$ in the BFS case is shown for the QC and the IBOF closure. The dimensionless isotropic matrix viscosity ${\mathbb { V}}^*_\mathsf{{M}}=2{\mathbb { P}}_2$ is shown as a reference. In addition, the dimensionless viscosity of the fiber suspension in case of isotropic fiber orientation $\mathbb {V}^*(\mathbb {N}_\mathsf{{iso}})$ is shown. In Fig. 11b the effective behavior is shown averaged over the whole domain. Three Figs. 11c–e show $\mu ^*$ at three different points in the cavity marked in Fig. 11a. It is pointed out that the anisotropic viscosity is only defined in the coupled approach. The designation decoupled in Fig. 11 means that $\mu ^*$ is calculated with the decoupled simulated fiber orientation but is not included in the calculation of the flow. Compared against the matrix behavior and as stated out before, the fibers both increase the viscosity isotropically and induce anisotropic behavior. Based on the special case of isotropic fiber orientation, it can be seen that the direction-dependent effect of fiber alignment on the viscosity can be negative. Note that the value of the isotropic matrix viscosity cannot be decreased by adding fibers.

Fig. 11

Polar diagrams of the direction-dependent dimensionless viscosity $\mu ^*$ of the fiber suspension in the $\varvec{ e}_1$–$\varvec{ e}_3$-plane both globally and locally at the points ${A}=(2.7,1.2$), ${B}=(3.2,1.2)$, and ${C}=(6,1.2)$, see Fig. 2 for details concerning $\varvec{ e}_i$

Figure 12 shows $\mu ^*$ at the additional point ${D}=(9.0,1.8$), which is located near the upper channel wall (see Fig. 11a). In this region, the fiber alignment in flow direction dominates, and thus its effect on effective viscosity can be assessed at best. Here, the effective viscosity is clearly lower than in case of isotropic fiber orientation.

Fig. 12

Polar diagram of the direction-dependent dimensionless viscosity $\mu ^*$ of the fiber suspension in the $\varvec{ e}_1$–$\varvec{ e}_3$-plane at the point ${D}=(9.0,1.8$), see Fig. 2 for details concerning $\varvec{ e}_i$

Moreover, the IBOF closure predicts higher values of viscosity compared to the QC. As known from the previous Sections, the QC leads to more extreme orientation states compared to the IBOF closure which predicts the orientation state more isotropic. This confirms the statement by Mezi et al. [43] that higher fiber alignment leads to lower viscosity compared to random orientation states. It is remarked that the viscous behavior of a fiber suspension is represented by a fourth-order tensor which defines a multidimensional and anisotropic problem. Globally, the shear viscosity shows approximately only a dependence on the closure method and not on the coupling (see Fig. 11b). This is due to the geometry of the cavity favoring in large portions of the flow domain the asymptotic orientation state, which only depends on the closure method when all other parameters are held constant. However, locally the difference between the coupled and decoupled anisotropic viscosity can be more extreme as shown in the Fig. 11c–e.

4.3 Solid mechanics

In the following, the anisotropic linear elastic properties induced by the fiber orientation are discussed, particularly regarding the impact of different closure methods and of the coupled analysis. This Section is limited to the BFS and to the methods described in Sect. 2.5. Note that the stationary fiber orientation state is assumed to describe the anisotropy in the manufactured composite after its fluid–solid transition. In Fig. 13 the direction-dependent Young’s modulus $\bar{E}$ is shown in the BFS for the QC and the IBOF closure. The isotropic stiffness of the matrix material ${\mathbb { C}}_\mathsf{{M}}$ is shown as a reference. Moreover, the effect of an isotropic fiber orientation state on the effective stiffness is shown by $\bar{{\mathbb { C}}}(\varvec{ N}_\mathsf{{iso}},{\mathbb { N}}_\mathsf{{iso}})$.

Fig. 13

Polar diagrams of the direction-dependent effective Young’s modulus $\bar{E}$ of the manufactured solid composite both globally and locally in the $\varvec{ e}_1$–$\varvec{ e}_2$-plane at the points ${A}=(2.7,1.2$), ${B}=(3.2,1.2)$, and ${C}=(6,1.2)$, see Fig. 2 for details concerning $\varvec{ e}_i$

In Fig. 13b the effective behavior is shown averaged over the whole domain. The three plots in Fig. 13c–e show $\bar{E}$ at three different points in the cavity marked in Fig. 13a. The anisotropy at point D is not shown here due to the similarity to the averaged behavior in Fig. 13b. The designation decoupled means that $\bar{E}$ is estimated with the decoupled simulated fiber orientation, and coupled means that the coupled simulated fiber orientation is used. It can be observed locally that the difference between the decoupled and the coupled approach is described by a rotation of the polar plots, while the shape stays unchanged, implying that the coupled simulation predicts a different spin of the evolving substructure. The mentioned rotation results from a different shear state influence the alignment caused by back coupling compared to the decoupled results. The shape of the polar plots provides information about the direction of the fiber alignment. Furthermore, it can be seen that the QC predicts a higher maximal stiffness compared to the IBOF closure which comes from the more extreme orientation state predicted by the QC. While the anisotropic stiffness varies widely at the points A, B, and C due to the coupled approach, the difference in a global sense is mainly caused by the chosen closure method. As mentioned before, in simple geometries the asymptotic fiber orientation close to the walls dominates and does not depend on the coupling. Globally, the maximum stiffness in the coupled case is slightly smaller than in the decoupled cases. This results from the flattening of $v_1^*$ which inhibits the evolution of $N_{11}$ in large areas of the BFS during mold filling.

4.4 Discussion of modeling and coupling

The results of the present study refer to the simplest possible modeling approach of fiber suspensions. This is justified because this is the only way to make a targeted assessment of the impact of coupling the fiber orientation to the flow. A too complex modeling describes the manufacturing realistically, but there is a superposition of many influencing factors preventing the aforementioned targeted assessment. Furthermore, the results founding on simple models can be useful for the quantification of various model extensions. Based on the numerical results, both the influence of the coupled approach and of choosing specific closure approximations can be quantified in the context of the anisotropy in the viscous and elastic behavior. The suitable simulation approach can be chosen based on defined accuracy requirements depending on the use of the manufactured part. Moreover, it is assumed that the Folgar–Tucker equation [1, 25] is sufficient for describing the evolution of the fiber orientation state. In addition, the premise of the present study is that the material model of Dinh and Armstrong [19] describes the behavior of a fiber suspension flow more realistic compared to the decoupled approach.

The phenomenon of deformation-induced anisotropy can also be observed in metal plasticity [9, 10]. In metal forming processes, the overall elastic and plastic properties are changing due to the deformation-induced reorientation of the crystal orientations on the grain scale (spin of the evolving substructure). Corresponding model approaches are (similar to models for fiber reinforced polymers) based on tensorial coefficients describing the orientation distribution of crystals for which evolution equations are solved [8]. For model approaches, it is referred to the aforementioned literature and the corresponding references therein.

5 Summary and outlook

In the present study, the mold filling process of a fiber suspension is modeled as a laminar, incompressible, isothermal flow of a Newtonian matrix fluid with rigid fibers and without phase transition. The description of the fiber orientation state is limited to the orientation tensors of the first kind and of the second and fourth order [1, 37]. Furthermore, the QC and the IBOF closure are investigated [15, 20]. Based on a simple CF and a BFS, the impact of coupling the fiber orientation to the base flow leading to an anisotropic viscous behavior is considered. The Dinh–Armstrong model [19] is used for realizing the coupling. Based on the Mori–Tanaka homogenization method [47], the influence of coupling is studied in view of the direction-dependent Young’s modulus. The present results show that the previously observed flattening of the velocity profile in the CF [43] is a local effect and that the asymptotic state can be explained based on the coupling term in the linear momentum balance. In case of the BFS flow, the influence of the coupling level can be traced back to the observations in the geometrically simpler CF. Locally, the fiber orientation changes significantly due to flow-fiber coupling. By observing the anisotropic viscosity, it is shown that the fibers have both an isotropic and an anisotropic impact on the behavior of the suspension. Furthermore, the differences in local anisotropic elastic properties between the coupled and decoupled approach are quantified. Globally, the flow-induced elastic anisotropy strongly depends on the considered flow geometry. For the two investigated cases of the present study, the asymptotic orientation state was found to be the dominant one, thus largely determining the resulting averaged Young’s modulus.

In future studies, the impact of various homogenization methods concerning viscosity and elasticity may be considered. Moreover, more realistic and more complex flow cases can be studied in combination with different closure methods and different fiber orientation evolution models. Furthermore, the simple model approach of the present work may be extended to investigate the influence of temperature, shear thinning matrix behavior, and of phase transition during the mold filling process.

Appendices

Symbols and abbreviations

Table 1 summarizes all used symbols and abbreviations introduced in the present paper.

Table 1 Frequently used symbols and abbreviations throughout the present paper

Appendix: IBOF closure terms

In this Section, the IBOF closure terms given in Heinen [31] are provided in such a way that the symmetry of ${\mathbb { N}}[\varvec{ D}]$ is ensured. It should be noted that the equations given in this manuscript refer to the incompressible case with $\mathrm {tr}(\varvec{ D})=\varvec{ D}\cdot \varvec{ I}=0$. Please note that the formulae given in Heinen [31] contain $\mathrm {tr}(\varvec{ D})$. In Eq. (37), the abbreviation $\varvec{ S}=\varvec{ N}^2$ is used,

$$\begin{aligned} {\mathbb { N}}_\mathsf{{IBOF}}[\varvec{ D}]&= \frac{2\beta _1}{3}\varvec{ D}+ \frac{\beta _2}{6}\big ((\varvec{ N}\cdot \varvec{ D})\varvec{ I}+ 2\varvec{ D}\varvec{ N}+ 2\varvec{ N}\varvec{ D}\big ) + \frac{\beta _3}{3}\big ((\varvec{ N}\cdot \varvec{ D})\varvec{ N}+ 2\varvec{ N}\varvec{ D}\varvec{ N}\big ) \nonumber \\&\quad + \frac{\beta _4}{6}\big ((\varvec{ S}\cdot \varvec{ D})\varvec{ I}+ 2\varvec{ D}\varvec{ S}+ 2\varvec{ S}\varvec{ D}\big ) + \frac{\beta _5}{6}\big ((\varvec{ S}\cdot \varvec{ D})\varvec{ N}+ (\varvec{ N}\cdot \varvec{ D})\varvec{ S}+ 2\varvec{ N}\varvec{ D}\varvec{ S}+ 2\varvec{ S}\varvec{ D}\varvec{ N}\big ) \nonumber \\&\quad + \frac{\beta _6}{3}\big ((\varvec{ S}\cdot \varvec{ D})\varvec{ S}+ 2\varvec{ S}\varvec{ D}\varvec{ S}\big ). \end{aligned}$$

(37)