Abstract
The anisotropic elastic properties of injection molded composites are fundamentally coupled to the flow of the fiber suspension during mold-filling. Regarding the modeling of mold-filling processes, both a decoupled and a flow–fiber coupled approach are possible. In the latter, the fiber-induced viscous anisotropy is considered in the computation of the flow field. This in turn influences the evolution of the fiber orientation compared to the decoupled case. This study investigates how flow–fiber coupling in mold-filling simulation affects the stress field in the solid composite under load based on the final elastic properties after fluid–solid transition. Furthermore, the effects of Newtonian and non-Newtonian polymer matrix behavior are investigated and compared. The entire process is modeled micromechanically unified based on mean-field homogenization, both for the fiber suspension and for the solid composite. Different numerical stabilization methods of the mold-filling simulation are discussed in detail. Short glass fibers with a typical aspect ratio of 20 and a volume fraction of 20% are considered, embedded in polypropylene matrix material. The results show that the flow–fiber coupling has a large effect on the fiber orientation tensor in the range of over ± 30% with respect to the decoupled simulation. As a consequence, the flow–fiber coupling affects the stress field in the solid composite under load in the range of over ± 10%. In addition, the predictions based on a non-Newtonian modeling of the matrix fluid differ significantly from the Newtonian setup and thus the necessity to consider the shear-thinning behavior is justified in a quantifiable manner.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Motivation and state of the art
Short-fiber reinforced composites are commonly used in lightweight design. The special case of adding fibers into a polymer matrix allows the mass-production of lightweight components with complex shapes while retaining the desired mechanical stiffness and strength. During injection molding—the manufacturing process through which such components are produced—the fibers flow within the polymer matrix and thereby change their orientation based on the experienced flow conditions. At the same time, a local change of the fiber orientation affects the overall rheological properties of the fluid, which become inhomogeneous anisotropic, and in turn the flow characteristics. This mutual flow–fiber interaction is subject of recent numerical research efforts addressed in the following, focussing on the effects of flow–fiber coupling on the fluid side. In the context of this work, flow–fiber coupling expresses that the evolution of fiber orientation is influenced by the effective anisotropic viscosity of the fiber suspension. Three main points can be identified in this context: The effect of the flow–fiber coupling on the flow field, the influenced fiber orientation evolution due to the changed flow conditions and finally the change of the mechanical properties of the composite, which depend on the local fiber orientation. How the flow–fiber coupling during mold-filling affects the stress state in the solid composite under load after fluid–solid transition is a question that received less attention in literature and is the objective of the present work. Since the correct prediction of the stress field in the manufactured composite is an essential part in engineering applications, the need for a flow–fiber coupled simulation has to be studied. In this context, the question also arises which influence the two-phase simulation of the actual mold filling has both on the fiber orientation and on the local anisotropic properties.
The fiber-induced anisotropic viscosity within the flow–fiber coupled approach causes changes of the velocity field during mold-filling. Latz et al. [1] investigated the flow–fiber coupling from a fluid mechanics perspective in a channel flow, a flow around a cylinder and in a contraction flow. Different coupling intensities were considered with the result, that the coupling effects are significant in the channel and in the contraction flow. It is shown that (e.g. for the channel flow) the stronger the coupling, the flatter the velocity profile. This flattening was already reported in the early studies of Altan et al. [2] and Tang and Altan [3]. The importance of accounting for flow–fiber coupling in mold-filling simulations was demonstrated in a low Reynolds number flow through a tapered channel by Krochak et al. [4]. Both isotropic and aligned orientation states were considered at the inlet, showing that the flow changes towards a plug flow because of flow–fiber coupling. Flow–fiber coupled mold-filling simulation based on probability density function was carried out by Mezi et al. [5] in 2D geometries and by Férec et al. [6] in 3D axisymmetric geometries. Both studies conclude that the influence of flow–fiber coupling on the velocity field is significant and the velocity profile flattens, as mentioned before. In addition, the difference between Newtonian and non-Newtonian matrix fluid is addressed by Mezi et al. [5]. Mezi et al. [7] observed a flattening of the velocity profile in the context of flow–fiber coupling for die swell flows. The results show that the swell ratio of the flow is affected by flow fiber coupling. By using a scalar rheologial model, Li and Luyé [8] studied the flow–fiber coupling effects based on mold-filling simulations of a rectangular plate. In addition, three different orientation evolution models were used in their study. They observed, that the coupling effects strongly depend on the chosen orientation evolution model. In this context, the classical Folgar–Tucker model [9, 10] showed less coupling effects than the reduced-strain closure model [11]. The aforementioned flattening of the velocity profile also occured. In addition, the study of Li and Luyé [12] shows that results based on flow–fiber coupling improve parameter optimization of fiber orientation models in the core region of the flow. Tseng and Favaloro [13] introduced the informed isotropic viscosity model in order to improve convergence compared to the classic models [14, 15]. It is shown for simple and complex geometries, that this model is capable of reproducing experimental findings and that the coupling effects on the flow field are not negligible. The informed isotropic viscosity model was used by Huang and Lai [16] to show that flow–fiber coupling influences the melt front behavior and that the coupling effects are locally different. Lee et al. [17] also used the informed isotropic viscosity model and studied the compression molding process of composite material. Sommer et al. [18] investigated the flow–fiber coupling effects in squeeze flow. The results show that only a flow–fiber coupled analysis is capable of predicting the physically correct anisotropic behavior of the suspension. Based on two-phase flow, Witteman et al. [19] implemented the flow–fiber coupling approach with a non-Newtonian, temperature- and curing-dependent viscosity model for fiber-laden thermosets. The coupled simulation leads to a better agreement of the pressure field with experimental measurements than the decoupled approach.
The flow–fiber coupling effects on the velocity field addressed above have a direct influence on the fiber orientation evolution. Chung and Kwon [20, 21] studied the flow–fiber coupling effects on both flow field and fiber orientation. Their results show that flow–fiber coupling clearly influences the fiber orientation prediction. Latz et al. [1] found that the stronger the coupling, the larger the region of isotropic orientation in the channel center region. Li and Luyé [8] observed, that the fiber orientation evolution is clearly influenced by the changed flow kinematics for the studied mold-filling process of a rectangular plate. Wang and Smith [22, 23] investigated the flow–fiber coupling regarding an additive manufacturing process. The fiber orientation evolution referred to the orthotropically closed Folgar–Tucker model and the coupling was realized based on the fourth-order fiber orientation tensor. The results indicate that the fiber-fiber interaction coefficient strongly affects the influence of flow–fiber coupling. Significant differences in the fiber orientation tensor were observed due to flow–fiber coupling. In contrast, Mezi et al. [5, 7] and Férec et al. [6] did not observe significant differences regarding the fiber orientation state between the decoupled and the coupled approach in their simulation setups.
Karl et al. [24] studied the effect of flow–fiber coupling on both velocity and fiber orientation. A simple channel flow and a flow over a backward-facing step was considered with a detailed analysis of the aforementioned velocity flattening. Consistent with the studies already addressed, large differences in fiber orientation became evident. Based on polar plots of the direction-dependent Young’s modulus [25] computed with the Mori–Tanaka model [26, 27], the flow–fiber coupling effects on the local elastic anisotropy are shown. In this context, the results of Wang and Smith [22, 23] demonstrate significant differences due to flow–fiber coupling in the engineering constants describing the effective elastic anisotropy. Wang and Smith [28] present a finite element procedure regarding flow–fiber coupling with the result that the differences caused by flow–fiber coupling can be significant. Differences up to 25–50% in the velocity field and differences up to 8% in the tensile modulus were observed, depending on the chosen parameters and geometries. Wang [29] improved the algorithm of Wang and Smith [28] by optimizing the scalar viscosity in order to consider higher fiber aspect ratios with less numerical difficulties.
1.2 Originality
This study investigates the differences between the decoupled and the coupled approach of fiber suspensions with focus on the stress field of the solid composite based on the final elastic properties depending on the local fiber orientation state. In addition, the influence of flow–fiber coupling on one side and the Newtonian and non-Newtonian modeling of the matrix fluid on the other side is investigated. A detailed analysis of the flow conditions is omitted, since the coupling effects were already studied in this context in the literature cited in Sect. 1.1. The content of this study can be summarized as follows:
-
Application of a unified mean-field homogenization procedure for both viscous fiber suspensions and solid fiber reinforced composites.
-
Detailed analysis of the two-phase mold-filling simulation effects on the local fiber orientation with respect to the alternative steady state approach.
-
Quantification of the flow–fiber coupling effects on the stress field of the solid composite representing the local anisotropic elastic properties considering both Newtonian and non-Newtonian matrix behavior during mold-filling.
-
Detailed documentation of the numerical procedure focusing on stabilization methods of mold-filling simulation.
-
In order to establish a uniform open-source simulation tool, the use of OpenFOAM® also for solid composite simulations besides Abaqus® is addressed.
1.3 Notation
Throughout this manuscript, a symbolic tensor notation is used. Scalar quantities are denoted by \(a,b,\ldots \) and \({\varvec{a}},{\varvec{b}},\ldots \) indicate vectors. Second-order tensors are represented by \({\varvec{A}},{\varvec{B}},{\varvec{\varepsilon }},{\varvec{\sigma }},\ldots \) and \({\mathbb {A}},{\mathbb {B}},\ldots \) refer to fourth-order tensors. Two different mappings of tensors are used and indicated by \({\varvec{A}}{\varvec{B}}\) and \({\mathbb {A}}[{\varvec{B}}]\), with \(A_{ik}B_{kj}\) and \(A_{ijkl}B_{kl}\) representing the Cartesian index notation. The dyadic product refers to  with the Cartesian index representation \(n_i n_j\). The Frobenius tensor norm is denoted by \({\Vert {\varvec{A}} \Vert =\sqrt{{\varvec{A}}\cdot {\varvec{A}}}}\) with the scalar product between equal order tensors \({{\varvec{A}}\cdot {\varvec{A}}=A_{ij}A_{ij}}\). The trace of a tensor \({\varvec{A}}\) is represented by \({\textrm{tr}({\varvec{A}})=A_{ii}}\).
with the Cartesian index representation \(n_i n_j\). The Frobenius tensor norm is denoted by \({\Vert {\varvec{A}} \Vert =\sqrt{{\varvec{A}}\cdot {\varvec{A}}}}\) with the scalar product between equal order tensors \({{\varvec{A}}\cdot {\varvec{A}}=A_{ij}A_{ij}}\). The trace of a tensor \({\varvec{A}}\) is represented by \({\textrm{tr}({\varvec{A}})=A_{ii}}\).
2 Governing equations
For both viscous fiber suspensions and solid fiber reinforced composites, the governing equations, material models and assumptions are addressed in the following. It should be noted that all governing equations must be interpreted in the context of the finite volume method. Regarding the numerical procedure, the reader is referred to Sect. 3.
2.1 Volume of fluid approach for viscous fiber suspensions
Throughout this study, the fiber orientation is described based on the second-order and fourth-order fiber orientation tensor \({\varvec{N}}\) and \({\mathbb {N}}\) of the first kind [10, 30]

In Eq. (1) the probability density function f depends on the direction \({\varvec{n}}\) defined on the unit sphere \(\mathcal{S}\), on the time t and the spatial position \({\varvec{x}}\). The surface element \(\textrm{d}S\) on \(\mathcal{S}\) is given by \({\textrm{d}S=\sin (\theta )\textrm{d}\theta \textrm{d}\varphi /4\pi }\), with \({\theta \in [0,\pi ]}\) and \({\varphi \in [0,2\pi )}\). During mold-filling the fiber orientation evolution is modeled based on the Folgar–Tucker equation [9, 10]
with the effective strain rate tensor \({\bar{{\varvec{D}}}}\), the effective spin tensor \({\bar{{\varvec{W}}}}\), the fiber interaction coefficient \(C_{\textsf {I}}\) and the second-order identity tensor \({\varvec{I}}\). The scalar shear rate is defined by \({\dot{{\bar{\gamma }}}=\sqrt{{\bar{{\varvec{D}}}}\cdot {\bar{{\varvec{D}}}}/2}}\) and the shape parameter refers to \({\xi =(\alpha ^2-1)/(\alpha ^2+1)}\), with \(\alpha \) denoting the fiber aspect ratio. The scalar shear rate is introduced consistently to previous studies [24, 31]; other definitions may be applied along with changing \(C_{\textsf {I}}\) accordingly to ensure the same fiber-fiber interaction strength. Since Eq. (2) depends on \({\mathbb {N}}\), an adequate closure method is required which can be selected from numerous approaches given in the literature, e.g., [32,33,34]. In this study the invariant-based optimal fitting closure (IBOF) [34], whose implementation details are addressed in Appendix A, is adopted. It should be noted that neutrally buoyant, isotropically interacting rigid short fibers are considered embedded in an incompressible matrix fluid without body forces [9, 35, 36]. Regarding further discussion, parameterizations, and admissible parameter ranges of second- and fourth-order orientation tensors of the first kind, the reader is referred to the recent work of Bauer and Böhlke [37].
In order to realize the flow–fiber coupling, the effective viscosity tensor \({\bar{{\mathbb {V}}}}\) of the fiber suspension is formulated in terms of fiber orientation tensors \({\varvec{N}}\) and \({\mathbb {N}}\). Throughout this study, the effective Cauchy stress tensor \({\bar{{\varvec{\sigma }}}}\) refers to a generalized incompressible Newtonian fluid. Furthermore, the Mori–Tanaka model [26, 38,39,40] is used reading
The effective pressure is denoted by \({\bar{p}}\), \({\mathbb {V}}_{\textsf {M}}\) stands for the viscosity tensor of the matrix fluid, \(c_{\textsf {F}}\) and \({c_{\textsf {M}}=1-c_{\textsf {F}}}\) refer to the fiber (F) and matrix (M) volume fraction. The polarization tensor \({\mathbb {P}}_0\) contains information about the fiber geometry and the matrix material and can be computed analytically for spheroidal fibers. In this work the expressions given in Ponte Castañeda and Willis [41] are adapted for viscosity and simplified for incompressible matrix behavior following Karl and Böhlke [40]. The inversion \({\mathbb {P}}_0^{-1}\) is defined on the symmetric deviatoric subset (symDev) for the considered case of incompressible suspensions with \({{\mathbb {P}}_0^{-1}{\mathbb {P}}_0={\mathbb {P}}_2}\) representing the identity on symDev for second-order tensors. The operator \(\langle \cdot \rangle _{\textsf {OA}}\) denotes the orientation averaging procedure (OA) [10] leading to the following expression simplified for the special case of incompressibility
with the coefficients \(b_1,\ldots ,b_5\) depending on the orientation averaged tensor \({\mathbb {P}}_0^{-1}\) [10]. As discussed by Karl et al. [24], the formulation of the fiber-induced viscous stress based on Eqs. (3) and (4) in general is not traceless for anisotropic fiber orientation, even for traceless \({\bar{{\varvec{D}}}}\) in the incompressible case. In the framework of the decoupled approach (\({c_{\textsf {F}}=0}\)), only \({\bar{{\mathbb {V}}}={\mathbb {V}}_{\textsf {M}}}\) is used and, therefore, the flow field is not influenced by the evolution of the fiber orientation distribution.
The mold-filling process is based on the volume of fluid method (VOF) covering the two-phase flow of fiber suspension and air. Details about this established method are not given here, but reference is made to the literature [42, 43]. Both phases are considered immiscible, isothermal, incompressible and without phase transition and body forces. The location of both phases is described by the scalar phase parameter \(\psi \) with the value \({\psi =1}\) indicating the fiber-laden melt and \({\psi =0}\) indicating the air phase. The following system of equations (5) is solved for \(\psi \), the effective velocity field \({\bar{{\varvec{v}}}}\) and \({{\bar{p}}}\)
with the additional force vector \({\varvec{f}}\) being present only in the fiber-laden melt or suspension (susp) for the flow–fiber coupled approach
Details about the implementation are given in Sect. 3. The surface tension of the fiber suspension is denoted by \(\sigma \) and the curvature \(\kappa \) is defined as follows [44]
Furthermore, the effective mass density \({\bar{\rho }}\) and the viscosity \(\mu \) are defined by the following adapted mixture rules representing phase-dependent fields
It should be noted that the fibers are considered within \({\bar{\rho }}\) but not within \(\mu \) and that \({\rho _{\textsf {susp}}=c_{\textsf {M}}\rho _{\textsf {M}}+c_{\textsf {F}}\rho _{\textsf {F}}}\) corresponds to Voigt’s average leading to the exact suspension’s density.
In Eq. (3) the matrix viscosity \({\mathbb {V}}_{\textsf {M}}\) is considered both Newtonian and non-Newtonian in the context of a generalized Newtonian fluid. Within the present study, the shear-thinning Cross-model [45] for the polymer matrix is implemented as follows to be compared against the Newtonian behavior [40, 46]
The Newtonian viscosity is denoted by \(\mu _0\) and m, n represent model parameters. It should be noted that the air phase is always modeled as a Newtonian fluid. In Eq. (9) the assumption of rigid fibers \({\langle {\varvec{D}}\rangle _{\textsf {F}}={\textbf{0}}}\) is used in order to express \(\dot{{\bar{\gamma }}}_{\textsf {M}}\) with respect to \({\bar{{\varvec{D}}}}\) and \(c_{\textsf {F}}\) using \({{\bar{{\varvec{D}}}}=(1-c_{\textsf {F}})\langle {\varvec{D}}\rangle _{\textsf {M}}}\). Since the flow–fiber coupling affects the constitutive behavior, \(\dot{{\bar{\gamma }}}_{\textsf {M}}\) is used instead of \(\dot{{\bar{\gamma }}}\) introduced in the context of the Folgar–Tucker equation (2). It should be noted that the fiber orientation evolution is considered only dependent on the macroscopic kinematic fields \({\bar{{\varvec{D}}}}\), \({\bar{{\varvec{W}}}}\) and \(\dot{{\bar{\gamma }}}\). As a consequence, the coupling effects on the fiber orientation evolution are only present based on changes in the flow field compared to the decoupled approach. This procedure ensures a comparable fiber orientation evolution in order to study the coupling effects purely due to viscous anisotropy.
2.2 Solid fiber reinforced composites
After fluid–solid transition, effective linear elastic behavior \({{\bar{{\varvec{\sigma }}}}=\bar{{\mathbb {C}}}[\bar{{\varvec{\varepsilon }}}]}\) is assumed for the solid fiber reinforced composite, with \({\bar{{\varvec{\varepsilon }}}}\) denoting the effective strain and \({\bar{{\mathbb {C}}}}\) representing the effective stiffness tensor. It is assumed that the geometry and fiber orientation do not change during the fluid–solid transition. For clarity, the basics regarding mean-field modeling are omitted here and the reader is referred to further literature, e.g., Nemat-Nasser and Hori [47] or Kanaun and Levin [48]. Based on the Mori–Tanaka model [26], the effective stiffness tensor reads \({{\bar{{\mathbb {C}}}}={\mathbb {C}}_{\textsf {M}}+{\bar{{\mathbb {R}}}}}\) with the abbreviation \({\bar{{\mathbb {R}}}}\) defined as follows [27, 40, 49]
It should be noted that only homogeneous and isotropic phases are considered. In Eq. (10), the abbreviation \(\delta {\mathbb {C}}\) refers to \({{\mathbb {C}}_{\textsf {F}}-{\mathbb {C}}_{\textsf {M}}}\) with the stiffness of the fiber material \({\mathbb {C}}_{\textsf {F}}\) and of the matrix material \({\mathbb {C}}_{\textsf {M}}\). The polarization tensor \({\mathbb {P}}_0\) can be computed analytically based on the expressions given in Ponte Castañeda and Willis [41]. Analogously, \(\langle \cdot \rangle _{\textsf {OA}}\) refers to the orientation averaging procedure given in Advani and Tucker [10].
The stationary balance of linear momentum without body force densities \({{\textbf{0}}=\textrm{div}({\bar{{\varvec{\sigma }}}})}\) is used as the governing equation for the effective displacement field \({\bar{{\varvec{u}}}}\)
The bulk modulus is represented by K and the shear modulus by G. Based on the right minor symmetry of \({\bar{{\mathbb {R}}}}\), the mapping \({\bar{{\mathbb {R}}}}[\textrm{grad}({\bar{{\varvec{u}}}})]\) inherently uses only the symmetric part of \(\textrm{grad}({\bar{{\varvec{u}}}})\) referring to \({\bar{{\varvec{\varepsilon }}}}\). The tensor \({\bar{{\mathbb {R}}}}\) contains the information about the local fiber orientation state based on orientation averaging. After solving Eq. (11) for \({\bar{{\varvec{u}}}}\), the effective strain is computed directly by the kinematic relation \({{\bar{{\varvec{\varepsilon }}}}=\mathrm {sym\,grad}({\bar{{\varvec{u}}}})}\) and the effective stress follows from \({{\bar{{\varvec{\sigma }}}}=\bar{{\mathbb {C}}}[\bar{{\varvec{\varepsilon }}}]}\).
2.3 Scale separation and requirements for homogenization
Fiber orientation tensors inherently represent the averaged orientation state, e.g., on every numerical grid cell in the context of coarse graining. Therefore, labeling \({\varvec{N}}\) and \({\mathbb {N}}\) as effective fields by \(\bar{(\cdot )}\) is omitted throughout this manuscript. All other fields are labeled as effective fields to emphasize that they are averages regarding the scale on which the orientation tensor description is valid. In this context, every grid cell used for numerical computation is seen as a statistically representative volume across which the described mean-field homogenization is performed. The spatial distribution of the fibers is assumed to be statistically homogeneous and the ergodic hypothesis is applied. In addition, the considered microstructure does not contain cracks or voids, the Hill-Mandel condition [50, 51] is assumed to be valid and phase-wise constant properties are used. Further information can be found in the literature, e.g., in Nemat-Nasser and Hori [47] or in Torquato [52]. Regarding the uniform mean-field homogenization of viscous fiber suspensions and solid short-fiber reinforced composites, reference is made to the recent work of Karl and Böhlke [40].
3 Numerical procedure
3.1 Mold-filling simulation using OpenFOAM®
Geometry considered for both the mold-filling simulation and for the solid composite simulation with the definition of the area of interest being the basis for the results in Sect. 4
For both fluid and solid simulations the 2D rib geometry shown in Fig. 1 is used. This generic geometry is inspired by the bifurcation flow of Haagh and van de Vosse [53] and represents a classic thin-walled component. The length h is \(2.5\cdot 10^{-3}\,~{\textrm{m}}\). The geometry is chosen such that the two ribs experience different flow states towards the end of the mold-filling process, which is discussed in detail in Sect. 4.1. It is shown that the two-phase simulation considering the actual mold-filling is necessary in order to predict the fiber orientation state correctly.
The implemented VOF solver is based on the interIsoFoam solver of OpenFOAM® (version 2106) for the isothermal mold-filling of two immiscible and incompressible fluids with Newtonian or non-Newtonian viscosity [54]. The solver in use differs from the interFoam solver by using the isoAdvector scheme improving the advection towards a sharp interface [55,56,57,58]. Within the fluid solver, volume forces due to gravity are neglected in the balance of linear momentum analogous to the solid solver. The implemented methods of stabilizing the mold-filling simulations are addressed in Sect. 3.4. Regarding the temporal discretization, the second-order implicit backward scheme is used with the time step  determined by the maximum Courant number \({\textrm{max}(\textrm{Co})=0.02}\). This value corresponds to the order of magnitude of the value of 0.05 proposed by Larsen et al. [58] for the related interFoam solver. To ensure sufficient accuracy,
determined by the maximum Courant number \({\textrm{max}(\textrm{Co})=0.02}\). This value corresponds to the order of magnitude of the value of 0.05 proposed by Larsen et al. [58] for the related interFoam solver. To ensure sufficient accuracy,  is limited by the maximum value of \(10^{-3}\,~{\textrm{s}}\). All simulations are stopped at the filling level of \(99.999\%\). In addition, only second-order spatial discretization schemes are used. For solving the systems of equations the multigrid solver GAMG is chosen with GaussSeidel as the smoothing method. In addition, \({{\bar{p}}}\) and \({\bar{{\varvec{v}}}}\) are computed based on the PISO algorithm with 10 correction steps and no momentum predictor step. As a result of a grid study 80 orthogonal and uniformly distributed cells per h are set to resolve the fields with sufficient accuracy.
is limited by the maximum value of \(10^{-3}\,~{\textrm{s}}\). All simulations are stopped at the filling level of \(99.999\%\). In addition, only second-order spatial discretization schemes are used. For solving the systems of equations the multigrid solver GAMG is chosen with GaussSeidel as the smoothing method. In addition, \({{\bar{p}}}\) and \({\bar{{\varvec{v}}}}\) are computed based on the PISO algorithm with 10 correction steps and no momentum predictor step. As a result of a grid study 80 orthogonal and uniformly distributed cells per h are set to resolve the fields with sufficient accuracy.
Throughout this study, polypropylene (PP) is considered as the thermoplastic polymer matrix with the melt density \({\rho _{\textsf {M}}=728\,~{\mathrm{kg/m^3}}}\) (\(\approx 0.8\) solid density [59] of \(910\,~{\mathrm{kg/m^3}}\) [60]). The Newtonian kinematic viscosity is set to \({\nu _{\textsf {M}}=0.779\,~{\mathrm{m^2/s}}}\) which corresponds to \(\nu _0\) in the shear-thinning Cross model given in Eq. (9) with the parameter values \({n=0.749}\) and \({m=17.366\cdot 10^{-3}}\) [61]. Please note that the kinematic viscosity \(\nu \) and the density \(\rho \) are used as input in OpenFOAM® instead of the dynamic viscosity \({\mu =\nu \rho }\). The surface tension is set to \({\sigma =0.028\,~{\mathrm{N/m}}}\) [62]. For the air phase the default parameters \({\nu _{\textsf {air}}=1.48\cdot 10^{-5}\,~{\mathrm{m^2/s}}}\) and \({\rho _{\textsf {air}}=1\,~{\mathrm{kg/m^3}}}\) are used. In this study glass fibers are considered with the density \({\rho _{\textsf {F}}=2540\,~{\mathrm{kg/m^3}}}\) [60]. By defining \(h,{\bar{v}}_{\textsf {b}},\nu _{\textsf {M}},\rho _{\textsf {M}},\sigma \) as the characteristic quantities, the Reynolds number (\(\textrm{Re}\)) and the capillary number (\(\textrm{Ca}\)) describing the problem have the following values
Based on the value of \(\textrm{Re}\), the mold-filling process approximately corresponds to creeping flow conditions and \(\textrm{Ca}\) shows that viscous forces are larger than surface tension forces. The aspect ratio of the short glass fibers equals \({\alpha =20}\) with \({C_{\textsf {I}}=0.01}\) as the fiber-fiber interaction parameter affecting the orientation tensor evolution given in Eq. (2). The fibers are considered with a volume fraction \({c_{\textsf {F}}=0.2}\) which corresponds to \(41.1\,~{\mathrm{wt-\%}}\) based on the solid densities. Analogous to Karl et al. [24], the thermodynamic consistency is checked during mold-filling based on the isothermal dissipation inequality \({{\bar{{\varvec{D}}}}\cdot \bar{{\mathbb {V}}}[{\bar{{\varvec{D}}}}]\ge 0}\).
The initial and boundary conditions for every field are summarized in Table 1 with the boundaries wall, inlet and outlet sketched in Fig. 1. The zeroGradient condition refers to a vanishing gradient normal to the respective boundary. The zeroGradient condition for \(\psi \) corresponds to a contact angle of 90\(^{\circ }\) at the wall. The boundary condition fixedFluxPressure adjusts the pressure gradient in order to get a flux on the boundary which is consistent with the velocity boundary condition [54]. At the inlet a parabolic velocity profile is set with the bulk velocity \({{\bar{v}}_{\textsf {b}}=0.1\,~{\mathrm{m/s}}}\) [53]. By choosing the standard interIsoFoam solver, pinning of the contact line is observed. However, experiments in comparable settings show that form-filling flows are achieved with the selected process data described above [63, 64]. The observed contact line pinning is most likely related to the large capillary number given in Eq. (12). Under large \(\textrm{Ca}\) number conditions it is known that a large deformation of the free surface area can occur before the occurrence of a moving contact line. As a result, the advancing contact angle, which is related to \(\textrm{Ca}\) through the Cox–Voinov law [65, 66], basically decouples from the static contact angle [67]. This physical process cannot be captured by the employed VOF formulation in which only the static contact angle is prescribed. In order to enable the corresponding simulations at high \(\textrm{Ca}\) with a moving contact line in the standard interIsoFoam solver a novel boundary condition, referred to as localAirVent, is implemented. The localAirVent boundary condition—which is inspired by a freely escaping air phase in previous mold flow simulations [68,69,70]—enables an outflow of air in an area around the contact point. The boundary condition airVentBC allows the air phase to leave the domain across the outlet until the boundary cells are almost filled with polymer. Then, the condition switches linearly from zeroGradient to the standard no-slip condition and prevents the suspension from flowing out. Both localAirVent and airVentBC are based on the following equation with the implemented blending function \(g(\psi )\) and the outward pointing unit normal vector \({\varvec{n}}\) at each boundary
The mixedPressureOut boundary condition used by, e.g., Ospald [70] refers to a constant reference pressure if the boundary cells are completely filled with air. If the boundary cells are completely filled with suspension, then the zeroGradient condition is applied. In between, a mixed boundary condition is applied until the cells are completely filled with suspension following the condition
with the reference pressure chosen as \({p_{\textsf {ref}}=0}\). All other boundary conditions listed in Table 1 are self-explaining and OpenFOAM® standard. The 2D flow is achieved by assigning the empty boundary condition to the front and back faces.
3.2 Solid composite simulation using Abaqus®
Regarding the solid composite simulations, the Young’s modulus of \(1.6\,~{\textrm{GPa}}\) is used for PP and \(73\,~{\textrm{GPa}}\) for the glass fibers [60]. The Poisson’s ratio of PP equals 0.4 and 0.22 for the glass fibers [60]. With these parameter values, the equations (10) and (11) are uniquely determined. The inlet is clamped with suppressed displacement and rotation. The displacement \({{\bar{u}}_1}=1.5\cdot 10^{-4}\,~{\textrm{m}}\) is applied at the two outlets of the ribs, which results in a bending of the whole structure. All details about the boundaries are illustrated in Fig. 1. It should be noted that the fluid–solid transition during and after the mold-filling process is assumed to occur instantly without modification of the fiber orientation.
The solid composite simulations throughout this study are mainly carried out with the commercial finite element software Abaqus® CAE Standard/Explicit (version 2020). The anisotropic stiffness corresponds to the algorithmic tangent within a user-material (UMAT) subroutine implemented in Fortran 90. The fiber orientation data corresponds to a predefined field as an additional input of the UMAT. Based on the 2D load case, the 4-node bi-linear plane strain element CPE4 is used for meshing the geometry shown in Fig. 1. As a result of a grid study 80 orthogonal and uniformly distributed cells per h are used to resolve the stress field sufficiently. Moreover, the mapping of the orientation data from the fluid to the solid mesh is done based on the nearest-neighbor procedure used by Gajek et al. [71] extended by the trace-preserving correction scheme of Kuzmin [72]. It should be noted that the orientation data is mapped from the cell centers of the openFOAM® mesh to the nodes of the Abaqus® mesh. Since the UMAT is used at the element integration points, the nodal orientation values are interpolated by Abaqus®. It is observed that elements with quadratic trial functions lead to negative eigenvalues of the system matrix. Therefore, using elements with linear trial functions is suggested.
3.3 Solid composite simulation using OpenFOAM®
As a basis of the present study the solids4foam toolbox [73,74,75] for OpenFOAM® is used. For further information regarding the finite volume method in solid mechanics the reader is referred to Cardiff and Demirdz̆ić [76] and the references therein. The Mori–Tanaka model given in Eq. (10) is implemented as a new solid model in the solids4foam toolbox. On the one hand, both fluid and solid simulations are possible in a uniform open-source environment and on the other hand, a comparison with finite element solvers can be made in view of anisotropic fiber-reinforced composites.
The material parameters are given in the section above. At the inlet, the fixedDisplacement boundary condition is used realizing the clamping. For the two ribs, the solidDirectionMixed boundary condition is used with \({{\bar{u}}_1=1.5\cdot 10^{-4}\,~{\textrm{m}}}\) as the horizontal displacement and free vertical displacement \({\bar{u}}_2\). For all other boundaries the solidTraction condition is set as zeroGradient. The plane strain state is achieved by assigning the empty boundary condition to the front and back faces of the geometry. For solving the system of equations the multigrid solver GAMG is chosen with diagonal-based incomplete Cholesky preconditioner as the smoothing method. All chosen spatial discretization schemes are of second order and 80 orthogonal and uniformly distributed cells per h are used based on a grid study. Please note that in this study the same mesh is found to be sufficiently accurate for the mold-filling simulations, the finite element and for the finite volume simulations. In order to correct possible interpolation errors, which may occur during the transition between the fluid and the solid mesh, the trace-preserving correction scheme of Kuzmin [72] is implemented analogously to the finite element procedure described above. In contrast to the finite element implementation, methods for stabilization must be actively implemented in this context, which is described in Sect. 3.5.
3.4 Fluid solver stabilization methods
In the following subsections methods of stabilizing the two-phase fluid solver for computing the flow–fiber coupled mold-filling process are addressed in detail. The discussion of the methods is adapted to the use of OpenFOAM® and is intended to support engineering practice implementing flow–fiber coupled computations. All of the shown methods are implemented to enable parallel computations.
3.4.1 Implicit-explicit splitting of the coupling term
In order to improve the stability, as many terms of \({\varvec{f}}\) given in Eq. (6) as possible should be discretized implicitly regarding the primary field \({\bar{{\varvec{v}}}}\). It turns out to be numerically unfavorable that gradients can only be discretized explicitly in OpenFOAM® and that the coupling term is dominated by velocity gradients [70]. The coupling term \({\varvec{f}}\) given in Eq. (6) can be rewritten as follows
Only one part of the second term on the right-hand side of Eq. (15) can be discretized implicitly by using the product rule and the incompressibility condition leading to
By using Eq. (16) and Eq. (15), the implemented splitting of \({\varvec{f}}\) reads
The implicit-explicit splitting of all other terms in the system of governing equations (5) for computing \(\psi ,{{\bar{p}}}\) and \({\bar{{\varvec{v}}}}\) is not changed and corresponds to the implementation of the basic solver interIsoFoam described in Sect. 3.1.
3.4.2 Treatment of the viscous stress
As already discussed by Karl et al. [24] the fiber-related part of the viscous stress
is not traceless in the case of anisotropic fiber orientation, even for traceless \({\bar{{\varvec{D}}}}\). As a consequence, additional contributions to the spherical stress \(-p{\varvec{I}}\) are present, which can be spatially strongly inhomogeneous with negative effects on the pressure solver convergence. Since the pressure acts as a Lagrangian multiplier for satisfying the incompressibility constraint, one can use, without loss of generality, the following expression for the fiber-related viscous stress
Since the mass balance \({\textrm{div}({\bar{{\varvec{v}}}})=0}\) is fulfilled in terms of fluxes over the cell faces, the cell-centered \({\bar{{\varvec{D}}}}\) is not necessarily traceless due to interpolation errors. Simulation results show that this error might be large close to the interface with the error decreasing to tolerable values as the distance from the interface increases. In order to ensure, that only traceless \({\bar{{\varvec{D}}}}\) is used within the viscous stress tensor, the following final expression is implemented [39]
3.4.3 Spatial restriction of the coupling term
In the following, the spatial restriction of \({\varvec{f}}\) given in Eq. (6) is described in detail. As discussed in the literature, e.g., [53, 77,78,79], the three-phase contact point (TPCP) shown in Fig. 2 is critical in view of stress singularities. Furthermore, the large material contrast of the air and melt phases combined with the coupling in the area of the phase front has an unfavorable effect. In order to obtain convergence, the coupling is switched on successively with increasing distance from the phase front. Therefore, anisotropic viscosity effects directly at the phase front cannot be taken into account with this procedure. But this is not critical since the analyzed orientation tensor further downstream is not significantly influenced by this gradual introduction of the flow–fiber coupling behind the phase front.
In order to circumvent interface-induced coupling instabilities, the following procedure is implemented with all areas shown in Fig. 2. The area \(V_{\textsf {susp}}\) occupied by the fiber suspension is divided into three sub-areas. In the area \(V_{\textsf {decoupled}}\) close to the interface, no flow–fiber coupling is present avoiding large explicit coupling terms. Next, in the transition zone \(V_{\textsf {trans}}\) the coupling strength is increased linearly with increasing distance from the interface. The full flow–fiber coupling is present in \(V_{\textsf {coupled}}\). As an input, \(d_{\textsf {min}}\) is set as the minimum distance between the phase front (interface) and the beginning of flow–fiber coupling. In addition, \(d_{\textsf {trans}}\) is set as an input representing the width of the transition area. In every time step, the positions of the interface grid cells \({\varvec{x}}_{\textsf {interface}}\) are detected by \({\Vert \textrm{grad}(\psi ) \Vert >5000\,~{\mathrm{m^{-1}}}}\), which turns out to be sufficiently large for the used mesh. Then, for every point \({{\varvec{x}}\in V_{\textsf {susp}}}\) the spatially restricted (sr) coupling term \({\varvec{f}}_{\textsf {sr}}\) is clearly determined as follows based on \({d=\Vert {\varvec{x}}-{\varvec{x}}_{\textsf {interface}} \Vert }\)
It should be noted that Eq. (21) refers to both the implicit and the explicit part of the coupling term. Within this study the distances are set to \({d_{\textsf {min}}=d_{\textsf {trans}}=h/10}\).
3.4.4 Under-relaxation of the explicit coupling term
Under-relaxation is a common method in computational fluid dynamics improving numerical convergence [80]. Throughout this study the explicit part of the coupling term is under-relaxed (ur) as follows
with the relaxation factor \({0<r<1}\), the coupling term of the previous time step \({\varvec{f}}_{\textsf {expl}}^{n}\) and \({\varvec{f}}_{\textsf {expl}}^{n+1}\) referring to the explicit coupling term depending on the updated fiber orientation tensor and flow kinematics. As a result of under-relaxation, the explicit coupling term is not used entirely updated in the linear-momentum balance. As described in the literature [80], the relaxation parameter r depends on the flow problem and, therefore, cannot be chosen a priori. Within this study it is observed that strong under-relaxation is necessary for strong flow–fiber coupling (\({c_{\textsf {F}}>0.1}\), \({\alpha >10}\)), even for kinematically simple channel flows. Throughout this study, \({r=0.05}\) is fixed for the simulation setup. There are no negative effects on the convergence due to this small value of r since both the fiber orientation and the flow field quickly reach stationary values. The simulations results show that the difference \({{\varvec{f}}_{\textsf {expl}}^{n+1}-{\varvec{f}}_{\textsf {expl}}^{n}}\) is only present around the transition region (see Sect. 3.4.3), in which the coupling is not considered fully present anyway.
3.4.5 Stabilizing the Folgar–Tucker equation
As discussed by Paschkewitz et al. [81], an explicit solution procedure of Eq. (2) may lead to instabilities, which are manifested by a loss of positive semi-definiteness and by invalid values of the orientation components. Therefore, as many terms as possible are discretized implicitly regarding \({\varvec{N}}\), as shown in Appendix A in order to make the manuscript self-contained. Throughout this study, no numerical issues in view of solving the Folgar–Tucker equation occur by applying the procedure addressed in Appendix A. Nevertheless, further possibilities for stabilizing and correcting the Folgar–Tucker equation are summarized below, which are useful for the reader in case of numerical issues.
Since the Folgar–Tucker equation represents a purely convective equation, an artificial diffusion term \({{\varvec{R}}_{\textsf {art}}= \beta \Delta {\varvec{N}}}\) can be used to stabilize the solution procedure with \(\beta \) representing the artificial diffusion. Mezi et al. [5] used this stabilization method within the Fokker-Planck equation for the probability density function f. Alternatively, artificial diffusion can be restricted to regions where \({\varvec{N}}\) loses its positive semi-definiteness [81, 82]
The parameter \(\beta \) can be modeled depending on the local grid spacing and a proper value depending on the flow problem [81, 82]. It should be noted that unsuitable values of \(\beta \) lead to numerical issues and, therefore, a parameter study is suggested [82]. The trace condition \({\textrm{tr}({\varvec{N}})=1}\) is not violated by adding artificial diffusion terms to the Folgar–Tucker equation. This can be easily shown by expanding the evolution equation for \({s{:}{=} \textrm{tr}({\varvec{N}})}\) given in Linn [83] by the artificial diffusion term as follows
Please note that the derivation of Eq. (24) requires \({{\mathbb {N}}[{\varvec{I}}]={\varvec{N}}}\) to be fulfilled by the closure in use. Since always physical initial conditions for the orientation state are used with \({s=1}\), the right-hand side of Eq. (24) vanishes. As a consequence, \({s=1}\) is preserved.
In addition to stabilizing the Folgar–Tucker equation, non-physical orientation tensor results can be corrected. The correction schemes refer to eigenvalues or diagonal components of \({\varvec{N}}\) violating the physical interval [0, 1]. Verweyst and Tucker [84] developed a procedure to correct the eigenvalues of \({\varvec{N}}\) after solving the Folgar–Tucker equation and before the orientation state is used for flow–fiber coupling. For a trace-preserving correction based on setting non-physical negative eigenvalues to zero, the reader is referred to Kuzmin [72] and the references therein for further correction schemes.
3.4.6 Remarks on the mesh and time discretization
Within this study, it is observed that homogeneous and orthogonal mesh cells are the most suitable for the two-phase mold-filling simulations in view of computation time. This is due to the fact that non-orthogonal cells require a smaller time step to obtain the same Courant number for similar mesh fineness. Furthermore, with respect to the coupling term, coarse grids lead to stable solution behavior for spatially strongly inhomogeneous fields. This is due to the fact that gradients are smoothed in this way and numerically unfavorable local peaks in the coupling term are thus prevented. Despite the stability, coarse meshes are not recommended for improving stability due to spatial inaccuracy.
As already described in Sect. 3.1 the second-order implicit backward scheme is used for time discretization. Although this is an unbounded scheme [54, 85], no instabilities in the context of time discretization are observed in this study. In case of stability issues, the bounded implicit Euler scheme [54] may be applied to stabilize the time integration. For progressive waves the numerical damping of the Euler scheme is addressed by Larsen et al. [58]. It should be noted that this first-order accurate method may only be applied if sufficient temporal resolution is ensured or if the integration leads to a steady state solution.
3.5 Solid solver stabilization methods
In order to make the manuscript self-contained, the standard implementation of Eq. (11) in solids4foam is explained below, which is extended by the Mori–Tanaka model for the simulation of anisotropic fiber-reinforced composites. In its most compact form, the linear momentum balance reads
In order to improve convergence, Laplacian terms are added to Eq. (25) as follows with both implicit and explicit treatment [74, 75]

As described by Shayegh [75], the first two terms do not influence the converged solution. The prefactor \({k=4G_{\textsf {F}}/3+K_{\textsf {F}}}\) is used [74, 86, 87] with the elastic properties of the fiber phase. During the study it is observed that a smaller chosen k, for example calculated with the elastic constants of the matrix, may have a negative effect on the convergence. In order to damp non-physical oscillations, the Rhie–Chow stabilization method [74, 76, 87,88,89] already implemented in solids4foam is applied. As a consequence, the linear momentum balance reads with the explicitly treated Rhie–Chow stabilization term [75, 76]

with a representing a scaling factor. A parameter study shows that the solids4foam default value \({a=0.1}\) is sufficient to damp the occurring numerical oscillations to an acceptable magnitude. It should be noted that both \(\Delta {\bar{{\varvec{u}}}}\) and \(\mathrm {div\,grad}({\bar{{\varvec{u}}}})\) represent Laplacians, but \(\mathrm {div\,grad}({\bar{{\varvec{u}}}})\) is used to express a different discretization compared to \(\Delta {\bar{{\varvec{u}}}}\).
In addition, the Laplacian term \(G_{\textsf {M}}\Delta {\bar{{\varvec{u}}}}\) being part of \(\textrm{div}({\bar{{\mathbb {C}}}}[\textrm{grad}({\bar{{\varvec{u}}}})])\) as given in Eq. (11) can be treated implicitly to further stabilize Eq. (27). Based on a comparison of a purely explicit treatment, no advantage is observed in terms of stability and computational time. Therefore, the explicit discretization of \(\textrm{div}({\bar{{\mathbb {C}}}}[\textrm{grad}({\bar{{\varvec{u}}}})])\) shown in Eq. (27) is implemented.
Temporal evolution of orientation tensor components \(N_{11},N_{22},N_{33}\) and phase parameter \(\psi \) at the beginning of the left rib in a and of the right rib in b (non-Newtonian coupled, points marked in top right plot of Fig. 3)
4 Results and discussion
4.1 Coupling effects on the fiber orientation
In Fig. 3 the fiber orientation field \({\varvec{N}}\) is shown in the area of interest defined in Fig. 1. For simplicity, only the results regarding the non-Newtonian case are shown with the decoupled approach in the left column and the coupled approach in the right column, respectively. The plots in Fig. 3 serve to clarify the orientation state as a basis for the solid composite simulations of Sect. 4.2, which are based on the fiber-induced anisotropic stiffness. This is important because the coupling effects will be analyzed in form of difference fields. By comparing both columns in Fig. 3 against each other one can see that the coupling effects (see Sect. 1.1) are reproduced, e.g., the distinct isotropic orientation in the horizontal channel center region caused by the flattening of the velocity profile. In the considered 2D flow, mainly \(N_{11}\) and \(N_{22}\) are influenced by the kinematics, whereas \(N_{33}\) evolves due to trace preservation. The component \(N_{12}\) provides information about the eigensystem of \({\varvec{N}}\) with \({N_{12}=0}\) referring to an eigensystem coinciding with the spatial axes. Regarding the 2D flow consideration, \({N_{13}=N_{23}=0}\) holds. The area of interest shown in Fig. 3 can be divided into two main parts, the lower horizontal area and the vertical ribs. Both parts can be simplified as a simple channel flow, in which the fibers align in the main shear direction. For the horizontal part, this direction is \({\varvec{e}}_1\) represented by large values of \(N_{11}\). For the vertical ribs, this direction is \({\varvec{e}}_2\) leading to large values of \(N_{22}\).
By comparing the final fiber orientation states below and inside both ribs at the filling level of \(99.999\%\), the influence of the different filling behavior is clearly visible: The left rib is completely filled first, while the right rib and the horizontal channel are not completely filled at this particular time step. Once the left rib is filled, no fiber orientation evolution is present inside and the kinematics in the area below change into a shear-dominated one leading to an alignment in \({\varvec{e}}_1\)-direction. This horizontal shear is not present in the area below the right rib since the horizontal channel is filled before the right rib. Therefore, \(N_{22}\) is the favored fiber orientation below the right rib caused by vertical shear and a deflection of the flow. In the following, the filling behavior of the two ribs is investigated further in a comparative manner.
In the top-right plot of Fig. 3 two points are marked for which the temporal fiber orientation evolution is investigated. For the point in the left rib, the diagonal components of \({\varvec{N}}\) are plotted over time in Fig. 4a and for the right rib in Fig. 4b, respectively. The analysis is restricted to the coupled non-Newtonian approach. Starting from the isotropic initial state marked with  the fiber orientation begins to evolve once the phase front (represented by \(\psi \)) passed the two considered points. In time interval
the fiber orientation begins to evolve once the phase front (represented by \(\psi \)) passed the two considered points. In time interval  shortly behind the phase front, a transient orientation state is shown for both points. Subsequently, the orientation evolves towards an asymptotic state at
shortly behind the phase front, a transient orientation state is shown for both points. Subsequently, the orientation evolves towards an asymptotic state at  , which describes the mold-filling process of both ribs and the horizontal channel without any part of the cavity being completely filled. It should be noted that the asymptotic state only depends on the given kinematics, the aspect ratio of the fibers and the fiber-fiber interaction strength [31]. Since the kinematics are different at the two points during time interval
, which describes the mold-filling process of both ribs and the horizontal channel without any part of the cavity being completely filled. It should be noted that the asymptotic state only depends on the given kinematics, the aspect ratio of the fibers and the fiber-fiber interaction strength [31]. Since the kinematics are different at the two points during time interval  , also the orientation state differs. Note that the orientation state observed during time interval
, also the orientation state differs. Note that the orientation state observed during time interval  corresponds to the state that would occur if the flow through the cavity at the two points were stationary, or in other words, if no two-phase simulation of the actual mold-filling process is carried out. At approximately \({t=0.58\,~{\textrm{s}}}\) the left rib is completely filled with suspension and, as already described above, the kinematics change into a shear-dominated one in the area around the considered point. This also affects the orientation evolution in the right rib at this time step since the flow is accelerating in the horizontal channel. Already a short time later at approximately \({t=0.62\,~{\textrm{s}}}\) the horizontal channel is also completely filled leading to a complete deflection of the flow into the right rib. Until the cavity is completely filled at \({t=0.69\,~{\textrm{s}}}\), this change in kinematics leads to a new orientation state at
corresponds to the state that would occur if the flow through the cavity at the two points were stationary, or in other words, if no two-phase simulation of the actual mold-filling process is carried out. At approximately \({t=0.58\,~{\textrm{s}}}\) the left rib is completely filled with suspension and, as already described above, the kinematics change into a shear-dominated one in the area around the considered point. This also affects the orientation evolution in the right rib at this time step since the flow is accelerating in the horizontal channel. Already a short time later at approximately \({t=0.62\,~{\textrm{s}}}\) the horizontal channel is also completely filled leading to a complete deflection of the flow into the right rib. Until the cavity is completely filled at \({t=0.69\,~{\textrm{s}}}\), this change in kinematics leads to a new orientation state at  defining the anisotropy of the manufactured part after fluid–solid transition. Since level
defining the anisotropy of the manufactured part after fluid–solid transition. Since level  is clearly different from
is clearly different from  , the necessity of simulating the actual mold-filling becomes apparent. A simulation based purely on the steady-state flow through the geometry cannot represent this change in kinematics due to the filling process and predicts the fiber orientation differently. Therefore, the filling of individual areas of the cavity must necessarily be taken into account in order to correctly predict the evolution of the fiber orientation and the associated anisotropy.
, the necessity of simulating the actual mold-filling becomes apparent. A simulation based purely on the steady-state flow through the geometry cannot represent this change in kinematics due to the filling process and predicts the fiber orientation differently. Therefore, the filling of individual areas of the cavity must necessarily be taken into account in order to correctly predict the evolution of the fiber orientation and the associated anisotropy.
In order to further quantify the mentioned differences between  and
and  in view of fiber orientation, the local anisotropic viscosity is investigated in the coupled approach. For this purpose, the following two measures \(e_{\textsf {V}}\) and \(e_{\textsf {V,aniso}}\) are defined, which quantify the difference between
in view of fiber orientation, the local anisotropic viscosity is investigated in the coupled approach. For this purpose, the following two measures \(e_{\textsf {V}}\) and \(e_{\textsf {V,aniso}}\) are defined, which quantify the difference between  (left rib fills quasi-stationary at \({t=0.5\,~{\textrm{s}}}\)) and
(left rib fills quasi-stationary at \({t=0.5\,~{\textrm{s}}}\)) and  (shear-dominated flow below left rib at \({t=0.69\,~{\textrm{s}}}\))
(shear-dominated flow below left rib at \({t=0.69\,~{\textrm{s}}}\))
The total viscosity difference is represented by \(e_{\textsf {V}}\), whereas \(e_{\textsf {V,aniso}}\) addresses the change of anisotropy, both as a scalar measure for simplicity. The anisotropic part of \({\bar{{\mathbb {V}}}}\) is defined as follows
with \({\mathbb {P}}_1\) representing the identity on spherical second-order tensors. In Fig. 5 the viscosity measures defined in Eq. (28) are shown for the left rib. The results indicate that the difference in orientation between  and
and  significantly affects the local effective viscosity and also significantly changes the degree of anisotropy.
significantly affects the local effective viscosity and also significantly changes the degree of anisotropy.
In the following, the analysis is restricted to the comparisons shown in Fig. 6 with the fiber orientation differences defined by Karl et al. [24]. In Fig. 6, vertical differences address the effects of flow–fiber coupling for both viscosity models, whereas horizontal differences account for the effect of the viscosity models for both decoupled and flow–fiber coupled approach. For all four cases, the range of values is given with respect to the area of interest.
Based on Fig. 15 in Appendix B.1, where additional fiber orientation results are provided, the local orientation differences with respect to different viscosity models in the coupled approach range from \(-\,40\) to \(41\%\), regarding the possible interval [0, 1] of \(N_{11},N_{22}\) and \(N_{33}\). In addition, Fig. 14 in Appendix B.1 shows the effect of the viscosity model for the decoupled approach with local orientation differences \(-\,27\) to \(30\%\). Therefore, one can state that for both the decoupled and the coupled approach, the viscosity model has a great influence on the local fiber orientation state. Furthermore, the relevance of the viscosity model changes with the flow–fiber coupling, as the range of values increases compared to the decoupled case. Please note that the latter statement only holds for flow cases in which the shear rate is sufficiently large to cause significant shear-thinning in the matrix fluid. This is given under the selected process conditions and is addressed in Appendix B.1 in the context of Fig. 16.
For the sake of clarity, only the difference fields regarding the pure effects of flow–fiber coupling for each viscosity model are provided in the present section. In Fig. 7 the local orientation difference between the decoupled and the coupled approach is shown for the Newtonian case. The same difference is given in Fig. 8 for the non-Newtonian matrix fluid. Areas highlighted in red indicate an alignment which is larger in the coupled case and blue areas indicate a stronger alignment in the decoupled case. By comparing Figs. 7 and 8 one can see that the difference fields show similar characteristics for both considered matrix viscosity models. Regarding the possible interval [0, 1] of \(N_{11},N_{22}\) and \(N_{33}\), the local effect of flow–fiber coupling ranges from \(-\,36\) to \(31\%\) for the Newtonian and from \(-\,37\) to \(38\%\) for the non-Newtonian case and, therefore, can be evaluated as significant. It can be seen that the flow–fiber coupling has approximately the same effect for both viscosity models. In the non-Newtonian case, the differences are slightly more distinct. However, this does not mean that the fiber orientation in the coupled case is almost identical for both viscosity models. In the coupled case, for example, the choice of viscosity model has a larger influence on the local fiber orientation than the flow–fiber coupling. This can be seen in Fig. 6 in view of the given ranges of values. Therefore, not only the coupling is crucial for the local evolution of the fiber orientation, but also the consideration of the shear-thinning behavior.
4.2 Coupling effects on the stress field
The fiber orientation states investigated above are now used within finite element simulations for solid composites. Independent of the fluid model during mold-filling, the solid composite is modeled linear elastic with its anisotropy completely defined by \({\varvec{N}}\) and \({\mathbb {N}}\). Thus, this study docks directly to the results of Karl et al. [24], which analyze the coupling effects on the local elastic anisotropy, but not on the stress field in the solid composite under load. Analogous to the previous section, Fig. 9 addresses the four investigated cases and the corresponding comparisons. In the following, the non-dimensional stress difference field  is considered with the respective definitions given in Fig. 9. Note that these definitions must be applied for each stress component \({ij=11,12,\ldots }\) individually. Again, horizontal differences address the influence of the viscosity model during mold filling for both decoupled and coupled approach, whereas vertical differences consider the effect of coupling for both viscosity models.
is considered with the respective definitions given in Fig. 9. Note that these definitions must be applied for each stress component \({ij=11,12,\ldots }\) individually. Again, horizontal differences address the influence of the viscosity model during mold filling for both decoupled and coupled approach, whereas vertical differences consider the effect of coupling for both viscosity models.
As a supplement, Fig. 17 in Appendix B.2 shows the stress field both for the decoupled and the coupled approach regarding the non-Newtonian case during mold filling. The corresponding stress difference field is given in Fig. 11 with the range of values from \(-\,10.59\) to \(14.92\%\). Analogous to the previous section, only the non-dimensional stress difference fields regarding the pure effects of flow–fiber coupling for each viscosity model are considered in the section at hand. For the Newtonian viscosity Fig. 10 addresses these coupling effects with the range \(-\,12\) to \(12.9\%\). All components not shown are zero due to the plane strain state and \({N_{13}=N_{23}=0}\). Both ranges indicate, that the coupling effect on the fiber orientation evolution during mold-filling has a significant influence on the local stress of the solid composite under loading after fluid–solid transition. Please note that normalization is done with each maximum stress component, which emphasizes the importance of the coupling in the context of the specified ranges. If stress peaks occur locally due to the geometry, even small differences in fiber orientation caused by flow–fiber coupling during mold-filling can lead to large differences in the stress field. This is the case in the area of the left rib, in combination with large differences in fiber orientation. There, kinematically complex flow conditions are additionally present, which lead to large differences in the fiber orientation, since viscous anisotropy effects are fully present. Even a small load without stress peaks can lead to significant differences in local stress in such areas, as is the case, e.g., in the area under the right rib. In summary, also against the background of the stress distribution, both the necessity of coupling and the consideration of shear-thinning matrix behavior are confirmed.
The difference fields regarding the influence of the viscosity model can be found in Appendix B.2. For the decoupled case the range of the local stress difference is \(-\,6.04\) to \(4.61\%\) as shown in Fig. 18 and for the coupled case \(-\,4.74\) to \(6.51\%\) as shown in Fig. 19. As a consequence, one can state that different viscosity models during mold-filling affect the local stress significantly both for the decoupled and the coupled approach. Compared to the previous section, the relevance of the viscosity model does not change remarkably with the flow–fiber coupling, as the range of values is comparable to the decoupled case. However, the difference between the stress fields based on the different viscosity models is not negligible. More details can be found in Appendix B.2.
Effective stress field \({\bar{{\varvec{\sigma }}}}\) along paths through the area of interest with respect to the coupled non-Newtonian case for both finite volume and finite element simulations (top: along \({x_2=h/2}\), bottom: along \({x_1=5h}\), paths marked in Fig. 12)
4.3 Abaqus® vs. OpenFOAM® for solid composite simulation
In this section the stress predictions based on the extended finite volume solver OpenFOAM® (FVM in the following) are presented. Furthermore, a comparison is made with the results based on finite element simulations with Abaqus® (FEM in the following). The analysis is limited to the coupled approach for non-Newtonian matrix viscosity since both flow–fiber coupling and shear-thinning behavior significantly affect the orientation and the stress field. In Fig. 12 the components of the effective stress tensor are shown for both FVM (left column) and FEM (right column). The results show that both fields look similar with variable differences in the peak values. In general, the component values show comparable magnitudes with the largest differences between FVM and FEM for \(\bar{\sigma }_{12}\) and \(\bar{\sigma }_{33}\). The largest differences of the respective stress components are present at the corners of the geometry where the peak values occur. Numerical differences are amplified there and especially the stability terms of the FVM described in Sect. 3.5 are effective there, since spatially large and strongly inhomogeneous gradients are present. To investigate the differences between FVM and FEM in more detail, Fig. 13 shows the components of the effective stress tensor along two paths. The two paths are shown in the upper left plot in Fig. 12 representing a cut through the horizontal channel at \({x_2=h/2}\) and through the left rib at \({x_1=5h}\), respectively. In the considered area of interest, the results of FVM and FEM show an overall good agreement.
For the problem given in this study, the results show that compared to the FEM, the extended FVM solids4foam toolbox is suitable for calculating the stress field in the solid composite. This makes it possible to carry out the simulation chain starting with the mold-filling up to the loading of the solid composite in the open-source code OpenFOAM®. Further advantages are the uniform environment, which enables standardized workflows, and the high flexibility, i.e. the possibility to expand the contained basic solvers. A disadvantage is that, depending on the problem and the code extension, suitable stabilization methods must be found and any parameters must generally be selected depending on the given problem. This goes hand in hand with a larger implementation effort compared to the implementation of an Abaqus® user-material subroutine.
As any further comparison between FVM and FEM is not the focus of the study, the reader is referred to the review article of Cardiff and Demirdžić [76] and the references therein. The work of Demirdz̆ić [90], taken as an example, compares FVM with FEM and evaluates FVM as outperforming FEM and as an equal alternative, depending on the problem. However, the disadvantage is listed that solid mechanics based on FVM is not widely used.
5 Summary and conclusion
In this study the effects of flow–fiber coupling during mold-filling are investigated in view of the stress field in the manufactured solid composite after fluid–solid transition. The two-phase mold-filling simulation of the fiber suspension is carried out with the finite volume solver OpenFOAM® based on an extended VOF solver interIsoFoam [54]. Various methods for numerical stabilization are implemented. The fiber orientation taken from mold-filling simulations is used for the solid composite defining its local anisotropic elastic behavior. The fiber orientation itself during mold-filling is simulated both with Newtonian and non-Newtonian matrix behavior and also with and without flow–fiber coupling. Both the viscous fiber suspension and the solid fiber reinforced composite are modeled micromechanically unified with the Mori–Tanaka mean-field model [26, 27, 38,39,40, 49]. The simulation of the solid composite is carried out with the finite element solver Abaqus® using an implemented subroutine for the anisotropic elastic behavior. In addition, the OpenFOAM® solids4foam toolbox [73,74,75] is extended for simulating the solid composite and the differences to the results from Abaqus® are discussed briefly.
The present study is based on the following main assumptions. The fiber geometry is assumed to be constant and the fibers are treated as rigid bodies during mold-filling. Based on the Folgar–Tucker equation with isotropic fiber-fiber interaction [9, 10], the fiber orientation tensor of the first kind and of second order [30] is assumed to be a sufficient measure of anisotropy. The closure problem is treated by using the IBOF closure [34] both for the Folgar–Tucker equation and for the orientation average procedure. The mold-filling process is modeled incompressible, isothermal and without fluid–solid transition. To account for two different polymer matrix behaviors during mold-filling, the polymer matrix is modeled as a generalized Newtonian fluid with rigid fibers, whereas the solid composite and the fibers within are modeled linear elastic. Both the fiber suspension and the solid composite are homogenized on the scale of a grid cell, which is seen as a representative volume element. Voids and cracks are excluded and the Hill-Mandel condition [50, 51] is assumed to be fulfilled on the grid cells. The present study is based on a double-rib geometry as a generic injection molding geometry.
Regarding the implemented methods for numerical stabilization the implicit-explicit splitting is concluded as important. If it is possible in a solver to treat the coupling term completely implicitly in the linear momentum balance, the greatest possible stability will be obtained. But this is not possible in OpenFOAM®, which is why further methods have to be implemented to enable suspension simulations with large fiber volume fractions and aspect ratios. The under-relaxation of the explicit part of the coupling term is observed to be a powerful method for flows in which low relaxation factors can be used without negatively influencing the solution behavior. If only relatively large relaxation factors are allowed to be used, a combination with the method of spatial restriction of the coupling term is recommended. Furthermore, the described treatment of the viscous stress can be used to improve the convergence of the pressure solver. It can be concluded that stabilizing the code strongly depends on the given problem and that a coordination of the methods is necessary. Within this study, the combination of all described stabilization methods leads to a robust numerical behavior, provided that the adaptation of the methods is problem-specific. Since this is difficult a priori, extensive preliminary studies are recommended.
The simulation results can be summarized as follows and the associated conclusions can be drawn:
-
For both the decoupled and the coupled case, the choice of the viscosity model has a non-negligible influence on the fiber orientation (decoupled: \(-\,27\) to \(30\%\), coupled: \(-\,40\) to \(41\%\)) and on the stress field in the solid composite (decoupled: \(-\,6\) to \(4.6\%\), coupled: \(-\,4.7\) to \(6.5\%\)). Since real polymer melts show a shear-thinning behavior, the necessity of this modeling can be quantifiably justified.
-
The differences in fiber orientation between the viscosity models are larger in the coupled case than in the decoupled case. In this context, differences in the stress field in the decoupled and coupled case are comparable. Thus, it can be concluded that the relevance of the shear-thinning behavior increases with coupling.
-
For both viscosity models considered, it is shown that the coupling has a significant influence on the fiber orientation (Newtonian: \(-\,36\) to \(31\%\), non-Newtonian: \(-\,37\) to \(38\%\)) and on the stress field (Newtonian: \(-\,12\) to \(12.9\%\), non-Newtonian: \(-\,10.6\) to \(14.9\%\)). Based on the fact that the anisotropic viscosity model describes the real fiber suspension more physically than the neglect of fiber-induced viscous anisotropy, the implementation of flow–fiber coupling is recommended.
-
The influence of flow–fiber coupling is quite comparable for both viscosity models. Only the comparison between the two viscosity models reveals the necessity of the shear-thinning behavior.
-
The two-phase simulation approach leads to distinct differences in the local fiber orientation compared to the steady-state flow through the geometry. Therefore, changes in kinematics due to the actual filling process have to be predicted by the simulation setup in order to estimate the local anisotropic properties.
-
A brief comparison between FVM and FEM shows that a uniform simulation environment in OpenFOAM® is suitable for both mold-filling and for solid composite simulations. The stress field predicted by the two numerical methods shows an overall good agreement in the considered area of interest.
Finally, it should be noted that the assumptions described above are aimed at considering only the effects of flow–fiber coupling on the fiber orientation and thus on the stress field in the solid. Influences that are more complex than the viscous behavior of the matrix are therefore not taken into account, such as the effects of temperature, fiber-induced anisotropic heat conduction and fluid–solid transition. In this context, the recent publication of Dietemann and Bierwisch [91] indicates that accurate rheological modeling has a larger impact on fiber orientation (and thus on the resulting stress field) than complex modeling of orientation dynamics. In addition, the anisotropic behavior is estimated based on mean-field homogenization which has advantages in terms of computational effort. In particular the mold-filling simulation requires a computational effective estimation of the anisotropic viscosity on each grid cell. On the other hand, critical stress peaks within the highly heterogeneous microstructure are not resolved by mean-field methods. As a consequence, the conclusions listed above have to be interpreted against this background. Moreover, it is noted that injection molding processes are often modeled as flows through narrow gaps, as discussed by, e.g., Tucker [92]. In the present work, this so-called Hele-Shaw simplification (see, e.g., Spurk and Aksel [93]) is deliberately omitted because the geometry under consideration is complex. Another point is that the fiber orientation dynamics can be influenced by small wall distance in such a way that the movement of the fibers is restricted. In the literature this is referred to as confined flow, for which the modeling of fiber orientation evolution was adapted in the studies of, e.g., Perez et al. [94] and Scheuer et al. [95].
Data availability
The data of this study are available from the corresponding author upon reasonable request.
References
Latz A, Strautins U, Niedziela D (2010) Comparative numerical study of two concentrated fiber suspension models. J Nonnewton Fluid Mech 165(13):764–781. https://doi.org/10.1016/j.jnnfm.2010.04.001
Altan MC, Güceri SI, Pipes RB (1992) Anisotropic channel flow of fiber suspensions. J Nonnewton Fluid Mech 42(1):65–83. https://doi.org/10.1016/0377-0257(92)80005-I
Tang L, Altan MC (1995) Entry flow of fiber suspensions in a straight channel. J Nonnewton Fluid Mech 56(2):183–216. https://doi.org/10.1016/0377-0257(94)01280-U
Krochak PJ, Olson JA, Martinez DM (2009) Fiber suspension flow in a tapered channel: the effect of flow/fiber coupling. Int J Multiph Flow 35(7):676–688. https://doi.org/10.1016/j.ijmultiphaseflow.2009.03.005
Mezi D, Ausias G, Advani SG, Férec J (2019) Fiber suspension in 2D nonhomogeneous flow: the effects of flow/fiber coupling for Newtonian and power-law suspending fluids. J Rheol 63(3):405–418. https://doi.org/10.1122/1.5081016
Férec J, Mezi D, Advani SG, Ausias G (2020) Axisymmetric flow simulations of fiber suspensions as described by 3D probability distribution function. J Nonnewton Fluid Mech 284:104367. https://doi.org/10.1016/j.jnnfm.2020.104367
Mezi D, Ausias G, Grohens Y, Férec J (2019) Numerical simulation and modeling of the die swell for fiber suspension flows. J Nonnewton Fluid Mech 274:104205. https://doi.org/10.1016/j.jnnfm.2019.104205
Li T, Luyé JF (2019) Flow–fiber coupled viscosity in injection molding simulations of short fiber reinforced thermoplastics. Int Polym Proc 34(2):158–171. https://doi.org/10.3139/217.3706
Folgar F, Tucker CL (1984) Orientation behavior of fibers in concentrated suspensions. J Reinf Plast Compos 3(2):98–119. https://doi.org/10.1177/073168448400300201
Advani SG, Tucker CL (1987) The use of tensors to describe and predict fiber orientation in short fiber composites. J Rheol 31(8):751–784. https://doi.org/10.1122/1.549945
Wang J, O’Gara JF, Tucker CL (2008) An objective model for slow orientation kinetics in concentrated fiber suspensions: theory and rheological evidence. J Rheol 52(5):1179–1200. https://doi.org/10.1122/1.2946437
Li T, Luyé JF (2018) Optimization of fiber orientation model parameters in the presence of flow–fiber coupling. J Compos Sci 2(4). https://doi.org/10.3390/jcs2040073
Tseng HC, Favaloro AJ (2019) The use of informed isotropic constitutive equation to simulate anisotropic rheological behaviors in fiber suspensions. J Rheol 63(2):263–274. https://doi.org/10.1122/1.5064727
Dinh SM, Armstrong RC (1984) A rheological equation of state for semi-concentrated fiber suspensions. J Rheol 28(3):207–227. https://doi.org/10.1122/1.549748
Lipscomb GG, Denn MM, Hur DU, Boger DV (1988) The flow of fiber suspensions in complex geometries. J Nonnewton Fluid Mech 26(3):297–325. https://doi.org/10.1016/0377-0257(88)80023-5
Huang CT, Lai CH (2020) Investigation on the coupling effects between flow and fibers on fiber-reinforced plastic (FRP) injection parts. Polymers 12(10). https://doi.org/10.3390/polym12102274
Lee S, Shin D, Kim G, Ji W (2022) Numerical model for compression molding process of hybridly laminated thermoplastic composites based on anisotropic rheology. Compos Part C Open Access 7:100215. https://doi.org/10.1016/j.jcomc.2021.100215
Sommer DE, Favaloro AJ, Pipes RB (2018) Coupling anisotropic viscosity and fiber orientation in applications to squeeze flow. J Rheol 62(3):669–679. https://doi.org/10.1122/1.5013098
Wittemann F, Maertens R, Kärger L, Henning F (2019) Injection molding simulation of short fiber reinforced thermosets with anisotropic and non-Newtonian flow behavior. Compos A Appl Sci Manuf 124:105476. https://doi.org/10.1016/j.compositesa.2019.105476
Chung DH, Kwon TH (2002) Numerical studies of fiber suspensions in an axisymmetric radial diverging flow: the effects of modeling and numerical assumptions. J Nonnewton Fluid Mech 107(1):67–96. https://doi.org/10.1016/S0377-0257(02)00142-8
Chung DH, Kwon TH (2002) Fiber orientation in the processing of polymer composites. Korea Aust Rheol J 14(4):175–188
Wang Z, Smith DE (2019) Simulation of mutually dependent polymer flow and fiber filled in polymer composite deposition additive manufacturing. In: Solid freeform fabrication 2019: proceedings of the 30th annual international solid freeform fabrication symposium—an additive manufacturing conference. https://doi.org/10.26153/tsw/17360
Wang Z, Smith DE (2021) A fully coupled simulation of planar deposition flow and fiber orientation in polymer composites additive manufacturing. Materials 14(10). https://doi.org/10.3390/ma14102596
Karl T, Gatti D, Böhlke T, Frohnapfel B (2021) Coupled simulation of flow-induced viscous and elastic anisotropy of short-fiber reinforced composites. Acta Mech 232(6):2249–2268. https://doi.org/10.1007/s00707-020-02897-z
Böhlke T, Brüggemann C (2001) Graphical representation of the generalized Hooke’s law. Tech Mech 21(2):145–158
Mori T, Tanaka K (1973) Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall 21(5):571–574. https://doi.org/10.1016/0001-6160(73)90064-3
Brylka B Charakterisierung und Modellierung der Steifigkeit von langfaserverstärktem Polypropylen. Doctoral thesis. Schriftenreihe Kontinuumsmechanik im Maschinenbau Band 10. Karlsruher Institut für Technologie (KIT). https://doi.org/10.5445/KSP/1000070061
Wang Z, Smith DE (2021) Finite element modelling of fully-coupled flow/fiber-orientation effects in polymer composite deposition additive manufacturing nozzle-extrudate flow. Compos B Eng 219:108811. https://doi.org/10.1016/j.compositesb.2021.108811
Wang Z (2022) Exploring the applicability of a simplified fully coupled flow/orientation algorithm developed for polymer composites extrusion deposition additive manufacturing. Int Polym Proc 37(1):106–119. https://doi.org/10.1515/ipp-2021-4186
Kanatani KI (1984) Distribution of directional data and fabric tensors. Int J Eng Sci 22(2):149–164. https://doi.org/10.1016/0020-7225(84)90090-9
Karl T, Gatti D, Frohnapfel B, Böhlke T (2021) Asymptotic fiber orientation states of the quadratically closed Folgar–Tucker equation and a subsequent closure improvement. J Rheol 65(5):999–1022. https://doi.org/10.1122/8.0000245
Advani SG, Tucker CL (1990) Closure approximations for three-dimensional structure tensors. J Rheol 34(3):367–386. https://doi.org/10.1122/1.550133
Cintra JS, Tucker CL (1995) Orthotropic closure approximations for flow-induced fiber orientation. J Rheol 39(6):1095–1122. https://doi.org/10.1122/1.550630
Chung DH, Kwon TH (2002) Invariant-based optimal fitting closure approximation for the numerical prediction of flow-induced fiber orientation. J Rheol 46(1):169–194. https://doi.org/10.1122/1.1423312
Jeffery GB (1922) The motion of ellipsoidal particles immersed in a viscous fluid. Proc R Soc Lond Ser A 102(715):161–179. https://doi.org/10.1098/rspa.1922.0078
Altan MC, Tang L (1993) Orientation tensors in simple flows of dilute suspensions of non-Brownian rigid ellipsoids, comparison of analytical and approximate solutions. Rheol Acta 32(3):227–244. https://doi.org/10.1007/BF00434187
Bauer JK, Böhlke T (2022) Variety of fiber orientation tensors. Math Mech Solids 27(7):1185–1211. https://doi.org/10.1177/10812865211057602
Bertóti R, Böhlke T (2017) Flow-induced anisotropic viscosity in short FRPs. Mech Adv Mater Mod Process 3(1). https://doi.org/10.1186/s40759-016-0016-7
Bertóti R, Wicht D, Hrymak A, Schneider M, Böhlke T (2021) A computational investigation of the effective viscosity of short-fiber reinforced thermoplastics by an FFT-based method. Eur J Mech B Fluids 90:99–113. https://doi.org/10.1016/j.euromechflu.2021.08.004
Karl T, Böhlke T (2022) Unified mean-field modeling of viscous short-fiber suspensions and solid short-fiber reinforced composites. Arch Appl Mech 92(12):3695–3727. https://doi.org/10.1007/s00419-022-02257-4
Ponte Castañeda P, Willis JR (1995) The effect of spatial distribution on the effective behavior of composite materials and cracked media. J Mech Phys Solids 43(12):1919–1951. https://doi.org/10.1016/0022-5096(95)00058-Q
Noh WF, Woodward P (1976) SLIC (Simple Line Interface Calculation). In: van de Vooren AI, Zandbergen PJ (eds) Proceedings of the fifth international conference on numerical methods in fluid dynamics June 28–July 2, Twente University, Enschede. Springer, Berlin, p 330–340. https://doi.org/10.1007/3-540-08004-X_336
Hirt CW, Nichols BD (1981) Volume of fluid (VOF) method for the dynamics of free boundaries. J Comput Phys 39(1):201–225. https://doi.org/10.1016/0021-9991(81)90145-5
Brackbill JU, Kothe DB, Zemach C (1992) A continuum method for modeling surface tension. J Comput Phys 100(2):335–354. https://doi.org/10.1016/0021-9991(92)90240-Y
Cross MM (1965) Rheology of non-Newtonian fluids: a new flow equation for pseudoplastic systems. J Colloid Sci 20(5):417–437. https://doi.org/10.1016/0095-8522(65)90022-X
Thevenin P, Perreux D (1996) The use of homogenization methods for estimating anisotropic viscosities of composite melts. Compos Sci Technol 56(5):595–603. https://doi.org/10.1016/0266-3538(96)00046-2
Nemat-Nasser S, Hori M (1993) Micromechanics: overall properties of heterogeneous materials, vol 37. North-Holland Series in Applied Mathematics and Mechanics, Amsterdam
Kanaun SK, Levin VM (2008) Self-consistent methods for composites: vol. 1: static problems of solid mechanics and its applications, vol 148. Springer, Dordrecht
Hessman PA, Welschinger F, Hornberger K, Böhlke T (2021) On mean field homogenization schemes for short fiber reinforced composites: unified formulation, application and benchmark. Int J Solids Struct 230–231:111141. https://doi.org/10.1016/j.ijsolstr.2021.111141
Hill R (1963) Elastic properties of reinforced solids: some theoretical principles. J Mech Phys Solids 11(5):357–372. https://doi.org/10.1016/0022-5096(63)90036-X
Mandel J (1980) Generalization dans R9 de la regle du potential plastique pour un element polycrystallin. Comptes rendus de l’Académie des sciences 290(22):481–484
Torquato S (2002) Random heterogeneous materials: microstructure and macroscopic properties. Interdisciplinary applied mathematics, vol 16. Springer, New York
Haagh GAAV, Van De Vosse FN (1998) Simulation of three-dimensional polymer mould filling processes using a pseudo-concentration method. Int J Numer Methods Fluids 28(9):1355–1369
OpenFOAM® (2022) OpenFOAM documentation version 2106. Consulted on February 09. https://www.openfoam.com/documentation/overview
Roenby J, Bredmose H, Jasak H (2016) A computational method for sharp interface advection. R Soc Open Sci 3(11):160405. https://doi.org/10.1098/rsos.160405
Scheufler H, Roenby J (2019) Accurate and efficient surface reconstruction from volume fraction data on general meshes. J Comput Phys 383:1–23. https://doi.org/10.1016/j.jcp.2019.01.009
Gamet L, Scala M, Roenby J, Scheufler H, Pierson JL (2020) Validation of volume-of-fluid OpenFOAM®isoAdvector solvers using single bubble benchmarks. Comput Fluids 213:104722. https://doi.org/10.1016/j.compfluid.2020.104722
Larsen B, Fuhrman D, Roenby J (2019) Performance of interFoam on the simulation of progressive waves. Coast Eng J 61(3):380–400. https://doi.org/10.1080/21664250.2019.1609713
Harper CA (2000) Modern plastics handbook, 1st edn. McGraw-Hill, New York
Schürmann H (2007) Konstruieren mit Faser-Kunststoff-Verbunden, 2nd edn. Springer, Berlin
Osswald TA, Rudolph N (2015) Polymer rheology: fundamentals and applications. Hanser, München
Osswald TA, Baur E, Brinkmann S, Oberbach K, Schmachtenberg E (2006) International plastics handbook: the resource for plastics engineers, 4th edn. Hanser, München
Farotti E, Natalini M (2018) Injection molding. Influence of process parameters on mechanical properties of polypropylene polymer. A first study. Procedia Struct Integr 8:256–264. AIAS2017—46th conference on stress analysis and mechanical engineering design, 6–9 Sept 2017, Pisa, Italy. https://doi.org/10.1016/j.prostr.2017.12.027
Wang J, Mao Q, Jiang N, Chen J (2022) Effects of injection molding parameters on properties of insert-injection molded polypropylene single-polymer composites. Polymers 14(1). https://doi.org/10.3390/polym14010023
Voinov OV (1976) Hydrodynamics of wetting. Fluid Dyn 11(5):714–721. https://doi.org/10.1007/BF01012963
Cox RG (1986) The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J Fluid Mech 168:169–194. https://doi.org/10.1017/S0022112086000332
Wörner M, Cai X, Alla H, Yue P (2018) A semi-analytical method to estimate the effective slip length of spreading spherical-cap shaped droplets using Cox theory. Fluid Dyn Res 50(3):035501. https://doi.org/10.1088/1873-7005/aaaef6
Hétu JF, Gao DM, Garcia-Rejon A, Salloum G (1998) 3D finite element method for the simulation of the filling stage in injection molding. Polym Eng Sci 38(2):223–236. https://doi.org/10.1002/pen.10183
Chang RY, Yang WH (2001) Numerical simulation of mold filling in injection molding using a three-dimensional finite volume approach. Int J Numer Methods Fluids 37(2):125–148. https://doi.org/10.1002/fld.166
Ospald F (2014) Numerical simulation of injection molding using OpenFOAM. Proc Appl Math Mech 14(1):673–674. https://doi.org/10.1002/pamm.201410320
Gajek S, Schneider M, Böhlke T (2021) An FE-DMN method for the multiscale analysis of short fiber reinforced plastic components. Comput Methods Appl Mech Eng 384:113952. https://doi.org/10.1016/j.cma.2021.113952
Kuzmin D (2018) planar and orthotropic closures for orientation tensors in fiber suspension flow models. SIAM J Appl Math 78(6):3040–3059. https://doi.org/10.1137/18M1175665
Cardiff P, Tuković Z̆. solids4foam-release Bitbucket repository. Consulted on 24 May 2022. https://bitbucket.org/philip_cardiff/solids4foam-release/src/master/
Cardiff P, Karac̆ A, De Jaeger P, Jasak H, Nagy J, Ivanković A et al (2018) An open-source finite volume toolbox for solid mechanics and fluid–solid interaction simulations. https://doi.org/10.48550/arXiv:1808.10736
Shayegh A (2020) Block-coupled Finite Volume algorithms: a solids4Foam tutorial. In: Nilsson H (ed) Proceedings of CFD with OpenSource software. https://doi.org/10.17196/OS_CFD#YEAR_2020
Cardiff P, Demirdz̆ić I (2021) Thirty years of the finite volume method for solid mechanics. Arch Comput Methods Eng 28(5):3721–3780. https://doi.org/10.1007/s11831-020-09523-0
Huilgol RR, You Z (2006) On the importance of the pressure dependence of viscosity in steady non-isothermal shearing flows of compressible and incompressible fluids and in the isothermal fountain flow. J Nonnewton Fluid Mech 136(2):106–117. https://doi.org/10.1016/j.jnnfm.2006.03.011
Lee SL, Liao WC (2008) Numerical simulation of a fountain flow on nonstaggered Cartesian grid system. Int J Heat Mass Transf 51(9):2433–2443. https://doi.org/10.1016/j.ijheatmasstransfer.2007.08.030
Borzenko EI, Shrager GR (2015) Effect of the type of boundary conditions on the three-phase contact line on the flow characteristics during filling of the channel. J Appl Mech Tech Phys 56(2):167–176. https://doi.org/10.1134/S0021894415020017
Ferziger JH, Perić M, Street RL (2020) Computational methods for fluid dynamics, 4th edn. Springer, Cham
Paschkewitz JS, Dubief Y, Dimitropoulos CD, Shaqfeh ESG, Moin P (2004) Numerical simulation of turbulent drag reduction using rigid fibres. J Fluid Mech 518:281–317. https://doi.org/10.1017/S0022112004001144
Min T, Yoo JY, Choi H (2001) Effect of spatial discretization schemes on numerical solutions of viscoelastic fluid flows. J Nonnewton Fluid Mech 100(1):27–47. https://doi.org/10.1016/S0377-0257(01)00128-8
Linn J (2005) The Folgar–Tucker model as a differential algebraic system for fiber orientation calculation. Berichte des Fraunhofer-Instituts für Techno- und Wirtschaftsmathematik (ITWM Report) (75). http://nbn-resolving.de/urn:nbn:de:hbz:386-kluedo-13808
Verweyst BE, Tucker CL (2002) Fiber suspensions in complex geometries: flow/orientation coupling. Can J Chem Eng 80(6):1093–1106. https://doi.org/10.1002/cjce.5450800611
Seng S, Monroy C, Malenica S (2017) On the use of Euler and Crank–Nicolson time-stepping schemes for seakeeping simulations in OpenFOAM. In: MARINE VII : proceedings of the VII international conference on computational methods in marine engineering, pp 905–920. https://upcommons.upc.edu/handle/2117/332090
Jasak H, Weller HG (2000) Application of the finite volume method and unstructured meshes to linear elasticity. Int J Numer Methods Eng 48(2):267–287
Cardiff P, Z̆ Tuković, Jasak H, Ivanković A (2016) A block-coupled finite volume methodology for linear elasticity and unstructured meshes. Comput Struct 175:100–122. https://doi.org/10.1016/j.compstruc.2016.07.004
Rhie CM, Chow WL (1983) Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J 21(11):1525–1532. https://doi.org/10.2514/3.8284
Demirdz̆ić I, Muzaferija S (1995) Numerical method for coupled fluid flow, heat transfer and stress analysis using unstructured moving meshes with cells of arbitrary topology. Comput Methods Appl Mech Eng. 125(1):235–255. https://doi.org/10.1016/0045-7825(95)00800-G
Demirdz̆ić I (2020) Finite volumes vs finite elements. There is a choice. Coupled Syst Mech 9(1):5–28. https://doi.org/10.12989/csm.2020.9.1.005
Dietemann B, Bierwisch C (2022) Predicting particle orientation: is an accurate flow field more important than the actual orientation model? J Nonnewton Fluid Mech 310:104927. https://doi.org/10.1016/j.jnnfm.2022.104927
Tucker CL (1991) Flow regimes for fiber suspensions in narrow gaps. J Nonnewton Fluid Mech 39(3):239–268. https://doi.org/10.1016/0377-0257(91)80017-E
Spurk JH, Aksel N (2020) Fluid mechanics, 3rd edn. Springer, Cham
Perez M, Scheuer A, Abisset-Chavanne E, Chinesta F, Keunings R (2016) A multi-scale description of orientation in simple shear flows of confined rod suspensions. J Nonnewton Fluid Mech 233:61–74. https://doi.org/10.1016/j.jnnfm.2016.01.011
Scheuer A, Abisset-Chavanne E, Chinesta F, Keunings R (2016) Second-gradient modelling of orientation development and rheology of dilute confined suspensions. J Nonnewton Fluid Mech 237:54–64. https://doi.org/10.1016/j.jnnfm.2016.10.004
Heinen K. Mikrostrukturelle Orientierungszustände strömender Polymerlösungen und Fasersuspensionen. Doctoral thesis. Technische Universität Dortmund. https://eldorado.tu-dortmund.de/handle/2003/24559
Ansys Granta EduPack® (2022) Datasheet for PP-GF40. Consulted on 12 July 2022. https://www.ansys.com/de-de/products/materials/granta-edupack
Acknowledgements
The partial financial support by the Friedrich und Elisabeth Boysen-Stiftung (Grant BOY-163) is gratefully acknowledged. The authors acknowledge support by the state of Baden-Württemberg through bwHPC.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
TK: Conceptualization, methodology, formal analysis, investigation, software, data curation, visualization, writing—original draft, writing—review and editing. JZ: Software. SD: Software. DG: Discussion, supervision, writing—review and editing. BF: Conceptualization, discussion, supervision, funding acquisition, writing—review and editing. TB: Conceptualization, discussion, supervision, funding acquisition, writing—review and editing. All authors read and approved the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendices
Appendix A: Implicit-explicit splitting of the Folgar–Tucker equation
In this supplementary section, the implicit-explicit splitting of the Folgar–Tucker equation is addressed. The implicit-explicit splitting of the IBOF closure terms [34] is given based on the work of Heinen [96] with respect to the symmetry-preserving representation of Karl et al. [24]. It should be noted that the incompressibility condition \({\textrm{tr}({\bar{{\varvec{D}}}})=0}\) is used within the closure terms. The Folgar–Tucker equation is solved for cells with \({\psi >0.99}\) avoiding anisotropic effects in cells, which could neither be clearly assigned to the air phase nor to the suspension. In addition, the Folgar–Tucker equation is solved in every time step before solving the system of governing equations (5) with the following splitting

The splitting of the IBOF closure terms reads
with the coefficients \(\beta _1,\ldots ,\beta _6\) depending on the invariants of \({\varvec{N}}\) as given in Chung and Kwon [34] and the abbreviation \({{\varvec{S}}={\varvec{N}}^2}\) or equivalently \({S_{ij}=N_{ik}N_{kj}}\). Both terms of \({\mathbb {N}}[{\bar{{\varvec{D}}}}]_{\textsf {impl}}\) were linearized \(({\varvec{N}}^n\cdot {\bar{{\varvec{D}}}}^n){\varvec{N}}^{n+1}\) and \(({\varvec{S}}^n\cdot {\bar{{\varvec{D}}}}^n){\varvec{N}}^{n+1}\) as suggested by Heinen [96], with n representing the time step index.
Appendix B: Supplementary results
1.1 B.1 Fiber orientation
In addition to Sect. 4.1, Figs. 14 and 15 address the local fiber orientation difference with respect to viscosity modeling. Figure 14 shows the difference between the non-Newtonian and Newtonian matrix fluid for the decoupled case, whereas Fig. 15 address the same difference for the coupled case. The fields in both figures look similar. This is because for the decoupled case, the non-Newtonian fluid has a flatter velocity profile than the Newtonian fluid. This phenomenon is exactly the same in the coupled case, in which the flow–fiber coupling flattens the velocity profile (see, e.g., [5, 24]). In the coupled case, however, the non-Newtonian velocity profile flattens more than in the Newtonian case, which is why the characteristics of the difference field correspond to the decoupled approach.
The differences regarding the two matrix fluid behaviors are caused by different shear rates. Especially in the channel center region, flattening causes less shear leading to less fiber alignment in the main shear direction. This phenomenon can be seen for \(N_{11}\) in the horizontal channel, where the Newtonian fluid results in larger values for \(N_{11}\) close to the center line compared to the non-Newtonian case (blue color). The same can be seen for \(N_{22}\) in inside the right rib. Furthermore, the difference fields vanish close to the channel walls, since the asymptotic orientation state being dominant there only depends on the kinematics, fiber aspect ratio \(\alpha \) and the fiber-fiber interaction strength \(C_{\textsf {I}}\) and not on the fluid model of the matrix. For further information regarding asymptotic states of the Folgar–Tucker equation, the reader is referred to Karl et al. [31].
The differences between the viscosity models addressed above depend on the shear-thinning behavior of the matrix fluid in the non-Newtonian case. In order quantify this, Fig. 16a shows the non-dimensional viscosity \(\mu (\dot{{\bar{\gamma }}}_{\textsf {M}})/\mu _0\) based on the Cross-model given in Eq. (9). In addition, the field of the effective matrix shear rate \(\dot{{\bar{\gamma }}}_{\textsf {M}}\) is shown in Fig. 16b with respect to the coupled non-Newtonian simulation during mold-filling (\({t=0.5\,~{\textrm{s}}}\)). It can be seen that the shear rate is locally so large that significant shear-thinning is present.
1.2 B.2 Stress field
In addition to the results of Sect. 4.2 the local effective stress field is given in Fig. 17. The left column refers to the stress analysis for the decoupled simulation and the right column refers to the coupled approach, both for non-Newtonian matrix behavior during mold filling. Since the elastic limit of the material in use (PA-GF40) is 60.2–\(87.9\,~{\textrm{MPa}}\) [97], the deformation is purely elastic.
The non-dimensional stress difference field regarding both viscosity models for the decoupled approach is given in Fig. 18. For the coupled approach, this difference field is shown in Fig. 19. Due to the prescribed boundary conditions (see Sect. 3.1), effects of the viscosity model mainly can be limited to  inside the horizontal channel and to
inside the horizontal channel and to  inside the ribs. These differences are directly linked to the previous section and caused by the flattening of the velocity profile. This flatting affects the fiber alignment by a decreased shear rate in the center region of the channels which influences the local stiffness. These local stiffness differences are represented by the local stress differences regarding the prescribed displacement boundary conditions.
inside the ribs. These differences are directly linked to the previous section and caused by the flattening of the velocity profile. This flatting affects the fiber alignment by a decreased shear rate in the center region of the channels which influences the local stiffness. These local stiffness differences are represented by the local stress differences regarding the prescribed displacement boundary conditions.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Karl, T., Zartmann, J., Dalpke, S. et al. Influence of flow–fiber coupling during mold-filling on the stress field in short-fiber reinforced composites. Comput Mech 71, 991–1013 (2023). https://doi.org/10.1007/s00466-023-02277-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-023-02277-z


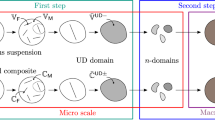







 and ranges of values with respect to the different mold-filling approaches
and ranges of values with respect to the different mold-filling approaches
 in the area of interest
in the area of interest
 in the area of interest
in the area of interest
 and ranges of values with respect to the different mold-filling approaches
and ranges of values with respect to the different mold-filling approaches
 in the area of interest
in the area of interest
 in the area of interest
in the area of interest


 in the area of interest
in the area of interest
 in the area of interest
in the area of interest


 in the area of interest
in the area of interest
 in the area of interest
in the area of interest