1 Introduction

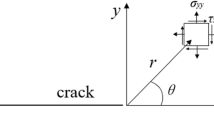
With the determination of durability and strength of structural elements with sharp notches and cracks, some difficulty is involved. According to theoretical solutions based on elasticity theory, around the concentrator tip, values of both stresses and strains go ad infinitum. Use of the regular method involving comparison of these values to permissible stresses or strains is pointless, and thus a completely different approach is required. Therefore, for forecasting the durability and strength of materials and structural elements with material defects, methods based on fracture mechanics are used. Determination of critical service loads most frequently requires knowledge of stress fields around the concentrator tip area where a local stress concentration is formed. In the literature, analytical solutions can be found which are based on elasticity theory, where particular components of stresses (in a polar coordinate system located in the concentrator tip, Fig. 1) are described by the following equation—\(\sigma _{ij} (r,\varphi )=\sum \nolimits _{n=1}^N {{K_{\mathrm{I}n} r}^{\lambda _{n} -1} f_{ij}^{\mathrm{I}} } (\varphi )+\,\sum \nolimits _{n=1}^N {{K_{\mathrm{II}n} r}^{\lambda _{n} -1} f_{ij}^{\mathrm{II}} } (\varphi )\) where \(f_{ij}^{\mathrm{I}} (\varphi ),f_{ij}^{\mathrm{II}} (\varphi )\) are known eigenfunctions including boundary conditions of the issue, \(\lambda _{n}\)—eigenvalues, n—number of terms of the asymptotic solution, \(K_{\mathrm{I}n}, K_{\mathrm{II}n}\)—stress intensity factors (SIFs).

Fig. 1
figure 1

Element with sharp corner

Full size image

The description of mechanical fields most frequently requires the use of the first power series term \((n=1,\lambda _{n} =\lambda _{1} =\lambda ,K_{\mathrm{I}n} =K_{\mathrm{I}1} =K_{\mathrm{I}} ,K_{\mathrm{II}n} =K_{\mathrm{II}1} =K_{\mathrm{II}} )\), including singular term—eigenvalue \(\lambda <1\). Concrete analytical solutions and methods of their obtaining for the sharp corners located in a homogeneous material can be found, e.g. in papers [1,2,3].

The qualitative nature of singular stress fields determines the exponent \(\lambda \), called eigenvalue. For the issue of a crack in a homogeneous material, it is always \(\lambda =1/2\) regardless of the mechanical properties of the material [1]. In papers, e.g. [3,4,5,6,7,8,9,10,11], concerning sharp corners with different boundary conditions, it was shown that the exponent can have values other than \(\lambda =1/2\).

The author of paper [3], using the eigenfunction expansion method, for the notch located in a homogeneous material obtained the so-called characteristic equation. The solution of this equation shows that the eigenvalue \(\lambda \) is not constant and depends on the notch tip angle. What is more, in the range of \(< 0,1>\) it occurs only once (single singular) and always belongs to a set of real numbers. In case if a sharp corner occurs in an inhomogeneous material, eigenvalues can be complex numbers—\(\lambda =\lambda _{r} +i\delta \). For the very first time, such fact was reported for a case of an interfacial crack in paper [4]. With the presence of an imaginary part \(\delta \) of the exponent \(\lambda \) characteristic oscillating terms of type sin[\(\delta \hbox {ln}(r)\)] and cos[\(\delta \hbox {ln}(r)\)] are introduced to the solution of stress and displacement fields, which increase the amplitude and “frequency” of changes in stresses and displacements, as the radius r goes to zero. Further investigations given, for example, in papers [5, 6], have shown that the real part of the eigenvalue is always constant and equals \(\lambda _{{r}}=1/2\), and the imaginary part depends on material constants. An other stress concentrator, frequently occurring in heterogeneous materials, is structural notch (Fig. 2). Such issue was dealt with by, for example, the authors of papers [7,8,9, 12]. On the basis of their investigations, it can be claimed that in the case of a notch located on the interface of a bi-material structure, stress and displacement fields can be described by both the real and the complex eigenvalue \(\lambda \). The value of the exponent \(\lambda \) depends on the notch geometry and material constants; however, also multiple singularities can occur.

To sum up, the qualitative nature of stress and displacement fields occurring around the sharp edge tip area is determined by eigenvalue \(\lambda \). Depending on a concentrator type (geometry, material parameters), local stress and displacement fields may have complex and real singularities, both single and multiple.

For forecasting of the fracture process, a quantitative determination of a singular stress field is necessary, and this is obtained by determination of stress intensity factors. The physical interpretation of SIFs was first presented by Irwin [13]. Definitions of SIFs, as well as methods of their calculation, depend on the qualitative nature of a singular stress field. For the sharp corners in a homogeneous material (eigenvalues always have real values—\(\lambda =\lambda _{r} \in R)\) stress intensity factors can be defined as follows [1,2,3]:

$$\begin{aligned} \left( {\sigma _{\varphi } +\text{ i }\tau _{r\varphi } } \right) _{\varphi =0} =\frac{K_{\mathrm{I}} +iK_{\mathrm{II}} }{\sqrt{2\pi } r^{1-\lambda _{r} }},\quad \lambda =\lambda _{r} \in R \end{aligned}$$
(1)

where \(K_{\mathrm{I}}\) and \(K_{\mathrm{II}}\) are factors for mode I and mode II loading, respectively, defined in the plane of symmetry of the corner.

In the literature, e.g. [6, 14,15,16,17,18], for the issue of notches and cracks located on the interface of a bi-material structure, many various definitions of SIFs can be found. In this paper, SIFs were defined as in paper [17]. In a paired definition (2), modification allowing for its application for a sharp corner, of any tip angle, located on the interface of a bi-material structure or a homogeneous material (assuming \(\delta =0\)) was introduced:

$$\begin{aligned} \left( {\sigma _{\varphi } +\text{ i }\tau _{r\varphi } } \right) _{\varphi =0} =\frac{K_{\mathrm{I}} +iK_{\mathrm{II}} }{\sqrt{2\pi } r^{1-\lambda _{r} }}\left( {\frac{r}{2a}} \right) ^{\text{ i }\delta }\text{ cosh }\left( {\pi \delta } \right) , \end{aligned}$$
(2)

where a is a characteristic dimension that can be considered as a crack length or a notch height.

It is worth noting that in the literature for the issue of sharp corners, for which stress fields are described as eigenvalue \(\lambda \ne 1/2\), factors \(K_{\mathrm{I}}\) and \(K_{\mathrm{II}}\) are often referred to as generalised stress intensity factors GSIF. In this paper, in order to avoid unnecessary confusion, the factors defined by formula (2) regardless of the value \(\lambda \) are always referred to as stress intensity factors SIFs.

When comparing the presented definitions of SIF—formula 1 and 2—it can be noticed that in the case of corners and cracks in a homogeneous material \(K_{\mathrm{I}}\) depends only on circumferential stresses, while \(K_{\mathrm{II}}\) depends only on tangential stresses. For the issue of a bi-material structure with a notch, the exponent \(\lambda \), as already mentioned, can have complex values. Such fact causes that factors \(K_{\mathrm{I}}\) and \(K_{\mathrm{II}}\) depend on tangential and circumferential stresses at the same time. In consequence, this makes the analytical description of local stress and displacement fields and calculation procedures for SIFs difficult.

As regards methods of determination of values of SIFs, a closed-form solution exists only for the issue of an element with a crack (in a homogeneous material and a bi-material structure) assuming that the element is subject to tensile or shear load applied in infinity. In the case of finite dimensions of the element or the presence of a complex external load condition, in order to determine values of sought factors it is necessary to use numerical methods.

In the literature, many papers related to the determination of stress intensity factors can be found. Usually, the following analytical and numerical methods are used:

  1. I.

    Determination of sought factors based on change of strain energy related to a virtual expansion of the crack [19].

  2. II.

    Determination of the value of integral J on the basis of numerical results [20].

  3. III.

    Application of special finite elements [21].

  4. IV.

    Comparison of stresses or displacements obtained from numerical solution (e.g. FEM) to a known analytical solution [22, 23].

Not all the methods mentioned can be used for elements with a corner of freely defined boundary conditions (e.g. method I is applicable only for elements with cracks), and some have certain limitations. Using, for example, method II, it is possible to determine only the value of integral J which is described by a quadratic function of two variables (sought factors \( K_{\mathrm{I}}\) and \(K_{\mathrm{II}}\)). Thus, as a result of a solution of such quadratic equation (or in the case of a structural notch—system of two equations) more than one set of correct solutions is obtained.

Regarding method III, when using commercial software for FEM modelling it is not always possible to simply apply own finite elements allowing for a direct determination of the sought factors.

Due to a fact that the purpose of this paper was to develop a universal method allowing for calculation of SIFs for sharp corners of freely defined boundary conditions (crack/notch in a homogeneous material or in a bi-material structure), method IV seems to be the justified choice. Use of such approach in most cases requires knowledge of an analytical description of the distribution of singular stress or displacement fields occurring around the corner tip area. This is cumbersome if the method is to be used for corners of various boundary conditions. Apart from that, it is not possible for all stress concentrators to directly compare analytical solutions (stresses/displacements) to a numerical solution. Such situation is encountered in cases of corners generating stress fields of complex singularities. This results from a fact that both factor \(K_{\mathrm{I}}\) and \(K_{\mathrm{II}}\) depend on tangential and normal stresses at the same time.

Therefore in this paper universal analytical functions of \(K_{\mathrm{I},\mathrm{II}(r)} =f\left( {\sigma _{\varphi \mathrm{FEM}} ,\tau _{r\varphi \mathrm{FEM}} ,\lambda } \right) \) type are developed. These functions, using extrapolation methods and in connection with a numerical solution (\(\sigma _{\varphi \mathrm{FEM}} ,\tau _{r\varphi \mathrm{FEM}}\)), allowed for SIFs’ determination of for any corner. Of course the developed functions are correlated with boundary conditions of the issue and the assumed SIFs’ definition. In the developed functions \(K_{\mathrm{I},\mathrm{II}(r)}\), a detailed form of that is presented in Sect. 3, eigenvalue \(\lambda \) is responsible for meeting boundary conditions. The eigenvalues are determined on the basis of the so-called characteristic equations. Characteristic equation and methodology of its obtaining (based on eigenfunction technique) is presented in Sect. 2. In the same Section, also analytical formulas combining stress intensity factors are given, defined using formula (2), with singular stress fields. The method of determination of SIFs, along with the developed criterion, selection of area from which the data obtained from FEM are applied to analytical functions, is described in Sect. 3. In order to verify the applied method, for a selected group of geometrical and material structures with sharp corner, stress intensity factors were determined and compared to data available in the literature. The description of analysed specimens with a notch and the method of their modelling using FEM are presented in Sect. 4. Obtained results and their discussion are given in Sect. 5.

2 Identification of parameters describing the qualitative and quantitative nature of singular stress fields

As already mentioned, the purpose of this paper is to develop a universal method of determination of stress intensity factors. Universality of the method is that it can be used for the issues of sharp corners of freely defined boundary conditions. Thus, this Section analyses the issues of a bi-material structure with a structural notch located on the interface (Fig. 2).

Fig. 2
figure 2

Area of a sharp notch tip in a bi-material structure

Full size image

Analytical solutions describing qualitative and quantitative features of singular stress fields obtained for such case can be considered as universal solutions of the issue of corner of any geometry and any structural properties. It can be noticed easily that in the obtained solution when assuming some special assumptions, solutions for the following issues are produced:

  • interfacial crack: \(\beta =0,\,\,\alpha =\gamma ;\)

  • notch in homogeneous material: \(\beta \ne 0,\,\,E_{1} =E_{2} ,\nu _{1} =\nu _{2} ;\)

  • crack in homogeneous material: \(\beta =0,\,\,\alpha =\gamma ,E_{1} =E_{2} ,\nu _{1} =\nu _{2}\).

An analytical description was obtained using the approach described by the authors of papers [24, 25]. In the applied method by using elasticity theory equations and Airy stress function, general asymptotic solutions are obtained describing individual components of stress and displacement fields:

$$\begin{aligned} u_{ri}= & {} r^{\lambda }\left( {A_{i} \text{ cos }\left( {\left( {\text{1 }+\lambda } \right) \varphi } \right) +B_{i} \text{ sin }\left( {\left( {\text{1 }+\lambda } \right) \varphi } \right) +C_{i} \text{ cos }\left( {\left( {\text{1 }-\lambda } \right) \varphi } \right) +D_{i} \text{ sin }\left( {\left( {\text{1 }-\lambda } \right) \varphi } \right) } \right) ,\nonumber \\ u_{\varphi i}= & {} r^{\lambda }\left( {-A_{i} \text{ sin }\left( {\left( {\text{1 }+\lambda } \right) \varphi } \right) +B_{i} \text{ cos }\left( {\left( {\text{1 }+\lambda } \right) \varphi } \right) -C_{i} \frac{\kappa _{i} +\lambda }{\kappa _{i} -\lambda } \text{ sin }\left( {\left( {\text{1 }-\lambda } \right) \varphi } \right) +D_{i} \frac{\kappa _{i} +\lambda }{\kappa _{i} -\lambda } \text{ cos }\left( {\left( {\text{1 }-\lambda } \right) \varphi } \right) } \right) , \nonumber \\ \sigma _{ri}= & {} r^{\lambda -1}\mu _{i} \left( A_{i} 2\lambda \cos \left( {\left( {1+\lambda } \right) \varphi } \right) +B_{i} 2\lambda \sin \left( {\left( {1+\lambda } \right) \varphi } \right) +C_{i} \left( {3-\lambda } \right) \frac{2\lambda }{\kappa _{i} -\lambda }\cos \left( \left( {1-\lambda } \right) \varphi \right) \right. \nonumber \\&\qquad \qquad \left. +D_{i} \left( {3-\lambda } \right) \frac{2\lambda }{\kappa _{i} -\lambda }\sin \left( {\left( {1-\lambda } \right) \varphi } \right) \right) ,\nonumber \\ \sigma _{\varphi i}= & {} r^{\lambda -1}\mu _{i} \left( -A_{i} 2\lambda \cos \left( {\left( {1+\lambda } \right) \varphi } \right) -B_{i} 2\lambda \sin \left( {\left( {1+\lambda } \right) \varphi } \right) +C_{i} \left( {1+\lambda } \right) \frac{2\lambda }{\kappa _{i} -\lambda }\cos \left( {\left( {1-\lambda } \right) \varphi } \right) \right. \nonumber \\&\qquad \qquad \left. +D_{i} \left( {1+\lambda } \right) \frac{2\lambda }{\kappa _{i} -\lambda }\sin \left( {\left( {1-\lambda } \right) \varphi } \right) \right) ,\nonumber \\ \tau _{r\varphi i}= & {} r^{\lambda -1}\mu _{i} \left( -A_{i} 2\lambda \sin \left( {\left( {1+\lambda } \right) \varphi } \right) +B_{i} 2\lambda \cos \left( {\left( {1+\lambda } \right) \varphi } \right) +C_{i} \left( {1-\lambda } \right) \frac{2\lambda }{\kappa _{i} -\lambda }\sin \left( {\left( {1-\lambda } \right) \varphi } \right) \right. \nonumber \\&\qquad \qquad \left. -D_{i} \left( {1-\lambda } \right) \frac{2\lambda }{\kappa _{i} -\lambda }\cos \left( {\left( {1-\lambda } \right) \varphi } \right) \right) \end{aligned}$$
(3)

where \(r,\varphi \)—coordinates in a polar coordinate system located in corner tip, \(\mu _{i} =\frac{E_{i} }{2\left( {1+\nu _{i} } \right) }\)—shear modulus \(\kappa _{i} =\left( {3-\nu _{i} } \right) /\left( {1+\nu _{i} } \right) \)—a plane stress, \(\kappa _{i} =\left( {3-4\nu _{i} } \right) \)—a plane strain, \(\nu _{i}\)—Poisson’s ratio, \(i=1,2\).

The method of determining Eq. (3) is discussed in detail, e.g. in [25].

Particular solution involves determination of eigenvalue \(\lambda \) and constants \(A_{i}\), \(B_{i}\), \(C_{i}\), \(D_{i}\). The sought values for the issue of structural notch (Fig. 2) were determined on the basis of both boundary and connection conditions:

  1. 1.

    along the interface, for \(\varphi = 0\);

  2. 2.

    \(u_{r1} =u_{r2} ;u_{\varphi 1} =u_{\varphi 2} ;\sigma _{\varphi 1} =\sigma _{\varphi 2} ;\tau _{r\varphi 1} =\tau _{r\varphi 2}\);

  3. 3.

    of upper surface of V-notch, for \(\varphi = \alpha \);

    $$\begin{aligned} \sigma _{\varphi 1} =\tau _{r\varphi 1} =0; \end{aligned}$$
  4. 4.

    of lower surface of V-notch, for \(\varphi = -\gamma \);

    $$\begin{aligned} \sigma _{\varphi 2} =\tau _{r\varphi 2} =0. \end{aligned}$$

Using formulas (3), the main matrix of the above boundary conditions can be formulated as:

$$\begin{aligned} M^{8\times 8}=\left[ {{\begin{array}{cc} {A^{4\times 4}} &{}\quad {B^{4\times 4}} \\ {C^{4\times 4}} &{}\quad {D^{4\times 4}} \\ \end{array} }} \right] , \end{aligned}$$
(4)

where

$$\begin{aligned} A^{4\times 4}= & {} \left[ {{\begin{array}{cccc} 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad {\frac{\kappa _{1} +\lambda }{\kappa _{1} -\lambda }} \\ {-2\lambda \mu _{1} } &{}\quad 0 &{}\quad {\left( {-\lambda -1} \right) \mu _{1} \left( {1-\frac{\kappa _{1} +\lambda }{\kappa _{1} -\lambda }} \right) } &{}\quad 0 \\ 0 &{}\quad {2\lambda \mu _{1} } &{}\quad 0 &{}\quad {\left( {1-\lambda } \right) \mu _{1} \left( {1-\frac{\kappa _{1} +\lambda }{\kappa _{1} -\lambda }} \right) } \\ \end{array} }} \right] ,\\ B^{4\times 4}= & {} \left[ {{\begin{array}{cccc} {-1} &{}\quad 0 &{}\quad {-1} &{}\quad 0 \\ 0 &{}\quad {-1} &{}\quad 0 &{}\quad {-\frac{\kappa _{2} +\lambda }{\kappa _{2} -\lambda }} \\ {2\lambda \mu _{2} } &{}\quad 0 &{}\quad {\left( {\lambda +1} \right) \mu _{2} \left( {1-\frac{\kappa _{2} +\lambda }{\kappa _{2} -\lambda }} \right) } &{}\quad 0 \\ 0 &{}\quad {-2\lambda \mu _{2} } &{}\quad 0 &{}\quad {\left( {\lambda -1} \right) \mu _{2} \left( {1-\frac{\kappa _{2} +\lambda }{\kappa _{2} -\lambda }} \right) } \\ \end{array} }} \right] ,\\ C^{4\times 4}= & {} \left[ {{\begin{array}{cccc} {-2\lambda \sin \left( {\alpha \left( {\lambda +1} \right) } \right) } &{}\quad {2\lambda \cos \left( {\alpha \left( {\lambda +1} \right) } \right) } &{}\quad {\left( {\lambda -1} \right) \left( {1-\frac{\kappa _{1} +\lambda }{\kappa _{1} -\lambda }} \right) \sin \left( {\alpha \left( {1-\lambda } \right) } \right) } &{}\quad {\left( {1-\lambda } \right) \left( {1-\frac{\kappa _{1} +\lambda }{\kappa _{1} -\lambda }} \right) \cos \left( {\alpha \left( {1-\lambda } \right) } \right) } \\ {-2\lambda \cos \left( {\alpha \left( {\lambda +1} \right) } \right) } &{}\quad {-2\lambda \sin \left( {\alpha \left( {\lambda +1} \right) } \right) } &{}\quad {\left( {-\lambda -1} \right) \left( {1-\frac{\kappa _{1} +\lambda }{\kappa _{1} -\lambda }} \right) \cos \left( {\alpha \left( {1-\lambda } \right) } \right) } &{}\quad {\left( {-\lambda -1} \right) \left( {1-\frac{\kappa _{1} +\lambda }{\kappa _{1} -\lambda }} \right) \sin \left( {\alpha \left( {1-\lambda } \right) } \right) } \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array} }} \right] ,\\ D^{4\times 4}= & {} \left[ {{\begin{array}{cccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {-2\lambda \sin \left( {\gamma \left( {\lambda +1} \right) } \right) } &{}\quad {2\lambda \cos \left( {\gamma \left( {\lambda +1} \right) } \right) } &{}\quad {\left( {\lambda -1} \right) \left( {1-\frac{\kappa _{2} +\lambda }{\kappa _{2} -\lambda }} \right) \sin \left( {\gamma \left( {1-\lambda } \right) } \right) } &{}\quad {\left( {1-\lambda } \right) \left( {1-\frac{\kappa _{2} +\lambda }{\kappa _{2} -\lambda }} \right) \cos \left( {\gamma \left( {1-\lambda } \right) } \right) } \\ {-2\lambda \cos \left( {\gamma \left( {\lambda +1} \right) } \right) } &{}\quad {-2\lambda \sin \left( {\gamma \left( {\lambda +1} \right) } \right) } &{}\quad {\left( {-\lambda -1} \right) \left( {1-\frac{\kappa _{2} +\lambda }{\kappa _{2} -\lambda }} \right) \cos \left( {\gamma \left( {1-\lambda } \right) } \right) } &{}\quad {\left( {-\lambda -1} \right) \left( {1-\frac{\kappa _{2} +\lambda }{\kappa _{2} -\lambda }} \right) \sin \left( {\gamma \left( {1-\lambda } \right) } \right) } \\ \end{array} }} \right] . \end{aligned}$$

From zeroing of a determinant of the main matrix of boundary conditions—\(\det \left| {M^{8\times 8} } \right| =0\)—eigenequation (5) was determined, subsequent radicals of which determine eigenvalues \(\lambda \),

$$\begin{aligned} H_{0} +\Gamma H_{1} +\Gamma ^{2}H_{2} =0, \end{aligned}$$
(5)

where

$$\begin{aligned} H_{o}= & {} \left( {1-2\lambda ^{2}+2\lambda ^{2}\text{ cos }\left( {2\alpha } \right) } \right) \left( {1-\lambda ^{2}+\lambda ^{2}\text{ cos }\left( {2\gamma } \right) -\text{ cos }\left( {2\gamma \lambda } \right) } \right) \\&-\kappa _{1} \left( {\begin{array}{l} \text{ cos }\left( {2\left( {-\alpha +\gamma } \right) \lambda } \right) +\text{ cos }\left( {2\left( {\alpha +\gamma } \right) \lambda } \right) +\text{ cos }\left( {2\alpha \lambda } \right) \left( {-2+4\lambda ^{2}\text{ sin }\left( \gamma \right) ^{2}} \right) \\ +2\left( {\lambda ^{2}\text{ sin }\left( \gamma \right) ^{2}-\text{ sin }\left( {\gamma \lambda } \right) ^{2}} \right) \kappa _{1}, \\ \end{array}} \right) , \\ H_{1}= & {} 5\lambda ^{2}+\text{ cos }\left( {2\alpha \lambda } \right) +\text{ cos }\left( {2\gamma \lambda } \right) -2\text{ cos }\left( {\left( {-\alpha +\gamma } \right) \lambda } \right) ^{2} \\&-\lambda ^{2}\left( {3\text{ cos }\left( {2\alpha } \right) -\text{ cos }\left( {2\left( {\alpha -\gamma } \right) } \right) +3\text{ cos }\left( {2\gamma } \right) +4\text{ cos }\left( {2\gamma \lambda } \right) \text{ sin }\left( \alpha \right) ^{2}+4\left( {\text{ cos }\left( {2\alpha \lambda } \right) +4\lambda ^{2}\text{ sin }\left( \alpha \right) ^{2}} \right) \text{ sin }\left( \gamma \right) ^{2}} \right) \\&+\kappa _{2} \left( \text{ cos }\left( {2\left( {\alpha +\gamma } \right) \lambda } \right) -\text{ cos }\left( {2\alpha \lambda } \right) +2\text{ sin }\left( {\gamma \lambda } \right) ^{2}-\lambda ^{2}\left( {1+\left( {\text{ cos }\left( {2\alpha } \right) +4\text{ cos }\left( {2\gamma \lambda } \right) \text{ sin }\left( \alpha \right) ^{2}-2\text{ sin }\left( \alpha \right) \text{ sin }\left( {\alpha -2\gamma } \right) } \right) } \right) \right) \\&+\kappa _{1} \left( {\begin{array}{l} \text{ cos }\left( {2\left( {\alpha +\gamma } \right) \lambda } \right) +4\lambda ^{2}\text{ cos }\left( \alpha \right) \text{ sin }\left( {\alpha -\gamma } \right) \text{ sin }\left( \gamma \right) +\text{ cos }\left( {2\alpha \lambda } \right) \left( {-1+4\lambda ^{2}\text{ sin }\left( \gamma \right) ^{2}} \right) +2\text{ sin }\left( {\gamma \lambda } \right) ^{2} \\ +\left( {\text{ cos }\left( {2\alpha \lambda } \right) +\text{ cos }\left( {2\gamma \lambda } \right) -2\text{ cos }\left( {\left( {-\alpha +\gamma } \right) \lambda } \right) ^{2}+4\lambda ^{2}\text{ cos }\left( {\alpha -\gamma } \right) \text{ sin }\left( \alpha \right) \text{ sin }\left( \gamma \right) } \right) \kappa _{2} \\ \end{array}} \right) , \\ H_{2}= & {} \left( {1-2\lambda ^{2}+2\lambda ^{2}\text{ cos }\left( {2\gamma } \right) } \right) \left( {1-\lambda ^{2}+\lambda ^{2}\text{ cos }\left( {2\alpha } \right) -\text{ cos }\left( {2\alpha \lambda } \right) } \right) \\&-\kappa _{2} \left( {\begin{array}{l} \text{ cos }\left( {2\left( {-\alpha +\gamma } \right) \lambda } \right) +\text{ cos }\left( {2\left( {\alpha +\gamma } \right) \lambda } \right) +\text{ cos }\left( {2\gamma \lambda } \right) \left( {-2+4\lambda ^{2}\text{ sin }\left( \alpha \right) ^{2}} \right) \\ +2\left( {\lambda ^{2}\text{ sin }\left( \alpha \right) ^{2}-\text{ sin }\left( {\alpha \lambda } \right) ^{2}} \right) \kappa _{2} \\ \end{array}} \right) , \\ \Gamma= & {} \frac{\mu _{1} }{\mu _{2} }. \end{aligned}$$

Constants \(A_{i}\), \(B_{i}\), \(C_{i}\), \(D_{i}\) were determined by solving the below system of Eqs. (6) (resulting from boundary conditions):

$$\begin{aligned} \left[ {M^{8\times 8}} \right] \left\{ {U^{8\times 1}} \right\} =\left\{ {0^{8\times 1}} \right\} , \end{aligned}$$
(6)

where \(\left\{ {U^{8\times 1}} \right\} ^{T}=\left\{ {A_{1} ,B_{1} ,C_{1} ,D_{1} ,A_{2} ,B_{2} ,C_{2} ,D_{2} } \right\} ,\left\{ {0^{8\times 1}} \right\} \)—zero matrix.

In order to avoid a trivial solution (\(A_{i}\), \(B_{i},\ldots =0\)), it was necessary to modify the main matrix \(\left[ {M^{8\times 8}} \right] \). This modification involved replacement of any two boundary conditions by the following formulas (7) resulting from the assumed definition of SIF (Eq. (2)):

$$\begin{aligned} \left. {\begin{array}{l} K_{o} =\lim \limits _{r\rightarrow 0} \sqrt{2\pi } r^{1-\lambda r}\sigma _{\varphi } (r,0)\left( {\cos ^{-1}\left( {\psi +\delta \ln \left( {\frac{r}{2a}} \right) } \right) } \right) \\ K_{o} =\lim \limits _{r\rightarrow 0} \sqrt{2\pi } r^{1-\lambda r}\tau _{r\varphi } (r,0)\left( {\sin ^{-1}\left( {\psi +\delta \ln \left( {\frac{r}{2a}} \right) } \right) } \right) \\ \end{array}} \right\} , \end{aligned}$$
(7)

where \(K_{o} =\cosh \left( {\pi \delta } \right) \sqrt{K_{\mathrm{I}}^{2}+K_{\mathrm{II}} ^{2}} ,\psi =\arctan \left( {\frac{K_{\mathrm{II}} }{K_{\mathrm{I}} }} \right) \).

After applying constants \(A_{i}\), \(B_{i}\), \(C_{i}\), \(D_{i}\) obtained using the above method for dependence (3), an analytical description of stress fields was obtained. Below is a special form of stress fields for angle \(\varphi =0\), i.e. in a plane for which SIF was defined,

$$\begin{aligned} \left. {\begin{array}{l} \sigma _{\varphi 1,2}{_{\varphi =0} } =\frac{1}{\sqrt{2\pi } }\sqrt{K_{\mathrm{I}}^{2}+K_{\mathrm{II}}^{2}} r^{\lambda _{r} -1}\text{ cos }\left( {\text{ arctan }\left( {\frac{K_{\mathrm{II}} }{K_{\mathrm{I}} }} \right) +\delta \text{ ln }\left( {\frac{r}{2a}} \right) } \right) \text{ cosh }\left( {\pi \delta } \right) \\ \tau _{r\varphi 1,2}{_{\varphi =0} } =\frac{1}{\sqrt{2\pi } }\sqrt{K_{\mathrm{I}}^{2}+K_{\mathrm{II}}^{2}} r^{\lambda _{r} -1}\text{ sin }\left( {\text{ arctan }\left( {\frac{K_{\mathrm{II}} }{K_{\mathrm{I}} }} \right) +\delta \text{ ln }\left( {\frac{r}{2a}} \right) } \right) \text{ cosh }\left( {\pi \delta } \right) \\ \end{array}} \right\} , \end{aligned}$$
(8)

When the exponent is a real value (\(\delta =0\)) relations (8) will be simplified to the following form—\(\sigma _{\varphi 1,2}{_{\varphi =0} } =\frac{1}{\sqrt{2\pi } }K_{\mathrm{I}} r^{\lambda _{r} -1},\,\,\tau _{r\varphi 1,2}{_{\varphi =0} } =\frac{1}{\sqrt{2\pi } }K_{\mathrm{II}} r^{\lambda _{r} -1}\).

Full description of stress fields for the issue of structural notch can be found, e.g. in paper [9].

Relation (8), combining stress intensity factors and a stress field, has been used to formulate function \(K_{\mathrm{I},\mathrm{II}(r)} =f\left( {\sigma _{\varphi \mathrm{FEM}} ,\tau _{r\varphi \mathrm{FEM}} ,\lambda } \right) \), which is discussed in the next Section.

3 Description of method used for the determination of SIFs

In this part of the paper forms of analytical functions used for the determination of SIFs are given, as well as a criterion for the selection of nodes from which numerical results of FEM are implemented to the analytical solution.

As regards the criterion for the selection of nodes, as is well known, if a diagram for—\(\sigma =Cr^{-b}\) type stresses—in a double logarithmic system is linear (Fig. 3), gradient of the line is b.

Fig. 3
figure 3

Graphical interpretation of singular stress fields of theoretical gradient b

Full size image

For the issue of stress concentrators generating complex singularities, components of stresses are always dependent on factors \(K_{\mathrm{I}}\) and \(K_{\mathrm{II}}\), at the same time, and therefore in order to use a regularity as shown in Fig. 3, it is necessary to determine [on the basis of Eq. (8)] the so-called combined stresses dependent only on a single factor:

$$\begin{aligned} \sigma _{\mathrm{I}\left( {r,0} \right) }= & {} \text{ sech }\left( {\pi \delta } \right) \left( {\sigma \text{ cos }\left( {\delta \text{ ln }\left( {\frac{r}{2a}} \right) } \right) +\tau \text{ sin }\left( {\delta \text{ ln }\left( {\frac{r}{2a}} \right) } \right) } \right) =\frac{K_{\mathrm{I}} }{\sqrt{2\pi } r^{1-\lambda _{r} }}, \end{aligned}$$
(9)
$$\begin{aligned} \sigma _{\mathrm{II}\left( {r,0} \right) }= & {} \text{ sech }\left[ {\pi \delta } \right] \left( {\tau \text{ cos }\left( {\delta \text{ ln }\left( {\frac{r}{2a}} \right) } \right) -\sigma \text{ sin }\left( {\delta \text{ ln }\left( {\frac{r}{2a}} \right) } \right) } \right) =\frac{K_{\mathrm{II}} }{\sqrt{2\pi } r^{1-\lambda _{r} }}. \end{aligned}$$
(10)

In Eqs. (9) and (10) by replacing \(\sigma , \tau \) with circumferential and tangential stresses, respectively, obtained from FEM, it is possible to calculate gradient b for all nodes. Of course, when determining SIF only pairs of nodes of a gradient corresponding to the theoretical ones are taken into account, i.e. \(b=\left( {\lambda _{r} -1} \right) \pm 0.01\).

The ‘combined stresses’ \(\sigma _{j\left( {r,0} \right) }\) at distance \(r_{m}\) and \(r_{m+1}\) from the tip of the notch can be formulated as:

$$\begin{aligned} \sigma _{j\left( {r_{m} ,0} \right) } =\frac{K_{\mathrm{I},\mathrm{II}(r)} }{\sqrt{2\pi } r^{1-\lambda _{r} }}\left( {1+br_{m} } \right) ,\sigma _{j\left( {r_{m+1} ,0} \right) } =\frac{K_{\mathrm{I},\mathrm{II}(r)} }{\sqrt{2\pi } r^{1-\lambda _{r} }}\left( {1+br_{m+1} } \right) . \end{aligned}$$
(11)

Using formulas (9–11) after simple mathematical transformations, functions (12) are obtained allowing for the determination of factors \(K_{\mathrm{I},\mathrm{II}(r)}\) (at a certain distance from the tip of the notch):

$$\begin{aligned} \left. {\begin{array}{l} K_{\mathrm{I}(r)} =\frac{\sqrt{2\pi } \left( {r_{m} r_{m+1} } \right) ^{1-\lambda _{r} }}{r_{m} -r_{m+1} }\text{ s }\text{ ech }\left( {\pi \delta } \right) \left( {\begin{array}{l} r_{m}^{\lambda _{r} }\left( {\sigma _{(r_{m+1} )} \text{ cos }\left( {\delta \text{ ln }\left( {\frac{r_{m+1} }{2a}} \right) } \right) +\tau _{(r_{m +1} )} \text{ sin }\left( {\delta \text{ ln }\left( {\frac{r_{m+1} }{2a}} \right) } \right) } \right) \\ -r_{m+1}^{\lambda _{r} }\left( {\sigma _{(r_{m} )} \text{ cos }\left( {\delta \text{ ln }\left( {\frac{r_{m} }{2a}} \right) } \right) +\tau _{(r_{m} )} \text{ sin }\left( {\delta \text{ ln }\left( {\frac{r_{m} }{2a}} \right) } \right) } \right) \\ \end{array}} \right) \\ K_{\mathrm{II}(r)} =\frac{\sqrt{2\pi } \left( {r_{m} r_{m+1} } \right) ^{1-\lambda _{r} }}{r_{m} -r_{m+1} }\text{ s }\text{ ech }\left( {\pi \delta } \right) \left( {\begin{array}{l} r_{m}^{\lambda _{r} }\left( {\tau _{(r_{m+1} )} \text{ cos }\left( {\delta \text{ ln }\left( {\frac{r_{m+1} }{2a}} \right) } \right) -\sigma _{(r_{m+1} )} \text{ sin }\left( {\delta \text{ ln }\left( {\frac{r_{m+1} }{2a}} \right) } \right) } \right) \\ -r_{m+1}^{\lambda _{r} }\left( {\tau _{(r_{m} )} \text{ cos }\left( {\delta \text{ ln }\left( {\frac{r_{m} }{2a}} \right) } \right) -\sigma _{(r_{m} )} \text{ sin }\left( {\delta \text{ ln }\left( {\frac{r_{m} }{2a}} \right) } \right) } \right) \\ \end{array}} \right) \\ \end{array}} \right\} , \end{aligned}$$
(12)

Factors \(K_{\mathrm{I},\mathrm{II}(r)}\) are calculated by replacing—\(\sigma _{(r_{m+1})}\), \(\sigma _{(r_{m})}\), \(\tau _{(r_{m+1} )} \tau _{(r_{m})}\)—in Eq. (12) respective values of circumferential and tangential stresses obtained from FEM in nodes with coordinates \(r_{m}\), \(r_{m+1}\).

It is worth noting that when the exponent \(\lambda \) is a real number (\(\delta =0\)) dependence, (12) is simplified to a form presented in paper [26].

The factor calculated using formula (12), for all \(m+1\) selected nodes of gradient \(b=\left( {\lambda _{r} -1} \right) \pm 0.01\), in theory should be identical. However, due to potential errors in numerical calculations the results can be slightly different. Thus in order to minimise an error it is possible to:

  • average results (13):

    $$\begin{aligned} \left. {\begin{array}{l} K_{\mathrm{I}} =\frac{\sum \nolimits _{m=1}^{m+1} {K_{\mathrm{I}(r)} } }{m+1} \\ K_{\mathrm{II}} =\frac{\sum \nolimits _{m=1}^{m+1} {K_{\mathrm{II}(r)} } }{m+1} \\ \end{array}} \right\} \end{aligned}$$
    (13)

  • determine, using linear regression, stress intensity factors for \(r=0\) (14):

    $$\begin{aligned} \left. {\begin{array}{l} K_{\mathrm{I}} =K_{\mathrm{I}(r=0)} =\frac{\sum \nolimits _{m=1}^{m+1} {K_{\mathrm{I}(r)} \sum \nolimits _{m=1}^{m+1} {r{_{n} }^{2} -\sum \nolimits _{m=1}^{m+1} {r_{n} \sum \nolimits _{m=1}^{m+1} {K_{\mathrm{I}(r)} r_{m} } } } } }{\left( {m+1} \right) \sum \nolimits _{m=1}^{m+1} {r{_{n} }^{2} -\left( {\sum \nolimits _{m=1}^{m+1} {r_{m} } } \right) ^{2}} } \\ K_{\mathrm{II}} =K_{\mathrm{II}(r=0)} =\frac{\sum \nolimits _{m=1}^{m+1} {K_{II(r)} \sum \nolimits _{m=1}^{m+1} {r{_{n} }^{2} -\sum \nolimits _{m=1}^{m+1} {r_{n} \sum \nolimits _{m=1}^{m+1} {K_{\mathrm{II}(r)} r_{m} } } } } }{\left( {m+1} \right) \sum \nolimits _{m=1}^{m+1} {r_{m}^{2} -\left( {\sum \nolimits _{m=1}^{m+1} {r_{m} } } \right) ^{2}} } \\ \end{array}} \right\} \end{aligned}$$
    (14)

Differences in the obtained results, according to the applied method of error minimizing—formulas (13) and (14), are discussed in Sect. 5.

4 Modelling of issues of sharp corners using finite element method

With the development of numerical methods, nowadays an FEM-based numerical approach is very often used. FEM, combined with analytical or experimental solutions, can be used, e.g., to study phenomena such as friction [27,28,29,30], liquid and heat flow [31,32,33] or piezoelectricity [34, 35]. This method can also be used to estimate the basic parameters of fracture mechanics, such as the stress intensity factor. So elements with sharp corners were modelled using FEM by means of ANSYS environment (mechanical APDL) application. In numerical simulations, two types of specimens were modelled:

  • a rectangular plate with an edge sharp corner under uniaxial tension (Fig. 4a);

  • a rectangular plate with a centre sharp corner subjected to uniform tensile (Fig. 4b) or pure shear loading (Fig. 5).

Fig. 4
figure 4

Geometry and method of fixing and loading of tension samples, a with the edge sharp corner, and b with the centre sharp corner

Full size image
Fig. 5
figure 5

Geometry and method of fixing and loading of specimens subjected to pure shear loading with the centre sharp corner

Full size image

For specimens with centre sharp corner, due to symmetry, only a right side of plates was modelled. In a plane of symmetry, the following was assumed: symmetry (for tension samples—Fig 4b) and anti-symmetry (for shear samples—Fig. 5) boundary conditions.

Specimens were modelled as a mesh of quadrangular eight-node finite elements of an increased concentration around the tip area (Fig. 6).

Fig. 6
figure 6

A typical finite element mesh used for modelling the specimens

Full size image

Moreover, the tip of the notch was surrounded by triangular (four-node) finite elements.

In all simulations, specimens were subjected to the same loads \(\sigma =1\), assuming the plane stress condition. Moreover, it was assumed that Poisson’s ratio is always \(\nu _{{1}}= \nu _{\mathrm {2}}=0.3\). Other geometrical and material parameters were variable. By changing the relative stiffness value \(E_{{1}}/E_{{2}}\), the issue of a sharp corner located either in a homogeneous material (\(E_{1} /E_{2} =1\)) or in a bi-material structure (\(E_{1} /E_{2} \ne 1\)) was modelled. By selecting values of angular dimensions accordingly, it was possible to develop models of specimens with:

  1. (a)

    crack—\(\alpha =\gamma =\pi ,\beta =0\);

  2. (b)

    notch symmetrical in relation to interface—\(\alpha =\gamma ,\beta \ne 0\).

Proportions of linear dimensions (a/w, h/w), according to a modelled issue, were selected so as to make it possible to compare the obtained results with data available in the literature.

5 Test results

In this part of the paper, stress intensity factors, calculated using the developed method, are presented. The obtained results, as far as it was possible, were compared to data available in the literature and the numerical solution obtained directly using the ANSYS application (this application allows for direct determination of SIF only for the issue of a crack in a homogeneous material).

Calculations were performed for the following cases of elements with sharp corners:

  • crack located in homogeneous material and bi-material structure;

  • symmetrical notch located in homogeneous material and bi-material structure.

For all cases, the calculated stress intensity factors were normalised in accordance with formula (15):

$$\begin{aligned} F_{j} =K_{\mathrm{I},\mathrm{II}} \text{ cosh }\left( {\pi \delta } \right) /\left( {\sigma \sqrt{\pi }a^{1-\lambda _{r} }} \right) , (j=\mathrm{I},\mathrm{II}). \end{aligned}$$
(15)

Values of exponents—\(\lambda =\lambda _{r} +i\delta \)—were calculated on the basis of Eq. (5). Below are the obtained results.

5.1 Results for specimens with crack

Normalised values of stress intensity factors \(F_{j}\) calculated for elements with central crack (Figs. 4b, 5, \(\alpha =\gamma =\pi ,\beta =0)\) are given in Table 1. Values of exponents calculated from Eq. (5) for various relative stiffness values are consistent with data available in the literature [20]. Singular stress fields have single real (\(E_{1} /E_{2} =1\)) or complex \(E_{1} /E_{2} \ne 1\) singularity.

Table 1 Values of normalised factors \(F_{j}\) and eigenvalues \(\lambda \) for specimens with central crack
Full size table

In numerical models, the following geometrical dimensions were adopted: \(a=1\), \(a/w=0.1\), \(h=w\). Such defined geometry is more or less consistent with the issue of a flat plate of infinite dimensions, with a central crack (the overall dimensions of the plate and the a/w ratio have been determined on the basis of numerical tests). Calculations were performed for two variants of load—tension and shear.

The obtained results were compared to the results produced directly by the ANSYS application and to the closed-form solution (16) [17]:

$$\begin{aligned} \left. {\begin{array}{l} K_{\mathrm{I}} =\sqrt{\pi a} \left( {\sigma ^{\infty }-2\delta \tau ^{\infty }} \right) /\cos \left( {\pi \delta } \right) \\ K_{\mathrm{II}} =\sqrt{\pi a} \left( {\tau ^{\infty }+2\delta \sigma ^{\infty }} \right) /\cos \left( {\pi \delta } \right) \\ \end{array}} \right\} , \end{aligned}$$
(16)

where \(\sigma ^{\infty },\tau ^{\infty }\) is the load applied on the edges of a plate of infinite dimensions.

By analysing the data given in Table 1, high consistency of the obtained results with reference results can be concluded. The maximum error was less than 2%.

Table 2 presents results of the investigation of elements with a single-sided side crack (Fig. 4a, \(\alpha =\gamma =\pi ,\beta =0\)). In numerical simulations, tension specimens of the following dimensions were modelled: \(h/w=3/2, a=1\). Calculations were performed for various values a/w and \(E_{{1}}/E_{{2}}\).

Table 2 Values of normalised factors \(F_{j}\) and eigenvalues \(\lambda \) for tension specimens with single-sided side crack
Full size table

The obtained results were compared to the results produced directly by the ANSYS application and to data available in the literature. Similar to the case of a central crack, satisfactory consistency in solutions was achieved.

Fig. 7
figure 7

The SIFs (a) and the ‘combined stresses’ versus r/a for tension specimens with central crack (\(a/w=10\), \(E_{{1}}/E_{{2}}=4)\)

Full size image

Figure 7a presents normalised SIFs values (points) calculated using relation (12) for nodes (having gradient consistent with the theoretical one) of various coordinates r. A broken line is used to mark trend lines. The obtained trend line, both for factor \(K_{\mathrm{I}I(r)}\) and \(K_{\mathrm{II}(r)}\), is actually a horizontal line. Therefore it can be concluded that final SIFs’ values can be determined by using both dependence (13), and (14). In this paper, dependence (14) is used. Such determined SIFs were applied to formula (8) and calculated, using dependences (9) and (10), the ‘combined stresses’. The resulting analytical solution (solid line) was compared to FEM solution (point), which is shown in Fig. 7b. Nodes with a slope consistent with the theoretical one are marked in black. On the basis of the obtained results, consistency of both solutions in a range of about 10% a can be concluded.

5.2 Results for specimens with notch

In this part of the paper, results for elements with both side (one-sided) and central notches (symmetrical \(\alpha =\gamma \)) are presented. Specimens of tip angles \(\beta =60^{\circ }\) and \(\beta =90^{\circ }\) were analysed. Calculations were performed for various values of relative stiffness \(E_{\mathrm {1}}/\hbox {E}_{\mathrm {2}}\). The eigenvalues \(\lambda \) determined using Eq. (5) are given in Table 3 and in a graphic form in Fig. 8. The obtained data are consistent with data available in the literature [37, 38].

Table 3 The eigenvalues \(\lambda =\lambda _{r} +i\delta \) determined for various values \(E_{\mathrm {1}}/E_{\mathrm {2}}\), (\(\beta =60^{\circ },\beta =90^{\circ }\))
Full size table
Fig. 8
figure 8

Solution of the characteristic Eq. (8) for, \(\beta =60^{\circ }\), \(\nu _{\mathrm {1}}=0.3\), \(\nu _{\mathrm {2}}=0.3\), (plane stress)

Full size image

On the basis of results presented in Table 3 and in Fig. 8, it can be concluded that for the analysed specimens, depending on the relative stiffness, the exponent \(\lambda \) within the range of 0 and 1 can take two real values or a single complex value. Thus local stress fields can be characterized by double real singularity or multiple complex singularity.

For the issue of a structural notch with a single complex singularity, stress intensity factors most often are defined in the same way as for the issue of an interfacial crack. When double real singularities occur, to describe local stress fields three approaches are used:

I. Use of a single factor related to the first singular term \(\lambda _{\mathrm {r1}}\), defined as follows [39, 40]:

$$\begin{aligned} K =\lim \limits _{r\rightarrow 0} \sqrt{2\pi } r^{1-\lambda _{r1} }\sigma _{\varphi } (r,0); \end{aligned}$$
(17)

II. Use of two factors related to the first singular term \(\lambda _{\mathrm {r1}}\) [41]:

$$\begin{aligned} \left. {\begin{array}{l} K_{\mathrm{I}} =\lim \limits _{r\rightarrow 0} \sqrt{2\pi } r^{1-\lambda _{r1} }\sigma _{\varphi } (r,0) \\ K_{\mathrm{II}} =\lim \limits _{r\rightarrow 0} \sqrt{2\pi } r^{1-\lambda _{r1} }\tau _{r\varphi } (r,0) \\ \end{array}} \right\} . \end{aligned}$$
(18)

III. Use of two factors, whereas the first is related to circumferential stresses and first singular term \(\lambda _{\mathrm {r1}}\), and the second to tangential stresses and second singular term \(\lambda _{\mathrm {r2}}\) [37]:

$$\begin{aligned} \left. {\begin{array}{l} K_{\mathrm{I}} =\lim \limits _{r\rightarrow 0} \sqrt{2\pi } r^{1-\lambda _{r1} }\sigma _{\varphi } (r,0) \\ K_{\mathrm{II}} =\lim \limits _{r\rightarrow 0} \sqrt{2\pi } r^{1-\lambda _{r2} }\tau _{r\varphi } (r,0) \\ \end{array}} \right\} . \end{aligned}$$
(19)

Analysing formulas (17)–(19), it is easy to see that only K and \(K_{\mathrm{I}}\) are equal. \(K_{\mathrm{II}}\) coefficients cannot be compared with each other. Moreover, by using methods I and II, in the case of multiple singularities, stress factor(s) are calculated only for the first singular term [39], or terms of a higher order [40, 42] additionally are determined.

In this paper, for the determination of stress intensity factors approach II was used. The obtained results were presented:

  • for tension specimens with side notch (Fig. 4a) in Table 4;

  • for tension specimens with central notch (Fig. 4b) in Table 5;

  • for pure shear specimens with central notch (Fig. 5) in Table 6.

In all calculations, the same proportions of linear and angular dimensions were adopted, as follows: \(a/w=0.4\), \(h/w=2\), \(\hbox {a}=1, \alpha =\gamma \). For cases in which a double real singularity occurred, SIFs were calculated for both singular terms. Factors were determined in two stages by using the method described in papers [40, 42]. At first factor for the first term \(K_{\mathrm{I},\mathrm{II}}^{(\lambda _{r1} )} \) (with exclusion of impact of the second term) was calculated. Then circumferential and tangential stresses obtained from FEM were summed with stresses calculated from formula (8). In formula (8), previously determined factors for the first term, \(K_{\mathrm{I},\mathrm{II}}^{(\lambda _{r1} )} \) were used. Stresses—\(\sigma ,\tau \)—summed in such way were applied to Eq. (12), and factors for the second singular term, \(K_{\mathrm{I},\mathrm{II}}^{(\lambda _{r2} )} \) were determined. The summed stresses also were used in formulas (9, 10). This allowed for selection of nodes of a gradient consistent with the theoretical, i.e. \(b=\left( {\lambda _{r2} -1} \right) \pm 0.01\). When calculating both \(K_{\mathrm{I},\mathrm{II}}^{(\lambda _{r1} )} \), and \(K_{\mathrm{I},\mathrm{II}}^{(\lambda _{r2} )}\) it was assumed that in the case of lack of nodes with a slope consistent with the theoretical value—\(b=\left( {\lambda _{ri} -1} \right) \pm 0.01\)—factors take zero-values.

Table 4 Values of normalised factors \(F_{j}\) for tension specimens with symmetrical one-sided side notch of tip angle \(\beta =60^{\circ }\) and \(\beta =90^{\circ }\)
Full size table
Table 5 Values of normalised factors \(F_{j}\) for tension specimens with symmetrical central notch of tip angle \(\beta =60^{\circ }\) and \(\beta =90^{\circ }\)
Full size table
Table 6 Values of normalised factors \(F_{j}\) for pure shear specimens with symmetrical central notch of tip angle \(\beta =60^{\circ }\) and \(\beta =90^{\circ }\)
Full size table

The obtained results, when possible, were compared to data available in the literature. Very good consistency of results for the issue of a notch in a homogeneous material was obtained the maximum error between the obtained results and data available in the literature was 0.65%. As regards a notch in a bi-material structure, due to differences occurring in a method of defining stress intensity factors, in the literature it is hard to find data which the obtained results could be compared to. The issues of structural notches of the same geometrical and material parameters as in the presented article were analysed in paper [37]. The authors defined SIFs in accordance with relation (19). In the presented paper, definitions of SIFs described by a formula (18) were adopted. Therefore it was possible to compare only factors \(K_{\mathrm{I}}\) (as mentioned before factors \(K_{\mathrm{II}}\) are defined differently and cannot be compared directly). Differences in the obtained results are about 1.5% (with the exclusion of the case of a notch with tip angle \(\beta =90^{\circ }\) and relative stiffness \(E_{\mathrm {1}}/E_{\mathrm {2}}=10, 100\) where the difference in results was about 4.5%).

Moreover in the paper variability of stress intensity factors calculated for selected nodes of various coordinate values r was estimated. The obtained results for the tension element with notch of tip angle \(\beta =90^{\circ }\) and relative stiffness \(E_{\mathrm {1}}/E_{\mathrm {2}} =10\), are shown in Fig. 9. Alike the issue of interface crack, the trend line is a horizontal line, and thus SIFs can be determined by using both relations (13) and (14).

Fig. 9
figure 9

The SIFs versus r/a for the tension specimens with one-sided notch (\(\beta =90^{\circ }, E_{\mathrm {1}}/E_{\mathrm {2}}=10\)): a calculated for the first singular term, and b calculated for the second singular term

Full size image

A structural notch, of such geometry and relative stiffness, generates stress fields having double real singularity. Therefore the paper analyses the influence of a number of singular terms used in an asymptotic description on the field of application of analytical solutions. Comparison of analytical solutions (8–10) to FEM solution is presented in Fig. 10.

Fig. 10
figure 10

The stresses versus r/a for tension specimens with one-sided notch (\(\beta =90^{\circ }, E_{\mathrm {1}}/E_{\mathrm {2}}=10\)): a determined for the first singular term (analytical solution—(9), (10)) and b determined for the first (dotted line), second (thin solid line) singular term, and summed values (thick solid line) for both singular terms (analytical solution (8))

Full size image

By analysing the results presented in Fig. 10, it can be concluded that the use of only the first singular term allows for description of stress fields in an area near the notch tip (about 0.1% a). Use of both singular terms increases the area by about 70% a. What is more, by using only the second singular term in the analytical description, a solution deviating significantly from the results produced using FEM is obtained.

6 Summary and conclusions

The novel method of determination of stress intensity factors was developed. In this method, factors are determined on the basis of a specially developed analytical function to which stresses obtained from FEM solution are implemented. Moreover, a criterion allowing for selection of nodes from which numerical data are used, was developed. Use of the criterion increases accuracy in calculations and allows for a use of a mesh for division to finite elements of smaller concentration. The proposed method, in connection with the criterion of selection of nodes, allows for determination of SIFs for elements with stress concentrators generating both real and complex singularities. Moreover, it is possible to determine SIFs for cases of sharp corners with multiple singularities. Undoubtedly an advantage of the proposed method is that it does not require knowledge of an analytical description of singular stress/displacement fields or connection of SIF to energy parameters. The only required parameter determining boundary conditions of the analysed issue is eigenvalue \(\lambda \). The method does not require the use of special finite elements either and can be used together with any commercial FEM software.

The paper presents stress intensity fields calculated for corners of various tip angles, relative stiffness, and relative notch height. The calculations were made for various alternatives of loading of specimens. The obtained results, when possible, were compared to data available in the literature. Very good consistency was obtained for the following types of stress concentrators: crack in a homogeneous material, interfacial crack, notch in a homogeneous material, notch located on the interface of a bi-material structure. Moreover, a part of the presented results is unique (no data available in the literature), e.g. elements with central notch in a bi-material structure subjected to shear and tension stresses. These results can be used for comparison by other scholars.