Refinement of the Maxwell formula for a composite reinforced by circular cross-section fibres. Part II: using Padé approximants

Abstract

The effective properties of the fiber-reinforced composite materials with fibers of circle cross section are investigated. The novel estimation for the effective coefficient of thermal conductivity refining the classical Maxwell formula is derived. The method of asymptotic homogenization is used. For an analytical solution of the periodically repeated cell problem the Schwarz alternating process (SAP) was employed. Convergence of this method was proved by S. Mikhlin, S. Sobolev, V. Mityushev. Unfortunately, the rate of the convergence is often slow, especially for nondilute high-contrast composite materials. For improving this drawback we used Padé approximations for various forms of SAP solutions with the following additive matching of obtained expressions. As a result, the solutions in our paper are obtained in a fairly simple and convenient form. They can be used even for a volume fraction of inclusion very near the physically possible maximum value as well as for high-contrast composite constituents. The results are confirmed by comparison with known numerical and asymptotic results.

1 Introduction

This work extends the previous part of the paper [1]. In the paper [1] a detailed review of the literature is given, the relevance of the considered problem of the modification of Maxwell’s formula is shown, and possible ways for its solution are described.

As it has been concluded in the first part of our investigations [1], in the case of the limiting large sizes of inclusions and conductivity, both MF and SAM do offer reliable results; they do not describe neither qualitatively nor quantitatively the behavior of the effective parameter and the emergence of an infinite physically confirmed cluster.

It means that the Schwarz alternating process in spite of its numerous benefits does not allow to study all related problems and requires modification. The latter requirement was already pointed out in the monograph [2]. In order to remove some drawbacks of SAM, Drygas et al. [2] employed a rigorous analysis based on infinite series. Our modification of the Schwarz alternating process (SAP) is based on the application of Padé approximants [3] to various forms of SAP solutions with additive matching of the obtained expressions. In result, our final form of solutions is simple and can be easily used in numerous applications.

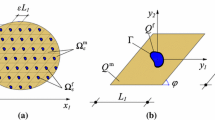
Moreover, in order to address the question: why solutions for an ideally periodic lattice of inclusions are required, if in practice one deals with imperfections considered here and beyond ideal cases. For example, a center of each fiber can randomly deviate within a circle of diameter d, whereas these circles themselves form a regular square lattice of the period l. Such kind of a microstructure is usually referred to as a shaking-geometry composite [4, 5]. In [4,5,6], it is shown that a regular lattice possesses the extreme effective properties among the corresponding shaking-geometry random structures. Therefore, a solution for the perfectly regular lattice can be considered as upper or lower bound on the effective transport coefficient.

This paper is organized as follows. Construction of the generalized relations for Maxwell’s formula using Padé approximants (PA) is described in Sect. 2. The analysis of the obtained corrections to the MF is provided in Sect. 3. Numerical results are analyzed in Sect. 4. Finally, Sect. 5 presents the concluding remarks.

When referencing formulas from [1], we use triple numbering, e.g., formula (1.2.2) is formula (2.2) from [1].

2 Construction of Padé approximant

We consider the formula $\lambda$ (1.4.2) obtained by the Schwarz alternating method (SAM) for the effective heat transfer parameter in part I of the paper:

$$\begin{aligned} q= & {} 1+2\,\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{3}+\cdots +\nonumber \\&+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{2}a^{6}}{4}\,\left( {1+\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}\;\sum \limits _{\ell =1}^\infty {S_{\ell } } \ell \sum \limits _{n=1}^\infty {\,\frac{\left( {-1} \right) ^{n+1}\left( {\pi \ell } \right) ^{4n-2}a^{8n-4}}{2^{2n-2}\left( {2n-1} \right) \,\left( {4n-1} \right) \,!}} \nonumber \\&+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{3}a^{8}}{16}\,\left( {1+\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}\sum \limits _{\ell =1}^\infty \, \ell \,\sum \limits _{j=1}^\infty {S_{j} } j\sum \limits _{m=1}^\infty {\,\frac{\left( {-1} \right) ^{m+1}\left( {\pi j} \right) ^{4m-2}a^{8m-4}}{\left( {2m-1} \right) \,\left( {4m-1} \right) \,!\left( {4m-3} \right) \,}} \nonumber \\&\times \left( {\left( {\uppi \ell } \right) ^{4\mathrm{m}-2}S_{\ell } + \sum \limits _{\mathrm{k}=1}^{\mathrm{m}} {\left( {-1} \right) ^{\ell +\mathrm{k}+1}\frac{\left( {4\mathrm{k}-3} \right) \,!}{2^{2\mathrm{k}-2}}\,\frac{\left( {\uppi \ell } \right) ^{4\mathrm{m}-4\mathrm{k}}}{\sinh \,\uppi \ell }} } \right) \,\sum \limits _{\mathrm{n}=1}^\infty {\,\frac{\left( {-1} \right) ^{\mathrm{n}+1}\left( {\uppi \ell } \right) ^{4\mathrm{n}-2}\mathrm{a}^{8\mathrm{n}-4}}{2^{2\mathrm{n}-1}\left( {2\mathrm{n}-1} \right) \,\left( {4\mathrm{n}-1} \right) \,!}}. \end{aligned}$$

(2.1)

In series (2.1), we leave the terms corresponding to $n=2$, $m=1$ of the series (1.4.7), (1.4.8), while, in the formula (1.4.5), we leave the terms of order not larger than $a^{18}$:

$$\begin{aligned} q= & {} 1+2\,\sum \limits _{j=1}^9 {\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{j}} a^{2j}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{2}a^{6}}{4}\,\left( {1+\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}\nonumber \\&\times \,\left( {\delta _{1}^{\left( 1 \right) } \,\frac{\pi ^{2}a^{4}}{4^{2}}+\delta _{1}^{\left( 2 \right) } \,\frac{\pi ^{6}a^{12}}{4^{6}}+\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}\,\delta _{2}^{\left( {11} \right) } \,\frac{\pi ^{4}a^{8}}{4^{4}}} \right) \nonumber \\= & {} 1+2\,\sum \limits _{j=1}^9 {\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{j}} +\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{4}a^{10}}{4^{3}}\,\left( {1+\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2} \nonumber \\&\times \,\left( {\updelta _{1}^{\left( 1 \right) } +\frac{\uppi ^{4}a^{8}}{4^{4}}\,\updelta _{1}^{\left( 2 \right) } +\frac{\uplambda -1}{\uplambda +1}\,\frac{\uppi ^{3}a^{6}}{4^{3}}\,\updelta _{2}^{\left( {11} \right) } } \right) . \end{aligned}$$

(2.2)

Then we present the truncated series in (2.2) as a sum of two components, so-called the straight and inversed component. To this aim, we use the following transformations:

• (i) we transform the truncated series (2.2) into PA $\left[ 0\big /18\right]$ with regard to parameter a (so-called inverse component):

  $$\begin{aligned} q_{[0/18]} \,\left( {\lambda \,,\, {a}} \right)= & {} \left[ 1-2\,\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}\,a^{2}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{2}a^{4}-2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{3}a^{6}\right. \nonumber \\&+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{4}a^{8} \nonumber \\&-\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{5}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\frac{\pi ^{4}}{4^{3}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{10}\nonumber \\&+\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{6}+2\,\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{5}}{4^{4}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{12}+\nonumber \\&-\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{7}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{5}\frac{\pi ^{6}}{4^{5}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{14}\nonumber \\&+\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{8}-\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{7}}{4^{6}}\delta _{2}^{\left( {11} \right) } } \right) \,a^{16}+\nonumber \\&\left. {-\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{9}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{8}}{4^{7}}\delta _{1}^{\left( 2 \right) } -2\,\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{5}\frac{\pi ^{8}}{4^{7}}\delta _{2}^{\left( {11} \right) } } \right) \,a^{18}} \right] ^{ - 1}\nonumber \\= & {} \left[ {1+2\,\sum \limits _{j=1}^9 {\,\left( {-\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{j}} -\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\frac{\pi ^{4}a^{10}}{4^{3}}\,\left( {1-\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}\delta _{1}^{\left( 1 \right) } } \right. \nonumber \\&\left. {-\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{7}a^{16}}{4^{6}}\,\left( {1-2\,\frac{\lambda -1}{\lambda +1}\frac{\pi a^{2}}{4}} \right) \,\delta _{2}^{\left( {11} \right) } -\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{8}a^{18}}{4^{7}} \, \delta _{1}^{\left( 2 \right) } } \right] ^{ - 1};\qquad \end{aligned}$$

  (2.3)

• (ii) we transform, using PA $\left[ 18\big /0\right]$, expression (2.2) as follows:

  $$\begin{aligned} q^{-1}\,\left( {\lambda ^{-\,1},\,{a}} \right)= & {} \left[ {1+2\,\sum \limits _{j=1}^9 {\,\left( {-\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{j}} -\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{4}a^{10}}{4^{3}}\,\left( {1-\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2} } \right. \nonumber \\&\left. {\times \,\left( {\updelta _{1}^{\left( 1 \right) } +\frac{\uppi ^{4}{a}^{8}}{4^{4}}\,\updelta _{1}^{\left( 2 \right) } -\frac{\uplambda -1}{\uplambda +1}\,\frac{\uppi ^{3}{a}^{6}}{4^{3}}\,\updelta _{2}^{\left( {11} \right) } } \right) } \right] ^{ - 1}. \end{aligned}$$

  We also transfer function $q^{-1}\,\left( {\lambda ^{-\,1},\,{a}} \right)$ into PA $\left[ 18/0\right]$, i.e., we obtain a new function $q^{-1}_{[18/0]}\,\left( {\lambda ^{-1},\,{a}}\right)$, the so-called straight component of the following form:

  $$\begin{aligned} q^{-1}_{[18/0]} \,\left( {\lambda ^{-\,1},\,{a}} \right)= & {} 1+2\,\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}\,a^{2}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{2}a^{4}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{3}a^{6}\nonumber \\&+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{4}a^{8}+\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{5}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\frac{\pi ^{4}}{4^{3}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{10}\nonumber \\&+\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{6}+2\,\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{5}}{4^{4}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{12}\nonumber \\&+\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{7}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{5}\frac{\pi ^{6}}{4^{5}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{14}\nonumber \\&+\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{8}-\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{7}}{4^{6}}\delta _{2}^{\left( {11} \right) } } \right) \,a^{16}\nonumber \\&+\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{9}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{8}}{4^{7}}\delta _{1}^{\left( 2 \right) } -2\,\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{8}}{4^{7}}\delta _{2}^{\left( {11} \right) } } \right) \,a^{18}\nonumber \\= & {} 1+2\,\sum \limits _{j=1}^9 {\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{j}} +\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\frac{\pi ^{4}a^{10}}{4^{3}}\,\left( {1+\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}\delta _{1}^{\left( 1 \right) } \nonumber \\&-\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{7}a^{16}}{4^{6}}\,\left( {1+\frac{\lambda -1}{\lambda +1}\frac{\pi a^{2}}{2}} \right) \,\delta _{2}^{\left( {11} \right) } +\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{8}a^{18}}{4^{7}}\,\delta _{1}^{\left( 2 \right) }; \end{aligned}$$

  (2.4)

• (iii) we match functions $q_{[0/18]} \,\left( {\lambda ,\,{a}} \right)$ and $q^{-1}_{[18/0]} \,\left( {\lambda ^{-\,1},\,{a}} \right)$ with regard to $\lambda$ in the following way:

  $$\begin{aligned} q\,\left( {{a},\,\lambda } \right) =\frac{1}{\lambda +1}\,q^{-1}_{[18/0]} \,\left( {\lambda ^{-\,1},\,{a}} \right) +\frac{\lambda }{\lambda +1}\,q_{[0/18]} \,\left( {\lambda ,\,{a}} \right) . \end{aligned}$$

This expression can be treated as three-point PA, because

• at $\lambda =0$ expression

  $$\begin{aligned} q\,\left( {{a},\,\lambda } \right) \;\Big |{_{\,\lambda =0} }= & {} q^{-1}_{[18/0]} \,\left( {\lambda ^{-\,1},\,{a}} \right) \;\Big | {_{\,\lambda =0} } =1+2\,\sum \limits _{j=1}^9 {\,\left( {-\frac{\pi a^{2}}{4}} \right) ^{j}} -\frac{\pi ^{4}a^{10}}{4^{3}}\,\left( {1-\frac{\pi a^{2}}{4}} \right) ^{2}\delta _{1}^{\left( 1 \right) } \\&-\frac{\pi ^{7}a^{16}}{4^{6}}\,\left( {1-\frac{\pi a^{2}}{2}} \right) \,\delta _{2}^{\left( {11} \right) } -\frac{\pi ^{8}a^{18}}{4^{7}}\,\delta _{1}^{\left( 2 \right) } \end{aligned}$$

  coincides with formula (2.2) at $\lambda =0$, with the order of accuracy $a^{14}$;

• at $\lambda =1$ one has

  $$\begin{aligned} q\,\left( {{a},\,\lambda } \right) \;\Big | {_{\,\lambda =1} } =\frac{1}{2}\,q^{-1}_{[18/0]} \,\left( {\lambda ^{-\,1},\,{a}} \right) \;\Big | {_{\,\lambda =1} } +\frac{1}{2}\,q_{[0/18]} \,\left( {\lambda ,\,{a}} \right) \;\Big | {_{\,\lambda =1} } \equiv 1; \end{aligned}$$

• at $\lambda \rightarrow \infty$ the series expansion of the equation

  $$\begin{aligned}&q\,\left( {{a},\,\lambda } \right) \;\Big |{_{\,\lambda \rightarrow \infty } } =q_{[0/18]} \,\left( {\lambda ,\,{a}} \right) \;\Big | {_{\,\lambda \rightarrow \infty } } \\&\quad =\frac{1}{1+2\,\sum \limits _{j=1}^9 {\,\left( {-\frac{\pi a^{2}}{4}} \right) ^{j}} -\frac{\pi ^{4}a^{10}}{4^{3}}\,\left( {1-\frac{\pi a^{2}}{4}} \right) ^{2}\delta _{1}^{\left( 1 \right) } -\frac{\pi ^{7}a^{16}}{4^{6}}\,\left( {1-\frac{\pi a^{2}}{2}} \right) \,\delta _{2}^{\left( {11} \right) } -\frac{\pi ^{8}a^{18}}{4^{7}}\,\delta _{1}^{\left( 2 \right) } }\\&\qquad \sim 1+2\,\sum \limits _{j=1}^9 {\,\frac{\pi a^{2j}}{4}} +\frac{\pi ^{4}a^{10}}{4^{3}}\,\left( {1+\frac{\pi a^{2}}{4}} \right) ^{2}\delta _{1}^{\left( 1 \right) } +\frac{\pi ^{7}a^{16}}{4^{6}}\,\left( {1+\frac{\pi a^{2}}{2}} \right) \,\delta _{2}^{\left( {11} \right) } +\frac{\pi ^{8}a^{18}}{4^{7}}\,\delta _{1}^{\left( 2 \right) } \end{aligned}$$

  coincides with expression (2.2) at $\lambda \rightarrow \infty$, with the order of accuracy $a^{18}$.

Therefore, combination of SAM-PA methods yields the following formulas for the effective heat transfer parameter:

$$\begin{aligned} q_{{\text {SAM-P}}}= & {} \frac{1}{\lambda +1}\,\left[ {1+2\,\sum \limits _{j=1}^9 {\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{j}} +\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\frac{\pi ^{4}a^{10}}{4^{3}}\,\left( {1+\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}\delta _{1}^{\left( 1 \right) } } \right. \nonumber \\&\left. {-\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{7}a^{16}}{4^{6}}\,\left( {1+2\,\frac{\lambda -1}{\lambda +1}\frac{\pi a^{2}}{4}} \right) \,\delta _{2}^{\left( {11} \right) } +\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{8}a^{18}}{4^{7}}\,\delta _{1}^{\left( 2 \right) } } \right] \nonumber \\&+\frac{\lambda }{\lambda +1}\,\left[ {1+2\,\sum \limits _{j=1}^9 {\,\left( {-\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{j}} -\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\frac{\pi ^{4}a^{10}}{4^{3}}\,\left( {1-\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}\delta _{1}^{\left( 1 \right) } } \right. \nonumber \\&\left. {-\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{7}a^{16}}{4^{6}}\,\left( {1-2\,\frac{\lambda -1}{\lambda +1}\frac{\pi a^{2}}{4}} \right) \,\delta _{2}^{\left( {11} \right) } -\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\frac{\pi ^{8}a^{18}}{4^{7}}\,\delta _{1}^{\left( 2 \right) } } \right] ^{ - 1}, \end{aligned}$$

(2.5)

where the quantities $\delta _{1}^{\left( 1 \right) }$, $\delta _{1}^{\left( 2 \right) }$, $\delta _{2}^{\left( {11} \right) }$ are defined by formulas (1.4.8) and take the following form:

$$\begin{aligned} \delta _{1}^{\left( 1 \right) }= & {} \frac{8}{3}\,\sum \limits _{\ell =1}^\infty {S_{\ell } } \ell ^{3};\nonumber \\ \delta _{1}^{\left( 2 \right) }= & {} -\frac{64}{945}\,\sum \limits _{\ell =1}^\infty {S_{\ell } } \ell ^{7};\nonumber \\ \delta _{2}^{\left( {11} \right) }= & {} \frac{32}{9}\sum \limits _{\ell =1}^\infty \, \left( {\left( {\pi \ell } \right) ^{2}S_{\ell } +\frac{\left( {-1} \right) ^{\ell +2}}{\sinh \,\pi \ell }} \right) \ell ^{3}\,\sum \limits _{j=1}^\infty {S_{j} } j^{3}. \end{aligned}$$

(2.6)

3 Analysis of the SAM-PA solution

In this Section we will carry out an analysis of the effective heat transfer parameter $q_{{\text {SAM-P}}}$ (2.5), (2.6).

• (i) We show that splitting of expression (2.5) into a series for $a\rightarrow 0$ coincides with the original expression (2.2) for the effective coefficient with accuracy of $a^{14}$ for arbitrary values of $\lambda$ (the error caused by the second correction term $\Delta _{2}$ is of order $a^{16})$. We have

  $$\begin{aligned}&q_{{\text {SAM-P}}} \sim 1+2\,\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}\,a^{2}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{2}a^{4}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{3}a^{6}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{4}a^{8}\nonumber \\&\quad +\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{5}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\frac{\pi ^{4}}{4^{3}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{10}+\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{6}+2\,\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{5}}{4^{4}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{12}\nonumber \\&\quad +\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{7}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{5}\frac{\pi ^{6}}{4^{5}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{14}\nonumber \\&\quad +\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{8}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{5}\frac{\pi ^{7}}{4^{6}}\delta _{2}^{\left( {11} \right) } } \right) \,a^{16}+O\,\left( {a^{18}} \right) \quad \hbox { for }a\rightarrow 0;\nonumber \\&q\sim 1+2\,\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}\,a^{2}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{2}a^{4}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{3}a^{6}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{4}a^{8}\nonumber \\&\quad +\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{5}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\frac{\pi ^{4}}{4^{3}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{10}+\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{6}+2\,\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{5}}{4^{4}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{12}\nonumber \\&\quad +\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{7}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{5}\frac{\pi ^{6}}{4^{5}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{14}\nonumber \\&\quad +\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{8}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{4}\frac{\pi ^{7}}{4^{6}}\delta _{2}^{\left( {11} \right) } } \right) \,a^{16}+O\,\left( {a^{18}} \right) \quad \hbox { for }a\rightarrow 0. \end{aligned}$$

  (3.1)

• (ii) The Keller theorem [7] holds for $q_{{\text {SAM-P}}}$ (2.5), since the terms of order $a^{16}$ inclusively satisfy the following condition:

  $$\begin{aligned}&q_{{\text {SAM-P}}} \,\left( {\lambda \,,\;a} \right) \sim 1+2\sum \limits _{i=1}^9 {\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) } ^{i}+\frac{16}{\pi }\,\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\left( {\frac{\pi a^{2}}{4}} \right) ^{5}\\&\quad \times \left[ {\left( {1+\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}\delta _{1}^{\left( 1 \right) } +\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{2}\left( {\frac{\pi a^{2}}{4}} \right) ^{3}\delta _{2}^{\left( {11} \right) } } \right] +O\,\left( {a^{20}} \right) \quad \hbox { for }a\rightarrow 0;\\&q_{{\text {SAM-P}}}^{-\,1} \,\left( {\lambda ^{-\,1}\,,\;a} \right) \sim 1+2\sum \limits _{i=1}^8 {\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) }^{i}+2\,\frac{\lambda -1}{\lambda +1}\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{9}\\&\quad +\frac{16}{\pi }\,\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\left( {\frac{\pi a^{2}}{4}} \right) ^{5}\\&\quad \times \left[ {\left( {1+\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{2}\delta _{1}^{\left( 1 \right) } +\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{2}\left( {\frac{\pi a^{2}}{4}} \right) ^{3}\delta _{2}^{\left( {11} \right) } } \right] +O\,\left( {a^{20}} \right) \quad \hbox { for }a\rightarrow 0, \end{aligned}$$

  i.e., we have

  $$\begin{aligned} q_{{\text {SAM-P}}} \,\left( {\lambda \,,\;a} \right) \sim q_{{\text {SAM-P}}}^{-\,1} \,\left( {\lambda ^{-\,1}\,,\;a} \right) +O\,\left( {a^{18}} \right) \quad \hbox { for }a\rightarrow 0. \end{aligned}$$

• (iii) Solution $q_{{\text {SAM-P}}}$ (2.5), (2.6) is within the Hashin–Shtrikman pitchfork [8,9,10], since for $1\le \lambda <\infty$ we have

  $$\begin{aligned} \frac{1-\frac{\pi a^{2}}{4}+\lambda \,\left( {1+\frac{\pi a^{2}}{4}} \right) }{1+\frac{\pi a^{2}}{4}+\lambda \,\left( {1-\frac{\pi a^{2}}{4}} \right) }=\underline{q}_\mathrm{H-S} \le q_{{\text {SAM-P}}} \le \overline{q} _\mathrm{H-S} =\lambda \,\frac{2-\frac{\pi a^{2}}{4}+\lambda \,\frac{\pi a^{2}}{4}}{\frac{\pi a^{2}}{4}+\lambda \,\left( {2-\frac{\pi a^{2}}{4}} \right) }, \end{aligned}$$

  where $\underline{q}_\mathrm{H-S}$ and $\overline{q}_\mathrm{H-S}$ denote lower and upper Hashin–Shtrikman bounds.

The left-hand side of the above inequality follows from comparison of the asymptotic formula $q_{{\text {SAM-P}}}$ (3.1) and $\underline{q}_\mathrm{H-S}$:

$$\begin{aligned}&\underline{q}_\mathrm{H-S} \sim 1+2\,\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}\,a^{2}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{2}a^{4}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{3}a^{6}+2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi a^{2}}{4}} \right) ^{4}a^{8}\nonumber \\&\quad +2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{5}\,a^{10}+o\,\left( {a^{10}} \right) \quad \hbox { for }a\rightarrow 0; \end{aligned}$$

(3.2)

$$\begin{aligned}&q_{{{\text {SAM-P}}}} \sim 1+2\,\frac{\uplambda -1}{\uplambda +1}\,\frac{\uppi }{4}\,a^{2}+2\,\left( {\frac{\uplambda -1}{\uplambda +1}\,\frac{\uppi }{4}} \right) ^{2}a^{4}+2\,\left( {\frac{\uplambda -1}{\uplambda +1}\,\frac{\uppi }{4}} \right) ^{3}a^{6}+2\,\left( {\frac{\uplambda -1}{\uplambda +1}\,\frac{\uppi a^{2}}{4}} \right) ^{4}a^{8}\nonumber \\&\quad +\left( {2\,\left( {\frac{\lambda -1}{\lambda +1}\,\frac{\pi }{4}} \right) ^{5}+\left( {\frac{\lambda -1}{\lambda +1}} \right) ^{3}\,\frac{\pi ^{4}}{4^{3}}\delta _{1}^{\left( 1 \right) } } \right) \,a^{10}+o\,\left( {a^{10}} \right) \quad \hbox { for }a\rightarrow 0, \end{aligned}$$

(3.3)

when $\lambda \ge 1$, $\delta _{1}^{\left( 1 \right) } >0$.

If $0\le \lambda \le 1$, the following estimation holds:

$$\begin{aligned} \uplambda \,\frac{2-\frac{\uppi a^{2}}{4}+\uplambda \,\frac{\uppi a^{2}}{4}}{\frac{\uppi a^{2}}{4}+\uplambda \,\left( {2-\frac{\uppi a^{2}}{4}} \right) }=\underline{{q}}_{\,\mathrm{H}-\mathrm{S}} \le {q}_{{{\text {SAM-P}}}} \le {\overline{{q}}} _{\,\mathrm{H}-\mathrm{S}} =\frac{1-\frac{\uppi {a}^{2}}{4}+\uplambda \,\left( {1+\frac{\uppi {a}^{2}}{4}} \right) }{1+\frac{\uppi {a}^{2}}{4}+\uplambda \,\left( {1-\frac{\uppi {a}^{2}}{4}} \right) }. \end{aligned}$$

The obtained inequality follows from (3.2), (3.3) for $\lambda \le 1$.

Figures 1, 2, 3, 4, 5, 6, and 7 present values of the effective heat transfer coefficients ${q}_{\mathrm{SAM}-\mathrm{P}}$, yielded by formulas (2.5), (2.6). The behavior of the effective ${q}_{\mathrm{SAM}-\mathrm{P}}$ parameter is of particular interest for the values of geometric and physical composite characteristics being closed to the limiting values. Therefore, we consider either very large (Figs. 3, 4) or very small (Figs. 1, 2) values of $\lambda$ conductivity and we take into account large values of a (Figs. 5, 6, 7).

Fig. 1

Effective heat transfer coefficient: $q_{{{\text {SAM-P}}}}$—SAM-PA; ${q}_{\mathrm{SAM\,(N)}}$—generalized SAM; $q_{\mathrm{as}\;\mathrm{s}}^{\left( 0 \right) }$—asymptotic solution (6.6.61) from [11], recast by the Keller formula [7]; $q_{\mathrm{MF}} \;\left( {\bar{{{q}}}_{\mathrm{H-S}} }\right)$—MF (upper Hashin–Shtrikman bound); $q_{\mathrm{as}}^{\left( 0 \right) }$—asymptotics (1.1.3)

Fig. 2

Effective heat transfer coefficient for inclusions of small conductivity $\lambda =2\times 10^{-3}: {q}_{{{\text {SAM-P}}}}$—SAM-PA; ${q}_{\mathrm{SAM}\,\left( \mathrm{N} \right) }$—generalized SAM; ${q}_{\mathrm{f}}$—formula (6.8.90) from [11]; ${q}_{\mathrm{MF}} \;\left( {\bar{{{q}}}_{\,\mathrm{H}-\mathrm{S}} } \right)$—MF (upper Hashin–Shtrikman bound); ${q}_{\mathrm{as}\;\mathrm{f}}^{\left( 0 \right) }$—asymptotic formula (49) from [12], recast by the Keller formula [7]

Fig. 3

Effective heat transfer coefficient for inclusions with large conductivity $\lambda =5\times 10^{2}$: ${q}_{\mathrm{SAM-P}}$—SAM-PA; ${q}_{\mathrm{SAM}\,\left( \mathrm{N} \right) }$—generalized SAM; ${q}_{\mathrm{f}}$–formula (6.8.90) from [11]; ${q}_{\mathrm{MF}} \;\left( {\underline{{q}}_{\,\mathrm{H-S}} } \right)$—MF (lower Hashin–Shtrikman bound); ${q}_{\mathrm{as}\;\mathrm{f}}^{\left( \infty \right) }$—asymptotic formula (49) from [12]

Fig. 4

Effective heat transfer coefficient for the absolutely conductive inclusions ($\lambda \rightarrow \infty )$: ${q}_{{{\text {SAM-P}}}}$—SAM-PA; ${q}_{\mathrm{SAM}\,\left( \mathrm{N} \right) }$–generalized SAM; ${q}_{\mathrm{as}\;\mathrm{s}}^{\left( \infty \right) }$—asymptotic solution (6.6.61) from [11]; ${q}_{\mathrm{num}}$—numerical solution [9]; ${q}_{\mathrm{MF}} \;\left( {\underline{{q}}_{\mathrm{H-S}} } \right)$—MF (lower Hashin–Shtrikman bound); ${q}_{\mathrm{as}}^{\left( \infty \right) }$—asymptotics (1.1.2)

Fig. 5

Effective heat transfer coefficient for large values of inclusions (${a}=0.9)$: ${q}_{{{\text {SAM-P}}}}$—SAM-PA; ${q}_{\mathrm{SAM}\,\left( \mathrm{N} \right) }$—generalized SAM; ${q}_{\mathrm{MF}} \;\left( {{q}_{\mathrm{H}-\mathrm{S}} } \right)$—MF (Hashin–Shtrikman bounds); ${q}_{\mathrm{as}\;\mathrm{f}}^{\left( \infty \right) } \;\left( {{q}_{\mathrm{as}\;\mathrm{f}}^{\left( 0 \right) } } \right)$—asymptotic formula (49) [12] (recast by Keller formula [7]); ${q}_{\mathrm{as}\;\mathrm{s}}^{\left( \infty \right) } \;\left( {{q}_{\mathrm{as}\;\mathrm{s}}^{\left( 0 \right) } } \right)$—asymptotic solution (6.6.61) from [11] (recast by Keller formula [7])

Fig. 6

Effective heat transfer coefficient for large values of inclusions ${a}=0.95$: ${q}_{{{\text {SAM-P}}}}$—SAM-PA; ${q}_{\mathrm{SAM}\,\left( \mathrm{N} \right) }$—generalized SAM; ${q}_{\mathrm{MF}} \;\left( {{q}_{\mathrm{H}-\mathrm{S}} } \right)$—MF (Hashin–Shtrikman bounds); ${q}_{\mathrm{as}\;\mathrm{f}}^{\left( \infty \right) } \;\left( {{q}_{\mathrm{as}\;\mathrm{f}}^{\left( 0 \right) } } \right)$—asymptotic formula (49) from [12] (recast by the Keller formula [7]); ${q}_{\mathrm{as}\;\mathrm{s}}^{\left( \infty \right) } \;\left( {{q}_{\mathrm{as}\;\mathrm{s}}^{\left( 0 \right) } } \right)$—asymptotic solution (6.6.61) from [11] (recast by Keller formula [7])

Fig. 7

Effective heat transfer coefficient for sizes of inclusions close to the maximum possible ${a}=0.995$: ${q}_{{{\text {SAM-P}}}}$—SAM-PA; ${q}_{\mathrm{SAM}\,\left( \mathrm{N} \right) }$—generalized SAM; ${q}_{\mathrm{MF}} \;\left( {{q}_{\mathrm{H-S}} } \right)$—MF (Hashin–Shtrikman bounds); ${q}_{\mathrm{as}\;\mathrm{f}}^{\left( \infty \right) } \;\left( {{q}_{\mathrm{as}\;\mathrm{f}}^{\left( 0 \right) } } \right)$—asymptotic formula (49) from [12] (recast by the Keller formula [7]); ${q}_{\mathrm{as}\;\mathrm{s}}^{\left( \infty \right) } \;\left( {{q}_{\mathrm{as}\;\mathrm{s}}^{\left( 0 \right) } } \right)$—asymptotic solution (6.6.61) from [11] (recast by Keller formula [7])

In Table 1, for average and large sizes of inclusions, the values of the effective heat transfer parameter are reported based on the carried out computations given in [11,12,13,14,15,16] for the case of absolutely conductive inclusions $\left( {\lambda \rightarrow \infty } \right)$. Further, they are compared with results of SAM-PA computations based on formulas (2.5), (2.6).

Table 2 reports the values of the averaged coefficient computed with a help of SAM-PA in contrast to the asymptotic solutions obtained in [11, 12, 15, 16] for inclusions of large sizes close to the limiting ones ($a\rightarrow 1)$ and for large conductivity $\lambda>>1$ (including the limiting case $\lambda \rightarrow \infty )$.

The so far carried out analysis of the obtained computational results allows to formulate the following statements.

• (i) The generalized SAM solution, with a help of the PA procedure, allows to essentially extend its area of applicability.

• (ii) The formulas of the effective parameter (2.5), (2.6) correctly describe qualitatively its changes for limiting values of the geometric and physical composite parameters and yield the quantitative estimation close to the asymptotic ones for the inclusions size close to 1.

• (iii) The formula SAM-PA preserves accuracy accepted by practice for inclusions of the arbitrary conductivity $(0\le \lambda <\infty$, $\lambda \rightarrow \infty )$ for the values $\le \mathrm {a} \le \, .996$.

4 Concluding remarks

The effective properties of the fiber-reinforced composite materials with fibers of circular cross section are investigated. The novel features of our research are concluded as:

• (i) Improvements of the SAM solution with a help of PA are developed.

• (ii) It is shown that the PA-modified solution does not change the structure of the effective heat transfer parameter. Namely, the following have been validated:

  • (a) Development into a series for small sizes of inclusions coincides with the input formula of the effective coefficient with accuracy up to the terms order of $a^{14}$ inclusively;

  • (b) The Keller theorem is satisfied asymptotically including terms of order ${a}^{16}$;

  • (c) The proposed result is within the Hashin–Shtrikman pitchfork.

• (iii) Analysis of the SAM-PA relations and comparison of our computational results with those obtained by others authors allow to conclude that the transformation of the N-iteration SAM solution with a help of PA essentially extends the area of its applicability. Namely, the N-iteration SAM solution describes the percolation transition and gives close to asymptotic values of the reduced parameter up to the size of inclusions “$a\approx 0.996$”.

Table 1 Effective heat transfer coefficient for absolutely conductive inclusions

Table 2 Effective heat transfer coefficient for large sizes of inclusions and large conductivity