Abstract
This paper presents two formulations of the segment method: one with absolute coordinates and the second with joint coordinates. The nonlinear equations of motion of slender links are derived from the Lagrange equations by means of the methods used in multibody systems. Values of forces and moments acting in the connections between the segments are defined using a new and unique procedure which enables the mutual interaction of bending and torsion to be considered. The models take into account the influence of the velocity of the internal fluid flow on the riser’s dynamics. The dynamic analysis of a riser with fluid flow requires calculation of the curvature by approximation of the Euler angles with polynomials of the second order. The influence of the sea environment, such as added mass of water, drag and buoyancy forces as well as sea current, is considered. In addition, the influence of torsion is discussed. Validation is carried out for both models by comparing the authors’ own results with those obtained from experimental measurements presented in the literature and from COMSOL, Riflex and Abaqus software. The validation is concerned with vibrations of cables and the riser with internal fluid flow as well as with frequencies of free and forced vibrations of a riser fully or partially submerged in water. The numerical effectiveness of both formulations is examined for dynamic analysis of the riser, whose top end is moving in a horizontal plane. Conclusions concerned with the effectiveness of both formulations of the segment method and the influence of torsional vibrations on numerical results are formulated.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The segment method is, in addition to the yet more popular finite element method, one of the discretisation methods for continuous systems used very widely in modelling systems with slender links. Initially, the segment method (SM) was developed by Huston and co-authors for modelling lines and cables and for analysing large deflections of slender links. Winget and Huston in [1] present a nonlinear, spatial model of a cable or chain, in which the continuous system is replaced by a series of links connected to each other by ball-and-socket joints. Closed kinematic sub-chains are left out of consideration. The position of each link is defined in relation to the preceding link. Hydrodynamic forces are included in the equations of motion. The calculations are carried out for a rotary crane with a payload hanging on a cable partly submerged in water. The extension of the method to systems with tree-like structures, still without closed sub-chains, is presented in [2]. In addition to relative angles, Euler parameters with relative angular velocities are also introduced for the description of system kinematics. The equations of motion are developed on the basis of the Lagrange form of d’Alembert’s principle. The method in these formulations does not account for the flexibility of cables. Flexibility of the system is taken into account in [3] by introducing three rotational and three translational springs at the connection point between the segments. The author considers small relative displacements which enable the interacting forces in the connection between two segments to be replaced by one force and one torque.
Paper [4] presents the generalisation and recapitulation of the results presented in [1,2,3], namely calculation of stiffness coefficients of rotary springs as well as derivation of the equations of motion, while the continuity of displacements is ensured. An extensive reference list (158 items) concerned with modelling of rigid and flexible multibody systems is included; however, no calculation example, as in [2, 3], is given.
The validation of the elaborated models is presented in [5] by using as an example a multilink pendulum with a lumped mass at its end. The authors compare their own results with an analytical solution for vibrations with small amplitudes and frequencies of free vibrations. In addition, results are compared with experimental measurements and with SEADYN computer simulation for the displacements of the end of the cable with a spherical body attached and submerged in water. All examples deal with planar models.
A computer program based on the formulations of the segment method was developed for spatial dynamic analysis of bodies and towing or hoisting cables partially or fully submerged in water [1,2,3,4,5].
Analysis of the influence of the water environment with special attention to hydrodynamic forces such as buoyancy, inertial forces and drag forces is discussed in [6]. Two cases are considered: buoy release and anchor drop. The discussion is limited to planar cases.
The application of the segment method to modelling of flexible systems is presented in [7, 8]. The first paper is concerned with theoretical aspects of the method and introduces springs connecting the segments together with a description of stiffness coefficient calculations. The second presents numerical examples and describes planar dynamics of a clamped and rotating beam. A large difference between the results obtained with those obtained using FEM can be seen; for the rotating beam, the differences are about 14%.
Problems connected with winding and unwinding cables with variable lengths are analysed in [9, 10]. Pay-out/reel-in phenomena occurring in many offshore systems are a difficult problem because they require changeable mass and length of segments to be taken into account. In order to eliminate problems with calculation of moments of inertia of the segments with varied lengths, the authors apply the lumped mass method and consider the motion of a cable towed by a vessel. Amirouch [11] describes a procedure for creating a structural matrix of connections of bodies in a tree-like structure when the segment method for dynamic analysis of systems undergoing large base motion is applied. The author uses Kane’s equations presented by Huston and others and describes the advantages of the method for computer implementation especially when the equations of motion are formulated for flexible systems with small relative deflections, yet no numerical examples are presented.
The segment method, due to its simple physical interpretation and easy computer implementation, has also been applied in modelling beams [12, 13], cranes [14], robot manipulators [15], railroad track structures [16, 17] and compliant mechanisms [18]. A variant of the SM called the flexible segment method (FSM) is presented in [19], and its application to dynamic analysis of risers is described in [20, 21].
It is important to note that also a different definition of cables is presented in the literature. Huston and co-authors in papers [1,2,3,4,5,6,7,8,9,10] treat cables as elements with bending and torsional flexibility. Shear and longitudinal flexibility are very rarely considered. A different definition of cables is used in the review paper [22], where cables are treated as elements consisting of helically twisted strands around the core wire. Cables considered in [22] are categorised according to their geometry, the method of considering friction among the wires and the way of formulating equilibrium equations. Three basic groups of models are distinguished. The first group consists of thin-rod models, initially without bending and torsional flexibilities [23, 24], which finally have been included [25, 26] by modelling individual wires as thin rods. Semi-continuous models [27,28,29], in which each layer of a twisted wire is modelled as an orthotropic cylinder, form the second group of models. The third includes beam models [30,31,32], in which solid beam theory is used in order to formulate the equilibrium equations. A review of research concerned with this subject can be found in [33, 34]. Large deflections of cables are considered in [35, 36]. The formulations of the segment method presented in our paper are closest to the third group of models discussed in [22].
Along with the development of the finite segment method, the rigid finite element method (RFEM) similar in approach has been developed in Poland [37, 38]. In both methods (SM and RFEM), a continuous system is replaced by a discrete system of rigid bodies, yet the methods differ above all in their origin and formalism. According to [1, 2], the segment method was initially used for analysis of large deflections of cables and ropes without analysis of flexibility effects. By contrast, the rigid finite element method from the very beginning was formulated for flexible systems with spring–damping elements, although the first research was concerned with small vibrations about the static equilibrium. The classical formulation assumes that each rigid element has six degrees of freedom described by absolute displacements (translational and rotational). The rigid elements are connected by means of three translational springs (limiting longitudinal and transverse displacements) and three rotational springs (limiting relative rotations). Thus, unlike in SM, RFEM does not ensure the continuity of displacements.
Large base motion is introduced in [39, 40] but only for planar systems, while the respective formulation for spatial systems is presented in [41,42,43,44,45]. The formulations described in these papers as well as in [46] also include a modification of the method which ensures the continuity of displacements. This modification can be considered as another formulation of the segment method different in formalism from that presented by Huston and his co-workers, since it uses Lagrange equations of the second order and homogenous transformations.
The rigid finite element method and its modified formulations are applied to dynamic analysis of a wide range of machines and mechanisms including manipulators [41, 42, 45, 47], beams [43, 44], cranes [48, 49], vehicles [50] and band saws [51].
RFEM formulated in joint coordinates is also applied by Szczotka [52,53,54,55] for dynamic analysis of offshore pipeline installations with special emphasis on the following installation techniques: S-lay, J-lay and reel lay.
Modification of the RFEM formulated in absolute coordinates, which takes into account, apart from bending and torsional flexibilities (like SM), also longitudinal flexibility, is applied to analysis of forced vibrations of risers in [56,57,58,59,60]. Paper [61] presents applications of the method to dynamic analysis of risers and a rotating flexible beam.
3D formulation of the segment method in joint coordinates, with consideration of bending flexibility when torsion is omitted, is presented in [62]. Numerical effectiveness of this formalism enabled the method to be applied to the solution of a dynamic optimisation problem of stabilisation of forces in the connection of a riser with a wellhead.
This paper discusses two formulations of the segment method which differ in the choice of generalised coordinates. The first formulation applies absolute coordinates, which means that the motion of each segment is described by means of six generalised coordinates: three translational and three rotational displacements. ZYX Euler angles are used in order to describe the geometry of the system. The second formulation uses joint coordinates; the motion of a segment is defined by three rotation angles about axes of the inertial system and by coordinates of the origin of the local coordinate system. The approach presented in the paper, in comparison with earlier research devoted to the segment method, involves the following new components:
Both formulations of the SM consistently use ZYX Euler angles measured in the global coordinate system. Formulations presented by other authors usually use relative angles defining the deflections with respect to the preceding segment.
The equations of motion are derived from the Lagrange equations of the second order. The kinetic energy of the flexible link when absolute coordinates are used is formulated by homogenous transformations, similarly to the RFEM [46].
The formulation of an original method for calculating moments in the connection of segments reflecting bending and torsion differs from previously published approaches. A special expression for the potential energy of deformation of rotary springs is formulated, which enables mutual interaction of torsion and bending to be considered. The presented formulation enables static and dynamic analysis to be carried out when large differences between the angles of segments occur. It should also be noted that the formulae defining bending and torsional moments are identical for both joint and absolute coordinates.
Formulae for consideration of the influence of the sea environment based on Morison equations are given in a compact form for both formulations of SM.
An algorithm enabling consideration of the influence of internal fluid flow on equations of motion and vibration of a riser is developed. Because of the step change of inclination angles of segments with respect to local or global reference systems (lack of continuity of the angles’ first derivative), special approximation curves are proposed in order to define the curvature of the riser.
The paper presents validation of the proposed model by means of the comparison of the authors’ own results with those presented by other researchers or obtained from professional FEM software packages for free and forced vibrations of cables and risers.
Moreover, the numerical effectiveness of both formulations of the segment method in riser modelling is compared, and conclusions are formulated.
2 Segment method—geometry of the system
The main idea of the segment method consists in replacing the continuous system with a finite number of rigid bodies—segments connected by means of rotary joints. Mass (inertial) features of the discretised link are assumed by rigid segments, while spring–damping elements are responsible for flexibility and damping. Depending on how the position of a chosen segment is described and thus on the choice of the generalised coordinates, two approaches to the description of the motion of the segment can be distinguished: based on absolute or joint coordinates.
Let us consider a homogenous beam-like link (Fig. 1). Discretisation of the link is carried out, as in the rigid finite element method [46], in two steps. First the link is divided into n elements with equal length \(\Delta \) (Fig. 1a)—points \(B_0 -B_n \), and then, massless and non-dimensional spring–damping elements (sdes) are placed in the middle of the segments—points \(A_{i}\), \(i=1,{\ldots },n\). As a result, a system of \(n+1\) segments (rfe 0 to rfe n) connected by means of n sdes (numbered from 1 to n) is obtained.
Discretisation of the rigid link into segments a primary division b secondary division
A local coordinate system is assigned to each segment, and its origin (Fig. 2) is placed in the preceding sde and treated as a ball-and-socket joint enabling three rotations.
Local coordinate system assigned to segment i
The orientation of the local coordinate system \({x}_{i}^{\prime } {y}_{i}^{\prime } {z}_{i}^{\prime } \) with respect to the system \({x}^{\prime }{y}^{\prime }{z}^{\prime }\), whose axes are parallel to the axes of the inertial system, is defined by means of ZYX Euler angles (Fig. 3).
ZYX Euler angles
The angles \(\psi _i =\varphi _{i,3},\theta _i =\varphi _{i,2},\gamma _i =\varphi _{i,1} \) called yaw, pitch and roll [63] describe rotations of the i-th segment about axes of system \({x}^{\prime }{y}^{\prime }{z}^{\prime }\) as follows. The segment i rotates by the angle \(\psi _i \) about the axis \({z}^{\prime }\), and thus, the system assigned to the segment assumes the position \({x^{\prime \prime }}{y}^{\prime \prime }{z}^{\prime }\). Such a system is rotated about the axis \({y}^{\prime \prime }\) by the angle \(\theta _i \) assuming the position \({x}^{\prime \prime \prime }{y}^{\prime \prime }{z}^{\prime \prime \prime }\). The last rotation by the angle \(\gamma _i \) about the axis \({x}^{\prime \prime \prime }={x}_{i}^{\prime }\) leads to the system associated with segment i with axes \({x}_i^{\prime } {y}_i^{\prime } {z}_i^{\prime }\). The position of the beginning of the segment, according to the choice of the generalised coordinates, is defined either by the coordinates \(x_i,y_i,z_i\) of the origin of the system \({x}_i^{\prime } {y}_i^{\prime } {z}_i^{\prime } \) with respect to the global coordinate system (for absolute coordinates), or depends on coordinates of the preceding segments when joint coordinates are chosen. Continuity of displacements at connecting points of the segments is required, and thus, when absolute coordinates are used, reactions in these connections are externalised and respective constraint equations are formulated. This is unnecessary when joint coordinates are used.
2.1 Absolute coordinates
In this case, the generalised coordinates of the i-th segment are the components of a vector with six elements:
where \(\mathbf{r}_i =\left[ {{\begin{array}{l} {x_i } \\ {y_i } \\ {z_i } \\ \end{array} }} \right] \) are the coordinates of point \(A_i \) with respect to the global coordinate system, \({\varvec{\upvarphi }}_i =\left[ {{\begin{array}{l} {\gamma _i } \\ {\theta _i } \\ {\psi _i } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {\varphi _{i,1} } \\ {\varphi _{i,2} } \\ {\varphi _{i,3} } \\ \end{array} }} \right] \) are the Euler angles about axes parallel to the axes of the global system.
The vector of generalised coordinates of the flexible link consists of \(N_A =6({n+1})\) components and takes the following form:
Transformation of coordinates from the local system \(\left\{ i \right\} ^{\prime }\) to the global system is carried out as follows:
where \(\mathbf{r}\) is the vector of coordinates of a chosen point of segment i in the global system { }, \(\mathbf{r}^{\prime }\) is the coordinate vector of this point with respect to the local coordinate system \(\{i\}'\)\(\mathbf {R}_i=\mathbf {R}_i^{(3)}\mathbf {R}_i^{(2)}\mathbf {R}_i^{(1)}\) is the rotation matrix, \(\mathbf {R}_i^{(3)} =\left[ \begin{array}{lll} {c\varphi _{i,3}}&{}\quad {-s\varphi _{i,3} }&{}\quad 0\\ {s\varphi _{i,3} }&{}\quad {c\varphi _{i,3} }&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} \right] ,\mathbf {R}_i^{(2)} =\left[ \begin{array}{lll} {c\varphi _{i,2} }&{}\quad 0&{}\quad {s\varphi _{i,2} } \\ 0&{}\quad 1&{}\quad 0 \\ {-s\varphi _{i,2} }&{}\quad 0&{}\quad {c\varphi _{i,2} } \\ \end{array} \right] ,\)\(\mathbf {R}_i^{(1)} =\left[ \begin{array}{lll} 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad {c\varphi _{i,1} }&{}\quad {-s\varphi _{i,1} } \\ 0&{}\quad {s\varphi _{i,1} }&{}\quad {c\varphi _{i,1} } \\ \end{array} \right] \), \(c\varphi _{i,j} ={\cos }\varphi _{i,j}, s\varphi _{i,j} ={\sin }\varphi _{i,j}\) for \(j=1,2,3\).
When using homogenous transformations, formula (3) can be written in compact form as
where \({\bar{\mathbf{r}}}=\left[ {{\begin{array}{l} \mathbf{r} \\ 1 \\ \end{array} }} \right] \), \({\bar{\mathbf{r}}}^{\prime }=\left[ {{\begin{array}{l} {\mathbf{r}^{\prime }} \\ 1 \\ \end{array} }} \right] \), \(\mathbf{B}_i =\left[ {{\begin{array}{ll} {\mathbf{R}_i }&{}\quad {\mathbf{r}_i } \\ 0&{}\quad 1 \\ \end{array} }} \right] \).
2.2 Joint coordinates
Vectors of the generalised coordinates of segments take the following form:
where \({\varvec{\upvarphi }}_i \) is defined in (1) and the vector of generalised coordinates of the whole link has \(N_J =3+3({n+1})\) components:
where \(\mathbf{r}_0 =\left[ {x_0 }\quad {y_0 }\quad {z_0 } \right] ^\mathrm{T}\) are the coordinates of point \(A_0\) with respect to the system { } (Fig. 4).
Flexible link as a system of \(n+1\) rfes and n sdes
The coordinates \(\mathbf{r}_i \) of point \(A_i \) can be calculated from the relation
and the vector \({\varvec{\upphi }}_j =\left[ {{\begin{array}{l} {c\varphi _{j,2} c\varphi _{j,3} } \\ {c\varphi _{j,2} s\varphi _{j,3} } \\ {-s\varphi _{j,2} } \\ \end{array} }} \right] \) is the first column of the matrix \(\mathbf{R}_i \).
Having taken into account these relations in formula (3), the following formula for transformation of coordinates, when joint coordinates are used, is obtained:
It can be easily seen that the number of generalised coordinates for absolute coordinates is almost twice the number of coordinates when joint coordinates are used (\(N_A =2N_J -6)\). However, the transformation of coordinates from system \(\{i\}^{{\prime }}\) to system { } can be simply carried out for absolute coordinates (formula (4)—one multiplication of a matrix by a vector), while in the case of joint coordinates it is more complex (formula (8)).
3 Lagrange operators, kinetic energy
The equations of motion are derived from the Lagrange equations of the second order in the form
where \(\varepsilon _j (T)=\frac{\hbox {d}}{\hbox {d}t}\frac{\partial T}{\partial {q}_j}\) is the Lagrange operator, T is the kinetic energy of the link, V is the potential energy of the link, D is the function describing dissipation of energy (damping), \(q_j,\dot{q}_j\) are generalised coordinates and velocities, respectively, \(Q_j\) are generalised forces, and N is the number of generalised coordinates.
In order to formulate the equations of motion, the kinetic and potential energies of the flexible link have to be defined, the dissipation function when damping is considered has to be formulated, and generalised forces resulting from gravity and external forces together with those reflecting the sea environment when the link is fully or partially submerged in the sea have to be introduced.
Due to the different way of defining the position of a chosen point according to the choice of the generalised coordinates, the kinetic energy and thus the Lagrange operators are defined differently. The kinetic energy of segment i can be presented in one of two equivalent forms:
where \(\hbox {tr}(\mathbf{A})\) means the trace of matrix \(\mathbf{A}\), \({\dot{\mathbf{r}}}=\frac{d\mathrm{r}}{dt}'\), \({\dot{\bar{\mathbf{r}}}}= \frac{d {\bar{\mathbf{r}}}}{dt}'\), \(m_i \) is the mass of i-th element.
Form (10a) will be used when the kinetic energy is calculated in joint coordinates and (10b) when absolute coordinates are used.
Thus, the respective transformations are presented separately for each type of generalised coordinates.
When calculating the kinetic energy from formulae (10), not only the mass of segment i but also added mass and mass of the internal fluid can be taken into account by introducing the following substitute linear density:
where \(A_r =A_\mathrm{out} -A_\mathrm{inn} \), \(A_\mathrm{inn},A_\mathrm{out}\) are cross-sectional areas of the inner and outer riser, respectively, \(\rho _r,\rho _f,\rho _w \) are material density of the riser, internal fluid and water, respectively, \(c_M\) is a coefficient.
3.1 Absolute coordinates
Having carried out transformations described in [46], the kinetic energy of the i-th segment can be written in the form
where \({\dot{\mathbf{B}}}=\frac{d\mathrm{B}_{i}}{dt}\), \(\mathbf{H}_i \) is the pseudo-inertial matrix of segment i,
The integrals occurring in the above formulae can account not only for the mass of the riser but also for internal fluid and the added mass of water as in (11). When the procedure from [46] is applied, and bearing in mind that the matrices \({\dot{\mathbf{B}_i}}\) depend on the vectors \(\mathbf{q}_{A,i} \) and \({\dot{\mathbf{q}}}_{A,i}\), the Lagrange operator can be written in the following matrix form:
where \(\mathbf{A}_i =\left( {a_{i,k,j} } \right) _{k,j=1,\ldots ,6} \), \(a_{i,k,j} =\hbox {tr}\left\{ {\mathbf{B}_{i,k} \mathbf{H}_i \mathbf{B}_{i,j} ^{T}} \right\} \),
The following notation is used:
The calculation of elements of the matrices \(\mathbf{A}_i \left( {\mathbf{q}_{A,i} } \right) \) and vectors \(\mathbf{h}_{A,i} \left( \mathbf{q}_{A,i} ,{\dot{\mathbf{q}}}_{A,i} \right) \) according to formula (13) can be easily algorithmised. Many of the elements are equal to zero.
The Lagrange operator of the whole flexible link can be written in the form
where \(\mathbf{M}_A =\hbox {diag}\left\{ {\mathbf{A}_0 \ldots \mathbf{A}_i \ldots \mathbf{A}_n } \right\} \), \(\mathbf{h}_A =\left[ {\mathbf{h}_0^T \ldots \mathbf{h}_i^T \ldots \mathbf{h}_n^T } \right] ^{T}\), and the matrices \(\mathbf{A}_i \) and vectors \(\mathbf{h}_i \) are defined in (13).
3.2 Joint coordinates
The kinetic energy of segment i is presented in form (10a). Bearing in mind (8), the following is obtained:
After transformations, the kinetic energy of the link can be written in the form
where \(d_{i} = l_{i} \sum \nolimits _{{j = i + 1}}^{n} m_{j} ;d_{{i,j}} = l_{i} l_{j} \sum \nolimits _{{l = {{\max }}\left\{ {i,j} \right\} + 1}}^{n} m_{i}\); \(m=\sum _{i=0}^{n} m_i\) is constant, and the Lagrange operators are as follows:
where \(i=0,1,\ldots ,n;j=1,2,3\);
The formulae are easy to program, and by summing the respective elements, the following is obtained:
where \(\mathbf{\varepsilon }_{{\varvec{\upvarphi }}_i } =\left[ {{\begin{array}{l} {\varepsilon _{i,1} } \\ {\varepsilon _{i,2} } \\ {\varepsilon _{i,3} } \\ \end{array} }} \right] \), \(\mathbf{M}_J \), \(\mathbf{h}_J \) are generated in the loop realising formulae (18a) and (18b).
4 Energy of spring deformation
The energy of spring deformation of sde i placed between segments \(i-1\) and i can be calculated from the formula
where \(\Delta {\varvec{\upphi }}_i^ =\left[ {{\begin{array}{l} {\Delta \gamma _i } \\ {\Delta \theta _i } \\ {\Delta \psi _i } \\ \end{array} }} \right] =\left[ {{\begin{array}{l} {\Delta \varphi _{i,1} } \\ {\Delta \varphi _{i,2} } \\ {\Delta \varphi _{i,3} } \\ \end{array} }} \right] \) is the vector of rotation angles for transformation from the coordinate system \(\left\{ {i-1} \right\} ^{\prime }\) to \(\left\{ i \right\} ^{{\prime }},\mathbf{C}_i =\hbox {diag}\left\{ {C_{i,1} C_{i,2} C_{i,3} } \right\} \), \(C_{i,1}\) is the torsional stiffness coefficient, \(C_{i,2},C_{i,3} \) are bending stiffness coefficients.
The angles \(\Delta \varphi _{i,j} \) occurring in (20) (Fig. 5) defining the transformation from system \(\{i\}^{\prime }\) to system \(\{{i-1}\}^{\prime }\) can be calculated from the following formulae:
where \(\left( {\mathbf{R}_{i,\Delta \phi } } \right) _{i,j} \) denotes the element of the i-th row and j-th column of the matrix \(\mathbf{R}_{i,\Delta \phi }\):
Thus, the following expressions are introduced in the equations of motion of the segments \(i-1\) and i:
for \(i=1,\ldots ,n;j=1,2,3\).
Notation for calculations of moments caused by bending and torsion
The derivatives \(\frac{\partial \Delta {\varvec{\upphi }} _i }{\partial \varphi _{i-1,j} }\) and \(\frac{\partial \Delta {\varvec{\upphi }}_i}{\partial \varphi _{i,j} }\) can be calculated as follows:
where \(\alpha _{i,2} =-\frac{1}{c\Delta \varphi _{i,2} }\), and then:
as well as:
where \(\alpha _{i,1} =\frac{1}{c\Delta \varphi _{i,1} c\Delta \varphi _{i,2} }\), \(\beta _{i,1} =s\Delta \varphi _{i,1} s\Delta \varphi _{i,2} \), \(\alpha _{i,3} =\frac{1}{c\Delta \varphi _{i,2} c\Delta \varphi _{i,3} }\), \(\beta _{i,3} =s\Delta \varphi _{i,2} s\Delta \varphi _{i,3}.\)
After the necessary transformations, the derivatives (22) can be written as:
where \(\mathop {\overline{\mathbf {M}}}_i =\left[ {{\begin{array}{l} {C_{i,1} \Delta \varphi _{i,1} } \\ {C_{i,2} \Delta \varphi _{i,2} } \\ {C_{i,3} \Delta \varphi _{i,3} } \\ \end{array} }} \right] \), \({\overline{\mathbf {D}}}_i =\left[ {{\begin{array}{l} {{\bar{\mathbf {d}}}_{i,1} } \\ {{\bar{\mathbf {d}}}_{i,2} } \\ {{\bar{\mathbf {d}}}_{i,3} } \\ \end{array} }} \right] \), \({\overline{\overline{\mathbf {D}}}}_i =\left[ {{\begin{array}{l} {\bar{\bar{\mathbf {d}}}}_{i,1} \\ {\bar{\bar{\mathbf {d}}}}_{i,2} \\ {\bar{\bar{\mathbf {d}}}}_{i,3} \\ \end{array} }} \right] \), \({\bar{\mathbf {d}}}_{i,j} =\left[ {{\begin{array}{l} {\bar{d}} _{i,j,1} \\ {\bar{d}} _{i,j,2} \\ {\bar{d}} _{i,j,3} \\ \end{array} }} \right] ^T\), \({\bar{\bar{\mathbf {d}}}}_{i,j} =\left[ {{\begin{array}{l} {\bar{\bar{{ d}}}}_{i,j,1} \\ {\bar{\bar{{ d}}}}_{i,j,2} \\ {\bar{\bar{{ d}}}}_{i,j,3} \\ \end{array} }} \right] ^T\).
It is important to stress that in both formulations of the segment method the expressions for the derivatives of energy of rotational springs have identical form (26) although their assignment to the respective equations of motion depends on the choice of the generalised coordinates.
In the case of absolute coordinates, the following expressions have to be added to the left sides of the equations of motion of segments \(0\ldots n\):
- A.
Segment 0
$$\begin{aligned} \mathbf {F}_{s,0}^{\left( A \right) } =\left[ {{\begin{array}{c} 0 \\ {{\overline{\mathbf {D}}}_1 {\overline{\mathbf {M}}}_1 } \\ \end{array} }} \right] \end{aligned}$$(27a) - B.
Segments \(1\ldots n-1\)
$$\begin{aligned} \mathbf {F}_{s,i}^{\left( A \right) } =\left[ {{\begin{array}{c} 0 \\ {\overline{\overline{\mathbf {D}}}_i {\overline{\mathbf {M}}}_i +{\overline{\mathbf {D}}}_{i+1} {\overline{\mathbf {M}}}_{i+1} } \\ \end{array} }} \right] \end{aligned}$$(27b) - C.
Segment n
When joint coordinates are used, the following expressions occur in the left sides of the Lagrange equations for the respective segments:
- A.
Segment 0
$$\begin{aligned} \mathbf {F}_{s,0}^{(J)} ={\overline{\mathbf {D}}}_1 {\overline{\mathbf {M}}}_1 \end{aligned}$$(28a) - B.
Segments \(1\ldots n-1\)
$$\begin{aligned} \mathbf {F}_{s,i}^{(J)} ={\overline{\overline{\mathbf {D}}}}_i {\overline{\mathbf {M}}}_i+{\overline{\mathbf {D}}}_{i+1} {\overline{\mathbf {M}}}_{i+1} \end{aligned}$$(28b) - C.
Segment n
$$\begin{aligned} \mathbf {F}_{s,n}^{(J)} = {\overline{\overline{\mathbf {D}}}}_n {\overline{\mathbf {M}}}_n \end{aligned}$$(28c)
The procedure for calculation of moments (vectors \({\overline{\mathbf {M}}}_i )\) acting on segments \(i-1\) and i is different from the approaches used in previous papers [52,53,54] and [58,59,60].
5 Gravity and buoyancy forces
The potential energy of gravity and buoyancy forces for segment i can be written as follows:
where \({\overline{m}}_i =\rho _r V_{r,i} +\rho _f V_{f,i} -\rho _w V_{w,i} \) is the substitute mass, \(\rho _r,V_{r,i} \) are the density and volume of the riser segments, respectively, \(\rho _f,V_{f,i} \) are the density and volume of the internal fluid, respectively, \(\rho _w ,V_{w,i} \) are the density and volume of the buoyancy water, \(y_{c,i} \) is the coordinate y of the centre of mass of segment i with respect to the system { }, g is the acceleration of gravity.
When the riser cross section is circular, then
where \(D_{\mathrm{inn}} \) is the inner diameter of the riser, and \(D_{\mathrm{out}}\) is the outer diameter of the riser.
Let \(\mathbf{r}_{c,i}^{\prime } \) be the vector defining the position of the centre of mass \({\overline{m}}_i \) with respect to the local coordinate system of segment i; thus, the coordinate \(y_{c,i} \) can be calculated as follows:
where \({{\varvec{\updelta }}}_2^T =\left[ 0\quad 1\quad 0 \right] \).
Therefore, the derivatives of (29) with respect to generalised coordinates are as follows:
- A.
when absolute coordinates are used:
$$\begin{aligned} \frac{\partial V_{g,i} }{\partial \mathbf{q}_{A,i} }={\overline{m}}_i g\left[ {{\begin{array}{l} {\mathbf{\delta }_2 } \\ {\mathbf{G}_{c,i} } \\ , \end{array} }} \right] =-\mathbf{Q}_{A,i}^{(g)}, \end{aligned}$$(32)where \(\mathbf{G}_{c,i} =\left[ {{\begin{array}{lll} {{{\varvec{\updelta }}}_2^T \mathbf{R}_{i,1} \mathbf{r}_{c,i}^{\prime } } \\ {{{\varvec{\updelta }}}_2^T \mathbf{R}_{i,2} \mathbf{r}_{c,i}^{\prime } } \\ {{{\varvec{\updelta }}}_2^T \mathbf{R}_{i,3} \mathbf{r}_{c,i}^{\prime } } \\ \end{array} }} \right] \);
- B.
when joint coordinates are used:
Thus, in case A due to gravity and buoyancy forces, the vector \(\mathbf{Q}_{A,i}^{(g)}\) occurs on the right side of the Lagrange equations of segment i, while in the case of joint coordinates on the right side of the equations corresponding to \(\mathbf{r}_0 \) there is a component \(\mathbf{Q}_{J,i,\mathbf{r}_0 }^{(g)}\), but in the equations corresponding to the segments \(0\ldots i\), there are vectors \(\mathbf{Q}_{J,i,{\varvec{\upvarphi }}_0 }^{(g)} \),..., \(\mathbf{Q}_{J,i,{\varvec{\upvarphi }}_j }^{(g)} \),..., \(\mathbf{Q}_{J,i,{\varvec{\upvarphi }}_i }^{(g)} \), respectively.
6 Drag forces
The Morison equation is used in order to take into account the hydrodynamic drag. The elementary drag force acting on a section with length \(\Delta \xi \)of segment i (Fig. 6) can be presented in the following form:
where \(\mathbf{S}_i^{{\prime }} =e_H \left[ {{\begin{array}{l} {D_x \left| {v_x^{{\prime }} } \right| v_x^{{\prime }} } \\ {D_{yz} v_y^{{\prime }} v_{yz}^{{\prime }} } \\ {D_{yz} v_z^{{\prime }} v_{yz}^{{\prime }} } \\ \end{array} }} \right] \),\(\hbox {}e_H =-\frac{1}{2}\rho _w D_\mathrm{out} \), \(v_{yz}^{{\prime }} =\sqrt{v_y^{{{\prime }}2} +v_z^{{{\prime }}2} }\), \(\mathbf{v}^{{\prime }} =\left[ {{\begin{array}{l} {v_x^{{\prime }} } \\ {v_y^{{\prime }} } \\ {v_z^{{\prime }} } \\ \end{array} }} \right] =\mathbf{R}_i^T \left( {\mathbf{v}-\mathbf{v}_w } \right) \), \(\mathbf{v}={\dot{\mathbf{r}}}\), \(\mathbf{{r}'}=\mathbf{{r}'}(\xi )\), \(\left[ {{\begin{array}{l} {\xi } \\ {\bar{y}} \\ {\bar{z}} \\ \end{array} }} \right] \)\({\bar{y}} ={\bar{y}}(\xi )\), \({\bar{z}}={\bar{z}} (\xi ), D_x \) is the coefficient of tangential drag, and \(D_{yz}\) is the coefficient of normal drag, and \(\mathbf{v}_w\) is the vector of water velocity.
Hydrodynamic drag force
The velocity vector \(\mathbf{v}\) with respect to the global system { } is expressed by the formulae:
The force (36) with respect to system { } can be written in the form
The generalised force resulting from the force \(d\mathbf{F}\) with respect to the generalised coordinate \(q_k \) is as follows:
The further approach depends on the generalised coordinates used.
6.1 Hydrodynamic drag in absolute coordinates
From (3), it follows that:
The velocity \(\mathbf{v}\) is calculated in this case from formula (35a).
Bearing in mind (34), (35) and (36), generalised forces corresponding to drag forces can be calculated in the following way:
where \(\mathbf{S}_i^ =\mathbf{R}_i \mathbf{S}_i^{\prime } \), and they can be written in compact form as follows:
where \(\mathbf{Q}_{{\varvec{\upvarphi }}_i }^{(H)} =\left[ {{\begin{array}{lll} {Q_{\varphi _{i,1} }^{(H)} }&{} {Q_{\varphi _{i,2} }^{(H)} }&{} {Q_{\varphi _{i,3} }^{(H)} } \\ \end{array} }} \right] ^{T}\).
This vector will be included in the right side of the equations of motion of segment i.
6.2 Hydrodynamic drag in joint coordinates
In this case, the velocity \(\mathbf{v}\) is calculated according to formula (35b). From (8), it follows that:
Taking into consideration the above formulae, the generalised forces can be calculated according to the following:
Hydrodynamic drag forces acting on segment i are reflected in the equations of motion by the following vectors occurring on the right hand side of the equations of motion:
- A.
Vector \(\mathbf{Q}_{i,\mathbf{r}_0 }^{(H)} \) from (42a) in equations corresponding to \(\mathbf{r}_0 \).
- B.
Vectors \(\mathbf{Q}_{i,{\varvec{\upvarphi }}_k }^{(H)} \), whose components are defined by (42b), in equations corresponding to \({\varvec{\upvarphi }}_k\) (\(k=0,{\ldots },i-1\)).
- B.
Vectors \(\mathbf{Q}_{i,{\varvec{\upvarphi }}_i }^{(H)} \), defined by (42c), in equations corresponding to \({\varvec{\upvarphi }}_i \).
6.3 Internal fluid flow in the riser
An inertial force acts on a segment dS of the riser (Fig. 7a), as presented in [49, 50]:
where s is the Lagrange coordinate defined in Fig. 7a, r is the vector of coordinates with respect to the inertial system { }, u is the velocity of the internal fluid with relation to the riser, \({\dot{\mathbf{u}}}\) is the acceleration of the fluid with relation to the riser.
Quantities r and s are defined in the segment method by the following formulae:
where \(\mathbf{r}_i \), \({\varvec{\upphi }}_i \) are defined in (1) and (7), \(\xi \) is the local coordinate along the direction of the \(x_i^{\prime } \) axis (Fig. 7b).
Load on the riser from internal flow
Having taken into account (44), the force due to the internal fluid flow in the riser acting on segment i can be presented in the form
According to (11), the component \(\rho _{f} A_\mathrm{inn} \mathop \int \nolimits _{0}^{l_{i}} {\ddot{\mathbf{r}}}\, {d}\xi \) has to be considered in the expression for the kinetic energy of segment i and is then included in Eq. (15) or (19). Therefore, only three other components have to be considered in the formula defining the force \({\bar{\mathbf{F}}}_i^u \) caused by the internal flow.
When it is additionally assumed that the velocity of the flow is constant u (\({\dot{\mathbf{u}}}=0)\), the following force has to be applied at the centre of the mass of segment i:
where \(m_i^f =\rho _f A_\mathrm{inn} l_i \) is the mass of the fluid inside segment i.
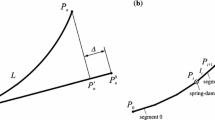
Bearing in mind (44a), one would obtain the following relation: \(\frac{\partial {\varvec{\upphi }}_i }{\partial \xi }=0\), which eliminates the second component of \(\mathbf{F}_i^u \) from the considerations. Thus, in the paper we propose the following approach which enables us to calculate \(\left( {\frac{\partial {\varvec{\upphi }}_i }{\partial \xi }} \right) _{\left| {\xi =\frac{l_i }{2}} \right. } \). Let us consider the situation in which the values \({\varvec{\upphi }}_i \) are known at three neighbouring points (Fig. 8) along the riser.
Notation used for calculating \(\frac{\partial \varphi _i }{\partial \xi }\)
A polynomial of the second order can be constructed through the points \(P_L,\;P_M,\;P_R\):
From the following:
the coefficients a, b, c can be determined, and then, the following can be calculated:
In order to calculate the curvature \(\left( {\frac{\partial {\varvec{\upphi }}_i }{\partial \xi }} \right) _{\left| {\xi =\frac{l_i }{2}} \right. } =\mathbf{k}_i \) inside the segments, the following is assumed:
for \(i=0\):
for \(i=1,2,\ldots ,n-1\):
for \(i=n\):
Bearing in mind that
the following formulae defining the generalised forces resulting from force \(\mathbf{F}_i^u \) are obtained:
A. for absolute coordinates, for \(i=0,1,{\ldots },n\):
where
B. for joint coordinates, for \(i=0,1,{\ldots },n\):
where
7 Constraints and synthesis of equations
Applications of the SM which will be presented in further sections require constraint equations reflecting the connection of both ends of the riser with the environment to be formulated. Moreover, when absolute coordinates are used, constraints have to be imposed on the connections between segments. The procedure that introduces constraint reactions into equations and formulates constraint equations for both types of coordinates is described below.
7.1 Absolute coordinates
In this case, generalised coordinates describing the motion of segments are independent. In order to connect segments at points \(A_i \) (Fig. 9), it is necessary to consider constraint reactions and to formulate constraint equations which eliminate translational relative motion of segments.
Constraint reactions: a general view of the riser, b reactions due to discretisation
Two reactions \(\mathbf{F}_i,\mathbf{F}_{i+1} \) for \(i=0,1,{\ldots },n\) act on each segment. \(\mathbf{F}_0 \) and \(\mathbf{F}_{n+1} \) represent external forces, \(\mathbf{F}_0 \) acts at the connection of the top end of the riser with a platform or a vessel, while \(\mathbf{F}_{n+1} \) reflects forces acting at the connection of the other end of the riser with the bottom of the sea. The following generalised forces are introduced in the equations of motion of segment i:
where \(\frac{\partial \mathbf{r}_{A_i } }{\partial \mathbf{q}_i }=\left[ {{\begin{array}{l} {\mathbf{I}_{3x3} } \\ \mathbf{0_{3x3} } \\ \end{array} }} \right] =\mathbf{D}_{i,i} \); \(\frac{\partial \mathbf{r}_{A_{i+1} } }{\partial \mathbf{q}_i }=\left[ {{\begin{array}{l} {\mathbf{I}_{3x3} } \\ {{\varvec{\upphi }}_i^{\prime } } \\ \end{array} }} \right] =\mathbf{D}_{i,i+1} \); \({\varvec{\upphi }}_i^{\prime } =l_i \left[ {{\begin{array}{l} {{\varvec{\upphi }} _{i,1}^T } \\ {{\varvec{\upphi }} _{i,2}^T } \\ {{\varvec{\upphi }} _{i,3}^T } \\ \end{array} }} \right] \).
Thus, the equations of motion of the system of segments \(0\ldots n\) take the following form:
where \(\mathbf{M}_A =\hbox {diag}\left\{ {\mathbf{A}_0^{\left( A \right) } \ldots \mathbf{A}_i^{\left( A \right) } \ldots \mathbf{A}_n^{\left( A \right) } } \right\} \),
The segments have to be connected with the environment—at points \(A_0 \) and \(A_{n+1} \), as well as between themselves. The constraint equations are assumed as follows:
where \({\bar{\mathbf{r}}}_0 (t)\) and \({\bar{\mathbf{r}}}_{n+1} (t)\) are known functions of time.
Having twice differentiated equations (55) with respect to time t, they can be presented in the acceleration form:
where \({\mathbf {g}}_{A} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\ddot{\mathbf {r}}}_{0} } \\ \vdots \\ \end{array} } \\ {{\mathbf {g}}_{{A,i}} } \\ {\begin{array}{*{20}c} \vdots \\ {{\mathbf {g}}_{{A,n}} } \\ {{\mathbf {g}}_{{A,n + 1}} +\ddot{\bar{\mathbf {{r}}}}_{{n + 1}} } \\ \end{array} } \\ \end{array} } \right] ,\qquad {\mathbf {g}}_{{A,i}} = - l_{i} \displaystyle \mathop \sum \nolimits _{{j = 1}}^{3} \mathop \sum \nolimits _{{k = 1}}^{3} {\varvec{\upphi }}_{{i,j,k}} {{\dot{\varphi }}}_{{i,j}} {{\dot{\varphi }}}_{{i,k}}\) for \(i=1,\ldots ,n+1\).
7.2 Joint coordinates
In this case, constraint equations refer only to points \(A_0\) and \(A_{n+1} \) because the choice of generalised coordinates ensures continuity of displacements at points \(A_1,{\ldots },A_n\).
Generalised forces resulting from external forces \(\mathbf{F}_0 \) and \(\mathbf{F}_{n+1} \) can be calculated according to the formulae:
Due to the following relation:
the reaction vector can be presented as follows:
where \(\mathbf{D}_J =\left[ {{\begin{array}{ll} {-\mathbf{I}}&{}\quad \mathbf{I} \\ 0&{}\quad {{\varvec{\upphi }}_0^{\prime } } \\ \vdots &{} \quad \vdots \\ 0&{}\quad {{\varvec{\upphi }}_i^{\prime } } \\ \vdots &{} \quad \vdots \\ 0&{} \quad {{\varvec{\upphi }}_n^{\prime } } \\ \end{array} }} \right] \), \(\mathbf{F}_J =\left[ {{\begin{array}{c} {\mathbf{F}_0 } \\ {\mathbf{F}_{n+1} } \\ \end{array} }} \right] \), \({\varvec{\upphi }}_i^{\prime } \) are defined in (53).
The constraint equations take the following form:
In view of (56), the constraint equations can be written in the acceleration form as follows:
where \({\mathbf {g}}_{J} = \left[ {\begin{array}{c} {{\mathbf {g}}_{{J,{\mathbf {r}}_{0} }} } \\ {{\mathbf {g}}_{{J,n + 1}} + \ddot{\bar{\mathbf {r}}}_{{n + 1}} } \\ \end{array} } \right] ,{\mathbf {g}}_{{J,{{{\mathbf {r}}}}_{0} }} = {\ddot{\mathbf {r}}}_{0}, {\mathbf {g}}_{{J,n + 1}} = \displaystyle {\mathop {\sum }\nolimits _{i = 0}^{n}} {\mathbf {g}}_{{A,i}}\).
Taking into account previous relations, the equations of motion can be written in the form
where \({\mathbf {M}}_j\) is defined in (20),
8 Model validation
Both formulations of the segment method should give identical numerical results for the same data. The numerical experiments carried out confirm this compatibility. Some small differences may occur when coefficients for the constraint stabilisation method are not chosen carefully enough (for absolute coordinates). Calculation times are different for simulations of identical problems of dynamics of risers, and the next section is devoted to these problems.
Validation is carried out in three steps: first, the results of the authors’ own simulations dealing with forced vibrations of a cable (beam) without consideration of the sea environment are compared with the results obtained by means of the software Abaqus. The next two steps of validation concerned with free vibrations of the riser with internal fluid flow are compared with those obtained by means of the finite element method (COMSOL program) presented in [64], and subsequently, the frequencies of free and forced vibrations are compared with the experimental measurements and calculations by means of the finite element method (RIFLEX program) presented in [65].
8.1 Vibrations of a cable
As mentioned above, the first validation example is concerned with forced vibrations of beams (cables) when no hydrodynamic forces are considered. Figure 10 shows the model of a beam and the load imposed on the beam considered.
Beam considered: a the model of the beam b course of the vertical force
The beam is loaded at its middle point M with a vertical force \(F_y \), the course of which is presented in Fig. 10b. Geometrical and mechanical properties of the beam are presented in Table 1.
Comparison of the authors’ own results obtained by SM for \(n=50\) elements with results obtained using Abaqus (3-node quadratic beam in space, hybrid formulation, B32H elements, \(n=50\)) is presented in Fig. 11.
Courses of displacements
Gravity forces have been omitted for numerical simulations, and the equations of motion have been integrated using the Runge–Kutta method with constant integration step \(h=0.0001\,\hbox {s}\). Very good compatibility of the results obtained by means of SM and FEM (Abaqus) can be observed.
Influence of the number of elements on the results obtained
The results presented in Fig. 12 show the influence of the number of segments into which the beam is discretised. It is important to note that already for \(n=10\) the results obtained differ from those obtained for \(n=50\) only by 1%. Differences between both formulations of SM are negligible.
The second example is concerned with analysis of forced vibrations with large amplitude of a line, shown in Fig. 13a, loaded with forces applied at its end (at point E). Forces in directions x and z act during 10 s, each in the way shown in Fig. 13b, while the force acting in the y direction during 50 s is constant and equals − 5000 N.
Line considered a model of the line b courses of forces acting at the end of the line
Parameters of the line considered are shown in Table 2.
Numerical simulations, using both the authors’ program and Abaqus, have been carried out for discretisation into \(n=50\) segments in the primary division. Comparison of the trajectory of point E is presented in Fig. 14, while Fig. 15 presents displacements of point E in the x, y and z directions.
Trajectory of point E calculated using Abaqus and SM in both formulations
Displacements of point E in respective directions: a\(x_E (t)\), b\(y_E (t)\), c\(z_E (t)\)
The equations of motion have been integrated using the Runge–Kutta method of the fourth order with constant integration step \(h=0.002\,\hbox {s}\). Analysis of the results presented in Figs. 15 and 16 shows very good compatibility of the results. Table 3 contains times of calculations (integration of the equations of motion) for both formulations of SM in relation to the number of discretisation segments. The following notation is used in the table: joint coordinates are denoted by “J”, and absolute coordinates are denoted by “A”. The influence of torsion is also examined for both formulations, and in order to compare the results, the case in which torsion is included is denoted by “3”, while “2” means that torsion is omitted. When joint coordinates “J” are used, the vector of generalised coordinates is in the form:
while for the absolute coordinates “A” the following takes place:
Times of calculations for SM in absolute coordinates (“A”) for \(n\le 50\) are longer than in joint coordinates (“J”). However, for \(n>50\) there is a reverse dependency, which means that then SM in absolute coordinates is more effective numerically.
8.2 Frequencies of free vibrations with consideration of internal fluid flow
Zhang et al. [64] discuss vibrations of risers subjected to axial tension, and among others, they analyse free vibrations of a straight vertical riser simply supported at both ends, with the parameters given in Table 4.
The coefficient \(i_T\) defines reinforcement of the pretension of the upper end of the riser:
where \({m}^{\prime }=\mathop \sum \nolimits _{i=0}^{n} m_i, m_i\) is defined by (28), \(g{m}^{\prime }\) is the force counterbalancing the weight of the riser and internal fluid in the sea.
Table 5 presents values of the first two frequencies of free vibrations of the riser analysed.
Results presented in [49] are obtained for the riser divided into 1500 elements (the authors do not give information about the type of elements, but presumably either shell or solid elements are used), and our results are obtained by means of the segment method (SM) with discretisation into \(n=50\) elements. It is important to note that the differences do not exceed 0.1%.
Table 6 presents the influence of the number of elements n on the results obtained only for \(i_T=1\).
8.3 Comparison of the results with those from experimental measurements and FEM calculations
Validation of the segment method is carried out on the basis of well-documented results of experimental measurements and numerical calculations presented in [66, 67]. The model of the riser analysed is shown in Fig. 16.
Models of the riser for validation a and c models used for frequencies of free vibrations, b model used for forced vibrations
Frequencies of free vibrations are calculated for cases (a) and (c), while in case (b) the top end of the riser performs a harmonic motion. Table 7 gives the parameters of the riser.
Table 8 presents the first three frequencies of free vibrations of the riser from Fig. 16a obtained by experimental measurements (E), the Riflex program (R) as in [66], the segment method (S), and calculated analytically (A) from the following formula:
where L is the length of the riser, i is the number of the free frequency. Using this formula, it is assumed that buoyancy forces act along the whole length of the riser.
Differences between values \(\omega _1\), \(\omega _2\), \(\omega _3\) from experimental measurements and calculated with the segment method are not larger than 5%.
Figure 17 presents the results of comparison of the forced vibrations for a riser from Fig. 16b when the upper end of the riser (point \(A_0\)) moves harmonically in a horizontal direction. The amplitude of the motion equals \(0.013\,\hbox {m}\) and its frequency is \(\omega _2 (E)=1.4771/\hbox {s}\). Good compatibility of the results of calculations and experimental measurements has been obtained both in the range of displacement and curvature amplitudes.
Amplitudes of: a displacements, b curvature of the forced harmonic motion
Table 9 presents vibration frequencies of the riser shown in Fig. 16c.
It can be seen that the differences, as in the case of using the Riflex package, are smaller than 10.5%.
In summary, the validation process has proved that the results obtained during the analysis of both free and forced vibrations are compatible with experimental measurements and the calculation results presented in [66] and [67]. Formulation of the segment method in joint coordinates has been used, and in order to calculate frequencies of free vibrations a procedure presented in [60] has been applied. Calculations were carried out on a mid-level PC with a 3.6 GHz processor, and the programs were written in Delphi.
9 Numerical simulations and effectiveness of SM
The dynamic problem for the riser presented in Fig. 18 is solved in order to compare the effectiveness of both formulations of the segment method.
Model of the riser
The top end of the riser moves in the xz plane along a trajectory similar to an ellipse (Fig. 19).
Motion of the top end of the riser: a trajectory, b\(x_0 (t),z_0 (t)\)
The translational motion of the bottom end of the riser (point \(A_{n+1})\) is not allowed. Parameters of the riser and environment are given in Table 10.
Notation is used as described in Sect. 8.1 (Eqs. (63–64)). It is assumed that the riser is loaded with the sea current along the z axis with constant velocity \(v_c =1\,\hbox {m}/\hbox {s}\). Figure 20 presents the shape of the riser and courses x(s) and z(s) for \(t=24\,\hbox {s}\). Courses for “J2” and “A2” as well as “J3” and “A3” coincide since the results obtained by both formulations are almost identical.
Shape of the riser for \(t=24\,\hbox {s}\): a 3D, bx(s), z(s)
Figures 21 and 22 present the influence of torsion on stresses in the middle of the riser length. The torsion influence is significant for stress, while its influence on displacements is negligible.
Bending stress in the middle of the riser: a\(\sigma _{xy} =M_3^{{\prime }}/wB\), b\(\sigma _{xz} =M_2^{{\prime }} /wB\), c\(\sigma _b =\sqrt{\sigma _{xy}^2 +\sigma _{xz}^2 }\), \(wB=\frac{\pi }{32}\left[ D_\mathrm{out}^4 -D_\mathrm{inn}^4 \right] D_\mathrm{out} \)
Stress \(\sigma _t =M_1^{\mathrm{{\prime }}} /wT\) due to torsion in the middle of the riser,
\(wT=\frac{\pi }{16}D_\mathrm{out}^3 \left[ {1-\left( {\frac{D_\mathrm{inn} }{D_\mathrm{out} }} \right) ^{4}} \right] ,\; M_1^{\mathrm{{\prime }}} ,M_2^{\mathrm{{\prime }}},M_3^{\mathrm{{\prime }}} \) are coordinates of the vector \({\bar{\mathbf{M}}}_i \) from (26). The bending and torsional stresses for \(t=24\,\hbox {s}\) along the riser are presented in Fig. 23.
Bending and torsional stresses for \(t = 24\) s a\(\sigma _{xy} \), b\(\sigma _{xz} \), c\(\sigma _t \)
The results presented in the above graphs are obtained for \(n=100\). The number of segments n into which the riser is divided is important, and thus, its influence on the bending stress in the middle of the riser is presented in Fig. 24.
Influence of n on bending stress \(\sigma _b \) at L / 2
The choice of generalised coordinates (“J” or “A”), and the decision whether the torsion is considered or not, directly influence the calculation time. Table 11 presents calculation times for different numbers of segments n for all four cases “J2”, “J3”, “A2” and “A3”.
The equations of motion were integrated by the Runge–Kutta method of the fourth order with constant integration step \(h=0.002\,\hbox {s}\) over time period \(\langle 0,36\,\hbox {s}\rangle \). Dependence of calculation time on number n is presented in Fig. 25.
Calculation time versus n
Having analysed the results presented in Table 11 and Fig. 25, it can be seen that shorter calculation times for \(n\ge 20\) are obtained when absolute coordinates are chosen. This effect is even larger when torsion is omitted.
9.1 Final remarks
The paper presents two formulations of the segment method: by means of joint and absolute coordinates. Analysis of published research shows that the formulation which uses joint coordinates is more frequent; however, formulation of the segment method for dynamic analysis of risers is simpler when absolute coordinates are applied.
Validation of the methods presented in Sect. 8 confirms the correctness of the formulated algorithms. The frequencies of free vibrations of the riser with consideration of the internal fluid flow calculated by means of the segment method are closely compatible with those obtained using the finite element method. Even for \(n\ge 25\), the differences are less than 0.1%. Also, a comparison of the authors’ own results with those obtained from experimental measurement and calculations carried out with the Riflex software package shows that the differences in frequencies of free vibrations are less than 5% for the riser of 9 m and 10.5% for the riser of 9.5 m with a spring at its bottom end. Equally good compatibility of results is obtained when vibrations forced by the harmonic motion of the top end are analysed.
Both formulations differ in numerical effectiveness. The calculations presented in Sect. 9 show that shorter calculation times are required when absolute coordinates are used. When the number of segments \(n\ge 40\), the calculation time for joint coordinates is almost 50% longer than when absolute coordinates are used.
Essential differences in both formulations of the segment method are presented in Table 12.
An important conclusion from the analysis of the numerical results is that when displacements and bending stress are analysed for typical risers, it is possible to leave torsion out of consideration. Neglecting torsion would result in further considerable shortening of calculation time. However, this can be done only when torsional vibrations are not important for fatigue analysis.
Results shown in Tables 3, 11 and 12 indicate that when n is large (dense discretisation), the formulation of the segment method in absolute coordinates (SM/A) is more effective than the formulation in joint coordinates (SM/J). When the sea environment is omitted, the effectiveness of MS/A is seen for \(n\ge 50\); this holds true even for \(n\ge 25\) when the sea environment is included. This dependency can be explained as follows. Times of calculations considerably depend on two factors:
dimension of the mass matrix \(N_A =6\left( {n+1} \right) \) for SM/A and \(N_J =3+3\left( {n+1} \right) \) for SM/J. In order to calculate the vector \({{\ddot{\mathbf{q}}}}\), it is necessary to solve either \(N_A +3\left( {n+1} \right) \) or \(N_J \) linear algebraic equations at each integration step. Therefore, calculation times are considerably shorter when the smaller number of equations in SM/J is solved.
number of arithmetic operations connected with generation of mass matrices, constraint equations and the vector of right hand sides of equations. In this case, SM/A is superior especially when the sea environment is considered. This is due to the fact that forces acting at segment i (also inertial forces) in SM/J also influence all preceding segments and thus lengthen the time of generation of the equations of motion.
Due to the reciprocal influence of both factors, the indication of numerical effectiveness of both formulations is equivocal. For a small number of n, the dimension of linear algebraic equations is more influential and thus SM/J is more effective, while for large n the generation times of the equations of motion are more influential and thus SM/A is more effective.
Whenever possible, it is more reasonable to apply formulation of the segment method in absolute coordinates and neglect torsion. A further reduction in calculation time can be expected if the specific form of the matrix \(\mathbf{D}\) (of reactions and constraints) is used in generating the equations of motion in absolute coordinates.
References
Winget, J.M., Huston, R.L.: Cable dynamics—a finite segment approach. Comput. Struct. 6, 475–480 (1976)
Huston, R.L., Passarello, C.E., Harlow, M.W.: Dynamics of multirigid-body systems. J. Appl. Mech. 45, 889–894 (1978)
Huston, R.L.: Flexibility effects in multibody systems. Mech. Res. Commun. 7, 261–268 (1980)
Huston, R.L.: Multi-body dynamics including the effect of flexibility and compliance. Comput. Struct. 14, 443–451 (1981)
Huston, R.L., Kamman, J.W.: Validation of finite segment cable models. Comput. Struct. 15(6), 653–660 (1982)
Kamman, J.W., Huston, R.L.: Advanced structural applications. Modelling of submerged cable dynamics. Comput. Struct. 20(1–2), 623–629 (1985)
Connely, J.D., Huston, R.L.: The dynamics of flexible multibody systems: a finite segment approach—I. Theoretical aspects. Comput. Struct. 50(2), 252–258 (1994)
Connely, J.D., Huston, R.L.: The dynamics of flexible multibody systems: a finite segment approach—II. Example problems. Comput. Struct. 50(2), 259–262 (1994)
Kamman, J.W., Huston, R.L.: Modeling of variable length towed and tethered cable structures. J. Guid. Control Dyn. 22(4), 602–608 (1999)
Kamman, J.W., Huston, R.L.: Multibody dynamics modelling of variable length cable systems. Multibody Syst. Dyn. 5, 21–221 (2001)
Amirouche, M.L.: Dynamic analysis of ‘tree-like’ structures undergoing large motions–a finite segment approach. Eng. Anal. 3(2), 111–117 (1986)
Yin, X., Du, S., Hu, J., Ding, J.: Analysis of dynamical buckling and post buckling for beams by finite segment method. Appl. Math. Mech. 26(9), 1181–1187 (2005)
Neves, A.C., Simoes, F.M.F., Pinto da Costa, A.: Vibrations of cracked beams: discrete mass and stiffness models. Comput. Struct. 168, 68–77 (2016)
Bak, M.K., Hansen, M.R.: Analysis of offshore knuckle boom crane–part one: modeling and parameter identification. Model. Identif. Control 34(4), 157–174 (2013)
Li, H., Zhang, X.: A method for modelling flexible manipulators: transfer matrix method with finite segments. Int. J. Comput. Inf. Eng. 10(6), 1086–1093 (2016)
Hamper, B.M., Recuero, M.A., Escalona, L.J., Shabana, A.A.: Use of finite element and finite segment methods in modeling rail flexibility: a comparative study. J. Comput. Nonlinear Dyn. 7, 041007-1–041007-11 (2012)
Hamper, B.M., Zaazaa, K.E., Shabana, A.A.: Modeling Railroad track structures using finite segment method. Acta Mech. 223(8), 1707–1721 (2012)
Turkkan, O.A., Su, H.-J.: A general and efficient multiple segment method for kinetostatic analysis of planar compliant mechanisms. Mech. Mach. Theory 112, 205–217 (2017)
Xu, X.-S., Wang, S.-W.: A flexible segment model based dynamics calculation method for free handing marine risers in re-entry. China Ocean Eng. 26(1), 139–152 (2012)
Xu, X.-S., Wang, S.-W., Lian, I.: Dynamic motion and tension of marine cables being laid during velocity change of mother vessel. China Ocean Eng. 27(5), 629–644 (2013)
Xu, X.-S., Yao, B.H., Ren, P.: Dynamic calculation for underwater moving slander bodies based of flexible segment model. Ocean Eng. 57, 111–127 (2013)
Spak, K., Agnes, G., Inman, D.: Cable modeling and internal damping developments. Appl. Mech. Rev. 65, 010801-1-18 (2013)
Triantafyllou, M.S.: Linear dynamics of cables and chains. Shock Vib. Dig. 16(3), 9–17 (1984)
Triantafyllou, M.S.: Dynamics of cables and chains. Shock Vib. Dig. 19(12), 3–5 (1987)
Velinsky, S.A.: On the design of wire rope. ASME J. Mech. Trans. 111(3), 382–388 (1989)
Sathikh, S., Moorthy, M.B.K., Krishnan, M.: A symmetric linear elastic model for helical wire strands under axisymmetric loads. J. Strain Anal. 31(5), 389–399 (1996)
Raoof, M., Hobbs, R.E.: Analysis of multilayered structural strands. J. Eng. Mech. 114(7), 1166–1182 (1988)
Jolicoeur, C., Cardou, A.: Semicontinuous mathematical model for bending of multilayered wire strands. J. Eng. Mech. 122(7), 643–650 (1996)
Crossley, J.A., Spencer, A.J.M., England, A.H.: Analytical solutions for bending and flexure of helically reinforced cylinders. Int. J. Solids Struct. 40, 777–806 (2003)
Ashkenazi, R., Weiss, M.P., Elata, D.: Torsion and bending stresses in wires of non-rotating tower crane ropes. OIPECC Bull. 87, 1157–1172 (2004)
Elata, D., Eshkenazy, R., Weiss, M.P.: The mechanical behavior of a wire rope with an independent wire rope core. Int. J. Solids Struct. 41, 1157–1172 (2004)
Usabiaga, H., Pagalday, J.M.: Analytical procedure for modeling recursively and wire by wire stranded ropes subjected to traction and torsion loads. Int. J. Solids Struct. 45, 5503–5520 (2008)
Rega, G.: Nonlinear vibrations of suspended cables—Part I: modeling and analysis. ASME Appl. Mech. Rev. 57(6), 443–478 (2004)
Rega, G.: Nonlinear vibrations of suspended cables—Part II: deterministic phenomena. ASME Appl. Mech. Rev. 57(6), 479–514 (2004)
Srinil, N., Rega, G., Chucheepsakul, S.: Three-dimensional non-linear coupling and dynamic tension in the large-amplitude free vibrations of arbitrarily sagged cables. J. Sound Vib. 269, 823–852 (2004)
Lacarbonara, W., Paolone, A., Vestroni, F.: Non-linear modal properties of non-shallow cables. Int. J. Nonlinear Mech. 42(3), 542–554 (2007)
Kruszewski, J.: Application of finite element method to calculations of ship structure vibrations (theory). European shipbuilding. J. Ship Tech. Soc. 3, 38–42 (1975)
Kruszewski, J., Gawroński, W., Wittbrodt, E., Najba,r F., Grabowski, S.: Metoda sztywnych elementów skończonych. (The rigid finite element method). Arkady, Warszawa (1975) (in Polish)
Wittbrodt, E.: Dynamika układów o zmiennej w czasie konfiguracji z zastosowaniem metody elementów skończonych. (Dynamics of systems with changing in time configuration analysed by the finite element method). Gdańsk University Press, No 354, Gdansk (1983) (in Polish)
Wojciech, S.: Dynamika płaskich mechanizmów dźwigniowych z uwzględnieniem podatności ogniw oraz tarcia i luzów w węzłach. (Dynamics of planar linkage mechanisms with consideration of both flexible links and friction as well as clearance in joints). Lodz Technical University Press, Monographs No 66, Lodz (1984) (in Polish)
Wojciech, S.: Dynamic analysis of manipulators with flexible links. Arch. Mech. Eng. XXXVII(3), 169–188 (1990)
Adamiec-Wójcik, I.: Dynamic analysis of manipulators with flexible links. PhD thesis, Strathclyde University, Glasgow (1992)
Wojciech, S., Adamiec-Wójcik, I.: Nonlinear vibrations of spatial viscoelastic beams. Acta Mech. 98, 15–25 (1993)
Wojciech, S., Adamiec-Wójcik, I.: Experimental and computational analysis of large amplitude vibrations of spatial viscoelastic beams. Acta Mech. 106, 127–136 (1994)
Wittbrodt, E., Wojciech, S.: Application of rigid finite element method to dynamic analysis of spatial systems. J. Guid. Control Dyn. 18(4), 891–898 (1995)
Wittbrodt, E., Adamiec-Wójcik, I., Wojciech, S.: Dynamics of Flexible Multibody Systems. Rigid Finite Element Method. Springer, Berlin (2006)
Płosa, J., Wojciech, S.: Dynamics of systems with changing configuration and with flexible beam-like links. Mech. Mach. Theory 35, 1515–1534 (2000)
Osiński, M., Wojciech, S.: Application of nonlinear optimisation methods to input shaping of the hoist drive of an offshore crane. Nonlinear Dyn. 17, 369–386 (1998)
Adamiec-Wójcik, I., Drąg, Ł., Wojciech, S., Metelski, M., Nadratowski, K.: A 3D model for static and dynamic analysis of an offshore knuckle boom crane. Appl. Math. Model. 66, 256–274 (2019)
Szczotka, M., Wojciech, S.: Application of joint coordinates and homogeneous transformations to modeling of vehicle dynamics. Nonlinear Dyn. 52(4), 377–393 (2008)
Wojnarowski, J., Adamiec-Wójcik, I.: Application of the rigid finite element method to modelling of free vibrations of band saw frame. Mech. Mach. Theory 40, 241–258 (2005)
Szczotka, M.: Pipe laying simulation with an active reel drive. Ocean Eng. 37, 539–548 (2010)
Szczotka, M.: Dynamic analysis of an offshore pipe laying operation using the reel method. Acta Mech. Sin. 27(1), 44–55 (2011)
Szczotka, M.: A modification n of the rigid finite element method and its application to the J-lay problem. Acta Mech. 220(1–4), 183–198 (2011)
Szczotka, M., Wojciech, S., Maczyński, A.: Mathematical model of a pipelay spread. Arch. Mech. Eng. 54(1), 27–46 (2007)
Adamiec-Wójcik, I., Wojciech, S., Wittbrodt, E.: Rigid finite element method in modelling of bending and longitudinal vibrations of ropes. Int. J. Appl. Mech. Eng. 17(3), 665–676 (2012)
Adamiec-Wójcik, I., Brzozowska, L., Wojciech, S.: Modification of the rigid finite element method in modeling dynamics of lines and risers. Arch. Mech. Eng. 60(3), 409–429 (2013)
Drag, Ł.: Model of an artificial neural network for payload positioning in sea waves. Ocean Eng. 115, 123–134 (2016)
Drąg, Ł.: Application of dynamic optimization to the trajectory of cable-suspended load. Nonlinear Dyn. 84(3), 1637–1653 (2016)
Drąg, Ł.: Application of dynamic optimisation to stabilise bending moments and top tension forces in risers. Nonlinear Dyn. 88(3), 2225–2239 (2017)
Adamiec-Wójcik, I., Drąg, Ł., Wojciech, S.: A new approach to the rigid finite element method in modeling spatial slender systems. Int. J. Struct. Stabil. Dyn. 18(2), 1850017-1–1850017-27 (2018)
Adamiec-Wójcik, I., Wojciech, S.: Application of the finite segment method to stabilisation of the force in a riser connection with a wellhead. Nonlinear Dyn. 93, 1853–1874 (2018)
Bauchau, O.A.: Flexible Multibody Dynamics. Springer, Heidelberg (2011)
Zhang, X., Gou, R., Yang, W., Chang, X.: Vortex-induced vibration dynamics of a flexible fluid convening marine riser subjected to axial harmonic tension. J. Braz. Soc. Mech. Sci. Eng. 40, 365 (2016)
Kaewunruen, S., Chiravatchradej, J., Chucheepsakols, S.: Nonlinear free vibrations of marine risers/pipes transporting fluid. Ocean Eng. 32, 417–440 (2005)
Yin, D., Lie, H., Russo, M., Grytoyr, G.: Drilling riser model tests for software verification. In: ASME 35th International Conference on Offshore Mechanical and Arctic Engineering, vol. 2: CFD and VIV():V002T08A032 (2016)
Yin, D., Lie, H., Russo, M., Grytoyr, G.: Drilling riser model tests for software verification. J. Offshore Mech. Arct. Eng. 140(1), 01170-1–011701-15 (2017)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Adamiec-Wójcik, I., Brzozowska, L. & Wojciech, S. Effectiveness of the segment method in absolute and joint coordinates when modelling risers. Acta Mech 231, 435–469 (2020). https://doi.org/10.1007/s00707-019-02532-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-019-02532-6