Flexural vibrations of geometrically nonlinear composite beams with interlayer slip

Abstract

This paper addresses moderately large vibrations of immovably supported three-layer composite beams. The layers of these structural members are elastically bonded, and as such, subjected to interlayer slip when excited. To capture the moderately large response, in the structural model a nonlinear axial strain-displacement relation is implemented. The Euler–Bernoulli kinematic assumptions are applied layerwise, and a linear interlaminar slip law is utilized. Accuracy and efficiency of the resulting nonlinear beam theory is validated by selective comparative plane stress finite element calculations. The outcomes of application examples demonstrate the grave effect of interlayer slip on the geometrically nonlinear dynamic response characteristic of layered beams.

1 Introduction

In various engineering applications, beams, plates and shells composed of several layers are used to optimize weight and load-bearing capacity of structures. The layers of composite members are bonded by, for instance, glue, bolts, or nails. In those cases, where the flexibility of the fastener is relatively large, rigid bond cannot be achieved and the layers slip against each other when loaded. The structural behavior becomes more complex than of homogeneous members, and thus, classical theories of analysis cannot be used anymore for response analysis.

This has been recognized a long time ago, and consequently, in the last decades various studies were devoted to the static analysis of beams and plates with interlayer slip subjected to lateral loading. The results of some early studies are summarized in the contributions of Pischl [25] and Goodman and Popov [14]. In Appendix B of Eurocode 5 [8], the $\gamma$-method [23], which is a simplified method to analyze the static response of layered structures with partial interaction, is included. The exact static analysis of composite beams with partial layer interaction was presented in Girhammar and Pan [10]. Static buckling of composite beams and beam columns was more recently treated, for example, in [6, 12, 21, 28]. In more sophisticated approaches, an inelastic relation between interlaminar shear traction and slip on the static deflection is considered. For instance, [24] describes an inelastic force-based finite element analysis of two-layer beams applying the assumptions of Timoshenko beam theory to each layer separately, and a higher-order beam theory for the inelastic analysis of composite beams with partial interaction can be found in [29]. An extension of the latter theory to geometric nonlinear beams was presented in [30]. Previously, in [26] a geometric nonlinear model for composite beams with partial interaction was introduced. Hozjan et al. [18] analyzed the geometrically and physically nonlinear static response of planar structures with partial interaction. Recently, in [2] the governing equations for predicting the moderately large static response of a fully restrained pinned-pinned beam were presented.

The dynamic behavior of composite beams with interlayer slip has been studied less frequently. In the pioneering paper of Girhammar and Pan [11], lateral vibrations of layered beams with interlayer slip were analyzed. Later, the same group provided an extension and generalization of this theory for the exact dynamic analysis of such structural members [13]. Adam et al. [3] developed an accelerated modal series solution of vibrations of flexibly bonded layered beams. Piezoelectric and thermo-piezoelectric vibrations of beams with interlayer slip were studied in [16, 17]. Challamel [5] treated lateral torsional vibrations of composite beams with partial interaction. The random dynamic response of an uncertain compound bridge subjected to moving loads was analyzed in [4]. Recently, Di Lorenzo et al. [22] presented an efficient procedure for the computation of lateral vibrations of discontinuous layered elastically bonded and non-classically supported beams.

A moderately large response in the presence of immovably supports causes nonlinear axial strains, i.e., the beam response becomes geometric nonlinear. In various studies, the influence of the membrane stress due to stretching of the central fiber on the dynamic response of homogeneous (e.g., [9, 31]) and layered beams (e.g., [15, 20]) has been considered. However, to the best knowledge of the authors, moderately large vibrations of beams with interlayer slip have not been analyzed yet. To fill this gap, in this contribution a theory for the analysis of the dynamic flexural response of composite beams with elastically bonded layers is presented, whose supports are rigidly held apart. In this theory, nonlinear axial strain-displacement relations are considered, which originate from moderately large vibrations of the member with horizontally restrained supports. In a common assumption, for each layer, the Euler–Bernoulli assumptions are assigned separately. To keep the derivations simple and clear, a three-layer composite beam with symmetrically disposed layers is considered. However, it should be noted that the proposed theory can be extended to beams with an arbitrary number of asymmetrically disposed layers.

The following paper is structured as follows. At first, the governing kinematic equations and their relation to the layerwise cross-sectional resultants of a three-layer composite beam are established. Conservation of momentum yields in combination of the cross-sectional resultants expressed in terms of the kinematic variables a set of coupled geometrically nonlinear equations of motion. Corresponding boundary conditions for various horizontally restrained beam ends are formulated. The proposed solution procedure is based on a modal expansion of the lateral deflection into the first few mode shapes of the corresponding linear beam. In an illustrative example, the transient response of a soft-hinged immovably supported member to a half-wave sinusoidally distributed time harmonic excitation is analyzed. In order to verify the proposed beam theory, the derived response is compared to the outcomes of an elaborate plane stress finite element analysis. The second example studies the nonlinear resonance of a beam with partial interaction, to show the effect of different load amplitudes and varying interlaminar stiffness on the amplitude frequency response of various kinematic variables and stress resultants.

2 Basic equations

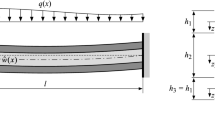
A single-span beam of length l in principal bending about the out of plane (y-)axis, composed of three elastically bonded layers with constant rectangular cross section along the central beam (x-)axis, is considered, as for instance shown in Fig. 1. Geometry and material parameters of the external layers are the same. That is,

$$\begin{aligned} h_1 = h_3 \, , \, A_1 = A_3 \, , \, E_1 = E_3 \, , \, \rho _1 = \rho _3 \, , \, EA_1 = EA_3 \, , \, EJ_1 = EJ_3 \end{aligned}$$

(1)

with $h_i$ denoting the thickness of the $i\hbox {th}$ layer, $A_i$ is the $i\hbox {th}$ layer cross-sectional area, $E_i$ the $i\hbox {th}$ layer Young’s modulus, $\rho _i$ the $i\hbox {th}$ layer density, $EA_i$ the $i\hbox {th}$ layer extensional stiffness, and $EJ_i$ the $i\hbox {th}$ layer bending stiffness. Subscript $i=1$ refers to quantities of the top layer, $i = 2$ to the central layer, and $i=3$ to the bottom layer. A time-varying distributed lateral load q(x, t) excites the structural member to flexural vibrations.

Fig. 1

Immovably supported three-layer beam with partial layer interaction

Since the bond between the layers is flexible, the layers displace against each other when the beam is deflected. This relative displacement between the top layer and the central layer, $\varDelta u_{12}$, and the central layer and the bottom layer, $\varDelta u_{23}$, is referred to as interlayer slip. Assuming that the layers are rigid in shear, Euler–Bernoulli theory is applied to each layer separately. This yields the lateral deflection $w_i$ and horizontal displacement $u_i$ at distance $z_i$ from the neutral axis of the $i\hbox {th}$ layer as [16]

$$\begin{aligned} w_i = w \, , \, u_i = u_i^{(0)} - z_i w_{,x} \qquad i = 1,2,3 \end{aligned}$$

(2)

with $(.)_{,x}$ indicating partial differentiation with respect to x, and $u_i^{(0)}$ is the $i\hbox {th}$ axial displacement at $z_i = 0$ (see Fig. 2). Expressing the axial displacements of the outer layers, $u_1^{(0)}$ and $u_3^{(0)}$, in terms of the central axial displacement $u_2^{(0)}$, cross-sectional rotation $w_{,x}$, and the interlayer slips $\varDelta u_{12}$ and $\varDelta u_{23}$, leads to [16]

$$\begin{aligned} u_1^{(0)} = u_2^{(0)} + dw_{,x} - \varDelta u_{12} \, , \,\, u_3^{(0)} = u_2^{(0)} - dw_{,x} + \varDelta u_{23} \end{aligned}$$

(3)

In these relations, d is the distance between the central axis and the neutral axis of the top/bottom layer, as shown in Fig. 2. In case of rectangular outer layers $d = (h_1+h_2)/2$.

Fig. 2

Deformed three-layer beam element at x and at time t (modified from [16])

Moderately large lateral vibrations in the presence of immovable supports strain the central axis, and thus, the axial strain-displacement relation becomes nonlinear (see e.g., [32]),

$$\begin{aligned} e_i = u_{i,x}^{(0)} + \frac{1}{2} w_{,x}^2 \, , \qquad i=1,2,3 \end{aligned}$$

(4)

The longitudinal strain at any fiber of the beam is therefore

$$\begin{aligned} \epsilon _i = e_i - z_i w_{,xx} = u_{i,x}^{(0)} + \frac{1}{2} w_{,x}^2 - z_i w_{,xx} \, , \qquad i=1,2,3 \end{aligned}$$

(5)

Assuming a constant slip modulus K, which is the same for both interfaces, the interlaminar shear traction $t_{s12}$ ($t_{s23}$) is linearly related to the interlayer slip $\varDelta u_{12}$ ($\varDelta u_{23}$), and in combination with the kinematic relations of Eq. (3) it follows that

$$\begin{aligned} t_{s12} = K \varDelta u_{12} = K \left( u_2^{(0)} - u_1^{(0)} + dw_{,x} \right) \, , \,\, t_{s23} = K \varDelta u_{23} = K \left( u_3^{(0)} - u_2^{(0)} + dw_{,x} \right) \end{aligned}$$

(6)

Application of Hooke’s law delivers the relation between the layerwise bending moment, $M_i$, and the layerwise axial force, $N_i$, respectively, and the kinematic quantities (see e.g., [32]),

$$\begin{aligned} M_i= & {} -EJ_i w_{,xx} \, , \qquad i=1,2,3 \end{aligned}$$

(7)

$$\begin{aligned} N_i= & {} EA_i e_i = EA_i \left( u_{i,x}^{(0)} + \frac{1}{2} w_{,x}^2 \right) \end{aligned}$$

(8)

The global stress resultants for the entire cross section (compare with Fig. 3) are composed of the layerwise quantities according to

$$\begin{aligned}&\displaystyle M = \sum \limits _i^3 M_i - (N_1 - N_3) d \end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle N = \sum \limits _{i=1}^3 N_i \end{aligned}$$

(10)

Fig. 3

Free-body diagram of a deformed infinitesimal three-layer beam element at time t. First-order (in red) and second-order (in blue) internal forces (color figure online)

No external axial load is applied to the beam, and thus, global axial force N (also referred to as membrane force) emerges from the nonlinear axial strains due to moderately large deflection w only. The effect of N on the dynamic response is captured through second-order analysis. That is, conservation of momentum in axial (x-) and transverse (z-)direction and conservation of angular momentum about the y-axis is applied to an infinitesimal beam element in its deformed state (shown in Fig. 3), yielding

$$\begin{aligned}&\displaystyle N_{,x} = 0 \end{aligned}$$

(11)

$$\begin{aligned}&\displaystyle T_{,x} + q = \mu {\ddot{w}} \end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle M_{,x} + N w_{,x} - T = 0 \end{aligned}$$

(13)

where $\mu = 2 \rho _1 A_1 + \rho _2 A_2$ denotes the mass per unit length, ${\ddot{w}}$ is the lateral acceleration, and T is the transverse cross-sectional force. In Eq. (11) the effect of longitudinal inertia and in Eq. (13) the effect of rotatory inertia have been omitted, thus limiting the analysis to the lower frequency range. Furthermore, in a common assumption of second-order analysis, the longitudinal force S has been replaced by the axial force N [27].

Equation (13) is differentiated with respect to x and subsequently combined with Eq. (12). Considering that according to Eq. (11) the axial force N is only a function of time t (and not of x) this results in

$$\begin{aligned} M_{,xx} + N w_{,xx} + q = \mu {\ddot{w}} \end{aligned}$$

(14)

In x-direction, omitting the longitudinal inertial, layerwise application of conservation of momentum yields [16]

$$\begin{aligned}&\displaystyle N_{1,x} + t_{s12} = 0 \end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle -N_{3,x} + t_{s23} = 0 \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle N_{2,x} - t_{s12} + t_{s23} = 0 \end{aligned}$$

(17)

3 Governing equations

3.1 Equations of motion

The equations of motion of this beam problem are obtained by expressing Eqs. (11), (14)–(17) in terms of the governing kinematic variables, i.e., lateral deflection w, interlayer slips $\varDelta u_{12}$ and $\varDelta u_{23}$, and axial displacement of the central axis $u_{2}^{(0)}$.

Inserting the expression for axial force N,

$$\begin{aligned}&\displaystyle N = EA_e\left( u_{2,x}^{(0)}+\frac{1}{2} w_{,x}^2\right) + EA_1(\varDelta u_{23,x}-\varDelta u_{12,x}) \end{aligned}$$

(18)

$$\begin{aligned}&\displaystyle EA_e = 2EA_1 + EA_2 \end{aligned}$$

(19)

which results from combining Eq. (10) with constitutive relation Eq. (8) and kinematic relation Eq. (3), into Eq. (11) leads to the first governing equation,

$$\begin{aligned} EA_e\left( u_{2,xx}^{(0)} + w_{,x} w_{,xx}\right) + EA_1(\varDelta u_{23,xx}-\varDelta u_{12,xx}) = 0 \end{aligned}$$

(20)

Next, in Eq. (9), $M_i$, $N_1$, and $N_3$ are substituted by Eqs. (7) and (8), respectively, and subsequently, variables $u_{1,x}^{(0)}$ and $u_{3,x}^{(0)}$ are replaced by the derivative of Eq. (3) with respect to x. This yields the total bending moment as

$$\begin{aligned} M = - {EJ_\infty }{w_{,xx}} + E{A_1}d\left( {\varDelta {u_{12,x}} + \varDelta {u_{23,x}}} \right) \end{aligned}$$

(21)

with

$$\begin{aligned} EJ_\infty = EJ_0 + 2d^2EA_1 \end{aligned}$$

(22)

denoting the bending stiffness of the rigidly bonded beam, and

$$\begin{aligned} EJ_0 = 2EJ_1 + EJ_2 \end{aligned}$$

(23)

is the bending stiffness of the non-composite beam, i.e., $K=0$. The second derivative of Eq. (21) with respect to x inserted into Eq. (14) leads to the second equation of motion,

$$\begin{aligned} - {EJ_\infty }{w_{,xxxx}} + E{A_1}d\left( {\varDelta {u_{12,xxx}} + \varDelta {u_{23,xxx}}} \right) + N{w_{,xx}} + q = \mu {\ddot{w}} \end{aligned}$$

(24)

Now, Eqs. (15), (16), and (17) are combined with constitutive relations Eqs. (8), (6) and kinematic relations Eq. (3), with the result

$$\begin{aligned}&\displaystyle \varDelta {u_{12,xx}} - \frac{K}{{E{A_1}}}\varDelta {u_{12}} - u_{2,xx}^{(0)} - {w_{,x}}{w_{,xx}} - d{w_{,xxx}} = 0 \end{aligned}$$

(25)

$$\begin{aligned}&\displaystyle \varDelta {u_{23,xx}} - \frac{K}{{E{A_1}}}\varDelta {u_{23}} + u_{2,xx}^{(0)} + {w_{,x}}{w_{,xx}} - d{w_{,xxx}} = 0 \end{aligned}$$

(26)

$$\begin{aligned}&\displaystyle \frac{K}{E{A_2}}\left( \varDelta {u_{23}} - \varDelta {u_{12}}\right) + {u_{2,xx}^{(0)} + w_{,x} w_{,xx}} = 0 \end{aligned}$$

(27)

One of the five coupled nonlinear partial differential equations of motion, Eqs. (20), (24)–(27) in terms of the four governing kinematic variables w, $\varDelta u_{12}$, $\varDelta u_{23}$, and $u_{2}^{(0)}$ are redundant because the sum of the underlying Eqs. (15) to (17) yields Eq. (11). Consequently, Eqs. (20), (25), and (26) are condensed to two equations, which are easier to solve. To this end, Eqs. (25) and (26) are summed up with the outcome

$$\begin{aligned} \varDelta {u_{23,xx}} + \varDelta {u_{12,xx}} - \frac{K}{{E{A_1}}}\left( {\varDelta {u_{23}} + \varDelta {u_{12}}} \right) - 2d{w_{,xxx}} = 0 \end{aligned}$$

(28)

Then, Eq. (25) is subtracted from Eq. (26). In the resulting expression, quantity $u_{2,xx}^{(0)} + {w_{,x}}{w_{,xx}}$ is eliminated by means of Eq. (20), yielding

$$\begin{aligned} \varDelta {u_{23,xx}} - \varDelta {u_{12,xx}} - {\delta ^2}\left( {\varDelta {u_{23}} - \varDelta {u_{12}}} \right) = 0 \end{aligned}$$

(29)

Parameter

$$\begin{aligned} {\delta ^2} = K\frac{{E{A_e}}}{{E{A_1}E{A_2}}} \end{aligned}$$

(30)

is proportional to K, and hence, can be considered as an indicator of the degree of composite action in longitudinal direction.

3.2 Boundary conditions

The equations of motion are solved in combination with the actual boundary conditions. Because this mixed initial-boundary value problem comprises one fourth-order differential equation (Eq. (24)) and three second-order differential equations (Eqs. (20), (28), (29)), for its solution five boundary conditions are to be specified at each end.

The ends of the considered structural members are immovably supported, i.e., at both ends the horizontal displacement of the central axis and the lateral deflection are zero,

$$\begin{aligned}&\displaystyle \left( u_2^{(0)}\right) _b = 0 \end{aligned}$$

(31)

$$\begin{aligned}&\displaystyle w_b = 0 \end{aligned}$$

(32)

and are either hinged supported without shear restraints, hard hinged supported, or clamped. Free-end boundary conditions are not considered because in moderately large beam vibrations axial force N is primarily a result of nonlinear stretching of the central fiber due to longitudinally fully restrained ends. In Eqs. (31) and (32), subscript b indicates quantities of the boundaries at $x=0$ and $x=l$.

Hinged support without shear restraints

When at a hinged end no shear restraints are applied (i.e., the slip between the layers is not restrained), the rotations of the layerwise cross section are not restrained, and consequently, the layerwise bending moments are zero, ${(M_i)}_b = 0$, $i = 1, 2, 3$. Eq. (7) facilitates to express this dynamic boundary condition in terms of kinematic quantity w as

$$\begin{aligned} (w_{,xx})_b = 0 \end{aligned}$$

(33)

At any hinged end, the overall bending moment is zero, $M_b = 0$. That is, according to Eq. (21) and considering Eq. (33)

$$\begin{aligned} {\left( {\varDelta {u_{12,x}} + \varDelta {u_{23,x}}} \right) _b} = 0 \end{aligned}$$

(34)

Since the interlayer slip is not constrained at the boundaries, at the beam end the horizontal support reaction, which corresponds to axial force N, is fully transferred into the central layer, i.e., $(N_2)_b = N$. Inserting Eqs. (8) and (18) into this relation yields the fifth boundary condition,

$$\begin{aligned} {\left( {\varDelta {u_{23,x}} - \varDelta {u_{12,x}}} \right) _b} + 2{\left( {u_{2,x}^{(0)} + \frac{1}{2}w_{,x}^2} \right) _b} = 0 \end{aligned}$$

(35)

which couples all kinematic variables of the problem.

Hard hinged support 

At a hard hinged support, an end plate prevents the relative displacement of the layers at the interface, i.e.,

$$\begin{aligned} (\varDelta {u_{12}})_b = (\varDelta {u_{23}})_b = 0 \end{aligned}$$

(36)

Thus, the shear tractions at the interfaces ${(t_{s12})}_b$ and ${(t_{s23})}_b$ are also zero. Boundary condition $M_b = 0$ can be expressed alternatively as compared with Eq. (21),

$$\begin{aligned} - {EJ_\infty }\left( {w_{,xx}}\right) _b + E{A_1}d\left( {\varDelta {u_{12,x}} + \varDelta {u_{23,x}}} \right) _b = 0 \end{aligned}$$

(37)

Rigidly clamped end 

A rigidly clamped end yields the slope of the lateral deflection zero,

$$\begin{aligned} (w_{,x})_b = 0 \end{aligned}$$

(38)

and slip at both interfaces is constrained,

$$\begin{aligned} (\varDelta {u_{12}})_b = (\varDelta {u_{23}})_b = 0 \end{aligned}$$

(39)

It should be noted here that the coupled differential equations Eqs. (24) and (28) can be condensed to a single sixth-order equation of motion in terms of deflection w. In this equation (Eq. (55)), the corresponding boundary conditions and stress resultants in terms of w are derived in Appendix A.

4 Solution procedure

The coupled set of differential equations of motion (Eqs. (20), (24), (28), (29)) is solved by expanding lateral deflection w(x, t) into the first NM mode shapes of the corresponding linearized beam problem (i.e., $N=0$) (see e.g., [1]),

$$\begin{aligned} w(x,t)=\sum \limits _{n=1}^{NM} \phi _n(x)Y_n(t) \end{aligned}$$

(40)

Mode shapes $\phi _n(x)$ are obtained easily from the homogeneous differential equation of motion of sixth order in terms of lateral deflection w of the corresponding linear beam problem (i.e., Eq. (55) with $N = 0$ and $q = 0$), as described comprehensively in [13]. The modal expansion of w is inserted into the ordinary differential Eqs. (20) and (28), which are subsequently solved in combination with Eq. (29) and the corresponding boundary conditions for $\varDelta {u_{12}}$, $\varDelta {u_{23}}$, and $u_2^{(0)}$ as a function of $Y_n$, $n = 1,\ldots ,NM$. With these variables available, axial force N is evaluated according to Eq. (18), yielding a nonlinear series in terms of $Y_n$. For this analysis, any value of $0 \le x \le l$ can be employed because N is constant along span l. The required derivatives of these in such a manner obtained series for w, $\varDelta {u_{12}}$, $\varDelta {u_{23}}$, and N are inserted into the partial differential equation Eq. (24). According to the rule of Galerkin (see e.g., [32]), this equation is successively multiplied by $\phi _m(x)$, $m = 1,\ldots ,NM$ and integrated over span l. The orthogonality conditions of the mode shapes $\phi _n(x)$ simplify considerably the resulting NM nonlinear ordinary differential equations in time t for unknown coordinates $Y_m$, $m = 1,\ldots ,NM$, which are coupled through the effect of axial force N. Eventually, these equations are solved by means of standard procedures of numerical analysis.

Subsequently, this procedure of analysis is exemplarily outlined for a hinged beam without shear restraints. Since the corresponding mode shapes are simply sine waves [3],

$$\begin{aligned} \phi _n(x)=\beta _n\sin \lambda _nx \, , \, \beta _n=\left[ \frac{\mu l}{2}\left( \frac{\alpha ^2}{EJ_\infty }+\frac{\lambda _n^2}{EJ_0}\right) \right] ^{-1/2} \, , \, \lambda _n=\frac{n\pi }{l} \, , \, n=1,\ldots ,\infty \end{aligned}$$

(41)

the solution of the ordinary differential equations Eqs. (20), (28), (29) in combination with the corresponding boundary conditions Eqs. (31), (34) and (35) at each end can be presented comprehensively in analytical form. The found series representation of $u_2^{(0)}$ is a quadratic function of $Y_n$ ($n = 1,\ldots ,NM$),

$$\begin{aligned} u_{2}^{(0)}(x,t) = - \sum \limits _{n=1}^{NM} \frac{{\lambda _n} ^2 {\beta _n}^2}{{8}} \left( \frac{ \sin \left( 2 \lambda _n x \right) }{\lambda _n} - \frac{4 {EA}_1 \left( (l-2 x) \sinh \left( \frac{\delta l}{2}\right) -l \sinh \left( \frac{1}{2} \delta (l-2 x)\right) \right) }{ 4 {EA}_1 \sinh \left( \frac{\delta l}{2}\right) + {EA}_2 \delta l \cosh \left( \frac{\delta l}{2}\right) }\right) {Y_n}^2 \end{aligned}$$

(42)

whereas $\varDelta {u_{12}}$ and $\varDelta {u_{23}}$ contain a linear and a quadratic term of unknown coordinates $Y_n$

$$\begin{aligned} \varDelta {u_{12}}(x,t)= & {} \sum \limits _{n=1}^{NM} {{\lambda _n}^2 \beta _n} \left( \frac{d \lambda _n \cos \left( \lambda _n x\right) }{{\lambda _n} ^2 + \frac{K}{{EA}_1}} - \frac{\beta _n l}{4} \frac{{EA}_e \sinh \left( \frac{1}{2} \delta (l-2 x)\right) }{4 {EA}_1 \sinh \left( \frac{\delta l}{2}\right) + {EA}_2 \delta l \cosh \left( \frac{\delta l}{2}\right) }Y_n\right) Y_n \end{aligned}$$

(43)

$$\begin{aligned} \varDelta {u_{23}}(x,t)= & {} \sum \limits _{n=1}^{NM} {{\lambda _n}^2 \beta _n } \left( \frac{d \lambda _n \cos \left( \lambda _n x\right) }{{\lambda _n} ^2 + \frac{K}{{EA}_1}} + \frac{\beta _n l}{4} \frac{{EA}_e \sinh \left( \frac{1}{2} \delta (l-2 x)\right) }{4 {EA}_1 \sinh \left( \frac{\delta l}{2}\right) + {EA}_2 \delta l \cosh \left( \frac{\delta l}{2}\right) }Y_n\right) Y_n \end{aligned}$$

(44)

The first derivative of the latter equations and of Eq. (40) is inserted into Eq. (18). Evaluation of this expression at, for instance, $x=0$ yields after some algebra axial force N in terms of $Y_r^2$ ($r = 1,\ldots ,NM$),

$$\begin{aligned} N(t)= \frac{{EA}_e}{4} \left( 1 - \frac{4 {EA}_1}{4 {EA}_1 + {EA}_2 \delta l \coth \left( \frac{\delta l}{2}\right) }\right) \sum _{r=1}^{NM} {\lambda _r}^2 {\beta _r}^2 {Y_r}^2(t) \end{aligned}$$

(45)

Multiplying the mode expanded fourth-order partial differential equation Eq. (24) by the $m\hbox {th}$ mode shape, $\phi _m$, integrating subsequently over span l, and considering the orthogonality relations of the mode shapes

$$\begin{aligned} \int \limits _0^l \mu \phi _n(x) \phi _m(x) dx = m_n \delta _{mn} \left( = \frac{\beta _n^2 \mu l}{2} \delta _{mn}\right) \end{aligned}$$

(46)

yields a coupled set of NM nonlinear ordinary differential equations for the modal coordinates $Y_n$,

$$\begin{aligned} {{\ddot{Y}}_n} + 2{\zeta _n}{\omega _n}{\dot{Y}_n} + \omega _n^2 Y_n + \frac{\lambda _n^2}{\mu } N {Y_n} = \frac{1}{m_n} {P_n} \, , \, n=1,\ldots ,NM \end{aligned}$$

(47)

In this equation, $\omega _n$ denotes the $n\hbox {th}$ natural circular frequency of the corresponding linearized simply supported beam with interlayer slip (see e.g., [3]),

$$\begin{aligned} \omega _n^2=\lambda _n^4(\lambda _n^2+\alpha ^2)\left[ \mu \left( \frac{\alpha ^2}{EJ_\infty }+\frac{\lambda _n^2}{EJ_0}\right) \right] ^{-1} \end{aligned}$$

(48)

with parameter $\alpha$ according to Eq. (56). $P_n$ is the $n\hbox {th}$ modal load,

$$\begin{aligned} m_n = \frac{{\beta _n}^2 \mu {l}}{2} \, , \, {P_n}(t) = \int \limits _0^l {{\phi _n}(x) q(x,t)dx} \end{aligned}$$

(49)

Viscous damping has been added modally to Eq. (47) via modal damping coefficient $\zeta _n$ [3].

5 Illustrative examples

In the following, the nonlinear dynamic response of a three-layer beam, whose ends are resting on hinged supports without shear restraints, subjected to a time harmonic half-wave sine load distribution with excitation frequency $\nu$,

$$\begin{aligned} q(x,t) = {q_0}\sin \frac{{\pi x}}{l}\sin \nu t \end{aligned}$$

(50)

is analyzed. Load q and the fundamental mode shape $\phi _1$ are affine, and thus, all modal loads except the fundamental one are zero,

$$\begin{aligned} {P_1} = \frac{{q_0 \beta _1 l}}{2}\sin \nu t \end{aligned}$$

(51)

For internal resonance, higher modes may contribute significantly to the total response due to mode interaction caused by the cubic terms in the modal equations. In the present study, internal resonance is not studied, and since ${P_n} = 0$$\forall$$n=2,\ldots ,\infty$, the contribution of the higher modes to the nonlinear forced dynamic response is negligible. Consequently, the coupled modal equations of motion reduce to a single equation in terms of the fundamental modal coordinate only,

$$\begin{aligned} {{\ddot{Y}}}_1 + 2{\zeta _1}{\omega _1}{{\dot{Y}}_1} + \omega _1^2{Y_1} + \frac{{\lambda _1}^4 {\beta _1}^2 {EA}_e}{4 \mu } \left( 1 - \frac{4 {EA}_1}{4 {EA}_1 + {EA}_2 \delta l \coth \left( \frac{\delta l}{2}\right) }\right) {Y_1}^3 = \frac{1}{m_1}{P_1} \end{aligned}$$

(52)

In particular, a three-layer beam of length $l=1.0~\hbox {m}$, layer thickness $h_1 = h_3 = 0.01~\hbox {m}$, $h_2 = 0.0102$, and width $b=0.1~\hbox {m}$ is considered. Young’s modulus of the external layers, $E_1 = E_3 = 7.0 \cdot 10^{10}~\hbox {N/m}^2$, is seven times larger than of the core, $E_2 = 1.0 \cdot 10^{10}~\hbox {N/m}^2$. To the interfaces, a slip modulus of $K = 1.0 \cdot 10^9~\hbox {N/m}^2$ is assigned. This setup of the cross section corresponds to a lateral composition parameter $\alpha$ (Eq. (56)) times l of $\alpha l = 13.3$, indicating a moderate lateral layer interaction [12]. The mass density of the top and the bottom layer $\rho _1 = \rho _3$ is $= 2700~\hbox {kg/m}^3$, and of the central layer $\rho _2 = 1000~\hbox {kg/m}^3$. Evaluation of Eq. (48) yields the first five natural circular frequency of the corresponding linear composite beam as

$$\begin{aligned} \begin{aligned} \omega _1&= 383.7~ {\hbox {rad/s}}, \,\, \omega _2 = 1107~{\hbox {rad/s}}, \,\, \omega _3 = 1994~{\hbox {rad/s}}, \\ \omega _4&= 3079~{\hbox {rad/s}}, \,\, \omega _5 = 4395~{\hbox {rad/s}} \end{aligned} \end{aligned}$$

(53)

5.1 Example 1: Transient response

In the first example, the transient response of this beam subjected to load q(x, t) according to Eq. (50) with load amplitude of $q_0 = 1.5 \cdot 10^{3}~\hbox {N/m}$ and excitation frequency $\nu = \omega _1$ is computed. The results of the proposed nonlinear dynamic beam theory are compared with the outcomes of a computationally much more expensive finite element (FE) analysis conducted in Abaqus Standard 6.13-2, in an effort to verify this theory. In this analysis, quadrilateral plane stress elements with eight nodes per element are used to discretize the layers, and the interlayer domain is discretized by linear cohesive elements with four nodes per element. To the normal stiffness of the cohesive elements a value of 1000 times the tangential stiffness is assigned, because in the beam model it is infinite. The tangential stiffness corresponds to the slip modulus K assigned to the beam model. In contrast to the beam model, where the thickness of the interlayers is zero, in the FE model the cohesive zones have a thickness of $0.1~\hbox {mm}$, i.e., $h_1 / 100$. The thickness of the midlayer, $h_2$, is reduced by two times the thickness of the cohesive zones (i.e., $h_2 = 0.01~\hbox {m}$), with the result that the total height of the FE model and the beam model are the same. The hinged supports at the ends of the central axis are implemented by means of kinematic couplings of the outer surfaces of the central layer to two additional nodes, which represent the left and right support, respectively. In total, the FE model exhibits about 30, 000 degrees of freedom (compared to one degree of freedom in terms of the single-mode Ritz approximation used to solve the beam equations). Geometric nonlinearity is accounted for by setting in Abaqus the NLGEOM option to ON. This triggers an incremental iterative solution procedure where equilibrium is established in the deformed configuration. For evaluating internal forces, Abaqus uses Cauchy (true) stress and the integral of the rate of deformation, ${\mathbf {D}}=\text {sym}\left( \frac{\partial {\mathbf {v}}}{\partial {\mathbf {x}}}\right)$, where ${\mathbf {v}}$ is the velocity at a point with current spatial coordinates ${\mathbf {x}}$ [7]. For the numerical integration of ${\mathbf {D}}$, the approach presented in [19] is used.

An eigenfrequency analysis yields the first five natural frequencies of the corresponding geometric linear FE model as follows,

$$\begin{aligned} \begin{aligned} \omega _1^{(FE)}&= 383.0~{\hbox {rad/s}}, \,\, \omega _2^{(FE)} = 1103~{\hbox {rad/s}}, \,\, \omega _3^{(FE)} = 1984~{\hbox {rad/s}}, \\ \omega _4^{(FE)}&= 3060~{\hbox {rad/s}}, \,\, \omega _5^{(FE)} = 4363~{\hbox {rad/s}} \end{aligned} \end{aligned}$$

(54)

Comparing these outcomes with the corresponding results of the beam theory, Eq. (53), shows that the first natural frequency of both approaches differs only by about $0.2 \%$. This small difference increases to about $0.8 \%$ for the fifth frequency.

The subsequent figures show the undamped nonlinear transient response of the beam. At first, in Fig. 4 the lateral deflection at midpan, $w(x=0.5l)$, normalized with respect to the nonlinear static response at midspan, $w_S(x=0.5 l)$, is shown as a function of the ratio time t over fundamental period $T_1 = 2 \pi /\omega _1$. The bold full black line represents the nonlinear outcome of the proposed beam theory. As observed, the midspan deflection increases until the maximum is obtained at $t/T_1 = 4.763$, then decreases to almost zero, then increases again, and so on. This kind of beat effect is a result of the geometric nonlinearity of the problem that yields the fundamental frequency amplitude dependent. In this figure, also the normalized midspan deflection of the corresponding linear member is depicted by a red graph. Since the excitation frequency corresponds to the first natural frequency, the response of the undamped linear beam grows unboundedly. Comparison of the linear and nonlinear deflection reveals even better the amplitude dependence of the fundamental frequency, leading to a reduction in the effective fundamental period of the nonlinear beam with increasing response amplitude. Additionally, the time history of the corresponding nonlinear midspan deflection of the FE model is shown by the thin blue line with circular markers. It is readily seen that the results of the beam and the FE approach are virtually identical. Comparison of the deflection resulting from the beam and FE model along the beam axis at normalized time instant $t/T_1 = 4.763$, depicted in Fig. 5, also verifies for this example problem the accuracy of the proposed beam theory.

Fig. 4

Time history of the normalized lateral midspan deflection. Outcome of the proposed nonlinear beam theory versus FE plane stress solution. Nonlinear and linear response

Fig. 5

Normalized lateral deflection along the beam axis at a certain time instant. Outcome of the proposed nonlinear beam theory versus FE plane stress solution

Figure 6 shows the upper and lower interlayer slip, $\varDelta u_{12}$ and $\varDelta u_{23}$, at the left beam end (i.e., $x = 0$) with respect to $t/T_1$. $\varDelta u_{12}$ and $\varDelta u_{23}$ are also normalized with respect to nonlinear static deflection at midspan, $w_S(0.5 l)$, to keep the difference in the order of magnitude of the considered displacement response quantities apparent. One interesting observation is that the nonlinearity due to moderately large vibrations causes the upper (black line) and lower (blue line) interlayer slip to become different. In contrast, in the linear beam both interlayer slips (red graph) are identical. The distribution of the normalized interlayer slips of the nonlinear beam over x at $t/T_1 = 4.763$ reveals that close to the beam ends $\varDelta u_{12}$ and $\varDelta u_{23}$ become different due to the geometric nonlinear membrane force N. Close to the beam center, where the beam deformation is small, both quantities are the same. The FE solution shown in Figs. 6 and 7 confirms again the accuracy of the proposed theory.

Fig. 6

Time history of the normalized interlayer slips at the left beam end. Outcome of the proposed nonlinear beam theory versus FE plane stress solution. Nonlinear and linear response

Fig. 7

Normalized interlayer slips and central longitudinal displacement along the beam axis at a certain time instant. Outcome of the proposed nonlinear beam theory versus FE plane stress solution

The longitudinal displacement of the central fiber $u_2^{(0)}$ at $x = 0.08 l$, again normalized with respect to $w_S(0.5 l)$, is displayed in Fig. 8. The peak value of $u_2^{(0)}$ appears at about $x = 0.08 l$, compared with the red graph in Fig. 7, which shows the distribution of $u_2^{(0)}$ over x at time instant $t/T_1 = 4.763$. The time history of $u_2^{(0)}(0.08 l)$ reflects the beat effect observed before. The prediction of $u_2^{(0)}(0.08 l)$ by the plane stress FE analysis, which is also shown in Figs. 7 and 8, coincides excellently with the results of the beam theory. In contrast to the previously discussed kinematic response variables, however, the local FE peak values of $u_2^{(0)}(0.08 l)$ are slightly larger than those of the beam response, as seen in Fig. 8. It should be noted that $u_2^{(0)}$ is the result of stretching of the central fiber, and thus, for the corresponding linear beam zero.

Fig. 8

Time history of the normalized central longitudinal displacement at $x = 0.08 l$. Outcome of the proposed nonlinear beam theory versus FE plane stress solution

Subsequently, the resulting internal forces are displayed and discussed. Figure 9 shows the time history of the membrane force N, and the layerwise axial forces $N_1$, $N_2$, and $N_3$, respectively, at midspan. The quantities are normalized to the nonlinear axial force $N_3$ at $x = 0.5 l$. While membrane force N and central layer force $N_2$ are always in tension (or zero), the axial forces of the faces, $N_1$ and $N_3$, alternate between tension and pressure. However, in contrast to the linear beam, the peaks in tension are larger than in compression, due to the presence of membrane force N. In Fig. 10, these axial forces at $t/T_1 = 4.763$ are plotted against the longitudinal coordinate x. According to this beam theory, the membrane force N is constant along the beam. At $x = 0$ and $x = l$, $N_1$ and $N_3$ are zero, and $N_2 = N$, as prescribed by the pertaining boundary conditions, compared with Eq. (34).

Fig. 9

Time history of various normalized axial forces at midspan

Fig. 10

Various normalized axial forces along the beam axis at a certain time instant

In Fig. 11, the overall bending moment M, and the layerwise bending moments $M_1$, $M_2$, and $M_3$ at midspan are depicted as a function of time ratio $t/T_1$. The static nonlinear overall bending moment $M_S$ at $x = 0.5 l$ is used to normalize these dynamic bending moments. In addition, the overall bending moment in the center of span l of the corresponding linear beam is also shown. The moments of the external layers, $M_1$ and $M_3$, which are proportional to the beam curvature $w_{,xx}$, are identical because these layers have the same bending stiffness. It is readily observed that the dynamic amplification of the overall bending moment at midspan is of the same magnitude as the one of the midspan deflection, compared with Fig. 4. To complete the insight into the nonlinear response behavior of the considered structural member, in Fig. 12 for a certain time instant the normalized overall and layerwise bending moments are plotted as a function of x.

Fig. 11

Time history of various normalized bending moments at midspan. Nonlinear and linear response

Fig. 12

Various normalized bending moments along the beam axis at a certain time instant

From the results of this example, it can be concluded that the proposed theory for immovably supported composite beams with interlayer slip predicts very accurately the nonlinear response of those members, validated through a comparative FE analysis.

5.2 Example 2: Nonlinear resonance

After having validated the proposed theory for a particular member, subsequently linear and nonlinear frequency response functions of the same but $5\%$ damped composite beam are derived by sweeping the excitation frequency $\nu$ in the vicinity of the fundamental frequency $\omega _1$ of the corresponding linear structure. At time $t=0$, the member is subjected to the harmonic load according to Eq. (50), and a time history analysis is conducted. After decay of the transient vibrations, the maximum of the steady-state response is recorded.

Figure 13 shows the nonlinear frequency response functions of the midspan deflection $\max |{w_p}(0.5l)|$ for three different load levels. These frequency response functions are normalized by means of the static midspan deflection of the corresponding geometric linear beam, subsequently referred to as $w_{SL}^{(ref)}(0.5 l)$. The excitation frequency $\nu$ is related to the fundamental frequency $\omega _1$ of the linear flexibly bonded beam, denoted as $\omega _1^{(ref)}$. The reference load amplitude $q_0^{(ref)}$ is the same as $q_0$ in the first example, i.e., $q_0^{(ref)} = 1.5 \cdot 10^{3}~\hbox {N/m}$. In two additional analyses, the load amplitudes are two times ($2 q_0^{(ref)}$) and ten over three times ($10 q_0^{(ref)}/3$), respectively, of the reference load. In this figure, also the amplitude function of the linear member with its maximum of 10.0 at resonance is shown by the dashed graph. As expected, the nonlinear beam behaves in the vicinity of the first natural frequency like a hard spring, and with increasing load amplitude the peak deflection deviates more from the linear counterpart. The reference load $q_0^{ref}$ yields for $\max |{w_p}(0.5l)| / w_{SL}^{(ref)}(0.5 l)$ a peak value of 9.15. For the two larger load amplitudes $2 q_0^{(ref)}$ and $10 q_0^{(ref)}/3$, the resonance curves exhibit in a certain frequency range multivalued amplitudes, and the entire solution splits into two stable and one unstable branch. However, in this and the subsequent figures only the stable response branches are depicted because the response has been found by time history analyses. Two different frequency sweeps are conducted to determine the two stable solutions. In the first sweep, starting at $\nu / \omega _1^{(ref)} = 0.1$, the excitation frequency is stepwise increased, and the last response of the current step is used as initial condition for the subsequent analysis with increased excitation frequency. In the second sweep, starting at $\nu / \omega _1^{(ref)} = 2.5$ the excitation frequency is stepwise reduced. Both sweeps are continued until that frequency where the well-known jump phenomenon occurs, i.e., the tangent of the amplitude functions becomes vertical. For load case $2 q_0^{(ref)}$, three solutions exist in the frequency range $1.18 \le \nu / \omega _1^{(ref)} \le 1.25$, the corresponding peak amplifications $\max |{w_p}(0.5l)| / w_{SL}(0.5 l)$ are 3.23 and 7.95, respectively. Further increase of the load amplitude to $10 q_0^{(ref)}/3$ increases also the frequency range of multivariate solutions (i.e., $1.25 \le \nu / \omega _1^{(ref)} \le 1.50$), however, the maximum deflection amplification reduces to 6.78 at $\nu / \omega _1^{(ref)} = 1.50$. The resonance curve of the largest load amplitude exhibits at $\nu / \omega _1^{(ref)} \approx 1 / 3$ some minor amplifications, an effect of subharmonic resonance well-known in highly nonlinear structural problems.

Fig. 13

Frequency response function of the normalized deflection at midspan. Variation of the load amplitude. Nonlinear and linear response

In Fig. 14, for the same load amplitudes the frequency response functions of interlayer slip $\varDelta u_{23}$ at $x = 0$ are presented, normalized with respect to $w_{SL}^{(ref)}(0.5 l)$. In contrast to the midspan deflection, the maximum of the steady-state solution of $\varDelta u_{23}$ becomes larger with increasing load amplitude (and thus, with increasing nonlinearity). The large increase in the interlayer slip at the beam ends in a geometric nonlinear response condition has already been observed in the previous example, compare with Figs. 6 and 7. Note that the frequency response functions of the interlayer slip $\varDelta u_{12}$ are identical with the one of $\varDelta u_{23}$, see also Fig. 7.

Fig. 14

Frequency response function of normalized interlayer slip at the left beam end. Variation of the load amplitude. Nonlinear and linear response

A similar response behavior is observed for the normalized steady-state longitudinal displacement $\max |{u_{2p}^{(0)}}(0.08l)| / w_{SL}(0.5 l)$, as seen in Fig. 15. This quantity is zero for the linear member and grows with increasing nonlinearity related to an increase in the load amplitude.

Fig. 15

Frequency response function of the normalized central longitudinal displacement at $x = 0.08 l$. Variation of the load amplitude

Figure 16 represents the resonance functions of the overall axial force N, and the layerwise axial forces $N_1$, $N_2$ and $N_1$ at midspan only for reference load $q_0^{(ref)}$. All steady-state internal forces are divided by the static axial force in the bottommost layer, at $x = l/2$ of the corresponding linear beam subjected to $q_0^{(ref)}$, referred to as reference axial force $N_{3SL}^{(ref)}(0.5l)$. Thus, in this representation the difference in magnitude of the various axial forces is maintained. As observed, the maximum of the layer quantity $N_3$ is about 2.69 times larger than of the resultant axial force N, and 38.8 times larger than $N_2$. To quantify the increase in the non-dimensional steady-state overall axial force with increasing load, in Fig. 17 the ratio $\max |{N_p}|$ over $N_{3SL}^{(ref)}$ is shown for load cases $q_0^{(ref)}$, $2 q_0^{(ref)}$, and $10 q_0^{(ref)}/3$. In contrast, the maximum of the amplitude function of the axial forces of the bottommost layer, $\max |{N_{3p}(0.5l)}| / N_{3SL}^{{(ref)}}(0.5l)$, is with 11.1 largest for load $q_0^{(ref)}$, and decreases slightly for the two larger load amplitudes, as revealed by Fig. 18. The amplification of this quantity in the linear beam is 10.0, and thus, smaller than in the three considered nonlinear responses.

Fig. 16

Frequency response function of various normalized axial forces at $x = 0.5 l$

Fig. 17

Frequency response function of the normalized overall axial force. Variation of the load amplitude

Fig. 18

Frequency response function of the normalized axial force in the bottom layer at midspan. Variation of the load amplitude. Nonlinear and linear response

The resonance curves of the overall bending moment at midspan shown in Fig. 19 are similar to the ones of the midspan deflection, compared with Fig. 13.

Fig. 19

Frequency response function of the normalized overall bending moment at midspan. Variation of the load amplitude. Nonlinear and linear response

Subsequently, the linear and nonlinear frequency response functions of the considered flexibly bonded beam ($\alpha l = 13.3$) subjected to reference load $q_0^{(ref)}$ are set in contrast to the outcomes of the rigidly bonded beam (i.e., $K = \infty$, and thus, $\alpha l = \infty$) and the unbonded beam (i.e., $K = \alpha l = 0$), both also subjected to $q_0^{(ref)}$. The fundamental frequency of the fully bonded member is 1.27 times larger and of the unbonded beam 2.78 times smaller than the one of the flexibly bonded structure (i.e., $\omega _1^{(ref)}$).

The deflection frequency response functions depicted in Fig. 20 represent the dynamic (de-)amplification with respect to the midspan deflection of the flexibly bonded linear beam, $w_{SL}^{(ref)}(0.5l)$. This figure reveals the large effect of the interlayer stiffness K on the global stiffness, and consequently, on the nonlinear dynamic structural response. As observed, the nonlinear quasistatic midspan deflection of the beam without bonded layers is 6.3 times larger than the static deflection of the flexibly bonded beam, and the nonlinear peak amplitude ratio is 21.0 compared to 9.15 of the reference structure. Because of the large flexibility of this member, its response characteristics becomes more nonlinear compared to the reference beam. That is, in a certain frequency range the response is multivariate with two stable and one unstable branch, and the effect of subharmonics at about one third of the fundamental frequency is more pronounced. By contrast, the fully bonded beam exhibits a nonlinear quasistatic midspan deflection of 0.63 times $w_{SL}^{(ref)}(0.5l)$, and a peak deflection amplitude amplification of 5.54 is predicted. In the flexibly and the rigidly bonded beam, the nonlinear peak deflection amplification is slightly smaller than in the linear counterpart, however, in the unbonded beam the difference between the linear and nonlinear peak amplification is large.

Fig. 20

Frequency response function of the normalized deflection at midspan. Variation of the interlayer stiffness. Nonlinear and linear response

According to Fig. 21, the nonlinear steady-state interlayer slip amplitude $\max |{\varDelta u_{23 p}}|$ at $x = 0$ of the unbonded structure is 6.66 times larger than the one of the flexibly bonded reference beam. It is also seen that in the unbonded nonlinear beam the peak amplification $\max |{\varDelta u_{23 p}}|(0) / w_{SL}^{(ref)}(0.5l)$ is much smaller than in the linear member, whereas in the flexibly bonded beam this response behavior is the other way around.

Fig. 21

Frequency response function of the normalized lower interlayer slip at the left beam end. Variation of the interlayer stiffness. Nonlinear and linear response

Figure 22 shows frequency response functions for the overall axial force N, normalized with respect to the static axial force of the bottom layer at midspan of the linear flexibly bonded beam, $N_{3SL}^{(ref)}(0.5l)$. The displayed results show that the maximum nonlinear overall axial force N of all beam configurations is of similar order of magnitude.

Fig. 22

Frequency response function of the normalized overall axial force. Variation of the interlayer stiffness

Since in the unbonded beam, no shear tractions can be transferred from the central layer to the external layers across the interfaces, the axial forces in the external layers, $N_1$ and $N_3$, are zero. Thus, Fig. 23 shows the midspan frequency response function of $N_3$ for the flexibly and the rigidly bonded beam. One interesting observation is that for both members the quasistatic internal force is almost the same. The maximum nonlinear response amplification of $N_3$ is 11.1 for the flexibly bonded member, compared to 12.2 for the beam without interlayer slip. The nonlinear peak of the frequency response function of $N_3 (0.5l)$ exceeds the linear one, which is in contrast to the response behavior of the peak deflection.

Fig. 23

Frequency response function of the normalized axial force in the bottom layer. Variation of the interlayer stiffness. Nonlinear and linear response

In the last figure, Fig. 24, the nonlinear and linear steady-state overall bending moment amplitude at $x = l/2$ divided by the static bending moment of the linear flexibly bonded beam is shown. While the nonlinear peak bending moments of the flexibly and the rigidly bonded structure (of about 9.4) are about the same, the maximum amplification of the unbonded beam is more than three times smaller compared to the other members. The reason is the large flexibility of the unbonded beam, by which means the membrane force $N = N_2$ becomes dominant in the transfer of the external load to the supports. Note that the resonance peak of the overall moment M is identical for the three linear beams because the system is statically determined, and thus, M is unaffected by the structural stiffness.

Fig. 24

Frequency response function of the normalized overall bending moment at midspan. Variation of the interlayer stiffness. Nonlinear and linear response

6 Summary and conclusions

In this paper, the equations of motion and corresponding boundary conditions for vibrating flexibly bonded three-layer composite beams on immovable supports have been derived. The proposed theory is based on a layerwise application of kinematic Euler–Bernoulli assumptions, a linear elastic relation between the interlayer slip and the interlayer shear traction, and a nonlinear strain-displacement relation for the central fiber. The latter relation accounts for stretching of the central fiber during moderately large lateral beam vibrations, which develop because the supports are rigidly held apart.

In a first illustrative example, it was shown that the proposed beam solution of the considered simply supported member without shear restraints and the outcomes of a comparative plane stress finite element analysis are in excellent agreement. As such validated, in the second illustrative example the proposed beam theory was used to derive frequency response functions for various kinematic response and internal force quantities. The results of this study demonstrate the significant impact of partial layer interaction on the nonlinear dynamic response of composite beams. Consequently, the benefit of the proposed theory for efficiently predicting moderately large vibrations of composite beams with interlayer slip is confirmed.

Appendix A: Governing equations in terms of the lateral deflection w and its derivatives

1.1 A.1 Equation of motion

In Eq. (24), ${\varDelta {u_{12,xxx}} + \varDelta {u_{23,xxx}}}$ is substituted by the expression obtained by differentiating Eq. (28) with respect to x and solved for ${\varDelta {u_{12,xxx}} + \varDelta {u_{23,xxx}}}$. Then, the resulting equation is differentiated two times with respect to x, and ${\varDelta {u_{12,xxx}} + \varDelta {u_{23,xxx}}}$ is replaced by the expression originating from rearranging Eq. (24). This analysis yields the following sixth-order partial differential equation,

$$\begin{aligned} w_{,xxxxxx}-\alpha ^2 \left( 1+\frac{N}{\alpha ^2EJ_0}\right) w_{,xxxx}+\frac{\alpha ^2N}{EJ_\infty }w_{,xx}+\frac{\mu }{EJ_0}{\ddot{w}}_{,xx}-\frac{\alpha ^2\mu }{EJ_\infty }{\ddot{w}}=\frac{1}{EJ_0}q_{,xx}-\frac{\alpha ^2}{EJ_\infty }q \end{aligned}$$

(55)

where parameter [16]

$$\begin{aligned} \alpha ^2 = K\frac{EJ_\infty }{EA_1EJ_0} \end{aligned}$$

(56)

is proportional to slip modulus K, and thus, defines the degree of lateral composite action. The practical range of this parameter is discussed in [12].

1.2 A.2 Stress resultants

Equations (15) and (16) are added and the shear tractions eliminated by Eq. (6). Differentiation of this expression with respect to x, and inserting $u_{1,x}^{(0)}$ and $u_{3,x}^{(0)}$ obtained from rearranging of Eq. (8) yields

$$\begin{aligned} N_{1,xx} - N_{3,xx} - \frac{K}{EA_1} (N_1 - N_3) + 2Kdw_{,xx} = 0 \end{aligned}$$

(57)

The difference of the axial forces in the upper and the lower layer follows from rewriting of Eq. (9) and substituting constitutive equation (7),

$$\begin{aligned} N_1 - N_3 = \frac{1}{d} \left( \sum \limits _{i=1}^3 M_i - M\right) = -\frac{1}{d} (EJ_0 w_{,xx} + M) \end{aligned}$$

(58)

Inserting Eq. (58) and its second derivative with respect to x into Eq. (57) leads to

$$\begin{aligned} w_{,xxxx} - \alpha ^2 w_{,xx} = -\frac{M_{,xx}}{EJ_0} + \frac{\alpha ^2 M}{EJ_\infty } \end{aligned}$$

(59)

Eventually, the overall bending moment M results from combination of Eq. (59) and Eq. (14) as

$$\begin{aligned} M = \frac{EJ_\infty }{\alpha ^2}\left[ w_{,xxxx} - \alpha ^2\left( 1+\frac{N}{\alpha ^2EJ_0}\right) w_{,xx} + \frac{1}{EJ_0}(\mu {\ddot{w}} - q)\right] \end{aligned}$$

(60)

The difference of the axial forces in the outer layers $N_1 - N_3$, which is subsequently needed for defining the boundary conditions, is found by substituting in Eq. (58) $M_i$ by Eq. (7) and M by Eq. (60),

$$\begin{aligned} N_1 - N_3 = -\frac{EJ_\infty }{d \alpha ^2} \left[ w_{,xxxx} - \alpha ^2 \left( 1- \frac{EJ_0 }{EJ_\infty } + \frac{N}{\alpha ^2 EJ_0}\right) w_{,xx} + \frac{1}{EJ_0}(\mu {\ddot{w}}-q) \right] \end{aligned}$$

(61)

Adding Eq. (15) and Eq. (16) reveals that the sum of the shear tractions at the interfaces $t_{s12} + t_{s23}$ is equal to $- (N_{1,x} - N_{3,x})$. Thus, Eq. (61) is differentiated with respect to x and multiplied by $(-1)$, leading to

$$\begin{aligned} t_{s12} + t_{s23} = \frac{EJ_\infty }{d \alpha ^2} \left[ w_{,xxxxx} - \alpha ^2 \left( 1- \frac{EJ_0}{EJ_\infty } + \frac{N}{\alpha ^2 EJ_0}\right) w_{,xxx} + \frac{1}{EJ_0}(\mu {\ddot{w}}_{,x}-q_{,x}) \right] \end{aligned}$$

(62)

1.3 A.3 Boundary conditions

Hinged support without shear restraints 

For the sixth-order boundary problem Eq. (55) at each beam end three boundary conditions must be prescribed. For a simply supported end $w_b=0$, $(w_{,xx})_b=0$, and $M_b = 0$, compared with Sect. 3.2. Equation (60) is used to express $M_b = 0$ in terms of variable w, i.e., $(EJ_0w_{,xxxx}-q)_b = 0$. In summary, the boundary conditions read

$$\begin{aligned} w_b=0 \, , \, (w_{,xx})_b=0 \, , \, (EJ_0w_{,xxxx}-q)_b = 0 \end{aligned}$$

(63)

Hard hinged support 

The boundary conditions for a hard hinged support are $w_b = 0$, $M_b = 0$, and $(\varDelta u_{12})_b = (\varDelta u_{23})_b = 0$. The latter conditions can be alternatively expressed as $(t_{s12} + t_{s23})_b = 0$. Utilizing Eqs. (60) and (62), respectively, the boundary conditions of a hard hinged support in terms of w read as

$$\begin{aligned} \begin{aligned}&w_b = 0 \, , \, \left[ w_{,xxxx}-\alpha ^2\left( 1+\frac{N}{\alpha ^2EJ_0}\right) w_{,xx}-\frac{1}{EJ_0} q \right] _b = 0 \, , \, \\&\left[ w_{,xxxxx} - \alpha ^2 \left( 1 - \frac{EJ_0}{EJ_\infty } + \frac{N}{\alpha ^2EJ_0}\right) w_{,xxx} + \frac{1}{EJ_0}(\mu {\ddot{w}}_{,x}-q_{,x}) \right] _b = 0 \end{aligned} \end{aligned}$$

(64)

Rigidly clamped end 

At a rigidly clamped end $w_b = 0$, $(w_{,x})_b = 0$, and $(\varDelta u_{12})_b = (\varDelta u_{23})_b = 0$, or alternatively $(t_{s12} + t_{s23})_b = 0$. Expressed in terms of w these conditions become

$$\begin{aligned} w_b = 0 \, , \, (w_{,x})_b = 0 \, , \, \left[ w_{,xxxxx} - \alpha ^2 \left( 1- \frac{EJ_0 }{EJ_\infty } + \frac{N}{\alpha ^2 EJ_0}\right) w_{,xxx} - \frac{1}{EJ_0}q_{,x} \right] _b = 0 \end{aligned}$$

(65)

1.4 A.4 Discussion

Equation (55) in combination with the pertinent boundary conditions can only be solved for w if the axial force N is the result of an external axial force applied at the boundary of the beam, such as in dynamic buckling analysis. In the current problem, however, the overall axial force N develops due to membrane strains as a result of immovable supports. Thus, according to Eq. (18), additionally to w the interlayer slips $\varDelta u_{12}$ and $\varDelta u_{23}$, and the axial displacement $u_2^{(0)}$ need to be solved simultaneously. This is only possible in an efficient manner with the coupled equations present in Sect. 3. However, the formulation of this boundary problem according to Eq. (55) reveals parameter $\alpha$, which is an important parameter to assess at the outset the vulnerability of the member to interlayer slip [12].