Skip to main content
SpringerLink
Log in

Calibration of a complete homogeneous polynomial yield function of six degrees for modeling orthotropic steel sheets

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

For better modeling plane-stress anisotropic plasticity of steel sheets, a direct calibration method is proposed and detailed for establishing a positive and convex sixth-order homogeneous polynomial yield function with up to sixteen independent material constants. The calibration method incorporates parameter identification, convexity testing, and if needed, an adjustment of an initially calibrated but non-convex yield function toward a convex one. Some advantages of the calibration method include (i) a systematic solution of only linear equations for the sixteen material constants of a steel sheet with various degrees of planar anisotropy, (ii) a practical numerical implementation of the necessary and sufficient conditions for convexity certification of the calibrated or adjusted yield function, and (iii) an incremental procedure using a parameterized version of the initially calibrated and non-convex yield function that can always lead to an approximate sixth-order yield function with guaranteed convexity. Results of applying the proposed calibration method to successfully obtain convex sixth-order yield functions are presented for three steel sheets with experimental measurement inputs from various types and numbers per type of uniaxial and biaxial tension tests.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

x, y, z :

The orthotropic material symmetry axes corresponding to the rolling (RD), transverse (TD), and normal (ND) directions of a thin sheet metal

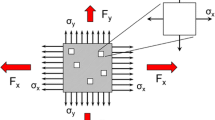
\(\sigma _x\), \(\sigma _y\), \(\tau _{xy}\) :

Three in-plane Cartesian (two normal and one shear) components of an applied Cauchy stress \(\pmb {\sigma }\) in the orthotropic coordinate system of the sheet metal

\(\varPhi _2\), \(A_1\),..., \(A_4\) :

Hill’s 1948 quadratic anisotropic yield function [9] in plane stress and its four material constants

\(\varPhi _4\), \(A_1\),..., \(A_9\) :

Gotoh’s 1977 fourth-order anisotropic yield function [6] in Cartesian stress components (\(\sigma _x\), \(\sigma _y\), \(\tau _{xy}\)) and its nine material constants

\(\varPhi _6\), \(A_1\),..., \(A_{16}\) :

The sixth-order homogeneous polynomial anisotropic yield function in Cartesian stress components (\(\sigma _x\), \(\sigma _y\), \(\tau _{xy}\)) and its sixteen material constants

\(\sigma _1\), \(\sigma _2\), \(\theta \) :

The so-called intrinsic variables of an applied plane stress \(\pmb {\sigma }\) according to Hill [12, 13], namely, the in-plane principal stresses (\(\sigma _1,\sigma _2\)) and the loading orientation angle \(\theta \) between \(\sigma _1 (\ge \sigma _2)\) and the rolling direction of the sheet metal

\(\sigma _{\theta }\), \(r_{\theta }\), \(\sigma _b\), \(r_b\) :

Yield stresses and plastic strain ratios under uniaxial tension (\(\sigma _1=\sigma _\theta > 0,\sigma _2=0\)) at the loading orientation angle \(\theta \); and yield stress and plastic strain ratio under equal biaxial tension (\(\sigma _1=\sigma _2=\sigma _b>0\))

\(\sigma _{p\theta }\), \(\sigma _{s\theta }\) :

Yield stresses under near plane-strain tension (\(\sigma _1=2\sigma _2=\sigma _{p\theta }>0\)) and under pure shear stress (\(\sigma _1=-\sigma _2=\sigma _{s\theta }>0\)) at the loading orientation angle \(\theta \)

\(\phi _{6}\), \(F(\theta ), G(\theta ),H(\theta ), N(\theta )\) :

The sixth-order yield function recast in intrinsic variables in a compact form of seven homogeneous principal stress terms and its four in-plane anisotropic functions. \(F_0\),...,\(F_6\), and so forth are the 25 nonzero Fourier cosine series coefficients of those four functions

\(\varPsi _{6A}\), \(\varPsi _{6B}\), \(\varPsi _{6C}\) :

Three sub-determinants or leading principal minors of the Hessian matrix of the sixth-order yield function \(\varPhi _6\) in Cartesian stress components (\(\sigma _x\), \(\sigma _y\), \(\tau _{xy}\))

\(\psi _{6A}\), \(\psi _{6B}\), \(\psi _{6C}\) :

Three sub-determinants \(\varPsi _{6A}\), \(\varPsi _{6B}\), \(\varPsi _{6C}\) of the Hessian matrix of the sixth-order yield function \(\varPhi _6\) recast in intrinsic variables (\(\sigma _1\), \(\sigma _2\), \(\theta \))

\(\rho \), \(\omega \) :

The polar coordinates for the two principal stresses \(\sigma _1\) and \(\sigma _2\)

References

  1. Ahmadi, A., Olshevsky, A., Parrilo, P., Tsitsiklis, J.: NP-hardness of deciding convexity of quartic polynomials and related problems. Math. Progr. Ser. A 137, 453–476 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Aretz, H., Hopperstad, O.S., Lademo, O.G.: Yield function calibration for orthotropic sheet metals based on uniaxial and plane strain tensile tests. J. Mat. Process. Technol. 186, 221–235 (2007)

    Article  Google Scholar 

  3. Barlat, F., Yoon, J.W., Cazacu, O.: On linear transformations of stress tensors for the description of plastic anisotropy. Int. J. Plast. 23(3), 876–896 (2007)

    Article  MATH  Google Scholar 

  4. Carrell, J.B.: Fundamentals of Linear Algebra, pp. 363–364. http://www.math.ubc.ca/~carrell/NB.pdf (2005). Accessed 26 Apr 2017

  5. Drucker, D.: Relations of experiments to mathematical theories of plasticity. J. Appl. Mech. 16, 349–357 (1949)

    MathSciNet  MATH  Google Scholar 

  6. Gotoh, M.: A theory of plastic anisotropy based on a yield function of fourth order (plane stress state)-I. Int. J. Mech. Sci. 19, 505–512 (1977)

    Article  MATH  Google Scholar 

  7. Gotoh, M.: A theory of plastic anisotropy based on a yield function of fourth order (plane stress state)-II. Int. J. Mech. Sci. 19, 513–520 (1977)

    Article  MATH  Google Scholar 

  8. Hershey, A.: The plasticity of an isotropic aggregate of anisotropic face centred cubic crystals. J. Appl. Mech. Trans. ASME 21, 241–249 (1954)

    MATH  Google Scholar 

  9. Hill, R.: A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. Lond. A193, 281–297 (1948)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hill, R.: The Mathematical Theory of Plasticity, p. 330. Clarendon Press, Oxford (1950)

    Google Scholar 

  11. Hill, R.: Theoretical plasticity of textured aggregates. Math. Proc. Camb. Philos. Soc. 85, 179–191 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  12. Hill, R.: Basic stress analysis of hyperbolic regimes in plastic media. Math. Proc. Camb. Philos. Soc 88, 359–369 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hill, R.: Constitutive modeling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 38, 403–417 (1990)

    Article  Google Scholar 

  14. Hosford, W.F.: A generalized isotropic yield criterion. J. Appl. Mech. Trans. ASME 39, 607–609 (1972)

    Article  Google Scholar 

  15. Hosford, W.F.: Comments on anisotropic yield criteria. Int. J. Mech. Sci. 27, 423–427 (1985)

    Article  Google Scholar 

  16. Hosford, W.F.: The Mechanics of Crystals and Textured Polycrystals. Oxford University Press, Oxford (1993)

    Google Scholar 

  17. Hu, W.: An orthotropic yield criterion in a 3-D general stress state. Int. J. Plast. 21, 1771–1796 (2005)

    Article  MATH  Google Scholar 

  18. Karafillis, A.P., Boyce, M.C.: A general anisotropic yield criterion using bounds and a transformation weighting tensor. J. Mech. Phys. Solids 41(12), 1859–1886 (1993)

    Article  MATH  Google Scholar 

  19. Logan, R., Hosford, W.: Upper-bound anisotropic yield locus calculations assuming pencil glide. Int. J. Mech. Sci. 22, 419–430 (1980)

    Article  Google Scholar 

  20. Savoie, J., MacEwen, S.R.: A sixth order inverse potential function for incorporation of crystallographic texture into predictions of properties of aluminum sheet. Textures Microstruct. 26–27, 495–512 (1996)

    Article  Google Scholar 

  21. Soare, S., Barlat, F.: Convex polynomial yield functions. J. Mech. Phys. Solids 58, 1804–1818 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  22. Soare, S., Yoon, J.W., Cazacu, O.: On the use of homogeneous polynomials to develop anisotropic yield functions with applications to sheet forming. Int. J. Plast. 24(6), 915–944 (2008)

    Article  MATH  Google Scholar 

  23. Tong, W.: Application of Gotoh’s orthotropic yield function for modeling advanced high-strength steel sheets. ASME J. Manuf. Sci. Eng. 138, 094502-1–094502-5 (2016)

    Google Scholar 

  24. Tong, W.: Generalized fourth-order Hill’s 1979 yield function for modeling sheet metals in plane stress. Acta Mech. 227(10), 2719–2733 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  25. Tong, W.: On the parameter identification of polynomial anisotropic yield functions. ASME J. Manuf. Sci. Eng. 138, 071002-1–071002-8 (2016)

    Google Scholar 

  26. Tong, W., Alharbi, M.: Comparative evaluation of non-associated quadratic and associated quartic plasticity models for orthotropic sheet metals. Int. J. Solids Struct. 128, 133–148 (2017)

    Article  Google Scholar 

  27. Van Houtte, P., Van Bael, A.: Convex plastic potentials of fourth and sixth rank for anisotropic materials. Int. J. Plast. 20, 1505–1524 (2004)

    Article  MATH  Google Scholar 

  28. Vegter, H., ten Horn, C., An, Y., Atzema, E., Pijlman, H., den Boogaard, T., Huetink, H.: Characterization and modelling of plastic material behaviour and its application in sheet metal forming simulation. In: Onate, E., Owen, D.R.J. (eds.) Proceedings of VII International Conference on Plasticity. Barcelona (2003)

  29. Yang, W.: A useful theorem for constructing convex yield function. J. Appl. Mech. ASME 47, 301–303 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  30. Yoshida, F., Hamasaki, H., Uemori, T.: A user-friendly 3D yield function to describe anisotropy of steel sheets. Int. J. Plast. 45, 119–139 (2013)

    Article  Google Scholar 

  31. Yoshida, F., Hamasaki, H., Uemori, T.: Modeling of anisotropic hardening of sheet metals including description of the Bauschinger effect. Int. J. Plast. 75, 170–188 (2015)

    Article  Google Scholar 

  32. Zhou, Y., Jonas, J., Savoie, J., Makinde, A., MacEwen, S.: Effect of texture on earing in FCC metals: finite element simulations. Int. J. Plast. 14(1–3), 117–138 (1998)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Lyle School of Engineering, Southern Methodist University, Dallas, TX, 75275-0337, USA

    Wei Tong

Authors
  1. Wei Tong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Tong.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tong, W. Calibration of a complete homogeneous polynomial yield function of six degrees for modeling orthotropic steel sheets. Acta Mech 229, 2495–2519 (2018). https://doi.org/10.1007/s00707-018-2113-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-018-2113-7

Search

Navigation