1 Introduction

The acceleration of anthropogenic greenhouse gas emissions, ensued from a rapid population growth and economic development, accounts for a major contribution to the global warming in the recent decades (IPCC 2014). In consequence, the hydrological cycle and thereafter availability of water resources across different areas of the world have been endangered (Kouhestani et al. 2016).

Precipitation as the driver of the hydrological cycle has been substantially influenced as a result of climate change (Tryhorn and DeGaetano 2011; Yang et al. 2023). Because of these already considerable changes in precipitation patterns over the past decades, water resources managers and planners in many regions have started to prepare and take measures to withstand or mitigate imminent changes in the climate conditions.

The first step to do this properly is to have accurate future climate predictions for a specific region. To that end, the so-called General Circulation Models (GCMs) are used. They are based on the theories underlying the atmospheric/oceanic physics. The GCMs simulation outcome is greatly affected by plausible realizations of future Greenhous Gas (GHG) concentrations (Sachindra et al. 2014) and for that reason they are usually driven by emission scenarios, which include the former Special Report on Emission Scenarios (SRES), and the more recent Representative Concentration Pathways (RCPs) that range from the relatively mild RCP2.6 to the most extreme RCP8.5, where the number expresses the power of the forcing global radiation in \(W/{m}^{2}\).

However, while GCMs provide reasonable simulations of hydro-climate variables at global scales with grid sizes of 1–3 degrees (~ 100-300 km), they still suffer from the resolution needed for generating local climate as required for water resources impacts studies at the watershed scale (Chen and Zhang 2021; Iizumi et al. 2011; Mandal et al. 2016). To overcome this inherent resolution limitation of most GCMs, the so-called downscaling techniques are used to derive predictand(s) at small scale from coarse-resolution predictors for being further used in local impact studies.

Downscaling methods are widely classified as either dynamic or statistical. Dynamic downscaling is based on some sort of nesting a finer scale regional climate model (RCM) (from a few kilometers to as much as 50 km) within the large-scale grid of a GCM (Wood et al. 2004) and drive the RCM with the boundary forcing of the parent GCM. The serious disadvantages of dynamic downscaling tools are high computational requirements, model complications, and their dependence on boundary conditions obtained from GCMs. Therefore, they are not as widely used as the class of statistical downscaling methods. The main assumption in statistical downscaling is that a stochastic or deterministic relationship, called a transfer model, exists between a GCM-predictor, e.g. geopotential height, moisture fluxes, sea surface temperatures, etc. and a local or regional predictand such as temperature and/or precipitation (Canon et al. 2011). Nonetheless, the extent to which the derived transfer function’s skill may change when applied to future climate projections has been a question of research (Dixon et al. 2016). Statistical downscaling is more adaptable and flexible owing to low computational demand, simple modeling structure, and easy modifications for application at various locations.

Statistical downscaling techniques developed until now, recognized as perfect prognosis (“prog”, PP) algorithms (Legasa et al. 2023), can be categorized into three groups: (1) classification/weather typing methods (Haberlandt et al. 2015; Hay et al. 1991; Hughes and Guttorp 1994; Mehrotra and Sharma 2010); (2) regression/ transfer function approaches (Kannan and Ghosh 2013; Maraun et al. 2010; von Storch et al. 1993; Wilby et al. 2002, 1999); and (3) weather generators (Caron et al. 2008; Eum and Simonovic 2012; King et al. 2015; Sharif and Burn 2006; Wilks 1999; Wilks and Wilby 1999). Among these PPs, regression/transfer functions model class, as epitomized in the well-known SDMS-software (Wilby et al. 2002, 1999), is probably the most widely used downscaling model. In spite of its countless applications in climate impact studies, SDSM and other statistical downscaling methods, in general, have serious limitations when it comes to the downscaling of daily precipitation, required as an input into almost all hydrological models, particularly with the purpose of local climate impact assessment on water resources. This is because daily precipitation exhibits spatiotemporal intermittence, highly skewed distribution, complex stochastic dependencies, and discrete characteristic reflected by wet and dry spells, particularly, in arid and semi-arid areas (Ramana et al. 2013). Additionally, precipitation is a highly uncertain and heterogeneous spatial phenomenon, occurring because of interwoven interactions between different climate variables.

As the climate variables simulated by the numerical models as well as downscaled precipitation often show a distinct systematic deviation from the true observed climate, postprocessing of the climate model outputs in such a manner to match the observed climate is inevitable (Christensen et al. 2008). Recognized as a postprocessing approach, bias correction methods (BCMs) that fall into the category of model output statistics (MOS) have been developed over the last decade (Gudmundsson et al. 2012) and increasingly being used in climate impact studies (Emami and Koch 2017; Fereidoon and Koch 2018).

The core methodology of this class of MOS is to apply some statistical transformations to the GCM/RCM predictors/outputs to correct for the named systematic biases. Even though bias correction methods have been criticized for being dependent on non-physical bases (Ngai et al. 2017), various statistical adjustment techniques have been developed and fine-tuned over the recent years thus far, including the delta change model (Hay et al. 1991), multiple linear regression (Hay and Clark 2003), local intensity scaling (Schmidli et al. 2006), monthly mean correction (Fowler and Kilsby 2007), gamma-gamma transformation (Sharma et al. 2007), fitted histogram equalization (Piani et al. 2010a), and quantile mapping (QM) (Ngai et al. 2017; Sachindra et al. 2014; Themeßl et al. 2012). Particularly, the latter has demonstrated to be an effective bias correction approach, as it can be used for all types of statistical distributions and can successfully adjust the biases in the quantiles, the mean, as well as the standard deviation and, in case of precipitation, wet/dry-spell frequency (Fang et al. 2015). As such, QM appears to outperform other methods to effectively adjust the systematic biases of RCM and GCM-simulated precipitation (Chen et al. 2013; Sun et al. 2011; Themeßl et al. 2012). Despite the fact that the viability of QM has been widely reported in the literature, instead, Maraun (2013) has asserted that the drizzle effect for areal means are overcorrected and area-mean extremes are overestimated as well as trends are affected by the QM algorithm. Nonetheless, different QM approaches have been developed to resolve the deficiencies of the classic QM algorithm (Adeyeri et al. 2020; Cannon et al. 2015).

There have been further developments regarding nonparametric statistical downscaling models over the last decades. Among the several conceptual and black box models developed over this period, coupled Discrete Wavelet Transforms (DWT) and Artificial Neural Network (ANN)-based models appear to be the most promising for simulating hydrologic processes and specifically for precipitation forecasting (Nourani et al. 2014).

Thus, nowadays, DWT has been gaining more attention as a versatile analysis tool, because of its capability to elucidate simultaneously both spectral and temporal information within a time-signal (Adeyeri and Ishola 2021; Adeyeri et al. 2019). Indeed, DWT resolves the basic drawbacks of classical Fourier analysis — which delivers only globally time-averaged frequency information (Markovic and Koch 2005) — by decomposing a time series into its sub-components at different scales (periods), producing a good local representation of the signal in both time and frequency domains, thereby providing further information about the structure of the physical process to be modelled (Partal and Cigizoglu 2009).

ANN has shown superiority over nonlinear regression techniques, because it can elicit complex patterns and relationships between predictors and predictand (Baghanam et al. 2018). The viable skill of ANN in simulation of the nonlinear and time-varying properties of atmospheric predictors at different scales has been demonstrated by downscaling studies in the literature (Chadwick et al. 2011; Dibike and Coulibaly 2006; Nourani et al. 2018; Okkan and Fistikoglu 2014; Okkan and Kirdemir 2016; Wilby and Wigley 1997).

A step further is to combine DWT and ANN to a so-called coupled DWT-ANN model that benefits from multi-scale signals as input data, thus providing a better forecast that would be possible with a single pattern input (Nourani et al. 2009a). A Wavelet-ANN coupled model was firstly developed by Aussem et al. (1998) for financial time series forecasting. For the purpose of rainfall prediction at different temporal scales, i.e. daily and monthly, Wavelet-ANN has been applied to some studies (Goyal 2014; Nourani et al. 2009b; Partal and Cigizoglu 2009; Shafaei et al. 2016). Underlying multi-resolution seasonality extracted by wavelet transforms (e.g. DWT, Wavelet-entropy) as being latter fed into an ANN has enhanced the capability of ANN in extracting various features of a time series (Baghanam et al. 2018).

As successful applications of QM have been well documented (Chen et al. 2013; Sun et al. 2011; Themeßl et al. 2012), we appointed QM to be linked to the DWT-ANN model for postprocessing of the daily future projected precipitation.

Moreover, successful applications of DWT have been well reported, for instance, for downscaling and forecasting of evapotranspiration (Kaheil et al. 2008), detecting and downscaling of wet areas (Kaheil and Creed 2009), spatial downscaling of radar-derived rainfall field (Nourani et al. 2020), and downscaling of daily precipitation (Kumar et al. 2021).

Likewise, ANN (Ahmed et al. 2015), and QM (Lafon et al. 2013) models have been already applied per se or in a coupled manner (i.e. DWT-ANN) (Baghanam et al. 2022; Nourani et al. 2009a) to simulate as well as to bias correct the simulated/downscaled precipitation data. Nonetheless, according to the authors’ best knowledge, they have not been used as a coupled model for statistical downscaling of daily precipitation.

Therefore, the objective of this study is to introduce and test a hybrid model of DWT, ANNs, and QM for the statistical downscaling of daily precipitation. For that purpose, we use historical (1978–2005) and future (2006–2100) data from eight selected GCMs, including NorESM1-M, CNRM-CM5, CSIRO-Mk3-6, GFDL-ESM2G, GFDL-ESM2M, HadGEM2-AO, HadGEM2-ES, and MPI-ESM-MR from the newest version of the Fifth Assessment Report (AR5) under Representative Concentration Pathways (RCPs) 2.6, 4.5, and 8.5.

The effectiveness of the DWT-ANN-QM approach is to be assessed through diverse evaluation criteria, encompassing Taylor diagrams, Quantile–Quantile plots, Empirical Cumulative Distribution Functions, and wet/dry spell analysis.

2 Study area

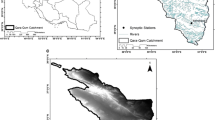
The Gharehsoo River Basin (GRB), located in northwestern Iran, covers an area about 4193 \({km}^{2}\) and extends between latitude 37° 46ʹ-38° 36ʹ N and longitude 47° 46ʹ- 48° 42 ʹ E (Fig. 1). As a semi-arid region, dry and wet seasons of the GRB are in the periods of May through October and November through April, respectively. According to historical daily records collected from synoptic meteorology stations of the Iran Meteorological Organization and rain gauge stations of the Iran Ministry of Energy in the study area (Table 1), 12 weather stations (Fig. 1b), distributed over the basin for the historic period 1978–2005, were selected.

Fig. 1
figure 1

(a) Map of world including the countries; (b) Iran’s map including the Gharehsoo River Basin (GRB); (c) spatial distribution of the average precipitation across the GRB for the reference period (1978–2005); (d) the digital elevation model (DEM) of the GRB

Full size image
Table 1 Annual precipitation statistics at the selected weather stations for the reference period 1978–2005
Full size table

Being equal to about one-third of the world’s average precipitation, the average annual precipitation in the GRB (Table 1), depending on weather station, varies from 267 to 357 mm that falls mainly in the winter months (November to April). According to the Köppen climate classification, the prevailing climate is cold and semi-arid (BSk).

The GRB presents a challenging environment for precipitation statistical downscaling due to its heterogeneous wet and dry spells and frequent extreme precipitation events. These characteristics often lead to deviations of precipitation from a Gaussian distribution, which is a fundamental assumption of many parametric statistical downscaling methods. Consequently, classical statistical transformation techniques like Box-Cox are inadequate for this region.

Moreover, being a mountainous area with a semi-arid climate, the GRB is particularly vulnerable to the impacts of climate change, as noted by Beniston (2003). Projections from the Intergovernmental Panel on Climate Change (IPCC) suggest a potential decrease in precipitation for the mid-latitude and subtropical dry regions such as the GRB (IPCC 2014). This anticipated decline in precipitation raises significant concerns about the future availability of water resources in the basin. As the precipitation of this basin varies greatly from the upstream to its downstream, providing a statistical downscaling that can effectively downscale the daily precipitation at a station level for such a complex terrain would be a stepping stone for perspective statistical downscaling studies aiming at downscaling of precipitation in semi-arid regions with highly complex terrains.

In light of these challenges, downscaling future daily precipitation at the local station becomes crucial. This downscaling process provides essential input data, allowing hydrological models to project future water yield accurately. In turn, this information empowers local authorities and decision-makers to devise effective strategies for water resource management, both in terms of mitigation and adaptation to the effects of climate change (Taie Semiromi and Koch 2020).

3 Methodology

3.1 Large-scale GCM/NCEP- datasets

In the current study, the climate predictors of eight GCMs, as listed in Table 2, including NorESM1-M, CNRM-CM5, CSIRO-Mk3-6, GFDL-ESM2G, GFDL-ESM2M, HadGEM2-AO, HadGEM2-ES, and MPI-ESM-MR from the newest version of the Fifth Assessment Report (AR5) of Intergovernmental Panel on Climate Change (IPCC) were employed.

Table 2 The GCMs used in this study and their properties
Full size table

These eight GCMs were chosen according to their better performance over Iran and the near neighbour countries such as Pakistan and Iraq and distant neighbour countries such as India (Afshar et al. 2017; Babar et al. 2015; Latif et al. 2018; Lee and Wang 2014; Mahmood et al. 2018; Prasanna 2015; Salman et al. 2018b; Xuan et al. 2017).

Considering that most of climate change impact assessments conducted in Iran, particularly those undertaken in the GRB (Javan et al. 2015), have benefited from large-scale predictors of the National Centers for Environmental Prediction and National Center for Atmospheric Research (NCEP/NCAR) reanalysis dataset 1 (Kalnay et al. 1996; Kistler et al. 2001), to draw a comparison between the results anticipated from this study with other studies undertaken in this region, we utilize this dataset on the eight-selected GCMs grid box (Table 3). NCEP-predictors are a global set of gridded weather data at a 2.5° by 2.5° horizontal resolution for the historic period available from 1948 until present.

Table 3 NCEP-reanalysis variables screened for the selection of appropriate predictors
Full size table

Due to the availability of the measured precipitation at the 12 weather stations for the period 1978–2005, the NCEP-predictors for the same period were employed. All predictors have been standardized before being screened by subtracting the long-term mean and dividing by the long-term standard deviation (Liu et al. 2011). GCM-predictors for the historic period 1978–2005 and future period 2006–2100 have been acquired from the CMIP5 data archive (https://esgf-data.dkrz.de/projects/esgf-dkrz/). The first ensemble member (r1i1p1) of each of the models has been chosen in this study. We used Climate Data Operator (CDO) program to remap the selected GCMs using a bilinear interpolation approach, which results in a smooth transformation (Salman et al. 2018a), to match the resolution of the NCEP/NCAR reanalysis predictors. The recent climate change studies are based on RCPs rather than SRES. The CMIP5-based scenarios produce a sustained combination of future population growth, technological advances, and socioeconomic parameters (Taylor et al. 2012). Three radiative forcing scenarios were used in the present study that consist of 1) RCP2.6 representing a rise in the radiative forcing to 2.6 (\(W/{m}^{2}\)) by year 2100, 2) RCP4.5, in which an increase of 4.5 \(W/{m}^{2}\) will be expected, and 3) RCP8.5, representing 8.5 \(W/{m}^{2}\) rise in the radiative forcing, as will be experienced by the end of the century (Kouhestani et al. 2016).

Thus, with the purpose of calibrating the proposed downscaling model, the potential NCEP-predictor-set consisting of 26 atmospheric variables (Table 3) was employed to be later processed for selecting the most suitable predictor(s) at each weather station. As the size of the basin covers approximately one NCEP grid box, only one grid-point of the NCEP-predictors was required.

3.2 Screening of the predictors

Choosing the most suitable large-scale predictors is known as the most crucial step in all kinds of statistical downscaling approaches (Huang et al. 2011; Wilby et al. 2002); as is the case especially for the downscaling of precipitation. According to recommendations of Khan et al. (2006), Huang et al. (2011b), and Mahmood and Babel (2014), some major considerations should be considered while screening the potential predictors, including (1) the monthly percentage of variance explaining the locally observed precipitation; (2) physical interconnection between predictors and local precipitation; (3) the predictor’s capability to carry climate change information; and (4) accurate representation of the potential predictors by climate models. Screening the most suitable predictors, we have adopted the stepwise approach following Mahmood and Babel (2014):

  1. (1)

    A correlation matrix between a predictand at a weather station, i.e. precipitation and NCEP-predictors (as listed in Table 3) was established and then highly correlated predictors, as indicated by a p-value < 0.05, were chosen and arranged in descending order.

  2. (2)

    The predictor with the strongest correlation with the predictand at a station, known as the Master/Super Predictor (MP/SP), was identified.

  3. (3)

    Each predictand and the MP were correlated with the remainder of the selected predictors to compute the partial correlation and correlation coefficients. Moreover, the correlation coefficients between individual selected predictors were computed. In this step, to calculate the partial correlation, depending on the number of the selected predictors, the following Equations (Eq. 1a and 1b) were used:

Partial correlation formula when there are two predictors (independent predictor, i.e. x and z as control predictor):

$${\mathrm{r}}_{\mathrm{xy}.\mathrm{z}}=\frac{{\mathrm{r}}_{\mathrm{xy}}-({\mathrm{r}}_{\mathrm{xz}}{\mathrm{r}}_{\mathrm{yz}})}{\sqrt{(1-{\mathrm{r}}_{\mathrm{xz}}^{2})(1-{\mathrm{r}}_{\mathrm{yz}}^{2}})}$$
(1a)

Partial correlation formula when there are more than two predictors:

$${\mathrm{r}}_{\mathrm{xy}.{\mathrm{z}}_{1}\dots {\mathrm{z}}_{\mathrm{n}}}=\frac{{\mathrm{P}}_{\mathrm{x},\mathrm{y}}}{\sqrt{{\mathrm{P}}_{\mathrm{xi}}{ \times \mathrm{ P}}_{\mathrm{yi}}}}$$
(1b)

where \({\mathrm{r}}_{\mathrm{xy}.{\mathrm{z}}_{1}\dots {\mathrm{z}}_{\mathrm{n}}}\) is partial correlation between \(\mathrm{x}\) and \(\mathrm{y}\) (predictand or dependent variable) in case of removing the correlation effects of the other independent variables or control predictors (\({\mathrm{z}}_{1}\dots {\mathrm{z}}_{\mathrm{n}}\)). \({\mathrm{P}}_{\mathrm{x},\mathrm{y}}\) is the inverse correlation between predictors x and y. \({\mathrm{P}}_{\mathrm{xi }}{\mathrm{and P}}_{\mathrm{yi}}\) show the inverse correlations of \(\mathrm{x}\) and \(\mathrm{y}\) predictors with themselves, respectively (Baba et al. 2004). In the present study, at weather stations with two selected predictors, the MP was used as a control predictor (Eq. 1a) and then we calculated the partial correlation for the other predictor. The same was applied to the other predictor for computing the partial correlation of the MP. However, at weather stations with more than two selected predictors, all predictors except one were considered as the control predictors (Eq. 1b) whereby the partial correlation was calculated for the predictor of interest. This procedure was repeated for the other predictors. Thus, the partial correlations were computed for all selected predators.

  1. (4)

    The predictors with high individual mutual correlation between 0.5 and 0.7, as suggested by Pallant (2007), were left out to eliminate any multicollinearity.

  2. (5)

    Finally, the percentage reduction (PR) was calculated (Eq. 2) for identification of the second most suitable predictor.

    $$\mathrm{PR}=\left(\frac{{P}_{r}-\mathrm{R}}{\mathrm{R}}\right)\times 100$$
    (2)

Where \({P}_{r}\) is the absolute partial correlation and \(\mathrm{R}\) indicates the absolute correlation coefficient.

The second most suitable predictor has only a very small multicollinearity with the MP. The third, fourth, and following-order suitable predictor can then be ascertained by calculating \(\mathrm{PR}\) for the remainder of the predictor-set. Likewise to most applications of statistical downscaling methods, between one to three predictors were identified to satisfactorily explain the predictand in calibration, while removing any existing multicollinearity (Mahmood and Babel 2013). The predictor-set chosen in this way was then used as input into the DWT.

3.3 Model development

3.3.1 Discrete Wavelet Transform (DWT)

In hydrological applications, discrete-time signal is the much more prevalent than a continuous-time signal process. Due to its localization properties in both time and scale, the DWT follows tracking of the time evolution of processes at different scales possible in the signal (Nourani et al. 2009a). The wavelet transform of a time series f (t) is expressed as:

$$f\left(a,b\right)=\frac{1}{\sqrt{a}}{\int }_{-\infty }^{\infty }f\left(t\right)\varphi \left(\frac{t-b}{a}\right)dt$$
(3)

where φ (t) states the original wavelet with effective length (t) that is normally quite shorter than the target time series f (t). The variable “\(\mathrm{a}\)” is the scale factor that demonstrates the properties of frequency as its variation escalates a spectrum and “\(\mathrm{b}\)” shows the translation in time so that its variation resembles the “sliding” of the wavelet over f (t). The wavelet spectrum is thus generally indicated in time–frequency domain. For low scales namely once |a|< < 1, the wavelet function is highly concentrated with frequency contents mostly in the higher frequency bands. On the contrary, if |a|> > 1, the wavelet is lengthened and, therefore consists of mostly low frequencies. Hence, for small scales, a more detailed view of the signal with a higher resolution is achieved, while for larger scales a more general view of the signal structure is resulted. The initial signal X (n) passes through two filters including low pass and high pass (Fig. S1) and as a result, two signals as Approximations (A) and Details (D) are emerged. The approximations are considered as the high-scale, low frequency elements of the signal, while the details are the low-scale, high frequency components. Customarily, the low frequency content of the signal (approximation, A) is the most prominent part. It shows the signal identity. The high frequency component (detail, D) is nuance. The decomposition process can be repeated, with successive approximations being decomposed in turn, so that one signal is broken down into many lower resolution components (Ramana et al. 2013).

The selection of appropriate mother wavelet is of paramount importance to decompose the signal. On this matter, Daubechies and Morlet wavelet transforms are known as the most commonly used mother wavelets in engineering applications. Daubechies wavelets represent a good balance between parsimony and information richness; they generate homogeneous events over the signal and findings have shown that most of prediction models can clearly identify them (Benaouda et al. 2006). In the current study, the Daubechies wavelet of order 4 (db4) was employed.

The decomposition level L = \({j}_{max}\) is determined as \(\mathrm{L}=\mathrm{int}[\mathrm{log}\left(\mathrm{N}\right)]\), where N is the time series length, respectively (Nourani et al. 2009a). In the current study N = 10,227, thus L = 4. As such, d1, d2, d3 and d4 are then the details and a4 denotes the low-scale approximation of the time series at that level (see Fig. S1, see Supplementary). These details and the approximation are then fed into the ANN-model.

For instance, the multiresolution decomposition of the NCEP standardized specific humidity at 500 hPa during 1978–2005, as one of the selected predictors for the downscaling of the precipitation, is illustrated (Fig. S2, see Supplementary). One can clearly notice how high frequency noise is filtered out in the a4-approximation, which should make the calibration of the ANN-QM downscaling process easier.

3.3.2 Artificial neural network model

In this study, Multi-layer Perceptrons (MLPs), which have been widely considered as the simplest and most commonly used neural network architectures, was employed. MLPs can be trained using several learning algorithms. In the present study, the Levenberg–Marquardt (LM) or damped Gauss–Newton method was used. It has often been found to be superior compared to other nonlinear optimization methods, like the classical back-projection method, although it needs more computer memory than other algorithms (Adamowski and Sun 2010).

When constructing an ANN model, the principal objective is to reach the optimum architecture of the ANN in a way that a satisfactory relationship between the input and output variables is obtained (Mislan et al. 2015). Deciding the number of layers and number of neurons in the hidden layers is then an important task of establishing the overall neural network architecture (Heaton 2008).

The selection of an appropriate architecture, i.e. number of hidden layers and neurons for the neural network will come down to trial and error. In practice, in most ANN engineering applications, the number of hidden layers is one (Heaton 2008) and this number was also used in this study. However, the number of neurons is more variable, as it depends also on the number of input signals used in the coupled DWT-ANN model, as discussed below.

3.4 Coupled wavelet and artificial neural network (DWT-ANN) model

The coupled wavelet and neural network (DWT-ANN) model developed here is an ANN model that benefits from the sub-series components of the DWT-multiresolution analysis of the original selected climate predictors. The different DWT-ANN models were then created using the approximations (a) and details (d) of the decomposed selected predictors (signals) – as mentioned, ranging between 1 and 3 at a weather station as input and the observed precipitation (predictand) as output (Fig. S3, see Supplementary). In other words, with the decomposition at level 4, favored here (Fig. S1, see Supplementary), 5 sub-signals, i.e. the a4 and the details d1, d2, d3 and d4 (see Eq. 1) were generated. Accordingly, depending on the weather station, the number of inputs ranges from 5 to 15. The skeleton of the 12 DWT-ANN models obtained conclusively for the different weather stations is described in Table 4.

Table 4 Skeleton of the developed DWT-ANN models using DWT level-4 decompositions of daily precipitation at the 12 weather stations and the calculated-RMSE in both DWT-ANN and DWT-ANN-QM model development stages in the training/calibration and testing/validation phases
Full size table

Likewise to other hydrological studies (e.g. Zare and Koch 2018), for creating the training and validation sub-sets, the historic period (1978–2005) at each weather station was divided into two parts, namely a training set (70% of the historic period) and a validation set (30% of the historic period). The model was fit to the training set and the fitted model was used to simulate the responses for the observations in the validation set. The resulting validation set error rate is typically assessed using Mean Squared Error (MSE) (James et al. 2013). In the light of benefiting from a long historical data record (e.g. 1978–2005), the developed DWT-ANN models can be adequately trained by capturing the extreme events that exist in the output layer (daily precipitation), implying that the extreme events for the future scenarios might be well projected accordingly. The 12 trained and validated DWT-ANN models were then forced with the approximations (a) and details (d) of the decomposed selected future predictors of the 8 GCMs and under 3 RCPs 2.6, 4.5, and 8.5, resulting in projecting the daily precipitation at the 12 stations for the future period 2006–2100.

3.5 Bias correction using quantile mapping (QM)

In the present study, the biases reflected in the historic- and future-simulated/projected precipitation by the 12 DWT-ANN models were then bias-corrected using quantile mapping based on empirical quantiles, which is available in the”qmap” R package (https://cran.r-project.org/web/packages/qmap/qmap.pdf). It should be noted that we used QM for correction of the mean, standard deviation, quantiles, and drizzle effects of the daily downscaled precipitation resulted from DWT-ANN.

The QM algorithm is resulted from the empirical transformation (Themeßl et al. 2012). The practical formidable problem of QM is to find a good approximation (transfer function h) for projecting simulated climate predictors \({P}_{m}\) onto observed ones \({P}_{o}\), i.e. (Piani et al. (2010b)

$${P}_{o}=h\left({P}_{m}\right)$$
(4)

Different methods have been provided in the literature to find an appropriate h (Gudmundsson et al. 2012). The most commonly used technique to approximate h is to apply empirical cumulative distribution functions (ECDFs) to the two sets of predictors which hopefully can be described by some known parametric distributions. As this is practically often not possible for different precipitation time series of a wide variety of climates (Gudmundsson et al. 2012; Themeßl et al. 2011; Wood et al. 2004), statistical transformations as an application of the probability integral transform (Angus 1994) are employed to get the biased corrected-simulated precipitation of \({\widehat{x}}_{m,p}\left(t\right)\) for a time period, expressed as follow:

$${\widehat{x}}_{m,p}\left(t\right)={F}_{o,h}^{-1}\left\{{F}_{m,h}\left[{x}_{m,p}(t)\right]\right\}$$
(5)

where \({F}_{o,h}\) and \({F}_{m,h}\) are the CDFs of observed (\({x}_{o,h}\)) and modeled (\({x}_{m,h}\)) data, respectively for the historical period, denoted by the subscript h (Cannon et al. 2015). Thus, the empirical CDFs are then estimated using tables of the empirical percentiles (Boe et al. 2007).

As the empirical CDFs, estimated from the calibration set (1978–1996), were approximated by tables of empirical percentiles, following the procedure of Boe et al. (2007), the values falling between the percentiles were approximated using a cubic interpolation approach.

Nonetheless, when the values of the projection scenarios (2006–2100), as simulated by DWT-ANN, were larger than the calibration values used to train the QM model, the maximum quantile of the empirical percentiles range, provided for the calibration period, was employed to correct these larger amounts of precipitation for the projection period (Boe et al. 2007; Gudmundsson et al. 2012; Themeßl et al. 2012). This possibility can somewhat allow flexibility to the QM model to correct the values that are higher than those not seen during the calibration period.

Afterwards, using the estimated parameters of the empirical QM transfer function (Eq. 5), obtained from the historical period (1978–2005), the future (up to year 2100) DWT-ANN projected daily precipitation data was bias-corrected. It should be noted that since there are different statistical distributions of wet and dry spells for the different months of the year, this bias correction was repeated for each month, i.e. 12 times and was used for the corresponding future projections for that month.

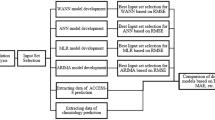
To evaluate the skill of QM in bias correction of the DWT-ANN-simulated precipitation, the historic period was systematically split into two sub-sets, out of which two-third of the dataset (1978–1996) was used for the calibration purpose and the remainder (1997–2005) was employed for the validation. Nonetheless, to procure the parameters of QM for bias correction of the daily future projected precipitation under the 8 GCMs, we trained QM using the whole historic period (1978–2005). The flow chart of the proposed methodology for simulation and prediction of daily precipitation, i.e. the working of the coupled DWT-ANN-QM model is illustrated in Fig. 2.

Fig. 2
figure 2

Flowchart of the DWT-ANN-QM coupled model for precipitation downscaling

Full size image

4 Results and discussion

4.1 Assessment of the DWT-ANN-QM model’s skill in downscaling and bias correction of the historic precipitation

As listed in Table 4, the performance of DWT-ANN and DWT-ANN-QM models is demonstrated in both calibration/training and validation/test steps in simulating and bias-correcting of daily precipitation at 12 weather stations and under the 8 GCMs. As RMSE, the objective function used for assessment, is directly proportional to the magnitude of the precipitation at each station, one can notice that the maximum and minimum RMSE were found for the stations with the maximum (e.g. Namin, Nir, and Pole Almas) and minimum (e.g. Samian, Abi Biglou, and Hir) of the precipitation, on average (see Table 1). It should be noted that RMSE of DWT-ANN-simulated precipitation for both training and test subsets under all GCMs at all stations is smaller than that of DWT-ANN-QM-simulated and bias corrected precipitation. The reason for this is that the objective function through which DWT-ANN is trained is RMSE, while the same is not true for the DWT-ANN-QM model in which QM was coupled to DWT-ANN. Therefore, a lower RMSE of DWT-ANN-simulated precipitation should not be seen as outperformance of DWT-ANN over DWT-ANN-QM. Due to the high-skill postprocess implemented using QM, the mean, standard deviation, and drizzle effects, as well as quantiles of uncorrected/simulated daily precipitation were rigorously corrected.

To better illustrate the skill of DWT-ANN-QM in downscaling of the historic precipitation, we employed the Taylor diagram (Taylor 2001), enabling us to draw an comparison between the historic precipitation (1978–2005) and the downscaled precipitation resulted from the 8 GCMs at each weather station. As illustrated in Fig. 3, all of the 8 GCM models manifested almost identical output, distributing within a specific region of the Taylor diagram. Nonetheless, based on the three statistics of the Taylor diagram, MPI-ESM-MR outperformed the other GCMs at 4 weather stations, including Abi Biglou, Ardebil, Nir, and Shams Abad. The same holds true for HadGEM2-AO at 3 stations, including Gilandeh, Hir, and Namin. Similarly, NorESM1-M yielded a better result at two stations, which are Kouzeh and Samian. CSIRO-Mk3-6, GFDL-ESM2G, and HadGEM2-ES could surpass the other GCMs at stations: Lay, Pole Almas, and Yamchi Olya, respectively. The remainder of GCMs, namely CNRM-CM5 and GFDL-ESM2M could not prove superiority over all other GCMs at all stations. Afshar et al. (2017) drew a comparison among 14 GCMs across the northeast of Iran via 4 statistical metrics \(.\) Their findings revealed that NorESM1-M and GFDL-ESM2G demonstrated a noticeable superiority over the other 12 GCMs, while CSIRO-Mk3-6 and HadGEM2-ES showed unsatisfactory results. Therefore, our results are partially corroborated by the study of Afshar et al. (2017). The discrepancy spotted between two studies can be attributed to two different prevailing climates of application areas, namely the GRB in the northwest of Iran (see Fig. 1a) and Kashafrood basin in the northeast of Iran, where Afshar et al. (2017) conducted their studies.

Fig. 3
figure 3

Taylor diagrams for the monthly downscaled precipitation using DWT-ANN-QM for the historic period (1978–2005) at the 12 weather stations under the 8 GCMs. Note that for each GCM, three statistics are plotted: (1) the Pearson correlation coefficient (demonstrating similarity in pattern between the historic and GCM-downscaled precipitation) is associated with the azimuthal angle (dotted black lines); (2) the centered RMSE in the GCM-downscaled precipitation is proportional to the distance from the hollow circle on the x-axis identified as “observed” (red contours); and (3) the standard deviation of the GCM-downscaled precipitation is proportional to the radial distance from the origin (dotted blue contours). The observed/historic standard deviation at each station is represented by the hollow circle on the x-axis joining to the y-axis using a solid black contour

Full size image

Compared with other state-of-the-art methods for statistical downscaling of precipitation, in particular the study conducted by Rashid et al. (2016), in which continuous wavelet transform (CWT) was employed in conjunction with Generalized Additive Model in Location, Scale and Shape (GAMLSS), a higher \({R}^{2}\) for both calibration (0.64) and validation (0.62) subsets was obtained. This is mainly ascribed to the fact that they forced the GAMLSS model with reanalysis NCEP/NCAR to downscale the historic period (1960–2010). Since the NCEP predictors resemble the observed data, GAMLSS could better simulate the historic precipitation. But in the present study, we aimed at projecting the precipitation in a changing climate for the future period. Thus, we forced DWT-ANN-QM with the selected historic predictors of the 8 GCMs that contain systematic bias. A meaningful comparison, however, between these two models can be only undertaken when both studies take advantage of the same dataset and application area.

To pinpoint the skill of QM in postprocessing the daily DWT-ANN-simulated precipitation, as driven by the 8 GCMs, in comparison with the daily historic precipitation, Quantile–quantile (Q-Q) plot (Gibbons and Chakraborti 2014) was deployed at each station and for both calibration (1978–1996) and validation (1997–2005) subsets. For the calibration period (Fig. 4), the quantiles of the corrected precipitation lie essentially on the slope-one line (R2 = 1), irrespective of the GCM used, indicating that the distributions of observed data on the one hand and those of the 8 GCMs on the other hand were practically identical. However, the quantiles of the uncorrected daily precipitation are highly deviated from the slope-one line (R2 = 1), indicating the viable effect of postprocessed made via QM (Chen et al. 2013; Themeßl et al. 2012). For the validation period (Fig. 5), the quintiles of the daily corrected precipitation are partially deviated from the 45-degree line, in particular for larger precipitation values, yet the R2 –values are close to one, again suggesting a promising implication of the QM model.

Fig. 4
figure 4

Q-Q plot of the daily observed, uncorrected-simulated (DWT-ANN), and corrected-simulated (DWT-ANN-QM) precipitation as driven by the 8 GCMs for the calibration period (1978–1996) at the 12 weather stations

Full size image
Fig. 5
figure 5

As in Fig. 4, but for the validation period (1997–2005). Note that R1-R8 denote the Pearson correlation between the quantiles of the observed precipitation (1997–2005) and that of the daily corrected-simulated precipitation (DWT-ANN-QM) as driven by the 8 GCMs for the same period

Full size image

As displayed in Fig. 5, a distinct deviation can be noticed for reproduction of the heavier amounts of precipitation for the validation set. For instance, this deviation, irrespective of overestimation and underestimation, from the observed precipitation occurred somewhere between 15 to 20 mm (e.g. 20 mm in Abi Biglou; 15 mm in Yamchi Olya), thus implying QM was not well trained for heavier amounts of precipitation. Owing to the fact that the GRB is located in a semi-arid region, length of wet spells is not generally so long that leads to a higher amount of precipitation. As a consequence, due to a low frequency of great amounts of precipitation witnessed during such a short period of validation subset (1997–2005), the QM algorithm could not well correct the larger values of daily precipitation. This deviation was demonstrated by the partial GCMs overestimation at Ardebil, Gilandeh, Lay, Namin, Nir, Pole Almas, Samian, Shams Abad, and Yamchi Olya stations and similarly by the partial GCMs underestimation at Abi Biglou, Hir, and Kouzeh stations. Therefore, it is of paramount importance to assess the skill of QM for correcting the daily simulated precipitation of humid climates, where sustained wet spells are frequent and so a great amount of precipitation is expected, which may result in a better training of QM.

In addition, as an inherent uncertainty of GCM outputs, tendency to overestimate wet days (Goddard et al. 2001; Nyunt et al. 2016) might be another reason why this apparent discrepancy between the observed and simulated-bias corrected precipitation was identified for higher amount of the precipitation.

As earlier mentioned, to hone the skill of QM for correction of the future projected precipitation (2006–2100) of DWT-ANN, we trained it using the complete historic period (1978–2005) instead, leading to capture more frequent heavier precipitation events while being trained.

4.2 Assessment of the DWT-ANN-QM model’s skill in reproduction of empirical cumulative distribution functions (ECDFs)

The empirical cumulative distribution functions (CDFs) of the daily historic precipitation, the daily uncorrected-simulated precipitation of DWT-ANN, and the daily corrected-simulated precipitation of DWT-ANN-QM, were illustrated for the calibration (1978–1996) (Fig. 6) and validation (1997–2005) (Fig. 7) subsets. As illustrated in Fig. 6, the ECDFs of the corrected-simulated precipitation for the calibration and validation periods, as driven by the eight GCMs, imitate closely those of the historic period. As shown, all of the corrected ECDS are very well matched to the observed ECDF so that they can be hard distinguished from each other; this is especially the case for the precipitation amounts exceeding 15–20 mm. By contrast, the uncorrected ECDFs are partially deviated from the observed ECDFs. Therefore, the positive effect of the bias correction with the QM algorithm is clearly demonstrated. Similarly, a comparison was drawn between the ECDFs of the historic precipitation and those of the projected by the precipitation driven by the eight future GCMs (Figs. S4-S6; see Supplementary) under RCPs 2.6, 4.5, and 8.5. As shown in Fig. S4, an overestimation of the projected precipitation resulted from increasing the projected wet spells (Fig. 8), relative to the historic precipitation, can be seen under RCP2.6 at all weather stations. The lowest discrepancy was found at Samian station, whereas the highest discrepancy was identified at Kouzeh and Gilandeh stations. Interestingly, Gilandeh, Kouzeh, and Samian stations indicated the lowest standard deviations (SDs) as calculated for the historic period (Table 1) amounting to 60, 65, and 67 mm, respectively. Nonetheless, the best match was recognized for Samian (Fig. S4j) that can be ascribed to a lower percentage reduction (PR) (Eq. 2) as listed in Table S1 (see Supplementary) for the two selected predictors rather than PR calculated for Kouzeh having one selected predictor and Gilandeh consisting of three selected predictors. The same holds true for the ECDFs of the precipitation projected under RCP4.5 (Fig. S5). As displayed for RCP8.5 (Fig. S6), at all stations, due to a considerable increase in wet days and thus precipitation amounts, a longer tail for the projected ECDFs can be discerned.

Fig. 6
figure 6

Empirical cumulative distribution functions (ECDFs) for the historic precipitation, uncorrected-simulated of DWT-ANN and corrected-simulated precipitation of DWT-ANN-QM for the calibration period (1978–1996), as driven by the 8 GCMs at the 12 weather stations

Full size image
Fig. 7
figure 7

As in Fig. 6, but for the validation period (1997–2005)

Full size image
Fig. 8
figure 8

Exceedance probability of the dry spells for the daily observed precipitation and historic corrected-simulated precipitation of DWT-ANN-QM as driven by the 8 GCMs

Full size image

4.3 Assessment of the DWT-ANN-QM model’s skill in simulation of dry and wet spells

Wet and dry spells analysis should also be taken into account for the assessment of the reliability of the proposed downscaling approach. Indeed, knowledge of the wet and dry spell lengths and frequencies are important in water resource planning and management, particularly, in countries relying on hydropower generation (She et al. 2016).

Throughout the literature, several definitions of wet/dry spell lengths are given; in this study the maximum number of consecutive days with precipitation greater/less than 0.1 mm/day, recommended for arid and low precipitation regions (Pervez and Henebry 2014), was considered as the threshold.

In Figs. 8 and 9, the empirical occurrence/exceedance probabilities of the dry and wet spell lengths fallowing Kannan and Ghosh (2013) were plotted, respectively at each weather station for both the historic and the DWT-ANN-QM simulated-bias corrected daily precipitation under all historic GCMs. The general pattern of the curves is typical for some hydrological extreme distribution observed in both figures. One may notice that the dry spells were better reproduced relative to the wet spells, although an overall overestimation of the exceedance probability and the lengths of the spells were nearly witnessed under all GCMs. The greatest mismatch can be seen for CNRM-CM5 (e.g. Ardebil, Hir, Kouzeh, Namin, Yamchi Olya), CSIRO-Mk3-6 (e.g. Abi Biglou, Nir), and GFDL-ESM2G (e.g. Gilandeh).

Fig. 9
figure 9

As Fig. 8, but for the wet spells

Full size image

Similarly, as shown in Fig. S7-S9 (see Supplementary), an overestimation for the exceedance probability and the length of dry spells were projected for RCP2.6, 4.5 and 8.5, respectively. The discrepancy between the historic wet spells and that of the future GCMs is much higher (Fig. S10-S12; see Supplementary). The reason for this peculiar behavior, which has also been reported in previous studies particularly in arid or semi-arid regions with often short rainfall bursts (Hu et al. 2013; Hughes and Guttorp 1994; Liu et al. 2011), may be due to the very short temporal dependence/small lag-correlation of the more extreme precipitation process (Hu et al. 2013). In addition, as precipitation tends to typify a Markov process (Katz 1977) in which a short memory or low temporal dependency is represented, especially in arid and semi-arid regions where the dry-spells constitute a quite longer length of a precipitation time series, thereby resulting in a higher occurrence probability.

As a consequence, the proposed coupled model could surpass reproduction of the dry spells rather than wet spells owing to this considerable probability of occurrence, while there are a much higher systematic overestimation between the historic and corrected-simulated wet spell occurrence probability (Fig. 9). This discrepancy can be also attributed to the poor skill of the QM model at correcting higher amount of precipitation because these events are exceptional and thus cannot adequately train the parameters of the QM model. As a result, QM cannot properly increase the amount of precipitation for the extreme events of the DWT-ANN simulated precipitation, but only an increase in the number of the wet days can counterbalance the underestimated extreme events in order to ensure a mean and standard deviation as witnessed for the historic period. Thus, the skill of QM in correction of storm events typifying intrinsic characteristic of precipitation in arid and semi-arid regions should be carefully taken into consideration.

In addition, as explained earlier for the mismatches witnessed for Fig. 5, GCM outputs have a propensity to over predict wet spells (Goddard et al. 2001; Nyunt et al. 2016). Hence, the longer tail of the projected wet spell over that of the observed wet spells in the present study may be explained by such an intrinsic uncertainty induced by the used GCMs. The poor performance of two statistical downscaling methods used by Liu et al. (2011) for simulation of wet spells has been also documented.

Based on our best knowledge, it is the first time that QM using empirical quantiles was fused with DWT-ANN. Nonetheless, for future studies, other QM approaches such as the quantile delta mapping, suggested by Cannon et al. (2015), may be used in combination with DWT-ANN for bias correction of downscaled precipitation in comparison with the QM using empirical quantiles, which was used in this study.

It should be noted, however, due to the internal variability of GCMs and RCMs, noticeable systematic biases can be expected, which most of bias correction methods suffer from shortcomings to resolve these biases (Adeyeri et al. 2020; Cannon 2016; Maraun 2012).

4.4 Projection of future precipitation via the DWT-ANN-QM model

We forced the DWT-ANN-QM model to downscale and bias correct the future precipitation (2006–2100) with the selected predictors of the 8 GCMs under the three emission scenarios RCP2.6, 4.5, and 8.5 at the 12 weather stations. The results of the middle future projection (2041–2070), however, in comparison with historic period (1978–2005) are here presented (Figs. 10, 11, 12, 13, 14, 15, 16). The projections of the near and distant future (2006–2040 and 2071–2100, respectively) are provided in Supplementary (Fig. S13-S18).

Fig. 10
figure 10

Averages of the monthly precipitation for the historic and the future GCMs-driven projections for the middle future (2041–2070) under the emission scenario RCP2.6

Full size image
Fig. 11
figure 11

As Fig. 10, but under the emission scenario RCP4.5

Full size image
Fig. 12
figure 12

As Fig. 10, but under the emission scenario RCP8.5

Full size image
Fig. 13
figure 13

Spatial distributions of relative change of the winter mean precipitation for the future time slice 2041–2070 in comparison with the reference period 1978–2005 under the 8 GCMs. Note that a positive and negative percentage indicate an increase and decline of the future winter precipitation compared with the reference period, respectively

Full size image
Fig. 14
figure 14

As in Fig. 13, but for spring

Full size image
Fig. 15
figure 15

As in Fig. 13, but for summer

Full size image
Fig. 16
figure 16

As in Fig. 13, but for fall

Full size image

Figure 10, 11, 12 illustrate, depending on the GCM used, the future monthly precipitation may increase or decrease relative to the historic period (1978–2005). These variabilities are much pronounced in wet seasons, i.e. from January to May. Overall, the average of the monthly precipitation will increase, particularly during wet months (e.g. November, December, January, and February) under RCP2.6 at all stations (Fig. 10). Under RCP4.5 (Fig. 11) the averages of the monthly precipitation will be less raised rather than that of RCP2.6. Nonetheless, a benevolent increase in the monthly average of the precipitation is projected under RCP8.5 (Fig. 12).

The reason for this peculiar behavior could be attributed to higher temperatures usually anticipated under RCP8.5, which in turn can lead to a higher amount of evapotranspiration, resulting in more precipitable water in the atmosphere. Hence, it will cause more propensity for precipitation occurrence (Huang et al. 2014), counteracting the generally witnessed decline in the precipitation during the historic period in the GRB (Ardabil Regional Water Authority 2013). Our findings are corroborated by Pendergrass et al. (2017) in which on basis of comparing RCP8.5 projections for the end of the twenty-first century with recent decades, precipitation variability rises 3–4% \({K}^{-1}\) globally, 4–5% \({K}^{-1}\) across land, and 2–4% \({K}^{-1}\) over ocean and is considerably robust on a range of time scales from daily to decadal. Furthermore, their results demonstrated that this increase in variability can be as high as the average of precipitation and lower than moisture and extreme precipitation as shown by nearly all models, areas, and time scales. The changes can be associated with rising in the atmospheric moisture, although it has been partially mitigated by weakening circulations. Thus, the discrepancy spotted between RCP4.5 and RCP8.5 in the current study can be attributed as a natural variability, even under a warmer climate.

The spatial variability of the middle future projected precipitation under the 8 GCMs relative to the historic precipitation at a seasonal scale has also been illustrated by Figs. 13, 14, 15, 16. Overall, the average of winter precipitation will rise under most of the GCMs and scenarios, although a decline in the future winter of 2041–2070 is anticipated for CSIRO-Mk3-6 (RCP2.6), GFDL-ESM2G (RCP4.5), GFDL-ESM2M (RCP8.5), and at some areas of the GRB under GFDL-ESM2G (RCP8.5), GFDL-ESM2M (RCP2.6), and GFDL-ESM2M (RCP4.5) (Fig. 13).

The maximum increase of the future winter is to be expected for CNRM-CM5 (RCP8.5), whereas the maximum decline for the same season covering the whole basin is anticipated to occur for CSIRO-Mk3-6 (RCP2.6).

The increase in the future precipitation, including the winter (September, December, January, February, March,) across the GRB has also been projected by Javan et al. (2015) in the light of employing the PRECIS (Providing REgional Climates for Impacts Studies) climate model and considering B2 as a SRES (Special Report on Emissions Scenarios) scenario.

The future spring precipitation is expected to be diminished, rather than the historic spring period of 1978–2005, under 16 GCMs/scenarios combinations (out of maximum possibilities: 8 GCMs × 3 RCPs), while a rise in the future spring precipitation has been projected under 8 GCMs/scenarios combinations (Fig. 14). The maximum rise and decline have been witnessed for GFDL-ESM2G (RCP4.5 and 8.5, yet with a partial difference in spatial distribution (see Fig. 14k-l)) and HadGEM2-ES (RCP8.5), respectively. In contrast to the future winter (Fig. 13), the future summer precipitation is projected to be considerably reduced under 20 GCMs/scenarios combinations, though 4 GCMs/scenarios show a rise in the precipitation (Fig. 15). The maximum reduction and increase relative to the historic summer period 1978–2005 are anticipated for CSIRO-Mk3-6 (RCP4.5) and HadGEM2-ES (RCP2.6), respectively. Compared with the historic precipitation of fall for the period 1978–2005, the future projected fall precipitation for 2041–2070 has been prognosticated to be increased and decreased under 16 and 2 GCMs/scenarios combinations, respectively (Fig. 16). Nonetheless, the future fall precipitation may increase or decrease, depending on the spatial distribution as projected for 6 GCMs/scenarios combinations, including NorESM1-M (RCP2.6), CNRM-CM5 (RCP8.5), GFDL-ESM2G (RCP2.6), HadGEM2-AO (RCP8.5), and HadGEM2-ES (RCP4.5 and RCP8.5).

In general, compared to our spatial analysis conducted for the four seasons hinting a rise in the future precipitation on average, the results of a large scale spatial projection of future precipitation (2020–2050) undertaken by Terink et al. (2013) are counterintuitive. They used nine GCMs and SRES A1B reflecting two time slices (2020–2030 and 2040–2050) to project different hydro-climate variables, including precipitation across the Middle East and North Africa (MENA). Having statistically downscaled the precipitation in the light of the GCMs, they have found that under the aforementioned future periods the annual precipitation is anticipated to be reduced around 5 to 10% across the GRB.

Corroborating partially our findings, the study performed by Modarres et al. (2018) indicated that some increases in precipitation, particularly maximum rainfall has been projected. They projected the variability of the maximum daily rainfall across the north and North West of Iran for the future period 2020–2049 under 6 GCMs and two scenarios A2 and B1. Their results showed that a change between -16 to 7% under scenario A2 can be expected for this region. Similarly, depending on the used GCM, maximum rainfall can vary from -16 to 10% under scenario B1, compared to the historic period (1981–2010). However, it should be noted that only one GCM grid covers the GRB as compared to the study of Modarres et al. (2018) where a quite larger region in size was investigated.

Moreover, to better spot the differences between the future scenarios and the historic precipitation, the averages of the annual projected precipitation at all weather stations and for all time slices under the 8 GCMs, relative to that of the historic period are provided in Table S2 (see Supplementary).

4.5 Limitations and considerations

The current research was undertaken in accordance with the historic and future climate predictors of 8 GCMs under climate change scenarios of RCPs 2.6, 4.5, and 8.5. Nonetheless, it is necessary to assess the validity and effectiveness of the proposed statistical downscaling approach, i.e. DWT-ANN-QM with more recent climate change scenarios, namely Shared Socioeconomic Pathways (SSPs), which represent climate change scenarios of projected socioeconomic global changes up to 2100 as per the IPCC Sixth Assessment Report on climate change in 2021. In this study, we employed the NCEP reanalysis parameters in order to ascertain the most important atmospheric parameters influencing daily precipitation in the GRB. As several newer reanalysis datasets have emerged such as ECMWF (European Centre for Medium-Range Weather Forecasts), MERRA-2 (), JRA-55 (Japanese 55-year Reanalysis), CFSR (Climate Forecast System Reanalysis), and 20CR (Twentieth Century Reanalysis), the efficacy of this statistical downscaling method should be further evaluated based on the predictor screening procedure applied to the predictors of the aforementioned reanalysis atmospheric parameters. In addition, as the simulation of dry-spells outperformed that of the wet-spells, we advise caution when using the proposed approach for the projection of the future wet-spells, which is of great importance in water resources management plans in a changing climate.

5 Conclusion

Despite substantial efforts in developing advanced statistical downscaling models, downscaling of daily precipitation from global climate models (GCMs) at the local/station level, particularly in arid and semi-arid regions, remains a significant challenge for climate change impact assessments. In this study, we proposed a novel nonparametric statistical downscaling model that integrates discrete wavelet transform (DWT), artificial neural networks (ANNs), and quantile mapping (QM) algorithms to both downscale and bias-correct historic (1978–2005) and future (2006–2100) daily precipitation at 12 weather stations in the Gharehsoo River Basin (GRB), northwestern Iran.

Our proposed coupled downscaling algorithm, DWT-ANN-QM, was rigorously assessed using various statistical measures, including Taylor diagrams, Q-Q plot analyses for calibration and validation subsets, and empirical cumulative distribution functions (ECDFs). Additionally, the model's performance in reproducing dry and wet spells for both historic and future periods was evaluated.

Findings revealed significant improvements in simulated precipitation with the implementation of the QM algorithm, particularly evidenced by Q-Q plot analyses and ECDF comparisons. While the coupled model satisfactorily reconstructed dry spells, there was a systematic overestimation of the exceedance probability and length of wet spells, attributed to insufficient training of the QM model for extreme precipitation events.

Overall, projections indicate an increase in future precipitation across the GRB, ranging from 10 to 17% depending on the weather station. Notably, the seasonal spatial distribution of future precipitation suggests increases in fall and winter, with declines projected for spring and summer.

The present study investigated historical and future climate predictors from 8 GCMs across RCP scenarios 2.6, 4.5, and 8.5. However, it is essential to evaluate the validity and efficacy of our proposed statistical downscaling approach, DWT-ANN-QM, using more recent climate change scenarios, particularly Shared Socioeconomic Pathways (SSPs). We utilized the NCEP reanalysis parameters to identify the most influential atmospheric parameters affecting daily precipitation in the GRB. With the emergence of newer reanalysis datasets such as ECMWF, MERRA-2, JRA-55, CFSR, and 20CR, further assessment of this statistical downscaling method is warranted, employing the given predictor screening procedure on the predictors of these reanalysis atmospheric parameters. Additionally, given the superior performance in simulating dry spells compared to wet spells, caution is advised when using our approach to project future wet spells, which holds significant implications for water resources management plans in a changing climate.

From a water resource management perspective, it is advisable to devise strategies for retaining floodwaters via enhancing sponge function of landscape and implementing managed aquifer recharge systems due to wetter winter and fall months as anticipated for the future in the GRB, thereby sustaining streamflow during anticipated drier spring and summer months.