1 Introduction

The impacts of climate change have gradually increased, and coupled with the aggravation caused by human activities, they have resulted in remarkable changes in the hydrological processes around the world (Liu et al. 2020). The Intergovernmental Panel on Climate Change’s (IPCC) Fifth Assessment Report (AR5) shows that the economic losses caused by extreme climate events will increase gradually (Brunner et al. 2017). Rainstorms are one of many extreme weather events, and they have features such as shorter durations and higher intensities (Li et al. 2019). The frequent occurrence of rainstorms increases the probability of urban waterlogging, and the disaster loss caused by urban waterlogging increases at an unprecedented rate (Alcamo et al. 2000; Fischer et al. 2016).

Over the last 100 years, the global rainfall situation has changed significantly. In particular, the extreme rainfall in the middle and high latitudes has increased significantly. With the increase of rainstorm events, all kinds of economic losses caused by heavy precipitation events around the world have increased significantly every year, which seriously threatens industrial and agricultural production and human daily life. Rainstorm contains many characteristics, and the correlation between various elements tends to be complex. Therefore, it is difficult to comprehensively reflect the characteristics of rainstorm through the analysis of single factors. Comprehensive analysis of rainstorm elements has become a trend in the field of precipitation research. According to research conducted by scholars, the maximum daily rainfall in most parts of the world exhibits an increasing trend, and the daily rainfall intensity is also increasing (Saini et al. 2020; Shree and Kumar 2018). Research on rainfall characteristics can directly reflect the temporal and spatial variations and periodic characteristics of regional rainfall. The commonly used methods include the sliding t-test, the Mann–Kendall trend test, and rescaled range (R/S) analysis (Lu et al. 2019). Sayemuzzanman and Jha (2014) analyzed the seasonal and annual rainfall trends in North Carolina in the USA. Their results revealed that there was a significant mutation in North Carolina from 1960 to 1970. Duhan and Pandey (2013) used statistical analysis to study the spatial and temporal variation characteristics of the annual rainfall in Madhya Pradesh, India. Their results revealed that the rainfall data from almost all of the rainfall stations from 1901 to 1978 exhibit a decreasing trend.

At present, most of the studies conducted on rainstorms have focused on the temporal and spatial distributions of rainfall and simulations of the waterlogging caused by urban rainstorms. In terms of rainstorm risk, increasing attention has been paid to the multivariate joint risk analysis method, which describes rainstorms from multiple perspectives (Pedro-Monzonís et al. 2015). Copula functions have been widely used in the fields of rainfall multivariate joint probability analysis and flood joint risk analysis because of their advantages, including a flexible structure and an unlimited marginal distribution type (Wang and Ren 2017). The theory and application of two-dimensional copula functions are relatively mature (Qian et al. 2017).

Ganguli and Reddy (2013) described the joint probability distribution of two variables and three variables (i.e., the peak discharge, flood volume, and flood duration) using various types of connection functions, and they discussed the characteristics of two return periods and tail correlation. Salvadori (2004) used two-dimensional Frank copula functions to simulate the joint probability distribution of the rainfall duration and rainfall intensity, deduced the isoline of the joint return period, and introduced the concept of the second return period.

The theory of three-dimensional and higher-dimensional copula functions is more complex due to the expansion of the dimensions and the nondependence among the variables, so is relatively lacking research in this area. In this study, several factors of rainfall were selected, and copula functions were used to determine the two-dimensional and three-dimensional joint distributions. Three indexes (i.e., the contribution rate of the rainfall in the flood season, the maximum daily rainfall, and the rainstorm frequency) were used to reveal the inherent probability distribution characteristics.

Taking the rainfall in the Taihu Lake Basin as the research object, this paper used the advantages of Copula function in constructing multi-dimensional joint distribution to reveal the characteristics of rainstorm under multivariable combination, so as to provide a scientific basis for reducing the uncertainty of rainstorm disaster frequency analysis and improving the level of risk management.

2 Study region and data selection

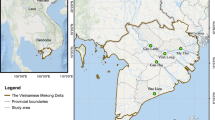
The Taihu Lake Basin is located in the southern part of the Yangtze River Delta in China (30°05′–32°08′N, 119°08′–121°55′E). The Taihu Basin is dominated by plains, accounting for two thirds of the total area. The basin covers four provinces: Jiangsu, Zhejiang, Shanghai, and Anhui. It has a total area of 36,900 km2. The climate of the basin is a typical semi-tropical monsoon climate. The annual mean temperature in the basin is about 15–17 °C and increases from north to south. The general situation of the study area is shown in Fig. 1.

Fig. 1
figure 1

Geographical location of the study area

Full size image

The daily rainfall datasets from 1955 to 2019 were obtained from the China Meteorological Data Shared Services System. Data from 11 stations were used in this study, and the information for the stations is presented in Table 1.

Table 1 Geographic coordinates of the rainfall stations
Full size table

3 Methodology

3.1 Mann–Kendall trend test

The Mann–Kendall trend test is a nonparametric testing method that does not require that the samples follow a certain distribution, and the results are not easily affected by outliers, so it is more suitable for revealing the change trend of hydrological time series (Hamed 2009).

Suppose X1, X2,…, Xn is the variable of the rainfall series, and n is the length of the rainfall series, i.e., the statistical year. The Mann–Kendall method defines the statistic S as

$$S=\sum_{i<j}{a}_{ij}$$
(1)
$${a}_{ij}=sgn\left({x}_{j}-{x}_{i}\right)=\left\{\begin{array}{c}\begin{array}{cc}1& \left({x}_{i}<{x}_{j}\right)\end{array}\\ \begin{array}{cc}0& \left({x}_{i}={x}_{j}\right)\end{array}\\ \begin{array}{cc}-1& \left({x}_{i}>{x}_{j}\right)\end{array}\end{array}\right.$$
(2)

When the number of samples n is relatively large, the statistic S generally exhibits a normal distribution and the mean value is 0. The variance is as follows:

$$\mathrm{Var}\left(S\right)=n\left(n-1\right)\left(2n+5\right)/18$$
(3)

The Mann–Kendall statistic Z can be obtained as follows:

$$Z=\left\{\begin{array}{c}(s-1) /\sqrt{\mathrm{var}\left(S\right)} (S>0)\\ 0 \left(S=0\right)\\ (s+1) /\sqrt{\mathrm{var}\left(S\right)} (S<0)\end{array}\right.$$
(4)

In the bilateral test, for the statistic Z, if Z > 0, the time series exhibits an upward trend; if Z < 0, the time series exhibits a downward trend. Given the confidence level α, if \(\left|Z\right|\ge {Z}_{1-\alpha /2}\) there is an obvious upward or downward trend in the confidence level α. In hydrological statistics, the confidence level α is usually selected as 0.05 (Lab 2005).

3.2 Multi-year moving average method

The moving average method is a smoothing prediction technology, which is mainly used to separate uncertain components and deterministic components. It can effectively eliminate random fluctuations in data and reduce the impact of random errors.

Assume that the original time series of an element is (x1, x2,…, xn), the new sequence becomes yk, N is the length of the time series, and its calculation formula is

$${y}_{k}=\frac{{x}_{k}+{x}_{k-1}+\dots +{x}_{k-(n-1)}}{n} k=n,n+1,\cdot \cdot \cdot ,N$$

3.3 Mann–Kendall mutation test

Suppose X1, X2,……, Xn is the time series variable and n is the length of the time series. It can be defined as

$${S}_{k}={\sum }_{i=1}^{k}{r}_{j},k=\mathrm{2,3},\cdots ,n$$
(5)

When Xj > Xi, ri = 1; and when Xj ≤ Xi, ri = 0 (j = 1,2,…,i).Where ri is the cumulative number of Xj greater than Xi(1 ≤ i ≤ j).

The statistic \({\mathrm{UF}}_{k}\) is defined as

$$\begin{array}{c}{\mathrm{UF}}_{k}=\left[{S}_{k}-E\left({S}_{k}\right)\right]/\left[\mathrm{Var}\left({S}_{k}\right)\right]\\ E\left({S}_{k}\right)=n(n-1)/4\\ \mathrm{Var}\left({S}_{k}\right)=n\left(n-1\right)\left(n+5\right)/72\end{array}$$
(6)

The time series Xn, Xn−1, ……, X1 is calculated again to obtain the statistical sequence Uʹk, and to make UBk = UFʹn−k (k = 1,2,……,n).

The time of the mutation can be determined by analyzing statistical sequences \({\mathrm{UF}}_{k}\) and \({\mathrm{UB}}_{k}\). If \({\mathrm{UF}}_{k}\) >0, the sequence exhibits an upward trend; if \({\mathrm{UF}}_{k}\) <0, the sequence exhibits a downward trend. If \({\mathrm{UF}}_{k}\) exceeds the critical value, the change trend is significant. If there is an intersection between \({\mathrm{UF}}_{k}\) and the curve and the intersection is between the critical lines of the 0.05 confidence level, then the time corresponding to the intersection is the start time of the mutation.

3.4 Construction of marginal distribution

In this study, the Poisson distribution (POISS), the general extreme value (GEV), the exponential distribution (EXP), the log-normal distribution (Ln2), and the Pearson type III distribution (P-III) were selected for the marginal distribution fitting (Poulin et al. 2007).

3.4.1 1. Poisson distribution

The Poisson distribution is a classical probability model that describes the frequency distribution of rare events. It is suitable for describing the number of random events per unit time. It can be regarded as the limit distribution of a binomial distribution.

The probability distribution of a random variable x obeying the Poisson distribution is.

$$P\left\{X=k\right\}=\frac{{\lambda }^{k}}{k!}{e}^{-\lambda }=1$$
(7)

According to the Poisson model, the probability of more than n rainstorms per year can be calculated as follows:

$$P\left(X\ge n\right)=1-{e}^{-\lambda }\sum_{k=0}^{n-1}\frac{{\lambda }^{k}}{k!}$$
(8)

3.4.2 2. Log-normal distribution

Suppose that the logarithm of the extreme value variable obeys a normal distribution; then if X is an extreme value variable, its logarithm y = lnX obeys the normal distribution, that is,

$$f\left(y\right)=\frac{1}{\sqrt{2\pi {\delta }_{y}}}{e}^{{-(y-{m}_{y})}^{2/2{\delta }_{y}^{2}}}$$
(9)

where \({m}_{y}\) and \({\delta }_{y}\) can be estimated using the following formula (Wong et al. 2010):

$${m}_{y}=\frac{1}{n} \sum_{i=1}^{n}\mathrm{ln}{x}_{i},{\delta }_{y}^{2}=\frac{1}{n}{\sum }_{i=1}^{n}{\left({\mathrm{ln}x}_{i}-{m}_{y}\right)}^{2}$$
(10)

3.4.3 3. General extreme value distribution

The general extreme value distribution has a good fitting effect for extreme hydrological events, and its probability density is (Sraj et al. 2015)

$$f\left(x\right)=\frac{1}{a}{\left[1+k(\frac{x-\mu }{a})\right]}^{-\frac{1}{k}-1}{{e}^{-\left[1-k(\frac{x-\mu }{a})\right]}}^{1/k}$$
(11)

where a is the scale parameter, k is the shape parameter, and \(\mu\) is the position parameter.

The distribution function is

$$F\left(x\right)=\mathrm{exp}\left\{{-\left[1+k\left(\frac{x-\mu }{a}\right)\right]}^{-\frac{1}{k}}\right\}$$
(12)

3.4.4 4. Exponential distribution

The probability density of the exponential distribution is

$$f\left(x\right)=\mathrm{\alpha }{e}^{-\alpha (x-\beta )} (\upbeta \le x<+\infty )$$
(13)

where \(\mathrm{\alpha and \beta }\) are the distribution parameters, \(\mathrm{\alpha }\) is the degree of dispersion, and \(\upbeta\) is the lower limit of the distribution.

The distribution function is

$$F\left(x\right)={\int }_{x}^{+\infty }f\left(x\right)\mathrm{d}x={e}^{-\alpha (x-\beta )}$$
(14)

3.4.5 5. Pearson type III distribution

The P-III distribution has the following probability density function:

$$f\left(x\right)=\frac{{\beta }^{\alpha }}{\Gamma \left(\mathrm{\alpha }\right)}{(x-b)}^{\alpha -1}{e}^{-\beta (x-b)} (b\le x)$$
(15)

where \(\mathrm{\alpha }\) is the shape parameter (\(\mathrm{\alpha }>0\)), \(\beta\) is the scale parameter (\(\beta >0)\), and \(b\) is the position parameter.

The estimation of the fitting effect of the edge distribution parameters can be conducted using the maximum likelihood method as follows:

$$\begin{array}{c}L\left(\theta \right)=\prod_{i=1}^{n}F\left({x}_{i};\theta \right)=\prod_{i=1}^{n}\frac{\partial F({x}_{i};\theta )}{\partial {x}_{i}}\\ \mathrm{ln}\left[L(\theta )\right]=\sum_{i=1}^{n}\mathrm{ln}\left[F({x}_{i};\theta )\right]\end{array}$$
(16)

where L(θ) is the likelihood function, F(xi; θ) is the marginal distribution density function, and θ is the parameter to be estimated. Furthermore, the Kolmogorov–Smirnov 2 (K-S2) test was used to test the goodness of fit of each marginal distribution and to determine the probability distribution function suitable for each index (Subimal 2010).

3.5 Construction of copula functions

3.5.1 Definition of a copula function

A copula function is a type of connection function that describes the correlation between variables by constructing the dependency structure between the variables. It is an effective function for connecting the marginal distribution and the joint distribution of variables. One of the advantages of the copula function is that it is not subject to the marginal distribution of the selection restrictions (Zhang 2014.).

If the random variables X1, X2, …, Xn obey the marginal distribution of Fx1, Fx2, …, Fxn, the joint distribution function is H (X1, X2, …, Xn). According to the Sklar theorem, there is copula joint function that combines n variables, that is,

$$H\left({x}_{1}\bullet \bullet \bullet ,{x}_{n}\right)=C\left({\mathrm{F}}_{{X}_{1}}\left({x}_{1}\right),\bullet \bullet \bullet ,{F}_{{X}_{n}}\left({x}_{n}\right)=C\left({u}_{1},\bullet \bullet \bullet ,{u}_{n}\right)\right)$$
(17)

where the marginal distribution function of the random variable Xi is Fxi (xi) = ui, (i = 1,2,…n). If Fx1, Fx2, …, Fxn are all continuous functions, then the copula function C is unique. In contrast, if C is an n-dimensional copula function, and Fx1, Fx2, …, Fxn are distribution functions, then the function H must be an n-dimensional joint probability. The distribution has a marginal distribution of Fx1, Fx2, …, Fxn.

Several common copula functions in the field of hydrology include the Archimedean copula, the elliptical copula, and the empirical copula functions. In hydrological analysis, the main method used is the Archimedean copula function. Its clear expression, few parameters, and simple structure make it superior (Yu and Xiong 2014).

When the Archimedean copula function contains only one parameter, it is a symmetric copula function. A n-dimensional copula Cn: [0,1]n → [0,1] can be defined as

$$\begin{array}{c}C\left({u}_{1},{u}_{2},\cdot \cdot \cdot ,{u}_{n}\right)={\varphi }^{-1}\left[\sum_{k=1}^{n}\varphi \left({u}_{k}\right)\right]={\varphi }^{-1}\left[\varphi \left({u}_{1}\right)+\varphi \left({u}_{2}\right)+\cdot \cdot \cdot \varphi \left({u}_{n}\right)\right]\\ {u}_{k}=\left[\mathrm{0,1}\right],k=\mathrm{1,2},\cdot \cdot \cdot n,\end{array}$$
(18)

where \(\varphi \left(\bullet \right)\) is the generating function of the Archimedean copula function and \({\varphi }^{-1}\) is the inverse function of \(\varphi\).

The Archimedean copula function does not necessarily have a density function. When the Archimedean copula function is an absolute continuous function, there is a density function. The expression is as follows:

$$c\left({u}_{1},{u}_{2},\cdot \cdot \cdot ,{u}_{n}\right)={\varphi }^{-1\left(n\right)}\left[\varphi \left({u}_{1}\right)+\varphi \left({u}_{2}\right)+\cdot \cdot \cdot +\varphi \left({u}_{n}\right)\right]\prod_{k=1}^{n}{\varphi }^{^{\prime}}\left({u}_{k}\right)$$
(19)

where \(\varphi\)−1(n) is the nth derivative of the inverse function of the generating function and \(\varphi \left(\cdot \right)\) is the first derivative of \(\varphi\). Common functions include the G–H copula, Clayton copula, and Frank copula functions. Their function expressions are shown in Table 2 (Latif and Mustafa 2020).

Table 2 Three Archimedean copula function forms
Full size table

The forms of the three-dimensional symmetric Archimedean copula function are shown in Table 3.

Table 3 Three-dimensional symmetric Archimedean copula function
Full size table

3.5.2 Parameter estimation of a copula function

Correlation index method

The parameters of a copula function can be estimated via kernel density estimation, the correlation index method, the inference for margins (IFM) method, and the exact maximum likelihood (EML) method (Akbari and Reddy 2019). In this study, the parameters were obtained by establishing the correlation between the Kendall rank correlation coefficient \(\uptau\) and the copula function parameter θ. The unified expression is as follows:

$$\uptau =4\int C\left(u,v\right)\mathrm{d}C\left(u,v\right)-1$$
(20)

Dependence formula for the Gumbel copula:

$$\uptau =1-\frac{1}{\uptheta };\mathrm{\theta \epsilon }[1,\infty )$$
(21)

Dependence formula for the Clayton copula:

$$\uptau =\frac{\uptheta }{2}+\uptheta ;\mathrm{\theta \epsilon }(0,\infty )$$
(22)

Dependence formula for the Frank copula:

$$\uptau =\frac{4}{\uptheta }\left[\frac{1}{\uptheta }{\int }_{0}^{\uptheta }\frac{\uptau }{\mathrm{exp}\left(\uptau \right)-1}\right];\mathrm{\theta \epsilon }\left[-\mathrm{1,1}\right]$$
(23)

Goodness-of-fit test

To verify the fitting degree between the theoretical calculation curve of the copula function and the empirical cumulative probability of the measured samples, it is necessary to test the goodness of fit of the constructed model. The evaluation of the goodness of fit is an important standard for selecting the optimal function of the distribution line. The commonly used indexes are the root mean square error (RMSE), the Akaike information criterion (AIC), and the Bayes information criterion (BIC).

3.5.3 1. RMSE method

In terms of testing the fitting effect of the copula function, the root-mean-square-error method is common. The smaller the RMSE value, the better the fitting effect of the copula function. The formula is as follows:

$${\text{RMSE}}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{\left({F}_{\mathrm{emp}}-C\right)}^{2}}$$
(24)

where \({F}_{\mathrm{emp}}\) is the empirical probability value, C is the theoretical probability value, and N is the length of the series.

The formula for the three-dimensional empirical frequency is

$$\begin{array}{c}{F}_{\mathrm{emp}}\left({x}_{i1},{x}_{i2},{x}_{i3}\right)=P\left({X}_{i1}\le {x}_{i1},{X}_{i2}\le {x}_{i2},{X}_{i3}\le {x}_{i3}\right)\\ =\left({\sum }_{j=1}^{n}{\sum }_{k=1}^{n}{\sum }_{l=1}^{n}{n}_{jkl}-0.44\right)/\left(n+0.12\right)\end{array}$$
(25)

where \({n}_{jkl}\) is the number of joint observations when \({X}_{i1\le }{x}_{i1},{X}_{i2\le }{x}_{i2},{X}_{i3\le }{x}_{i3}\) is satisfied at the same time (Filipova et al. 2018).

3.5.4 2. AIC method

The AIC method is an algorithm based on information measurement, which is suitable for testing the copula model obtained using the maximum likelihood estimation method. The formula is as follows:

$$\mathrm{AIC}=n\mathrm{log}\left(\mathrm{MSE}\right)+2m$$
(26)

wherem is the number of parameters and n is the sample capacity. The smaller the AIC value, the better the fitting effect of the copula function.

3.5.5 3. BIC method

Similar to the AIC method, the BIC method also includes two parts: the fitting deviation and the instability caused by the number of parameters. The formula is as follows:

$$\mathrm{BIC}=n\mathrm{log}\left(\mathrm{MSE}\right)+m\mathrm{log}(n)$$
(27)

wherem is the number of parameters and n is the sample capacity. The smaller the BIC value, the better the fitting effect of the copula function.

4 Results and discussion

4.1 Variation trends of the rainfall indexes

4.1.1 Variation trend of the contribution rate of the rainfall in the flood season

The contribution rate of the rainfall in the flood season in the Taihu Lake Basin and seven subregions were tested using the Mann–Kendall trend test. The results are shown in Table 4. As can be seen from the table, the contribution rate of the rainfall in the flood season in the Taihu Lake Basin and each subregion is decreasing; the value in West Zhejiang Province passes the 95% significance test, exhibiting a significant decreasing trend. Due to the high level of urbanization in the Taihu Lake Basin, the rain island effect is more significant, and the evaporation is also greatly increased. The Taihu Lake Basin is located in the subtropical monsoon region, which has more solar radiation and more evaporation (Zhai et al. 2020). This reduces the rainfall in the flood season.

Table 4 Trend test table for the contribution rate of the rainfall in the flood season
Full size table

4.1.2 Variation trend of the rainstorm frequency

The Mann–Kendall trend test method was used to test the trend of the rainstorm frequency in the Taihu Basin and seven subregions. The test results are shown in Table 5. As can be seen from the table, except for in the Taihu region, the rainstorm frequency in each subregion in the Taihu Lake Basin exhibits an increasing trend, and the rainstorm frequencies in the Wuchengxiyu and Yangchengdianmao regions pass the 95% significance test, exhibiting significant increasing trends. The Z value of the trend test for the entire Taihu Basin is 1.13, which indicates that the rainstorm frequency in the entire Taihu Basin exhibits an insignificant increasing trend.

Table 5 Trend test table for rainstorm frequency
Full size table

As can be seen from the above analysis, the rainstorm frequency in each subregion in the Taihu Basin is increasing, except for in the Huxi region. This may be due to the rain island effect caused by urbanization, which increases the frequency of the rainstorm events in urban areas. However, the evaporation in the Taihu Basin is higher in the east than in the west. The Huxi region is located in the western part of the Taihu Basin, which makes the evaporation in this region lower, thus reducing the condensation nodules and water vapor condensation over the cities in this region, resulting in a lower rainstorm frequency.

4.1.3 Variation trend of the maximum daily rainfall

The Mann–Kendall trend test method was used to test the trend of the maximum daily rainfall in the Taihu Basin and seven subregions. The test results are shown in Table 6. As can be seen from the table, the maximum daily rainfall in the Huxi and Pudongpuxi regions shows decreasing trend, while that in the other districts exhibits an increasing trend. Among them, the maximum daily rainfall in the Yangchengdianmao region passes the 95% significance test, exhibiting a significant increasing trend. The Z value of the trend test for the entire Taihu Basin is 0.41, which indicates that the annual rainfall in the entire Taihu Basin exhibits an insignificant increasing trend.

Table 6 Trend test table for the maximum daily rainfall
Full size table

As can be seen from the above analysis, the maximum daily rainfall in the Taihu Lake Basin has obvious regional differences. Because the maximum daily rainfall mostly occurs in the flood season, the maximum daily rainfall can be caused by convective rain, and there are regional differences in the surface water entering the atmosphere through evaporation in the different areas, so the maximum daily rainfall in each subregion is different.

4.1.4 Linear regression analysis

Five-year moving average analysis demonstrates that the contribution rate of rainfall in flood season shows a downward trend, and the rainfall frequency and maximum daily rainfall generally show an upward trend, resulting in an increased risk of flood events, as shown in Fig. 2. This conclusion is consistent with the trend calculated by Mann–Kendall method. Rainfall frequency and maximum daily rainfall tend to increase during the study period with the rising risk of urban flood, so it is necessary to make a thorough analysis about the rainfall indicators to provide scientific data for flood control and disaster reduction in urban areas.

Fig. 2
figure 2

Temporal trend of a contribution rate of rainfall in flood season; b rainfall frequency; c maximum daily rainfall

Full size image

4.2 Mutation point detection

As can be seen from Fig. 3, at the end of the 1950s, UF(k) and UB(k) intersected, and then, UF(k) exceeded the critical straight line, indicating that the rainfall in the next year had a significant mutation at the end of the 1950s. After that, the UF(k) and UB(k) curves intersected many times after the 1990s, and the rainfall exhibited a certain volatility.

Fig. 3
figure 3

Mann–Kendall mutation analysis results of the annual rainfall in the Taihu Basin

Full size image

4.3 Results of two-dimensional joint copula function

4.3.1 Measurement of the dependence

The Pearson γ, Spearman ρ, and Kendall τ values were used to measure the dependence between several pairs of variables: the contribution rate of the rainfall in the flood season and the maximum daily rainfall, the contribution rate of the rainfall in the flood season and the rainstorm frequency, and the maximum daily rainfall and the rainstorm frequency. The calculation results are shown in Table 7.

Table 7 Dependence between variables
Full size table

As can be seen, there are close correlations between the contribution rate of the rainfall in the flood season (C), the maximum daily rainfall (M), and the rainstorm frequency (F), so joint probability characteristic analysis of the flood variables can be carried out.

4.3.2 Selection of the marginal distribution

Appropriate distribution functions and parameters were used to draw the probability distribution curve for each rainfall factors (Fig. 4). The tops of the cumulative probability distribution curves of the three characteristic factors have a gentle change trend, that is, the occurrence of 6–7 rainstorms in a year, a maximum daily rainfall of 140–160 mm, and rainfall contribution rates of 0.75–0.8 in the flood season are rare. The cumulative probability curve of the maximum daily rainfall is the steepest, and the rainfall is mainly concentrated between 60 and 120 mm, with a cumulative probability of 0.9. That is, the maximum daily rainfall for nearly 58 years is within the range of the 65 year research period of 1955–2019. The variation trend of the top of the cumulative probability curve of the contribution rate of the rainfall in the flood season is relatively consistent with that of the middle part, and the distribution is relatively uniform, which means there is no obvious concentrated range.

Fig. 4
figure 4

Univariate distributions of the rainfall indexes: a the rainstorm frequency, b the maximum rainfall, c the contribution rate of the rainfall in the flood season

Full size image

The maximum likelihood function was used for the parameter estimation of the probability distribution functions of the rainfall indexes, and the Kolmogorov–Smirnov test was used to evaluate whether the fitting function can pass the 0.05 significance test. If the P value is greater than the significance level, the greater the P value, the more likely it is to pass the test.

Table 8 shows that the EXP distribution only passes the test for the contribution rate of the rainfall in the flood season, and the difference between the P value and the 0.05 significance level is small, indicating that the fitting effect is weak. The Poisson distribution is suitable for fitting the rainstorm frequency. The fitting effect of the GEV distribution for the contribution rate of the rainfall in the flood season is particularly obvious. Both the P-III distribution and the Ln2 distribution pass the fitting test for the two indexes, and the fitting accuracy of the Ln2 distribution for the maximum daily rainfall is relatively high. The fitting curves for the marginal distributions of the three variables are shown in Fig. 5. As shown in Fig. 5, the points of empirical frequency and theoretical frequency are basically distributed near the 45-degree line evenly, which indicates the fitting effect of three indicators’ marginal distribution function is well.

Table 8 K-S test of the marginal function fitting
Full size table
Fig. 5
figure 5

Fitting curves for the marginal distributions of the three variables

Full size image

Table 9 shows the values of the marginal distribution parameters of the characteristic rainfall variables.

Table 9 Parameters and P values of the marginal distribution
Full size table

4.3.3 Parameter estimation and goodness-of-fit test

The parameters were obtained through parameter estimation, and the theoretical frequency values of the Clayton copula, Gumbel copula, and Frank copula functions were calculated. The copula functions with the best fitting degree were determined by comparing their the RMSE, AIC, and BIC values, which were used to construct the joint distribution of the rainfall indexes. The calculated parameter values and the goodness of fit evaluation values are shown in Table 10. As can be seen from the table, the RMSE, AIC, and BIC indexes of the Frank copula function are the smallest, so the Frank copula function was selected to build the two-dimensional joint distribution model.

Table 10 Index values for evaluating the goodness of fit
Full size table

4.3.4 Joint probability analysis of the rainfall indexes

The Frank copula function was used to calculate the joint distribution function for the three rainfall factors. The conditional risk probability was calculated according to the formula. The risk probability of the other two variables was calculated based on the contribution rate of the rainfall in the flood season. Figure 6 shows the conditional probability distribution map and its isoline map for the rainfall frequency and the maximum daily rainfall when the contribution rate of the rainfall in the flood season is equal to 0.65. According to Fig. 6a, the joint probability increases as the rainfall frequency and maximum daily rainfall increase. From the joint probability contour map in Fig. 6b, the probability values of the different index value combinations can be seen more clearly. The greater the rainfall frequency and the maximum daily rainfall, the greater the joint probability value. When the rainfall frequency remains unchanged, the probability increases with increasing maximum daily rainfall. Similarly, when the maximum daily rainfall remains unchanged, the joint probability increases with increasing rainfall frequency.

Fig. 6
figure 6

Conditional risk probability when the contribution rate of the rainfall in the flood season is equal to 0.65

Full size image

Figure 7 shows the conditional probability distribution map and its isoline map for the rainfall frequency and maximum daily rainfall when the contribution rate of the rainfall in the flood season is greater than or equal to 0.65.

Fig. 7
figure 7

Conditional risk probability when the contribution rate of the rainfall in the flood season is greater than 0.65

Full size image

As can be seen from Figs. 6 and 7, compared with the probability distribution under the condition that a single variable is equal to a certain designed value, the probability diagram under the corresponding condition that a single variable is less than or equal to a certain design value is taller and fatter, indicating that the probability of the risk of being greater than or equal to a certain design value under the latter condition is higher.

There is a strong correlation among the three rainfall variables. The use of the joint distribution of the multiple variables to describe the relationship between the different rainfall eigenvalues can more comprehensively describe the rainfall events and improve the analysis accuracy.

4.4 Results of three-dimensional joint copula function

The Frank copula formula was used to solve the Frank copula joint probability for the study area, and then, a three-dimensional rainfall characteristic map with the rainfall factors as the x–y-z axes and the copula joint probability of the study area as the distribution value C was drawn using the surf code in MATLAB, as shown in Fig. 8.

Fig. 8
figure 8

a Cumulative probability of the three dimensional Copula function. b Fitting of empirical joint probability and Copula joint probability

Full size image

As can be seen from Fig. 8b, the Frank copula function’s three-dimensional joint probability is concentrated near the 45-degree straight line, with little difference from the actual distribution, and the fitting result is reliable. When the joint cumulative probability is between 0.8 and 0.9, the deviation is relatively large and the fitting error is relatively obvious. The copula joint probability does not exhibit a synchronous change trend with the rainfall factors. For example, when X–Y-Z is (0.5, 0.5, 0.5), if all of the factors have the same influence on the copula value, the copula value should be 0.5. As can be seen from the figure, the corresponding value at this point is less than 0.5.

The multivariable joint distribution diagram is designed to present the probability changes between variables. For example, the midpoints (0.74, 0.58, 0.42, 0.54) in Fig. 8a show that when the cumulative probability of rainfall frequency is 0.74, the cumulative probability of maximum daily rainfall and contribution rate of rainfall in flood season are 0.58 and 0.42, respectively, and the corresponding Frank copula value is 0.54.

The difference of X–Y-Z values demonstrates the asynchrony of rainstorm variables in the cumulative distribution. In other words, the relatively larger rainfall frequency corresponds to the smaller maximum daily rainfall and contribution rate of rainfall in flood season, which leads to the lag of Y–Z axis in the cumulative probability with the probability of this situation being 0.54. The information contained after copula combination is much richer than what is provided by a single variable in Fig. 5. Apart from more various information provided by its combination, the links between elements are highlighted. Using copula function to combine multi-dimensional elements of rainstorm can broaden the joint research direction of multi-element rainstorm.

According to the value of Frank copula, Fig. 8 was divided into three parts: A, B, and C, as shown in Fig. 8a. In area A, which has a Frank copula value of 0–0.38, the rainstorm frequency and maximum daily rainfall are larger in the figure. That is, when the copula value is 0.38, the values of X and Y are greater than 0.5, while C is less than 0.2, demonstrating an obvious lag and indicating that in the years with lower rainstorm frequencies, lower maximum daily rainfall values, and lower contribution rates of the rainfall in the flood season, the contribution rate of the rainfall in the flood season plays a relatively important role in the comprehensive characteristics of the rainfall.

Area A obviously protrudes into the region with a high rainstorm frequency. That is, when Y and Z (the maximum daily rainfall and the contribution rate of the rainfall in the flood season) change uniformly, a relatively large X (the rainfall frequency) is required to make the copula probability value correspond to the Y and Z values, which indicates that the maximum daily rainfall and the contribution rate of the rainfall in the flood season are the main factors affecting the copula joint probability. This also shows that if the maximum daily rainfall and the contribution rate of the rainfall in the flood season are small in a certain year, the rainfall frequency has little influence on the comprehensive characteristics of the rainfall in this year.

In area B, the variation trend of the rainstorm characteristics is that when the X value increases positively, the Y value decreases negatively, and the Z value is distributed in the range of 0.48–0.65 and approaches 0.65. Area B is triangular, with the top on the right, and the Z value and X value approach the right apex of the triangle. The corresponding actual rainfall characteristics are as follows. In a year with less rainfall, the rainfall frequency is relatively large, but the maximum daily rainfall is relatively small, which results in a small amount of rainfall compared with the historical records but accounts for a large proportion of the rainfall in this year. Therefore, the contribution rate of the rainfall in the flood season is relatively high.

As can be seen from area C, the cumulative distribution of the copula increases with as the cumulative probability value of the marginal distribution of each rainfall factor increases, which conforms to the objective fact of the cumulative probability distribution.

Area C shows that the rainstorm frequency (X) and maximum daily rainfall (Y) are relatively large, and the contribution rate of the rainfall in the flood season (Z) is relatively consistent with the copula joint probability value. This indicates that when the copula function is 0.74–0.96, the rainstorm frequency and maximum daily rainfall have the opposite effect; when one of the two factors has a weak effect on the copula function value, the other has a relatively strong effect.

5 Conclusions

Based on the indivisibility of the rainfall factors, in this study we used the copula joint distribution function to discuss the probability distribution characteristics of the rainfall factors in the study area. The conclusions of this study are as follows.

  1. 1.

    In terms of the change trend, the annual rainfall and the contribution rate of the rainfall in the flood season in the Taihu Lake Basin exhibited a non-significant decreasing trend. The abrupt change point of the annual rainfall in the Taihu Lake Basin appeared at the end of the 1950s, and it fluctuated after the 1990s.

  2. 2.

    With regard to the selection of the marginal distribution, the Poisson distribution is suitable for the probability fitting of the rainstorm frequency, the log-normal distribution is suitable for simulating the maximum daily rainfall, and the general extreme value distribution is more accurate for fitting the contribution rate of the rainfall in the flood season.

  3. 3.

    A three-dimensional joint distribution of the rainfall indexes was established, and the Frank copula function was found to be more suitable for the probability calculation based on the RMSE tests.

  4. 4.

    By calculating the conditional risk probability, the probability of the risk under the condition of being greater than or equal to a certain design value is larger.

  5. 5.

    The three-dimensional joint copula function reflects more of the information than the single variable distribution function and highlights the relationship between the factors, which is a part of rainfall research that must be explored further.