1 Introduction

Water is vital to all life and livelihood applications [1, 2]. Rain is a natural and vital component of the climate system, connecting processes on land, in the atmosphere, and in the ocean. Rain plays an important role in both the planetary water and energy balances. However, it is one of the components most badly impacted by climate change. Recent significant hydrological events, such as floods, droughts, freshwater scarcity, water pollution, and groundwater depletion, have emphasized changes in rainfall distribution and magnitude caused by climate change [3,4,5,6,7].

Forecasting rainfall is challenging and demanding, with a lot of factors that lead to uncertainty. Internationally, many attempts have been made to predict its behavioral pattern using various techniques [7]. Data was a set of observations of random, discrete, real, non-negative variables. The selected model can predict future occurrences, most of which are critical, statistical, and/or analytical-approximate in nature. The projecting future values employs an acceptable mathematical strategy for extrapolating future data, which is dependent on external factors and chronologically organized numerical information [8].

As a modeling technique, ARIMA has proved beneficial for predicting a range of hydro meteorological parameters [9]. Time-series data is modeled and forecasted using a variety of statistical methodologies. Those commonly used include ARIMA, moving average, exponential smoothing, regression analysis, and Fourier series analysis [10,11,12]. ARIMA was conducted in numerous studies [8, 12, 13], ARIMA is a linear model assuming that time series data is stationary [14]. As a result, nonlinearities and non-stationarities in the data are only partially captured. ARIMA models successfully account for serial linear correlation among observations, whereas Seasonal Auto Regressive Integrated Moving Average (SARIMA) models can adequately represent time series with simple periodic non-stationarity both within and across seasons [14]. The SARIMA modeling methodology was introduced as the preferred statistical method, utilizing data gathered from observations collected over a significant time period. The most difficult investigation is to forecast the temperature because of their time and space variation [15]. Besides seasonal influences, rainfall is also affected by many external factors, such as El Niño-Southern Oscillation (ENSO), temperature, wind, moisture-bearing winds, ocean currents, distance inland from the coast, and mountain ranges.

The SARIMAX model is a sophisticated and useful statistical technique for analyzing and forecasting time series data, particularly when it is impacted by seasonality and external factors. It is based on the Seasonal ARIMA (SARIMA) model, which generalizes the ARIMA model by including seasonality and allows the introduction of exogenous variables, or external influences, that may have a significant impact on the series being analyzed. Various studies have reveal to the ways identify rainfall prediction, as shown by Spessa et al. [16], Qian et al. [17], Adiwijaya et al. [18], Valipour [19]. The VMD region is undergoing rapid social, economic and environmental transitions. Water availability is critical to these transitions. The Vietnamese Mekong Delta depends highly on rain-fed agriculture in its semi-mountainous and coastal regions and also facing recurring cycles of drought [4, 5, 20, 21]. Besides that, annual rainfall was considered as the most important climatic elements that influences water irrigation and water supplies. Therefore, annual rainfall forecasting plays an important role in the planning and water resources management.

In this context, the primary objective of this study is to develop and refine a forecasting model that accurately predicts annual rainfall trends in the VMD, using the historical rainfall data collected from 12 meteorological stations over a 45-year period (1978–2022). By assessing a series of SARIMAX models, this research aims to identify the most suitable model (s) based on criteria such as the ACF, PACF, AIC, and the SBC. Further, the study seeks to evaluate the effectiveness of these models in capturing the non-linear and non-stationary nature of rainfall, considering the impact of external factors such as the ENSO, temperature variations, and geographical influences. This research aims to provide reliable, interpretable, and location-specific forecasts of near-term precipitation, thereby contributing to the effective planning and water resources management in the VMD, a region critically dependent on rain-fed agriculture and increasingly challenged by climate variability.

2 Methodology

2.1 Study area and data collection

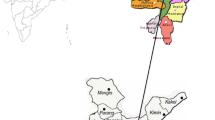
The Vietnamese Mekong Delta (VMD) is the southernmost region of Vietnam and its one of the most nationally important areas (Fig. 1). The 13 provinces that make up the VMD, account for 12% (39,200 km2) of the national territory and one-fifth of Vietnam's population [22]. The region produces for 51% of the rice crop, 65% of aquaculture, 70% of fruit, 95% of exported rice, and 60% of exported fish. The region has become a society and an engineered production landscape dependent, where water plays a key role in its economic, social and environmental development. Increases in population, urbanization, industrialization, agricultural expansion and restructuring, increased living standards and aquacultural production have in turn increased the demand for water. Moreover, the VMD is recognized as pivotal region for agriculture and aquaculture especially susceptible to climate change. In particular impact pose a substantial risk to impoverished communities, ethnic minorities, and women.

Fig. 1
figure 1

Location of study area

Full size image

The VMD experiences a tropical monsoon climate, with a high annual rainfall and large seasonal variability split into 2 distinct seasons. During the rainy seasons, the upper parts of the delta suffer from floods, whilst during the dry season, the coastal provinces suffer from saline intrusion. Approximately 5% of the water in the VMD comes from rain [23]. Whilst the total annual rainfall in Vietnam has not changed significantly since 1960, in some provinces of the VMD rainfall has increased during the rainy season and decreased during the dry season. This has important impacts for flood and drought management.

For the region rainfall forecasting is an important means for water resource management and the prevention of future disasters, mitigating floods, landslides and droughts and determining the potential of rainwater harvesting. The compounding impacts of upstream dam construction, downstream degraded, depleted and polluted water resources, and climate change, has made the accurate prediction of future rainfall for the VMD an increasingly important task in national security, regional policy making, and decision-making. Datasets from the official meteorological stations were used to assess the changes in rainfall characteristics

The annual rainfall data was obtained at 5 gauges (Bạc Lieu, Can Tho, Cao Lanh, Ca Mau and My Tho) from 1978 to 2022.

2.2 Box Jenkins Algorithm

The proposed approach uses data from the past to provide predictions. Using the ARIMA self-projecting time series predicting model, it is expected to find a best models that will approximately generate the rainfall patterns. The main objective of the Box-Jenkins Forecasting Method is to find a suitable formula that will minimize the residuals and has no pattern. The effects of climate change on various environmental variables have been widely observed in various regions around the world namely, rainfall, temperature, humidity, vapor, wind. Among these variables, rainfall was the most concerned climate change effect variable due to its nonhomogeneous distributions in time and in space [24]. The steps for the SARIMA model were as illustrated in Fig. 2.

Fig. 2
figure 2

SARIMA algorithm flowchart

Full size image

SARIMA model components

  • Autoregression (AR): Autoregression uses past values of a time series to predict present values.

  • Moving average (MA): The moving average continues to model past errors in predictions.

  • Integration (I): Integration is always used to keep the time series steady.

  • Seasonal component (S): The seasonal component represents variations that occur at regular intervals.

2.3 ARIMA, and seasonal ARIMA, and season ARIMAX models

ARIMA (p, d, q) is a traditional time series forecasting model, first introduced by Box and Jenkins in the 1970 [25]. They which created a multiplicative version of the Autoregressive Integrated Moving Average (ARIMA). The ARIMA model also has three components: p, d, and q, which stand for "autoregressive", "differencing", and "moving average", respectively. If the ARIMA (p, d, q) constructs under consideration with the seasonal nature of the time series. The general multiplicative Seasonal ARIMA is showed as SARIMA (p, d, q) (P, D, Q)s [26]; in which p, d, q denotes non-seasonal AR order, denotes non-seasonal differencing, and denotes non-seasonal MA order, respectively; P, D, Q denote denotes seasonal AR order, denotes seasonal differencing and denotes seasonal MA order, respectively; and s denotes the time span of repeating seasonal pattern. One of the model limitations is its inability to incorporate exogenous variables that could impact the time series data. Although SARIMA considers seasonal factors, it is also limited by not considering exogenous factors (temperature, vapor, and the effects of ENSO phenomena. Therefore, to address this issue, the SARIMAX model was developed. The ARIMA, SARIMA, and SARIMAX are shown in Eqs. 1–3.

$${y}_{t}=c+\sum_{n=1}^{p}{\alpha }_{n}{y}_{t-n}+\sum_{n=1}^{q}{\theta }_{n}{\epsilon }_{t-n}+{\epsilon }_{t}$$
(1)
$${y}_{t}=c+\sum_{n=1}^{p}{\alpha }_{n}{y}_{t-n}+\sum_{n=1}^{q}{\theta }_{n}{\epsilon }_{t-n}+\sum_{i=1}^{Q}{\upeta }_{n}{\epsilon }_{t-sn}+{\epsilon }_{t}$$
(2)
$${y}_{t}=c+\sum_{n=1}^{p}{\alpha }_{n}{y}_{t-n}+\sum_{n=1}^{q}{\theta }_{n}{\epsilon }_{t-n}+\sum_{i=1}^{Q}{\upeta }_{n}{\epsilon }_{t-sn}+\sum_{i=1}^{r}{\beta }_{n}{x}_{{n}_{t}}+{\epsilon }_{t}$$
(3)

where, \({y}_{t}\), and c denote the lag term, the intercept of model, respectively. \({\varepsilon }_{t}, r,\text{ and }x\) denote the random error at time t, the number of exogenous variables, and the exogenous variable, respectively.

When a seasonal factor impacts a series, a seasonal pattern is created. Seasonality is of a fixed and known period that might display an increasing trend to a decreasing trend [10]. The annual rainfall series in the study area shows that it is cyclical because the annual rainfall series shows some years within this study with low rainfall and some years that alternate with heavy rainfall.

2.4 Model identification (selection of model order)

Initially, the original data was tested to an augmented Dickey-Fuller (ADF) test to determine stationarity stationary using unit root and stationary tests; if the results showed a non-stationary series, a differenced transformation would establish stationarity.

To determine preliminary values for the autoregressive order p, the order of differencing d, the moving average order q, and the seasonal parameters P, D, and Q. The autocorrelation function (ACF), partial autocorrelation function (PACF), and inverse autocorrelation function (IACF) are the most essential components [27]. The ACF assesses the level of linear dependency between observations in a time series separated by a lag q. The PACF identifies how many auto-regressive terms (p) are required. The IACF detect over-differences, and if the data are over-differenced, the IACF resembles an ACF from a non-stationarity process. The selection of the best proposal models involved the use of the Likelihood, Akaike Information Criterion (AIC), with consideration given to the model with the lowest AIC. The mathematical formulation for the AIC is defined as:

$$AIC= -2\text{log}L+2m$$
(4)

where, m = (p + q + P + Q) is the number of terms estimated in the model and L denotes the likelihood function of ARIMA models and it is a monotonically decreasing function of the sum of squared residuals.

The mathematical formulation for SBC is defined as

$$SBC= -2\text{log}L+m\text{ln}(n)$$
(5)

where, n denotes the number of observations.

2.5 Model performance measurement

Model performance was measured to assess the regeneration capability based on various statistical measures such as Nash-Sutcliff coefficient (Nash) and Root Mean Square Error mean (RMSEM). The highest of Nash value and the lowest of RMSEM were selected. Nash and Sutcliffe [28] proposed an alternative goodness-of-fit Nash index, which is often referred to as the efficiency index as shown in Eq.

$$Nash=1-\frac{\sum_{i=1}^{n}{({y}_{i}-{x}_{i})}^{2}}{\sum_{i=1}^{n}{({x}_{i}-\bar{x })}^{2}}$$
(6)
$$RMSEM=\frac{\sqrt{\frac{1}{n}\sum_{i=1}^{n}{({x}_{i}-{y}_{i})}^{2}}}{\bar{x} }$$
(7)

where, \({x}_{i},{y}_{i}, \bar{x }, and n\) denote observed data, predicted data, mean of observed data, and observed size, respectively.

3 Results

3.1 Impact of climatic factors on rainfall variability in the VMD

Here we explore the intricate dynamics of precipitation in the VMD, highlighting the significant influence of various factors including the ENSO, wind, temperature, and moisture on rainfall patterns. Numerous studies have demonstrated that the ENSO phase has an impact on rainfall in the VMD as well. Thus, we adopted the NOAA definition that an El Niño (or La Niña) event occurs. The intensity of El Niño events was further categorized as very strong (ONI ≥2 °C), strong (1.5–1.9 °C), moderate (1.0–1.4 °C), and weak (0.5–0.9 °C), and similarly for La Niña events based on the corresponding negative values [29]. A higher ONI means it has a trend of El Nino level and a lower INO means it trend of La Nina. Figures 3 and 4 and Table 3 show the correlation test among rainfall station with Oceanic Niño Index (ONI) (Appendix 2). It can be seen that the annual rainfall at Cao Lanh, My Tho, and Bac Lieu stations have positively correlated to ONI at 95% confidence level, with correlation coefficients of –0.53, –0.51, and –0.31, respectively. However, the correlation between annual rainfall at Can Tho and Ca Mau and ONI is low and without significant statistics. As a result, we decided to use the SARIMA model for the study's five research regions. The annual rainfall time series data (1978–2022) was plotted in Fig. 5 over 45 years at five meteorological stations in the VMD. It was found that annual rainfall at 12 stations were non-stationary except My Tho station using Unit root and stationarity tests. We observed time series go down and increase alternately. Some factors affected to annual rainfall by using correlation test. Therefore, we expected SARIMA model can predict annual rainfall.

Fig. 3
figure 3

Scatter plots for Spearman correlation tests of Annual rainfall at Bac Lieu, My Tho, and Cao Lanh with ONI

Full size image
Fig. 4
figure 4

Scatter plots for Spearman correlation tests of Annual rainfall at Bac Lieu, My Tho, and Cao Lanh with ONI

Full size image
Fig. 5
figure 5

Time series of annual rainfall at: a Bac Lieu, b Can Tho, c Cao Lanh, d Ca Mau, and d My Tho. On inspecting in this figure, we note the cycle (seasonal factor). This is confirmed by very high spikes at and around seasonal lags ranging from 10 to 12

Full size image

3.2 Model development and forecasting analysis for rainfall prediction

The data was divided into two sets, training and test data. Data from 1978 to 1988/1989 were used as training data while the rest of the data were used as test data for consistency and reliability of our model. The annual rainfall time series has been built by a seasonal ARIMA model and predicts the rainfall patterns for the next years ranging from 5 to 15 years. Specifically, in a seasonal ARIMA model, the parameters D and d, other parameters P, Q, p, and q can be preliminarily identified from the autocorrelation function (ACF), Partial Autocorrelation function (PACF) and inverse autocorrelation function (IACF) of the stationary processing series. The best SARIMA models are selected from the potential models: (1) SARIMA 1-SARIMA 16 for all station: (2) SARIMA 1-SARIMA 32 for My Tho station (Table 1). The suitable model is selected based on the lowest Likelihood. However, we only selected 5 stations that can be used for good forecasting based on the Nash and RMSEM values shown in Table 2. SARIMA models performed very good at Bac Lieu and Can Tho stations with Nash of 0.87 and 0.83, respectively. The RMSEM index is also found to be quite small at these two stations. SARIMA (1,1,1)(2,1,1)11 were proposed for Bac Lieu, Cao Lanh and Ca Mau while SARIMA (1,1,1)(2,1,1)12 were proposed for Can Tho and My Tho for prediction. We conducted prediction for the next 15 years for Bac Lieu, Can Tho and Cao Lanh, respectively; 8- and 10-years annual rainfall  predictions for Ca Mau and My Tho stations, respectively. Figures 6 and 7 show the prediction of annual rainfall for five stations.

Fig. 6
figure 6

Predictions annual rainfall using SARIMA models: a) Bac Lieu and b Can Tho

Full size image
Fig. 7
figure 7

Predictions annual rainfall using SARIMA models: a Cao Lanh, b Ca Mau, and c My Tho

Full size image
Table 1 Potential SARIMA models
Full size table
Table 2 Results of selecting the best prediction model for 5 stations
Full size table

To verify the suitability of the model, we plot the autocorrelation values of the residual against lag as shown in Figs. 8 and 9 (Appendix 1). We note that on inspection of Fig. 8, there is no spike at any lag showing that the residual process is random. We therefore accept Seasonal SARIMA (1, 1, 1) (2, 1, 1)11 for Bac Lieu, Cao Lanh, and Ca Mau, and SARIMA (1, 1, 1) (2, 1, 1)12 Can Tho and My Tho as the most appropriate modes for prediction rainfall in 5 stations in the VMD.

Fig. 8
figure 8

Autocorrelogram and Partial autocorrelogram charts of SARIMA models: Bac Lieu (a–d) and Can Tho (e–h)

Full size image

4 Discussion

In this study, the SARIMA models showed good efficacy in predicting annual rainfall across the VMD, as evidenced by the Nash and RMSEM values for each station. These performance metrics highlighted the reliability of SARIMA models for forecasting purposes for this region. Bac Lieu and Can Tho stations showed high performance which suggested that rainfall patterns in these areas can be predicted with a considerable degree of accuracy using these models. Specific regional climatic factors such as seasonal variability and trend patterns could be attributed for the high predictabilities of these models in these areas that aligned well with the assumptions underlying SARIMA models. Many studies have also reported similar results. Ramli et al. [30] employed these models for rainfall prediction in Aceh, Indonesia, highlighting their applicability across various time periods. The study achieved promising results in terms of predictive accuracy, that was evaluated using Nash-Sutcliffe Efficiency and PBIAS (IIETA) metrics [30]. This study demonstrated the model's effectiveness in forecasting rainfall with different time series data lengths. The main outcome of their study showed that shorter, more recent time series provide more accurate predictions. Furthermore, Martínez-Acosta et al. [31] demonstrated the SARIMA model's capability to generate synthetic monthly rainfall series that closely match observed data in the Sinú River Watershed in Colombia [30]. In this study, the SARIMA model was particularly used for its ability to address the seasonal behavior of rainfall, highlighting the importance of selecting appropriate models that can capture the inherent temporal nature of precipitation in specific areas, and concluded that reliable rainfall forecasts, are important for planning and decision-making processes related to water resource utilization and agricultural activities.

The observed strong correlations between the ONI station and annual rainfall patterns at Cao Lanh, My Tho, and Bac Lieu stations in the VMD significantly emphasized the critical role El Niño and La Niña phases play in influencing rainfall variability within this region [31]. There are studies that have demonstrated the broader global impact of the ENSO on precipitation patterns [32, 33]. During El Niño events, certain regions experience significantly reduced rainfall, that leads to drought conditions, while during the La Niña phases there is often incidents of increased rainfall, which results in flooding of the regions that are affected by it [34, 35]. Dai and Wigley [36], showed the variability of precipitation and temperature extremes in relation to ENSO cycles, hence demonstrating the significant correlations that highlight their role in affecting the global climatic conditions [36, 37]. By integrating ENSO phases into rainfall forecasting and climate models, researchers and policymakers can significantly enhance the accuracy and reliability of these predictions. In regions like the VMD, where agriculture and water management are critical to socioeconomic stability, incorporating ENSO-related insights into planning and operational frameworks can lead to the development of more resilient agricultural practices and water management systems and thus could greatly aid in mitigating the adverse effects of climate change, ultimately contributing to the sustainability and resilience of vulnerable regions against the backdrop of global climate dynamics.

The rainfall time series are non-stationary at all but one station (My Tho) which presents a significant challenge to traditional forecasting models. This non-stationarity, indicative of changing mean and variance over time, further necessitates the use of advanced models like SARIMA that can accommodate such complexities. The application of unit root and stationarity tests to identify these characteristics is crucial for selecting the appropriate model and ensuring forecasting accuracy, highlighting the importance of preliminary data analysis in the modeling process. SARIMA models stand out as a particularly effective solution in this context, given their design to accommodate the seasonal fluctuations and non-stationary nature of time series data. Moreover, the key role of preliminary data analysis, that consist of the application of unit root and stationarity tests such as the ADF, cannot be underestimated [38,39,40]. Such tests are instrumental in assessing the stationarity of a time series, that helps to guide in the selection of an appropriate modeling approach which is customized based on characteristics of data. In this study, we also conducted ADF test, that helped in strengthening the reliability and accuracy of the forecasting outcomes from this study. In this context, Box, Jenkins, and Reinsel's work on time series analysis has laid the groundwork for the use of ARIMA models in dealing with non-stationary data, which emphasizes the importance of identifying the nature of data before model selection [14]. Furthermore, Brockwell and Davis [41] extended this approach by introducing SARIMA models as an extension of ARIMA to specifically address the problems associated with the seasonal data. This shows the evolution of statistical methods to accommodate complex data characteristics in the analysis [41]. In our study, the observed spikes observed at the seasonal lags provided us with the requisite information for selecting the appropriate SARIMA model configurations. This very particular characteristic defines the SARIMA model’s capacity to incorporate seasonal variability into its forecasts. Moreover, the adaptability of the SARIMA model also extends to incorporating external climatic factors, that in this study were ENSO phases, that influence rainfall patterns in the VMD, demonstrates the its capability to forecast with greater precision. In this context, Chiew et al. [42] have analyzed the ENSO's impact on Australian rainfall patterns using the understanding of ENSO phases to improve rainfall predictions using such models [42]. Similarly, Morid et al. [43] highlights the potential of incorporating ENSO indicators into forecasting models to anticipate and mitigate drought impacts in Iran [43]. Furthermore, the integration of SARIMA models with external climatic factors like ENSO phases aligns with the approach taken by Poveda et al., [44]. This study investigated the influence of ENSO on Colombian hydrology and water resources and showed that their models were able to capture a broader spectrum of climatic variability, using ENSO indicators thereby enhancing the robustness and reliability of their forecasts.

The ability to forecast rainfall with high accuracy is instrumental in informing a range of essential activities, from agricultural planning to flood management and drought preparedness in this region. In agricultural planning, accurate rainfall forecasts enable farmers to make informed decisions regarding the timing of planting and harvesting, leading to improved yields and reduced risk of crop failure. This is particularly important in VMD, which is critically dependent on rice cultivation and is thus, sensitive to small fluctuations in water availability. Pavelic et al. [45] demonstrated the impact of improved hydrological forecasting to benefit irrigation scheduling, hence enhancing water use efficiency and crop productivity in agricultural systems [45]. Flood management is another crucial area where reliable rainfall predictions have a substantial impact. The VMD is prone to annual flooding due to its geographical location and topographical characteristics [46, 47]. Advanced forecasting models that accurately predict rainfall shall help in the timely implementation of flood mitigation strategies, such as evacuation plans, and the reinforcement of flood defenses and the operation of dams and reservoirs. Tingsanchali et al. [48] highlighted the importance of flood forecasting and management in reducing the vulnerability of river basins to flooding, hence emphasizing the role of accurate weather predictions [48]. Similarly, for drought preparedness, it is important to foresee periods of low rainfall which allows for the proactive management of water resources, so that water supplies are conserved and optimally distributed during times of scarcity. This is also very critical for maintaining agricultural productivity and supporting the livelihoods of communities within the VMD. Wilhite et al. [49] examined the effectiveness of drought early warning systems and their significance in drought risk management. They illustrated the benefits of incorporating accurate climate forecasts into water resource planning [49].

When the data has strong seasonal patterns, SARIMA models perform better than ARIMA models. SARIMA models can accommodate several seasonal cycles, such as weekly, monthly, and yearly patterns. SARIMA takes more parameters to estimate than ARIMA, which can complicate the process. The SARIMA model presupposes that seasonal patterns remain stable and constant throughout time, which may be unrealistic for some data. Another downside is that they may underperform when dealing with non-seasonal data. Moreover, the SARIMA model's limitations is that it can only identify linear relationships in the time series data. Future research must focus on exploring models that can incorporate additional climatic variables, external variables (such as Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors (SARIMAX) model) and provide longer-term forecasts. Also, the impact of climate change on rainfall predictability also warrants investigation, as does the potential for integrating machine learning techniques to enhance forecasting accuracy. Abbot and Marohasy [50], employed artificial neural networks to predict rainfall in the Murray-Darling Basin, Australia, highlighting the potential of complex algorithms to capture the nonlinear relationships inherent in climate data [50]. Trenberth [51] illustrated the complexities of understanding precipitation forecasts under changing climatic conditions, hence emphasizing the need for robust forecasting models [51]. Studies have used machine learning techniques in forecasting precipitation. Yin et al. [52] used support vector machines for the forecasting precipitation and thus highlighted the usefulness of machine learning techniques [52]. Xingjian Shi et al. [53] using convolutional LSTM networks highlighted the enormous possibilities of combining ML with climatic data for precipitation forecasting [53]. Therefore, future research in the VMD must therefore prioritize the development of hybrid models that integrate the traditional climatic models with machine learning algorithms. This approach would facilitate a much deeper understanding of climate dynamics and shall offer more reliable forecasts, critical for preparing for and mitigating the effects of climate variability and change.

5 Conclusions

In this study, we predicted the annual rainfall in the VMD, using SARIMA models. The results demonstrated that these models are effective at capturing the peculiarities of rainfall patterns across various stations, in the VMD. For Bac Lieu, Cao Lanh, and Ca Mau stations, the SARIMA (1, 1, 1) (2, 1, 1)11 configuration was identified as the most effective. While as, for Can Tho and My Tho stations, the SARIMA (1, 1, 1) (2, 1, 1)12 model was observed as the best choice. The accuracy of these models was evident in their correlation with observed annual rainfall data at key stations, particularly Bac Lieu and Can Tho. This highlighted their potential to be used for significantly enhancing the rainfall forecasting accuracy in the region. These findings also contributed to a more specific understanding of the region's climatic variability demonstrated by local variations, and paved the way for more informed water resource management strategies. By using accurate rainfall predictions, stakeholders can better navigate agricultural planning, flood management, and drought preparedness, thereby strengthening the region's resilience against climatic fluctuations. Looking ahead, the path for future research is clear. The exploration of more sophisticated models that encompass a wider array of climatic variables stands as a promising avenue for enhancing long-term forecast capabilities. Additionally, the pressing need to examine the implications of climate change on rainfall predictability is evident, as is the potential for integrating cutting-edge machine learning techniques to further refine forecasting accuracy. Such endeavors will deepen our understanding of climate dynamics in the VMD and advance the state of rainfall forecasting models, thus ensuring they remain robust in the face of changing climatic conditions.