Abstract
A large body of scientific research has demonstrated a changing climate, which affects river flow regimes and extreme flood frequencies and magnitudes. The magnitude and frequency of extreme events are of critical importance in the evaluation of river systems to inform flood risk reduction under current and future conditions. The global climate projections from the Coupled Model Intercomparison Project, Phase 5 (CMIP5) datasets were used by the Variable Infiltration Capacity (VIC) land surface model to produce a runoff dataset, implementing a Bias-Correction Spatial Disaggregation (BCSD) approach. The resulting runoff was then used as input to the Routing Application for Parallel computatIon of Discharge (RAPID) river routing model to simulate daily flows within all 1.2 million Mississippi River Basin river reaches for years 1950 through 2099. This research effort analyzed the performance of the models for the historical time period, comparing with the observations at 64 gage locations for 16 different climate models. A recurrence interval analysis was performed to determine the 2-, 5-, 10-, 50-, 100-, 500-, and 1000-year events within both the historical and projected time periods, highlighting the relative changes predicted into the future. Anticipated seasonal changes are demonstrated by comparing monthly average streamflows for three different time periods (1951–2005, 2006–2049, and 2050–2099). Results indicate that the hydrologic conditions of the Lower Mississippi River are not stationary. Based on all 16 models considered in this study, the median of the model projections shows an 8% increase in the 100-year return period discharge at Vicksburg, Mississippi, into the future time period, although the full range of 16 models varies widely from − 11 to + 85% change in the 100-year discharge in the future.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
While climate change has been empirically proven, it remains critical to evaluate the effect that the non-stationary conditions due to climate change will have on the Earth and its human population (Intergovernmental Panel on Climate Change [IPCC], Masson-Delmotte et al. 2019). Although geophysical processes and the hydroclimate are inherently non-stationary, historical observations can be represented by stationary stochastic models. Therefore, referring to the hydroclimate as non-stationary designates a break in that trend, requiring a complex deterministic characterization of the process (Lins 2012). This non-stationarity is affected by anthropogenic contributions, as atmospheric water-holding capacity is expected to increase with temperature from rising global emissions, thus more extreme precipitation events become more likely to occur (Min et al. 2011). Across the Northern Hemisphere, such increases in greenhouse gases have contributed to two-thirds of the intensification of precipitation events from the latter twentieth century onwards (Min et al. 2011). In the contiguous United States, precipitation rates in the heaviest one percent of rain events increased twenty percent over the last century (1901–2000) according to Kunkel et al. (2008). This research suggests that heavy downpours will also increase: “1-in-20-year occurrences are projected to occur about every 4 to 15 years by the end of this century, depending on location, and the 1-in-20-year heavy downpour is expected to be between 10 and 25% heavier by the end of the century than it is now” (Kunkel et al. 2008). Increases in extreme precipitation events pose serious challenges to both human populations and the environment, rendering it critical to accurately model potentially destructive extreme events, such as floods.
Gudmundsson, et al. demonstrated that externally forced climate change has globally adjusted both the mean and extreme river flows, presenting new challenges for water management and flood protection (2021). Several studies have used the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP) simulation results (simulation experiment 2a by Gosling et al. 2017, and phase 2b Frieler et al. 2017) to evaluate streamflow projections at both the global and regional scales. Krysanova et al. emphasize the importance of evaluating model projections over the historical time period (2020, 2018). Some studies evaluate the models with an expectation that the temporal fluctuations of streamflow would match the pattern of the observations. Even when converting the data to annual values, a different sequence of wet and dry years than was observed can cause a model to appear to perform poorly. However, some studies avoid this expectation by evaluating the model results for longer term trends or through methods independent of the temporal sequence of streamflows. For example, Kiesel et al. evaluated model performance for the Danube River separately for the 10 warmest, 10 coldest, 10 wettest, and 10 driest years (2020). The analysis presented below (Section 3.2) does not expect the temporal sequence of the model flows to match the observations, but rather it calculates the residual errors across the statistical distributions of modeled and observed streamflows.
The Mississippi River Basin (MRB) is the USA’ largest watershed, covering all or part of 31 states, or 41% of the contiguous United States. This area comprises approximately 3,298,800 km2 (Tavakoly et al. 2017). The Mississippi River provides critical services to the USA: the efficient waterway annually provides half a trillion dollars to the economy and 1.3 million jobs (Bridges 2019). Around 18 million people rely on the river for their water supply, and many million live within the basin area. It holds 25% of the USA’ hydropower, 25% of North America’s fish species, and 60% of North America’s bird population (Bridges 2019). The Great Mississippi River Flood of 1927 was the most destructive flood in U.S. history, inundating 68,000 km2 and displacing hundreds of thousands of people. The Great Flood of 2011 was of a similar size to the floods of 1927 and 1937, but there was far less destruction due to the major federal investment following the 1927 flood. Protection from future Mississippi River floods continues to be a national priority.
Future flood projections of MRB with respect to climate change have been the subject of a few case studies (e.g., Krysanova et al. 2020 and Zaherpour et al. 2018), although it has mostly been limited to the Upper Mississippi River Basin (UMRB). Jha et al. (2006) showed that the UMRB is located at the intersection of three major air masses (Pacific, Arctic, and Gulf of Mexico) driving the climate of North America and is therefore very sensitive to climate change (2006). Historical analyses from the Holocene and U.S. Geological Survey (USGS) lake sediment cores suggest significant climate change conditions (Jha et al. 2006). Layering in the sediment records indicates that flooding magnitudes are sensitive to climatic changes, revealing that large floods are commonly associated with the beginning of warm and dry seasons (Knox 2002). The same sediment data showed the longer the term of warmer conditions, the more small floods of high short-term variability (Knox 2002). Changes in precipitation and other climate conditions could also have major environmental consequences. Some of the in-depth recent studies on climate change and streamflow analysis are limited to small- or regional-scale modeling (e. g. Dahl et al. 2021, Johnson et al. 2015, Park et al. 2011, Verma et al. 2015, and Huang et al. 2020). Our study is the first to use a high-resolution stream network to quantify climate change effects on an entire river system, using 1.2 million river reaches to represent all streams and tributaries for the entire MRB.
For this purpose, a set of varying climate simulations was executed using the Routing Application Parallel Discharge (RAPID) river routing model (David et al. 2011). The Coupled Model Intercomparison Project (CMIP) consists of Atmosphere–Ocean General Circulation Models (AOGCMs) that include decadal hindcast and prediction simulations, as well as long-term simulations and atmosphere-only simulations (Taylor et al. 2012). This divides the four greenhouse gas trajectories described by the IPCC as Representative Concentration Pathway (RCP) scenarios, which have values of 2.6, 4.5, 6.0, and 8.5, referring to the peak radiative forcing in W/m2. The Variable Infiltration Capacity (VIC) land surface model was set up to downscale and bias-correct raw Coupled Model Intercomparison Project, Phase 5 (CMIP5) precipitation and temperature using Bias-Correction Spatial Disaggregation (BCSD; Reclamation 2014). Runoff data was generated for 31 AOGCMs with four aforementioned RCP scenarios. In this study, the runoff data were obtained for 16 selected global climate models with RCP 4.5 (Masui et al. 2011) from 1950 through 2099. In Tavakoly et al., RAPID was used to simulate streamflow in the MRB for 1.2 million river reaches across a decade of data in order to understand both the challenges and successes in continental flow computation of river discharge across the MRB (2017 and 2021). The performance of using VIC runoff, driven by observed meteorological data, in the RAPID model is demonstrated in Tavakoly et al. (2017), Follum et al. (2017), and Tavakoly et al. (2021). Our study takes this RAPID model setup from Tavakoly et al. and applies it to the climate projections found in the CMIP5 dataset (2017). The results are then analyzed through recurrence intervals and seasonal variation at different USGS and U.S. Army Corps of Engineers (USACE) gage locations.
To the authors’ knowledge, there has not been a comprehensive study covering climate projections and future flood conditions at the continental scale of the MRB using high-resolution vector-based river networks. The capability to run such large-scale river routing is made possible by the advancement in numerical modeling on supercomputer parallelization, which will be further discussed in Section 2.
2 Methodology
The CMIP is a global scientific effort to standardize and compare projections of the earth’s climate. Climate models have been developed by various science groups around the world in support of CMIP. Multiple phases of CMIP have occurred and are ongoing (Eyring et al. 2019). The research documented in this paper uses results of the CMIP Phase 5 (CMIP5), because it is the most recent effort with available hydrology data including the BCSD runoff dataset. The different models within CMIP5 shared common forcings, such as emission levels, and performed simulations to calculate climate conditions such as precipitation and temperature values. The CMIP5 modeling results start in the year 1950 and continue through the year 2099. The time period 1950 to 2005 used observed climate forcings and is called the historic time period. Model simulations of 2006–2099 use projected forcings according to four different emission scenarios. Emission scenarios are labeled by their RCP. RCP 2.6 assumes global annual greenhouse gas emissions peak between 2010–2020 and then decline. RCP 4.5 assumes a peak in emissions around 2040, and RCP 6.0 assumes a peak around 2080. RCP 8.5 assumes emissions continue to rise throughout the twenty-first century.
Due to resource and practical limitations, this initial effort could not compute and evaluate streamflow for all models and all scenarios. This effort chose the intermediate RCP 4.5 scenario as opposed to either extreme (RCP 2.6 or RCP 8.5), and as RCP 6.0 had less available hydrology data. Sixteen of the 31 available climate models were chosen for this analysis, as listed in Table 1. The selection of the 16 CMIP5 climate models used in this analysis was based on accuracy rankings available within the literature for either precipitation or runoff. Törnqvist et al. ranked 22 CMIP5 models for the Lake Baikal basin based on monthly precipitation, temperature, evapotranspiration, and runoff (2014). Similarly, Ahmadalipour et al. analyzed the performance of 20 models for the Columbia River Basin regarding monthly and daily precipitation and temperature parameters (2015).
This effort utilized the hydrologic data available for CMIP5 computed by Reclamation (2014) using the VIC hydrologic model (Liang et al. 1994; and Nijssen et al. 1997), version 4.1.2. In particular, the gridded VIC runoff data was used here as input for streamflow computations. Hydrologic processing of the CMIP5 modeling data included Bias-Correction and Spatial Disaggregation (BCSD) as well as a technique to time-disaggregate monthly BCSD climate projections into daily VIC weather inputs (Reclamation 2014). The VIC products selected for this study use a specific statistical downscaling approach (BCSD) to downscale (and bias-correct) raw CMIP5 precipitation and temperature outputs. After BCSD, the downscaled precipitation and temperature values have the same monthly distribution compared to the chosen gridded observation (Maurer et al. 2002); this effort was primarily led by the Bureau of Reclamation. More details can be found in the Reclamation technical report (Reclamation 2014). The downscaled precipitation and temperature values are then used to drive the 12 km VIC model used by the National Center for Atmospheric Research. The CMIP5-BCSD-VIC was not further bias-corrected.
Runoff products from the BCSD-VIC model were then used to drive the RAPID river routing model in this study. The RAPID model is capable of calculating streamflow at a continental scale by routing the volumetric runoff data through a high resolution of streams. The RAPID model uses a vector-based computation of the Muskingum method within each river segment. This model has been applied to study nitrogen transport in large-scale river networks (Tavakoly et al. 2016; 2019), detection and attribution analysis (Forbes et al. 2019), and flood simulation over the continental scale river network (Salas et al. 2018; Tavakoly et al. 2017).
This study takes geospatial RAPID parameters from Tavakoly et al. and inputs from the climate projections in the CMIP5-BCSD-VIC runoff dataset to simulate daily streamflows throughout the MRB and analyze recurrence interval relationships and seasonal variations at different USGS and USACE gage locations (2017). Using RAPIDpy, a Python interface for pre and post processing for RAPID, a static weight table was created to distribute the VIC runoff data to each individual catchment based on the catchment area within each grid cell (Snow et al. 2016). For each daily time step, the volumetric runoff was calculated for each catchment. The Muskingum parameters k and x for each river segment were used from the previously calibrated effort for the MRB (Tavakoly et al. 2017). The daily computations were performed using the Topaz supercomputer at the U.S. Army Engineer Research and Development Center. Due to streamflow initialization effects, the first year of simulation was discarded from the analysis of results.
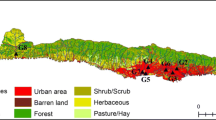
The daily flows were extracted at 64 different locations around the MRB for analysis, as shown in Fig. 1. The flowlines used by RAPID and shown in the figure are from the NHDPlus river network (McKay et al. 2012). Observed data also existed at each of the 64 locations, which were obtained from the USGS National Water Information System (NWIS) and from the Memphis and Vicksburg U.S. Army Corps of Engineers District Offices. Three of the locations (Vicksburg, MS; Metropolis, IL; and Thebes, IL) were chosen strategically to evaluate combined effects from very large areas of the MRB. The Vicksburg station is on the main stem of the Lower Mississippi River below the confluences with most of the large tributary basins. The Metropolis station is on the Ohio River near its mouth, and the Thebes location is on the Mississippi River upstream of the confluence with the Ohio River.
3 Results
The primary purpose in evaluating the simulation results is to highlight the relative changes and the uncertainty that can be expected for future river conditions. An analysis of changes between the historical and future time periods begins with a linear regression calculation of an ensemble, as described in the first section below. The second section will evaluate the performance during the historical time period using a residual sum of squares calculation across the statistical distribution of streamflows. The third section will analyze the changes in the streamflow distributions between the historical and future time periods. The fourth section will evaluate the extremely high streamflow events and explore the changes and uncertainty in those magnitudes. Lastly, the fifth section will investigate the relative changes in seasonal streamflow behavior between the historical and future time periods.
3.1 Calculation of an ensemble of model results
A representative ensemble was calculated using a linear regression method as described in Crawford et al. (2019), shown in Eq. 1.
where y is the ensemble prediction, i is time, j is for each independent model (p = 16), x is the individual model result, and the vector β = (β0, β1, …, βp) contains the regression coefficients.
The β coefficients were found using a Generalized Reduced Gradient solver (Lasdon et al. 1974) in a least-squares regression approach, fitting the 16 models’ annual averages with the observed annual averages for the time period 1951 to 2005 at each of the 64 gage locations. Using annual values is in line with Krysanova et al., who recommended the calculation of the ensemble was better suitable for mean annual values (2020). Table 2 below shows the values for the β coefficients at the three selected locations and also the average of the β coefficients across all 64 gage locations. At the three selected locations, we see that the ensemble calculation consistently gives a relatively high weight (high β coefficient) to model CCSM4 (≥ 0.15 in each case). Model GISS-E2-R had the highest β coefficient at both the Thebes and Vicksburg locations. A simple arithmetic mean of the models would be equivalent to a β coefficient (β1, …, βp) of 0.0625 across each model, which is a reference value for comparing which models received higher/lower coefficients in the ensemble calculation than a simpler ensemble mean approach.
The resulting β coefficients, at each of the 64 gage locations, were used to calculate the ensemble for each date of the entire simulated time period through 2099. The ensemble results for the three locations are shown in Fig. 2. The authors recommend the coefficient weighting used in the ensemble calculation should not be used for evaluating or comparing the performance of a model. A model may do very well at matching the distribution of observed streamflows, but if the timing of simulated wet and dry years does not line up with the observed timing of wet and dry years it could receive a low β coefficient value. In this work, the model performance is evaluated based on the distribution of flows, as discussed in the next section. One other note is that the ensemble results are smoother than the models. When fitting the ensemble to the observations, the high and low values for particular years are not as extreme as an individual model.
3.2 Evaluation of modeling performance
This section of the report evaluates how well the routed climate modeling results were able to replicate the historical time period. As defined in the CMIP5 documentation the historical time period 1950 to 2005 includes common emission-forcing data across the GCMs (Reclamation 2014). It is not reasonable to compare model results and recorded streamflows within each year due to the variations in meteorological conditions generated by each GCM at any particular time. Furthermore, simulations are not expected to match observations at any specific time or match the temporal sequence of wet and dry years. For example, it is not anticipated that the temporal fluctuations of the climate models will produce a dry year in 1992 followed by a wet year in 1993, as was observed for the Mississippi River. Rather, the focus is on comparing the distribution of simulated and recorded streamflows over the historical time period in its entirety. The ability of the modeled streamflows to match the distribution of observed streamflows is of interest.
Here, we directly calculate the differences between the distribution of the observed streamflows with each model’s distribution through the historical time period (1951–2005). The distributions were characterized using the statistical software R and the standard “stats” package within R (2018). Using the “quantile” function, each distribution was represented by 99 values from the 1st to 99th percentiles, using daily values from 1951 to 2005. The distribution of the observed data and each of the 16 models was found for each of the 64 gage locations. The residual errors between the observations and each model were calculated for each percentile in the distribution, and the sum of the squares of the residuals was calculated (Morgan and Tatar 1972). This approach, as shown in Eq. 1, provides a direct way to analyze how well each model’s results fit the observed distribution of streamflows at each location.
where S is the residual sum of squares, j is each independent model (p = 16), k and m represent the range of percentiles over which the summation is performed, zk is the value in the observed distribution at the kth percentile, and ẑj,k is the value of the distribution in the jth model at the kth percentile.
The residual sum of squares error was compared across models to rank them 1 to 16 (1 being the model that had the lowest error and 16 having the highest error). For example, looking at the lowest and highest error sums at the Vicksburg location, the models IPSL-CM5A-MR, BCC-CSM1-1-M, MRI-CGCM3, and MIROC5 were the 1st, 2nd, 15th, and 16th ranked models, respectively. From the red and orange symbols of Fig. 3, you can see how the MIROC5 and MRI-CGCM3 models, respectively, have portions of the distribution where they are significantly further away from the black line of observations, compared to the green and blue symbols for the IPSL-CM5A-MR and BCC-CSM1-1-M results, respectively, at Vicksburg. This ranking process, based on the sum of the squares method, was performed at each of the 64 gage locations. The full table of ranking results for each model at each gage location can be seen in the Appendix.
The performance of the models across the basin can be compared by calculating an average rank across all locations, as shown by the gray bars in Fig. 4. The models with the best average ranks across locations were CSIRO-Mk3-6–0 and BCC-CSM1-1-M with average ranks of 5.9 and 6.7, respectively. Models with relatively poor average rankings were GISS-E2-R (average rank of 11.0) and MRI-CGCM3 (average rank of 10.7). The same procedure was calculated again using only 9 values to represent each distribution, instead of 99, in order to see the influence of the distribution characterization (i.e., the summation is performed for 9 terms: k = 10, 20, … 90). These are shown by the blue bars in Fig. 4. Lastly, the same procedure was also performed focusing only on the upper 10 pecentiles (i.e., the summation is performed for k = 90, 91, … 99) in order to evaluate how well the models match the higher end of the observation distribution (orange bars in Fig. 4). In general, the average ranking of the models is somewhat consistent across the three different methods. For example, the GFDL-ESM2G model has an average ranking between 7.47 and 7.61 for all three methods.
Focusing on the distribution which uses 99 percentile values, a further analysis tallied the number of locations that each model was ranked in first place. Here, the IPSL-CM5A-MR model stood out above the others, being ranked first at 14 different gage locations out of 64. Behind it, CSIRO-Mk3-6–0 was ranked first at 9 locations, and CCSM4, GISS-E2-R, and MPI-ESM-LR were ranked first at 6 locations each. The IPSL-CM5A-MR model is used below in Sections 3.3 and 3.4, because it had the lowest error at the most locations. For the three primary locations highlighted in this work, IPSL-CM5A-MR was ranked the best at Vicksburg, 2nd at Thebes, and 10th at Metropolis.
3.3 Changes in streamflow distributions over time
The modeling results can also be evaluated for changes over time. The percentile distributions of streamflow for three time periods are represented in Fig. 5 using the model IPSL-CM5A-MR at the three selected locations. The three time periods include 1951–2005 in blue; 2006–2049 in red; and 2050–2099 in green, while the observations for the historical time period 1951–2005 are shown in black. In general, spots in a dataset exhibiting a more horizontal behavior indicate a larger percentage of the flows at that discharge, whereas a more vertical behavior indicates that there is a relatively small percentage of flows at that discharge. Additionally, a time period shown higher than another time period indicates that the discharges are higher across that range of percentiles. Of particular interest here is to compare the relative changes in the modeling results across the three time periods. Observations from the IPSL-CM5A-MR results are discussed by location in the paragraphs below. An overall observation is that the future changes in discharge are not expected to be uniform across the distribution. One cannot simply state that all of the discharges are projected to go up or down.
Comparison of observed and simulated streamflow (m3/s) distributions for different time periods for the IPSL-CM5A-MR model for a Thebes, b Metropolis, and c Vicksburg stations. In each figure, the blue symbols show the location’s simulated streamflow distribution for the time period 1950–2005, the red symbols for 2006–2049, and the green symbols for 2050–2099
The Thebes results in Fig. 5a show that the future time periods have higher discharges for much of the upper percentiles compared to the historical time period since the blue symbols are below the other two colors. However, the right-most point for the 99th percentile shows that all three time periods have approximately the same discharges for that most extreme part of the distribution. This indicates that the 99th percentile of discharge is not projected to change much in the future for the IPSL-CM5A-MR model at Thebes. The 99th percentile discharges for the 1951–2005, 2006–2049, and 2050–2099 time periods are 20,100 m3/s; 19,800 m3/s (− 1.5%); and 19,600 m3/s (− 2.5%), respectively.
The Metropolis results in Fig. 5b show some discrepancies between the observed discharges and the IPSL-CM5A-MR model results for much of the distribution. For the Metropolis location, the IPSL-CM5A-MR model error was ranked 10th out of the 16 models, according to the method described above in Section 3.2. This model’s results at Metropolis show that the lower 60% of the distribution exhibit negligible change into the future time periods. At the 60th percentile, there is a noticeable separation where the future time periods are expected to have lower discharges until about the 90th percentile. However, the most extreme percentile (99th) shows that the future time period is expected to have higher streamflows at the extreme. The 99th percentile discharges for the 1951 − 2005, 2006 − 2049, and 2050 − 2099 time periods are projected to be 28,800 m3/s; 29,800 m3/s (+ 6.4%); and 31,700 m3/s (+ 13.2%), respectively.
The Vicksburg modeling results in Fig. 5c show relatively little change from the historical time period (1951–2005) to the first future time period (2006–2049). However, there are noticeable changes for the second future time period (2050–2099) shown in green, with portions of the distribution having higher streamflows and other portions lower. The future discharges for 2050–2099 are expected to be lower for the 40th to the 90th percentiles in the IPSL-CM5A-MR results at Vicksburg. But at the upper end of the distribution, the 2050–2099 discharges are expected to be higher than the historical period. The 99th percentile streamflow for 1951–2005 is 49,700 m3/s while it is 49,100 m3/s (− 1.2%) for 2006–2049 and 51,700 m3/s (+ 4.0%) for 2050–2099.
3.4 Annual maximums and recurrence relationships
Additional attention is given here to the extremely high streamflow magnitudes and the annual maximums. The upper tail of the streamflow distribution contains helpful information for many water resource management questions related to how flooding risks could be impacted by climate change. Figure 6 shows the annual maximums for each of the 16 GCMs with the light-gray lines; model IPSL-CM5A-MR is highlighted in blue. The green line represents the median of the 16 simulated maximums for each year, and the observed annual maximums are shown by the black line. When looking at the highest of the peaks within the model results (gray lines) of Fig. 6, there is an increase in the frequency and magnitude of the most extreme events. In each location, there was an increase in the highest annual maximum discharge event across the three time periods of 1951–2005, 2006–2049, and 2050–2099. For the Thebes location, the highest annual maximum from 1951–2005 was 43,741 m3/s using model FGOALS-g2, 2006–2049 was 50,059 m3/s using model FGOALS-g2, and 2050–2099 was 57,360 m3/s using model GFDL-CM3. For the Metropolis location, the highest annual maximum from 1951 to 2005 was 60,733 m3/s using model MPI-ESM-LR, 2006–2049 was 75,222 m3/s using model NorESM1-M, and 2050–2099 was 102,028 m3/s using model GISS-E2-R. For the Vicksburg location, the highest annual maximum from 1951 to 2005 was 91,437 m3/s using model MPI-ESM-LR, from 2006 to 2049 was 101,353 m3/s using model GFDL-ESM2G, and 2050–2099 with 123,861 m3/s with model GISS-E2-R.
Annual maximum streamflows for a Thebes, b Metropolis, and c Vicksburg. At each location, the black line shows the time series of observed annual max, the light gray lines show all of the annual maximums from all models, the blue line highlights model IPSL-CM5A-MR, and the green line shows the time series of the median annual max among the 16 models
A recurrence interval analysis was performed in order to quantitatively compare the extremely high streamflows across models and time periods, as well as relative to observations. Annual maximums were used with a generalized extreme value routine of the R statistical software to estimate the 2-, 5-, 10-, 50-, 100-, 500-, and 1000-year return interval streamflows (Gilleland and Katz 2016). Figure 7 shows the observed and simulated return interval streamflows for the historical time period 1951–2005 in the left column and the comparison between historical and future time periods in the right column. In the left column, the light gray lines represent the individual models, the dashed black line represents the historical observations, and the blue solid line is the median of the 16 GCM values at each return interval. The right column of Fig. 7 shows a comparison between the return interval streamflows of the future time period and the historical time period. The difference between the solid red and solid blue lines identifies the change between the historical and future time periods for each return interval. That relative difference is then applied to the recurrence interval relationship based on the observations to estimate the projected future streamflows for each return interval, shown by the solid black line. For the historical time period (1951–2005), there were some large differences between the recurrence interval relationship for the observations and the median of the 16 models; for example, the blue lines of Fig. 7a–c show significant deviation from the observations. Therefore, this effort focused on the relative difference in the modeling results between the historical (1951–2005) and future (2006–2099) recurrence interval relationships. There is general agreement among many of the simulations that the extreme streamflows of the future time period will be higher than the historical time period, especially for Metropolis and Vicksburg. The figure for Thebes indicates an increase in the 2-year through 100-year streamflows, but then not much change for the 500- and 1000-year return intervals, since the blue and red solid lines are on top of one another.
Return interval streamflows for historical (a, b, c) and future (d, e, f) time periods. The left figures (a, b, c) show the modeled and observed recurrence relationships for the historical time period 1951–2005. The right figures (d, e, f) show dashed lines for the range of models and solid lines for the median of the models for both the historical (1951–2005) and future (2006–2099) recurrence relationships. The solid black line takes the relative future change in the models projected onto the historical observations
Uncertainties associated with the streamflow simulations are visible across the recurrence interval relationships. The recurrence figures show that the extreme streamflows of the observed data are nearly always less than the extreme streamflows of the simulations. Zaherpour et al. also found an overestimation of runoff and recommended it be addressed by the global scale hydrological modeling community (2018). Figures 6 and 7 show large differences between gray lines representing a wide spread of the model values. This spread across the different GCMs is largely attributed to variations in the input data for the RAPID model, since the RAPID model parameters were unchanged between GCMs for this effort. Therefore the input data to the RAPID model is a major source of uncertainty. The authors also acknowledge uncertainties within the RAPID model due to the lack of reservoir regulation and routing, but these are not as large as the uncertainties from the RAPID input data. Uncertainty in the RAPID input data includes both the meteorological variations and the hydrologic modeling uncertainty. Although the GCM results have been bias-corrected and spatially downscaled for both precipitation and temperature, the macroscale hydrologic model used to generate runoff did not undergo comprehensive calibration. Hundecha et al. (2020) and Hattermann et al. (2018) state that the climate model uncertainty is very large and much greater than hydrologic modeling uncertainty. Even with these uncertainties in mind, relative changes across the historical and future time periods still exhibit important findings. Future work to improve the accuracy of climate or hydrologic modeling would be very valuable.
At all three locations, the median of the models showed a higher discharge event for the 100-year recurrence interval than the historical observations. The results show an increase of 8.5% in the 100-year recurrence interval flow for the Mississippi River at Thebes, a 10.9% increase at Metropolis, and an 8.0% increase at Vicksburg. Eleven out of the 16 models show an increase in the 100-year discharge at Thebes, 12 show an increase at Metropolis, and 12 show an increase at Vicksburg (Table 3).
Changes to the 100-year return period discharge are shown in Fig. 8 for the two future time periods, 2006–2049 and 2050–2099, relative to the historical time period 1951–2005 at each of the gage locations from the model ensemble (Fig. 8a and b) and IPSL-CM5A-MR simulation (Fig. 8c and d) results. The ensemble of the 16 models was described in Section 3.1. The IPSL-CM5A-MR was also selected for mapping the 100-year return period discharge, because it had the most locations where it was ranked highest. Both ensemble and IPSL-CM5A-MR models show increasing of the 100-year return period discharge for a majority of the locations in the time period 2006–2049 and 2050–2099. The IPSL-CM5A-MR model tends to show a higher increase for the 100-year flood in comparison to the ensemble results. The ensemble model predicts the lowest increase of the 100-year discharge in the Ohio and Tennessee Regions (Regions 5 and 6) among other MRB major regions. The average percent changes from 1951–2005 to 2006–2049 and 1951–2005 to 2050–2099 are 10% and 5%, respectively, averaged across gage locations in this region. Regions 10 (Missouri Region) and 11 (Arkansas-White-Red Region) show the largest increase in the 100-year recurrence interval discharge with both the IPSL-CM5A-MR and the ensemble model. These two major basins are hydrologically very important. The Missouri Region is heavily regulated by the largest dams of the USA and the High Plains Aquifer underlies part of the Missouri, the Arkansas-White-Red, and the Texas Gulf Coast Regions. Therefore, any future variation in the hydrology of these basins due to climate change can impact both reservoir operations and groundwater.
Comparison of 100-year flood events over 64 gages. a Percent changes between 1951–2005 and 2006–2049 using the model ensemble. b Percent changes between 1951–2005 and 2050–2099 using the model ensemble. c Percent changes between 1951–2005 and 2006–2049 using the IPSL-CM5A-MR model. d Percent changes between 1951–2005 and 2050–2099 using the IPSL-CM5A-MR model
3.5 Seasonal analysis
This section evaluates seasonal differences within the simulated results for the three time periods: 1951–2005, 2006–2049, and 2050–2099. The box-and-whisker plots of Fig. 9 show the general distribution of monthly-average streamflows for each of the three time periods for all 16 models. To clarify, the first red box and whisker on the left of the figure represent 880 values (16 × 55), all of the 16 models’ January values for all of the 55 years 1951–2005 at that location. Looking first at the historical time period 1951–2005, the annual cycle of generally higher springtime streamflow and lower autumn streamflow is apparent in the pattern. The following paragraphs describe observations from these results (1) by location and then (2) across all three locations overall.
3.5.1 Results by location
Figure 9 shows that the Thebes location is expected to see increases in average discharge for the months of January through July. Thebes’ discharges for September and October are projected to have slight declines into the future, while August, November, and December may experience relatively little change.
The Metropolis monthly average discharges are projected to have steady increases for January and February, as shown in Fig. 9. March does not show a significant change between the first (1951–2005) and second (2006–2049) time periods, but then there is a significant increase into the third (2050–2099) time period. The April median shows an increase from the first to the second time periods but then a slight decline into the third time period. May, June, and December may increase while July through November show relatively little change in monthly discharges into the future.
The Vicksburg discharges in Fig. 9 are influenced by combinations of the Thebes and Metropolis behaviors as well as other tributaries. For example, the September through November discharges at Vicksburg show decreases which are likely influenced by the Thebes declines in those months. The large increase in March discharge between the second and third time periods can be seen at Vicksburg, which is similar to the March pattern at Metropolis. The months of January through August are projected to have increasing discharges. The 25th and 75th percentiles show that the month of December is expected to remain generally consistent.
3.5.2 Overall results
This section focuses on the consistent observations from the results across all three of the locations shown in Fig. 9. All three locations show an increase in the spring streamflows into the future time periods. On the other hand, the late summer and autumn months show relatively little change or slight decreases in discharge, meaning the months with high discharges will become significantly higher. This is likely due to the greenhouse effect where warmer air temperatures are able to carry more moisture and thus produce more rainfall. This has important implications that times of surface water abundance will generally grow in abundance while times of low water levels could remain low.
The increases in streamflow have important implications about the transport capacity through these locations. The simulated results indicate that the overall volume of water will increase for the future time periods, since increases are larger than decreases overall. The increased volume of water would imply that an increased amount of constituents could be transported in the future. Indeed some constituents such as suspended sediment, which are not linearly related to discharge, could increase significantly in the future, if you assume consistent sediment delivery from the watershed. That is, since the concentration of sediment generally increases with discharge and the months of high discharge will see large increases relative to other months, the overall potential for transporting sediment could increase more than linearly with water volume change.
4 Conclusions
Processed CMIP5 daily total runoff data (i.e., VIC driven by BCSD) were used in the RAPID model to simulate daily flows in 1.2 million river segments over the entire MRB from 1950 to 2099. The following list of conclusions can be drawn from this effort:
-
Models vary significantly from the recorded flows during the historical time period. This is primarily due to the uncertainties in inputs for the RAPID model, as is demonstrated by the wide range of climate model results.
-
A linear regression ensemble was calculated, using the annual averages of the 16 models over the historical time period 1951–2005. The ensemble is generally smoother than the individual models; the high and low values for particular years are not as extreme as an individual model.
-
A direct calculation of the residual sum of squares error for each model’s distribution compared to observations was performed at each location. The models were ranked to determine their performance across the basin. The IPSL-CM5A-MR model was ranked the best at the most number of locations, 14 different gage locations out of 64.
-
The future changes in discharge are not expected to be uniform across the distribution. For the locations we evaluated, it would be incorrect to simply state that all of the discharges are projected to go up or down.
-
When looking at the extremely high flows in the model results of Fig. 6, some climate models predict that the extreme peak events will occur at greater magnitudes, or at higher frequencies, in the future. However, Table 3 shows that some models show a decrease in extremely high flows.
-
The recurrence interval analysis generally shows an overestimation of the upper tail model discharges for the historical time period in comparison with the observations. The primary causes of the overestimation should be investigated further, as recommended by Zaherpour et al. (2018).
-
Results from this effort can be used to attribute contributing influences between the Ohio River and the Mississippi River above the confluence at Cairo, IL. At all three locations, the median of the models showed a higher discharge event for the 100-year recurrence interval than the historical observations. Based on the 16 models considered in this study, the median of the model results shows an increase of 8.5% in the 100-year recurrence interval flow for the Mississippi River at Thebes, a 10.9% increase at Metropolis, and an 8.0% increase at Vicksburg. The uncertainty is large, though; for example, the future 100-year return period discharge at Vicksburg ranges from − 11 to + 85% across models. Future efforts to reduce the uncertainty in the climate and hydrologic models are recommended.
-
Results indicate that the hydrologic conditions of the Mississippi River are not stationary and that discharges associated with the extreme events are projected to likely increase in the future. 11 of the 16 models show an increase in the 100-year return period discharge at Thebes, and 12 out of 16 show an increase at Metropolis and Vicksburg.
-
Seasonal analysis of the simulated results indicates that the spring months with high discharges will become significantly higher while the months with low discharges will remain relatively consistent.
-
Increases in streamflow into the future indicate the potential for increased constituent transport.
-
This work establishes a continental-scale modeling framework and a point of comparison for future analysis of Mississippi River Basin streamflows. Future efforts could incorporate climate and hydrologic model improvements to compare with the results and uncertainty in this work.
Data availability
Geospatial RAPID inputs are publically available at (https://zenodo.org/record/322886#.X3tCAGhKhPY). CMIP5 climate projection data were obtained from the downscaled CMIP3 and CMIP5 Climate and Hydrology Projections archive at http://gdo-dcp.ucllnl.org/downscaled_cmip_projections.
Code availability
The RAPID model is available on GitHub (http://rapid-hub.org/).
References
Ahmadalipour A, Rana A, Moradkhani H, Sharma A (2015) Multi-criteria evaluation of CMIP5 GCMs for climate change impact analysis. Theoret Appl Climatol 128(1–2):71–78. https://doi.org/10.1007/s00704-015-1695-4
Bridges T (2019) Flood Control and risk reduction. presentation, congress on charting a new course for the Mississippi River watershed, December 3, 2019
Crawford J, Venkataraman K, Booth J (2019) Developing climate model ensembles: a comparative case study. J Hydrol 568:160–173
Dahl TA, Kendall AD, Hyndman DW (2021) Climate and hydrologic ensembling lead to differing streamflow and sediment yield predictions. Clim Change 165:8. https://doi.org/10.1007/s10584-021-03011-5
David CH, Maidment DR, Niu GY, Yang ZL, Habets F, Eijkhout V (2011) River network routing on the NHDPlus dataset. J Hydrometeorol 12(5):913–934. https://doi.org/10.1175/2011JHM1345
Eyring V, Flato G, Lamarque JF, Meehl J, Senior C, Stouffner R, Taylor K (2019) Status of the Coupled Model Intercomparison Project Phase 6 (CMIP6) and goals of the workshop. https://cmip6workshop19.sciencesconf.org/data/CMIP6_CMIP6AnalysisWorkshop_Barcelona_190325_FINAL.pdf. Accessed in May 2021
Follum ML, Tavakoly AA, Niemann JD, Snow AD (2017) AutoRAPID: a model for prompt streamflow estimation and flood inundation mapping over regional to continental extents. JAWRA J Am Water Resour Assoc 53(2):280–299. https://doi.org/10.1111/1752-1688.12476
Forbes WL, Mao LJ, Ricciuto DM, Kao SC, Shi X, Tavakoly AA, Jin M, Guo W, Zhao T, Wang Y, Thornton PE (2019) Streamflow in the Columbia River Basin: quantifying changes over the period 1951–2008 and determining the drivers of those changes. Water Resour Res 55:6640–6652. https://doi.org/10.1029/2018WR024256
Frieler K, Lange S, Piontek F, Reyer CP, Schewe J, Warszawski L, Zhao F, Chini L, Denvil S, Emanuel K, Geiger T (2017) Assessing the impacts of 1.5 C global warming–simulation protocol of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2b). Geosci Model Dev 10(12):4321–45
Gelfan A, Gustafsson D, Motovilov Y, Arheimer B, Kalugin A, Krylenko I, Lavrenov A (2017) Climate change impact on the water regime of two great Arctic rivers: modeling and uncertainty issues. Clim Change 141:499–515. https://doi.org/10.1007/s10584-016-1710-5
Gilleland E, Katz R (2016) extRemes 20: An extreme value analysis package in R. J Stat Software 72(8):1–39. https://doi.org/10.18637/jss.v072.i08
Gosling S, Müller Schmied H, Betts R, Chang J, Ciais P, Dankers R, Döll P, Eisner S, Flörke M, Gerten D, Grillakis M, Hanasaki N, Hagemann S, Huang M, Huang Z, Jerez S, Kim H, Koutroulis A, Leng G, Liu X, Masaki Y, Montavez P, Morfopoulos C, Oki T, Papadimitriou L, Pokhrel Y, Portmann FT, Orth R, Ostberg S, Satoh Y, Seneviratne S, Sommer P, Stacke T, Tang Q, Tsanis I, Wada Y, Zhou T, Büchner M, Schewe J, Zhao F (2017) ISIMIP2a simulation data from water (global) sector. https://doi.org/10.5880/PIK.2017.010
Gudmundsson L, Boulange J, Do HX, Gosling SN, Grillakis MG, Koutroulis AG, Leonard M, Liu J, Müller Schmied H, Papadimitriou L, Pokhrel Y (2021) Globally observed trends in mean and extreme river flow attributed to climate change. Science 371(6534):1159–1162. https://doi.org/10.1126/science.aba3996
Hattermann FF, Vetter T, Breuer L, Su B, Daggupati P, Donnelly C, Fekete B, Flörke F, Gosling SN, Hoffmann P, Liersch S (2018) Sources of uncertainty in hydrological climate impact assessment: a cross-scale study. Environ Res Lett 13(1):015006
Huang S, Shah H, Naz BS, Shrestha N, Mishra V, Daggupati P, Ghimire U, Vetter T (2020) Impacts of hydrological model calibration on projected hydrological changes under climate change—a multi-model assessment in three large river basins. Clim Change 163(3):1143–1164
Hundecha Y, Arheimer B, Berg P, Capell R, Musuuza J, Pechlivanidis I, Photiadou C (2020) Effect of model calibration strategy on climate projections of hydrological indicators at a continental scale. Clim Change 163(3):1287–1306
Jha M, Arnold JG, Gassman PW, Giorgi F, Gu RR (2006) Climate change sensitivity assessment on Upper Mississippi River Basin streamflows using SWAT 1. J Am Water Resour Assoc 42:997–1015
Johnson T, Butcher J, Deb D, Faizullabhoy M, Hummel P, Kittle J, McGinnis S, Mearns LO, Nover D, Parker A, Sarkar S, Srinivasan R, Tuppad P, Warren M, Weaver C, Witt J (2015) Modeling streamflow and water quality sensitivity to climate change and urban development in 20 US watersheds. J Am Water Resour Assoc 51:1321–1341. https://doi.org/10.1111/1752-1688.12308
Kiesel J, Stanzel P, Kling H, Fohrer N, Jähnig SC, Pechlivanidis I (2020) Streamflow-based evaluation of climate model sub-selection methods. Clim Change 163(3):1267–1285
Knox JC (2002) Sensitivity of large Upper Mississippi River floods to climate change. https://gsa.confex.com/gsa/2002AM/webprogram/Paper46957.html. Accessed in May 2021
Krysanova V, Donnelly C, Gelfan A, Gerten D, Arheimer B, Hattermann F (2018) Kundzewicz ZW (2018) How the performance of hydrological models relates to credibility of projections under climate change. Hydrol Sci J 63(5):696–720. https://doi.org/10.1080/02626667.2018.1446214
Krysanova V, Zaherpour J, Didovets I, Gosling SN, Gerten D, Hanasaki N, Müller Schmied H, Pokhrel Y, Satoh Y, Tang Q, Wada Y (2020) How evaluation of global hydrological models can help to improve credibility of river discharge projections under climate change. Clim Change 163(3):1353–1377. https://doi.org/10.1007/s10584-020-02840-0
Kunkel KE, Bromirski PD, Brooks HE, Cavazos T, Douglas AV, Easterling DR, Emanuel KA, Groisman PY, Holland GJ, Knutson TR, Kossin JP, Komar PD, Levinson DH, Smith RL (2008) Observed changes in weather and climate extremes. In: Weather and Climate Extremes in a Changing Climate: Regions of Focus: North America, Hawaii, Caribbean, and U.S. Pacific Islands [Karl TR, et al (eds)]. Synthesis and Assessment Product 3.3. U.S. Climate Change Science Program, Washington DC, 35–80
Lasdon LS, Fox RL, Ratner MW (1974) Nonlinear optimization using the generalized reduced gradient method. Revue française d’automatique, informatique, recherche opérationnelle. Recherche Opérationnelle 8(V3):73–103
Liang X, Lettenmaier DP, Wood EF, Burges SJ (1994) A Simple Hydrologically Based Model of Land Surface Water and Energy Fluxes for General Circulation Models. J Geophys Res 99:14415–14428. https://doi.org/10.1029/94JD00483
Lins H (2012) A note on stationarity and nonstationarity. World Meteorological Organization, Commission for Hydrology, Advisory Working Group, available at: http://www.wmo.int/pages/prog/hwrp/chy/chy14/documents/ms/Stationarity_and_Nonstationarity.pdf. Accessed 1 Feb 2019
Masson-Delmotte V, Zhai P, Pörtner HO, Roberts D, Skea J, Shukla PR, Pirani A, Moufouma-Okia W, Péan C, Pidcock R (2019) Intergovernmental Panel on Climate Change. Available online: https://www.ipcc.ch/site/assets/uploads/sites/2/2019/06/SR15_Full_Report_High_Res.pdf
Masui T, Matsumoto K, Hijioka Y, Kinoshita T, Nozawa T, Ishiwatari S, Kato E, Shukla PR, Yamagata Y, Kainuma M (2011) An emission pathway for stabilization at 6 Wm−2 radiative forcing. Clim Change 109:59. https://doi.org/10.1007/s10584-011-0150-5
Maurer EP, Wood AW, Adam JC, Lettenmaier DP, Nijssen B (2002) A long-term hydrologically-based data set of land surface fluxes and states for the conterminous United States. J Clim 15:3237–3251
McKay L, Bondelid T, Rea A, Johnston C, Moore R, Deward T (2012) NHDPlus Version 2: User Guide. National Operational Hydrologic Remote Sensing Center, Washington, D.C.
Min SK, Zhang X, Zwiers FW, Hegerl GC (2011) Human contribution to more-intense precipitation extremes. Nature 470:378–381
Morgan JA, Tatar JF (1972) Calculation of the residual sum of squares for all possible regressions. Technometrics 14(2):317–325
Nijssen B, Lettenmaier DP, Liang X, Wetzel SW, Wood EF (1997) Streamflow simulation for continental-scale river basins. Water Resour Res 33(4):711–724
Park JY, Park MJ, Ahn SR, Park GA, Yi JE, Kim GS, Srinivasan R, Kim SJ (2011) Assessment of Future Climate Change Impacts on Water Quantity and Quality for a Mountainous Dam Watershed Using SWAT. Transactions of ASABE 54(4):1725–1737. https://doi.org/10.13031/2013.39843
Pechlivanidis IG, Arheimer B, Donnelly C, Hundecha Y, Huang S, Aich V, Samaniego L, Eisner S, Shi P (2017) Analysis of hydrological extremes at different hydro-climatic regimes under present and future conditions. Clim Change 141(3):467–481. https://doi.org/10.1007/s10584-016-1723-0
R Core Team (2018). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/
Reclamation (2014) Downscaled CMIP3 and CMIP5 Hydrology Projections – Release of Hydrology Projections, Comparison with Preceding Information and Summary of User Needs. U.S. Department of the Interior, Bureau of Reclamation, pp 110, http://gdo-dcp.ucllnl.org/downscaled_cmip_projections/techmemo/BCSD5HydrologyMemo.pdf
Salas FR, Somos-Valenzuela MA, Dugger A, Maidment DR, Gochis DJ, David CH, Yu W, Ding D, Clark EP, Noman N (2018) Towards real-time continental scale streamflow simulation in continuous and discrete space. JAWRA J Am Water Res Assoc 54(1):7–27
Snow AD, Christensen SD, Swain NR, Nelson J, Ames DP, Jones NL, Ding D, Noman N, David CH, Pappenberger F (2016) A High-Resolution National Hydrologic Forecast System Downscaled from a Global Ensemble Land Surface Model. J Am Water Resour Assoc 52:1–15. https://doi.org/10.1111/1752-1688.12434
Tavakoly AA, Maidment DR, McClelland J, Whiteaker T, Yang ZL, Griffin C, David CH, Meyer L (2016) A GIS Framework for Regional Modeling of Riverine Nitrogen Transport: Case study, San Antonio and Guadalupe Basins. J Am Water Resour Assoc 52:1–15. https://doi.org/10.1111/1752-1688.12355
Tavakoly AA, Snow AD, David CH, Follum ML, Maidment DR, Yang ZL (2017) Continental Scale River Flow Modeling of the Mississippi River Basin Using High-Resolution NHDPlus Dataset. J Am Water Resour Assoc 53:258–279. https://doi.org/10.1111/1752-1688.12456
Tavakoly AA, Habets F, Saleh F, Yang ZL, Bourgeois C, Maidment DR (2019) An Integrated Framework to Model Nitrate Contaminants with Interactions of Agriculture, Groundwater, and Surface Water at Regional Scales: The STICS-Eaudyssée Coupled Models Applied over the Seine River Basin. J Hydrol 568:943–958. https://doi.org/10.1016/j.jhydrol.2018.11.061
Tavakoly A, Gutenson J, Lewis J, Follum M, Rajib A, LaHatte W, Hamilton C (2021) Direct Integration of numerous dams and reservoirs outflow in continental scale hydrologic modeling. Water Res Res 57(9):e2020WR029544. https://doi.org/10.1029/2020WR029544
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Törnqvist R, Jarsjö J, Pietroń J, Bring A, Rogberg P, Asokan SM, Destouni G (2014) Evolution of the hydro-climate system in the Lake Baikal Basin. J Hydrol 519:1953–1962. https://doi.org/10.1016/j.jhydrol.2014.09.074
USGS (U.S. Geological Survey), 1999a. Evidence of Climate Change Over the Last 10,000 Years From the Sediments of Lakes in the Upper Mississippi Basin. U.S. Geological Survey Fact Sheet FS-059-99. Available at http://pubs.usgs.gov/fs/fs-0059-99/. Accessed in June 2005
USGS (U.S. Geological Survey) (1999b) Evidence of Climate Change Over the Last 10,000 Years From the Sediments of Lakes in the Upper Mississippi Basin. U.S. Geological Survey Fact Sheet FS-059–99. http://pubs.usgs.gov/fs/fs-0059-99/. Accessed in May 2021
Verma S, Bhattarai R, Bosch NS, Cooke RC, Kalita PK, Markus M (2015) Climate change impacts on flow, sediment and nutrient export in a Great Lakes watershed using SWAT. Clean-Soil AirWater 43:1464–1474. https://doi.org/10.1002/clen.201400724
Zaherpour J, Gosling SN, Mount N, Schmied HM, Veldkamp TI, Dankers R, Eisner S, Gerten D, Gudmundsson L, Haddeland I, Hanasaki N (2018) Worldwide evaluation of mean and extreme runoff from six global-scale hydrological models that account for human impacts. Environ Res Lett 13(6):065015
Acknowledgements
We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modeling groups (listed in Table 1 of this paper) for producing and making available their model output. For CMIP, the U.S. Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led the development of software infrastructure in partnership with the Global Organization for Earth System Science Portals.
Funding
This effort was supported by the Mississippi River Geomorphology and Potamology Program of the U.S. Army Corps of Engineers Mississippi Valley Division.
Author information
Authors and Affiliations
Contributions
James W. Lewis: Conceptualization, Funding Acquisition, Data Curation, Methodology, Visualization, Writing—Original Draft. Sara E. Lytle: Validation, Formal analysis, Visualization, Writing—Review and Editing. Ahmad A. Tavakoly: Data Curation, Methodology, Software, Validation, Visualization, Resources, Writing—Review and Editing.
Corresponding author
Ethics declarations
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The following Table 4 shows the ranking results for each model at each gage location. The headers of the table show the USGS site number and the stream segment’s COMID (based on the NHDPlus river network). For each gage location, the models are ranked 1 through 16 based on the residual sum of squares method across the 99 percentiles, as described in Section 3.2. A rank of 1 shows the best performing model at that location with the lowest residual sum of squares error, while a rank of 16 corresponds to the highest residual sum error.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lewis, J.W., Lytle, S.E. & Tavakoly, A.A. Climate change projections of continental-scale streamflow across the Mississippi River Basin. Theor Appl Climatol 151, 1013–1034 (2023). https://doi.org/10.1007/s00704-022-04243-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-022-04243-w