1 Introduction

Reliable hydrological projections, especially at the regional scale, are of particular importance for developing climate adaptation strategies for different water-related sectors, such as water supply, hydropower production and agriculture. Nowadays, the hydrological projections are usually generated following a complex modelling chain, including the Representative Concentration Pathway (RCP) scenarios, global circulation models (GCMs), statistical or dynamical downscaling, bias correction methods and hydrological models (HMs) (Olsson et al. 2016 and Krysanova et al. 2016). This modelling chain can lead to large uncertainty of hydrological projections, depending on the selection of the climate scenarios, climate and hydrological models as well as the downscaling and bias correction methods (Kundzewicz et al. 2017). Hence, it is becoming more common to use multi-model assessment to provide more robust projections accounting for the uncertainties from different sources (Chen et al. 2012; Dobler et al. 2012; Lawrence and Haddeland 2011; Meresa and Romanowicz 2017; Vetter et al. 2015).

In order to inter-compare the climate impact projections in a consistent manner, the second phase of the Inter-Sectoral Impact Model Intercomparison project (ISIMIP2) was launched, where in the Water-Regional sector 9 regional HMs, 4 RCPs and 5 GCMs were applied to investigate the climate impacts on river discharge and hydrological extremes in 12 large-scale river basins worldwide (Krysanova and Hattermann 2017). The results showed that the largest uncertainty was generally attributed to GCMs for most river basins while the HMs contributed notably to the uncertainty of projections for some snow-dominant basins or for low flows (Vetter et al. 2017, Pechlivanidis et al. 2017).

Using multi-model ensembles in regional climate impact assessments, such as in the ISIMIP2 project, has led to great progress in quantification of the HM uncertainty. However, the HM uncertainty originates from different sources, e.g., varying levels of model complexity (Orth et al. 2015), different representation of hydrological processes in models (Hagemann et al. 2013), hydrological parameter uncertainty (Ficklin and Barnhart 2014) and the choice of calibration/validation parameters and methods (Finger et al. 2015). Using multiple HMs allows to consider the uncertainty sources of model complexity and representation of hydrological processes, but still cannot account for the uncertainty sources from calibration methods and the resulting parameterizations.

The aim of calibrating HMs is to estimate the model parameter values that provide the best possible hydrological results of interest. However, it is still under discussion whether a good performance of HMs in the historical period increases confidence in projected impacts under climate change and decreases uncertainty of projections related to HMs. Hattermann et al. (2017) and Gosling et al. (2017) compared the hydrological projections for 12 large-scale river basins using an ensemble of calibrated regional HMs and an ensemble of uncalibrated global HMs. They found that the regional HMs performed better than global HMs in the historical period, and the total projection uncertainty was substantially smaller when using regional HMs than that based on global HMs. In contrast, several studies suggested that good performance of a HM in today’s climate did not guarantee robust results under different climates due to poorly designed calibration procedures (Coron et al. 2014), equifinality using many calibration parameters (Her et al., 2019) and changes in parameter ranges under different climate conditions (Merz et al., 2011). However, Fowler et al. (2016) found that the conceptual models might be more capable to project discharges under non-static conditions if they were calibrated in different climatic conditions simultaneously. The special issue of Hydrological Sciences Journal on “Modelling temporally-variable catchments” (Thirel et al. 2015) contributed valuable case studies of testing a range of catchment models under changing climate and anthropogenic conditions with improved calibration methods and process understanding.

Based on the discussion, Krysanova et al. (2018) analysed results of recent climate impact studies and arguments in literature pro and contra the importance of good model performance in the historical period for projecting impacts, and suggested 5 main steps for an appropriate calibration and validation procedure of hydrological models which were supposed to be used for climate impact studies. The 5 steps are (1) to evaluate the quality of observational data and take into account uncertainty in the input data, (2) to calibrate the models using differential split-sample approach simultaneously for periods with different climates, (3) to validate model performance at multiple sites within the catchment and for multiple variables, (4) to validate whether or not the models can reproduce the hydrological indicators of interest and (5) to validate for any observed trends (or lack of trends) or for a proxy climate period (i.e. the observed climate in a certain period that is similar to the projected future climate). After the validation, weighting of HMs based on their performance and excluding the poorly performed HMs were suggested to project the impacts driven by an ensemble of climate projections.

The 5-step calibration/validation is obviously a more enhanced procedure than the simple and widely used calibration/validation, i.e. when the models are calibrated only against discharge at the outlet gauge. However, the case studies are still lacking to answer the research questions: (a) whether the enhanced calibration/validation procedure increases robustness of models applied for climate impact assessment compared to the simple calibration method, (b) whether impacts based on two calibration/validation methods are different and to what extent and (c) whether better performing hydrological models after the enhanced procedure would help reducing the uncertainty related to HMs. Hence, this study aimed to investigate the influence of the enhanced calibration/validation procedure on (1) hydrological projections for annual high flow (HF, indicated by the runoff quantile Q10), median flow (MF, indicated by Q50) and low flow (LF, indicated by Q90) and (2) the uncertainty contribution of HMs using 3 HMs (SWIM, SWAT and VIC) for the Rhine, Upper Yellow and Upper Mississippi basins.

The selection of HMs and basins was based on the different uncertainty contributions of HMs found in the ISIMIP2 project, where the simple calibration/validation method was applied. For example, the HMs showed high agreement on significant changes for high and low flows for the Rhine, an agreement of no significant changes for the Upper Mississippi and disagreement on projected changes for the Upper Yellow under the RCP 4.5 and 8.5 scenarios (Vetter et al. 2017). In order to retain the selection basis, we kept the simulation results from the ISIMIP2 project as the reference. In this study, we re-calibrated/validated the HMs following the enhanced method, investigated climate impacts on HF, MF and LF driven by the same climate outputs from 5 GCMs and 4 RCPs used in the ISIMIP2 project, and compared the projected changes and uncertainty contribution of HMs based on both calibration/validation methods for all basins and models.

2 Study area

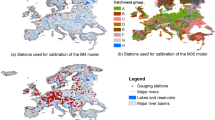
In this study, we selected three river basins (Fig. 1) located on different continents: Upper Mississippi (444,000 km2), Rhine (160,000 km2) and Upper Yellow (121,000 km2). Later in the text, the word “Upper” will be omitted for better readability. In the ISIMIP2 studies, the observed discharge time series at the outlet gauges, i.e. Alton, Lobith and Tangnaihai, were used for calibration and validation of HMs for these three basins, and then projections for discharge were analysed at these gauges under climate scenarios. Since calibration/validation at multiple sites is required in the enhanced calibration/validation approach (Krysanova et al. 2018), we selected several intermediate gauges to evaluate the model performance for sub-regions of each basin in this study (Fig. 1).

Fig. 1
figure 1

The digital elevation models of the studied river basins. a Mississippi. b Rhine. c Yellow. a–c The location of discharge gauges. d The location of river basins

Full size image

The selected basins differ in the geographic and climatic characteristics (Fig. 1). The Yellow basin has the highest elevation, with a mean value of approximately 4125 m a.s.l. This basin is situated in the coldest and driest region among the three, with the long-term (1971–2000) mean temperature and annual precipitation of − 2 °C and 506 mm, respectively. It belongs to the alpine (montane) climate according to the Köppen climate classification scheme (Peel et al. 2007). The mean elevation of the Rhine and Mississippi basins does not differ substantially, ranging from 300 to 500 m a.s.l. However, the Rhine basin is located in the oceanic climate region except its southern part situated in the alpine region whereas the Mississippi is located in the warm summer continental climate. It is a little warmer and wetter in the Rhine basin (mean temperature/annual precipitation of 8.7 °C/1038 mm) than in the Mississippi (mean temperature/annual precipitation of 7.3 °C/967 mm).

Due to the distinct climatic characteristics, the three basins also differ in their hydrological regimes. The Yellow basin generates the smallest annual runoff among the three, with the long-term average of 169 mm. It receives more than 80% of rainfall from May to September leading to distinct high flow season in summer and low flow season in winter. The mean annual runoff in the Mississippi is about 257 mm and the high/low flow seasons are not as distinct as in the Yellow. The high flow season expands from spring to summer, resulting from both snowmelt and convective rainfall. In the Rhine basin, the annual runoff is the largest, more than 450 mm. High flows mainly occur in winter and spring due to precipitation and snowmelt, whereas low flows occur in autumn due to high evapotranspiration and relatively low precipitation. However, the seasonal fluctuations in the Rhine are not so pronounced compared to other two rivers. More detailed information on these three basins is given by Krysanova and Hattermann et al. (2017).

3 Method and data

3.1 Hydrological models

In this study, we applied 3 HMs with different levels of complexity. They are two process-based hydrological models SWAT (Soil and Water Assessment Tool) and SWIM (Soil and Water Integrated Model) and one land surface model with the full hydrological cycle VIC (Variable Infiltration Capacity model). A more detailed description of these models is given in Krysanova and Hattermann (2017). These models have showed satisfactory and comparable performances in terms of river discharge for various large river basins worldwide located in different geographic zones ranging from tropics to Arctic regions (Huang et al., 2017). Here, we only provide some general information on each model to highlight their differences.

3.1.1 SWAT

The Soil and Water Assessment Tool (SWAT, Arnold et al. 1998) is a continuous-time semi-distributed process-based hydrological simulator for water flows and nutrient transport at river basin scale. A basin is discretized into sub-basins and Hydrological Response Units (HRUs, areas with a unique combination of land use, soil and slope classes). SWAT treats each process at HRU level on a daily or sub-daily time step to provide aggregated inputs into a river network (Neitsch et al. 2011). Usually, it uses daily minimum and maximum temperature as well as daily precipitation as input. In this study, the Penman-Monteith and variable storage routing (Williams 1969) approaches are applied to calculate potential evapotranspiration (PET) and river routing. For snowmelt, SWAT uses an approach similar to degree-day method, with consideration of snow-pack temperature and seasonally varied melt factors. SWAT estimates runoff from frozen soil when the temperature in the first soil layer is less than 0 °C. The model increases runoff for frozen soils but still allows significant infiltration when the frozen soils are dry (Neitsch et al. 2011).

3.1.2 SWIM

SWIM (Soil and Water Integrated Model, Krysanova et al. 1998) is an ecohydrological continuous-time semi-distributed model of intermediate complexity applied with the daily time step. It was developed based on SWAT-1993 (Arnold et al. 1993) and MATSALU (Krysanova et al. 1989) specifically for climate and land use change impact assessment in mesoscale and large river basins. Different from the SWAT model, it needs six climate parameters as input: mean, maximum and minimum temperature, precipitation, relative humidity and solar radiation. The hydrotopes, which are similar as HRU in SWAT, are sets of elementary units in a subbasin with homogeneous soil and land use types. PET is estimated using the method of Priestley-Taylor (Priestley and Taylor 1972). An extended degree-day method is used to compute snowmelt, and the Muskingum approach is applied to route the runoff from subbasins into river network. Since SWIM inherits the soil module from the SWAT model, the frozen soil algorithm is the same as the one in SWAT.

3.1.3 VIC

VIC (Variable Infiltration Capacity, Liang et al. 1994) is a semi-distributed hydrological model for large-scale applications, and it solves both the surface energy balance and water balance equations. The land surface processes are modelled at a grid of large cells accounting for the sub-grid heterogeneity (e.g. in elevation, land cover). The climate input data are maximum and minimum temperature, precipitation, relative humidity and wind speed. PET is calculated using the Penman-Monteith equation. Snowmelt from the canopy snowpack is simulated using an energy balance model (Andreadis et al. 2009). The runoff processes are represented through variable infiltration curve, parameterization of subgrid variability in soil moisture holding capacity and nonlinear baseflow. The Cherkauer and Lettenmaier (1999) frozen soil algorithm in VIC solves the thermal fluxes first to predict the soil layer temperature, which determines soil layer ice content. Both the liquid and ice content are used to calculate infiltration for each soil layer but only the liquid water content is used for soil moisture drainage. The routing of water flow is performed using the unit hydrograph principle within the grid cells and linearized St. Venant’s equations for the stream channels using a stand-alone routing model (Lohmann et al. 1996).

3.2 Data

The morphological and climatic input data used in this study was the same as in the ISIMIP2 project, so all detailed information on the input data can be found in Krysanova and Hattermann (2017). The climate scenarios are the bias corrected outputs from 5 GCMs: HadGEM2-ES, IPSL-CM5A-LR, MIROC-ESM-CHEM, GFDL-ESM2M and NorESM1-M considering all 4 RCP scenarios: RCP2.6, RCP4.5, RCP6.0 and RCP8.5 (Hempel et al. 2013). The observed discharge data to calibrate/validate HMs were obtained from the Global Runoff Data Centre (GRDC) for the Rhine and Mississippi and from the national yearbooks for the Yellow.

3.3 Calibration and validation procedure

Krysanova and Hattermann (2017) provided details on the modelled hydrological processes and the calibration and validation procedure in the ISIMIP2 project. All 3 HMs were setup using global datasets for topography, land use and soil and they were forced by the WATCH (Water and Global Change) reanalysis climate forcing data (Weedon et al. 2011). Water management was ignored in the model setup due to lack of detailed information at large scale. They were calibrated in a simple manner, i.e. only against time series of monthly discharge at the outlet gauge in each catchment for a continuous period of 8–10 years selected from the period of 1951–2000. In this study, we used the same input data and the same model setup but followed the enhanced calibration and validation procedure suggested by Krysanova et al. (2018) as described in the next sub-sections.

3.3.1 Evaluation of the quality of climate and discharge data

We firstly compared the daily mean, maximum and minimum temperature, precipitation and radiation from the WATCH forcing data with the interpolated observations at the sub-catchment scale (Supplementary material, part A). For the Rhine, the bias in temperature was small (< 0.5 °C) in all sub-catchments except the bias in the maximum temperature for the sub-catchment of Rheinfelden. The bias in precipitation ranged from 0–9% in all sub-catchments whereas the correlation (r2) between WATCH and observed data was about 0.46 to 0.64. Radiation from WATCH was also underestimated by about 14% for the whole basin. For the Mississippi, the temperature and precipitation from WATCH in all sub-catchments were overestimated by 0.5–1 °C and by 11–19%, respectively. For the Yellow basin, an underestimation of temperature by 0.2–1.44 °C and a low correlation (r2 < 0.55) between WATCH and observed precipitation were found.

We also checked the availability and homogeneity of daily and annual discharge data by visual hydrograph inspection, which is probably the most thorough method (Crochemore et al. 2020). We found that the observed annual discharge at gauge Huangheyan in the Yellow River was very low with even zero discharge values in several years without substantial decrease in the observed precipitation (Supplementary material, part B). Zheng et al. (2009) estimated that land cover change was responsible for more than 70% of the streamflow reduction in the source region of the Yellow in 1990s.The land cover changes, e.g. the grassland degradation, were caused by both climate change and human activities, such as excessive grazing (Zhou et al. 2003). As our hydrological modelling did not include the information of land cover changes, especially those caused by human activities, we excluded this gauge from calibration/validation and climate impact analysis.

3.3.2 Calibration of HMs for periods with different climates

In order to find periods with different climates, we plotted the 1-, 5- and 10-year moving average time series of mean temperature and precipitation of the WATCH data for the 3 basins and distinguished the warm, cold, wet and dry years using the long-term average temperature and precipitation (Supplementary material, part C). Strong inter-annual variability of both temperature and precipitation was found for all basins, and the variability of moving average time series decreased with increasing window sizes. The 5-year moving average time series showed more distinct climate than the 10-year ones, and a selection of 5 years gave a sufficiently long period for calibration. As a result, we selected one 5-year warm and dry period and one 5-year cold and wet period for each basin (Table 1). In total, there were 10-year time series for calibration including two distinct climatic conditions of 5 years each.

Table 1 The calibration and validation results after the simple and enhanced calibration/validation using the WATCH-forcing data as input. Good performance indicated by KGE ≥ 0.7 and |PBIAS| ≤ 10% is presented with italic font
Full size table

Since we aimed to calibrate the models at multi-sites and for different climatic conditions, the objective function θ of optimization was formulated as:

$$ \theta =\left(1-{\mathrm{KGE}}_{\mathrm{cold}\ \mathrm{and}\ \mathrm{wet}\ \mathrm{period}}\right)+\left(1-{\mathrm{KGE}}_{\mathrm{warm}\ \mathrm{and}\ \mathrm{dry}\ \mathrm{period}}\right) $$
(1)

where KGE is the Kling-Gupta efficiency (Kling, 2012) calculated from daily discharge time series. The KGE for the two distinct climates is a weighted sum of KGE of all selected gauges (Eqs. 2 and 3).

$$ {\mathrm{KGE}}_{\mathrm{cold}\ \mathrm{and}\ \mathrm{wet}\ \mathrm{period}}={\sum}_{i=1}^n\left(\frac{{\mathrm{Area}}_i}{\sum_{i=1}^n{\mathrm{Area}}_i}\times {\mathrm{KGE}}_{\mathrm{i},\mathrm{cold}\ \mathrm{and}\ \mathrm{wet}\ \mathrm{period}}\right) $$
(2)
$$ {\mathrm{KGE}}_{\mathrm{warm}\ \mathrm{and}\ \mathrm{dry}\ \mathrm{period}}={\sum}_{i=1}^n\left(\frac{{\mathrm{Area}}_{\mathrm{i}}}{\sum_{i=1}^n{\mathrm{Area}}_{\mathrm{i}}}\times {\mathrm{KGE}}_{\mathrm{i},\mathrm{warm}\ \mathrm{and}\ \mathrm{dry}\ \mathrm{period}}\right) $$
(3)

where n is the number of gauges selected in each basin and Area is the drainage area of each sub-catchment.

3.3.3 Validation of HMs

Since the calibration periods using the simple and enhanced calibration methods were different, we applied a long-term period 1971–2000 for validation for the sake of simplicity. Note that this period also covered the calibration period. Firstly, we validated the models in terms of daily KGE, percent bias (PBIAS) of the whole hydrograph and KGE of annual HF, MF and LF for all selected gauges. Secondly, we compared the monthly actual evapotranspiration (AET) for the whole basins with the satellite products from the Global Land Evaporation Amsterdam Model (GLEAM, Miralles et al. 2011). In addition, r2 between the simulated and GLEAM data was calculated at the sub-basin or grid level depending on the spatial representation of HMs. Finally, we identified the significant trends in the observed and simulated time series of annual HF, MF and LF using the Mann-Kendall (MK) test (Mann, 1945; Kendall, 1975). The differences between the observed and simulated significant trends were reported.

3.3.4 Analysis of runoff changes and uncertainties under climate scenarios

In this study, we followed the approach used by Vetter et al. (2017) to analyse the runoff changes and the sources of uncertainties. We selected the periods 1971–2000, 2010–2039 (indicated by 2010 in the results), 2040–2069 (2040) and 2070–2099 (2070) as the reference and three scenario periods.

The annual HF, MF and LF in the reference and scenario periods were firstly calculated using the daily time series simulated by each combination of RCPs, GCMs and HMs. The changes were evaluated between the median values of each indicator in the reference and scenario period. The statistical significance of changes (p < 0.05 significance level) was tested using the Wilcoxon signed-rank test of package stats of the R statistical software. We calculated the ensemble medians, ensemble means as well as weighted ensemble means of changes from the 15 combinations of GCMs and HMs under each RCP scenario and in each scenario period. The weights to calculate the weighted ensemble means were the normalized KGE of the three HMs in the validation period for each river basin, so that the higher KGE gave the higher weight to the HM, which performed better for the basin. Another option to assign the weights was to exclude poorly performing model(s) with KGE lower than the satisfactory threshold of 0.5 from the HM ensemble (strict weighting).

The ANOVA method was used to decompose 3 sources of uncertainty in projected hydrological changes, i.e. from GCMs, RCPs and HMs. A subsampling method was used to avoid biases, which were introduced because the three uncertainty sources had different sample sizes (5 GCMs, 4 RCPs and 3 HMs). A detailed description of the ANOVA and the subsampling methods can be found in Vetter et al. (2015). The ANOVA method gave the shares of uncertainty related to the 3 sources as well as their interaction terms. In order to analyse the uncertainty related to a specific source, all interaction terms were split by equal shares and added to the respective factors. For example, the uncertainty contribution of the interaction term between GCMs and RCPs was divided by 2 and added to the uncertainties of both factors, respectively.

4 Results

4.1 Calibration and validation

Table 1 lists all results in terms of KGE and PBIAS in the calibration and validation periods based on the enhanced method, as well as the validation results based on the simple method. In general, the HMs showed various performances in different locations and climatic conditions when the enhanced method was applied. For the Mississippi basin, all models could simulate discharge at the outlet gauge well with KGE larger than 0.77 and |PBIAS| lower than 10% in all periods. The model performance for the intermediate gauges was generally weaker, especially for Wisconsin using SWAT and St. Paul using SWIM. Different model performances for 2 calibration periods with different climate conditions can be seen for the Valley City using the SWAT model.

For the Rhine basin, VIC showed good results (KGE > 0.7 and |PBIAS| ≤ 10%) for all gauges in all periods (except Rockenau in cold and wet period). The SWIM model also reproduced discharge well for all gauges in the cold and wet period but showed weaker performance in some intermediate gauges in the warm and dry period. The results from the SWAT model were not satisfactory, especially for the snow dominant catchment Rheinfelden.

For the Yellow basin, SWIM showed good model performance in all periods for all gauges except the most upstream one. The VIC model had problems to simulate water balance for all gauges in calibration periods, indicated by |PBIAS| larger than 10%, while SWAT could not perform well for this catchment in terms of KGE (< 0.55) and PBIAS. As the models had problems to simulate the water balance well for certain gauges in this basin, this might be due to the effects of land cover changes which were not implemented in the models, as discussed previously.

In addition to the KGE for daily discharges, KGE for annual HF, MF and LF was calculated in the period 1971–2000 to validate the hydrological indicators of interest in this study (Table 1). Similar to the simulation results based on the simple calibration method for these basins (Huang et al. 2017), the high flows were generally better simulated than the low flows. All models performed well for all hydrological indicators at the outlets of the Mississippi and Rhine, with KGE ranging from 0.62 to 0.91. SWIM and VIC showed satisfactory KGE ranging from 0.58 to 0.66 for the outlet of the Yellow basin, but SWAT performed weaker for this river, with KGE ranging from 0.09 to 0.66. In general, the models performed better for the outlet gauges than for the intermediate ones mainly due to higher weight given to the outlet gauge in the calibration objective function.

The same criteria calculated in the simulations based on the simple calibration approach were compared with the results based on the enhanced calibration in the validation period (Table 1). Since only discharge at the outlet gauges was simulated based on the simple calibration in the previous studies (Krysanova and Hattermann 2017), we focused on the results for the gauges Alton (Mississippi), Lobith (Rhine) and Tangnaihai (Yellow) hereafter. In most cases, the validation results based on the enhanced method outperformed the ones based on the simple method in terms of KGE, probably because the models were calibrated against daily discharges in this study instead of monthly discharges. In addition, calibration for two periods with different climates gave a better balance of model performance in a long period, which covered various climate conditions. However, slightly larger |PBIAS| was found in the results of SWIM and VIC for the Mississippi and VIC for the Yellow compared to the simulations based on the simple method. This was probably due to the difference of calibration objective functions, as the enhanced method was a compromise of errors from all sub-basins and the simple method only concerned about performance at the outlets. Finally, we noticed that the SWAT model showed poor performance with KGE lower than 0.5 and |PBIAS| > 10% for the Rhine and Yellow using both calibration/validation methods. Hence, we should assign a lower weight to the SWAT results or even exclude this model in the later climate impact analysis according to the suggestions in Krysanova et al. (2018).

The comparison between the simulated and GLEAM monthly AET for three basins in the period 1980–2000 is presented in Supplementary material, part D. It should be noted that the GLEAM data is not an observed dataset either but estimates using satellite data as input. In general, the correlations between the simulated and the GLEAM data were good (r2 > 0.7) in most areas for all models. At monthly scale, the simulated AET had good agreement with the GLEAM data in winter months, while in summer months, there were notable differences between the modelled AET and the GLEAM estimates for the Mississippi using SWIM and VIC, and for the Rhine using SWAT and VIC. The overestimation of AET using SWIM for the Mississippi and the underestimation using SWAT for the Rhine can explain the PBIAS of the simulations in the validation period. The overestimation of AET and small PBIAS using VIC for the Rhine may also indicate that the GLEAM estimates were not accurate for this basin. Since the modelled results highly relied on the quality of the climatic and discharge data, whereas the performance of GLEAM was affected by the climatic and vegetation data as well as the estimation methods, the comparison results showed the uncertainty of AET estimates for these basins, especially in the summer period.

Supplementary material, part E lists the statistically significant trends identified in the observed and simulated time series in the period 1971–2000. There were no significant trends at the 3 outlet gauges in both the observed and simulated discharge time series. In total, there were only 3 statistically significant positive trends at gauges Clinton (Mississippi) and Frankfurt (Rhine) for LF and at Rockenau (Rhine) for MF based on the observed data. Statistically significant negative trends were found for LF at 2 intermediate gauges in the Yellow basin. However, the observed significant trends were not reproduced by the models except the one at Frankfurt by the SWAT model. This suggests that there is a good agreement on trends between observations and model simulations for the outlet gauges, but quite weak agreement for some of the intermediate ones.

4.2 Influence of calibration methods on projected changes in HF, MF and LF

The percent changes of HF, MF and LF in the 3 scenario periods relative to the reference period were calculated based on the discharge time series simulated by the HMs after both simple and enhanced calibration. Supplementary material, part F shows the relative changes for each combination of GCMs and HMs under 4 RCP scenarios, and compares results between the calibration methods in each period. In order to better interpret the results, we counted the numbers of significant positive/negative and insignificant positive/negative changes, and calculated the ensemble medians, ensemble means as well as weighted ensemble means of the 15 combinations of GCMs and HMs under each RCP scenario and for each scenario period. The comparisons of simulation results between the calibration methods are shown in the Supplementary material, part G for RCPs 2.6, 4.5 and 6.0 and in Fig. 2 for the RCP 8.5 scenario.

Fig. 2
figure 2

Comparison of numbers of projections with positive significant changes (dark blue bars), positive insignificant changes (light blue bars), negative significant changes (red bars) and negative insignificant changes (orange bars) for high flow (HF), median flow (MF) and low flow (LF) using five global climate models and three hydrological models, which were calibrated using the simple (sim.) and enhanced (enh.) methods, under the RCP 8.5 scenario for three scenario periods. The black, green and brown dots show the ensemble median, mean and weighted mean of relative changes, respectively

Full size image

Among the 3 river basins, the influence of calibration procedure on hydrological changes is most notable for the Mississippi. Forty-two percent of the 540 combinations of projections (4 RCPs × 5 GCMs × 3 HMs × 3 periods × 3 indicators) indicated positive changes based on the simple calibration while there were 65% projections showing positive changes based on the enhanced calibration. The number of insignificant positive changes increased by 14%. The increased positive changes can be found for all RCPs and hydrological indicators during the last 2 periods.

A moderate influence of the calibration procedure was found for the Rhine and the Yellow basins. In the Rhine, the number of positive changes increased by about 8% of all 540 results in the simulations based on the enhanced calibration, and the new positive changes occurred mainly under RCP 6.0 for MF. For the Yellow River, about 51% and 57% of all simulation results indicated decrease in discharge in simulations based on the simple and enhanced calibration, respectively. About 3% of the new negative changes were found under the RCP 2.6 scenario (Supplementary material, part G).

Figure 2 and Supplementary material, part G also compare the ensemble medians, means and weighted means of relative changes (see the dots in the figures) using both calibration methods. For the Mississippi basin, the influence of calibration methods led to contradictory changing directions for the ensemble statistics in many cases. For example, under RCP 6.0, the projections after the enhanced calibration show increase in all indicators (except the LF at the end of the century), while the projections after the simple calibration show decrease in all indicators (except the HF at the beginning of the century). For other changes where the changing directions were consistent using both calibration methods, the positive changes were more pronounced, and the negative changes were weaker based on the enhanced calibration than those based on the simple calibration. For the Yellow and Rhine basins, the 2 calibration methods hardly led to contradictory changing directions.

Part H in Supplementary material highlights the moderate (5–10%) and stronsg (> 10%) differences of ensemble results based on 2 calibration methods for 3 indicators in all basins. Moderate to strong influences (differences up to 23% for ensemble medians, means and weighted means) of the calibration methods were found for the Mississippi, especially for the far future period, but for the Rhine and Yellow the influences were minor to moderate, not exceeding 10% in all cases.

In addition, the weighted ensemble means were affected differently by the calibration methods for some cases compared to the median. For example, the ensemble means and medians differed substantially after the simple calibration for the LF of the Yellow under RCP 8.5 but they showed good agreement after the enhanced calibration (Fig. 2). Thus, we also investigated the effects of the strict weighting method, i.e. setting the weight of zero to the SWAT results for the Yellow and Rhine due to its poor performance in these basins in the validation period, and setting the weights to the SWIM and VIC results based on their KGE values. As shown in Table (a), (c) and (d) of Part H in Supplementary material, the difference between the ensemble medians based on the 2 calibration methods was positive (up to 10%) for the LF of the Yellow; the difference between the ensemble weighted means was negative (down to − 7%) and the difference of the strict weighted ensemble means became even stronger (down to − 16%) under RCP 8.5. The results imply that the selection of ensemble statistics could also lead to different projection results, especially when the performance of HMs differs substantially.

Finally, we compared the ensemble means of relative changes for the monthly discharges in the far future period under RCP 8.5 based on the 2 calibration methods to have a better overview of the effects on seasonal dynamics (Supplementary material, part I). In general, the monthly results complied well with the mean annual results of indicators. The effects of calibration methods were moderate for the Mississippi in all months, where the relative changes based on the enhanced method were higher than those based on the simple one by 5–16%. The effects of calibration methods were minor to moderate for the Yellow basin, and the relative changes based on the enhanced method were lower than those based on the simple one especially in the winter low flow season, e.g. lower by 15% in February. The effects were minor for the Rhine in all months with the difference in relative changes between the 2 methods not exceeding 5%.

4.3 Influence of calibration/validation methods on sources of uncertainty

We plotted the sum of the squares of variation in all 30-year periods to illustrate the development of total uncertainty of the climate impact results (Fig. 3), where the variation was defined as the spread between the relative change (in percent) of each model combination and the ensemble mean of all combinations (4 RCPs × 5 GCMs × 2 or 3 HMs) following the strict weighting method, i.e. we excluded the SWAT model from the ANOVA analysis for the Rhine and Yellow due to its poor performance in these basins.

Fig. 3
figure 3

Comparison of sums of squares of variation (blue colour) of an ensemble of relative changes (4 RCPs × 5 GCMs × 2 or 3 HMs) in high flow (HF), median flow (MF) and low flow (LF) and the shares of uncertainty related to hydrological models (red colour) between the simulations based on the simple (solid line) and enhanced (dashed line) calibrations for all 30-year periods from 2007 to 2099. The ANOVA analysis includes all projections from all 3 HMs for the Mississippi but excludes the projections of the SWAT model for the Rhine and Yellow due to its poor performance in the validation period

Full size image

In general, the total uncertainty for LF was up to 4 times larger than for HF and MF and it increased with time in all basins. The total uncertainty of projections for the Rhine is the smallest among the three basins, and the total uncertainty for the LF of the Mississippi is the largest. There was a minor difference in the total uncertainty between the simulations based on the two calibration methods in most cases, except the results for the LF in the Mississippi, where the total uncertainty was decreased by approximately 50% after the enhanced calibration due to smaller positive changes simulated by the SWIM and VIC models and smaller negative changes simulated by the SWAT model compared with the results based on the simple calibration.

Figure 3 also shows the shares of the uncertainty related to HMs, revealing the influence of calibration procedures on the projected hydrological changes. The shares of the GCMs and RCPs uncertainties are not presented in this Figure as there are no changes in the climate scenarios, which served as input for both simulations. In general, the effect of calibration procedure on the shares of the uncertainty related to HMs was more notable compared to the effect on the total uncertainty. The shares of uncertainty decreased for all hydrological indicators and periods, especially for LF but with an exception for the HF in the Rhine for the last 10 years. For the LF in the Mississippi, the decrease in the shares of uncertainty could be mainly attributed to the decrease in the total uncertainty from HMs. Namely, higher agreement of LF changes from HMs (see the spread of LF changes projected by all HMs in Supplementary material, part F) were obtained based on the enhanced calibration procedure compared to the results based on the simple one. For other indicators, where the total uncertainty was similar using both calibration methods, changes in the shares of uncertainty were mainly due to the response of HMs to different climate scenarios. Namely, the projections from the same HM but driven by different GCMs differed more substantially after the enhanced calibration than the ones after the simple calibration (see Supplementary material, part F). Hence, the shares of uncertainty related to GCMs increased, and the shares of uncertainty related to HMs decreased. This result also indicates that the HMs after the enhanced calibration are more sensitive to different climate conditions in these river basins and these HMs may be more capable to project hydrological changes under climate scenarios.

The ANOVA results including all RCPs, GCMs and HMs are shown in Supplementary material, part J. The total uncertainty was increased substantially for the Rhine and Yellow in this case, indicating that the SWAT model gave different hydrological change projections compared with the other 2 models. For the Rhine basin, the shares of uncertainty showed different patterns, i.e. it increased for the HF and LF but decreased for the MF after the enhanced calibration. In addition, there are high shares of uncertainty (50–75%) for the Rhine (red lines) in the first few years, probably because the SWAT model needed a long spin-up period and could not simulate the discharge properly in these years. This result shows that the poorly performing models could contribute large shares to the total uncertainty and thus influence the HM share of uncertainty substantially.

5 Discussion

In this study, we analysed the quality of the WATCH forcing data and the observed discharge data for each sub-basin before the enhanced calibration of HMs. The errors in the WATCH-forcing data showed potential difficulties for simulation of discharge at different locations simultaneously with the daily time step in the studied basins. To solve the problem of the WATCH-forcing data, we could use a new EWEMBI climate dataset (EartH2Observe, WATCH-Forcing-Data-ERA-Interim and European Reanalysis (ERA)-Interim data Merged and Bias-corrected for ISIMIP) (Lange 2019) generated as meteorological input for impact model inter-comparison studies (e.g. Huang et al. 2019). It integrates the climate variables from different reanalysis datasets, which have the best estimates among the available reanalysis data. However, the bias-corrected climate scenarios based on the EWEMBI dataset include only 2 RCPs and 4 GCMs (Huang et al. 2019), so they do not provide enough climate projections for a robust uncertainty analysis. Since the main objective of this study was to investigate the influence of the enhanced calibration/validation procedures on hydrological projections and uncertainty contribution from HMs, rather than to update the previous hydrological projections, we still applied the WATCH forcing data in this study and implemented the complete enhanced calibration/validation procedure suggested by Krysanova et al. (2018).

Besides the errors introduced in the meteorological input data, the calibration/validation results of the HMs indicated that there were other spatial input data that might influence the spatial distribution of runoff simulations. For example, the SWIM and SWAT models showed weaker validation results than the VIC model for some sub-basins of Mississippi, but all models showed similar results at the outlet. The reasons might be that the two soil-based models, SWIM and SWAT heavily depend on the quality of soil information, which is often difficult to validate at large scale. In contrast, the VIC model, with a more conceptual soil module, performed quite robust in reproducing the spatial distribution of runoff in this basin compared to the other 2 models. Hence, the quality of large-scale soil data should also be evaluated if the local information is available.

Another important reason why it is difficult to obtain good calibration/validation results for all intermediate gauges is that we did not consider the land cover changes and water management in our hydrological modelling. For example, the land cover changes affected the runoff generation in the whole Upper Yellow basin according to Zheng et al. (2009). In addition, the natural river processes in many large river systems are often interrupted by a series of dams and locks (e.g. the Mississippi, see more information in Walker, 2010) and the effects of the artificial interruption are hard to estimate without detailed information, especially at the daily timestep. For example, the SWAT model applied a target release approach (Arnold et al. 2011) to control the outflow from reservoirs listed in the National Inventory of Dams as implemented in the Hydrologic and Water Quality System (HAWQS) for the Mississippi river (Yen et al. 2016). However, it can still lead to obvious discrepancies in simulated streamflow at the daily timestep because SWAT, being a hydrological model, cannot handle strict reservoir control rules as the hydraulic models could do. The lack of detailed water management information can partly explain the difficulties of simulating low flows in all 3 rivers using both the simple and enhanced calibration procedures (see section 4 in this study and Huang et al. 2017).

Finally, we used simple approaches to describe some of the hydrological processes in our modelling. For example, the models do not simulate explicitly the natural river buffering effects of lake Constance in the Rhine, and only calibrate river routing parameters for the whole basin. The snow/glacier and soil processes may also contribute errors as we did not validate these processes specifically.

It is evident that the calibrated parameters can be biased, no matter which calibration/validation procedure was applied, due to errors in input data, lack of land cover change and water management information and their implementation, and simplification of some hydrological processes. The biased parameters will further affect the hydrological projections under climate scenarios. However, given the present input data and hydrological models, we expected smaller bias in the calibrated parameters using the enhanced method when compared with the simple one, as the enhanced method has more controls under changing climate conditions and in the spatial distribution of hydrological processes.

In this study, we presented only an example of application of the enhanced calibration/validation procedure following the suggestions of Krysanova et al. (2018), which leads to increased robustness of the models and improves the credibility of impacts. The method used in this study could be applied also in other climate impact assessments, and it could be modified or adjusted based on the objectives of future studies. For example, using mean discharge instead of drainage area in the objective functions (Eqs. 2 and 3) would give higher weights to the upmost gauges in the basins to improve the results for headwaters, especially when the simulated discharge in these sub-catchments is also used as indicator in climate impact assessment. However, the applied enhanced calibration/validation procedure is only a step forward towards more robust hydrological modelling for climate impact assessment. Long-term efforts of the whole hydrology community are required to solve the problems related to observation data and improving the modelling approaches (see Blöschl et al. 2019). The improvement of data relates not only to climatic and hydrological data but also to information on water management/reservoir operation, which could be directly implemented in the modelling or used to estimate the naturalized river discharge.

In this study, it was encouraging to see that the total uncertainty for LF, which was the largest among all indicators, reduced substantially for the Yellow and Mississippi when the model parametrizations after the enhanced calibration were applied (Supplementary material, part J). The HMs after the enhanced calibration generally performed better than the models after the simple calibration. However, the SWAT model did not perform well for the Rhine and Yellow compared with the other 2 models after both calibration methods. Hence, the projections from this model were questionable, and they did influence the ensemble means with and without weighting assignments, the total uncertainty and the shares of uncertainty related to HMs. Though several previous studies (e.g. Coron et al. 2014) suggest that good performance of a HM in today’s climate does not guarantee robust results under climate change conditions, the enhanced calibration, which considers contrast climate conditions, improves the model transferability and robustness, and therefore the hydrological projections from the models with good performance after the enhanced calibration should be more reliable. Hence, we can conclude that the well performed HMs after carefully designed calibration/validation have a potential to reduce the total uncertainty of future projections as well as the shares of uncertainty related to HMs, especially for LF, which are difficult to reproduce in the historical period.

Finally, we should acknowledge that we applied only 3 HMs in this study instead of 9 models used in the previous ISIMIP2 studies for 12 large basins. The outcomes obtained above may be modified if more HMs are applied in these and other river basins, and if all applied models would show good performance in the validation period. In addition, we should always keep in mind that good performance of a model does not only mean good reproduction of river discharge at the outlet gauge for a certain calibration/validation period, but also includes good representation of other water balance components, simulation capability under contrast climate conditions and in different sub-regions.

6 Summary and conclusions

In this study, we applied 3 hydrological models (SWAT, SWIM and VIC) to simulate the daily discharge in 3 large river basins (the Upper Mississippi, the Rhine and the Upper Yellow). The models were calibrated only against the discharge at the outlets in previous studies (simple calibration), and they were calibrated again for multi-sites and contrasting climatic conditions simultaneously in this study (enhanced calibration). After the enhanced calibration, we validated the models not only in terms of KGE and PBIAS for daily hydrographs and water balance, but also in terms of KGE and the temporal trends for hydrological indicators of interest (high, median and low flows). The validation results showed that the models could reproduce the daily discharge well (KGE ≥ 0.7 and |PBIAS| ≤ 10%) and capture the temporal trends of indicators at the outlets, except the SWAT model for the Rhine and Yellow. The simulated actual evapotranspiration was also compared with that from the satellite-based GLEAM products, and they had good agreement spatially and in winter months, but weaker agreement for summer months. The validated models were then applied to simulate changes in hydrological indicators driven by an ensemble of climate projections from 5 GCMs under 4 RCP scenarios. The projection results after the enhanced calibration/validation were compared with the results simulated using the same climate scenarios and the HMs after the simple calibration.

The comparison of the projections showed that the enhanced calibration procedure of HMs affected the number of positive/negative changes significantly for the Mississippi and moderately for the Yellow and the Rhine. There was an increase in the number of positive changes by about 23% and 8% of the total 540 projections in the Mississippi and Rhine, respectively, while a decrease in the number of positive changes by 6% in the Yellow. Similarly, the influences of the calibration procedure on the ensemble medians and means were moderate to strong for the Mississippi (differences up to 23%), minor to moderate (differences up to 10%) for the Yellow and negligible (mostly < 5%) for the Rhine. When the weighted mean was estimated from only two well performing models, the differences for LF in the Yellow have increased (up to 16%). The total uncertainty reduced significantly for LF projections in the Mississippi, and the shares of uncertainty related to HMs decreased for projections of all indicators in all river basins after the enhanced calibration when the strict weighting method was used.

Summarizing the results, the main findings of this study are the following:

  • The enhanced calibration/validation method has moderate to strong effects on the projections for some hydrological indicators in two investigated basins (the Mississippi and Yellow), compared with the projections based on the simple calibration/validation method.

  • The uncertainty of hydrological projections related to hydrological models is notably reduced for all indicators and in all basins after the enhanced calibration when only the well performing models are used.

  • The enhanced calibration/validation method is thus recommended in advance of climate impact assessments, especially when HMs after simple calibration contribute large uncertainty in climate projections. The hydrological projections based on the well performing models after the enhanced calibration are thus generally more credible for stakeholders, as the transferability of models to future climate improves.

In our view, this study could be extended to include more HMs with different levels of complexity and more river basins with different geomorphological and climate characteristics, in order to confirm or modify our results. This requires more extensive cooperation between modellers using different HMs, and more attention on the calibration/validation procedure of the models before they are applied for climate impact assessment.