1 Introduction

Predicting floods and streamflow, in general, is one of the most critical tasks of hydrological modeling. This is quite a difficult modeling task, owing to the highly nonlinear, time- and spatially varying nature of the underlying process (Cheng et al. 2020). In addition, it is time-consuming and costly to measure the processes that affect streamflow, particularly in tributaries and snow-fed rivers, which means that the use of remotely sensed data is inevitable for accurate forecasts (Yang et al. 2007). The available data is often noisy, incomplete, or entirely missing. In addition, there is often an urgent need for high-quality modeling results (Havlíček et al. 2013). Hence, it is more satisfactory to use univariate artificial intelligence (AI) techniques in which the preceding streamflow records are merely used to construct a predictive model (Zhang et al. 2018).

In recent decades, there has been considerable research on the use of AI techniques such as artificial neural networks (ANNs), extreme learning machine, and support vector machines to develop predictive models and identify the underlying hydrological pattern amongst a set of empirically observed variables (Govindaraju 2000; Raghavendra and Deka 2014; Yaseen et al. 2019; Boucher et al. 2020). Although the task is known as system identification, modelers have failed to discover a physically interpretable relationship for the desired phenomenon in many cases. This is mainly due to the black-box characteristics of most of the AI techniques which may model the process through implicit networks of data and parameters. To tackle the problem, recent studies have recommended gray-box techniques such as genetic programming (GP) (Giustolisi 2004; Nourani et al. 2014; Bozorg-Haddad et al. 2017; Herath et al. 2021).

GP is an emerging AI technique that applies evolutionary algorithms to identify explicit relationships for a given process (Koza 1992). It has different variants including (but not limited to) monolithic GP, gene expression programming, linear GP, multistage, and multigene GP. In all types, a population of random solutions (programs) is formed at the outset and then, the genetic items of each program are progressively changed to achieve the desired solution. Hydrologists have frequently used GP as a symbolic regression tool (Danandeh Mehr et al. 2018; Mohammad-Azari et al. 2020). Examples include the use of GP for rainfall-runoff modeling (Babovic and Keijzer 2002; Havlíček et al. 2013), groundwater simulation (Fallah-Mehdipour et al. 2014), forecasting meteorological variables (Kisi and Shiri 2011; Citakoglu et al. 2020), water quality prediction (Bozorg-Haddad et al. 2017), soil temperature modeling (Kisi et al. 2017), and spatial distribution of flow depth in fluvial rivers (Yan et al. 2021).

The current GP literature shows that several studies have also attempted to apply GP for univariate streamflow forecasting (e.g., Sivapragasam et al. 2008; Guven 2009; Wang et al. 2009; Al-Juboori and Guven 2016; Danandeh Mehr and Demirel 2016). Overall, its ability to extract explicit formulas has been reported as its main advantage over other AI techniques (Karimi et al. 2016, 2019; Herath et al. 2021). However, it may fail to model the streamflow process, particularly in long-term forecasts. To increase the predictive accuracy of GP, the most recent studies suggest hybrid GP models that can better tackle nonstationary features of streamflow time series (Danandeh Mehr et al. 2018). The key objective of the present study is therefore to improve the efficiency of univariate streamflow forecasting models through introducing a new hybrid GP model. In this study, we, first, developed a set of GP models for one-step-ahead streamflow forecasting in a lake-river system in cold climate conditions for a catchment in North-Eastern Finland. The models cover both short- (daily) and long-term (weekly and monthly) forecasting horizons and were compared with seasonal autoregressive integrated moving average (SARIMA) models developed as the benchmark. A new ensemble model, called GP-SARIMA, is additionally introduced to enhance the predictive accuracy of the standalone models for monthly streamflow forecasting. To select effective predictors, the study benefits from both autocorrelation and average mutual information (AMI) techniques.

1.1 Main contributions

The primary contributions are twofold. First, this study, for the first time, investigates the predictive capabilities of GP and SARIMA models for streamflow forecasting in a boreal lake-river system. Next, a new ensemble evolutionary model, called GP-SARIMA, is proposed for monthly streamflow forecasting that is superior to standalone GP and SARIMA models and meets both accuracy and simplicity conditions. Compared to metaheuristic optimized AI models existing in the literature, the proposed model is explicitly having a less computational burden that makes it more appropriate to be implemented in practice.

2 Methodology

2.1 Overview of GP

GP is an evolutionary modeling approach in which random computer programs are created and improved to solve a given problem (Koza 1992). The computer programs have a tree structure comprising a root/function node, inner nodes, branches, and terminal nodes (leaves). Figure 1 demonstrates a GP tree and the associated mathematical expression. The main steps required to develop a GP-based forecasting model include (i) selection of input variables, (ii) educated guess about modeling functions (mathematical or Boolean), and (iii) appropriate tuning of evolutionary operators (Hrnjica and Danandeh Mehr 2019). Skilled decision-making during these steps helps the GP algorithm to evolve precise models and decrease the time of computations.

Fig. 1
figure 1

An exemplary genome and its mathematical expression

Full size image

Regardless of the kind of problem, the GP algorithm starts with the random establishment of the initial programs known as potential solutions. At that point, the programs are sorted based on their goodness of fitness, and the ones demonstrating higher suitability are chosen as parents subjected to the evolutionary operations of crossover and mutation (Koza 1992). During crossover, two top parents combine their branches and create two offspring that may show higher fitness than their parents. In mutation operation, only a single parent is chosen, and an offspring is created by substituting some of its genetic materials with the new materials. Among the initial parents, the individual(s) showing the highest fitness is transferred directly to the new set of programs. The modeler defines the probability of GP operations. For a symbolic regression task, as is the case in this study, a high crossover rate is generally selected so that it is substantially greater than the mutation and reproduction rates. Since there is no universal way to determine these rates, one may use a trial-and-error procedure to optimize their values. For details about the GP algorithm and its applications in hydrology, the reader is referred to Danandeh Mehr et al. (2018).

2.2 Overview of SARIMA

Classic autoregressive time series modeling techniques such as autoregressive moving average (ARMA), autoregressive integrated moving average (ARIMA), and seasonal autoregressive integrated moving average (SARIMA) could be used as alternatives for univariate streamflow modeling (Terzi and Ergin 2014; Valipour 2015; Mehdizadeh and Sales 2018). The pertinent literature shows SARIMA outweighs its counterparts as it can handle both potential trend and periodicity features in streamflow series (Moeeni et al. 2017). However, its performance is highly sensitive to selecting a correct periodic term in the model calibration stage.

A SARIMA model is structured by combining additional seasonal terms into ARIMA structure (Box et al. 2015). The model is commonly expressed as SARIMA(p,d,q)(P,D,Q)m in which p, d, and q are non-seasonal components; P, D, and Q are the seasonal backshifts and the letter m denotes the number of samples in a year (e.g., m = 12 for monthly data). Equation (1) expresses an example of a first-order SARIMA model without a constant for a set of quarterly data (i.e., m = 4).

$$SARIMA {(\mathrm{1,1},1)(\mathrm{1,1},1)}_{4}: (1-{\phi }_{1}B) (1-{\Phi }_{1}{B}^{4})(1-B)(1-{B}^{4})yt=(1+{\theta }_{1}B) (1+{\Theta }_{1}{B}^{4}){\varepsilon }_{t}$$
(1)

where \({\phi }_{1}\) and \({\theta }_{1}\) are the parameters of non-seasonal and \({\Phi }_{1}\) and \({\Theta }_{1}\) are the parameters of seasonal components of the model. The term \({\varepsilon }_{t}\) is white noise (Bender and Simonovic 1994).

It is seen that the additional seasonal terms are simply multiplied by the non-seasonal terms. Like ARIMA modeling, the seasonal backshift parameters (\(\Phi\) and \(\Theta\)) can be determined through either a correlogram analysis or from an analytical stationarity test such as augmented Dickey-Fuller (ADF). For more details about parameter tuning in SARIMA, the interested reader is referred to Bender and Simonovic (1994).

2.3 The proposed evolutionary GP-SARIMA model

Predictive performance is of the utmost importance to a hydrological model. Ensemble learning algorithms typically combine the forecasts from multiple models and are designed to outweigh any contributing ensemble member. Applications of different types of ensemble AI techniques in hydrology have been recently reviewed by Zounemat-Kermani et al. (2021). This study introduces the ensemble GP-SARIMA model in which the prediction process is composed of three main stages (Fig. 2). The correlogram and mutual information analysis are implemented in the first stage to determine the potential lags (predictors). Then, both target and input vectors are normalized to secure the development of dimensionally accurate solutions. In the second stage, the ad hoc modeling phase, the SARIMA, and GP techniques are run to evolve initial solutions. To this end, Gretl and GPdotNET v5.0 (Hrnjica and Danandeh Mehr 2019) tools can be used, respectively. In this phase, the most effective input (Qt-m) is determined concerning the average impact of each input in the best solutions as suggested by Uyumaz et al. (2014). The GP result in this phase is a dimensionless vector of streamflow, but the SARIMA forecasts streamflow with the same dimension of the input series (here m3/s). In the last phase, the GP engine is rerun so that the most influential input, the initial GP forecast, and the normalized SARIMA forecast are used as the new predictors. This acts as post-processing to reduce the initial models’ errors. As both GP and SARIMA are explicit models, the ensemble model remains explicit; however, the results are dimensionless and need to be denormalized. Compared to hybrid simulation-metaheuristic optimization models (e.g., Yaseen et al. 2017), the new model has a less computational burden. This makes it faster than metaheuristic optimization models. However, it increases the likelihood of traping GP in local optima, and thus, the modeler needs to control the model against the overfitting problem.

Fig. 2
figure 2

Flowchart of the proposed GP-SARIMA streamflow forecasting model

Full size image

2.4 Average mutual information (AMI)

A set of optimal time delays (lags) leads a predictive AI model to a robust solution. On the contrary, inefficient or redundant lags may result in poor or complex models. Many optimal lag selection methods fail to perform properly owing to the inherent hypothesis of linearity or intense redundancy between the lags (Darudi et al. 2013). In previous studies, autocorrelation analysis of the streamflow series has been commonly employed to identify the optimum lags (e.g., Rezaie-Balf et al. 2019). However, the information distilled from autocorrelation analysis merely represents collinearity among the current and preceding discharge amount. Thus, the method might fail to extract efficient inputs in a nonlinear process (Danandeh Mehr and Gandomi 2021). To cope with this drawback, the average mutual information (AMI) that could be judged as a nonlinear generalization of the autocorrelation function was additionally considered in this study. This criterion (Eq. 2), aka auto mutual information, is generally used to find time delayed coordinates that are as independent of each other as possible (Fraser and Swinney 1986).

$$AMI ({Q}_{t}, {Q}_{t+\tau })=\sum\nolimits_{i.j}{P}_{i,j}(\tau )log (\frac{{P}_{i,j}(\tau )}{{P}_{i}.{P}_{j}})$$
(2)

where \({P}_{i}\) is the probability of \({Q}_{t}\) in bin i of the histogram constructed from the data points and \({P}_{i,j}(\tau )\) is the probability that \({Q}_{t}\) is in bin i and \({Q}_{t+\tau }\) is in bin j. As merely the joint probability \({P}_{i,j}(\tau )\) depends on \(\tau\), and thus, the AMI function also depends on how the histograms are constructed, i.e., the width and position of the bins.

3 Study area and data

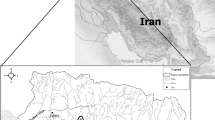
Essential to the fulfillment of a hydrological model is its stochastic feature. Construction of regulators such as a dam is just one way to lose the stochasticity of streamflow. Therefore, the implementation of the new models should be assessed on a case-by-case basis. When deciding on a catchment, it should be taken into account that flow measurements are not regulated or adjusted before or at the location of a stream gauge. Accordingly, implementation of the GP and SARIMA for daily, weekly, and monthly univariate streamflow modeling was carried out using observations from the Palojärvi gauging station located on the unbuilt headwater of the Oulujoki River system in North-Eastern Finland (Fig. 3). The region is northern boreal with seasonal snow and soil frost and does not contain any glaciers or permafrost. Oulujoki river catchment is strongly seasonally affected. Limited baseflow during winter months and spring floods during the snow melting period at April-May, and summer baseflow during July-August. Having a length of about 107 km, the Oulujoki is one of the largest lake-river systems (catchment area = 22,500 km2) in Finland (Salojärvi et al. 1982). At the point of Palojärvi gauging station (7,186,061 N, 3,635,282 E), the catchment area is about 264 km2. The upstream area from the gauging station has a high lake/pond percentage that significantly affects the runoff regime. Daily streamflow data at the station is recorded since 1983 by Finnish Environment Institute (SYKE), and data is openly available at the national OIVA-database.

Fig. 3
figure 3

Study area and location of Palojärvi gauging station

Full size image

The observed daily, weekly, and monthly streamflow hydrographs used in this study are shown in Fig. 4. Of the total observations, the first 70% and last 30% were used to train and test the evolved models. Table 1 represents the associated statistical features. Prior to importing the datasets to the GP engine, we normalized the predictor/target vectors so that they are within the range of 0.0 to 1.0 (i.e., min-max normalization approach).

Fig. 4
figure 4

Observed Streamflow at Palojärvi gauging station

Full size image
Table 1 Statistical features of the observed streamflow in Palojärvi gauging station
Full size table

4 Criteria for performance appraisal

Numerical metrics utilized to evaluate models’ performance have been reviewed by Biondi et al. (2012). A combination of absolute value error and normalized goodness-of-fit statistics is currently recommended to assess hydrological models (Ritter and Munoz-Carpena 2013). Therefore, in addition to graphical results, we implement root mean square error (RMSE) as an absolute error statistic and Nash-Sutcliffe efficiency (NSE) as a normalized efficiency value in this study. Mathematical expressions of the indices are presented below:

$$NSE=1-\frac{{\sum }_{i=1}^{n}({X}_{i}^{obs}-{X}_{i}^{pre}{)}^{2}}{{\sum }_{i=1}^{n}({X}_{i}^{obs}-{X}_{mean}^{obs}{)}^{2}}$$
(3)
$$RMSE=\sqrt{\frac{{\sum }_{i=1}^{n}({X}_{i}^{obs}-{X}_{i}^{pre}{)}^{2}}{n}}$$
(4)

where \({X}_{i}^{obs}\)= observed streamflow at the time i, \({X}_{i}^{pre}\) = predicted streamflow at the time i,\({X}_{mean}^{obs}\) = mean observed streamflow, and n is the number of arrays at each vector.

5 Results and discussion

As previously mentioned, effective lags were selected with respect to both linear and nonlinear correlations throughout the correlogram and mutual information analysis. To this end, we calculated AMI measure for the target streamflow series. At first, the joint likelihood between the observed discharge at time t (Qt) and its preceding 62 steps (i.e., Qt-τ, τ = 1, 2, …, 62) was calculated. Then, the associated AMI values were attained using Eq. (2). Figure 5 illustrates the AMI values attained for the observed daily, weekly, and monthly streamflow series. Overall, the figure demonstrates that the AMI values generally decrease by increasing the number of lags. It contains an oscillating pattern at weekly and monthly time scales. Regarding the daily and weekly timeseries, the greatest AMI value stood at the first lag; however, at the monthly scale, the maximum AMI was attained at lag #12. This implies that monthly streamflow in the river relies heavily on the past year’s value than that of the previous months. Considering the AMI threshold of 0.25, 0.1, and 0.035 as well as the attained correlogram (see Fig. 6), the most effective inputs for one-step-ahead daily, weekly, and monthly univariate streamflow forecasting are shown in Eqs. (5) to (7).

Fig. 5
figure 5

The AMI (left panels) and joint probability (right panels) amongst the observed streamflow data at the study site

Full size image
Fig. 6
figure 6

Autocorrelation function (ACF) and partial autocorrelation functions (PACF) of the observed a daily, b weekly, and c monthly streamflow in the study site

Full size image
$$Q_{td}\:=f\left(Q_{td-1},\;Q_{td-2},\;Q_{td-3},\;Q_{td-4},\;Q_{td-5}\right)$$
(5)
$$Q_{tw}\:=f\left(Q_{tw-1},\;Q_{tw-38},\;Q_{tw-39},\;Q_{tw-40},\;Q_{tw-41}\right)$$
(6)
$$Q_{tm}=f\left(Q_{tm-1},\;Q_{tm-2},\;Q_{tm-4},\;Q_{tm-12},\;Q_{tm-32},\;Q_{tm-33}\right)\;$$
(7)

where Qtd, Qtw, and Qtm denote mean daily, mean weekly, and mean monthly streamflow, respectively.

5.1 Results of standalone GP and SARIMA models

As illustrated in Fig. 2, the efficient streamflow vectors (shown in Eqs. (5) to (7)) were imported as the inputs for the GP engine. Apart from input/target vectors, the modeler needs to define a set of functions, random numbers, aka floating-point, and rates of evolutionary operators to run GP. Considering the given time scales, the evolutionary algorithm can generate various formulae representing the lake-river’s streamflow time series. Here, we employed the basic arithmetic (+ , /, × , and -), trigonometric, and exponential functions. Table 2 summarizes the setup features for GPdotNET v5.0, a non-commercial GP tool. It is worth mentioning that the main evolutionary parameters (i.e., crossover, mutation rate, and reproduction) were optimized through a trial-and-error strategy.

Table 2 Parameters used to run GPdotNET
Full size table

To cope with the overfitting problem in the GP, we ran the GP with lower trees at the first trials and then, linearly increased the maximum three depth up to six (see Table 2). Meanwhile, the mean fitness value throughout gene productions was checked to end the run. This is a kind of supervised control in which the evolutionary process is ended once either a weaker solution is created, or the number of generations passes a user-defined maximum number of generations.

The mathematical expressions of the best GP solutions are tabulated in Table 3. It is clear from the table that the best model does not necessarily comprise all the predefined effective lags and functions. For instance, the best daily model was attained via a nonlinear combination of the first two lags although up to five lags were considered as potential input vectors. Similarly, the weekly model indicates that the first and 38th lags are more informative inputs among those given in Eq. (6). This is due to interior evolutionary function optimization of the GP algorithm that allows it to optimize its shape by eliminating less efficient inputs/functions existing in the user-specified search space at each time scale. Considering the monthly time scale, GP produces the most complex model (in terms of both numbers of inputs and functional nodes) that utilizes all the predefined input vectors. The flexibility of GP structure against the given inputs or functions is one of its advantages over SARIMA which has a fixed structure.

Table 3 GP models evolved for one-step-ahead streamflow forecasting for the study site
Full size table

To attain the best SARIMA models at each time scale, the first step is to estimate the order of autoregressive, moving average, and integration components. To this end, the ADF test and a visual inspection of correlograms (see Fig. 6) were respectively utilized in this study. The p values of the ADF test (see Table 4) less than 5% implied that the observed streamflow hydrographs could be regarded as stationary series.

Table 4 Performance appraisal of the evolved SARIMA models using observations at the training set
Full size table

In Figs. 6a and b, the sudden drops in the first lag of the partial autocorrelation functions indicate the insignificant correlation after the first lag. Thus, a seasonal autoregressive process of order one and period one could be considered. Figure 5c exhibits the highest strength of the serial correlations at lag 12. Following Danandeh Mehr and Gandomi (2021), multiple combinations of seasonal (p, d, q) and non-seasonal parameters (P, D, Q) were tested in this study to select the best SARIMA model. The model which shows the smallest corrected Akaike information criterion (AICc) in the training period and RMSE in the testing period was selected as the best solution. Table 4 summarizes some of the best SARIMA combination trials.

According to the results, the SARIMA (1,1,1)(1,0,1), SARIMA (1,0,1)(0,0,0), and SARIMA (2.0.2)(2,0,2) are respectively the best autoregressive models for daily, weekly, and monthly streamflow forecasting for the study site. The results of the weekly scale indicated that the best performing SARIMA model has no seasonal component and the order of integration of the non-seasonal portion is equal to zero which means ARMA could effortlessly model weekly mean streamflow series.

For performance appraisal, the best GP and SARIMA models’ hydrographs are depicted in Fig. 7, and the associated goodness-of-fit values are tabulated in Table 5. From Fig. 7, it is seen that both GP and SARIMA precisely capture the oscillating regime of the observed daily flow in the snow-dominated lake-river system. According to the goodness-of-fit results in the daily model, both the GP and SARIMA offer similar predictive accuracy (NSE = 0.997) with the lower error between the model and observed data in the testing period. Comparing to the results of a similar study (see Abdollahi et al. 2017) that applies GP to model daily streamflow in a hot climate (NSE = 0.94), our findings indicate that GP (and even SARIMA) exhibits better performance (NSE = 0.99) in cold climates.

Fig. 7
figure 7

The observed compared with modeled streamflow data during both training and testing periods

Full size image
Table 5 Performance values of the best GP and SARIMA models used for univariate streamflow forecasting in the study site
Full size table

At the weekly time scale, global peak and local maxima were better forecasted by the SARIMA. In contrast, GP exhibited higher efficiency in tracing peak monthly streamflow values. According to the fitness criteria, the GP identifies the weekly and monthly flow process better than SARIMA during the training period; however, they suffer from low efficiency in the testing period. Regarding the higher performance of the SARIMA during the testing period, it must be highlighted that such results could be due to the relatively lower number of testing observations and the higher variance of the training observations that include the global maximum.

5.2 Results of the proposed GP-SARIMA model for long-term streamflow forecasting

Following the methodology flowchart, the SARIMA (1,1,1)(2,1,0), the best GP outputs, and the most effective lag (i.e., Qt-12) were utilized as predictors for the rolling forecast of monthly streamflow using GP-SARIMA. Running this model through the same training (testing) period, we get an NSE of 0.715 (0.483) and RMSE equals 1.437 (1.817) m3/s. In comparison to the goodness-of-fit values given in Table 5, GP-SARIMA is superior to the standalone GP and SARIMA models. Compared to the best SARIMA, the proposed ensemble model yielded an approximately 25 and 20% reduction in RMSE in the training and testing periods, respectively. Cross-correlation analysis between the new predictors (best GP and SARIMA models) and the target streamflow series showed that they have a higher correlation (0.67 and 0.63 for GP and SARIMA, respectively) than standalone models’ inputs (maximum of 0.56 for Qt-12). Since all these models generally utilize autocorrelation of the time series, the mentioned higher correlation could be considered as the origin of the improvement of the performance of the ensemble model compared to the standalone models. The observed and forecasted monthly streamflow series and the associated scatter plots during the training and testing periods were depicted and compared in Fig. 7.

Overall, the forecasts mimic the strong fluctuation of the observed streamflow series even though significant errors are observed in the prediction of some of the peaks throughout the year. It is seen that the SARIMA suffers from low-variance forecasts unable to capture peak flows. This result agrees with that of Danandeh Mehr and Gandomi (2021) in which SARIMA was applied to model the Sedre River flow in Turkey. Such drawback at the estimation of high discharge values might be due to the existence of strong deviation during the snow melting months so that the linear SARIMA cannot capture it. For such months during the testing period, Fig. 8c demonstrates that the SARIMA forecasts are converged to a false local maximum of around 6.0 m3/s. By contrast, the GP, and in particular, the ensemble GP-SARIMA were not trapped into such maxima. Although GP-SARIMA considerably diminishes the residuals, it still underestimates the observed high flows. Such difference could be due to intramonthly accumulated snow water equivalent that is difficult to be distilled from historical streamflow data using univariate AI models. Therefore, the use of exogenous inputs such as snow cover extent or depth for long-term streamflow forecasting in snow-fed rivers is recommended.

Fig. 8
figure 8

Monthly streamflow hydrograph (a) and the associated scatter plots in the b training and c testing periods

Full size image

To explore the contribution of each input in the best evolved GP-SARIMA model, its tree expression is shown in Fig. 9. In this model, Qtm-12, GP, and SARIMA are the normalized values of the 12-month antecedent observed streamflow, concurrent GP, and SARIMA forecasts, respectively. The constant 1.11 represents the summation of two random floating points (0.47 and 0.64) attained in the terminal nodes of the raw GP-SARIMA model. It is seen that the Qtm-12 and GP solution appeared two times in this model. Therefore, they could be counted as the most dominant variables among the pre-specified predictors.

Fig. 9
figure 9

The GP-SARIMA model evolved for univariate streamflow forecasting in the study site

Full size image

6 Conclusion

Many studies have proved that AI techniques outperform classical time series models for streamflow forecasting. While tackling nonstationary features of a given time series is the utmost important issue in univariate streamflow modeling using classical autoregressive models, selecting a suitable AI technique, finding the more efficient inputs (i.e., lags), and being heedful of the common overfitting challenge are some of the critical concerns that a modeler should contemplate in time series modeling using AI techniques (Thapa et al. 2020). In this study, the abilities of GP and SARIMA for one-step-ahead daily, weekly, and monthly streamflow forecasting in the headwaters of the Oulujoki River were investigated. The comparative performance appraisal of the models showed a good and more or less the same accuracy for both GP and SARIMA models in daily streamflow forecasting. The techniques also showed acceptable performance for weekly streamflow forecasting with a slight superiority of SARIMA over GP during the testing period. Our results also revealed that the standalone techniques are not suitable for monthly streamflow modeling in the case study lake-river system. This drawback was attributed to the effect of snow melting during spring months that creates extreme oscillating structure in the monthly streamflow hydrograph so that the models, particularly SARIMA, cannot model the streamflow series 1 month in advance. Consequently, they underestimate maxima/peak streamflow in the study site. To enhance the prediction accuracy at the monthly time scale, an ensemble univariate GP-SARIMA model was introduced. The associated results demonstrated a significant improvement in the predictive accuracy of the GP and SARIMA. Therefore, we concluded that the ensemble strategy is more robust than standalone methods, being less likely to be trapped into a false local maximum.

From an evolutionary programming perspective, the GPdotNET running experiences indicated that using more complex functions or deep GP trees would not essentially enhance the models’ accuracy. Contrariwise, it may lead the algorithm to be trapped in a local optimum (i.e., over-fitted solution) during the initial generations. Benefiting from the function optimization feature, GP yielded in simpler models than SARIMA, particularly for short-term forecasting. Although the GP-SARIMA model was superior to GP and SARIMA, the attained results emphasize the necessity of applying further efforts to improve model accuracy in long-term forecasting.

The present study was limited to the use of (i) univariate modeling strategy (i.e., observed streamflow data is used as both input and target variables) and (ii) classic GP as the nonlinear regression technique. At monthly timescale, the evolved models generally underestimated the streamflow hydrograph. This highlights the necessity for further investigations either on the modeling strategy or the training approach. For long-term (weekly, monthly, or seasonal) streamflow prediction in boreal rivers, one may investigate the use of multivariate models so that they would better reflect intramonthly snow water equivalent proportion (Yang et al. 2009). In addition, future studies can consider more robust GP variants such as multigene GP or multistage GP that might better handle streamflow series in boreal lake-river systems. It was well-documented that AI-based models are case-sensitive, and their generalization ability depends on the range and type of data used to train/test the desired model. Thus, it could be informative if the efficiency of GP-SARIMA to model intermittent rivers has been checked in a similar study.