1 Introduction

Understanding the variability of hydrometeorological variables in water-stressed environments like in East Africa is fundamental in addressing water challenges, especially in the context of climate and land use change. The prediction of climate variability in such a tropical region remains challenging (e.g., Vera et al. 2013).

The understanding of hydrometeorological variability requires improved knowledge of the interaction between the atmospheric and terrestrial branches of the hydrological cycle. Regional climate modeling allows investigating the dependency of hydrometeorological variables to land use and land surface properties (Ge et al. 2007). The validation of regional climate model (RCM) modeling approaches requires observational data of several components of the water cycle, e.g., precipitation, evapotranspiration, runoff, and soil moisture, which are difficult to obtain in a data-scarce region like Kenya, East Africa.

Precipitation is considered to be the crucial hydrometeorological variable in East Africa and is characterized by large spatio-temporal variability (Endris et al. 2013; Gitau et al. 2013). Zhang (2007) used the Weather Research and Forecasting (WRF) model (Skamarock et al. 2008) at 60 km horizontal resolution to investigate the hydrological cycle in East Africa, with emphasis on model result sensitivity to different radiation schemes, for the period 1994 to 1998. He found the WRF model to be suitable in reproducing the average East African climate and its interannual variability. Pohl et al. (2011) tested a number of WRF model settings (i.e., physical parameterization, land use categories, domain size and number of vertical levels) in simulating the seasonal water cycle over the Equatorial East Africa for 1999. In their study, they found WRF simulations of a spatial resolution of 12 km were closest to that from the Global Precipitation Climatology Project daily (GPCP-1dd) gridded rainfall product, when combining the Kain Fritsch (KF) cumulus scheme with the WRF Single-Moment 6-class (WSM6) microphysics, Asymmetric Convective Model (ACM2) planetary boundary layer, Dudhia short wave radiation, and the Rapid Radiative Transfer Model (RRTM) long wave radiation scheme. Most recently, the WRF model was used as one of the ten participating RCMs at 50 km horizontal resolution in the Coordinated Regional Climate Downscaling Experiment (CORDEX) to simulate the characteristics of rainfall patterns over East Africa (Endris et al. 2013). The CORDEX experiment results indicated that the WRF based on KF cumulus convection, WRF Single-Moment 5-class (WSM5) microphysics, Yonsei University (YSU) planetary boundary, Dudhia short wave radiation, and RRTM long wave radiation schemes overestimated rainfall far above all the other RCMs that were assessed. Accordingly, there is a large sensitivity of WRF model results to the choice of physics parameterizations for East Africa. Little attempt was made in previous studies to investigate the impact of variation of the horizontal resolution of the RCM. Pohl et al. (2011) stated that the horizontal resolution of the RCM could influence the results of simulations in this region; moreover, they particularly highlighted the need to study the intraseasonal variability in this region and to conduct further sensitivity experiments with models like WRF due to the relatively high uncertainties associated with the model physics and domain geometry. Our study contributes to fill this gap.

RCM studies for this region are scarce, and there is no consensus on a suitable configuration and horizontal resolution that will be accurate in successfully reproducing observed regional climate characteristics (e.g., Pohl et al. 2011; Endris et al. 2013). The present study focuses on the Tana River basin (TRB) of Kenya (Fig. 1). This study region was chosen due to the availability of station data and for its crucial role in the Kenyan economy. TRB is an extensive agricultural area and contributes to about 57 % of the country’s hydropower (e.g., Oludhe et al. 2013). Extending the work of Pohl et al. (2011), we further test the performance of the WRF model in reproducing observed precipitation and temperature in the TRB for the period 2011 to 2014, based on gridded observations as well as station data. The impact of the horizontal resolution and land use classification is specifically addressed.

Fig. 1
figure 1

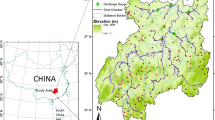
Map of the study area and location of the meteorological stations (Nyeri, Embu, Meru, Thika, Garissa, Makindu, and Lamu) marked as red dots (see Table 1 for the exact locations), with the inset boundary showing the Tana River basin (TRB), Kenya. The dotted rectangular boundaries mark the representative portion or whole portion of upper Tana (UT), middle Tana (MT), and lower Tana (LT). The map of Africa (top) is processed from Natural Earth data (www.naturalearthdata.com)

Full size image

Section 2 provides a brief description of the study area, the observational datasets, the model, and experimental setup. Section 3 documents the sensitivity of simulated monthly precipitation and mean temperature to the horizontal resolution and land use classifications. A summary and conclusion is given in Section 4.

2 Study area, observational datasets, model, and experimental details

2.1 Study area

The TRB lies between the latitudes 0° 0′ 53″ S and 3° 0′ 00″ S and between the longitudes 37° 00′ 00″ E and 41° 00′ 00″ E (Fig. 1) with a total catchment area of about 126,000 km2 (Knoop et al. 2012). It hosts the longest river in Kenya, the Tana River which is appriximately 1000 km long. The climate of the TRB is typical of East Africa and varies from arid in the lowlands to semi-humid in the highlands and coastal areas (Dinku et al. 2011). In this study, the TRB is divided into three parts: the upper, middle, and lower TRB, with precipitation characteristics primarily influenced by topography (Knoop et al. 2012). Averaged annual rainfall and temperature in each of these three parts of the TRB are investigated using station datasets recognized by the World Meteorological Organization (WMO) and operated by the Kenya Meteorological Department (KMD; Table 1). Nyeri, Meru, Embu, and Thika stations are grouped under upper TRB, Garissa and Makindu stations are associated with middle TRB, and Lamu station is in the lower TRB (Fig. 1). The areas around the upper TRB, middle TRB, and lower TRB are marked and labeled as UT, MT, and LT, respectively, in Fig. 1 for further spatially averaged analyses.

Table 1 List of selected meteorological stations in the Tana River basin (TRB), mean annual precipitation amount (1970 to2014) and annual mean temperature (2000 to2014)
Full size table

The upper TRB lies between 400 m.a.s.l. on the eastern part of the catchment and 5199 m.a.s.l. on Mount Kenya (Geertsema et al. 2009). It receives the highest annual rainfall, between 900 and 1300 mm on average (see Table 1). The middle part of the TRB is semi-arid to arid with an altitude of less than 1300 m.a.s.l. (Knoop et al. 2012). This area receives the smallest amount of annual rainfall on average (less than 550 mm). The lower part of the TRB is at an altitude of less than 500 m.a.s.l. and is bordered on the southeast with a coastal strip (the Indian Ocean). Averaged annual rainfall in this part is about 960 mm. Precipitation observed at the stations and in the TRB region described above depends on the location and proximity to Mount Kenya (0° 9′ 0″ S and 37° 18′ 36″ E), the Aberdares (0° 37′ 48″ S and 36° 4′ 36″ E), and the Indian Ocean. The montainous regions are influenced by the leeward-windward phenomena where stations such as Nyeri and Thika west of Mount Kenya are considered to be to on its leeward side, compared with Meru, which is on the windward side. In this situation, Meru station record a higher annual precipitation than Nyeri, which is at a higher altitude (Table 1).

Like most areas in East Africa, the TRB experiences a bimodal rainfall seasonal pattern (Oludhe et al. 2013; Kitheka 2014). The first season, locally known as the “long rains,” falls during the months of March to May (MAM); while the second season, locally known as “short rains,” falls during the months of October to December (OND). The “long rains” are thought to produce greater rainfall amounts than the “short rains” and be characterized by a lower interannual variability (Camberlin and Okoola 2003). As the Equator disects Kenya, these seasons result from the north-south oscillation of the Intertropical Convergence Zone (ITCZ) twice in a year (e.g., Ogallo 1988; King’uyu et al. 2000; Nicholson 1996; Indeje et al. 2000; McSweeney et al. 2010; Kitheka 2014) although it is suggested that the OND season may be associated with either the Congo air boundary or the convergence of trade winds over the western Indian Ocean (Nicholson 2014).

The precipitation over the TRB has generally been decreasing since the 1997/1998 El Niño rains in Kenya, with the 2011 to 2014 recording below normal mean annual precipitation 80 % of the time (see purple box in Fig. 2). It is seen that the middle and lower TRB (which are in low altitude areas) were dry during the whole period of 2011 to 2014, possibly related to a failure of influx of moisture from the Indian Ocean and a weakening of the Mascarene High (Ogwang et al. 2015). This is consistent with earlier studies in this region (e.g., Williams and Funk 2011) showing a precipitation decrease from 1980 to 2009. This situation is projected to continue. This calls for proper management of the available TRB water resources if this trend is likely to persist.

Fig. 2
figure 2

Annual mean rainfall anomalies for stations located in TRB (see Fig. 1) based on the 1970 to 2014 average. The purple box shows the period 2011 to 2014 characterized with mostly below normal rainfall

Full size image

The temperature over the study region strongly depends on altitude. The upper part temperatures associated with the central highlands are much colder than those at the middle or lower parts, which are associated with the coastal regions. In particular, the annual mean temperature over Nyeri, Meru, and Thika (upper TRB) are 17.7, 18.5, and 20.2 °C, respectively, while over Lamu (lower TRB), it is 27.7 °C (Table 1). This is consistent with earlier studies that found that the upper and middle/lower TRB are characterized with annual temperatures of 15 and 29 °C, respectively (e.g., McSweeney et al. 2010). However, monthly temperature in the middle and lower parts of the TRB can be up to 33 °C (Omambia et al. 2014).

2.2 Observational datasets

This section presents the observational datasets that are used in Sect. 3 to validate WRF simulation results.

2.2.1 Precipitation observations

The satellite estimates of Tropical Rainfall Measuring Mission (TRMM; 3B42 v7 derived daily at 0.25° horizontal resolution, 1998 to 2015; Huffman et al. 2007), the gridded Climate Research Unit (CRU v3.23, monthly at 0.5° horizontal resolution, 1901 to 2014; Harris et al. 2014) and station data for 2011 to 2014 are used. The accuracy of TRMM- and CRU-gridded products for our study region is assessed in terms of its suitability as a proxy for in situ observation data. This is because the region is characterized by a coarse network of meteorological stations.

Some studies investigated the suitability of both satellite and gridded precipitation datasets compared with interpolated station data for the East African region (e.g., Anyah et al. 2006; Anyah and Semazzi 2007; Dinku et al. 2011; Nicholson 2014), and their results suggest that these datasets mimic the rainfall climatology of the region reasonably.

TRMM and station derived monthly precipitation time series have a correlation coefficient (r) of 0.9 and root mean square error (RMSE) of 1.4 mm/day. On the other hand, CRU- and station-derived monthly precipitation time series have an r of 0.7 and RMSE of 2.2 mm/day. The two global products capture the in situ observed seasonal and annual evolution of precipitation quite well (Fig. 3a–c). The bimodal regime of precipitation is well depicted in the upper and middle TRB, but weakly in the lower TRB in both CRU and TRMM. During the MAM, both CRU and TRMM indicate the peak month as April in the upper and middle TRB, but as May for the lower TRB. Both CRU and TRMM agree well with station-based precipitation in indicating the OND peak month as November for the upper and middle TRB. However, during the study period, the two datasets underestimate OND rains in the lower TRB. In the upper and middle TRB (Fig. 3a, b), the driest season falls during June to September. However, CRU does not agree with station data in the monthly mean amount for the upper TRB during the dry seasons. This is unusual as it is expected that there should be good agreement during the dry season between global datasets. In the lower TRB, both CRU and TRMM agree well with station data in depicting the driest season to occur during January and February. In general, CRU overestimates the station precipitation rates in some seasons (e.g., Fig. 3; Riddle and Cook 2008).

Fig. 3
figure 3

Annual cycle of monthly precipitation averaged for the period 2011 to 2014 at location of the stations over the a upper (Nyeri, Meru, Embu, Thika), b middle (Garissa, Makindu), and c lower (Lamu) Tana, derived from station data, TRMM and CRU

Full size image

The precipitation regime in the TRB can therefore be categorized into two groups: (i) the traditional bimodal, MAM and OND seasons for inland stations (upper and middle TRB) and (ii) bimodal, April, May, and June (AMJ) and OND for coastal stations (lower TRB). However, in this study, we consider the two traditional seasons to apply for the whole TRB (i.e., the first group).

In general, TRMM exhibits higher performance compared with CRU and mimics station rainfall more closely; therefore, TRMM is considered in subsequent assessment of the spatial and temporal analysis of the simulated area- and time-averaged precipitation in this study.

2.2.2 Temperature observations

The Climate Research University (CRU v3.23, monthly at 0.5 °C horizontal resolution, 1901 to 2014; Harris et al. 2014) and station data for the period 2011 to 2014 are used. Only four of the meteorological stations named in Sect. 2.2.1, i.e., Nyeri, Meru, Thika, and Lamu had complete records of temperature data.

CRU and station monthly mean temperatures are in close correspondence (r = 0.9) but show relatively high deviations in terms of their magnitudes (RMSE = 2.2 °C) for 2011 to 2014 (see the corresponding scatterplot Fig. 4). CRU temperature is slightly colder compared with station temperature, with a percent bias (Pbias) of about −0.3 % (pooling all four stations together). CRU captures well the annual cycle of temperature over all the stations considered (r > 0.8). At selected sites, the CRU temperatures are warmer at Meru (Pbias = 13.5 %) and Thika (Pbias = 4.3 %) but colder at Nyeri (Pbias = −15.6 %). At Lamu, there is a good agreement between CRU and station temperatures (Pbias = −0.2 %).

Fig. 4
figure 4

Monthly gridded mean temperature from CRU compared with monthly mean temperature at selected stations over the TRB (Nyeri, Thika, Meru, and Lamu) for 2011 to 2014

Full size image

The shortcoming observed in CRU versus station data may be attributed to very few station data records that are assimilated in the global datasets (Christy et al. 2009). Furthermore, CRU has a tendency to overestimate temperature in regions with complex topography, which are characterized by an uneven network of stations (e.g., Laux et al. 2012). In this study, however, CRU is used to assess the simulated spatial and temporal area- and time-averaged temperature.

2.3 Model

The WRF model is a mesoscale numerical model designed for operational forecasting and atmospheric research needs with several physical parameterization schemes available. In this study, WRF v3.5 is used. Details about WRF physics parameterizations (i.e., cumulus convection, microphysics, surface layer, planetary boundary layer atmospheric radiation, and land surface model schemes) can be found in Skamarock et al. (2008). The model also offers an option of selecting between two land use categories or classifications: the US Geological Survey (USGS; 24 classes; Anderson et al. 1976) and the Moderate Resolution Imaging Spectroradiometer (MODIS; 20 classes; Friedl et al. 2002). The USGS-based land use dataset was developed using the global 1-km resolution Advanced Very High Resolution Radiometer (AVHRR) satellite sensor from April 1992 to March 1993 (e.g., Anderson et al. 1976; Liang et al. 2005). The MODIS-based land use dataset is also at 1-km resolution but uses the International Geosphere-Biosphere Program (IGBP) classification and was defined in 2001–2002 (Friedl et al. 2002). The experimental details and choice of our parameterization is explained in the following section.

2.3.1 Experimental setup

The model domain for all our experiments covers the region 12° S–13° N; 22–53° E, which encompasses most of East Africa (Fig. 5). The white box in Fig. 5 delineates the study region (3° S–1 N; 36–41° E) shown in Fig. 1, and the associated details are described in Sect. 2.1. Note that it circumscribes the TRB (see purple contour line in Fig. 5). The domain size was chosen in order to reduce computational costs. It is also considered to resolve the mesoscale forcings associated with mountains, coastlines, lakes, and vegetation characteristics that influence the region’s local climate (Giorgi and Mearns 1999).

Fig. 5
figure 5

WRF model domains at a 50-km (left) and b 25-km (right) horizontal resolution showing the elevation from the WRF preprocessing. The white box (3° S–1° N; 36–41° E) delineates the study region encompassing the TRB (purple contour line)

Full size image

Two different horizontal resolutions are considered here (50 and 25 km; see Fig. 5a, b, respectively). Two different land use representations (USGS and MODIS) are also considered. This provides a total of four WRF experiments here referred to as: MODIS25, MODIS50, USGS25, and USGS50.

In MODIS50 and USGS50, the model domain (Fig. 5b) consists of 70 × 60 grid points in the west-east and south-north directions. The MODIS25 and USGS25 model domain (Fig. 5a) have 140 × 120 grid points in the west-east and north-south directions. Figure 5 shows the elevation from the WRF preprocessing in which most of the TRB (middle and lower part) have an elevation of less than 750 m.a.s.l.

All simulations are initialized on 1 November 2010, including a spin-up period of 2 months and cover a 4-year period from 2011 to 2014. According to Giorgi and Mearns (1999), a 2-month spin-up period should be long enough for the model to bring the atmospheric fields into dynamic equilibrium.

The physical and dynamical options are similar for all experiments. The chosen physical parameterizations are based on earlier studies (e.g., Riddle and Cook 2008; Pohl et al. 2011; Endris et al. 2013). The Kain Fritsch (KF) cumulus scheme (Kain 2004), the WRF Single-Moment v6 (WSM6), and microphysics (Hong and Lim 2006) are selected. The WSM6, for instance, is considered suitable for high-resolution simulations and is able to represent ice, snow, and graupel. In the case of the planetary boundary layer scheme, the v2 of the Asymmetric Convective Model (ACM2), which is characterized by nonlocal upward and local downward mixing (Pleim 2007), is considered a good compromise. For radiation schemes, the New Goddard radiation scheme (Chou and Suarez 1999) is selected for both long- and short-wave options. The Noah land surface model option is used for the land surface processes (Chen and Dudhia 2001).

All experiments use 40 vertical levels up to 20 hPa (approximately 26 km vertical height above the surface). The model integration for MODIS50 and USGS50 is 200 s while that of the MODIS25 and USGS25 is 100 s. The ERA-Interim (Uppala et al. 2008) reanalyses from the European Centre for Medium-Range Weather Forecasts (ECMWF) provide the initial and lateral boundary conditions for the WRF simulations which are updated every six hours.

2.3.2 Land use distribution in the TRB

Figure 6 illustrates the distribution of the dominant mean land use category in each model grid over the TRB from the four WRF experiments as depicted in the land use classifications. MODIS and USGS land use datasets classify the regions slightly differently but show reasonable agreement in the portions of the savannas.

Fig. 6
figure 6

The dominant land use category in each grid point over the TRB a in MODIS25 and b in MODIS50, c USGS25, and d USGS50 during the period 2011 to 2014

Full size image

Note that within each model grid, the most dominant land use category from the land use map (24 categories for USGS and 20 for MODIS) in terms of contributing area is chosen for that grid (Liang et al. 2005). Accordingly, there are 9 out of the 20 for MODIS25 and only 5 out of 20 land use categories for MODIS50 over the TRB (Fig. 6a, b). Both the MODIS-driven experiments classify the TRB to be covered by 70 % savannas and grasslands. According to the global land cover characteristics (GLCC) classification these two categories are of herbaceous type with forest canopy cover between 10 and 30 %. As an example, MODIS25 classifies regions around Nyeri, Embu, Meru, and Thika to be dominated by evergreen broadleaf forestland and woody savanna. In the case of the USGS WRF-driven experiments, USGS25 and USGS50 display 7 out of 24 and 5 out of 24 land use categories, respectively (Fig. 6c, d). The dominant land use categories for TRB based on USGS classification are the shrublands and croplands/woodland mosaic constituting about 80 % of the total area. The GLCC classifies shrublands as lands characterized by xerophytic vegetative types with woody systems and desert-like features. USGS25 describes the area around Nyeri, Embu, Meru, and Thika to be savanna and deciduous broadleaf forest, which is in contrast with the MODIS classification.

Compared with USGS25, MODIS25 provides a more heterogeneous spatial pattern (Fig. 6a), which is attributed to enhanced sensitivity of MODIS land use to horizontal resolution in comparison with USGS land use (Pohl et al. 2011).

2.4 Validation

The simulation results are compared with station, satellite rainfall (TRMM), and gridded temperature (CRU) datasets. The four WRF model configurations are evaluated based on monthly time series from which the correlation coefficient, RMSE, and Pbias are computed. To investigate which of the WRF configurations better represents the spatio-temporal rainfall distribution over the study area, spatial correlation between monthly sums of simulated and observed precipitation are computed. Apart from the monthly time series, we also use time-averaged spatial distribution maps and the Taylor diagram (Taylor 2001) to analyze further the level of correspondence between simulated and observed precipitation and temperature. Each point in this diagram is described by the standard deviation (radial distance of the point from the origin), which is a measure of the intensity and variability of the patterns, the RMSE error (distance from the observation), and the correlation coefficient (the angle between the x-axis and the point). Our analysis focuses on the statistics of (i) both the MAM and OND seasons averaged for 2011 to 2014 and (ii) the individual years for every season. Each modeled variable is normalized by dividing both its RMSE and the standard deviation by the standard deviation of the corresponding observations (given as a reference and plotted at a unit distance from the origin on the x-axis).

3 Results of performance analysis and discussion

In this section, the four modeled WRF simulations are compared with the in situ measurements and gridded datasets. Precipitation is considered with a focus on both MAM and OND seasons, together with its interannual evolution. A discussion on temperature follows thereafter.

3.1 Precipitation

3.1.1 Model results versus station data

All configurations of the WRF model capture the interannual and seasonal cycle of precipitation as recorded at the stations during the simulation period, but do not simulate the absolute values. All configurations capture well both MAM and OND rain seasons and the dry seasons for the respective regions of the catchment. In particular, precipitation in the upper and middle part of the TRB is generally underestimated, whereas in the lower part it is clearly overestimated (Fig. 7), as in Pohl et al. (2011).

Fig. 7
figure 7

Monthly precipitation (mm/day) averaged over the respective stations over the TRB a upper Tana, b middle Tana, and c lower Tana (see Table 1) for the period 2011 to 2014, derived from the station data and the four WRF simulations with MODIS and USGS land use datasets at 50 km and 25 km horizontal resolution, respectively

Full size image

In the upper TRB (UT), the total precipitation derived from the stations for the 4 years (2011 to 2014; Fig. 7a) was 4242 mm. Against this estimation, MODIS50 simulated 2216 mm while USGS50 provided a value of 1885 mm. On the other hand, MODIS25 produced 3639 mm compared with 2272 mm yielded by USGS25. Thus, the MODIS-driven experiments produced more precipitation than their counterparts. Based on these cumulative totals, the impact of increasing the horizontal resolution in this section of the study area is seen. This behavior is replicated in the annual totals.

In the middle TRB (MT), which is represented by Garissa and Makindu meteorological stations, a comparable performance to that seen at the UT is noted, except in term of horizontal resolution. The derived cumulated station rainfall for the entire period (Fig. 7b) is 1425 mm. MODIS50 (USGS50) simulated approximately 843 mm (766 mm) and MODIS25 (USGS25) at the same time recorded 803 mm (568 mm). In terms of the annual totals, the MODIS-driven experiments are closest that of the station especially for 2011 and 2012 while all experiments seriously underestimated the 2013 and 2014 station rainfall.

In the lower TRB (LT), which is represented by Lamu meteorological station, there is significant overestimation of precipitation (Fig. 7c). The MODIS50 and USGS50 yield the highest total amounts. In terms of the annual totals, all the experiments simulated approximately equal amounts in 2011 and 2012. In general, over this region, MODIS50 had the highest total amount of 2500 mm in 2013 while MODIS25 simulated 2000 mm in 2014.

Figure 8a shows the total seasonal amounts over the UT. During the MAM season, the scenario described above is replicated while the situation is different during the OND season. For the OND rains, MODIS25 overestimated the station rainfall for the years 2011 and 2012 by 56 and 25 mm, respectively. In 2013 and 2014, only MODIS25 showed a good correspondence to station-derived precipitation.

Fig. 8
figure 8

Total seasonal (MAM, OND) precipitation for individual years: a averaged over stations in upper Tana, b averaged over stations in middle Tana, c averaged over the station in lower Tana, and d spatially averaged over the study region

Full size image

Figure 8b shows the seasonal amounts for the MT region. During the MAM season, there was mixed performance for all the four experiments. For instance, MODIS50 simulated more precipitation than MODIS25 during 2011, 2013, and 2014, while USGS50 simulated more precipitation than USGS25. During the OND season, the MODIS-driven experiments record more or less equal amounts. There is thus little impact of model resolution in this case.

The overestimation seen over the LT arises primarily from the MAM season and less from the OND season (Fig. 8c). During OND, most of the experiments produced more or less equal amounts with exception of MODIS25.

From the aforementioned analysis, we note that the impact of increasing the horizontal resolution is more pronounced in the mountainous UT region than either the arid and semi-arid middle or the plain coastal LT. This can be attributed to the local forcings of the topography in the UT region leading to more realistically simulated orographically induced convective precipitation (e.g., Lee et al. 2004; Xue et al. 2007). MODIS25 is able to resolve the orographic precipitation better than USGS25 though they are all at the same horizontal resolution. In the MT, a significant orographic lifting of air mass in not expected. The area is an arid region meaning that the air above this region is mostly dry. Any other processes, such as convectional lifting, can still be weak. The overestimation in the LT may be attributed to the impact of the Indian Ocean wind regimes, which may cause more precipitation at the coast.

3.1.2 Model results versus gridded data

Annual cycle and interannual variability

Simulated annual cycle of monthly averaged precipitation (2011 to 2014) in the study region (Fig. 1; see white box in Fig. 5) is reasonably close to that from TRMM for all considered WRF configurations (r > 0.9 with 95 % confidence interval and p value <0.001; Fig. 9). The climatological seasonal peaks in April and November are well captured as well as the two dry seasons of January–February and June–September also mentioned in Sect. 3.1.1. All four configurations equally underestimate the monthly mean precipitation, as seen in Sect. 3.1.1. This can be attributed to the diverse land surface characteristics and elevation over the catchment which is not factored into the spatial averaging. However, it is not uncommon for most RCMs to underestimate precipitation in tropical regions. It is known that precipitation in a complex terrain area like that of TRB varies within short distances and thus taking an average for the whole region overshadows the local effects. Figure 10 shows the monthly time series of precipitation in the study region estimated from TRMM and simulated in the four configurations for the period 2011 to 2014. The WRF model in all considered configurations generally captures the interannual and seasonal evolution of precipitation in a good correspondence to TRMM. The two known rainfall seasons of MAM and OND are generally well depicted. It is only during the MAM season of 2014 in which all the WRF model simulations lag the rain peak by 1 month.

Fig. 9
figure 9

Annual cycle of monthly averaged precipitation (mm/day) over the study area averaged for the period 2011 to 2014, derived from TRMM and the four WRF simulations

Full size image
Fig. 10
figure 10

Monthly precipitation (mm/day) spatially averaged over the study region (see Fig. 1) for the period 2011 to 2014, derived from TRMM and the four WRF simulations

Full size image

Spatial correlation

The spatial correlation coefficients between the four WRF configurations and TRMM are calculated over the study area (Table 2).

Table 2 Spatial correlation coefficients between monthly sums of precipitation derived by TRMM and the four WRF experiments for the months of March to May (MAM) and October to December (OND) during 2011 to 2014 over the study area
Full size table

The results show diverse representation of the spatial distribution of rainfall during both rainy seasons. During MAM, all the four WRF configurations exhibit high consistencies at the end of the season, reaching correlation coefficients up to 0.9 during 2013 and 2014. For March and April, the correlation coefficients are consistently smaller and in most cases less than 0.5.

There is diverse level of consistency during OND. The highest level of inconsistencies by all the four WRF configurations is in 2011. MODIS25 is consistent in representing the October rainfall distribution (r > 0.6). The other configurations have lower performance than MODIS25.

In general, all the four WRF configurations show significant limitations in representing the peak months of April and November rainfall distribution over the study area during the individual years.

Seasonal totals and averages

The seasonal total amount of spatially averaged precipitation, derived from the monthly time series are shown in Fig. 8d. There is diverse performance by the four WRF experiments during the MAM season over the individual years. The total seasonal amounts for the period 2011 to 2014 for the four WRF experiments are: MODIS50 simulated 571 mm while USGS50 simulated 520 mm. MODIS25 simulated 544 mm while USGS25 simulated 534 mm. The corresponding total derived TRMM precipitation is 882 mm. The four WRF configurations simulated almost equal seasonal amounts over the individual years.

During OND season, MODIS50 simulated 683 mm, while USGS50 simulated 559 mm. MODIS25 simulated 817 mm, while USGS25 had 567 mm. These simulated seasonal amounts are compared to that derived from TRMM for the same period (2011–2014). MODIS25 consistently simulates more seasonal amounts than MODIS50, USGS50, and USGS25 and simulates amounts that are closer to TRMM.

With spatial averaging, over the area covering the region UT and LT, the results found are similar to those highlighted in Sect. 3.1.1 for both MAM and OND. We apply a Taylor diagram-based performance analysis (Taylor 2001) for an in-depth study of differences between modeled and observed precipitation. Figure 11 shows normalized statistics (i.e., the pattern correlation (r), RMSE, and the standard deviation (σ)) of the seasonal mean rainfall of the four WRF experiments with respect to TRMM estimates for the period 2011 to 2014. During MAM season, all the four experiments overestimated the magnitude of the interannual variation relative to TRMM with normalized standard deviations of approximately 1.5 and RMSE values of between 1 and 1.5. MODIS25 show a relatively high pattern of correlation (r > 0.6) and a lower normalized RMSE compared with the other experiments, consistent with the monthly correlation coefficients given in Table 2.

Fig. 11
figure 11

Normalized pattern statistics based on comparison of monthly mean precipitation for MAM and OND grid points for the four WRF experiments to TRMM estimates, averaged for the period 2011 to 2014

Full size image

In the case of OND, USGS50 showed the highest spatial variability and the lowest pattern correlation compared with USGS25, MODIS50, and MODIS25. The latter three experiments have similar equal normalized RMSE values. MODIS25 shows a slightly higher pattern correlation (Fig. 11).

Time-averaged precipitation

Considering the time-averaged precipitation for individual years, during the MAM season (Fig. 12), the WRF model in all configurations is generally wetter along the lower parts south-west of the catchment (coastal strip) compared with TRMM. On the other hand, in the north-west (in the vicinity of Mt. Kenya, upper TRB) and middle of TRB, the WRF model is relatively drier than TRMM, which is consistent with the monthly series of Fig. 7. The interannual and seasonal variability of precipitation is evident from the seasonal spatial maps (Fig. 12). In 2011, all the WRF configurations were very dry compared with TRMM in general, and more specifically in the MT. During 2012 and 2013, all WRF experiments captured well the precipitation maximum (related to TRMM), with MODIS25 displaying the closest patterns to that of TRMM. In 2014, however, MODIS25 shows the lowest performance in the MT.

Fig. 12
figure 12

Precipitation maps of the study area averaged for MAM season for the period 2011 to 2014, derived from a TRMM and the four WRF simulations: b MODIS25, c MODIS50, d USGS25, and e USGS50. The red contour line delineates the TRB

Full size image

During OND season (Fig. 13), we notice a closer spatial patterns compared with that observed in TRMM. All WRF experiments capture the precipitation maximum (north-west of the TRB) while being wetter along the lower TRB (coastal strip). It is seen that the MODIS configurations (MODIS25 and MODIS50) are consistently wetter than USGS configurations (USGS25 and USGS50), which is in line with the results presented in Sect. 3.1.2. In general, the simulated and observed precipitation show a decline over the years, with 2011 being the wettest while 2013 and 2014 are drier among the four considered years (Fig. 13). The OND season thus depicts more interannual variability which is in agreement with earlier studies like Camberlin and Okoola (2003).

Fig. 13
figure 13

Same as Fig. 12 but averaged for OND season

Full size image

Normalized statistical comparison of the time-averaged precipitation to the corresponding TRMM estimates summarizes the MAM spatial maps (Fig. 14a). In 2011, all the four WRF experiments had weak pattern correlations (r < 0.2). In 2012, there were fairly reasonable spatial pattern correlations (r ≈ 0.4). The pattern correlations of the four WRF experiments were higher in 2013 and 2014, ranging from approximately 0.5 to 0.8, but showing diverse standard deviation (1.8 ≤ σ ≤ 3.3). MODIS25, in general, displayed the highest pattern correlations for the 2 years.

Fig. 14
figure 14

Normalized pattern statistics summarizing the seasonal precipitation spatial maps a for MAM and b for OND

Full size image

In the case of OND, all four experiments show similar performance in terms of spatial variability with standard deviations (1 ≤ σ ≤ 2) and pattern correlation (r < 0.6) (Fig. 14b). Unlike for MAM, no clear inferences can be drawn for the different years.

In general, the WRF experiments are underestimate precipitation across the whole study region. The dry bias is less in MODIS25, followed by MODIS50, USGS25, and USGS50. This is in agreement with Pohl et al. (2011) who also found MODIS comparatively wetter than USGS. Increasing the horizontal resolution improved the simulated precipitation, except for the MT, as was also deduced in Sect. 3.1.1. MODIS25 can be considered to provide reasonable precipitation simulations as it shows best pattern correlations and smallest RMSE values.

3.1.3 Simulated latent heat and sensible heat

Figure 15 shows the differences in the simulated latent heat between the MODIS and USGS simulations for the MAM and OND seasons, averaged over 2011 to 2014. There are similar spatial patterns in the simulated differences for the MAM and OND season. MODIS25 simulates more latent heat than USGS25 in most of the upper TRB, but less in the middle TRB. The same applies for MODIS50; however, it simulates more latent heat than USG50 in the middle TRB.

Fig. 15
figure 15

Difference in mean seasonal latent heat (LH) over the study area, averaged for the period 2011 to 2014 a MODIS25 minus USGS25 for MAM, b MODIS25 minus USGS25 for OND, c MODIS50 minus USGS50 for MAM, and d MODIS50 minus USGS50 for OND

Full size image

Since all experiments have common parameterizations, it is speculated that the increased latent heat in the MODIS experiments leads to increased precipitation in comparison with the USGS experiments. In particular, MODIS25 produces more precipitation, especially over regions with complex topography. As expected, a close relationship of sensible heat with temperature was found (not shown).

3.2 Temperature

3.2.1 Model results versus station data

The WRF model in all configurations captures well the interannual evolution of temperature compared with that observed at the respective stations (Fig. 16) (r > 0.6). However, the monthly mean temperatures simulated in the four configurations are colder compared with station temperatures with a MAE values between 1 and 5 °C.

Fig. 16
figure 16

Monthly mean temperature (°C) at a Nyeri, b Meru, c Thika, and d Lamu for the period 2011 to 2014, derived from station data and the four WRF simulations

Full size image

The WRF simulations accounted for the air temperature decrease with altitude. All the WRF configurations simulated the lowest temperatures over Nyeri, which is located at the highest altitude of all stations. The highest temperatures are simulated at Lamu, which is at the lowest altitude. The difference between the simulated height and the actual station altitude (i.e., the station terrain heights minus model terrain heights) are shown in Table 3 with the corresponding decreases in surface air temperature. There is little impact of the model horizontal resolution on the simulated temperatures. The biases of all WRF experiments are high, on average about 9 °C at Nyeri, about 6 °C at Thika, 3 °C at Lamu, and 2 °C at Meru. There is no clear relation tendency of the biases based on altitude of the stations.

Table 3 Difference between the model grid point and actual station terrain height and the corresponding decrease in temperature of selected stations in TRB
Full size table

Resolutions of 50 and 25 km are not sufficient to capture differences in temperature between the stations related to orography and land surface. This is in agreement with Sheridan et al. (2010). The results shown as time series can also be confirmed in the seasonal average maps (Online resources 1 & 2).

3.2.2 Model results versus gridded data

Annual cycle and interannual variability

The spatially averaged monthly mean temperature over the study region exhibit correlation coefficients of r > 0.7 for all four WRF configurations, compared with CRU.

All the WRF configurations capture reasonably well the seasonality of monthly mean, maximum and minimum temperature. In line with the results for the stations, WRF simulates similar values for the spatially averaged temperature (Fig. 17). There is a relatively good agreement between CRU and the minimum temperature, but a significant (cold) bias can be found for maximum and mean temperature. This cold bias in the WRF simulations was noted in previous studies (Abdallah et al. 2015). All the WRF configurations show similar spatial variability and amplitudes (1 < σ < 1.2, 0.2 < RMSE < 0.4) over the studied years, as well as having high correlation patterns (r > 0.9) (Fig. 18).

Fig. 17
figure 17

Monthly mean temperature spatially averaged over the study area (see Fig. 1) for the period 2011 to 2014, derived from CRU and the four WRF simulations: a minimum, b maximum, and c mean of maximum and minimum

Full size image
Fig. 18
figure 18

Normalized statistical comparison of seasonally spatially averaged mean temperature over TRB for the period 2011 to 2014, derived from CRU and the four WRF simulations, a for MAM season and b for OND season

Full size image

4 Summary and conclusion

In the present study, the ability of the WRF model driven by the ERA-Interim lateral boundary conditions to reproduce the seasonal and interannual variability of hydrometeorological variables in the TRB is assessed. We performed four WRF simulations experiments for the period 2011 to 2014 in order to assess the impact of two different land use classifications (MODIS and USGS) and two horizontal resolutions (50 and 25 km) on simulated precipitation and temperature. The performance of the model was investigated with respect to station and gridded (TRMM, CRU) data over the TRB.

All the four WRF model configurations reasonably reproduced the spatial patterns and temporal evolution (seasonality) of both TRMM-derived precipitation and CRU-derived temperature over the study region. Significant cold model biases were found when compared with observation stations as well as the CRU data, independently of the WRF configuration. The limited accuracy in simulating temperature might not only be due to deficiencies of the WRF, but also due to deficiencies of the CRU dataset (interpolation limitations) in representing the actual temperature in such a mountainous region with a low density of observation stations. In terms of precipitation, the MODIS25 revealed the closest correspondence to the observations in relation to more latent heat.

Supported by the results of this study, we draw the following conclusions: (i) the choice of the land use data (i.e., MODIS or USGS) as well as the resolution (50 or 25 km) may significantly impact on simulated precipitation, but not so much on simulated temperature; and (ii) TRMM is a good surrogate for observation data in East Africa, where the observation network is sparse.

Based on our study, a qualified guess on a suited WRF model configuration for the region of Kenya is suggested. This is the prerequisite for CPU-demanding long-term regional climate simulations, which are important for climate change impact research, and particularly for water availability and agricultural studies.