1 Introduction

In recent years, the number of so-called objective circulation type classification systems has increased rapidly (Huth et al. 2008). New computing options and other novel methods have emerged in the last two decades along with large digital meteorological databases. This has produced a whole new range of classifications based on new analytical methods and concepts. On the other hand, proven manual classification systems (subjective systems) have been abandoned, in most cases, even though their practical and scientific value was significant. Unsurprisingly, some researchers decided to make existing manual circulation typologies objective (e.g., Cawley and Dorling 1996). Two examples of well-known classification systems in Europe are the Grosswetterlagen (James 2007) and the Lamb systems (Jenkinson and Collison 1977). Even less-renowned local classification systems can be made objective and there is a purpose to that. This is exactly the case with the well-known Polish manual classification system developed by Osuchowska-Klein (1975).

The main purpose of this study was to create a 24-h objective classification system based on the existing subjective Osuchowska-Klein classification system. This classification approach is used to evaluate circulation patterns over Poland and it is commonly applied in synoptic climatological studies. The calendar with Osuchowska-Klein types is available for the 1901–1998 time periods. Unfortunately, it has not been produced since 1999. This classification system has been selected for two additional reasons. First, it provides a relatively good assessment of meteorological phenomena over Poland. This is especially true of extreme weather events (Osuchowska-Klein 1978). Second, it consists of a relatively small number of patterns/types (13 patterns), which makes it possible for it to be used even with short data series.

The system's only flaw described in some publications is the fact that Type X (the 14th type— unclassified) occurs relatively frequently and its frequency of occurrence can reach several percent. This is especially true of synoptic situations, which often produce extreme air temperatures. Type X can be eliminated by making the Osuchowska-Klein classification system objective.

2 Data

The original Osuchowska-Klein circulation type classification system is based on 13 patterns that depend on the location of main pressure centers over Europe, which determine air mass movements over Poland (Osuchowska-Klein 1975). The following 13 classified patterns (types) and one unclassified pattern (type) have been identified: A—Western cyclonic, CB—Northwestern cyclonic, D—Southwestern cyclonic, B—Southern cyclonic, F—Southeastern cyclonic, C2D—Western anticyclonic, D2C—Southwestern and Southern anticyclonic, G—Central anticyclonic, E2C—Northwestern anticyclonic, E0—Northeastern and eastern cyclonic, E—Northeastern and eastern anticyclonic, E1—Southeastern and eastern anticyclonic, BE—Southern transitional between cyclonic and anticyclonic, X—unclassified.

European circulation patterns were initially produced by the Osuchowska-Klein method as part of this research study and then expressed as normalized values of sea level pressure across a regular 5° × 5° grid over an area ranging from 45°W to 60°E and from 30°N to 75°N. Observed daily atmospheric circulation (i.e., normalized values for the same domain) from January 1948 to December 2007 (based on NCEP/NCAR Reanalysis) was determined in the same way.

3 Methodology and results

The method applied in our study is based on case-based reasoning systems rooted in fuzzy set theory. Case-based reasoning is a method for solving problems by remembering similar previous situations and reusing information and knowledge about those situations (Hansen 2000, based on: Kolodner 1993; Leake 1996). It enables one to indicate similarity between a compared case (the synoptic situation on a given day) and a pattern (any of the 13 patterns in the Osuchowska-Klein classification system). This type of fuzzy logic methodology was used to determine circulation types based on the Osuchowska-Klein classification system for arrays of observed situations. The approach was applied to information acquired about the level of similarity between the features of a given case and those of a set pattern. This type of information is encoded in the so-called membership function (see further part of the text). Fuzzy logic emulates the work of experts performing comparative analysis.

The main purpose of our methodology was to create an objective calendar based on the Osuchowska-Klein classification system. A fuzzy logic approach was applied to the daily atmospheric circulation classification calendar. In a classic statement of logic, an answer is either true or false. In fuzzy logic, an expression may be true to a certain degree. An “objective” classification calendar was produced by identifying the given Osuchowska-Klein circulation pattern that best matches a given case (i.e., daily sea level pressure map). This was accomplished by calculating a similarity measure (the so-called degree of fulfillment) of each given case to each given pattern. Normalization was performed in order to make the patterns and cases comparable. European circulation patterns generated via the Osuchowska-Klein method were expressed as normalized values of sea level pressure across a regular 5° × 5° grid over an area ranging from 45°W to 60°E and from 30°N to 75°N. In order to normalize the pressure over the selected area, an expression of the following form (Han and Kamber 2001) was used:

$$ a \prime = \frac{{a - {a_{{min}}}}}{{{a_{{max}}} - {a_{{min}}}}}\left( {{{a \prime }_{{max}}} - {{a \prime }_{{min}}}} \right) + {a \prime _{{min}}} $$

where:

a max :

Maximum pressure value over domain

a min :

Minimum pressure value over domain

a′ max :

Maximum value of normalized pressure over domain

a′ min :

Minimum value of normalized pressure over domain

a :

Pressure value at the given grid point

a′ :

Normalized pressure value at the given grid point

In the study, the highest normalized pressure a′ max assumes a value of 1 while the lowest value of normalized pressure a′ min equals 0.

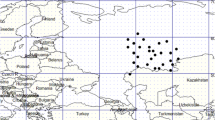
Observed cases of daily atmospheric circulation (i.e., normalized values for the same domain with the same resolution as the model patterns) from January 1948 to December 2007 (based on NCEP/NCAR Reanalysis) were expressed in the same way. Circulation patterns are distinguished by their typical locations of cyclones and anticyclones over the domain of interest. Taking into account the location of cyclones and anticyclones as well as the boundaries that separate centers of pressure (key determinants of weather), a set of grid points that clearly defines each pattern was selected. For the purpose of this study, a sub-domain ranging from 0°E to 40°E and from 40°N to 65°N was defined. The synoptic situation in the sub-domain affects the weather over Poland the most (Fig. 1). Figure 1 also shows grid point locations that clearly define one of the patterns of interest (Type D2C). Six grid point classes ν for cyclones, anticyclones, and areas that separate pressure centers inside and outside the sub-domain were created.

Fig. 1
figure 1

Membership function (Hansen 2000); see text for discussion

Full size image

The degree of fulfillment of a given case to a pattern was obtained in a few steps. At the beginning, the difference x 1  − x 2 between observed normalized pressure x 2 and that of the Osuchowska-Klein pattern x 1 was calculated for each selected grid point of each pattern. Then, in order to obtain the similarity μ between x 1 and x 2 at each selected grid point, a so-called membership function was constructed. In order to compare continuous fields such as pressure, a membership function such as the one shown in Fig. 2 (where constant c = 0.125) was used (Hansen 2000). The membership function enables one to calculate the degree of similarity of pressure as a function of the difference x 1  − x 2 between the normalized value of pressure of the pattern x 1 and the normalized value of pressure of the given case x 2 at each grid point of the set of locations that define the pattern. In our study, \( \mu \equiv {\mu_{\nu }}\left( {j,{ }k} \right) \) is the similarity at each selected grid point estimated using the membership function, and established for ranges of differences x 1  − x 2 between case t and pattern k for individual location j and class ν. For every grid point class ν of the pattern k, the degree of fulfillment \( {D_{{k\nu }}} \) was calculated as follows: inside the sub-domain, most of the selected locations should fit the pattern while at locations outside the sub-domain, at least a few values at selected grid points can be expected to fit the pattern. For this reason, different values of the weight \( {\gamma_{\nu }} \) for selected locations inside and outside the sub-domain were taken into consideration in our analysis. Satisfactory results were obtained for \( {\gamma_{\nu }} = 0.{4} \) inside the sub-domain and for \( {\gamma_{\nu }} = 0.{7} \) outside the sub-domain for each circulation pattern. The degree of fulfillment \( {D_{{k\nu }}} \) (Driankov et al. 1996; Bardossy et al. 1995) was expressed as a combination of OR (F o ) as well as (F a ) functions. In fuzzy set theory, the function F o takes the following form (Dubois and Prade 1980):

$$ {F_o}({\mu_{\nu }}(1,k),{\mu_{\nu }}(2,k)) = {\mu_{\nu }}(1,k) + {\mu_{\nu }}(2,k) - {\mu_{\nu }}(1,k)\;{\mu_{\nu }}(2,k) $$

and recursively as:

$$ {F_o}({\mu_{\nu }}(1,k), \ldots, \;{\mu_{\nu }}(j,k)) = {F_o}({F_o}({\mu_{\nu }}(1,k), \ldots, {\mu_{\nu }}(j - 1,k)),{ }{\mu_{\nu }}(j,k)). $$
Fig. 2
figure 2

Example of grid point location describing the D2C type over the area of interest (domain and sub-domain)

Full size image

While the function F a is expressed as (Bardossy and Disse 1993)

$$ {F_a}({\mu_{\nu }}(1,k), \ldots, { }{\mu_{\nu }}(m,k)) = { }{\Pi^m}_{{j = 1}}{\mu_{\nu }}(j,k). $$

The degree of fulfillment \( {D_{{k\nu }}} \) was calculated using the following equation (Driankov et al. (1996)):

$$ {D_k}_{\nu } = {\gamma_{\nu }}{F_o}({\mu_{\nu }}(1,k), \ldots, { }{\mu_{\nu }}(j,k)) + (1 - {\gamma_{\nu }}){F_a}({\mu_{\nu }}(1,k), \ldots, { }{\mu_{\nu }}(j,k)). $$

The next step was to calculate the degree of fulfillment D k that showed similarity between the case to be classified and the pattern of interest—the degree of similarity of the circulation observed to a given type of classification (Bardossy et al. 1995). The degree of fulfillment D k corresponding to pattern k and the case of day t is the product of the \( {D_{{k\nu }}} \) values obtained for every class ν:

$$ {D_k} = \Pi_{{\upsilon = 1}}^n{D_{{k\nu }}} $$

where n = 6 is the number of classes.

Finally, values of D k for each pattern and the case of day t were compared in order to select the circulation type of the observed situation t. The largest value of the degree of fulfillment D k for a compared case indicated the type of circulation pattern on any given day. This means that the pattern k for which the degree of fulfillment D k takes on the maximum value is selected as the circulation pattern for day t.

It must be noted that minimum similarity thresholds were not defined by the method where a given situation is assigned to one of 13 predefined Osuchowska-Klein classification types. For this very reason, the objective method does not take Type X (unclassified) into account. Another reason for this was that the days on which Type X was supposed to occur, according to the subjective method, were not compared.

4 Validation

Validation turned out to be one of the most difficult tasks. The authors wanted to compare the obtained results with the Osuchowska-Klein subjective calendar. Circulation types, described using the subjective method, were compared multiple times for each day from 1951 to 1998, applying different parameters generated by the fuzzy logic method. Although the comparison itself was quite simple—the number of cases obtained for all 13 types via the objective method was compared with that obtained via the subjective method—it needs to be emphasized that this type of analysis cannot be fully reliable. The most basic reason for this is the lack of the same initial materials in the two cases. The original “subjective” calendar was based on daily synoptic maps of Europe but it is not clear whether these maps were based on several observations (mean of several observations per day) or just based on a particular observation time each given day. Thus, it was decided to use mean daily grid data in the study. As a result, the circulation type obtained for a given day is a consequence of the situation, which took place at the main observation times. An example of this would be a comparison of a daily average of a synoptic situation and one point in time (e.g., 12 UTC) where, it turns out, the differences observed on the maps are not significant. In summary, it must be stated that the validation procedure was not carried out using the same initial data set, which would have produced similar, but not exactly the same, results from the very start.

Two different validation methods have been applied. The first was based on a statistical approach while the second consisted of a simple analysis of the contingency table supported by a simple comparison of the cases involved (comparison of both calendars and corresponding cases/days, i.e., subjective and objective ones).

4.1 The first “statistical method”

The first method consisted of a chi-square goodness of fit test (which is the sum of differences between calculated and expected outcome frequencies, Wilks 2006) and a chi-square test of independence (Kendall and Stuart 1973).

The chi-square test was used to compare the subjective method and the objective method to see if they produce consistent results (distribution of types). The following formula was used:

$$ {\chi^2} = \sum\limits_{{n = 1}}^m {\frac{{{{({O_n} - {E_n})}^2}}}{{{E_n}}}} $$

where:

O n :

Number of cases of a given type (pattern) n based on the objective method

E n :

Number of cases of a given type (pattern) n based on the subjective method

n :

Ranges from 1 to m; m = 13

The calculated chi-square value is markedly larger than the threshold value, which is 5.226 for the confidence level p = 0.95 and 12° of freedom. In light of this result, the objective method appears to be erroneous (not consistent). In the case of our data, this test does not seem to be sufficient. For this very reason, another test was then used, the chi-square test for independence. The formula shown below (Kendall and Stuart 1973):

$$ {{\chi^{{2}}} = \sum\limits_i {\sum\limits_j {\frac{{n_{{ij}}^{{2}}}}{{{n_{{i{.}}}}{n_{{{.}j}}}}}} } - {1}} $$

where:

n ij :

Frequencies

n i. :

Raw totals

n .j :

Column totals

was used to calculate the X2 value (X2 = 22,022), which exceeds even the largest threshold values many times over, given the number of degrees of freedom. The very large chi-square value indicates a strong relationship between the parameters (types) of both distributions. It was validated by the value of Pearson's coefficient of contingency (P = 0.751; Kendall and Stuart 1973), as well as by the value of a chi-square alternative (Kendall and Stuart 1973) called Tschuprow's T (T = 0.328).

In spite of unambiguous test results produced by both methods (i.e., subjective and objective), which show a highly consistent distribution of circulation types, still get the feeling that results are still somehow insufficient.

From our point of view, considering the nature of circulation phenomena, chi-square does not show which method is better. It only shows if the results produced by the two methods are in agreement. An analysis of the contingency table, which has been discussed to a significant extent (see below), shows which classification types are “confused” most often. An analysis of specific cases shows that the identification and assignment of a classification type to a given synoptic situation is neither easy nor unambiguous.

It must be noted that when certain cases (synoptic situations, specific days) are compared directly, the objective method appears to rely more on the boundaries of pressure systems than on the locations of pressure system centers. This is especially true of Central Europe, including Poland, where centers of both high as well as low-pressure systems rarely linger over the region.

4.2 The second “simple comparison approach”

The analysis of the contingency table produced a very nice surprise, with most of the circulation types described for 1951–1998, using both methods, being identical. This mainly applies to types G, E2C, and E, which were in agreement with types described subjectively in as many as about 50% of the cases (Table 1). Therefore, the challenge was dealing with types whose similarity level was the smallest, ranging from 20% to 30% (types B, D2C, E0). Air-pressure distributions were analyzed in order to find possible reasons for these large differences. The answer, however, turned out to be quite ambiguous. In some cases, the use of grid points was a limitation compared to using a map where all values are continuous, such as in the case of a synoptic map, the type used for subjective evaluation. In other cases, such as on June 30, 1991 (Fig. 3), the air-pressure pattern over Europe was so complex that the proposed control point could not possibly show differences correctly. As a result, subjective and objective circulation types were entirely different from each other, even though they identified two very similar situations (D2C and C2D). It appears that other domains and control points ought to be tested in order to improve the results. However, even a choice of the best possible parameters will not preclude differences, which will be produced via a better objective evaluation of a given circulation type by means of fuzzy logic. This approach will also identify similar types (e.g., E0 and E or D2C and C2D).

Table 1 Percentage of cases of types generated via the subjective method and the objective method (100%—number of cases of a particular type based on the objective method)
Full size table
Fig. 3
figure 3

Situation on June 30, 1991; observed situation and set pattern matched by the subjective/manual and objective methods

Full size image

Fuzzy logic circulation types calendar based on the Osuchowska-Klein scheme for the entire investigated period 1951–2006 is available on the web site: http://www.klimat.geo.uj.edu.pl/circulation.htm. The original Osuchowska-Klein circulation types calendar for the period of 1951–1975 (the only period of the whole accessible series permitted to be published) is also available at the mentioned address.

5 Conclusions

Fuzzy logic appears to be quite a promising and effective approach for the identification of circulation types. The results obtained in this study confirmed that fuzzy logic can be used to make traditional (subjective) classification methods objective. The Osuchowska-Klein classification approach has also been useful in this study.

The nature of fuzzy logic allows for the flexible matching of a type with a given pattern. It imitates the way a synoptic meteorologist looks at a synoptic pattern. The fuzzy logic method takes into account the distribution and spatial relationships found across a pressure system. Absolute values of air pressure, though significant, are not the fundamental matching feature. Therefore, it is always necessary to normalize data before use.

Methods based on fuzzy logic, much like other objective methods, require a long testing period. They allow for the best parameter values to be identified. Nevertheless, even the best set of parameters selected will make the new “objective” classification different from the manual one.

The results of this study have shown that there exists a real problem of an “undefined class” created by the traditional approach. It is equally important to define threshold values, above which the matching of the case and the pattern would be out of the question. Despite the imperfections of the method presented herein, it must be said that its use allows for the definition of types while taking into account areas located between pressure centers, which happens to be very important in the case of Poland. These types of situations are commonly encountered over the area of interest and shape of the weather in the region.