1 Introduction

Large-scale atmospheric circulation is an important feature of the Earth’s climate system. In some regions, prevailing wind directions provide stable and predictable weather conditions. Other regions are influenced by recurring large-scale oscillations on timescales of seasons (e.g. the South East Asian monsoon) or multiple years (e.g. El Niño–Southern Oscillation). Understanding the relationship between large-scale circulation and local weather phenomena has been in human interest at least since the antiquity.

Circulation type classification is an approach to classify the various different states of atmospheric circulation occurring during a period into a discrete number of classes, usually called circulation types (CT). There are very many classification methods. The EU COST Action 733 “Harmonisation and Applications of Weather Type Classifications for European regions” (Philipp et al. 2016) made an intercomparison of 35 different classification methods. They also produced a catalog of CTs (cost733cat, Philipp et al. 2010) based on the ERA-40 reanalysis as well as a software package (cost733class) to apply the classification methods to new data. One conclusion was that there is no single classification method that is optimal for all applications.

Classification methods can be divided into two main categories: subjective and objective methods. Subjective methods usually involve a pre-defined set of CTs, for example different strengths of prevailing zonal, meridional, cyclonic or anti-cyclonic patterns. In the early days one would then manually compare and place the observed map in the group with the CT which is most similar. Examples of early subjective methods are the Hess–Brezowski Grosswetterlagen (Hess and Brezowsky 1952) centered on Germany, and the Lamb weather types (Lamb 1972) focusing on the British Isles. Objective methods involve computing CTs that, depending on a given metric, minimises the spread within each CT. This group can be further divided (following the terminology used in Philipp et al. 2010) into methods based on eigenvectors (e.g. empirical orthogonal functions), leader algorithms or optimisation algorithms. The latter includes various different methods such as k-means clustering and self-organising maps.

The majority of the literature on circulation type classification unsurprisingly deals with observed historical weather. The first classifications were based more or less directly on data from meteorological stations, and as station density improved gridded observational datasets could be used. Nowadays classification is typically applied using more advanced products, such as atmospheric reanalyses, where a numerical model system employing data assimilation is fed with multiple sources of data, including for example also data from satellites, ships, buoys and aircraft. With multi-decadal datasets available, trends in circulation type statistics can also be detected (e.g. Corti et al. 1999; Cahynová and Huth 2016).

General circulation model (GCM) simulations have also been examined using circulation type classification methods. This can be done to investigate circulation biases in multi-model ensembles (e.g. Huth 2000; Pastor and Casado 2012; Stryhal and Huth 2019; Cannon 2020) as well as to identify possible changes in large-scale circulation under future climate change scenarios (e.g. Belleflamme et al. 2013; Riediger and Gratzki 2014).

Because global climate models do not represent fine scale processes due to their coarse spatial resolution, dynamical downscaling is used by a regional model to develop fine-scale weather inside a regional domain. Unlike for regional models in numerical weather prediction, for climate scenarios there are naturally no observations to assimilate, so the regional climate model is allowed to develop its own fine-scale representation of the weather inside the domain, only constrained on the boundary by the global model. Note that if techniques such as spectral nudging (von Storch et al. 2000) are used, the regional model can also be constrained to follow the global model on the coarse scales inside the domain.

One question in regional climate modelling that needs to be addressed is how the dynamical downscaling performed by the RCM affects the circulation. Sanchez-Gomez et al. (2009) found that regional models over Europe (from the ENSEMBLES EU FP7 project) reproduce the large-scale circulation patterns and statistics quite well, but that the ensemble spread was larger in summer due to differences in model setups and larger internal variability. Vautard et al. (2020) examined spatial correlation of daily mean sea-level pressure in 55 simulations from the Euro-CORDEX ensemble (Jacob et al. 2014, 2020) and their corresponding 8 GCMs and found that the day-to-day pattern correlation was strongest in winter (median values \(>0.9\) for all simulations) and lower in summer (medians 0.6–0.9). This can be explained by the European region in winter being controlled by the North Atlantic Oscillation (NAO, e.g. Sieck and Jacob 2016) which gives a strong predominantly westerly flow so that the RCMs are consistently provided with strong signals on the western boundary. This means that the regional models have less time to develop internal circulation before an airmass that enters on the western boundary exits the domain on the eastern boundary. This in turn means that differences in RCM setups have greater impact in the summer season (confirmed by e.g. Plavcová and Kyselý 2011 for Central Europe).

With its many participating modelling groups, the Euro-CORDEX ensemble Jacob et al. (2014, 2020) is the largest ensemble of regional climate models. It presents a great opportunity for evaluating the possible effects of downscaling on atmospheric circulation, both for the historical period and under future climate scenarios. The questions we would like to address with this paper are the following:

  • How does dynamical downscaling affect the circulation inside the domain?

  • How do results differ between various GCM-RCM combinations?

  • What are the changes in circulation in a future climate scenario?

  • Are the results sensitive to choice of classification method?

The paper is organised as follows: Data is presented in Sect. 2, methods and statistical measures in Sect. 3, results and discussion in Sect. 4 and summary and conclusion in Sect. 5.

2 Data

We retrieved daily mean sea-level pressure (psl) from Euro-CORDEX RCMs (EUR-11 domain) for the historical period as well as the RCP4.5 Thomson et al. (2011) and RCP8.5 (Riahi et al. 2011) scenarios. Their corresponding boundary simulations from CMIP5 GCMs were also retrieved. The command-line tool SyndaFootnote 1 was used to automate the retrieval of RCM and GCM data from ESGF. As reference, data from the ERA5 reanalysis for years 1979–2020 (Hersbach et al. 2018) and the back-extension 1950–1978 (preliminary version, Bell et al. 2020) was downloaded from the Copernicus Climate Change Service (C3S) Climate Data Store. The time period selected was year 1950 (or as early as available for the regional models) until 2100. The full reanalysis period was used as reference for all regional models, regardless of their simulation lengths. While there are multiple different reanalysis datasets available, and uncertainty between different reanalysis is interesting, such an investigation is outside the scope of this study, and is also covered in other literature such as Stryhal and Huth (2017), Cannon (2020) and Brands (2021).

We chose to focus on Europe because of the large number of regional model simulations available in the Euro-CORDEX ensemble. In addition, this region has strong variability in atmospheric circulation, as shown in Fig. 1. Because the classification software we use (cost733class, see Sect. 3) requires data to be on a regular grid, we selected the domain \(-19.5^\circ \) to \(40.5^\circ \) longitude and \(41^\circ \) to \(69^\circ \) latitude, shown in Fig. 1. As we are dealing with large-scale circulation features, we do not need the fine spatial resolution that the regional model provides and can instead use a coarser grid. This saves computational resources which allows prioritising a large ensemble instead of fine spatial resolution. The grid spacing was set to \(\varDelta x=2^\circ \) and \(\varDelta y=1^\circ \) in order to sample approximately the same horizontal distance in both directions, yielding an almost quadratic domain (\(31\times 29\) grid points). This also has the advantage of avoiding being close to the domain borders for most of the area, possibly allowing the regional models to develop more independent circulation.

Fig. 1
figure 1

Standard deviation of daily mean sea-level pressure (hPa) from ERA5 over the northern hemisphere. The four panels show values for the four seasons (Dec–Feb, Mar–May, Jun–Aug and Sep–Oct) for years 1950–2020. The selected study region is shown as the white rectangle in the middle and the domains of the 11 regional models from CORDEX are shown as dashed lines around it

Full size image

For all simulations the mean sea-level pressure data was interpolated to the same grid (specified above) using bilinear interpolation. We also tried conservative remapping but because many of the regional models do not include the vertices for their grid in the metadata this could not be applied universally. We compared conservative remapping with bilinear for the ERA5 dataset as well as two of the RCMs and the difference in pressure was less than \(1\%\) for all timesteps and grid points. This is not surprising because the pressure field is a rather smooth field, compared to e.g. precipitation. We therefore settled on bilinear interpolation for all simulations.

The full list of simulations used is available in Fig. 2. Note that many of the GCM and RCM models are represented in multiple simulations in different combinations of GCMs and RCMs. This list is based on availability of daily sea-level pressure as well as geopotential height at 500 hPa (which we finally did not use due to lack of time). Compared to the full Euro-CORDEX ensemble, we excluded simulations driven by r3i1p1 of ICHEC-EC-EARTH because in the GCM data the psl variable incorrectly contained surface pressure instead of sea-level pressure. We also excluded simulations based on r1i1p1 of CNRM-CM5 in combination with v1 simulations from CNRM-ALADIN53 and DMI-HIRHAM5 due to issues documented in the errata table.Footnote 2

For the analysis of future climate scenarios, we focus on the RCP8.5 scenario (Riahi et al. 2011), which has higher greenhouse gas concentrations. We selected this scenario mainly for two reasons: (1) RCP8.5 has the strongest projected future climate change, so we expect changes in circulation to be clearer and more statistically robust; (2) RCP8.5 has most simulations in the Euro-CORDEX ensemble (65 vs 28/25 for RCP2.6/4.5 respectivelyFootnote 3). However, as it may be of interest to climate services, we have also performed some of the analysis on the RCP4.5 ensemble. This smaller ensemble (Table S1 in the supplementary material) consists of 21 ensemble members after applying the same exclusion rules as for RCP8.5 mentioned above.

We deliberately chose not to include downscaled reanalysis simulations. While they are useful for evaluation of individual models, the choice to select downscaled GCM data is more representative of what a person working in e.g. national climate services would use. There the climate change assessments are usually based on comparisons of future and historical simulations from global climate models downscaled by regional models. In such context, one often face the challenge of creating an ensemble of regional model simulations by removing model combinations which do not satisfactorily represent observed recent climate. We hope that the results presented in this article may help in such decisions by providing information about model skill in reproduction of atmospheric large-scale circulation statistics.

Fig. 2
figure 2

List of simulations used. The first 11 models are CMIP5 GCMs, the 12th model is the ERA5 reanalysis and models 13–69 are Euro-CORDEX RCMs downscaled from GCMs 1 to 11. The format of each simulation name follows “{Number in list}_{Global model group − Global model name}_{Ensemble member}_{Regional model group − Regional model name}_{Dataset version}”. Ensemble member rn is short for rni1p1

Full size image

3 Methods

For each dataset and day separately, the spatial mean for the whole domain (“field mean”, the operator fldmean in CDO, Schulzweida 2019) was subtracted to form a dataset of anomalies, in accordance with Hansen and Belušić (2021). The same value is subtracted from all grid points within the domain (but varying from day to day and model to model). This preserves the differences in the pressure field, in essence meaning that wind directions and wind speeds are not altered, while at the same time removing trends and annual cycle in domain-wide mean pressure, making it possible to apply one classification for the all seasons and years.

In order to make sure that model states from all models are represented in the classification step, the anomalies from all 69 simulations listed in Fig. 2 (i.e. GCMs, RCMs and reanalysis) were concatenated and then fed to a circulation type classification method. We were limited to a maximum of 256 GiB RAM and 84 h per job (i.e. per classification method), so we chose to perform the classification (calculate the CTs) based on the historical period only. This amounts to over 3600 years for all 69 simulations performed together in one classification.

We applied three classification methods using the cost733class software (Philipp et al. 2016): distributed k-means (DKM), Grosswettertypes (GWT) and Simulated annealing and diversified randomisation clustering (typically abbreviated SANDRA, but we use SAN in our results to be brief). As mentioned in the introduction, the method GWT is a subjective method using predefined circulation types. DKM and SAN are optimisation algorithms. Detailed descriptions of the methods are available in Philipp et al. (2016) and Tveito et al. (2016). Each method was used with three different number of CTs: 10, 18 and 27.

After obtaining circulation types for a classification method, days for the future scenario were assigned to its closest CT by minimising the Euclidean distance between the observed day and the CT. This is available in the cost733class software as the method named ASC (presumably “assign centroids”, from here on just “assign”). We tested the assign method on historical data, by comparing the time-series obtained directly by the multi-millennial classification with classifications using the assign method, and got identical results. Because we are subtracting the spatial mean within the domain for each day, any trend in the mean field is removed. We argue that this in combination with the large size of the dataset should mean a low risk of future circulation states not being representable by the CTs from the historical period. We did however perform a test using the explained variation metric of Philipp et al. (2014) (their Section 8.1). If the future circulation would not be representable by the CTs computed from the historical period, there would be a reduction in the explained variation for the future period. Out of all GCM-RCM combinations, only three showed a reduction, and the largest reduction was only \(-0.004\) (\(-0.4\) percentage points). In fact, the median change in explained variation is \(+0.0056\), i.e. a small increase in explained variation in the future. Because we use the same CTs for the historical and future period, our analysis of future data is therefore focusing on changes in CT frequency.

Note that for the subjective classification method GWT, we do not use ASC, but rather classify all datasets separately, as justified in Stryhal and Huth (2019). GWT is a correlation-based method, while ASC uses Euclidian distance as default measure (we later learned that it is possible to use pattern correlation as an option). We tested the sensitivity to this by inconsistently applying ASC with Euclidian distance to CTs from the correlation-based GWT and observed that about 20% of the days were assigned to another class than the ones from the multi-millennial classification.

While we have produced results for all three methods, we choose to present results mainly from the SAN method because it has shown good results in other studies (Jacobeit et al. 2017; Stryhal and Huth 2019; Hansen and Belušić 2021). We also discuss the sensitivity of the results to the choice of method. We focus on 10 CTs, because (compared to a larger number of CTs) it gives more distinct CTs and therefore lower risk of misclassification. It also results in a more manageable number of figures and is easier to present the results and analyse visually. Results from other methods and number of CTs are available in the supplementary material.

3.1 Measures

The monthly occurrences of the circulation types from the simulations are of interest, and especially we want to compare these occurrences with those of the ERA5 reanalysis. We define the mean absolute error between the monthly frequency for a simulation and ERA5 as

$$\begin{aligned} {{\mathrm {MAE}}}_s= & {} \sum _{c = 1}^{n_{\mathrm {CT}}}\Bigg (\frac{1}{2n_{\mathcal {M}}} \sum _{m \in {\mathcal {M}}} \left| f_{\mathrm {model}}(s,c,m)\right. \nonumber \\&\left. - f_{{\mathrm {ERA5}}}({\mathrm {ERA5}},c,m)\right| \Bigg ), \end{aligned}$$
(1)

where m are the months in a season \({\mathcal {M}} \subseteq \) {Annual, DJF, MAM, JJA, SON} with \(n_{\mathcal {M}} = \{12,3,3,3,3\}\), f(s, c, m) is the monthly climatological (i.e. the multi-year monthly mean) frequency of a CT. Note that the number of days used when calculating the frequency \(f_{s,c,m}\) depends on which calendar the simulation has used (360/365/365.25 days per year). The division by 2 outside the innermost summation is used to avoid double-counting errors (otherwise when one day is classified incorrectly it would count as a positive bias in one CT and a negative bias in another CT). Finally, c is the CT (1 to \(n_c \in \{10, 18,27\}\)) and s specifies the simulation.

Each of the RCM and GCM models have several simulations, and we define the mean absolute error for a model as the mean of the mean absolute error for the simulations that corresponds to a given model:

$$\begin{aligned} {{\mathrm {MAE}}}_{{\mathrm {model}}} = \frac{1}{n_{{\mathrm {model}}}} \sum _{s = 1}^{n_{{\mathrm {model}}}} {{\mathrm {MAE}}}_s. \end{aligned}$$
(2)

Here, \(n_{{\mathrm {model}}}\) is the number of simulations to consider for that particular model (RCM or GCM).

To measure the spread of mean absolute errors for different simulations performed by the same model, we use the inter-quartile range, IQR, which is defined as the 75-percentile minus the 25-percentile:

$$\begin{aligned} IQR_{{\mathrm {model}}}=\, & {} P_{75\%}(\{{{\mathrm {MAE}}}_1,\ldots ,{{\mathrm {MAE}}}_{n_{{\mathrm {model}}}}\})\nonumber \\&-P_{25\%}(\{{{\mathrm {MAE}}}_1,\ldots ,{{\mathrm {MAE}}}_{n_{{\mathrm {model}}}}\}). \end{aligned}$$
(3)

We emphasise that the respective \(\text {MAE}_n\), for \( n={1,\ldots ,n_{{\mathrm {model}}}}\) are already climatological mean errors, so the IQR here is a measure of the spread of different simulations, and not the inter-annual variability within simulations.

4 Results and discussion

The circulation types are given by plotting the mean values of all simulation days associated with each circulation type and method. This is also referred to as centroid in the literature. CTs from SAN10 are shown in Fig. 3, and others in the supplementary material. Below we present the results related to the four research questions stated in Sect. 1.

Fig. 3
figure 3

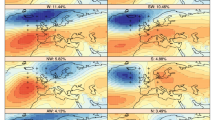
Centroids of anomalies (daily spatial mean subtracted) for each CT from SAN10. The mean frequencies in all 69 datasets are shown in parentheses. In the tables we additionally refer to some of these patterns according to their wind direction or characteristic pressure patterns: 1. south-westerly (SW), 2. weak north-westerly (NW), 3. west-northwesterly (WNW), 4. Iberian high (IbH), 5. Central-Eastern European high (CEH), 6. Scandinavian low (ScL), 7. weak, 8. south-southeasterly (SSE), 9. weak easterly (E), 10. strong west-southwesterly (WSW)

Full size image

4.1 Differences between GCM-RCM combinations

Fig. 4
figure 4

Annual distribution of method SAN with 10 circulation types for the historical period. The mean frequencies in all 69 datasets are shown in parentheses. ERA5 is shown as a black line. The ensemble mean of the models is shown as a red line, with the 25–75 percentile spread of the model ensemble shown as light red shading

Full size image

The annual distribution of CT frequencies with method SAN10 is presented in Fig. 4. Most model combinations follow ERA5 climatology rather well but a few exceptions can be noted. First of all, many simulations over-represent the frequency of the weak easterly flow of CT9 (in Fig. S2 in the Supplementary these can be identified as MIROC-MIROC5 (green) and CNRM-CERFACS-CNRM-CM5 (red) and MOHC-HadGEM2-ES (yellow, autumn only) and their downscaled simulations). They also show a corresponding under-representation of strong westerly flow (CT3 and CT10). Simulations based on NCC-NorESM1-M show (again in Fig. S2) a slightly opposite behaviour, with over-representation of the strong westerly flow (especially in the winter half of the year) of CT3 and CT10. We would have expected the too zonal storm tracks in CMIP5 models (described by e.g. Zappa et al. 2013) to show up as a negative bias in CT1, but that is only apparent for a few simulations. Though the model selection in Euro-CORDEX has not specifically been made to reduce this bias, it is unlikely that regional modellers choose GCMs with strong zonal biases, as it affects many climate variables, for example precipitation. The relatively small number of GCMs can possibly also make it easy to avoid GCMs with the worst biases.

Because of the large number of simulations, Figs. 4 and S2 are mainly useful to illustrate the general agreement of the ensemble, as well as for Fig. S2 to identify outliers in models or seasons. For more quantifiable results we therefore aggregated the mean absolute errors in CT frequencies (defined in Eq. 2) for the simulations relative to ERA5. These are presented in Table 1 for the whole year and within the seasons DJF, MAM, JJA and SON separately. The aggregation to GCMs and RCMs show that CCCma-CanESM2 r1 and MIROC-MIROC5 r1 have the largest errors, with more than 15% of days in all seasons in different CT than ERA5 climatology.

We compared the biases in Table 1 with the horizontal resolutions of the models,Footnote 4 hypothesising that coarser models would deviate more from reanalysis than finer ones. The MAE as a function of GCM resolution is shown in Fig. S1 in the supplementary material. The correlation values are larger for the winter (0.45) and spring (0.38) seasons. This can explain some of the results, as the model with finest resolution (ICHEC-EC-EARTH, 1.12 degrees) performs the best and the coarsest (CCCma-CanESM2 at 2.8 degrees) performs second worst. However, the worst model is in the middle resolution-wise (MIROC-MIROC5 at 1.4 degrees), and MPI-M-MPI-ESM-LR is second best in all seasons despite its somewhat coarser resolution (1.87 degrees), so this unsurprisingly does not explain all differences.

Table 1 Mean absolute error in frequency of occurrence (lower is better)
Full size table

4.2 Circulation changes after downscaling

When looking at the annual distributions of CT frequencies in Fig. 4 and in Table 1 in the previous section, it becomes clear that different models (both GCMs and RCMs) have different biases in circulation statistics relative to ERA5. Following the terminology used in e.g. Hawkins and Sutton (2009), the uncertainty in regional climate model simulations consists of a combination of model process uncertainty (due to e.g. different parameterisations) from the GCMs as well as from the RCMs, internal variability (e.g. phase of NAO), as well as scenario uncertainty for the future.

Fig. 5
figure 5

Mean absolute error of CT frequencies before (GCMs, shown as filled symbols) and after downscaling (RCMs, shown as letters A–K) for different seasons. The x axis shows the error relative to ERA5 and the y axis relative to the respective GCM. For example, a value of 0.1 means that \(10\%\) of the days in the multi-year climatologies are classified in a different CT (from ERA5 or GCM)

Full size image
Fig. 6
figure 6

Downscaling impact on mean absolute error of CT frequencies relative to ERA5 for different seasons. The RCMs are shown as letters A–K with the colour of the respective GCM. The black point is the mean value for the ensemble in both directions, and its coordinates are given below the season name. The x axis shows difference in error between the RCM error from ERA5 and its respective GCM’s error from ERA5. The y axis shows the mean absolute error from the respective GCM. For example, a value of 0.1 means that \(10\%\) of the days in the multi-year climatologies are classified in a different CT (from ERA5 or GCM)

Full size image

To illustrate the regional models’ process uncertainty we calculated the mean absolute error in CT frequency both before and after downscaling following Eq. 1. This is presented in Fig. 5. In Fig. 6, the difference between the MAE relative to ERA5 for the GCMs and their respective RCMs is calculated. In general, these figures show that the errors relative to ERA5 vary depending on the model combination, but also that there are simulations where the downscaling alters the circulation considerably.

The two GCMs which have multiple ensemble members, ICHEC-EC-EARTH and MPI-M-MPI-ESM-LR (individual members shown with different plot symbols) can be used to give a brief impression of the effect of internal variability, though limited due to the small number. Figure 5 shows that although the members from each GCM start out with quite similar biases relative to ERA5, the resulting downscaled results show a larger spread relative to ERA5. This spread (on the x axis) can sometimes even be larger (for example in summer with MPI-M-MPI-ESM-LR downscaled with SMHI-RCA4) than the differences between different GCMs. For more details on this we refer to Table S2 in the Supplementary material.

ICHEC-EC-EARTH is the best-performing global model for all seasons except winter, where MPI-M-MPI-ESM-LR and IPSL-IPSL-CM5A-MR are among the best. It should be noted that ICHEC-EC-EARTH is based on the same dynamical core as the ERA5 reanalysis (the IFS model), so ideally one could compare with other reanalysis as well. This is supported by Stryhal and Huth (2017) who compared 32 CMIP5 GCMs and five reanalyses and found that ICHEC-EC-EARTH has the smallest bias, and that it was smallest when compared to ERA-40 and ERA-20C. Brands (2021) used simulations from both CMIP5 and CMIP6 as well the two reanalyses ERA-Interim and JRA-55 and found that ICHEC-EC-EARTH performs among the best in both the CMIP5 and CMIP6 ensembles, and that they are closer to ERA-Interim than JRA-55.

The GCM MIROC-MIROC5 has the largest departure from ERA5 (rightmost on the x axis) in all seasons, and the downscaling with GERICS-REMO2015 (the green E on top) modifies the (JJA) circulation the most of all included simulations (uppermost on the y axis).

Altered circulation is in principle a good thing, as it means that the regional model is able to develop its own circulation, in particular in summer when the background flow is weak. Even though the downscaled results can be argued to be more realistic one may question if such a large alteration of circulation as seen with MIROC-MIROC5 is desirable (for MIROC-MIROC5 in summer \(\sim {}25\%\) of all days are classified in a different CT after downscaling with GERICS-REMO2015). In particular, a large alteration by the regional model poses a problem for the one-way nesting approach used in the CORDEX experiments. This assumes that the large-scale representation of the global model is not strongly altered by interaction with local scales represented by the regional model (e.g. Vautard et al. 2020). Breaking this assumption may invalidate the regional model setup, and lead to non-negligible inconsistencies in e.g. energy and water budgets between the global and regional model. Any large alteration for days with non-weak background flow would need to be fed back to the global model in a two-way (coupled) nesting approach.

Comparing the different seasons in Figs. 5 and 6, it is clear that the inter-model spread (excluding GCM+RCM combinations that utilise MIROC-MIROC5) is largest in summer. In winter, the regional models tend to follow the global models more closely (lines have short extent in the vertical), while in summer they are more spread out. This is in agreement with previous literature findings (e.g. Plavcová and Kyselý 2011; Sieck and Jacob 2016) and the stronger background flow (e.g. CT1 and CT3 during winter).

The regional model IPSL-WRF381P has the largest modifications for all GCMs where it is available. For the five simulations by IPSL-WRF381P, the error relative to ERA5 is increasing in 17 out of 20 GCM-season combinations (except in summer when downscaling MOHC-HadGEM2-ES and CNRM-CERFACS-CNRM-CM5 and in spring when downscaling ICHEC-EC-EARTH). This may be related to biases in the WRF model system, as discussed by Pontoppidan et al. (2019). von Trentini et al. (2019) also notes that many studies have excluded the IPSL-WRF model due to large biases in different variables.

Table 2 Added value in representation of circulation frequency distribution of the RCMs relative to ERA5
Full size table

Table 2 presents the ensemble fraction that show an improvement relative to ERA5 after downscaling. Here we can see a tendency that most RCMs improve the circulation representation in the summer season. This can possibly point to an added value of the regional models, in that their more detailed representation of surface processes (e.g. evaporation) and topographic features can improve also the larger-scale circulation statistics. The improvements are most of the time smaller than the spread among the simulations from the same model, with the exception of DMI-HIRHAM5 which has significant improvement in all seasons except spring.

Fig. 7
figure 7

Contribution of the error from different CTs, illustrated by the number of simulations (y axis) where the respective CT (x axis) has more than \(20\%\) of the total error

Full size image

In Fig. 7, we show which circulation types contribute more often to the error in the winter and summer seasons, based on the mean absolute error from ERA5 for all 68 simulations. In winter, CT1 and CT10 contribute most often, while in summer, CT2 and CT9 are the most common. These are among the top contributors to the error also before downscaling (see Supplementary Figs. S2 and S3).

Fig. 8
figure 8

Distribution of mean absolute error [fraction of days classified differently] for different CTs in winter (DJF) and summer (JJA). (−) indicates a significant reduction in error (mean below zero) after downscaling and (+) indicates significant increase in error (mean above zero). “( )” indicates no statistically significant change. The significance level used is 1%. The percentages show the fraction of ensemble members with mean change in absolute error (1) below zero and (2) above zero. For example, for CT8 there is a significant decrease in the error in the winter season and a significant increase in error in summer after downscaling

Full size image

Until now, we have seen how the downscaling alters the mean absolute error relative to ERA5 and the corresponding GCM aggregated over all CTs. Analysing the downscaling impact on the error of the 10 CTs separately, Fig. 8 shows that most CTs do not show a statistically significant change for the ensemble as a whole. There is however statistically significant reduction in bias for CT8 (south-southeasterly) in winter and CT9 (weak easterly) in summer, with 77% and 63% of the ensemble improving, respectively. There is also significant increase in bias for CT1 (south-westerly) in both seasons, CT2 (weak north-westerly) in winter and CT8 (south-southeasterly) in summer.

We would then like to know how the downscaling by specific models affects the statistics for specific CTs. If the alteration of the downscaling is small enough, the RCMs should mostly remain in the same CT as their corresponding GCM. However, with a large alteration as seen in by e.g. IPSL-WRF381P in Figs. 5 and 6, some days will be classified to other CTs than the one of the GCM.

Fig. 9
figure 9

Distribution of CTs after downscaling in season DJF. The different CTs are shown in the different panels (1–5 on the top row and 6–10 on the bottom row). The vertical axis shows the fraction of days which are classified as the same CT in the downscaled simulation as in the GCM. The 11 RCMs are shown as different bars (A–K) on the horizontal axis. Example: In the top left panel, the A bar (CLMcom-CCLM4-8-17) has a value of 0.8. This means that for all simulations with model A when its GCMs have CT1 before downscaling, the pressure patterns of model A produces the same CT1 in 80% of the cases

Full size image
Fig. 10
figure 10

Same as Fig. 9 for season JJA. CT1 and CT10 have below 1 day per month on average for all members during JJA (cf. Fig. 4) and are not shown

Full size image

To examine this, we start with selecting all days when a GCM is classified as a given CT. For example, the GCM CCCma-CanESM2 is, during winter (DJF), classified to CT1 a total of 916 times (19th of January 1950, 27th of January 1950, 28th of January 1950 and so on with the latest assignment the 27th of December 2005). Now we are interested in which CTs these 916 dates were classified to by the respective downscaled versions of the GCM, i.e. the RCMs CLMcom-CCLM4-8-17 (letter A) and GERICS-REMO2015 (letter E). These RCMs were classified “correctly” (in agreement with the GCM) to CT1 in 790 and 666 dates respectively, 86.2% and 72.7% of the 916 days. 78 and 119 dates were classified to CT10. The last 48 and 131 days were classified to other CTs: (4, 5, 6, 7, 8) for A and (4, 5, 6, 7, 8, 9) for E.

We repeat this task for all GCMs with their respective RCMs and CTs, and group the results into CTs (panels) and RCMs (columns) (resulting in Figs. S25 and S26 in the supplementary). For all CTs and GCMs with corresponding RCMs, we sum up and normalise so that a value of 1 on the vertical axis would mean that all days in the regional model are classified to the same CT as the global model. In addition, only frequencies above 1 days per month are shown.

Figures S25 and S26 are then summarised in Figs. 9 and 10. Here, the CTs before downscaling are shown, with RCMs on the horizontal axis and the agreement (fraction of days classified to the same CT in the downscaled simulation as the GCM) on the vertical axis. For most RCMs (bars A–K), the simulations remain in the same CT after downscaling in about 50–80% of the cases, and generally more often in winter than in summer. IPSL-WRF381P (column G) however has the lowest mean agreement, meaning that it alters the CT classification more often than any other model. The lowest value is from ICTP-RegCM4-6 (column F) for CT8 in summer, but this model is performing similar to the others for the winter season. From the resulting CT distributions (Supplementary Figs. S25 and S26), we see that the dates are mainly classified to CT5, CT7 and CT9, where the GCM MOHC-HadGEM2-ES (yellow colour) deviates most.

It is also worth noting that there is not a clear one-to-one relationship between the alterations, e.g. in winter, CT7 is most often changed to CT4, but CT4 is roughly equally probable to turn into CT3, CT7 and CT10, while CT10 does not turn into CT7 at all. This is evident from looking at the patterns in Fig. 3, where CT7 has rather weak gradients, and therefore may mean that the influence from the global model has shorter reach from the boundary, in turn allowing the regional model to develop internal circulation more freely. One should, however, be careful in interpreting too much about causality from Figs. S25 and S26.

4.3 Future climate scenario changes

As described in Sect. 3, we have applied the assign method to the simulations for the future scenarios RCP8.5 (57 members) and RCP4.5 (21 members). The temporal evolution of seasonal occurrence of each CT is shown in Figs. 11 (DJF) and 12 (JJA). It is clear that ERA5 is outside the 25–75% spread for many of the classes, though one must also remember that there is only one realisation of historical weather, meaning that inter-annual variability plays a great role. Many CTs also exhibit multi-decadal oscillations, which are averaged out in our MAE analysis. Climate model simulations are not expected to reproduce circulation statistics on a year-to-year basis, so we decided to use the full ERA5 period (1950–2020) for all regional model simulations regardless of their simulation length. It is possible that the simulations which start in 1970 (13 out of 57 regional simulations in the ensemble) may appear more biased due to phases in decadal variability and shorter sampling period. There are also trends in the ERA5 CT frequencies. The strongest trend in ERA5 is the increase in CT5 (Central-Eastern European high) in summer, which is opposite to the weak reduction shown by the regional climate model ensemble. It should be noted that the pressure gradients in this CT is rather weak and is therefore more sensitive to small differences.

For changes into the future, we compared the frequencies in the years 1971–2000 and 2071–2100 for each model in a two-sided t-test with \(p<0.05\) and summarise the results in Table 3. Changes in frequency are mostly found in the summer season, with a statistically significant increase in CT2 (north-westerly flow) for 49% of the ensemble members and decreases in CT5 (Central-Eastern European high, \(79\%\) of the ensemble), CT6 (Scandinavian low, \(61\%\)) and CT8 (south-southeasterly, \(58\%\)). The last column in the table shows that there is in general a high agreement on sign between RCMs and their corresponding boundary GCM, with higher agreement in the winter season. It is worth noting that Figs. 11 and 12 use a 20-year moving average, which means that inter-annual variability is not displayed. This implies that while for instance CT3 in winter seems to have a positive trend for multiple simulations, only \(14\%\) of the ensemble members have a statistically significant increase from the t-test (which does not use the moving average).

Comparing the two different scenarios RCP4.5 and RCP8.5, the winter season is mostly dominated by multi-decadal variability, and no clear trends are visible in the ensemble means. In the summer season, trends in ensemble means have the same signs for both scenarios, with RCP8.5 unsurprisingly showing larger change than RCP4.5 (in particular CT5 and CT6 but also CT2 and CT8). As a small bonus, the historical period can be used to briefly illustrate the effect of ensemble size, because the 21 ensemble members of the historical period (dashed blue line) are a subsample of the 57 member ensemble (red line). In the first 20 years (1950–1969), the agreement is lower, which is likely due to the fact that some model simulations (by ICTP-RegCM4-6 and SMHI-RCA4) begin in 1970, resulting in ensemble sizes of 15 and 45 for RCP4.5 and RCP8.5, respectively, for this period. After 1970, the ensemble means are following closely, indicating that ensemble mean circulation statistics are robust already with the smaller sample of 21 members. Further sensitivity analysis with even smaller subsets could be conducted systematically, for example when there are computational restrictions necessitating an even smaller subset, such as for convection-permitting modelling, but such an analysis is outside the scope of this study.

Since we have subtracted the field mean anomaly we disregard changes in the mean pressure field in the domain. There can still be changes within each circulation type over time, for example with regards to position of high and low pressure centres. Circulation type classification may not be the ideal method to deal with this, and could be supplemented with methods for tracking the position of individual pressure centres, e.g. using band pass filtering, which could be the subject of a different investigation.

Fig. 11
figure 11

Frequencies (days per season, on y axis) of CTs 1–10 for the DJF season years 1950–2100 (on x axis, consisting of historical simulation followed by RCP8.5) for the different simulations. ERA5 is shown as a black line. A 20-year moving average is applied when drawing the lines. The ensemble mean of all historical+RCP8.5 simulations are shown as a solid red line. The 25–75 percentile spread of the RCP8.5 ensemble is shown as light red shading. In addition, the ensemble mean of the smaller RCP4.5 ensemble is shown as a dashed blue line. Classification method used is SAN10

Full size image
Fig. 12
figure 12

Same as Fig. 11 but for the JJA season. CTs 1 and 10 have very low frequencies (less than 1 day per month) and are not shown

Full size image
Table 3 Future changes in seasonal frequency (DJF on top and JJA below) for the 10 CTs of SAN10
Full size table

4.4 Sensitivity to choice of classification method

We initially performed the study with three methods: GWT, DKM and SAN, but the resulting CTs of DKM and SAN were virtually identical. (The CTs from SAN10 and DKM10 are shown in Fig. 3 and Supplementary Fig. S3, respectively, but note the different order of CTs.) Consequently the statistics were also very similar, so we have chosen to only present a limited selection of results in the supplementary material.

We wanted to investigate the sensitivity of the MAE values to the choice of method and number of classes. This is shown in Fig. 13. First we note that the results from DKM and SAN are very similar, which is to be expected due to the similarity of the CTs. Secondly, there is a clear difference between the DJF and JJA seasons, with SAN and DKM showing considerably smaller errors in the summer season, while GWT is more consistent over the year. This could be because our classification was performed for the whole year, and since CT1 and CT10 are not present in the summer season, the effective number of CTs which the days can be classified to is lowered, and thus we have a smaller potential for misclassification. Since GWT uses predefined CTs, this method is not affected by this. Unsurprisingly, a higher number of CTs yield lower absolute errors due to the fewer number of days in each class.

Just like in Table 3 for SAN10, we also analysed changes in seasonal frequency of the CTs for method GWT10. This is presented in Supplementary Table S3. As expected from the SAN10 results, the summer season shows the largest change. For GWT10 the summer season in the future scenario sees an increase in frequency of the northwesterly and northerly CTs (53% and 37% of the ensemble, respectively) and a decrease in southwesterly, southerly and cyclonic patterns (39%, 53% and 37% of the ensemble, respectively).

The results shown in Fig. 5 can be further aggregated to the different RCMs and GCMs and sorted in order of increasing MAE. This is presented in Supplementary Table S3 and S4 (DJF and JJA, respectively) for all three methods (SAN, DKM and GWT) and the three different number of classes (10, 18 and 27). In terms of model ranking we can conclude that the results are similar for the different methods, and that the number of classes has a larger impact than the choice of classification method.

Fig. 13
figure 13

Distribution of the MAE values (x axis) for all 57 RCM simulations and all CTs, but for three different methods (DKM, GWT and SAN, in colours), three different number of classes (10, 18 and 27, shown as different panel rows) and two seasons (DJF and JJA, shown as panels in the horizontal). Note that all CTs are used as individual data points, instead of summed up as in Fig. 5, which explains the different magnitude of the MAE values

Full size image

For most GCMs the GWT10 method produces the smallest errors. This is especially visible in the timeseries plots for GWT10 (Figs. S27 and S28), where the frequencies in the model ensemble are much closer to ERA5. This can partly be explained by GWT utilising a predefined set of CTs. For this particular domain and/or set of models, as shown in Fig. S1 in the supplementary, this results in a very high fraction of the data being classified as the westerly CT1 (\(21\%\)) or southwesterly CT2 (\(18\%\)), which reduces the possibilities for misclassifications overall. In contrast, the CTs produced by SAN10 may have this fraction of the data (\(21\%+18\%\)) spread over a larger number of CTs. From Fig. 3 we can speculate about CTs 1, 3, 4, 10 and possibly 6, but we have not performed a more detailed analysis on how specific days distribute to specific CTs in the different methods.

While having a higher number of somewhat similar CTs increases the risk of misclassification, it does enable a more detailed evaluation. Depending on the focus of the study one can therefore argue that the CTs produced by either GWT or SAN/DKM are more suitable, and that the user should carefully weigh the benefits of each set of CTs.

5 Summary and conclusion

We applied circulation type classification to 57 regional climate model simulations from the Euro-CORDEX ensemble and their 11 corresponding global climate model simulations from CMIP5, as well as the ERA5 reanalysis. We focus on the circulation within the domain and therefore removed the domain-wide mean pressure for each day and simulation separately. In terms of added value, we have shown that dynamical downscaling improves the representation of large-scale circulation in summer, but also in other seasons for several model combinations.

We found that most simulations produce the seasonality of the circulation types quite well, but that some models have large biases. In particular, easterly flow is over-represented and the westerly flow is under-represented by the GCMs MIROC-MIROC5 and CNRM-CERFACS-CNRM-CM5 and with their respective downscaled simulations. Simulations based on ICHEC-EC-EARTH and MPI-M-MPI-ESM-LR show most consistent good results for all seasons. Comparing before and after downscaling, most regional model results remain in the same CT as the boundary data from the global model. A notable exception is IPSL-WRF381P which changes the circulation more often than any other of the included RCMs.

We found that the dynamical downscaling performed by some model combinations have considerable negative impact on the error relative to ERA5. This finding has implications for users of regional model data, such as climate services, in that one cannot take it for granted that a good representation of circulation in the global model means that it is also good in the regional model. This also means that it may not be enough to perform an analysis of large-scale circulation for the GCM data, but that it may need to be performed for the RCM as well.

Under the high future greenhouse gas concentration scenario RCP8.5, many simulations show statistically significant changes in CT frequency by the end of the 21st century for the summer season. The agreement is largest for increase in frequency of north-westerly flow and decrease of Central-Eastern European high, Scandinavian low as well as south-southeasterly flow. The regional models usually preserve the sign of change in frequency from the global model (\(>70\%\) agreement for 7 out of 10 CTs and \(>60\%\) for all CTs).

Our results are not particularly sensitive to choice of circulation classification method and the regional models appear in very similar order (sorted by error relative to ERA5) regardless of choice of method and number of CTs.

In our analysis of future scenario simulations, we limited ourselves to the annual frequency. One could imagine that some circulation types may shift their occurrence from one season to another. It could also be interesting to use the same method to explore circulation changes in regional climate model ensembles in other regions. While none of the other CORDEX domains currently have as many members (or as fine spatial resolution) as the Euro-CORDEX ensemble, other regions have other dominant circulation features, such as for example the South East Asian monsoon, or the circumpolar circulations of the Arctic and Antarctic. It will also be exciting to see what new regional simulations downscaled from CMIP6 will bring.