Third-order sparse grid generalized spectral elements on hexagonal cells for uniform-speed advection in a plane

Abstract

This paper investigates sparse grids on a hexagonal cell structure using a Local-Galerkin method (LGM) or generalized spectral element method (SEM). Such methods allow sparse grids to be used, known as serendipity grids in square cells. This means that not all points of the full grid are used. Using a high-order polynomial, some points of each cell are eliminated in the discretization, and thus saving Central Processing Unit (CPU) time. Here a sparse SEM scheme is proposed for hexagonal cells. It uses a representation of fields by second-order polynomials and achieves third-order accuracy. As SEM, LGM is strictly local for explicit time integration. This makes LGM more suitable for multiprocessing computers compared with classical Galerkin methods. The computer time depends on the possible timestep and program implementation. Assuming that these do not change when going to a sparse grid, the potential saving of computer time due to sparseness is 1:2. The projected CPU saving in 3-D from sparseness is by a factor of 3:8. A new spectral procedure is used in this paper, called the implied spectral equation (ISE). This procedure allows for some collocation points to use any finite difference scheme of high order and the time derivatives of other spectral coefficients are implied.

Appendix 1

1.1 A system of indices for second-order hexagonal cells creating a compact grid representation and the 1-D grids for plane waves

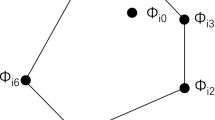
This appendix introduces an alternative system of indices to that used in Sects. 2 and 3. The grid is shown in Fig. 12 and it differs from Fig. 1 by assigning different numbers to the points. Each point has two indices i and k, where i indicates the hexagon and k indicated the position of a point within the hexagon. k = 0 indicates the center point of the hexagonal cell. The index i can be a structured index i = (i′, j′) (i′, j′ = 0, 1, 2, 3, …) or unstructured. The structured case is shown in Fig. 12, where the grids and their center points are indicated by the double index (i’, j’). The advantage of a structured grid notation is that neighboring grids are always known. For example, in Fig. 12 the cell (i′, j′+ 1) is always above the cell (i′, j′). Our definition can also be applied to the unstructured grid case. In the unstructured case a list is needed indicating the six neighbouring hexagons to the hexagon i. The grid based compact grid pointed out in the following can be used with structures and unstructured index i, where Fig. 12 refers to the structured case i = (i′, j′).

Fig. 12

As Fig. 1 except that with new indices creating a compact grid. Black points and points with thick circles are dynamic points, those with thin circles are diagnostic points. The points shown in black are the points for compact representation. They do not belong to any other hexagon and each dynamic point appears as a compact point of some hexagons

Let the side length of the hexagon be s. For the corner nodes ${\mathbf{r}}_{i,k}$ (k = 1, 3, 5, 7, 9, 11) we have

$$ {\mathbf{r}}_{i,k} = {\mathbf{r}}_{i,0} + \left( {s \cdot \cos \left( {\pi + \left( {k - 1} \right)\tfrac{\pi }{3}} \right),s \cdot { \sin }\left( {\pi + \left( {k - 1} \right)\tfrac{\pi }{3}} \right)} \right) $$

(27)

The edge nodes k = 2, 4, 6, 8, 12 are obtained by

$$ {\mathbf{r}}_{i,k} = {\mathbf{r}}_{i,k - 1} + \tfrac{\sqrt 3 }{2}\left( {s \cdot \cos \tfrac{\pi }{3},s \cdot { \sin }\tfrac{\pi }{3}} \right) $$

(28)

For the diagnostic inner points k = 13 to 18, we have

$$ \begin{aligned} {\mathbf{r}}_{i,k} & = {\mathbf{r}}_{i,0} + \tfrac{1}{2}\left( {s \cdot \cos \left( {\pi + \left( {2k - 25 - 1} \right)\tfrac{\pi }{6}} \right),s \cdot { \sin }\left( {\pi + \left( {2k - 25 - 1} \right)\tfrac{\pi }{6}} \right)} \right) \\ & = {\mathbf{r}}_{i,0} - \tfrac{1}{2}\left( {s \cdot \cos \left( {\tfrac{k - 1}{3}\pi } \right),s \cdot { \sin }\left( {\tfrac{k - 1}{3}\pi } \right)} \right) \\ \end{aligned} $$

(29)

The full grid consists for each i of all points k = 0 to 18. The points numbering 13, 14, 15, 16, 17, 18 are unused in the sparse grid. The sparse grid collocation therefore consists of the points i, k (k = 0 to 12) which are the mid-point k = 0 and points on the boundary. The sparse grid is redundant, as all points with k > 0 belong to more than one hexagon. For example in Fig. 12, the point 9_i′,j′, is also point 1_{i′+1,j′+1} and 5_i′,j′+1. The point 10_i′,j′ belongs only to one other hexagon: i′, j′+ 1. These redundant points of the collocation grid can be used to represent discontinuous functions.

The index is defined with respect to the orthogonal basis ${\mathbf{i}}_{s}$ and ${\mathbf{j}}_{s}$ shown in Fig. 12. This method of indexing is suitable for model areas being approximately square. A rhomboidal area can be achieved by changing the definition of the basis ${\mathbf{i}}_{s}$ and ${\mathbf{j}}_{s}$ shown in Fig. 12.

It was shown by Steppeler (1979) that the anisotropy of the square grid can lead to the deformation of structures, such as the destruction of the symmetry of a circular wave. It may be useful to show the connection to 1-D discretizations. In Fig. 13, two vectors ${\mathbf{n}}_{1}$ and ${\mathbf{n}}_{2}$ are given and for each of these directions grid lines are shown in Fig. 13b, c which meet hexagonal grid points and thus determine a 1-D grid. Figure 13 shows the lines and the 1-D grids created by them. ${\mathbf{n}}_{1}$ and ${\mathbf{n}}_{2}$ form a 30° angle. The situation is similar as with square grids, where two 1-D grids are generated by lines forming a 45° angle. For square grids, the implied grids have grid lengths of dx in x direction and for the 45° line the grid length $dx' = \tfrac{dx}{\sqrt 2 }$. For the square the grids seen by a plane wave in the direction of either x or the diagonal are all the same, as each line determines the same grid.

Fig. 13

Two examples of lines resulting in 1-D grids for two directions. The combined grid which is seen by a plane wave in the directions of the arrows ${\mathbf{n}}_{1} = \left( {\cos 60^\circ ,\sin 60^\circ } \right) = \left( {\tfrac{1}{2},\tfrac{\sqrt 3 }{2}} \right)$ and ${\mathbf{n}}_{2} = \left( {\cos 30^\circ ,\sin 30^\circ } \right) = \left( {\tfrac{\sqrt 3 }{2},\tfrac{1}{2}} \right)$ is shown in (d) and (e)

For 1-D grids in the direction of ${\mathbf{n}}_{1}$ generated by hexagonal grids, three types of irregular grid appear, shown in Fig. 13b. A plane wave in the directions ${\mathbf{n}}_{1}$ or ${\mathbf{n}}_{2}$ sees one of the two grids (Fig. 13d, e). They have the average resolution dx′ ($\tfrac{3}{8}s$ for Fig. 13d and $\tfrac{\sqrt 3 }{4}s$ for Fig. 13e). This is of higher resolution than each of the original grids shown in Fig. 13b, c. It has also a higher resolution than the underlying regular square grid of resolution $\tfrac{1}{2}s$. For the gradients of the fluxes at corner points in ${\mathbf{n}}_{1}$ or ${\mathbf{n}}_{2}$ direction, the o2o3 scheme proposed in this paper uses one-sided derivatives and averages them over the three directions shown in Fig. 5. For a structure being smooth in the direction vertical to ${\mathbf{n}}_{1}$ or ${\mathbf{n}}_{2}$, the derivative at one point uses points forming a different grid for each of the lines indicated in Fig. 13. Thus, the resolution of a plane wave is that of the 1-D grids shown in Fig. 13d, e. The irregularity of the plane wave grids is of a small scale which means that while some points are near to each other, they have large differences in grid length. The pattern of small and larger grid lengths repeats itself. These grids have a higher resolution than the plane wave grids for the square.

It was shown by Steppeler and Klemp (2017) for the example of centered differences that such small-scale irregularity gives a quality of simulation corresponding to the average grid length. It can be seen that the average grid for plane waves is smaller than the grid used on the hexagonal sides. The values of the average grids given above should be compared to those corresponding to the square grid. For the square grid, we obtain $\tfrac{s}{2}$ and $\tfrac{s}{2\sqrt 2 }$ for the averaged resolutions in two directions. The relation of the two grids is 1.17 for the hexagon and 1.47 for the square. These numbers are a measure of the isotropy of the grid, which is higher for hexagons. The maximum plane wave grid length is also smaller for the hexagon (0.433 s) than for the square (0.5 s). The maximum of the two grids for different directions of plane waves is the resolution of the scheme. A small resolution in just one direction is not useful except for the case that the nature of the solution requires a deformed grid.

The indices of the inherent 1-D grids and their computation from the hexagonal indices can be seen from Fig. 13b, d or c, e. The hexagonal version of the grid for the method o3o3 (Steppeler et al. 2019) is obtained from the o2o3 hexagonal grid by having four instead three points on each edge and the center point no longer carries an amplitude.