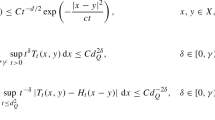Abstract
We study Hardy spaces associated with a general multidimensional Bessel operator \(\mathbb {B}_\nu \). This operator depends on a multiparameter of type \(\nu \) that is usually restricted to a product of half-lines. Here we deal with the Bessel operator in the general context, with no restrictions on the type parameter. We define the Hardy space \(H^1\) for \(\mathbb {B}_\nu \) in terms of the maximal operator of the semigroup of operators \(\exp (-t\mathbb {B}_\nu )\). Then we prove that, in general, \(H^1\) admits an atomic decomposition of local type.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\nu = (\nu _1, \ldots ,\nu _d) \in \mathbb {R}^d\), \(d\ge 1\), and consider the multidimensional Bessel differential operator
acting on functions on \(\mathbb {R}_+^d=(0,\infty )^d\). Operator \(\mathbb {B}_\nu \) is formally symmetric in \(L^2(\mathbb {R}_+^d, d\mu _\nu )\), where
1.1 Hardy spaces associated with the classical Bessel operator
When \(\nu \in (-1, \infty )^d\) there exists a classical self-adjoint extension of \(\mathbb {B}_\nu \) (acting initially on \(C_c^2(\mathbb {R}_+^d)\)), from now on denoted by \(\mathbb {B}_\nu ^\mathrm{{cls}}\) [16, 19]. The operator \(\mathbb {B}_\nu ^\mathrm{{cls}}\) is the infinitesimal generator of the classical Bessel semigroup of operators \(\mathbb {W}_{t,\nu }^\mathrm{{cls}} = \exp (-t \mathbb {B}_\nu ^\mathrm{{cls}})\), which has the integral representation \(\mathbb {W}_{t,\nu }^\mathrm{{cls}} f(x) = \int _{\mathbb {R}_+^d} \mathbb {W}_{t,\nu }^\mathrm{{cls}}(x,y) f(y) \, d\mu _\nu (y)\), \(t>0\). It is well known that
for \(x,y\in \mathbb {R}_+^d\) and \(t>0\), where \(I_\tau \) denotes the modified Bessel function of the first kind and order \(\tau > -1\), cf. [26]. The classical Bessel kernel satisfies the lower and upper Gaussian bounds, i.e.
with some constants \(c_1,c_2, C_1, C_2 >0\), where \(B(x,\sqrt{t}) = \left\{ y\in \mathbb {R}_+^d \ : \ |x-y| < \sqrt{t} \right\} \).
Recently, harmonic analysis related to the classical Bessel operator has been extensively developed, see e.g. [1,2,3,4,5,6, 8, 12, 14, 19, 20] and references therein. In particular, the Hardy space
associated with \(\mathbb {B}_\nu ^\mathrm{{cls}}\) and its characterizations have been studied. An especially useful result is the characterization of \(H^1(\mathbb {B}_\nu ^\mathrm{{cls}})\) by atomic decomposition, which was proved in [5] in the one-dimensional case and then extended to higher dimensions in [12]. This atomic characterization also follows from a more general result from [11]. This result states, in particular, that every function \(f\in H^1(\mathbb {B}_\nu ^\mathrm{{cls}})\) can be represented as \(f = \sum _k \lambda _k a_k\), where \(\sum _k \left| \lambda _k \right| \simeq \left\| f \right\| _{H^1(\mathbb {B}_\nu ^\mathrm{{cls}})}\) and \(a_k\) are the classical atoms on the space of homogeneous type \((\mathbb {R}_+^d, |\cdot |, d\mu _\nu )\), that is there exist balls \(B_k\) such that
We say that the atoms \(a_k\) satisfy localization, size and cancellation conditions [9].
The main goal of this paper is to prove an atomic decomposition theorem for the Hardy space associated with the multidimensional Bessel operator \(\mathbb {B}_\nu \) in the general situation, admitting all \(\nu \in \mathbb {R}^d\). For a precise definition of the operator \(\mathbb {B}_\nu \) see in Sect. 1.3. According to the best of the author’s knowledge the theory of Hardy spaces for the Bessel operator for the full range of the parameter has never been studied. The most general results are known for \(\nu _j > -1\), and a vast majority of them are restricted to \(\nu _j\ge -1/2\), \(j=1,\ldots ,d\). Our atomic decomposition theorem is a starting point for developing this theory in a general Bessel context and the first step towards proving other characterizations of \(H^1(\mathbb {B}_\nu )\). Note that one of the difficulties in the general situation is that the measure is not locally finite, in particular it does not satisfy the standard doubling condition. Theory of Hardy spaces or Calderón-Zygmund operators for spaces with non-doubling measure is far more difficult and less known. It has been developed only quite recently, see e.g. [17, 18, 23, 24, 27]. Usually an essential assumption in this theory is the polynomial growth condition \(\mu (B(x,r)) \le C r^n\). But this condition fails for \(\mu _\nu \) unless \(\nu \in (-1,\infty )^d\), since otherwise there are balls of arbitrarily small radius and infinite measure. For the same reason, our measure does not satisfy the property known in the literature as a local doubling condition, considered for instance in [7]. Another obstacle is that, in general, operators considered in the literature are generators of semigroups of operators whose integral kernels satisfy the upper Gaussian bounds. This is not the case of \(\mathbb {B}_\nu \) if \(\nu \notin (-1,\infty )^d\). Nevertheless we overcome these difficulties and give an atomic decomposition of the Hardy space associated with the general multidimensional Bessel operator \(\mathbb {B}_\nu \) for any \(\nu \in \mathbb {R}^d\).
1.2 The exotic Bessel operator
Recall that \(d\mu (x) = x^{2\nu +1} dx\). When we take \(\nu \in ((-\infty ,1){\setminus }\left\{ 0 \right\} )^d\) in (1.1), then there exists a self-adjoint extension of \(\mathbb {B}_\nu \), denoted by \(\mathbb {B}_\nu ^\mathrm{{exo}}\) and called the exotic Bessel operator [19]. It is quite remarkable that for the parameter \(\nu \in ((-1,1){\setminus }\left\{ 0 \right\} )^d\) there exist both, the classical and the exotic, self-adjoint extensions of \(\mathbb {B}_\nu \), which differ significantly. We denote by \(\mathbb {W}_{t,\nu }^\mathrm{{exo}}= \exp (-t\mathbb {B}_\nu ^\mathrm{{exo}})\) the semigroup of operators generated by \(\mathbb {B}_\nu ^\mathrm{{exo}}\). It is known that the exotic semigroup kernel can be expressed in a simple way in terms of the classical one, namely
It turns out that if \(0<\nu _j<1\) then the so-called pencil phenomenon occurs. In the one-dimensional situation this means that for any fixed \(t>0\) the operator \(W_{t,\nu _j}^\mathrm{{exo}}\) is well defined on \(L^p(\mathbb {R}_+,d\mu _{\nu _j})\) and maps this space into itself if and only if \(\nu _j+1<p<(\nu _j+1)/\nu _j\). Therefore there is no reason in studying the theory of Hardy spaces for the exotic Bessel operator in the case \(\nu \in (0,1)^d\). For more details see the discussion in [19, Sec. 4] or in [4]. Thus, from now on we shall consider the operator \(\mathbb {B}_\nu ^\mathrm{{exo}}\) only for \(\nu \in (-\infty ,0)^d\).
For the sake of convenience we shall write \(\mathbb {B}_{-\nu }^\mathrm{{exo}}\), where \(\nu \in (0,\infty )^d\). Hence, we will use such notation in the rest of the paper.
1.3 Main results
We consider a general multidimensional Bessel operator \(\mathbb {B}_\nu =L_1 +\cdots + L_d\), \(d\ge 1\), where each \(L_i\) is either one-dimensional classical Bessel operator \(B_{\nu _i}^\mathrm{{cls}}\) for \(\nu _i\in (-1,\infty )\) or one-dimensional exotic Bessel operator \(B_{-\nu _i}^\mathrm{{exo}}\) for \(\nu _i \in (0,\infty )\) (acting on the ith coordinate variable, see Sect. 4.1 for details). Since \(B_{\nu _i}^\mathrm{{cls}}\) and \(B_{-\nu _i}^\mathrm{{exo}}\) are self-adjoint operators, \(\mathbb {B}_\nu \) is well defined and essentially self-adjoint [21, Thm. 7.23]. To simplify the notation, by changing the coordinates, we shall consider \(\mathbb {B}_\nu = \mathbb {B}_{\nu _c}^\mathrm{{cls}} + \mathbb {B}_{-\nu _e}^\mathrm{{exo}}\), where \(\nu =(\nu _c,-\nu _e)\in (-1,\infty )^{d_1}\times (-\infty ,0)^{d_2}\) and \(d_1+d_2=d\). Then
As we mentioned above, the case \(d_1\ge 1\) and \(d_2=0\), that is the classical case, is well known and slightly different from the context involving the exotic Bessel operator. Therefore we will consider \(d_1\ge 0\) and \(d_2\ge 1\).
Denote by \(\mathbb {W}_{t,\nu } = \exp (-t\mathbb {B}_\nu )\) the semigroup of operators generated by \(\mathbb {B}_\nu \). Clearly, the semigroup \(\mathbb {W}_{t,\nu }\) has the integral representation
where
We define the Hardy space for the operator \(\mathbb {B}_\nu \) by means of the maximal operator associated with the semigroup of operators \(\left\{ \mathbb {W}_{t,\nu } \right\} \),
We will prove that elements of \(H^1(\mathbb {B}_\nu )\) have an atomic decomposition, where atoms are either classical atoms (1.4) or some additional atoms of the form \(\mu _\nu (Q)^{-1}\mathbb {1}_Q\) for some cube \(Q\subset \mathbb {R}_+^d\). Such atoms \(\mu _\nu (Q)^{-1}\mathbb {1}_Q\) are called ”local atoms” and notice that they do not satisfy cancellation condition. More precisely, we will show that every function \(f\in \) \(H^1(\mathbb {B}_\nu )\) belongs also to the local atomic Hardy space \(H^1_\mathrm{{at}}(\mathcal {Q}, \mu _\nu )\) associated with some family of cubes \(\mathcal {Q}\) in \(\mathbb {R}_+^d\). That means that f can be decomposed into a sum \(f=\sum _{k} \lambda _k a_k\), where \(\sum _k |\lambda _k| < \infty \) and \(a_k\) are either classical atoms described in (1.4) and supported in cubes \(Q\in \mathcal {Q}\) or atoms of the form \(a_k = \mu _\nu (Q)^{-1}\mathbb {1}_Q\), \(Q\in \mathcal {Q}\).
For the general Bessel operator \(\mathbb {B}_\nu \) let us define the family of cubes \(\mathcal {Q}_{\mathbb {B}}\) which arises as follows. Let \(\mathcal {D}=\left\{ [2^n,2^{n+1}] \ : \ n\in \mathbb {Z} \right\} \) be the collection of all closed dyadic intervals in \(\mathbb {R}_+\). Consider a family \(\left\{ \mathbb {R}_+^{d_1}\times Q_1\times \cdots \times Q_{d_2}: Q_i \in \mathcal {D} \right\} \). Then tile each cylinder \(\mathbb {R}_+^{d_1}\times Q_1\times \ldots \times Q_{d_2}\) with countably many cubes having diameters equal to the smallest of the diameters of \(Q_1,\ldots ,Q_{d_2}\). The family \(\mathcal {Q}_{\mathbb {B}}\) consists of all of these smaller cubes. For a rigorous definition of \(\mathcal {Q}_{\mathbb {B}}\) see Sect. 4.
The main result of this paper is the following.
Theorem 1.1
Let \(d_1\ge 0\), \(d_2\ge 1\). Assume that \(\nu _c \in (-1,\infty )^{d_1}\) and \(\nu _e\in (0,\infty )^{d_2}\). Then \(H^1(\mathbb {B}_{\nu _c}^\mathrm{{cls}} + \mathbb {B}_{-\nu _e}^\mathrm{{exo}})\) and \(H^1_\mathrm{{at}}(\mathcal {Q}_{\mathbb {B}}, \mu _\nu )\) are isomorphic as Banach spaces.
In the proof we will use only general properties of \(\mathbb {B}_{\nu _c}^\mathrm{{cls}}\) and \(\mathbb {B}_{-\nu _e}^\mathrm{{exo}}\), therefore some auxiliary results in Sects. 3 and 4 will be formulated in a more general context. Moreover, we introduce universal conditions on a semigroup kernel so that the product case can be deduced from a lower-dimensional information. The methods we use have roots in [15], however in that paper the Lebesgue measure case is considered, and here we need to adapt them to our situation, which requires some effort.
1.4 Organization of the paper
Section 2 contains definitions and notation used in the paper. Also, some auxiliary results are proved there. In Sect. 3 we consider a general self-adjoint and nonnegative operator L, which generates a semigroup of operators possessing an integral representation. We present general assumptions on the semigroup integral kernel and some family of cubes that are sufficient to prove an atomic decomposition of local type for \(H^1(L)\). Section 4 is devoted to a similar atomic characterization in a product situation. More precisely, we slightly generalize conditions from Sect. 3 and show that if (lower-dimensional) component operators \(L_1,L_2\) satisfy them, then the operator \(L=L_1+L_2\) also does. Hence, one may deduce the result for the sum of operators by checking “one-dimensional” conditions. Finally, in Sect. 5, we prove Theorem 1.1.
Throughout the paper we use standard notation. In particular, C and c at each occurrence denote some positive constants independent of relevant quantities. Values of C and c may change from line to line. Further, we write \(\alpha \simeq \beta \) if there exists a positive constant C, independent of significant quantities, such that \(C^{-1} \alpha \le \beta \le C \alpha \).
2 Preliminaries
2.1 Notation and terminology
We consider the metric measure space \((\mathbb {R}_+^d, |\cdot |, d\mu _{\nu })\), where \(|\cdot |\) stands for the standard Euclidean metric. It is well known that if \(\nu \in (-1,\infty )^d\), then \(\mu _\nu \) possesses the doubling property, i.e. there exists \(C>0\) such that
where \(B(x,r) = \left\{ y\in \mathbb {R}_+^d \ : \ |x-y| < r \right\} \).
Since both the space and the measure have product structure, it is convenient to use cubes and cuboids rather than balls. Thus denote by
the cuboid centered at \(z\in \mathbb {R}_+^d\) having axial radii \(r_1,\ldots ,r_d >0\). When \(r_1=\ldots =r_d=r\) the cuboid becomes a cube which we denote briefly by Q(z, r). We denote by \(d_Q\) the Euclidean diameter of a cuboid Q.
Definition 2.1
We call a family \(\mathcal {Q}\) of cuboids in \(\mathbb {R}^d\) an admissible covering if there exist \(C_1, C_2 >0\) such that:
-
1.
\(\mathbb {R}_+^d = \bigcup _{Q\in \mathcal {Q}} Q\),
-
2.
if \(Q_1, Q_2 \in \mathcal {Q}\) and \(Q_1\ne Q_2\) , then \(\mu _\nu (Q_1\cap Q_2) = 0\),
-
3.
if \(Q = Q(z;r_1,\ldots ,r_d)\in \mathcal {Q}\), then \(r_i\le C_1 r_j\) for \(i,j \in \left\{ 1,\ldots ,d \right\} \),
-
4.
if \(Q_1, Q_2 \in \mathcal {Q}\) and \(Q_1 \cap Q_2 \ne \emptyset \), then \(C_2^{-1} d_{Q_1} \le d_{Q_2}\le C_2 d_{Q_1}\).
Observe that item 3 means that admissible cuboids are uniformly bounded deformations of cubes. In fact, we shall often use only cubes. From now on we always assume that \(\mathcal {Q}\) is an admissible covering of \(\mathbb {R}_+^d\).
Given a cuboid Q, by \(Q^*\) we denote a (slight) enlargement of Q. More precisely, if \(Q=(z;r_1,\ldots ,r_d)\), then \(Q^*:= Q(z; \kappa r_1,\ldots ,\kappa r_d)\), where \(\kappa >1\) is a fixed constant. Let \(\mathcal {Q}\) be a given admissible covering of \(\mathbb {R}_+^d\). We fix \(\kappa =\kappa (\mathcal {Q})\) sufficiently close to 1, so that for any \(Q_1,Q_2 \in \mathcal {Q}\),
The family \(\left\{ Q^{***} \right\} _{Q\in \mathcal {Q}}\) is a finite covering of \(\mathbb {R}_+^d\),
For \(Q\in \mathcal {Q}\) denote \(N(Q) = \left\{ \widetilde{Q} \in \mathcal {Q}\ : \ \widetilde{Q} \cap Q \ne \emptyset , \right\} \) (all neighbors of the cuboid Q), and \(\widetilde{N}(Q) = \bigcup _{\widetilde{Q} \in N(Q)} \widetilde{Q}\).
For the covering \(\mathcal {Q}\) as above consider functions \(\psi _Q\in C^1(\mathbb {R}_+^d)\) satisfying
It is straightforward to see that such a family \(\left\{ \psi _Q \right\} _{Q\in \mathcal {Q}}\) exists. We call it a partition of unity related to \(\mathcal {Q}\).
We now define suitable atoms and a local atomic Hardy space \(H^1_\mathrm{{at}}(\mathcal {Q},\mu _\nu )\) related to \(\mathcal {Q}\).
Definition 2.2
A function \(a :\mathbb {R}_+^d \rightarrow \mathbb {C}\) is a \((\mathcal {Q},\mu _\nu )\)-atom if:
-
(i)
either there is \(Q\in \mathcal {Q}\) and a cube \(K\subset Q^{*}\), such that
$$\mathrm {supp}\, a \subseteq K, \ \ \left\| a \right\| _\infty \le \mu _\nu (K)^{-1}, \ \ \int a\, d\mu _\nu = 0;$$ -
(ii)
or there exists \(Q\in \mathcal {Q}\) such that
$$a = \mu _\nu (Q)^{-1}\mathbb {1}_Q.$$
The atoms as in (ii) are called local atoms.
Having \((\mathcal {Q}, \mu _\nu )\)-atoms at our disposal, we define the local atomic Hardy space \(H^1_\mathrm{{at}}(\mathcal {Q}, \mu _\nu )\) related to \(\mathcal {Q}\) in the standard way. Namely, a function f belongs to \(H^1_\mathrm{{at}}(\mathcal {Q}, \mu _\nu )\) if it has an atomic decomposition \(f = \sum _k \lambda _k a_k\) with \(\sum _k |\lambda _k| <\infty \) and \(a_k\) being \((\mathcal {Q},\mu _\nu )\)-atoms. The norm in \(H^1_\mathrm{{at}}(\mathcal {Q},\mu _\nu )\) is given by
where the infimum is taken over all possible representations of f as above. Note that \(H^1_\mathrm{{at}}(\mathcal {Q}, \mu _\nu )\) is a Banach space.
2.2 Auxiliary results
Lemma 2.3
Let \(d=1\) and \(\nu \in \mathbb {R}\). The following estimates hold.
-
(a)
If \( \nu > -1\), then
$$\begin{aligned} \mu _\nu (B(x,r)) \simeq \left( 1 \wedge \frac{r}{x} \right) (x+r)^{2\nu +2}, \qquad x,r >0. \end{aligned}$$ -
(b)
If \( \nu = -1\), then
$$\begin{aligned} \mu _\nu (B(x,r)) \simeq \log \frac{x+r}{x-r}, \qquad x>r >0. \end{aligned}$$ -
(c)
If \( \nu < -1\), then
$$\begin{aligned} \mu _\nu (B(x,r)) \simeq \left( 1 \wedge \frac{r}{x} \right) (x-r)^{2\nu +2}, \qquad x> r >0. \end{aligned}$$
Proof
(a) If \(r>x\), then
When \(x\ge r > x/2\), we have
Finally, if \(r\le x/2\), then \(x+r \simeq x \simeq x-r\). Therefore, applying the Mean Value Theorem,
The proof of (b) is straightforward. We pass to proving (c). If \(x>r>x/2\), then
since now \(2\nu +2<0\).
When \(r\le x/2\), we proceed similarly as in the corresponding part of the proof of (a) above. The conclusion follows.\(\square \)
Corollary 2.4
Let \(d=1\). Then
-
(a)
for each \(\nu \in \mathbb {R}\),
$$\begin{aligned} \mu _\nu (B(x,r)) \simeq r x^{2\nu +1}, \qquad 0< r < x/2; \end{aligned}$$ -
(b)
for each \(\nu > -1\),
$$\begin{aligned} \mu _\nu (B(x,r)) \simeq r (x+r)^{2\nu +1}, \qquad x,r > 0. \end{aligned}$$
Proof
(a) Since \(r<x/2\), we have that \(x+r\simeq x -r \simeq x\) and for \(\nu \ne -1\) the claim readily follows from (a) and (c) of Lemma 2.3. To cover \(\nu =-1\), use Lemma 2.3(b) and then observe that by the Mean Value Theorem \(\log (x+r)-\log (x-r) \simeq r/x\). Part (b) is a simple reformulation of Lemma 2.3(a).
As a consequence of the above results we obtain the following.
Corollary 2.5
Let \(d\ge 1\) and \(\nu \in \mathbb {R}^d\). Then
Moreover, if \(\nu \in (-1,\infty )^d\), then
Lemma 2.6
Let \(\mathcal {Q}\) be an admissible covering of \(\mathbb {R}_+^d\). Assume that \(\nu \in (-1,\infty )^d\) and \(Q \in \mathcal {Q}\). Let \(y\in Q^*\). Then for each \(\delta \in (0, \min (1/2, \nu _1+1,\ldots ,\nu _d+1))\) and each \(c>0\)
and
where the constant C is independent of Q and y.
Proof
Let \(Q=Q_1\times \ldots \times Q_d\), with \(d_Q\simeq d_{Q_1} \simeq \ldots \simeq d_{Q_d}\). First we prove (2.4). To do that we need some auxiliary estimates.
Case 1: \(\nu _i\ge -1/2\). Applying Corollary 2.4(b) we have
Case 2: \(\nu _i\in (-1,-1/2)\). In this case, since \(\delta /d-1-\nu _i<0\), using Corollary 2.4(b) we obtain
To get (2.4) we use Corollary 2.5, (2.6) and (2.7) obtaining
Next, we prove (2.5) by induction with respect to the dimension d.
Step 1. Suppose \(d=1\). We consider two cases.
Case 1: \(\nu \ge -1/2\). Using Corollary 2.4(b) we see that the left hand side of (2.5) is controlled by
The last inequality follows from the relation \(|x-y|\ge cd_Q\), since \(x\in (Q^{**})^c\) and \(y\in Q^*\).
Case 2: \(\nu \in (-1,-1/2)\). In this case we again apply Corollary 2.4(b) to bound the left hand side of (2.5) by
Step 2. Let \(d > 1\) be fixed. Suppose \(\nu =(\nu _1,\widetilde{\nu }) = (\nu _1,\nu _2,\ldots ,\nu _d) \in (-1,\infty )^d\) and \(Q = Q_1\times \widetilde{Q}\), where \(d_Q\simeq d_{Q_1}\simeq d_{\widetilde{Q}}\). We use the notation \(\mathbb {x}= (x_1,\widetilde{x}), \mathbb {y}=(y_1,\widetilde{y}) \in \mathbb {R}_+ \times \mathbb {R}_+^{d-1}\). Assume that (2.5) holds for \(\widetilde{Q}\), that is for every \(0< \delta ' < \min (1/2, \nu _2 +1, \ldots , \nu _d+1)\) and \(c>0\) there exists \(C>0\) such that
Here C does not depend on \(\widetilde{Q}\). Take \(\delta \in (0, \min (1/2, \nu _1+1,\ldots ,\nu _d+1))\). We split the set \((Q^{**})^c = S_1 \cup S_2 \cup S_3\), where
and write
To estimate \(J_1\) we apply Corollary 2.5(b), (2.8) and (2.4) with some small \(\varepsilon >0\) such that \(\delta +\varepsilon < \min (1/2,\nu _1 +1, \cdots ,\nu _d+1)\). We get
We deal with \(J_2\) similarly, but this time using (2.4) for the integral over the cube \(\widetilde{Q}\) and Step 1 for the integral over \(Q_1\). This gives
Treating \(J_3\) we apply (2.8) and Step 1 and obtain
This completes the proof.
2.3 Local Hardy space
In this subsection we consider \(\nu \in (-1,\infty )^d\). Let \(\tau >0\) be fixed. We are interested in decomposing into atoms a function f such that
In the classical case of the Laplace operator on \(\mathbb {R}^d\) equipped with Lebesgue measure, if one restricts the supremum to \(0<t\le \tau ^2\) in the maximal operator, then one obtains an atomic space with the classical atoms complemented with atoms of the form \(|B|^{-1}\mathbb {1}_B\), where the ball B has radius \(\tau \), c.f. [13].
It turns out that a similar phenomenon occurs in case of the classical Bessel operator. More precisely, (2.9) holds if and only if \(f = \sum _k \lambda _k a_k\), where \(\sum _k \left| \lambda _k \right| <\infty \) and \(a_k\) are either the classical atoms or local atoms at scale \(\tau \). The latter are atoms a supported in a cube Q of diameter comparable to \(\tau \) such that \(\left\| a \right\| _\infty \le \mu _\nu (Q)^{-1}\) but we do not impose cancellation condition. In other words one could say that these atoms built the space \(H^1_\mathrm{{at}}(\mathcal {Q}^{\{\tau \}},\mu _\nu )\) introduced in Sect. 2.1, where \(\mathcal {Q}^{\{\tau \}}\) is a covering of \(\mathbb {R}_+^d\) by cubes with diameter \(\tau \). The next proposition states a local atomic decomposition theorem that will be suitable for the proof of our main result. This proposition can be obtained by known methods based on Uchiyama [25, Cor. 1’]. We refer the reader also to [12, Sec. 4], where the authors check assumptions of Uchiyama’s Theorem in the classical Bessel framework for the whole range of the parameter \(\nu \in (-1,\infty )^d\). For the sake of completeness, below we present a sketch of the proof.
Let \(\mathcal {Q}^{\left\{ \tau \right\} }\) be a section of \(\mathbb {R}_+^d\) consisting of cuboids, which have diameter uniformly comparable to \(\tau \), i.e. there exists a positive constant C such that \(C^{-1} \tau \le d_Q \le C \tau \) for every \(Q\in \mathcal {Q}^{\left\{ \tau \right\} }\).
Proposition 2.7
There exists \(C>0\) independent of \(\tau \) such that:
-
(a)
For every classical atom a supported in \(K\subset Q^*\) or atom of the form \(a=\mu _\nu (Q)^{-1}\mathbb {1}_{Q}\), where \(Q\in \mathcal {Q}^{\left\{ \tau \right\} }\), we have
$$\begin{aligned} \left\| \sup _{t\le \tau ^2}\left| \mathbb {W}_{t,\nu }^\mathrm{{cls}} a \right| \right\| _{L^1(\mathbb {R}_+^d,d\mu _\nu )} \le C. \end{aligned}$$ -
(b)
If \(f\in L^1_\mathrm{{loc}}(\mathbb {R}_+^d, d\mu _\nu )\) is such that \(\mathrm {supp}f \subseteq Q^*\), \(Q\in \mathcal {Q}^{\left\{ \tau \right\} }\), and
$$\begin{aligned} \left\| \sup _{t\le \tau ^2}\left| \mathbb {W}_{t,\nu }^\mathrm{{cls}} f \right| \right\| _{L^1(Q^*,d\mu _\nu )}=M<\infty , \end{aligned}$$then there exist a sequence \(\lambda _k\) and \((\mathcal {Q}^{\left\{ \tau \right\} },\mu _\nu )\)-atoms \(a_k\), such that \(f = \sum _k \lambda _k a_k\), \(\sum _k \left| \lambda _k \right| \le C M\), and \(a_k\) are either the classical atoms supported in \(Q^{*}\) or \(a_k = \mu _\nu (Q)^{-1}\mathbb {1}_{Q}\). The sum above converges in \(L^1\) norm.
Proof
(a) If a is a classical atom satisfying cancellation condition, then the statement follows from [12, Prop. 4.1]. So assume that \(a=\mu _\nu (Q)^{-1}\mathbb {1}_Q\). The maximal operator associated with \(\mathbb {W}_{t,\nu }^\mathrm{{cls}}\) is bounded on \(L^p(\mathbb {R}_+^d,d\mu _\nu )\) for \(p>1\), by Stein’s general maximal theorem for semigroups of operators [22, p. 73]. Hence, using this fact and the Schwarz inequality,
To estimate the norm on \((Q^{**})^c\) observe that \(|x-y| > rsim \tau \) when \(y\in Q\) and \(x\in (Q^{**})^c\). Applying (1.2) and (2.5) with sufficiently small \(\varepsilon >0\) we obtain
since \(d_Q \simeq \tau \).
(b) Assume that \(f\in L^1_\mathrm{{loc}}(\mathbb {R}_+^d, d\mu _\nu )\) and \(\mathrm {supp}f \subset Q^*\). Consider \(X=Q^*\) as a space. Define \(\lambda _0 = \int f d\mu _\nu \) and \(g = f - \lambda _0 \mu _\nu (Q)^{-1}\mathbb {1}_Q\). Notice that
and
Therefore \(\left\| g \right\| _{L^1(Q^{*},d\mu _\nu )} \le 2 \left\| f \right\| _{L^1(Q^*,d\mu _\nu )} \le 2M\). Moreover, \(\left\| \sup _{t\le \tau ^2} \left| \mathbb {W}_{t,\nu }^\mathrm{{cls}} g \right| \right\| _{L^1(Q^*,d\mu _\nu )} \le C M\). Indeed, using (a) and (2.10) we have
For \(t>\tau ^2\), by (1.2) we obtain
We used the fact that by the doubling property of \(\mu _\nu \) we have \(\mu _{\nu }(B(x,\tau )) \simeq \mu _{\nu }(Q^*)\) for \(x\in Q^{*}\).
Repeating the proof of [12, Prop. 4.1], where the authors use Uchiyama’s Theorem [25, Cor. 1’], we conclude that the function g may be decomposed as
where \(a_k\) are atoms supported in \(X=Q^*\) and satisfy cancellation condition. The sum above converges in \(L^1\) norm, since \(\left\| a_k \right\| _{L^1(\mathbb {R}_+^d,d\mu _\nu )} \le 1\). The constant atom \(\mu _\nu (Q^*)^{-1}\mathbb {1}_{Q^*}\) appears since \(\mu _\nu (X) = \mu _\nu (Q^*) < \infty \), see [25, Sec. 2]. However, by (2.11) we get \(\widetilde{\lambda } = 0\). Further, \(\inf \sum _k |\lambda _k| \simeq \left\| \sup _{t >0} \left| \mathbb {W}_{t,\nu }^\mathrm{{cls}} g \right| \right\| _{L^1(Q^*,d\mu _\nu )} \le CM\), which combined with (2.10) gives the desired conclusion.
3 Local atomic decomposition
3.1 Local atomic decomposition theorem
We now consider an operator \(L:D(L) \subset L^2(\mathbb {R}_+^d, d\mu _\nu ) \rightarrow L^2(\mathbb {R}_+^d, d\mu _\nu )\), where D(L) is the domain of L. Assume that L is self-adjoint and nonnegative. Denote by \(T_t = \exp \left( -tL \right) \) the semigroup generated by L and suppose there exists a nonegative integral kernel \(T_t(x,y)\), such that for every \(f\in L^1(\mathbb {R}_+^d, d\mu _\nu )\), \(T_tf(x) = \int _{\mathbb {R}_+^d} T_t(x,y) f(y) d\mu _\nu (y)\), \(t>0\). We consider the maximal Hardy space for the operator LFootnote 1.
For \(\nu \in (-1,\infty )^d\), an admissible covering \(\mathcal {Q}\), and the semigroup \(\left\{ T_t \right\} \) we consider the following conditions.
Let us emphasize that the constants C, c in these above conditions are independent of \(Q\in \mathcal {Q}\).
The main result of this section is the following.
Theorem 3.1
Let \(\nu \in (-1,\infty )^d\). Assume that \(L, \left\{ T_t \right\} \) with an admissible covering \(\mathcal {Q}\) satisfy (\(A_0\)), (\(A_1'\)) and (\(A_2'\)). Then \(H^1(L)\) and \(H^1_\mathrm{{at}}(\mathcal {Q}, \mu _\nu )\) are isomorphic as Banach spaces.
To prove Theorem 3.1 we need one more lemma.
Lemma 3.2
Let \(\nu \in (-1,\infty )^d\). Assume that \(\left\{ T_t \right\} \) and \(\mathcal {Q}\) satisfy conditions (\(A_0\)), (\(A_1'\)) and a family \(\left\{ \psi _Q \right\} _{Q\in \mathcal {Q}}\) satisfies (2.3). Then
Proof
First, we prove (3.1). Let \(Q\in \mathcal {Q}\) and take \(y\in Q^*\). Notice that if \(x\in Q^{**}\) then in particular \(x\in \widetilde{N}(Q)\), hence we may use (\(A_0\)). We have
since \(\mu _\nu (B(x,d_Q)) \simeq \mu _\nu (Q)\), \(x\in Q^*\), by the doubling property of \(\mu _\nu \).
Next we show (3.2). Let \(y\in \mathbb {R}_+^d\). There exists \(Q_0\in \mathcal {Q}\) such that \(y\in Q_0\). Recall that \(N(Q_0) = \left\{ Q\in \mathcal {Q}\ : \ Q\cap Q_0 \ne \emptyset \right\} \). We write
To estimate \(S_2\) we use \(0\le \psi _Q \le 1\) and (\(A_1'\)), getting
To treat \(S_1\), write \(Q=Q_1\times \cdots \times Q_d\). We claim that, given \(j = 1,\cdots ,d\), and \(\varepsilon _j\in (0,2\nu _j+2)\), for \(x_j\in \widetilde{N}(Q_j)\), \(y_j\in Q_j^*\) one has the bound
that holds with C independent of \(Q\in \mathcal {Q}\), \(x_j\) and \(y_j\). This will be verified in a moment. Now choose \(\varepsilon _j\), \(j=1,\ldots ,d\), such that \(\varepsilon _j\in (0,2\nu _j+2)\) and \(\varepsilon :=\sum _j \varepsilon _j < 1\). Using (\(A_0\)), the Mean Value Theorem for \(\psi _Q\), (2.3), Corollary 2.5 and then (3.3) we obtain
since \(d_{Q_j} \simeq d_Q\) for \(j=1,\ldots ,d\).
It remains to show (3.3). We will consider several cases and subcases.
Case 1: \(\nu _j \ge -1/2\). In this case, by Corollary 2.4(b) we have
Case 1a: \(x_j < |x_j-y_j|/2\). We have
Case 1b: \(x_j \ge |x_j-y_j|/2\). Here we obtain
Case 2: \(\nu _j \in (-1,-1/2)\) and \(Cd_Q \ge x_j\). Using Corollary 2.4(b) we get
Case 2a: \(x_j < |x_j-y_j|/2\). We write
Case 2b: \(|x_j-y_j|/2 < x_j\). In this case
Case 3: \(\nu _j \in (-1,-1/2)\) and \(Cd_Q < x_j\). Here we have
This finishes proving (3.3).
3.2 Proof of Theorem 3.1
We shall prove the two inclusions.
First inclusion. Let \(f\in H^1_\mathrm{{at}}(\mathcal {Q},\mu _\nu )\). Obviously \(\left\| f \right\| _{L^1(X,d\mu _\nu )}\le \left\| f \right\| _{H^1_\mathrm{{at}}({\mathcal {Q}},\mu _{\nu })}\). We need to show \(\left\| \sup _{t>0}\left| T_t f \right| \right\| _{L^1(\mathbb {R}_+^d,d\mu _{\nu })} \le C \left\| f \right\| _{H^1_\mathrm{{at}}({\mathcal {Q}},\mu _{\nu })}\). It is enough to check that \(\left\| \sup _{t>0} |T_t a| \right\| _{L^1(\mathbb {R}_+^d,d\mu _{\nu })} \le C\) for every \((\mathcal {Q},\mu _{\nu })\)-atom a, where C does not depend on a. Indeed, by (\(A_0\)) and (\(A_1'\)) we know that linear operator \(T_t\), for fixed \(t>0\), is bounded on \(L^1(X,d\mu _\nu )\), hence it is continuous. Moreover, taking the supremum is sub-additive and \(\left\| a \right\| _{L^1(X,d\mu _\nu )}\le 1\).
Take an atom a associated with a cuboid \(Q\in \mathcal {Q}\), see Definition 2.2. Using (\(A_1'\)), (3.1), (\(A_2'\)) and Proposition 2.7(a) with \(\tau =d_Q\) we get
Second inclusion. Let \(f\in H^1(L)\). We shall prove \(\left\| f \right\| _{H^1_\mathrm{{at}}({\mathcal {Q}},\mu _{\nu })} \le C \left\| \sup _{t>0}\left| T_t f \right| \right\| _{L^1(\mathbb {R}_+^d,d\mu _{\nu })}\). Let \(\psi _Q\) be a partition of unity related to \(\mathcal {Q}\), see (2.3). Then \(f = \sum _{Q \in \mathcal {Q}} \psi _Q f\). Denote \(f_Q = \psi _Q f\) and notice that \(\mathrm {supp}\, f_Q \subset Q^{*}\). We have
Clearly,
Using (\(A_2'\)),
By (3.2),
Combining (3.5) – (3.7) with (3.4) we arrive at
Now we apply Proposition 2.7(b) for each \(f_Q\) separately with \(\tau =d_Q\). For each \(f_Q\) we obtain a sequence \(\lambda _{k}^Q\) and atoms \(a_{k}^Q\) such that
Observe that for each Q the atoms \(a_{k}^Q\) are either local atoms of the form \(\mu _\nu (Q)^{-1}\mathbb {1}_Q\) or classical atoms supported in \(Q^*\), therefore they are indeed \((\mathcal {Q},\mu _{\nu })\)-atoms. Finally we have that
where the series converges absolutely in \(L^1\), since \(\left\| a_k^Q \right\| _{L^1(\mathbb {R}_+^d,d\mu _\nu )}\le 1\) and by Proposition 2.7(b) and (3.8),
4 Local atomic decomposition in the product case
4.1 Product of local atomic Hardy spaces
In this section we consider operators of the form \(L=L_1 +\cdots + L_N\), where each \(L_i\) acts nontrivially only on the variable \(x_i \in X_i = \mathbb {R}_+^{d_i}\). We introduce conditions on the kernels of the semigroups generated by \(L_i\), and admissible coverings \(\mathcal {Q}_i\) of \(X_i\), which are sufficient to prove the local atomic decomposition theorem for the Hardy space \(H^1(L)\).
More precisely, we consider \(X = X_1 \times \cdots \times X_N = \mathbb {R}_+^{d_1} \times \cdots \times \mathbb {R}_+^{d_N} = \mathbb {R}_+^d\). We equip the space X with the Euclidean metric and the measure \(d\mu _\nu (x) = x^{2\nu +1} dx\), where \(\nu = (\nu _1, \ldots , \nu _N)\) and \(\nu _i = (\nu _{i,1}, \ldots ,\nu _{i,d_i})\in (-1,\infty )^{d_i}\) for \(i=1, \ldots ,N\). Assume that \(L_i: D(L_i) \subset L^2(X_i, d\mu _{\nu _i}) \rightarrow L^2(X_i, d\mu _{\nu _i})\) is a nonnegative and self-adjoint operator, as in Sect. 3.1. Slightly abusing the notation we keep the symbol
for the operator on \(L^2(X, d\mu _\nu )\), where I denotes the identity operator on the corresponding subspace, and we define
Since the operators \(L_i\) are self-adjoint, the operator L is well defined and essentially self-adjoint, see e.g. [21, Thm. 7.23].
We denote by \(T_t^{[i]}(x_i,y_i)\), \(x_i,y_i \in X_i\), the integral kernel of \(T_t^{[i]} = \exp \left( -tL_i \right) \).
Given two admissible coverings \(\mathcal {Q}_1\) and \(\mathcal {Q}_2\) of \(X_1\) and \(X_2\), respectively, we would like to produce an admissible covering on \(X_1\times X_2\). However, the products \(\left\{ Q_1 \times Q_2 \ : \ Q_1 \in \mathcal {Q}_1, Q_2 \in \mathcal {Q}_2 \right\} \) do not form an admissible covering (in general item 3 of Definition 2.1 fails). Therefore, we need a finer construction. We split each \(Q=Q_1\times Q_2\) (without loss of generality let us assume that \(d_{Q_1} > d_{Q_2}\)) into cuboids \(Q^{j}\), \(j=1,\ldots ,M\), such that all of them have diameters comparable to \(d_{Q_2}\). Then the cuboids \(Q^{j} = Q_1^{j}\times Q_2\), \(j=1,\ldots ,M,\) satisfy:
-
\(Q = \bigcup _{j=1}^M Q^{j}\),
-
\(\mu _\nu (Q^{i} \cap Q^{j}) = 0\) for \(i,j \in \left\{ 1,\ldots ,M \right\} \), \(i\ne j\),
-
each \(Q^{j}\) satisfies condition 3 of Definition 2.1.
Definition 4.1
The admissible covering of \(X_1\times X_2\) described in the above construction will be called the product admissible covering and denoted by \(\mathcal {Q}_1 \boxtimes \mathcal {Q}_2\).
As an example, consider the family \(\mathcal {D}= \left\{ [2^n,2^{n+1}] \ : \ n\in \mathbb {Z} \right\} \), which is an admissible covering of \(\mathbb {R}_+\). The product admissible covering \(\mathcal {D}\boxtimes \mathcal {D}\) of \(\mathbb {R}_+^2\) is illustrated by Fig. 1 below.
For a product admissible covering \(\mathcal {Q}_1 \boxtimes \mathcal {Q}_2\) we also fix a new \(\kappa \) such that (2.2) is fulfilled. The covering \(\mathcal {Q}_1\boxtimes \ldots \boxtimes \mathcal {Q}_N\) of \(X_1\times \ldots \times X_N\) is constructed as above by induction.
Remark 4.2
The collection of all the smaller cuboids \(Q_1^{j}\) emerging from splitting the cuboid \(Q_1\) and described before Definition 4.1 forms an admissible covering of \(\mathbb {R}_+^{d_1}\).
We introduce modifications of conditions (\(A_1'\)), (\(A_2'\)). For the semigroup of operators \(\left\{ S_t \right\} \) and an admissible covering \(\mathcal {Q}\) we consider the following conditions. There exists \(\gamma \in (0,1/3)\) such that:
and
Notice that if \(\left\{ S_t \right\} \) and \(\mathcal {Q}\) satisfy (\(A_1\)) and (\(A_2\)), then (\(A_1'\)) and (\(A_2'\)) also hold. We shall assume that each \(T_t^{[i]}(x_i,y_i)\) , \(i=1,\ldots ,N\), and the corresponding admissible covering \(\mathcal {Q}_i\) satisfy conditions (\(A_0\))–(\(A_2\)).
Remark 4.3
Condition (\(A_1\)) for negative \(\delta \in (-\gamma ,0)\) is automatically satisfied if the kernels \(T_t^{[i]}(x_i,y_i)\) satisfy the upper Gaussian estimates, that is the bound of condition (\(A_0\)) for all \(x_i,y_i\in X_i\). This is a direct consequence of (2.5).
Our main result in this section is the following.
Theorem 4.4
Let L be as in (4.1) and assume that for each \(i=1,\ldots ,N\), the kernel \(T_t^{[i]}(x_i,y_i)\) together with the corresponding admissible covering \(\mathcal {Q}_i\) satisfy conditions (\(A_0\)) – (\(A_2\)). Then
and the corresponding norms are equivalent.
Proof
We will show the following claim. If conditions (\(A_0\)) – (\(A_2\)) hold for \(T_t^{[i]}(x_i,y_i)\) together with admissible coverings \(\mathcal {Q}_i\) for \(i=1,2\), then (\(A_0\)) – (\(A_2\)) also hold for \(T_t(x,y) = T_t^{[1]}(x_1,y_1)T_t^{[2]}(x_2,y_2)\), together with \(\mathcal {Q}= \mathcal {Q}_1 \boxtimes \mathcal {Q}_2\). This is enough, since by simple induction we shall get that in the general case \(T_t(x,y) = T_t^{[1]}(x_1,y_1)\ldots T_t^{[N]}(x_N,y_N)\) with \(\mathcal {Q}_1 \boxtimes \ldots \boxtimes \mathcal {Q}_N\) satisfy (\(A_0\)) – (\(A_2\)), and consequently, the assumptions of Theorem 3.1 will be fulfilled.
To prove the claim let \(T_t^{[i]}(x_i,y_i)\) and \(\mathcal {Q}_i\) satisfy (\(A_0\)) – (\(A_2\)) with \(\gamma _i\) for \(i=1,2\). Let \(0< \gamma < \min (\gamma _1,\gamma _2, \nu _{1,1}+1,\ldots ,\nu _{1,d_1}+1,\nu _{2,1}+1,\ldots ,\nu _{2,d_2}+1)\). Suppose that \(\mathcal {Q}\ni Q \subseteq Q_1 \times Q_2\), where \(Q_1 \in \mathcal {Q}_1\), \(Q_2 \in \mathcal {Q}_2\). Without loss of generality we may assume that \(d_{Q_1} \ge d_{Q_2}\). Hence \(Q=K\times Q_2\), where \(K\subseteq Q_1\) is a cuboid emerging from the very construction of \(\mathcal {Q}_1\boxtimes \mathcal {Q}_2\), see the description preceding Definition 4.1 and Fig. 2 below. Denote by \(z=(z_1,z_2)\) the center of \(Q = K\times Q_2\).
Verification of (\(A_0\)). Notice that if \(x=(x_1,x_2) \in N(Q)\), then in particular \( x_1\in \widetilde{N}(Q_1)\) and \( x_2\in \widetilde{N}(Q_2)\). Similarly, if \(y = (y_1,y_2)\in Q^*\), then \(y_1\in Q_1^{*}\) and \(y_2\in Q_2^*\). Therefore, for such x, y we may use (\(A_0\)) for each of \(T_t^{[1]}(x_1,y_1)\) and \(T_t^{[2]}(x_2,y_2)\) obtaining (\(A_0\)) for \(T_t(x,y) = T_t^{[1]}(x_1,y_1) T_t^{[2]}(x_2,y_2)\).
Verification of (\(A_1\)). Fix \(\delta \in (-\gamma ,\gamma )\). Let  . Recall that \(d_Q \simeq d_K \simeq d_{Q_2} \le d_{Q_1}\). Decompose \((Q^{**})^c = S_1\cup S_2 \cup S_3 \cup S_4 \cup S_5\), where
. Recall that \(d_Q \simeq d_K \simeq d_{Q_2} \le d_{Q_1}\). Decompose \((Q^{**})^c = S_1\cup S_2 \cup S_3 \cup S_4 \cup S_5\), where
We start with estimating the integral over \(S_1\). We shall consider two cases.
Case 1: \(\delta \in (-\gamma ,0]\). In this case we take a small \(\varepsilon >0\) such that \(\delta -\varepsilon > -\gamma \). Using (\(A_1\)) for \(T_t^{[1]}(x_1,y_1)\), (\(A_0\)) for \(T_t^{[2]}(x_2,y_2)\) and then (2.4), we have
since \(d_{Q_1} \ge d_{Q_{2}} \simeq d_Q\).
Case 2: \(\delta \in (0,\gamma )\). Then, again using (\(A_1\)) for \(T_t^{[1]}(x_1,y_1)\), (\(A_0\)) for \(T_t^{[2]}(x_2,y_2)\) and then (2.4) we have
The integral over \(S_2\) is treated similarly. Indeed we take a small \(\varepsilon >0\) such that \(\delta -\varepsilon >-\gamma \). We apply (\(A_0\)) for \(T_t^{[1]}(x_1,y_1)\) and then (2.4), and (\(A_1\)) for \(T_t^{[2]}(x_2,y_2)\). We get
since \(d_K \simeq d_{Q_2}\simeq d_Q\). By Remark 4.2 we were allowed to use Lemma 2.6 for the cuboid K.
To estimate the integral over \(S_3\) notice that since \(x_1\in Q_1^{**}\) we may use (\(A_0\)) for \(T_t^{[1]}(x_1,y_1)\). Let \(\varepsilon >0\) be such that \(\delta +\varepsilon < \gamma \). Then we use (\(A_1\)) for \(T_t^{[2]}(x_2,y_2)\) and (2.5) and arrive at
Treating the integral over \(S_4\) we make use of (\(A_1\)) for both \(T_t^{[1]}(x_1,y_1)\) and \(T_t^{[2]}(x_2,y_2)\). We get
Turning to the last integral over \(S_5\) we consider two cases.
Case 1: \(\delta \in (-\gamma ,0]\). Take \(\varepsilon >0\) such that \(\delta -\varepsilon > -\gamma \). We use (\(A_0\)) for \(T_t^{[1]}(x_1,y_1)\) and \(T_t^{[2]}(x_2,y_2)\), and then Lemma 2.6 getting
since \(d_K \simeq d_{Q_{2}} \simeq d_Q\).
Case 2: \(\delta \in (0,\gamma )\). Let \(\varepsilon >0\) be such that \(\delta +\varepsilon < \gamma \). Using (\(A_0\)) for \(T_t^{[1]}(x_1,y_1)\), \(T_t^{[2]}(x_2,y_2)\) and then Lemma 2.6 we obtain
Condition (\(A_1\)) is now verified.
Verification of (\(A_2\)). Fix \(\delta \in [0,\gamma )\). Let  . In this proof \(\mathbb {W}_{t,\nu }^\mathrm{{cls}}\) will be the classical Bessel semigroup on \(\mathbb {R}_+^{d_1}\), \(\mathbb {R}_+^{d_2}\) or on \(\mathbb {R}_+^{d_1+d_2}\), depending on the context. First, notice that by (\(A_0\)) and (2.4), for any given constant \(c>1\) and \(i=1,2\), we have
. In this proof \(\mathbb {W}_{t,\nu }^\mathrm{{cls}}\) will be the classical Bessel semigroup on \(\mathbb {R}_+^{d_1}\), \(\mathbb {R}_+^{d_2}\) or on \(\mathbb {R}_+^{d_1+d_2}\), depending on the context. First, notice that by (\(A_0\)) and (2.4), for any given constant \(c>1\) and \(i=1,2\), we have

Since \(\mathbb {W}_{t,\nu }^\mathrm{{cls}}(x,y) = \mathbb {W}_{t,\nu _1}^\mathrm{{cls}}(x_1,y_1)\mathbb {W}_{t,\nu _2}^\mathrm{{cls}}(x_2,y_2)\), by the triangle inequality we have

where

Applying (\(A_0\)) for \(T_t^{[1]}(x_1,y_1)\) and then (2.4), and (\(A_2\)) together with (4.2) for \(T_t^{[2]}(x_2,y_2)\), gives

since \(0 \le \delta< \gamma < \min (\gamma _1,\gamma _2)\).
Similarly, by (1.2), (2.4), (\(A_2\)) and (4.2), we have

since \(d_{Q_1} \ge d_{Q_2} \simeq d_Q\). This finishes verification of (\(A_2\)).
The proof of Theorem 4.4 is complete.
4.2 Product of local and nonlocal atomic Hardy space
As we have mentioned, all atoms of the Hardy space \(H^1(\mathbb {B}_{\nu _1}^\mathrm{{cls}})\) satisfy cancellation condition, i.e. they are nonlocal atoms. However, if we consider the product \(\mathbb {R}_+^d = \mathbb {R}_+^{d_1} \times \mathbb {R}_+^{d_2}\) with the measure \(\mu _\nu = \mu _{\nu _1}\otimes \mu _{\nu _2}\) and the operator \(L= \mathbb {B}_{\nu _1}^\mathrm{{cls}} + L_2\), where the semigroup \(\mathbb {K}_t := \exp (-tL_2)\) generated by \(L_2\), together with an admissible covering \(\mathcal {Q}_2\) satisfy conditions (\(A_0\)) – (\(A_2\)) on \(\mathbb {R}_+^{d_2}\), then the resulting Hardy space \(H^1(L)\) shall have local character.
Let \(\mathbb {R}_+^{d_1}\boxtimes \mathcal {Q}_2\) be the admissible covering that arises by splitting all the cylinders \(\mathbb {R}_+^{d_1} \times Q_2\), \(Q_2 \in \mathcal {Q}_2\), into countably many cubes \(Q_{1,n} \times Q_2\), where \(Q_{1,n} = Q(z_n, d_{Q_2}/2)\). Denote by \(\mathbb {T}_t=\exp (-tL)\) the semigroup of operators generated by the operator L. There exists an integral kernel associated with \(\left\{ \mathbb {T}_t \right\} \) satisfying
We will prove the following.
Proposition 4.5
Let \(\nu =(\nu _1,\nu _2)\in (-1,\infty )^{d_1}\times (-1,\infty )^{d_2}\) and let \(L_2\) and L be as above. Assume that for \(\mathbb {K}_t(x_2,y_2)\) and an admissible covering \(\mathcal {Q}_2\) of \(\mathbb {R}_+^{d_2}\) conditions (\(A_0\)) – (\(A_2\)) hold. Then (\(A_0\)) – (\(A_2\)) are satisfied for \(\mathbb {T}_t(x,y)\) and \(\mathcal {Q}_L:=\mathbb {R}_+^{d_1}\boxtimes \mathcal {Q}_2\).
Combining Proposition 4.5 with Theorem 4.4 we get the following.
Corollary 4.6
Let \(\nu = (\nu _1,\nu _2)\in (-1,\infty )^{d_1}\times (-1,\infty )^{d_2}\) and let \(L_2, L\) be as above. Assume that \(\mathbb {K}_t(x_2,y_2)\) with an admissible covering \(\mathcal {Q}_2\) of \(\mathbb {R}_+^{d_2}\) satisfy (\(A_0\)) – (\(A_2\)). Then the spaces \(H^1(L)\) and \(H^1_\mathrm{{at}}(\mathbb {R}^{d_1}\boxtimes \mathcal {Q}_2, \mu _\nu )\) are isomorphic as Banach spaces.
Now we pass to proving Proposition 4.5.
Proof
Verification of (\(A_0\)). Let \(\mathcal {Q}_L \ni Q \subset \mathbb {R}_+^{d_1}\times Q_2\), where \(Q_2\in \mathcal {Q}_2\). We take \(y\in Q^*\) and \( x \in \widetilde{N}(Q)\). Since \( x_2\in \widetilde{N}(Q_2)\), \(y_2\in Q_2^*\), we know that (\(A_0\)) holds for \(\mathbb {K}_t(x_2,y_2)\). Moreover, \(\mathbb {W}^\mathrm{{cls}}_{t,\nu _1}(x_1,y_1)\) satisfies (1.2), hence (\(A_0\)) for \(\mathbb {T}_t(x,y)\) follows.
To verify (\(A_1\)) and (\(A_2\)) suppose that \(\gamma \) is as in (\(A_1\)) for \(\mathbb {K}_t(x_2,y_2)\) and \(\mathcal {Q}_2\), and let \(0< \gamma ' < \min (\gamma , \nu _{1,1}+1, \ldots , \nu _{1,d_1}+1,\nu _{2,1}+1,\ldots ,\nu _{2,d_2}+1)\). Let \(\mathcal {Q}_L\ni Q = Q_1\times Q_2 \subset \mathbb {R}_+^{d_1}\times Q_2\) and take \(y = (y_1,y_2)\in Q^*\). Recall that \(d_{Q_1}\simeq d_{Q_2} \simeq d_Q\).
Verification of (\(A_1\)). Let \(\delta \in (-\gamma ',\gamma ')\). In what follows \(\varepsilon >0\) will be always a fixed constant such that \(\delta -\varepsilon >-\gamma '\) and \(\delta +\varepsilon <\gamma '\). We decompose \((Q^{**})^c = S_1 \cup S_2\cup S_3 \), where
To deal with the integral over \(S_1\) we consider two cases.
Case 1: \(\delta \in (-\gamma ',0]\). We use (\(A_1\)) for \(\mathbb {K}_t(x_2,y_2)\), (1.2) for \(\mathbb {W}^\mathrm{{cls}}_{t,\nu _1}(x_1,y_1)\) and (2.4), getting
Case 2: \(\delta \in (0,\gamma ')\). By (\(A_1\)) for \(\mathbb {K}_t(x_2,y_2)\), (1.2) for \(\mathbb {W}^\mathrm{{cls}}_{t,\nu _1}(x_1,y_1)\) and (2.4) we obtain
To estimate the integral over \(S_2\) we again consider the two cases.
Case 1: \(\delta \in (-\gamma ,0]\). Using (\(A_0\)) for \(\mathbb {K}_t(x_2,y_2)\) and (1.2) for the classical Bessel semigroup kernel, and then applying (2.5) and (2.4) we arrive at
Case 2: \(\delta \in (0,\gamma ')\). In this case we use (\(A_0\)), (1.2) and Lemma 2.6, getting
Finally, to treat the integral over \(S_3\) we use (\(A_1\)) for \(\mathbb {K}_t(x_2,y_2)\), (1.2) for \(\mathbb {W}^\mathrm{{cls}}_{t,\nu _1}(x_1,y_1)\) and (2.5) obtaining
Verification of (\(A_2\)). Let \(\delta \in [0,\gamma ')\) and fix \(\varepsilon >0\) such that \(\delta +\varepsilon < \gamma '\). We write \(\mathbb {W}_{t,\nu }^\mathrm{{cls}}(x,y) = \mathbb {W}_{t,\nu _1}^\mathrm{{cls}}(x_1,y_1)\mathbb {W}_{t,\nu _2}^\mathrm{{cls}}(x_2,y_2)\). By (\(A_2\)) for \(\mathbb {K}_t(x_2,y_2)\) and (1.2) for \(\mathbb {W}_{t,\nu _1}^\mathrm{{cls}}(x_1,y_1)\) and (2.4), we have
The conclusion follows.
5 Atomic Hardy space for the general Bessel operator
In this section we prove Theorem 1.1. Recall that we consider the operator \(\mathbb {B}_\nu = \mathbb {B}_{\nu _c}^\mathrm{{cls}} + \mathbb {B}_{-\nu _e}^\mathrm{{exo}}\) acting on functions defined on the space \(X=\mathbb {R}_+^{d_1}\times \mathbb {R}_+^{d_2} = \mathbb {R}_+^d\) equipped with the measure \(\mu _{\nu } = \mu _{(\nu _c,-\nu _e)} := \mu _{\nu _c}\otimes \mu _{-\nu _e}\), where \(\nu _c \in (-1,\infty )^{d_1}\), \(\nu _e \in (0,\infty )^{d_2}\) and \(d_1\ge 0\), \(d_2\ge 1\). We use the notation \(\nu _c = (\nu _1,\ldots ,\nu _{d_1})\), \(\nu _e=(\nu _{d_1+1},\ldots ,\nu _{d_1+d_2})\) and \(\mathbb {x}= (\mathbb {x}_1,\mathbb {x}_2),\mathbb {y}=(\mathbb {y}_1,\mathbb {y}_2) \in \mathbb {R}_+^{d_1}\times \mathbb {R}_+^{d_2}\). Moreover, we write \(\mathbb {x}^{2\nu +1} = \mathbb {x}_1^{2\nu _c+1}\mathbb {x}_2^{-2\nu _e+1} := x_1^{2\nu _1+1} \ldots x_{d_1}^{2\nu _{d_1}+1} x_{d_1+1}^{-2\nu _{d_1+1}+1}\ldots x_{d_1+d_2}^{-2\nu _{d_1+d_2}+1}\).
Observe that
where \(\widetilde{f}(\mathbb {y}) = \mathbb {y}_2^{-4\nu _e} f(\mathbb {y})\), \(\mathbb {T}_t(\mathbb {x},\mathbb {y}) = \mathbb {W}_{t,\nu _c}^\mathrm{{cls}}(\mathbb {x}_1,\mathbb {y}_1) \mathbb {K}_t(\mathbb {x}_2,\mathbb {y}_2)\), and
From the above we see that \(f\in H^{1}(\mathbb {B}_{\nu })\) if and only if \(\sup _{t>0} |\mathbb {T}_t \widetilde{f}| \in L^1(X,d\mu _{(\nu _c,\nu _e)})\). To prove Theorem 1.1 we need the following.
Proposition 5.1
Let \(\mathcal {D}= \left\{ [2^n,2^{n+1}] \ : \ n\in \mathbb {Z} \right\} \) be the admissible covering of \(\mathbb {R}_+\). Assume \(\nu \in (0,\infty )\) and let
Then \(K_{t,\nu }\) with \(\mathcal {D}\) satisfy conditions (\(A_0\)) – (\(A_2\)).
In the proof we will need the following standard asymptotics of the modified Bessel function \(I_\tau \), see e.g. [26, p. 203-204],
Proof
To verify (\(A_0\)) – (\(A_2\)) for \(K_{t,\nu }\) with \(\mathcal {D}\), let \(\mathcal {D}\ni Q = [2^n,2^{n+1}]\) for some \(n\in \mathbb {Z}\) and take \(y\in Q^*\).
Verification of (\(A_0\)). We consider \( x\in \widetilde{N}(Q)\). Notice that then \(x^{-1}y \simeq 1\), hence \(K_{t,\nu }(x,y) = (x^{-1}y)^{2\nu } W_{t,\nu }^\mathrm{{cls}}(x,y) \simeq W_{t,\nu }^\mathrm{{cls}}(x,y)\). Therefore
since the kernel \(W_{t,\nu }^\mathrm{{cls}}(x,y)\) is non-negative and satisfies the Gaussian estimate (1.2).
Verification of (\(A_1\)). Suppose \(0< \gamma < \min (1/2,\nu )\) and take \(\delta \in (-\gamma ,\gamma )\). We write
To treat \(I_1\) we use (5.3) and (5.4).
since \(\delta -\nu <0\) and \(y\simeq d_Q\).
To deal with \(I_2\) we use (5.3) and (5.5). Observing that \(xy\le cd_Q^2 \le c |x-y|^2\), we get
since \(y\simeq d_Q\), and we choose N large enough so that \(\delta -\nu +N \ge 0\).
Treating \(I_3\) we observe that \(x\ge 2d_Q\) implies \(|x-y| \simeq x\). Then using (5.3) and (5.5) we obtain
by taking N sufficiently large and since \(y\simeq d_Q\).
Verification of (\(A_2\)). Let \(0<\gamma < \min (1/2,\nu )\) and take \(\delta \in [0,\gamma )\). Notice that here \(x\simeq y \simeq d_Q\). Moreover, \(t\le d_Q^2 \le c xy \). Using (5.3), (1.1), (5.5) and the Mean Value Theorem, we obtain
since \(y\simeq d_Q\) and \(\delta < 1/2\); here \(\xi _{x,y}\) denotes a point between x and y.
Lemma 5.2
Let \(\nu =(\nu _c,-\nu _e)\), where \(\nu _c\in (-1,\infty )^{d_1}\), and \(\nu _e\in (0,\infty )^{d_2}\). Let \(f\in L^1(X,d\mu _\nu )\). Then
The proof of Lemma 5.2 is presented in Appendix.
Proof of Theorem 1.1. Recall that \(\mathcal {Q}_\mathbb {B}= \mathbb {R}_+^{d_1} \boxtimes \underbrace{\mathcal {D}\boxtimes \ldots \boxtimes \mathcal {D}}_{d_2 \text { times }}\). In view of (5.1) we have
where \(\widetilde{f}(\mathbb {y}) = \mathbb {y}_2^{-4\nu _e}f(\mathbb {y})\). Observe that
Combining Proposition 5.1 with Proposition 4.5 and Theorem 4.4 we infer that \(\sup _{t>0} |\mathbb {T}_t\widetilde{f}| \in L^1(X,d\mu _{(\nu _c,\nu _e)})\) if and only if there exist a sequence \(\lambda _k\) and \((\mathcal {Q}_{\mathbb {B}},\mu _{(\nu _c,\nu _e)})\)-atoms \(\widetilde{a}_k\) such that
and
Hence, f belongs to \(H^1(\mathbb {B}_{\nu })\) if and only if it has a decomposition
Notice, that since \(\widetilde{f}\in H^1_\mathrm{{at}}(\mathcal {Q}_{\mathbb {B}},\mu _{(\nu _c,\nu _e)})\) and \(\mathbb {T}_t\) satisfies (\(A_0\))–(\(A_2\)), we have
(see the first inequality in the proof of Theorem 3.1). Moreover, in the view of Lemma 5.2 we have that
By (5.6) – (5.10) we get that \(\left\| f \right\| _{H^1(\mathbb {B}\nu )} \simeq \inf \sum _k |\lambda _k| \). Thus it suffices to show that functions of the form \(a_k(\mathbb {y}) = \widetilde{a}_k(\mathbb {y}) \mathbb {y}_2^{4\nu _e}\) are \((\mathcal {Q}_\mathbb {B},\mu _{(\nu _c,-\nu _e)})\)-atoms after a modification by multiplying by some function which is comparable to a constant.
Suppose first that \(\widetilde{a}_k = \mu _{(\nu _c,\nu _e)}(Q)^{-1}\mathbb {1}_Q\) for some cube \(\mathcal {Q}_\mathbb {B}\ni Q = Q_1 \times Q_2 \subset \mathbb {R}_+^{d_1} \times [2^{n_1},2^{n_1+1}]\times \cdots \times [2^{n_{d_2}},2^{n_{d_2}+1}]\). Without loss of generality we may assume that \(n_1 = \min _i{n_i}\) and that \(d_Q \simeq 2^{n_1} \simeq d_{Q_1} \simeq d_{Q_2} \). Denote by \(\mathbb {z}\) the center of Q. Then
where \(\mu _{(\nu _c,-\nu _e)}(Q)^{-1} \mathbb {1}_Q(\mathbb {y})\) is \((\mathcal {Q}_\mathbb {B},\mu _{(\nu _c,-\nu _e)})\)-atom. Using Corollary 2.4(a), for \(\mathbb {y}_2\in Q_2\) we obtain
since \(y_i \simeq z_i\) for \(i=d_1+1,\ldots ,d_1+d_2\). Notice that the above estimate is uniform in \(Q_2\).
On the other hand, if \(\widetilde{a}_k\) is a \((\mathcal {Q}_\mathbb {B},\mu _{(\nu _c,\nu _e)})\)-atom of the form (i) from Definition 2.2 associated with a cube \(\mathcal {Q}_\mathbb {B}\ni Q = Q_1 \times Q_2 \subset \mathbb {R}_+^{d_1} \times [2^{n_1},2^{n_1+1}]\times \ldots \times [2^{n_{d_2}},2^{n_{d_2}+1}]\) as above, then the function \(a_k(\mathbb {y}) = \mathbb {y}_2^{4\nu _e}\widetilde{a}_k(\mathbb {y})\) satisfies:
-
1.
\(\mathrm {supp}\ a_k \subseteq K = K_1\times K_2 \subseteq Q^*,\) (Suppose that \(K_2 = Q(\mathbb {w},r_{d_1+1}. \ldots , r_{d_1+d_2}) \subset [2^{n_1},2^{n_1+1}]\times \cdots \times [2^{n_{d_2}},2^{n_{d_2}+1}] \).)
-
2.
similarly as in (5.11), since \(r_i < w_i/2\) for \(i=d_1+1,\ldots , d_1+d_2\), we use Corollary 2.4(a) and have
$$\begin{aligned} \begin{aligned} \left\| a_k \right\| _\infty&= \text {ess sup}_{\mathbb {y}\in K} \mathbb {y}_2^{4\nu _e} \left| \widetilde{a}_k(\mathbb {y}) \right| \le \text {ess sup}_{\mathbb {y}\in K} \mathbb {y}_2^{4\nu _e} \left\| \widetilde{a}_k \right\| _\infty \\&\le \mu _{(\nu _c,-\nu _e)}(K)^{-1} \text {ess sup}_{\mathbb {y}_2\in K_2} \mathbb {y}_2^{4\nu _e} \frac{\mu _{-\nu _e}(K_2)}{\mu _{\nu _e}(K_2)} \\&\simeq \mu _{(\nu _c,-\nu _e)}(K)^{-1} \text {ess sup}_{\mathbb {y}_2\in K_2} \prod _{i=d_1+1}^{d_1+d_2} y_i^{4\nu _i} \frac{ w_i^{-2\nu _i+1} \cdot r_i }{w_i^{2\nu _i+1} \cdot r_i} \\&\simeq \mu _{(\nu _c,-\nu _e)}(K)^{-1} \text {ess sup}_{\mathbb {y}_2\in K_2} \prod _{i=d_1+1}^{d_1+d_2} y_i^{4\nu _i} w_i^{-4\nu _i} \le C \mu _{(\nu _c,-\nu _e)}(K)^{-1}, \end{aligned} \end{aligned}$$where the constant C does not depend on \(K_2\). In the last inequality we used the fact that \(y_i\simeq w_i\) for \(i=d_1+1,\ldots ,d_1+d_2\), when \(y_i,w_i\in [2^{n_i}, 2^{n_i+1}]\).
-
3.
$$\begin{aligned}\int a_k(\mathbb {y}) d\mu _{(\nu _c,-\nu _e)}(\mathbb {y}) = \int \widetilde{a}_k(\mathbb {y}) d\mu _{(\nu _c,\nu _e)}(\mathbb {y}) = 0. \end{aligned}$$
This finishes the proof. \(\square \)
Notes
Notice that for many operators, i.e. which satisfy the upper gaussian estimates, the property \(\left\| f \right\| _{L^1(\mathbb {R}_+^d,d\mu _\nu )} \le \left\| \sup \left| T_t f \right| \right\| _{L^1(\mathbb {R}_+^d, d\mu _\nu )}\) hold, therefore in these cases one may put \( \left\| f \right\| _{H^1(L)} : = \left\| \sup _{t>0} \left| T_t f \right| \right\| _{L^1(\mathbb {R}_+^d, d\mu _\nu )}\)
References
Betancor, J.J., Buraczewski, D., Fariña, J.C., Martínez, T., Torrea, J.L.: Riesz transforms related to Bessel operators. Proc. R. Soc. Edinburgh Sect. A 137, 701–725 (2007)
Betancor, J.J., Castro, A.J., Curbelo, J.: Spectral multipliers for multidimensional Bessel operators. J. Fourier Anal. Appl. 17, 932–975 (2011)
Betancor, J.J., Castro, A.J., Nowak, A.: Calderón–Zygmund operators in the Bessel setting. Monatsh. Math. 167, 375–403 (2012)
Betancor, J.J., De León-Contreras, M.: Parabolic equations involving Bessel operators and singular integrals. Int. Equ. Oper. Theory 90 (2018), Art. 18, 58
Betancor, J.J., Dziubański, J., Torrea, J.L.: On Hardy spaces associated with Bessel operators. J. Anal. Math. 107, 195–219 (2009)
Betancor, J.J., Harboure, E., Nowak, A., Viviani, B.: Mapping properties of fundamental operators in harmonic analysis related to Bessel operators. Studia Math. 197, 101–140 (2010)
Carbonaro, A., Mauceri, G., Meda, S.: \(H^1\) and BMO for certain locally doubling metric measure spaces. Ann. Sci. Norm. Super. Pisa Cl. Sci. (5) 8, 543–582 (2009)
Castro, A.J., Szarek, T.Z.: Calderón–Zygmund operators in the Bessel setting for all possible type indices. Acta Math. Sin. (Engl. Ser.) 30, 637–648 (2014)
Coifman, R.R., Weiss, G.: Extensions of Hardy spaces and their use in analysis. Bull. Am. Math. Soc. 83, 569–645 (1977)
Duoandikoetxea, J.: Fourier Analysis, Graduate Studies in Mathematics, vol. 29. American Mathematical Society, Providence, RI (2001). Translated and revised from the 1995 Spanish original by David Cruz-Uribe
Dziubański, J., Preisner, M.: Hardy spaces for semigroups with Gaussian bounds. Ann. Mat. Pura Appl. (4) 197, 965–987 (2018)
Dziubański, J., Preisner, M., Wróbel, B.: Multivariate Hörmander-type multiplier theorem for the Hankel transform. J. Fourier Anal. Appl. 19, 417–437 (2013)
Goldberg, D.: A local version of real Hardy spaces. Duke Math. J. 46, 27–42 (1979)
Kania, E., Preisner, M.: Sharp multiplier theorem for multidimensional Bessel operators. J. Fourier Anal. Appl. 25, 2419–2446 (2019)
Kania-Strojec, E., Plewa, P., Preisner, M.: Local atomic decompositions for multidimensional Hardy spaces. Rev. Mat. Complut. 34, 409–434 (2021)
Muckenhoupt, B., Stein, E.M.: Classical expansions and their relation to conjugate harmonic functions. Trans. Am. Math. Soc. 118, 17–92 (1965)
Nazarov, F., Treil, S., Volberg, A.: Weak type estimates and Cotlar inequalities for Calderón–Zygmund operators on nonhomogeneous spaces. Int. Math. Res. Not. 463–487
Nazarov, F., Treil, S., Volberg, A.: The \(Tb\)-theorem on non-homogeneous spaces. Acta Math. 190, 151–239 (2003)
Nowak, A., Sjögren, P., Szarek, T.Z.: Maximal operators of exotic and non-exotic Laguerre and other semigroups associated with classical orthogonal expansions. Adv. Math. 318, 307–354 (2017)
Nowak, A., Stempak, K.: Potential operators associated with Hankel and Hankel–Dunkl transforms. J. Anal. Math. 131, 277–321 (2017)
Schmüdgen, K.: Unbounded Self-Adjoint Operators on Hilbert Space, Graduate Texts in Mathematics, vol. 265. Springer, Dordrecht (2012)
Stein, E.M.: Topics in Harmonic Analysis Related to the Littlewood–Paley Theory, Annals of Mathematics Studies. Princeton University Press, Princeton (1970)
Tolsa, X.: BMO, \(H^1\), and Calderón–Zygmund operators for non doubling measures. Math. Ann. 319, 89–149 (2001)
Tolsa, X.: The space \(H^1\) for nondoubling measures in terms of a grand maximal operator. Trans. Am. Math. Soc. 355, 315–348 (2003)
Uchiyama, A.: A maximal function characterization of \(H^{p}\) on the space of homogeneous type. Trans. Am. Math. Soc. 262, 579–592 (1980)
Watson, G.N.: A Treatise on the Theory of Bessel Functions. Cambridge Mathematical Library, Cambridge University Press, Cambridge (1995). Reprint of the second (1944) edition
Yang, D., Yang, D., Hu, G.: The Hardy Space \(H^1\) with Non-doubling Measures and Their Applications. Lecture Notes in Mathematics, vol. 2084. Springer, Cham (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Karlheinz Gröchenig.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research is supported by the Grant OPUS 2017/25/B/ST1/00599 from the National Science Centre (Narodowe Centrum Nauki), Poland.
Appendix
Appendix
In this Appendix we prove Lemma 5.2. The proof goes by standard methods, but for the convenience of the reader we present details. Actually we prove a more general result, Lemma 5.6, from which Lemma 5.2 follows immediately. Recall that \(\mathbb {W}_{t,\nu }(\mathbb {x},\mathbb {y})= \mathbb {W}_{t,\nu _c}^\mathrm{{cls}}(\mathbb {x}_1,\mathbb {y}_1)\cdot \mathbb {W}_{t,-\nu _e}^\mathrm{{exo}}(\mathbb {x}_2,\mathbb {y}_2)\), where \(\nu =(\nu _c,-\nu _e)\), and \(\nu _c\in (-1,\infty )^{d_1}\), and \(\nu _e\in (0,\infty )^{d_2}\). We start with the following lemma.
Lemma 5.3
Let \(\nu \in (-1,\infty )^d\). There exists a sequence \(\left\{ t_n \right\} _n\) such that \(t_n \rightarrow 0\) and for every \(r>0\) we have:
for a.e. \(x\in X\).
Proof
To prove (5.12) we use (1.2) and the symmetry of \(\mathbb {W}^\mathrm{{cls}}_{t_n, \nu }(x,y)\), having
In order to prove (5.13), observe that for \(f\in L^2(X,d\mu _\nu )\) we have that \(\lim _{t \rightarrow 0}\mathbb {W}^\mathrm{{cls}}_{t, \nu } f\) converges to f in \(L^2(X,d\mu _\nu )\), so we can choose a sequence with a.e. convergence. Applying this to functions \(f_n(x) = \chi _{Q(0,n)}(x)\) and using a diagonal argument we obtain a sequence \(\left\{ t_n \right\} _n\), which goes to 0, and such that for a.e. \(x\in X\) we have
and (5.13) follows from (5.14) and (5.12).
Proposition 5.4
Let \(\nu \in (-1,\infty )^d\) and \(f\in C_c(X)\). There exists a sequence \(\left\{ t_n \right\} _n\) such that \(t_n\rightarrow 0\) and for almost every \(x\in X\),
Proof
By the Lebesgue differentiation theorem we have
for almost every \(x\in X\), since \(f\in C_c(X)\). Consider the set A of points \(x \in X\) such that we have (5.15), and, additionally, (5.12)–(5.13) hold for all rational \(r > 0\). Obviously, such set has full measure. Fix \(\varepsilon > 0\) and \(x \in A\). We will show that \(\left| \mathbb {W}^\mathrm{{cls}}_{t_n, \nu }f(x) -f (x) \right| \le C\varepsilon \) for large \(n\in \mathbb {N}\). Let \(r > 0\) be a fixed rational number such that for \(s < r\) we have
Assume that \(\sqrt{t_n} < r\) for large n. We write
Applying (5.13) we obtain that \(\left| I_1 \right| < \varepsilon \) for \(t_n\) small enough.
To treat \(I_2\) we use that \(f\in C_c(X)\) and (5.12), having \(\left| I_2 \right| <\varepsilon \) for \(t_n\) small enough.
To estimate \(I_3\) we apply (1.2). Hence, by (5.16), since \(\sqrt{t_n} < r\), we obtain
To deal with \(I_4\) let \(N=\lceil \log _2(r/\sqrt{t_n}) \rceil \), so that \(r \le \sqrt{t_n} 2^N \le 2r.\) Define
for \(k=1,\ldots ,N\). Notice, that by (2.1) we have \(\mu _\nu (B(x,r2^{-k}))/ \mu _\nu (B(x,r2^{-N})) \le C_0^{N-k+1}\). Using (1.2), (5.16), we get
by taking large \(M\in \mathbb {N}\).
Lemma 5.5
Let \(f\in C_c(X)\). There exists a sequence \(\left\{ t_n \right\} _n\) such that \(t_n\rightarrow 0\) and for almost every \(\mathbb {x}\in X\),
Proof
Take \(f\in C_c(X)\) and let \(\left\{ t_n \right\} _n\) be as in Lemma 5.4 for \(\mathbb {W}_{t,(\nu _c,\nu _e)}^\mathrm{{cls}}\). By Lemma 5.4 and (1.5) we obtain
since \( F(\mathbb {x}) = \mathbb {x}_2^{-2\nu _e} f(\mathbb {x})\in C_c(X)\).
Lemma 5.6
Let \(f\in L^1(X,d\mu _\nu )\). There exists a sequence \(\left\{ t_n \right\} _n\) such that \(t_n\rightarrow 0\) and for almost every \(\mathbb {x}\in X\),
Proof
It was proved in [19, Thm. 4.1] that the maximal operator \(\sup _{t>0} \left| \mathbb {W}_{t,\nu } f \right| \) is weak type (1,1). Hence, by [10, Thm. 2.2] we know that the set \(\{f\in L^1(X,d\mu _\nu ):\lim _{t\rightarrow 0} \mathbb {W}_{t,\nu } f(\mathbb {x}) =f(\mathbb {x}) \, a.e. \}\) is closed in \(L^1(X,d\mu _\nu )\). Combining this with Lemma 5.5 and the fact that \(C_c(X)\) is dense in \(L^1(X,d\mu _\nu )\) we get the desired result.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kania-Strojec, E. The atomic Hardy space for a general Bessel operator . Monatsh Math 196, 785–822 (2021). https://doi.org/10.1007/s00605-021-01603-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00605-021-01603-y