1 Introduction

Geothermal energy is widely regarded as a sustainable and environmentally friendly energy source, particularly in regions with high tectonic activity. Taiwan, situated at the convergence of two active tectonic plates, has abundant geothermal-energy reserves. However, unlike many geothermal fields globally situated in igneous- and sedimentary-rock formations, Taiwan's prospective geothermal resources are predominantly found in areas with slate, which is a type of metamorphic rock (Song and Lu 2018; Lu et al. 2020; Weng et al. 2023). Slate differs from igneous and sedimentary rocks because it exhibits significant anisotropy and heterogeneity. These distinctive characteristics have a substantial influence on the thermal–mechanical behavior and propagation of fractures under tectonic stress and hydraulic stimulation within the slate geothermal reservoir.

The presence of a sheet-like planar structure, known as foliation, in slate significantly influences the mechanical characteristics of the rock and the manner in which fractures propagate within it. Researchers have conducted a series of tests, including tensile, uniaxial compression, and triaxial-compression tests, to evaluate the mechanical characteristics of slate (Niandou et al. 1997; Tien and Kuo 2001; Bagheripour et al. 2011; Debecker and Vervoort 2009; McLamore and Gray 1967; Nasseri et al. 2003; Saeidi et al. 2013; Stoeckhert et al. 2015; Tan et al. 2015; Vervoort et al. 2014; Weng et al. 2020; Weng et al. 2022). The collective findings from these studies reveal that the strength and deformation properties of slate are strongly dependent on the orientation angle, denoted as θ, which represents the angle between the foliation and major loading direction. Notably, the shear strength of slate has a nonlinear relationship with the orientation angle θ. It exhibits a U-shaped curve, with the highest strength occurring at θ = 0° or 90°, while the lowest strength is typically observed at angles within the range of 30°–60°. Furthermore, previous studies indicate three main failure patterns: splitting, sliding, and mixed modes, observed under compressive loads. These patterns are thought to be influenced by the textures and mineralogical characteristics of the rocks (Debecker and Vervoort 2009; Li et al. 2012; Heng et al. 2015; Zhang et al. 2023; Liu et al. 2023a, b). Although the anisotropic behavior of slate has been extensively studied, the impact of high temperatures on its mechanical properties remains uncertain, and an adequate thermal–mechanical coupling failure criterion for slate is required.

Numerous researchers have conducted extensive high-temperature triaxial tests on a diverse range of rock types including granite, limestone, marble, metamorphic sandstone, sandstone, and slate (Masri et al. 2014; Zhang et al. 2015; Xu et al. 2017; Meng et al. 2017; Xu and Karakus 2018; Yang et al. 2019; Meng et al. 2020; Qin et al. 2020; Wong et al. 2020; Shan et al. 2021; Zhu et al. 2021; Jiang et al. 2021; Jiang et al. 2022; Zhou et al. 2022; Liu et al. 2023a, b). These experiments have covered a wide temperature spectrum, ranging from room temperature to as high as 1000 °C. The resulting data have played a pivotal role in the development of various theoretical models for establishing strength–temperature correlations, as listed in Table 1. Zhang et al. (2015) observed that Carthage-marble strength decreased with increasing temperature, whereas Crab Orchard sandstone exhibited a peak strength at 100 °C, with both rock types experiencing significant strength reductions at 180 °C. Wong et al. (2020) studied the effects of thermal damage and observed that temperature variations have complex influences on rocks, impacting microcracks, water evaporation, and material composition. Meng et al. (2020) tested limestone and showed that its peak strength decreased linearly with increasing temperature. Qin et al. (2020) conducted tests on granite, revealing nonlinear relationships between the temperature and axial differential stress peak values, with maximum values occurring at 600 °C under certain confining pressures.

Table 1 Summary of high-temperature triaxial-test studies on various rocks
Full size table

For anisotropic rocks, Masri et al. (2014) investigated the temperature effect on the mechanical behavior of Tournemire shale across a wide temperature range of 20–250 °C while focusing on two distinct loading orientations: one parallel and the other perpendicular to the bedding planes. Their results revealed that as the temperature increased, both the compressive strength and Young's modulus of the rock were notably reduced. Furthermore, temperature fluctuations were found to influence the anisotropic response associated with the bedding-plane deformation. Meng et al. (2017) conducted a series of triaxial-compression tests on slate, investigating its behavior at four distinct temperatures, ranging from 20 to 120 °C. Their results demonstrated that high confining pressures mitigated the thermal effects on the mechanical properties of the rock; however, the anisotropic response of slate was not explored. Jiang et al. (2022) conducted high-temperature triaxial-compression tests on slate and provided valuable insights into its mechanical properties. They explored the impact of temperature (ranging from 20 to 150 °C) and bedding angle (ranging from 0° to 90°) on the rock specimens. Their analysis revealed that, for rock samples with the same orientation angle, the degree of damage increased with increasing temperature. Additionally, they observed an anisotropic trend in rock strength, characterized by either a V- or W-shaped relationship with the foliation angle. In summary, these high-temperature triaxial tests provided valuable insights into the effects of temperature on the mechanical properties of various rock types. These findings emphasize the need for tailored testing to understand the thermal–mechanical interactions of rocks.

To assess the mechanical behavior of slate within the context of geothermal-reservoir operation, this study aims to establish an anisotropic thermal–mechanical coupling failure criterion (ATMFC) for slate. Slate samples with varying foliation angles were extracted from deep boreholes located at a geothermal site in Taiwan. Subsequently, a series of triaxial-compression tests was conducted under various confining pressures and temperatures to investigate the shear-strength characteristics of the slate. Direct-shear tests were conducted to determine the shear strength along the slate foliation planes. By integrating these test results, an ATMFC is proposed, which is validated against both the test data and prior research findings. These results are expected to facilitate the evaluation of geothermal development in slate areas.

2 Rock Material and Specimen Preparation

The rock specimens studied were slate from a geothermal site in Taitung County, Taiwan, with the highest temperature of 139 °C, belonging to the Hongye Formation (Fig. 1a). The Hongye Formation comprises slate and metasandstone. Field observations indicated that the foliation of the slate core was well developed and planar. Rock specimens were sampled from two nearby boreholes in the range of 200–800 m. According to the analysis results of the physical properties, the unit weight was approximately 2650 kg/m3, and the porosity was approximately 1.20%. The foliation dip angles of the specimens varied from 15° to 84°. Petrographic analysis demonstrated that the sampled slate mainly consisted of sheet-like clay minerals, mica, and quartz (CGSMOEA 2023). The backscattered electron image shows that the foliation was well developed and smooth (Fig. 1b). The thermal conductivity of the slate at 200 °C was 2.39 W/m K and the specific heat was 1.049 J/g °C.

Fig. 1
figure 1

Slate sample utilized in this study

Full size image

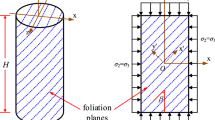
Cylindrical specimens 61 mm in diameter and at least 146 mm in height were prepared for the triaxial tests. The specimens were meticulously prepared following the standards outlined in ASTM D7012-14 and ISRM (1981) for material testing. The preparation process is described below:

  1. (a)

    The slate core was carefully extracted from the core box and cut using a double-edged core cutting machine with a blade separation of 140 mm. It was ensured that the length-to-diameter ratio (L/D) fell within the range of 2.0–2.5.

  2. (b)

    During the double-edged cutting, special attention was given to ensuring that the core axis was perpendicular to the blade and that the flatness of both ends of the cylindrical specimen did not exceed 0.2 mm.

  3. (c)

    After the cutting, the loading angle of the slate specimen was measured and documented. Subsequently, it was wrapped in plastic to protect it from weathering and await further testing in the rock triaxial test.

In addition, the specimens for direct-shear testing had the same diameter of 61 mm, with a minimum height of 65 mm. A total of 34 triaxial specimens and 10 direct-shear specimens were prepared for this study.

3 Laboratory Tests

3.1 Direct-Shear Test

To determine the shear strength of the foliation, direct-shear tests were performed using a rock direct-shear apparatus (Fig. 2a). This apparatus was equipped with a pair of MTS hydraulic actuators that could apply both vertical (normal) and horizontal (shear) loads, reaching up to 100 kN, and had a displacement capacity of 150 mm. The applied loads were controlled using an MTS servo-control system. Load variation was measured using load cells, and vertical displacement was tracked using two vertical linear variable differential transformers (LVDTs). Additionally, two other LVDTs were utilized to measure horizontal displacement with an accuracy of ± 0.2 mm. The LVDTs were mounted onto the loading frame using magnetic bases throughout the testing process.

Fig. 2
figure 2

Direct-shear test of slate foliation. a Direct-shear testing apparatus; b top view of the HY slate specimen; c profile view of the HY slate specimen after casting of gypsum

Full size image

In terms of specimen orientation, all foliation planes were centrally situated within a 10-mm-thick shear zone (Fig. 2b, c). This shear zone was consistently maintained in horizontal alignment within the shear box, and its void was filled with rigid gypsum. The design of the direct-shear tests considered engineering applicability; thus, it encompassed normal stress levels ranging from 1.2 to 20.2 MPa. Consequently, the obtained experimental data were relevant across a broad spectrum of overburden conditions. Subsequently, the shear velocity was set as 1 mm/min. During the test, the shear force and shear displacement were measured based on load cells, and LVDTs were used to measure the displacements. Ten specimens were tested under the designated normal stress levels to obtain the foliation failure envelope.

3.2 Rock Triaxial Test

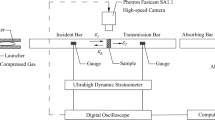
To investigate the thermomechanical characteristics of the slate, experiments were performed on a high-temperature and high-pressure rock triaxial apparatus, the MTS 815 system (Fig. 3). The apparatus can apply an axial load with a maximum capacity of 2669 kN. The loading rates ranged from 0.001 to 30 mm/min and the precision was set at 0.0005 mm/min. A confining-pressure intensifier was used to provide the internal confining pressure of the triaxial cell, and pressure was applied to the fluid to reach the target confining pressure with a maximum pressure of 83 MPa. The axial and hydrostatic stresses were under servo control, which enabled the execution of tests with the designated stress paths. A temperature-control module was used to control the furnace heater. The operating temperature of the machine had a maximum of 200 °C. To measure the deformation of the specimen, two axial extensometers and a circumferential extensometer were used to measure the specimen displacement in the axial and lateral directions, respectively (Fig. 4). The measurement accuracy of the extensometer was 0.01 mm.

Fig. 3
figure 3

High-pressure and high-temperature rock triaxial testing system

Full size image
Fig. 4
figure 4

Measurement of axial and radial strain in a rock sample. One circumferential and two axial extensometers are configured to capture both the radial and axial deformations of the specimen, respectively

Full size image

The triaxial tests were strategically designed to align with engineering applications, encompassing a confining-pressure range of 5–25 MPa. This range corresponded to overburden depths spanning approximately 200–1000 m, making the experimental data pertinent to a broad spectrum of engineering endeavors. All tests adhered to the conventional triaxial compressive procedure ASTM D7012-14 (2014), comprising two stages: hydraulic compression and deviatoric compression. Throughout the hydraulic compression stage, the confining pressure ascended at a rate of 1 MPa/min. Once the targeted confining pressure was attained, it remained constant while the axial load persisted at a subsequent displacement rate of 0.002 mm/min. 13 tests were carried out at a consistent room temperature of 25 °C to explore the failure envelope of slate across different orientation angles.

Subsequently, a total of 20 tests were conducted at a high temperature of 100 °C, with one test performed at 200 °C, to assess the thermal effect on the anisotropic strength variation of slate. The heating process was initiated before the hydraulic compression stage, with the temperature increasing at approximately 1.25 °C/min, as verified by the thermometer. Upon reaching the designated temperature, the stability of the extensometer reading was confirmed for over an hour, indicating uniform heating of the test specimen to the target temperature. Subsequently, the test procedure followed the aforementioned triaxial compressive procedure. Due to the limited number of available specimens, the majority were utilized for testing at the elevated temperature of 100 °C to investigate the anisotropic failure envelope.

4 Test Results

4.1 Results of Direct-Shear Test

Figure 5 shows the results of the direct-shear test on the slate foliation under different normal stresses ranging from 1.2 to 20.2 MPa. The results indicated that the shear strength and shear stiffness of the foliation increased with normal stress (Fig. 5a). Figure 5b illustrates the variations in the vertical displacements during the shearing process. At lower normal stresses, below 7.7 MPa, it exhibits shear dilation. However, as the normal stress increases, the extent of shear dilation gradually diminishes, ultimately transitioning into shear contraction at normal stresses exceeding 15.2 MPa. According to the results, Fig. 5c presents the failure envelope of the slate foliation. The failure envelope of the foliation can be described using the Mohr–Coulomb failure criterion, with the foliation having a friction angle (ϕ) of 27.8° and cohesion (c) of 1.89 MPa.

Fig. 5
figure 5

Results of direct-shear test for HY slate foliation

Full size image

4.2 Results of Triaxial Test

Figure 6 shows the stress–strain curves from the triaxial tests conducted under confining pressures varying from 5 to 25 MPa. The specimen number is denoted in the HY-orientation angle-confining pressure–temperature format. A total of 13 tests at a room temperature of 25 °C were carried out and eight typical stress–strain curves were selected, as shown in Fig. 6a. Furthermore, a total of 21 tests at high temperatures of 100 °C and 200 °C were conducted, and 18 representative curves are shown in Fig. 6b. The results indicate that the slate consistently demonstrated brittle behavior within the designated range of confining pressure, whether tested at room or elevated temperatures. Notably, the peak strength of the slate was influenced by both confining pressure and loading angle. Tables 2 and 3 present the comprehensive details of the test conditions for each specimen.

Fig. 6
figure 6

Measured stress–strain curves of the triaxial tests under different confining pressures and temperatures

Full size image
Table 2 Summary of triaxial-compression test results at 25 °C
Full size table
Table 3 Summary of triaxial-compression test results at 100 °C and 200 °C
Full size table

Figure 7 shows the failure patterns of the specimens after the triaxial tests. Three failure modes were observed based on the failure patterns: splitting, sliding, and mixed. At a room temperature of 25 °C, the specimens subjected to high and low orientation angles, specifically HY 84-20-25, HY 83-25-25, and HY 15-25-25, exhibited a split-mode failure, characterized by a primary fracture penetrating the multilayer foliation (Fig. 7a). Conversely, in the case of specimens HY 55-20-25, and HY 49-25-25, sliding failure was observed along the foliation. Additionally, specimens HY 55-5-25 and HY 56-10-25 exhibited a mixed failure mode, indicative of a combination of sliding and split failures. The three failure modes were also observed in the failure patterns at a temperature of 100 °C (Fig. 7b). The specifics of the corresponding failure modes of the specimens are presented in Tables 2 and 3.

Fig. 7
figure 7

Failure patterns of slate specimen after the triaxial test

Full size image

The relationship between the major principal strength under different orientation angles and the corresponding failure modes was further investigated, and is plotted in Fig. 8. Similar to the results of previous research, in cases where the orientation angle falls within a specific range (approximately 20°–60°), the strength of the slate was primarily dominated by the foliation strength, leading to sliding failure along the foliation. Conversely, outside this range, the strength was affected by the intrinsic properties of the rock material, resulting in either splitting or mixed failure modes. As the confining pressure increased, the sliding range decreased. These phenomena were consistently observed across a wide range of temperatures.

Fig. 8
figure 8

Relationship between the failure modes and orientation angles at different temperatures

Full size image

4.3 Effect of Temperature on the Strength

To evaluate the temperature effect on the shear strength of slate, Fig. 9 illustrates the variations of strength under different orientation angles at 25 and 100 °C, supplementing the data obtained from the experiments. Based on previous research (Tien and Kuo 2001), U-shaped curves were plotted to depict how the failure principal stress varied with the orientation angle. The trendlines are solely employed to indicate potential variations in slate strength. A proposed failure criterion will be introduced in the next section. Figure 9a–e illustrates the variations in strength across a range of confining pressures from 5 to 25 MPa. The results revealed significant strength reductions due to high temperature when the orientation angle was within both low and high values (θ < 10° and θ > 70°). Conversely, marginal thermal degradation was observed when the orientation angle was within the range of 10°–70°. This strength variation appeared to be closely linked to the specific failure modes that were exhibited. In cases where the orientation angle was within the range of 10°–70°, the strength of the slate was primarily governed by the shear strength of the foliation, i.e., sliding failure along the foliation, which exhibited only mild sensitivity to temperature fluctuations. However, in situations where the orientation angle was either low or high, the primary influence on the strength originated from the intrinsic characteristics of the rock material, resulting in split-mode failure. In these cases, the elevated temperatures significantly diminished the intrinsic strength of the rock material perpendicular to the foliation plane. A higher temperature lowered the strength anisotropy of the slate, i.e., the effect of the orientation angle became less significant. These phenomena could be observed in the test results for the entire range of confining pressures, which provide a basis for establishing an ATMFC.

Fig. 9
figure 9

Influence of temperature on shear strength at various orientation angles and confining pressures

Full size image

5 Proposed Anisotropic Thermal–Mechanical Coupling Failure Criterion

Based on the test results, this study adopted a two-step approach to establish a criterion for assessing ATMFC in slates. In the initial step, a failure criterion for transversely isotropic rocks was adopted to characterize the shear strength of rock specimens at different orientation angles θ under varying confining pressures. In the subsequent step, thermal degradation was considered, resulting in the formulation of an ATMFC. The validity of the proposed criterion was substantiated by the test results of this and other relevant studies.

5.1 Failure Criterion of Foliated Metamorphic Rock

Based on the existing failure criterion for transversely isotropic rocks (Jaeger 1960, Tien and Kuo 2001), the major principal stress for sliding along the foliation can be expressed as:

$${\sigma }_{1(\theta )}={\sigma }_{3}+\frac{2\left({c}_{j}+{\sigma }_{3}tan{\phi }_{j}\right)}{sin\left(2\theta \right)\left(1-tan\theta tan{\phi }_{j}\right)},$$
(1)

where \({c}_{j}\) is the cohesion of the foliation, and \({\phi }_{j}\) is the friction angle of the foliation. Furthermore, the minimum strength of slate occurs at the critical weak plane of \((45^\circ +{\phi }_{j}/2\)).

The Hoek–Brown criterion (Hoek and Brown 1980) was adopted to describe the failure envelope of the rock material at θ = 0° and 90°. The strength at different orientation angles, θ, can be described as follows:

$${\sigma }_{1(\theta )}={\sigma }_{3}+\frac{k\sqrt{m{\sigma }_{3}{\sigma }_{\text{c}}+{{\sigma }_{c}}^{2}}}{{cos}^{4}\theta +k{sin}^{4}\theta +2nk{sin}^{2}\theta {cos}^{2}\theta },$$
(2)

where m is the parameter in the Hoek–Brown criterion, \({\sigma }_{c}\) represents the uniaxial compressive strengths of the rock at θ = 0° or 90°, and k and n are the strength ratio and transverse anisotropy parameters, respectively. These are defined as follows:

$$n=\left(\frac{{E}_{\left(90\right)}}{{2G}^{\prime}}-{\nu }^{\prime}\right),$$
(3)
$$k=\frac{{\sigma }_{\left.1(0^\circ \right)}-{\sigma }_{3}}{{\sigma }_{\left.1(90^\circ \right)}-{\sigma }_{3}},$$
(4)

where \({E}_{\left(90\right)}\) is the Young’s modulus of rock at θ = 90°, \({G}{\prime}\) is the shear modulus for the plane normal to the foliation. \({\nu }{\prime}\) is the Poisson’s ratio, which describes the transverse strain within the foliation induced by normal stress acting perpendicular to the foliation plane.

In the case of a substantial orientation angle (θ > 60°), the influence of the value \({cos}^{4}\theta\) can be disregarded (while \(k\) should exceed 0.1), simplifying Eq. 2 as follows:

$${\sigma }_{\left.1(\theta \right)}={\sigma }_{3}+\left({\sigma }_{\left.1(90^\circ \right)}-{\sigma }_{3}\right)\times \frac{1}{{sin}^{4}\theta +2n{cos}^{2}\theta {sin}^{2}\theta }.$$
(5)

The transverse anisotropy parameter, n, can be derived from the results of a compression test conducted within a θ range of approximately 60°–80°.

Based on the results of the direct-shear test, the cohesion and friction angles of the foliation were 1.89 MPa and 27.8°, respectively. Consequently, using Eq. 1, the major principal stress induced by sliding at 25 °C under varying confining pressures was calculated and plotted, as shown in Fig. 10. The minimum strength of slate under different confining stresses can be determined from the foliation strength at the critical weak plane of \((45^\circ +{\phi }_{j}/2\)). For the nonsliding range, triaxial tests under confining pressures of 15 and 20 MPa were used to calibrate the required parameters of Eq. 2. By combining the two equations, the failure criterion of the slate at 25 °C was obtained, exhibiting a U-shaped curve (Fig. 10a). Figure 10a illustrates that under a confining pressure of 5 MPa, sliding failure occurred within the θ range of 5°–57°. As the confining pressure increased, the sliding failure range decreased. This phenomenon is also observed in experimental results from other studies on transversely isotropic rocks (Tien and Kuo 2001; Chiou et al. 2013; Asadi and Bagheripour 2015; Alsuwaidi et al. 2021; Weng et al. 2022). The results demonstrated good agreement between the predicted values and experimental data, achieving a determination coefficient (R2) of 0.907 (Fig. 10b). The detailed material parameters for the adopted criteria are listed in Table 4.

Fig. 10
figure 10

Comparison of the experimental and predicted shear strengths of slate at 25 °C

Full size image
Table 4 Parameters of transversely isotropic failure criteria
Full size table

Figure 11 illustrates the predicted shear strength at a temperature of 100 °C under confining pressures from 5 to 25 MPa. Owing to the lack of direct-shear test results at high temperatures, high-temperature triaxial tests were employed to calibrate all requisite material parameters. Table 4 lists the material parameters of the criterion at 100 °C. Figure 11a shows that the adopted criterion provided a reasonable prediction based on the experimental data. Although certain discrepancies were noticeable within the data points corresponding to 5 and 25 MPa, the overarching pattern could reflect anisotropic strength variations. The predictions were further substantiated by the determination coefficient (R2) of 0.778, as illustrated in Fig. 11b, thereby affirming the capability of the adopted criterion to predict strength variations at 100 °C.

Fig. 11
figure 11

Comparison of the experimental and predicted shear strengths of slate at 100 °C

Full size image

5.2 Anisotropic Thermal–Mechanical Coupling Failure Criterion

The ATMFC for slate is proposed based on the thermal effect described in Sect. 4.3, and it comprises two distinct components: sliding and non-sliding failures. In the case of sliding failure, thermal degradation was marginally significant; as such, Eq. (1) was employed to characterize the strength of foliation at room or elevated temperatures. Conversely, for non-sliding failure, to account for the thermal degradation of the rock material within the temperature range of 25–200 °C, Eq. (2) was adapted as follows:

$${\sigma }_{1\left(\theta ,T\right)}={\sigma }_{3}+\frac{k\sqrt{m{\sigma }_{3}{\sigma }_{c(25^\circ{\rm C} )}+{{\sigma }_{c(25^\circ{\rm C} )}}^{2}}}{{cos}^{4}\theta +k{sin}^{4}\theta +2nk{sin}^{2}\theta {cos}^{2}\theta }\times \left(1+\frac{\left(\eta -1\right)}{\omega \cdot \left[1+{e}^{\left({T}_{i}-T\right)\gamma }\right]}\right),$$
(6)

where \({\sigma }_{1\left(\theta ,T\right)}\) is the maximum principal stress varying with temperature T and orientation angle \(\theta\), Ti is the characteristic temperature for thermal degradation, and γ is the degradation parameter. \(\eta\) and \(\omega\) are the strength and strength-reduction ratios under a particular orientation angle between the specified temperatures, which are defined as follows:

$$\eta =\frac{{\sigma }_{1\left(\theta ,{T}_{2}\right)}}{{\sigma }_{1\left(\theta ,{T}_{1}\right)}},$$
(7)
$$\omega =\frac{{\sigma }_{1\left(\theta ,{T}_{1}\right)}-{\sigma }_{1\left(\theta ,{T}_{2}\right)}}{{\sigma }_{1\left(\theta ,{T}_{1}\right)}-{\sigma }_{1\left(\theta ,{T}_{max}\right)}}.$$
(8)

The uniaxial compressive strength at 25 °C, 100 °C, and 200 °C were chosen as \({\sigma }_{1\left(\theta ,{T}_{1}\right)}, {\sigma }_{1\left(\theta ,{T}_{2}\right)}, \text{and}\, { \sigma }_{1\left(\theta ,{T}_{max}\right)}\), respectively. Figure 12 shows the proposed thermal-degradation curves for the slate under different confining pressures. The primary degradation occurs in the range of 60–110 °C. To investigate the influence of parameters γ and Ti on the proposed failure criterion, a sensitivity analysis was performed. Figure 13a shows the influence of degradation parameter γ on major principal stress at failure. As the value of parameter γ rises, the degree of strength degradation notably increases from lower to higher temperatures, resulting in a steeper thermal-induced degradation curve. As the characteristic temperature Ti gradually increases, the thermal-induced degradation curve retains its consistent shape while shifting horizontally toward the higher temperature zone (Fig. 13b). Conversely, a decrease in Ti results in the curve shifting horizontally toward the lower temperature zone.

Fig. 12
figure 12

The proposed thermal-degradation model on the shear strength of slate

Full size image
Fig. 13
figure 13

Influence of parameters γ and Ti on the proposed failure criterion

Full size image

In the context of the suggested ATMFC, ten material parameters (\({c}_{j,25^\circ{\rm C} }\), \({\phi }_{j,25^\circ{\rm C} }\), \({\sigma }_{c,25^\circ{\rm C} }\), \({\sigma }_{c,100^\circ{\rm C} }\), \({\sigma }_{c,200^\circ{\rm C} }\), \(m\), \(k\), n, Ti, and γ) are necessary, and these can be ascertained through the following test results. The two parameters related to the foliation strength, \({c}_{j,25^\circ{\rm C} }\) and \({\phi }_{j,25^\circ{\rm C} }\), could be obtained from the direct-shear tests of foliation. The uniaxial compressive strength at different temperatures, \({\sigma }_{c,25^\circ{\rm C} }\), \({\sigma }_{c,100^\circ{\rm C} }\), and \({\sigma }_{c,200^\circ{\rm C} }\), could be measured through uniaxial compression tests or point load tests at θ = 0° or 90°. The parameters \(m\), n, and \(k\) could be calibrated through triaxial tests at different orientation angles. The two parameters for thermal degradation, Ti and γ, could be obtained from the triaxial test at different temperatures under a certain orientation angle. Table 5 summarizes the proposed criterion and the required material parameters.

Table 5 Material parameters of the proposed anisotropic thermal–mechanical coupling failure criterion (ATMFC)
Full size table

In practical applications, the parameters can be determined using the following procedure. Initially, three direct-shear tests are conducted on the slate foliation at room temperature, yielding the strength parameters for the foliation, \({c}_{j,25^\circ{\rm C} }\) and \({\phi }_{j,25^\circ{\rm C} }\). Subsequently, to ascertain the values of parameters \(m\), \(k\), n, and \({\sigma }_{c,25^\circ{\rm C} }\), a minimum of four triaxial-compression tests are performed under varying confining pressures, all at room temperature. It is recommended to select one specimen with θ ranging from 0° to 10° and two specimens with θ between 60° and 90°.A more extensive set of experiments is required for high-temperature triaxial tests, encompassing at least four tests at 100 °C or 200 °C, all under a consistent confining pressure. These tests serve to establish the thermal-degradation curve, as shown in Fig. 12, subsequently enabling the determination of \({\sigma }_{c,100^\circ{\rm C} }\), \({\sigma }_{c,200^\circ{\rm C} }\), Ti, and γ.

5.3 Criterion Validation and Prediction

The slate test results were used to evaluate the validity of the proposed model. The required parameters were derived from the direct-shear and triaxial test data of the HY slate, as presented in Table 5. For the temperature-degradation curve, the characteristic temperature Ti was 85 °C, and the degradation parameter γ was 0.102. A comparison of the experimental and predicted values of the failure criterion showed that the coefficient of determination, R2 = 0.863, as shown in Fig. 14. Figure 15 shows the failure envelope of the proposed criterion, along with the triaxial-test data of the HY slate for each confining pressure. Notably, the proposed criterion offered reasonable predictions for thermal–mechanical coupling failure, particularly within the confining pressure range of 15–25 MPa. In addition, a three-dimensional surface diagram illustrates the temperature-orientation angle-failure principal stress relationship as per the proposed criterion, showing the anisotropic thermal-degradation features of the slate across different confining pressures (Fig. 16).

Fig. 14
figure 14

Comparison of the experimental and predicted shear strengths of slate at different temperatures

Full size image
Fig. 15
figure 15

Comparison of the experimental and predicted shear strengths of slate considering diverse orientation angles, temperatures, and confining pressures

Full size image
Fig. 16
figure 16

A three-dimensional illustration depicting the interplay between temperature, orientation angle, and the principal stress at failure, with corresponding test results for slate plotted within the same figure

Full size image

To substantiate the applicability of ATMFC, this study gathered a comprehensive dataset comprising triaxial-test results for three anisotropic rocks spanning various temperatures, orientation angles, and confining pressures. Masri et al. (2014) conducted high-temperature triaxial tests on Tournemire shale exclusively investigating the orientation angles of 0° and 90°. These tests covered a wide range of confining pressures, from 0 to 20 MPa, and temperatures spanning from 20 to 250 °C, comprising a total of 40 test sets. Figure 17 shows the ATMFC predictions for temperature-induced rock degradation under various confining pressures at the orientation angles of 0° and 90°. Noteworthy is the alignment of ATMFC predictions with experimental observations. Zhou et al. (2023) conducted high-temperature true triaxial tests on gneiss granite, covering orientation angles ranging from 0° to 60° and temperatures spanning 25–200 °C under a confining pressure of 20 MPa. The results presented in Fig. 18 indicate thermal degradation at an orientation of θ = 0°. However, at θ = 30° (representing sliding failure along foliation), the strength remains relatively constant across temperatures. The ATMFC reasonably predicted this behavior. Furthermore, Rybacki et al. (2015) conducted high-temperature triaxial tests on Dotternhausen shale at an orientation of 90°, with temperatures ranging from 20 to 300 °C under a confining pressure of 50 MPa. Figure 19 illustrates that the ATMFC provided reasonable predictions of the thermal degradation behavior. The required parameters for thermal degradation for the three rocks are listed in Table 6. In summary, the proposed criterion demonstrates its effectiveness in predicting the strength of anisotropic rocks under varying conditions of orientation angle, temperature, and confining pressure, as evidenced by its agreement with experimental results.

Fig. 17
figure 17

Comparison of the experimental and predicted shear strengths of Tournemire shale under different confining pressures and temperatures. Test data from Masri et al. (2014)

Full size image
Fig. 18
figure 18

Comparison of the experimental and predicted shear strengths of gneiss granite under different temperatures and orientation angles. Test data from Zhou et al. (2023)

Full size image
Fig. 19
figure 19

Comparison of the experimental and predicted shear strengths of Dotternhausen shale under different temperatures. Test data from Rybacki et al. (2015)

Full size image
Table 6 Material parameters of the thermal gradation for transversely isotropic rocks
Full size table

6 Conclusions

This study aimed to assess the mechanical behavior of slate within the context of geothermal-reservoir operation and establish an ATMFC for slate. Slate samples obtained from a geothermal site in Taiwan were subjected to a series of direct-shear and triaxial-compression tests at various confining pressures and temperatures. The results showed that the orientation angle within a specific range significantly influenced the strength of the slate, primarily owing to the foliation strength. Beyond this range, intrinsic rock properties led to different failure modes. The effect of the confining pressure was also observed, with increased pressure reducing the sliding range.

Elevated temperatures significantly diminished the strength anisotropy of the slate, a phenomenon consistently observed at different temperatures and confining pressures. These findings provided a foundation for the development of an ATMFC. The validity of the proposed criterion, which incorporates both the orientation angle and thermal-degradation effects, was demonstrated through experimental results. A three-dimensional surface diagram was used to visualize the relationship between the temperature, orientation angle, and failure principal stress, highlighting the anisotropic thermal-degradation characteristics of slate under varying confining pressures.

In summary, the proposed criterion successfully predicted the strength of anisotropic rocks at different orientation angles, temperatures, and confining pressures. This provided valuable insights for the evaluation of geothermal development in slate areas and enhanced the understanding of the thermal–mechanical behavior of these materials in geothermal reservoirs. However, it is noted that most triaxial tests were limited to 25 °C and 100 °C due to constraints related to the availability of rock samples. In future research, a broader range of metamorphic-rock samples will be collected and tested across a wider range of temperatures to ensure the robustness and practical applicability of the proposed criterion. Furthermore, integrating this criterion into discrete element programs will enable a more comprehensive analysis of the thermal–hydraulic–mechanical conditions at actual geothermal sites.