Skip to main content
SpringerLink
Log in

When Large Deformation Analysis Meets Large Deformation Phenomenon: Comparative Study and Improvement

  • Original Paper
  • Published:
Rock Mechanics and Rock Engineering Aims and scope Submit manuscript

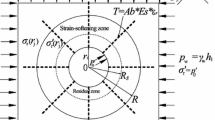
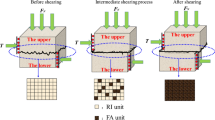
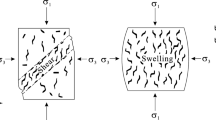
Abstract

Large deformation phenomena in rock engineering are commonly key bottlenecks impeding engineering progress. Correspondingly, large deformation analysis in rock mechanics has a widespread impact on mechanism understanding, prevention, and control guidance. Various large deformation schemes broadly categorized as hypoelastic- and hyperelastic-based models exist in the literature and software. Without an understanding of the capabilities and demerits of these schemes, the diversity in choices inadvertently leads to pitfalls, placing engineering endeavors at a disadvantage. In this work, we review and compare the most prevalent schemes (including PK2-Green, Jaumann, Green–Naghdi, Truesdell, and hyperelastic-based schemes) from perspective of rock mechanics, with an emphasis on their application in rock engineering, and further develop a hyperelastic-based large deformation scheme (marked as Cauchy-Ln scheme) based on Cauchy stress and Hencky logarithm strain. The proposed model realizes the separation of material nonlinearity and geometry nonlinearity. Several typical large deformation phenomena in rock engineering are studied. The relationships between large deformation phenomena and large deformation analyses are clarified under different circumstances. Especially under large strain conditions, the PK2-Green scheme is enfeebled, and the hypoelastic-based scheme should be used with caution. For rock material with an apparent pressure-sensitive effect, the proposed Cauchy-Ln scheme is superior.

Highlights

  • The connections between large deformation phenomenon and large deformation analysis are delineated.

  • Prevalent large deformation schemes are compared from a rock mechanics perspective with an emphasis on application in rock engineering.

  • A newly hyperelastic-based large deformation numerical model, enhancing compatibility with rocks, is developed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Data availability

All data and codes are available from the corresponding author upon reasonable request.

Abbreviations

\({\mathbb{a}}\) :

Spatial tangent modulus

\({\varvec{b}}^{{\text{e}}}\) :

Elastic left Cauchy–Green deformation tensor

\({\varvec{b}}\) :

Body force

\( {\mathbb{D}}^{{\text{e}}}\) :

Linear isotropic elasticity tensor

\( {\mathbb{D}}^{{{\text{ep}}}}\) :

Elastoplastic tangent modulus

\({\varvec{d}}\) :

Rate of deformation tensor

\( {\varvec{d}}^{{\text{e}}}\) :

Rate of elastic deformation tensor

\( {\varvec{d}}^{{\text{p}}}\) :

Rate of plastic deformation tensor

\(E\) :

Young’s modulus

\({\varvec{E}}\) :

Green strain tensor

\({\varvec{e}}\) :

Eulerian Hencky strain tensor

\({\varvec{F}}\) :

Deformation gradient tensor

\({\varvec{I}}\) :

Second-order identity tensor

\(J\) :

Jacobian of the deformation gradient

\({\varvec{l}}\) :

Velocity gradient tensor

\({\varvec{P}}\) :

First Piola–Kirchhoff stress tensor

\(q\) :

Hardening force

\({\varvec{R}}\) :

Rotation tensor

\({\varvec{S}}\) :

Second Piola–Kirchhoff stress tensor

\({\varvec{t}}\) :

Surface traction vector

\({\varvec{U}}\) :

Right stretch tensor

\({\varvec{u}}\) :

Displacement vector

\({\varvec{V}}\) :

Left stretch tensor

\({\varvec{w}}\) :

Spin tensor

x :

Position vector in current configuration

X :

Position vector in initial configuration

\(\gamma\) :

Plastic multiplier

\({\varvec{\varepsilon}}\) :

Infinitesimal strain tensor

\( {\varvec{\varepsilon}}^{{\text{e}}}\) :

Elastic strain tensor

\( {\varvec{\varepsilon}}^{{\text{p}}}\) :

Plastic strain tensor

\( \overline{\varepsilon }^{{\text{p}}}\) :

Effective plastic strain

\(\theta\) :

Frictional angle

\(\vartheta\) :

Dilatancy angle

\(\nu\) :

Poisson’s ratio

\({\varvec{\sigma}}\) :

Cauchy stress tensor

\({\varvec{\sigma}}^{\nabla }\) :

The specific stress rate of Cauchy stress

\({\varvec{\tau}}\) :

Kirchhoff stress tensor

\(\psi\) :

Strain density per unit reference volume

\({\Phi }\) :

Yield function

\({\Psi }\) :

Flow potential

\({\varvec{\varOmega}}\) :

Angular velocity tensor

References

  • Abe Y, Yamada S, Hoshi K, Kyoya T (2024) Reconstruction of Cam–Clay model based on multiplicative decomposition of the deformation gradient. Comput Geotech 166:105958

    Article  Google Scholar 

  • Barla G, Bonini M, Semeraro M (2011) Analysis of the behaviour of a yield-control support system in squeezing rock. Tunn Undergr Space Technol 26(1):146–154

    Article  Google Scholar 

  • Bathe K, Ramm E, Wilson EL (1975) Finite element formulations for large deformation dynamic analysis. Int J Numer Meth Eng 9(2):353–386

    Article  Google Scholar 

  • Belytschko T, Liu WK, Moran B, Elkhodary K (2013) Nonlinear finite elements for continua and structures. Wiley, Hoboken

    Google Scholar 

  • Bennett KC, Regueiro RA, Borja RI (2016) Finite strain elastoplasticity considering the Eshelby stress for materials undergoing plastic volume change. Int J Plast 77:214–245

    Article  Google Scholar 

  • Bennett KC, Regueiro RA, Luscher DJ (2019) Anisotropic finite hyper-elastoplasticity of geomaterials with Drucker-Prager/cap type constitutive model formulation. Int J Plast 123:224–250

    Article  Google Scholar 

  • Cabezas EE, Celentano DJ (2004) Experimental and numerical analysis of the tensile test using sheet specimens. Finite Elem Anal Des 40(5):555–575

    Article  Google Scholar 

  • Cavers DS (1981) Simple methods to analyze buckling of rock slopes. Rock Mech 14(2):87–104

    Article  Google Scholar 

  • Chen WF (1975) Limit analysis and soil plasticity. Elsevier, Amsterdam

    Google Scholar 

  • Chen Z, He C, Xu G, Ma G, Wu D (2019) A case study on the asymmetric deformation characteristics and mechanical behavior of deep-buried tunnel in phyllite. Rock Mech Rock Eng 52(11):4527–4545

    Article  Google Scholar 

  • Cheng X, Tang C, Zhuang D (2022) A finite-strain viscoelastic-damage numerical model for time-dependent failure and instability of rocks. Comput Geotech 143:104596

    Article  Google Scholar 

  • Eterovic AL, Bathe K (1990) A hyperelastic-based large strain elasto-plastic constitutive formulation with combined isotropic-kinematic hardening using the logarithmic stress and strain measures. Int J Numer Meth Eng 30(6):1099–1114

    Article  Google Scholar 

  • Gadala MS, Wang J (2000) Computational implementation of stress integration in Fe analysis of elasto-plastic large deformation problems. Finite Elem Anal Des 35(4):379–396

    Article  Google Scholar 

  • Ghasemi M, Corkum AG, Gorrell GA (2021) Ground surface rock buckling: analysis of collected cases and failure mechanisms. Bull Eng Geol Environ 80(6):4255–4276

    Article  Google Scholar 

  • Green AE, Naghdi PM (1971) Some remarks on elastic-plastic deformation at finite strain. Int J Eng Sci 9(12):1219–1229

    Article  Google Scholar 

  • Guan K, Zhu W, Wei J, Liu X, Niu L, Wang X (2018) A finite strain numerical procedure for a circular tunnel in strain-softening rock mass with large deformation. Int J Rock Mech Min 112:266–280

    Article  Google Scholar 

  • Guo H, Chen X, He M, Xi S, Tang J (2010) Frictional contact algorithm study on the numerical simulation of large deformations in deep soft rock tunnels. Min Sci Technol (china) 20(4):524–529

    Article  Google Scholar 

  • Hashiguchi K (2019) Multiplicative hyperelastic-based plasticity for finite elastoplastic deformation/sliding: a comprehensive review. Arch Comput Method E 26(3):597–637

    Article  Google Scholar 

  • He M, Gong W, Wang J et al (2014) Development of a novel energy-absorbing bolt with extraordinarily large elongation and constant resistance. Int J Rock Mech Min 67:29–42

    Article  Google Scholar 

  • Ji W, Waas AM, Bazant ZP (2013) On the importance of work-conjugacy and objective stress rates in finite deformation incremental finite element analysis. J Appl Mech. https://doi.org/10.1115/1.4007828

    Article  Google Scholar 

  • Jing L (2003) A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int J Rock Mech Min 40(3):283–353

    Article  Google Scholar 

  • Kazakidis VN (2002) Confinement effects and energy balance analyses for buckling failure under eccentric loading conditions. Rock Mech Rock Eng 35(2):115–126

    Article  Google Scholar 

  • Kojić M, Bathe K (1987) Studies of finite element procedures—stress solution of a closed elastic strain path with stretching and shearing using the updated Lagrangian Jaumann formulation. Comput Struct 26(1):175–179

    Article  Google Scholar 

  • Korobeynikov SN (2023) Families of hooke-like isotropic hyperelastic material models and their rate formulations. Arch Appl Mech 93(10):3863–3893

    Article  Google Scholar 

  • Le Pense S, Arson C, Pouya A (2016) A fully coupled damage-plasticity model for unsaturated geomaterials accounting for the ductile-brittle transition in drying clayey soils. Int J Solids Struct 91:102–114

    Article  Google Scholar 

  • Li Z, Lv Q, Zhu H, Hu J, Feng J, He M (2019) Laboratory testing and modeling of a high-displacement cable bolt. Int J Geomech 19(7):4019078

    Article  Google Scholar 

  • Li G, Cheng X, Hu L, Tang C (2021) The material-structure duality of rock mass: insight from numerical modeling. Int J Rock Mech Min 144:104821

    Article  Google Scholar 

  • Liu C, Hong H (1999) Non-oscillation criteria for hypoelastic models under simple shear deformation. J Elasticity 57(3):201–241

    Article  Google Scholar 

  • Longère P (2019) Numerical integration of rate constitutive equations in presence of large strains and rotations. Mech Res Commun 95:61–66

    Article  Google Scholar 

  • Meng L, Li T, Jiang Y, Wang R, Li Y (2013) Characteristics and mechanisms of large deformation in the Zhegu mountain tunnel on the Sichuan-Tibet Highway. Tunn Undergr Space Technol 37:157–164

    Article  Google Scholar 

  • Meschke G, Liu WN (1999) A re-formulation of the exponential algorithm for finite strain plasticity in terms of Cauchy stresses. Comput Method Appl M 173(1):167–187

    Article  Google Scholar 

  • Montáns FJ, Bathe K (2005) Computational issues in large strain elasto-plasticity: an algorithm for mixed hardening and plastic spin. Int J Numer Methods Eng 63(2):159–196

    Article  Google Scholar 

  • Okazawa S (2010) Structural bifurcation for ductile necking localization. Int J Nonlinear Mech 45(1):35–41

    Article  Google Scholar 

  • Ortlepp WD (2001) The behaviour of tunnels at great depth under large static and dynamic pressures. Tunn Undergr Space Technol 16(1):41–48

    Article  Google Scholar 

  • Perić D, Owen DRJ, Honnor ME (1992) A model for finite strain elasto-plasticity based on logarithmic strains: computational issues. Comput Methods Appl Mech Eng 94(1):35–61

    Article  Google Scholar 

  • Rosales Garzon SE (2016) Analytical solution for assessing continuum buckling in sedimentary rock slopes based on the tangent-modulus theory. Int J Rock Mech Min 90:53–61

    Article  Google Scholar 

  • Simo JC (1992) Algorithms for static and dynamic multiplicative plasticity that preserve the classical return mapping schemes of the infinitesimal theory. Comput Methods Appl Mech Eng 99(1):61–112

    Article  Google Scholar 

  • Simo JC, Armero F (1992) Geometrically non-linear enhanced strain mixed methods and the method of incompatible modes. Int J Numer Methods Eng 33(7):1413–1449

    Article  Google Scholar 

  • Vrakas A, Anagnostou G (2014) A finite strain closed-form solution for the elastoplastic ground response curve in tunnelling. Int J Numer Anal Methods Geomech 38(11):1131–1148

    Article  Google Scholar 

  • Vrakas A, Anagnostou G (2015) A simple equation for obtaining finite strain solutions from small strain analyses of tunnels with very large convergences. Géotechnique 65(11):936–944

    Article  Google Scholar 

  • Wang M, Zhang N, Li J, Ma L, Fan P (2015) Computational method of large deformation and its application in deep mining tunnel. Tunn Undergr Space Technol 50:47–53

    Article  CAS  Google Scholar 

  • Wang M, Li S, Yuan C et al (2021) A manifold Lagrangian integration point method for large deformation failure modelling of rock slopes. Comput Geotech 129:103875

    Article  Google Scholar 

  • Xu C, Xia C (2021) A new large strain approach for predicting tunnel deformation in strain-softening rock mass based on the generalized Zhang-Zhu strength criterion. Int J Rock Mech Min 143:104786

    Article  Google Scholar 

  • Xu C, Xia C, Han C (2021) Modified ground response curve (GRC) in strain-softening rock mass based on the generalized Zhang-Zhu strength criterion considering over-excavation. Undergr Space 6(5):585–602

    Article  Google Scholar 

  • Yamakawa Y (2022) Hyperelastic constitutive models for geomaterials: extension of existing models to include finite strains and their comparison. Comput Geotech 143:104600

    Article  Google Scholar 

  • Yuan W, Wang H, Zhang W, Dai B, Liu K, Wang Y (2021) Particle finite element method implementation for large deformation analysis using Abaqus. Acta Geotech 16(8):2449–2462

    Article  Google Scholar 

  • Zhang Q, Wang H, Jiang Y, Lu M, Jiang B (2019) A numerical large strain solution for circular tunnels excavated in strain-softening rock masses. Comput Geotech 114:103142

    Article  Google Scholar 

  • Zhang Q, Wang X, Jiang B, Liu R, Li G (2021) A finite strain solution for strain-softening rock mass around circular roadways. Tunn Undergr Space Technol 111:103873

    Article  Google Scholar 

  • Zhao Y, Feng X, Jiang Q et al (2021) Large deformation control of deep roadways in fractured hard rock based on cracking-restraint method. Rock Mech Rock Eng 54(5):2559–2580

    Article  Google Scholar 

  • Zhao R, Li C, Zhou L, Zheng H (2022) A sequential linear complementarity problem for multisurface plasticity. Appl Math Model 103:557–579

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to express their gratitude to the two anonymous reviewers and editors for their meticulous, professional, and insightful comments.

Funding

This work is supported in part by GHfund A (2023020122702), the China Postdoctoral Science Foundation (2023TQ0025), the Chinese Universities Scientific Fund (Z1090124057), and the National Natural Science Foundation of China (42050201, 41941018).

Author information

Authors and Affiliations

  1. College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling, 712100, China

    Xiaofeng Cheng

  2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, 116024, China

    Xiaofeng Cheng & Chun’an Tang

  3. School of Civil and Resources Engineering, University of Science and Technology Beijing, Beijing, 100083, China

    Xianhui Feng

Authors
  1. Xiaofeng Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chun’an Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xianhui Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaofeng Cheng.

Ethics declarations

Conflict of interest

The authors declare they have no conflicts of interest to this work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cheng, X., Tang, C. & Feng, X. When Large Deformation Analysis Meets Large Deformation Phenomenon: Comparative Study and Improvement. Rock Mech Rock Eng (2024). https://doi.org/10.1007/s00603-024-03912-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00603-024-03912-8

Keywords

Search

Navigation