A Simplified Approach to Estimate Anchoring Capacity of Blocky Rock Mass with Pressure Arch Theory

Abstract

In this paper, a simplified method for predicting rock mass resistance against tensile forces from rock anchors (anchor) is presented. The interaction of anchors and rock mass was investigated using three-dimensional discontinuous numerical modelling. Several patterns of rock discontinuities were assumed in the numerical modelling while a single anchor is embedded in it. The numerical results show that the existence of a discontinuity set sub-parallel to the anchor significantly improves the rock mass resistance against the tensile force from the anchors. This phenomenon is due to the rock block interlocking at the sub-parallel discontinuity set. Rock block interlocking generates a zone of stress concentration inside the rock mass which has an arch shape (i.e., a pressure arch), resisting against the anchor's tensile force. The load-bearing capacity of the pressure arch plays a significant role in the resistance of the rock mass against the forces from the rock anchor. A voussoir beam analogy was utilised to study the load-bearing capacity of the pressure arch. A simplified analytical approach was developed to assess the load-bearing capacity of the voussoir beams. Then, it was used in combination with the weight of the mobilised rock mass by the anchor to assess the maximum anchoring resistance of the rock mass (anchoring capacity). The suggested method was calibrated by numerical modelling and relevant published pull-out test results. The technique developed in this paper shows the significance of rock block size, shear behaviour of rock discontinuities, Young's modulus of the rock mass, and uniaxial compressive and tensile strength of the intact rock in anchoring capacity of rock masses.

Highlights

• A theoretical framework is presented on how rock mass and rock anchors interact based on numerical modelling.

• An analytical method is developed to calculate the anchoring capacity of a rock mass which has at least one joint set sub-parallel to the anchor.

• The importance of the rock block size and the shear behaviour of rock discontinuities in determining the anchoring capacity of the rock mass is discussed.

1 Introduction

Rock anchors are implemented in different engineering practices such as anchoring hanging bridges, the foundations of wind turbines, foundations of high-voltage electricity masts, ski, and gondola masts. Rock anchors are used to transfer the tensile force deep into the rock mass. They might be designed to function as passive (not post-tensioned) or active (post-tensioned) anchors, while they can be a single anchor or act in a group. The current study focuses on the behaviour of a single passive rock anchor (hereafter "the anchor" for brevity).

According to Brown (2015), anchor design has not changed since the 1970s. The anchors are controlled against four modes of failure which include (Littlejohn and Bruce 1975, 1976):

• Mode A: tensile failure of steel materials

• Mode B: failure at the grout‒steel interface, which leads to a loose bond between streel and grout

• Mode C: failure at the rock‒grout interface which leads to a loose bond between grout and rock

• Mode D: rock mass uplift.

The ultimate tensile load of an anchor is the minimum of the tensile load which is obtained from the above-mentioned modes of failure. This paper is focused on failure mode D and how to estimate it for a specific type of rock mass. Here, the minimum tensile force from an anchor which can cause a mode D failure in the rock mass is denoted as the "anchoring capacity of the rock mass" or simply the anchoring capacity.

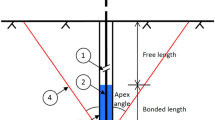
Design methods for assessing the failure modes A, B and C are summarised and discussed by Brown (2015) and Littlejohn and Bruce (1975, 1976). The traditional method for designing anchors against mode D failure is to assume that the tensile force of the anchor is resisted by the weight of the rock mass located inside an imaginary cone where the anchor is located at the axis of the cone—the so-called cone method. The apex of the cone can be located at either the anchor base or the middle of the bond length. The apex angle of the cone can vary between 60 and 90 degrees (Littlejohn and Bruce 1975, 1976). However, studies regarding the failure mode D are inadequate, limiting our understanding regarding the interaction of the anchors and rock mass.

Saliman and Schaefer (1968) carried out four tests on anchors with a length of 1.52 m embedded in sedimentary rocks (mostly shale). In all the cases, the failure happened by uplift of rock blocks (failure mode D) and rock-grout interface (failure mode C). The cone shape of the failure for the uplifted rock mass was inferred from the pattern and orientation of the cracking, joint opening, and rock mass bulging on the ground surface. To obtain the shape of the cone, they used the radius of the bulged rock mass on the ground surface and calculated the apex angle for an idealised cone which has its apex point located in either the anchor base or the middle of the bond length. This led to obtaining different apex angles for the cones: 62‒100 degrees and 33‒62 degrees if the apex of the failure cone is located at the middle of the bond length and the anchor base, respectively.

Brown (1970) carried out several tests on anchors embedded in laminated dolomite. It was not possible to identify the shape of the mass uplifted by the anchors. However, a large area at the ground surface was moved by the anchors. This was considered as an indication of the separation of the rock mass at the horizontal bedding planes.

Bruce (1976) carried out extensive tests on the anchors and managed to carry out at least seven tests where the anchors failed by mode D. The rock mass was laminated sandstone with two sets of sub-vertical joints which were perpendicular to each other. He used a similar approach to Saliman and Schaefer (1968) to calculate the volume of the failure cone. It led to an apex angle of 117‒144 degrees and 90–114 degrees, respectively, for the cone having its apex point at the middle of the bond length and the anchor base. Assuming the unit weight of 0.025 MN/m³ for the rock mass, the measured anchoring resistance was 14–56 and 7–29 times the cone weight, if the apex point was located at the middle of the bond length and the anchor base, respectively. Bruce (1976) reported that realistic estimation of the radius of the cone is not straightforward for the following reasons:

• In several tests, the shape of the disturbed area on the ground surface was more elliptical than circular. Therefore, the mean value of the ellipsoid's radius is reported as the radius of the cone base.

• In certain cases, the assumed volume of the cone was exaggerated since the shape of the bulged area at the ground surface was a very narrow ellipsoid.

In addition, Bruce (1976) made an interesting observation that, in the anchors with mode D failure, there is a short-length at the anchor base where a failure model B or C is observed. Therefore, the apex of the failure cone should not be located at the anchor base. Based on this observation from Bruce (1976), the more appropriate location for the cone's apex is above the anchor base where the mode C or D failure stops.

More recently, Thomas-Lepine (2014) carried out pull-out tests on 50 rebars with embedded lengths of 0.5–1.5 m into the rock mass in a dolomite open pit mine in Norway. Among all the tests, only 21 showed failure mode D. He observed that among the bolts with the D-type failure, two different mechanisms are visible as follows:

• A pre-existing rock block liberated by the tensile force of the anchor: this type of failure happened when the anchors were embedded mainly inside a single rock block. The rock block was liberated from the host rock by the pull-out force.

• Cracking and disintegration of the rock mass in the vicinity of the anchor: this failure happened when the rock mass consisted of smaller blocks. With increasing uplift force, the rock blocks interlock with each other and move upward. Finally, the interlocked blocks are failed, leading to the release of the anchors.

This observation shows the importance of the block size in the interaction mechanism of the rock mass and anchors.

Figure 1a depicts the ratio of the anchor pull-out force to the cone weight from the test data reported by Bruce (1976) and Thomas-Lepine (2014). The cone weight was calculated assuming an apex angle of 90 degrees with the apex located at the anchor base; the rock mass has a unit weight of 2500 kg/m³. A best fitting line on the data was also presented. Note that the vertical axis is in logarithmic scale. As it is clear, the pull-out forces from the tests are larger than the cone weight. However, with increasing anchor length, the differences decrease.

Fig. 1

Pull-out force obtained from the filed tests versus (a) anchor length, (b) Q-value, (c) GSI and (d) RQD. The data are from Bruce (1976) and Thomas-Lepine (2014)

To decrease the underestimation of the anchoring capacity by the cone method, Wyllie (1999) suggested utilising the rock mass tensile strength calculated via the Hoek‒Brown criterion (Hoek 1983) acting at the surface of the cone when field tests are not available. To utilise the tensile resistance of the rock mass on the surface of the cone, it is required to have a correlation between the rock mass quality (for example, the GSI value of the rock mass (Hoek et al. 2013)) and the anchoring capacity of the rock mass. To investigate this, Fig. 1b–d shows the anchoring capacity of the rock mass obtained by Thomas-Lepine (2014) from field tests versus the rock mass quality at the test location. The rock mass quality was assessed by the Q value (Barton et al. 1974), GSI (Hoek et al. 2013) and RQD (Deere 1964). The anchoring resistance of the rock mass was normalised to the anchor length since the anchors had different lengths. It is visible that there are no clear correlations between the traditional rock mass quality classes and the anchoring capacity of the rock mass. In spite of the fact that we only show a single dataset in Fig. 1b–d (from a dolomite rock mass), it is possible to conclude that finding any correlation between the known rock mass quality classes and the anchoring capacity of the rock mass is not straightforward and requires extensive anchor pull-out tests on different rock masses.

The key challenge in the cone method is to find the correct apex angle. There is no agreement between authors regarding the apex angle and how geological structures might affect it. For example, Bruce (1977) suggests an apex angle of 60–90 degrees while Wyllie (1999) argues that the apex angle can be increased to 120 degrees in hard rocks. In addition, the apex angle changes if the apex point is located at the anchor base or at the middle of the bond length. In the traditional cone method, the apex angle of the cones as mentioned by several authors is associated with the rock mass structures and the main discrepancy arises in the question of which orientation of the geological structures leads to the most and least favourable condition regarding the anchoring capacity of the rock mass. According to Wyllie (1999), the most and least favourable conditions are when the geological structures have a right angle with the anchor and are parallel to the anchor, respectively. However, Littlejohn and Bruce (1977) argued that the geological structures which have a right angle with the anchor have the most unfavourable effect on the anchoring capacity. Wyllie (1999) drew his conclusion by considering how the joint dip angle might contribute to the apex angle of the cone, while Littlejohn and Bruce’s (1977) conclusions were based on tests on laminated sedimentary rocks. To have a better understanding, the effect of the rock mass structures will be investigated by the numerical modelling in this manuscript (Sect. 2).

Dados (1984) studied the rock mass and anchor interaction in a granitic rock mass with horizontal and vertical joints. Through comparing the field observations and physical modelling in the laboratory, he developed a technique to assess the rock mass anchoring capacity. He showed that in this kind of rock mass, the radius of the bulged rock mass area in the ground surface is approximately equal to the anchor length. As soon as the uplift force is applied, the rock blocks detach at the horizontal joints, and the vertical joints are opening in the upper part while they are closing in the lower part. He observed that rock block interlocking generates a continuous plate subjected to a concentrated single load in the middle. Using the bending versus deflection relationship for a continuous plate, he suggested a formula to calculate the anchoring capacity of the rock mass. Through the field testing of anchors, he suggested a relationship to adjust the intact rock's Young's modulus to implement it into the calculations based on the RQD and anchor length.

Serrano and Olalla (1999) utilised the Hoek–Brown failure criterion (Hoek and Brown 1980) to identify rupture surface around an anchor under tensile loading when the failure is limited only to mode D. The rupture surface is a locus of points around an anchor where the rock mass has the lowest strength against the tensile load of the anchor. According to the analysis, depending on the slenderness ratio (diameter to length ratio) of the anchor and the rock mass quality (defined by a factor which depends on the Hoek–Brown parameters of the rock masses) two different types of the rupture surfaces might be observed, denoted as short and long anchor behaviour in the article. For the short anchors, the rupture surface has a hyperbolic shape with starting point at the anchor base. The long anchors have complex rupture surface, a hyperbolic shaped cone is limited to the upper part (similar to the short anchor) but a cylindrical rupture surface in the lower part. For the rock anchors which are the main focus of the current paper, the long anchor approach is valid (they always have length to diameter ration over 25), and according to the developed method by Serrano and Olalla (1999) the anchoring capacity of the rock mass can be estimated as the shear resistance of the rock mass at the wall of the borehole. This approach, however, is limited only to the rock masses at which the Hoek–Brown failure criterion is applicable (homogenous and isotropic rock mass) meaning that either the rock blocks are much larger than the anchor length, or the rock blocks are extremely smaller than the anchor. For practical anchor length in the industry (typically 3–10 m), this implies rock masses comprised mostly of blocks smaller than 10 cm or larger than 9–30 m which are rarely encountered in the construction sites in hard rocks.

Because of the challenges in simulating rock mass-anchor interaction in the laboratory or performing controlled field tests, numerical modelling is an attractive feasible alternative. Panton (2016) carried out an extensive numerical analysis to find the most appropriate numerical approach for simulating rock mass-anchor interaction. He noticed that a continuous numerical approach does not lead to acceptable results. In continuous models, the major part of the anchor fails by the debonding of the anchor, except at a portion of the anchor base. Later, with increasing pull-out force, a tensile failure zone develops at the anchor base, propagating in a cone shape towards the ground surface. This contradicts the observations in the field tests, where the rock mass uplifting and failure starts from the ground surface (e.g., Bruce 1976). With increasing pull-out force, the anchor load sinks further down towards the base, while at the same time the volume of the rock mass being uplifted by the anchor increases.

Panton (2016) showed that implementing rock joints explicitly in the analysis can help to study anchor and rock mass interaction, especially when the rock mass discontinuity system is simulated by a Discrete Fracture Network system (DFN) (Dershowitz 1984). The study shows that a rock mass with sub-vertical and sub-horizontal joints has a slightly higher anchoring capacity than a rock mass with inclined joints. Decreasing the fracture intensity (number of fractures per unit volume of rock mass) improves slightly the rock mass anchoring capacity. He also showed that, when considering the rock joint persistence, it is possible to calculate the maximum fully removable rock block using the statistical approaches of DFN. His numerical models show that the calculated volume of the removable blocks is conservative enough to represent the anchoring capacity of the rock mass.

Discontinuous numerical modelling can be a suitable tool to study rock mass-anchor interaction, as demonstrated by Panton (2016). However, it takes a lot of time to carry out site investigations to get the required inputs and conduct the modelling itself. In addition, in a very complex numerical model, it will be difficult to judge the significance of the numerical outcomes; for example, studying the relevance of the different rock mass properties on the anchoring capacity. Moreover, most of the time rock engineers are dealing with selecting a proper site for rock mass anchoring in the early phases of the design. Since we lack the fundamental knowledge of the anchors and rock mass interactions in different rock masses, conducting such a job can be quite challenging.

Hence, it is required first to understand fundamentally the rock mass and anchor interactions in a simple manner. Also, such a simple technique might help in smaller projects to calculate the ground anchoring capacity with an acceptable factor of safety, avoiding the conservative technique of the cone method (without utilising numerical modelling). Moreover, it might pave the way towards having a better understanding of rock mass and anchor interaction, helping in the earlier phases of projects to select appropriate sites for rock mass anchoring.

To this end, this paper focuses on investigating the interaction mechanism between fully bonded anchors and rock masses through three-dimensional discontinuous numerical modelling. The study is limited to type D failure mode of a single anchor, while considering different orientations and conditions for rock discontinuities in the models. The numerical results demonstrate that when the rock mass forms sub-parallel joints with the anchor, the rock blocks interlock with each other under the tensile force of the anchor, and create a zone of high stress concentration, known as a pressure arch. In such a condition, the load-carrying capacity of the pressure arches will control the anchoring capacity of the rock mass. The paper continues to develop an analytical approach to assess the anchoring capacity of rock masses based on the load-bearing capacity of the pressure arches and the distribution of rock blocks along the anchor. The developed method is calibrated against the numerical models and published field tests. Additionally, a discussion is presented about the correlation of the outcomes from this research work with the current state-of-the-art in anchor design and its limitations.

2 Interaction of Rock Mass and Anchors—Numerical Modelling

Three-dimensional (3D) numerical modelling was carried out with considering explicitly the rock discontinuities by 3DEC code (Itasca 2016 and 2019 versions: 5.2 and 7.0). The scope of the numerical modelling is limited to investigate the interaction between fully grouted anchors with blocky rock masses. A range of the properties were assumed for the rock masses which are generally encountered in the Scandinavian shield, hard blocky rock masses. For the sake of simplicity, the rock mass always has 3 joint sets with dip/dip directions as presented in Table 1, divided into four different rock mass classes according to the dip and dip-direction of the joint sets. Properties of intact rock and rock joints are summarised in Table 1. The anchors were modelled as cable elements and their mechanical properties are provided in Table 2. Rock anchors with lengths of 2, 4 and 5 m are modelled for each class of rock masses.

Table 1 Rock mass properties of the numerical models*

Table 2 Mechanical properties of the cable elements used in the numerical modelling

To ensure that the failure of the anchoring system is only dominated by the rock mass failure (failure mode D), sufficiently high values of bond shear resistances between steel, grout and rock and the yield strength of the anchor were assumed.

The rock mass is consolidated under its own weight and all the vertical boundaries of the model are constrained in the normal direction (Fig. 2a). The base of the model is constrained in the vertical and all horizontal directions. Therefore, the horizontal stresses are generated due to the Poisson's effect, leading to equal horizontal stresses in the x and y directions in the model.

Fig. 2

(a) Geometry of the models in 3DEC and (b) cross-section A-A showing the location of the monitoring points

After running the model to initial equilibrium, a constant velocity was applied to the top of the anchor in the vertical direction, pulling the anchor upward. The anchor load and displacement, stresses within the rock blocks and their displacements were monitored during pull-out of the anchor. Figure 2b shows the location of the monitoring points in the model, placed in an organised pattern with a distance of 1 m from each other; they are extended 5 m in both the X and Y directions.

The rock blocks are assumed to obey elastic behaviour, while the rock joints have only frictional resistance. It was assumed that the uniaxial compressive strength of the intact rock is 100 MPa. Considering the scale effect on the strength of the rock blocks, modelling was stopped when the maximum principal stress near the anchor reached 50 MPa (50% of the uniaxial compressive strength of the intact rock according to the observation by Martin (1997)). This means that the rock block has failed in compression mode. This assumption might be conservative since we are ignoring the effect of the confining stresses. However, as it will be demonstrated later, when the rock blocks interlock by the anchor force the stress state becomes uniaxial and the stresses in the other directions are neglectable. Similarly, it was assumed that uniaxial tensile strength of the intact rock is − 4 MPa. In the models if the minimum principal stress reaches − 4 MPa in the rock blocks at the vicinity of the anchor, the model was stopped.

Figure 3a–c show the pull-out force versus the anchor top displacement (which is approximately equal to the vertical displacement of the rock block located exactly at the anchor top in the ground surface) for the models with joint spacing 0.5 m, joint friction angle 30 degrees and joint dilation angle of 2 degrees. Two different failure mechanisms were observed in the models. Models with rock mass classes of 60–45–35 were failed by the rock joint shearing and uplifting of the rock blocks by the anchor. Since the shearing in the joints is governed by elastic-perfect plastic behaviour, the anchor load is standing almost constant after failure while the displacement increases. In all other models, i.e. with rock mass classes of 90–90–00, 90–60–00 and 90–30–00, the anchoring system was failed by the tensile failure of the rock blocks hosting the anchor (tensile failure mechanism). These models show approximately linear behaviour with increasing pull-out force, up until the model's cycle was stopped due to the tensile failure in a rock block at the vicinity of the anchor base.

Fig. 3

Pull-out force versus anchor displacement for different anchor length: (a) 2 m, (b) 4 m, (c) 5 m. (d) Anchoring capacity of different rock mass classes obtained by numerical models. In all the presented results, the rock joints have spacing of 0.5 m, friction and dilation angle of 30 and 2°, respectively

As shown in Fig. 3d, the anchoring capacity is dependent significantly on the rock joints' dip angles (see the rock mass classes in Table 1), and the anchor length. The rock mass class 90–90–00, containing two vertical joint sets, has the highest anchoring capacity (Fig. 3d), regardless of the anchor length. The rock masses with one sub-vertical joint set (classes 90–60–00 and 90–30–00) have a lower anchoring capacity than class 90–90–00. Between the classes 90–60–00 and 90–30–00 which have only one vertical joint set, class 90–30–00 has a higher anchoring capacity, which contains an inclined joint set of 30 degrees in dip compared to the 60 degrees inclined joint in rock mass class 90–60–00. This means that between the rock mass classes 90–60–00 and 90–30–00, the one which has a less inclined joint set has a smaller anchoring capacity. Rock mass class 60–45–35 shows slightly higher anchoring capacity compared to class 90–60–00 but less than rock mass class 90–30–00.

Based on the traditional method of the cone weight (as described in Sect. 1), the anchoring capacity of the modelled rock classes should follow the dip angle of the rock joints. Considering the recommendations from Wyllie (1999), the anchoring capacity of the modelled rock mass classes should follow this order from the lowest anchoring capacity to the highest: class 90–90–00, 90–60–00, 90–30–00 and 60–45–35. However, numerical modelling shows that the anchoring capacity follows the following order from lowest to highest: 90–60–00, 60–45–35, 90–30–00 and 90–90–00 (Fig. 3d). The numerical results show that rock masses which have rock discontinuity sets parallel to the anchor have the highest anchoring capacity, contradicting the hypothesis from the cone method. The reason for such discrepancy is that the rock block interlocking effect is ignored in the cone method.

Interlocking of the rock blocks under the uplift force of an anchor happens in the rock mass with joints which are sub-parallel to the anchor (referred to as sub-vertical in this paper since the installed anchors are vertical) in the rock mass classes 90–90–00, 90–60–00 and 90–30–00.

If an anchor is embedded inside a rock block, the tensile load of the anchor pushes the block to move upward. If the block does not slide along the sub-vertical joints, it will rotate the two adjacent rock blocks outward from the anchor (Fig. 4a). The rotation causes the neighbouring blocks to interlock with each other, a mechanism first observed by Dados (1984) in physical modelling of rock anchoring in the laboratory. Block interlocking generates a zone of high compressive horizontal stress concentration with an arch shaped line of the thrust (i.e., a pressure arch). The arch shape of the thrust line makes the generated horizontal forces in two different sides of the rock blocks (F_h) to be offset by a distance z, generating a moment which resists the anchor force. Below we present that numerical modelling shows a similar rock block interlocking mechanism in the rock masses with sub-vertical joints under anchor pull-out (rock mass classes 90–90–00, 90–60–00 and 90–30–00).

Fig. 4

(a) The interlocking mechanism of rock block under the tensile forces from an anchor when the rock mass has sub-parallel discontinuities with the anchor. A vertical cross-section parallel with X-axis in the middle of the numerical model with rock mass class 90-30-00 and anchor length of 4 m showing: (b) horizontal displacement, (c) horizontal stress distribution in the cross-section and (d) formation of the pressure due to block rotation and interlocking. The compressive stresses are shown as negative values

Figure 4b shows the horizontal displacement of rock mass class 90–30–00 with the anchor length of 4 m at pull-out forces of 0.5 MN. In the two most upper rows of blocks a spatial pattern of the horizontal displacements can be seen: fluctuations in the horizontal displacement along rock blocks parallel with the anchor. Inside each of these blocks the horizontal displacement in two different directions is observed, indicating that the blocks have the tendency to rotate out from the block uplifted by the anchor force, causing them to interlock. Figure 4b, c shows the generated horizontal pressure arch. The thrust line of the pressure arch is also highlighted in Fig. 4d, which represents the location of the total force generated inside the pressure arch with horizontal projection of F_h.

It should be noted that all the rock mass classes for which rock block interlocking occurred failed under the anchor load by tensile failure mechanism. However, in the rock mass classes with no block interlocking effect, the rock mass failed by shearing along the blocks and uplifting of them.

Figure 4 is an example showing how the anchor load is transferred to a rock mass containing a joint set which is sub-parallel with the anchor. Similar behaviour was also observed in the rock mass classes 90–90–00, 90–60–00 and 90–30–00 for anchor lengths of 2, 4 and 5 m. To investigate the interlocking effect in more detail, relevant rock mass properties including rock block size, friction and dilation angle of the rock joints were considered in series of sensitivity analysis. Figure 5 shows sensitivity analysis over anchoring capacity of different rock mass classes when an anchor with length of 4 m was installed.

Fig. 5

Sensitivity analysis with numerical modelling of an anchor with 4 m length: (a) anchoring capacity versus dilation angle while friction angle is 30° and joint spacing is 0.5 m, (b) anchoring capacity versus friction angle while the dilation is 2° and (c) anchoring capacity versus joint spacing while friction angle and dilation angle are 30° and 2°, respectively

Figure 5a shows that when there is no dilation within rock joints the anchoring capacity follows the hypothesis by Wyllie (1999) where it is only associated with the weight of the blocks hanging from the anchor and no block interlocking is happening. However, with a dilation angle as small as approximately 2 degrees, rock block interlocking happens, thereby significantly improving the anchoring capacity of the rock mass. However, further increasing of the dilation angle up to 10 degrees does not improve the anchoring capacity significantly, as the failure is mostly controlled by the tensile strength of rock blocks. Similarly, Fig. 5b shows that increasing the friction angle does not improve the anchoring capacity in rock classes with interlocking effect. However, in the rock mass class 60–45–35 where the failure mechanism is rock block sliding, increasing the friction angle improves anchoring capacity. In rock mass class 60–45–35, since the confining stresses over the sliding joints is low, the improvement in anchoring capacity due to increase in the friction angle has diminishing returns.

Figure 5a, b reveals that the anchoring capacity in rock mass classes that exhibit the interlocking effect is not sensitive to the frictional resistance of the rock joints, while a very small amount of dilation in rock joints is required to utilise the block interlocking effect. In rock mass class 60–45–35 where the rock mass fails by the block sliding and uplifting, both friction and dilation angles improves the anchoring capacity.

Figure 5c shows that when the joint spacing is equal 0.2 m, the anchoring capacity is almost equal in all the rock masses, indicating that interlocking does not improve the rock mass anchoring capacity. However, with increasing rock block size (joint spacing), the anchoring capacity improves in rock classes of 90–90–00, 90–60–00 and 90–30–00, with the rock class 90–30–00 showing the largest improvement rate. In the rock class 60–45–35 at which the anchoring capacity is controlled by the shearing along the joints, increasing the block size improves the anchoring capacity but rate of the improvement is less than other classes with block interlocking effect.

Figure 5a–c shows that block size and dilation angle are the most important factors in controlling anchoring capacity of the rock mass in comparison to the friction angle.

The classical cone model assumes that the involved rock around an anchor has a conical shape. However, numerical modelling is suggestive of a rather frustum geometry: a cone where it is cut by a plane parallel with the ground surface at the anchor base, but the apex point of the cone is in a point far deeper than anchor base. The horizontal cross-section of the frustum at the anchor base is shown in Fig. 6a–d (denoted as base plate) consisting of rows of interlocked rock blocks. In rock mass class 90–90–00 where the rock blocks are cubical, interlocking happens in both directions, forming a circular shaped base plate. However, in rock mass class 90–60–00 and 90–30–00 the base plate's shape is half elliptical where largest diameter of the ellipsoid is along the interlocking direction. In rock mass class 60–45–35 where rock block interlocking does not happen, the base plate has a triangular shape. The number of the interlocked rock block rows in the anchor base is associated with the anchor length to joint spacing ratio regardless of the friction and dilation angles (Fig. 6e, note that several points are located on top of each other in this graph).

Fig. 6

Horizontal cross-sections in the base of the numerical model with anchor length of 4 m showing vertical displacement of the rock blocks, from red to ward blue colour the displacements decrease. The directions where rock blocks are interlocked are shown and formed parallel rock pressure arches which are uplifted by the anchor force is also marked. (a) shows the cross-section for rock mass class 90–90–00, (b) rock mass class 90–60–00, (c) rock mass class 90–30–00, (d) rock mass class 60–45–35 and (e) presents the results from all the numerical models run in this manuscript which was showing rock block interlocking which includes the number of formed parallel pressure arches versus the anchor length to joint spacing rations. It should be noted that several points are matching on top of each other

The change in the anchor load inside a rock block is equal to the tensile load transferred to that block by the anchor. Figure 7 shows the anchor load transferred to the rock blocks for different rock mass classes along a 4 m long anchor. As it is visible, in rock mass class 90–90–00 the anchor load is almost evenly transferred into the rock blocks along the anchor while in rest of the classes, the largest anchor load is transferred to the rock block located around the anchor base. Rock mass classes of 90–90–00, 90–60–00 and 90–30–00 were failed by tensile failure of the rock block at the anchor base under anchor pull-out force. In rock mass class 90–90–00 almost all the blocks at which the anchor passed through showed tensile failure simultaneously. In conclusion, in the rock classes with interlocking if the generated pressure arch exhibits sufficient load bearing capacity, the anchoring capacity will be directly governed by the tensile strength of the rock blocks and the cross-section of the block in direction perpendicular to the anchor where the tensile failure develops. In this condition, the tensile failure of the rock blocks at the anchor base will liberate the anchor base and hence the loading in the upper proration of the anchor will increase dramatically, leading to the mode D of anchor failure. As observed in the field tests by Thomas-Lepine (2012) in several tests the rock mass shows sudden cracking and disintegration of the rock blocks in the vicinity of the anchors.

Fig. 7

The anchor load transferred to each rock block located along anchor with length of 4 m installed in different rock mass classes with joint spacing of 0.5 m, friction angle of 30° and dilation angle of 2°

As demonstrated by the numerical studies above, the kay issue in assessing the anchoring capacity of the rock masses with the block interlocking effect is estimating the load bearing capacity of the pressure arch formed in the anchor base in comparison to the tensile strength of the rock blocks. The stability and load bearing capacity of the pressure arches has been studied by the voussoir beam theory in rock engineering. The load bearing capacity of the voussoir beams has been investigated by numerical modelling and physical modelling in the laboratory, as well as several analytical methods (e.g. Brady and Brown 1985; Sofianos 1996; Diederich and Kaiser 1999; Sofianos and Kaipeni 1998; Talesnick et al. 2007; Tsesarsky 2012; Shabanimashcool and Li 2015; Paraskevi and Sofianos 2018).

This paper proposes a simplified version of the analytical method developed by Shabanimashcool and Li (2015) for studying the load bearing capacity of the pressure arches (Appendix 1) and also demonstrates how the simplified method for the voussoir beam analysis in combination with the tensile strength of the rock blocks can be used to find out anchoring resistance along an anchor (Appendix 2). This methodology is used in Sect. 3 to assess anchoring capacity of a rock mass which was calibrated by numerical results and published field test data.

3 Anchoring Capacity of Rock Mass

This section first discusses the theory of anchor–rock mass interaction. An analytical approach is presented which can be utilised to obtain the anchoring capacity of a rock mass containing sub-parallel joint sets with the anchor.

3.1 Rock Mass and Anchor Interaction

When an anchor is subjected to uplift force, shear stresses develop in the contact of the anchor and grout as well as the grout and rock. The shear stress has its peak value at the location of the anchor top, and it decreases exponentially with distance along the anchor (Farmer 1975; Li 2018). Therefore, if there is no failure (modes A to D) in the anchor‒rock mass system, the tensile force from the anchor is transferred into the rock mass at a short distance along the anchor.

Figure 8 shows schematically, the axial anchor force and the shear stress distribution at the anchor‒grout and grout–rock contacts according to the analogy developed by Farmer (1975) and Li and Stillborg (1999). Initially, the anchor pull-out load is P₁ which leads to exponentially descending axial load along the anchor and shear stress distribution in the contact of steel-grout or grout–rock (brown line in Fig. 8a, b). With increasing the pull-out force gradually to P₂ (blue line in Fig. 8a) the shear stress at either the steel‒grout or the grout‒rock contact (whichever has the lower shear resistance) can reach its maximum value (τ_m) and then fail. Therefore, the anchor debonds from the grout or rock and the shear stress at the contact decreases to a residual value. The residual shear strength is constant along the debonded stretch of the anchor (Fig. 8a, b). The axial anchor force decreases linearly along the debonded length. A zone along the anchor where the shear strength is mobilised is denoted as the active length in the figure. The active length increases with increasing the anchor pull-out force.

Fig. 8

Interaction of anchor and rock mass: (a) distribution of the tensile axial force along the anchor, (b) distribution of the shear stress at either anchor–grout or grout–rock contacts along the anchor length and (c) comparing anchor tensile load and anchoring resistance of rock mass. Blue line shows the condition at which the anchor pull-out force is P₁. With increasing the pull-out force from P₁ to P₂ a zone along the anchor debonds from the grout as the anchoring resistance of the rock mass is larger than the anchor load transferred into the block (for example ΔR_i ≥ ΔP_i)

Figure 8c compares the anchoring resistance of the rock mass to the pull-out force of the anchor. Assume that between the anchor length of l₁ and l₂ there is a rock block i which the anchor is interacting with. The load which is transferred from the anchor to the block i is ΔP_i = P_l1 - P_l2. In Fig. 8c the anchoring resistance of the rock mass is shown by R. The anchoring resistance of the rock mass at the location of block i is denoted as ΔR_i. If ΔR_i > ΔP_i, then the maximum load that can be transferred to block i is controlled by the shear resistance of the grout‒anchor and grout‒rock contacts or the tensile strength of the anchor steel. If ΔR_i < ΔP_i, then the rock mass can fail. Therefore, the anchor load between the length of l₁ and l₂ can never exceed R_l2. This phenomenon can happen particularly at the shallow part of the anchor where anchoring resistance of the rock mass is low. As a result, the load distribution along the anchor will not follow the theoretical exponential assumptions.

Consider that an anchor with length of L is embedded vertically inside a rock mass, passing through N blocks. The anchoring capacity of the rock mass for this condition is determined by the cumulative anchoring resistance of the N rock blocks as follows:

$${R}_{ult}= \sum_{i=1}^{N}R\left({l}_{i}\right),$$

(1)

where R(l_i) is the anchoring resistance at the location of block i which is located at the depth of l_i. A similar approach was used by Serrano and Olalla (1999) in which the anchoring resistance of the rock mass is obtained by integration of the rock mass strength along a rupture surface developed due to the tensile force of anchor. If the rock mass has the potential for block interlocking (containing at least one joint set sub-parallel with the anchor, as demonstrated in Sect. 2), then R(l_i) depends on the load-bearing capacity of the pressure arch formed due to rock block interlocking, the weight of the rock mass located above the pressure arch, and the tensile strength of the rock blocks:

$$R\left({l}_{i}\right)= {\mathrm{min}[W(l}_{i})+ {R}_{int}\left({l}_{i}\right); \quad and \quad {R}_{tens}\left({l}_{i}\right)],$$

(2)

where W(l_i) is the weight of the rock blocks that are mobilised by the pressure arch (located above the pressure arch) and pushed upwards by it (Fig. 9a), R_int (li) is the load-bearing capacity of the pressure arch formed at the depth of l_i (which will be investigated by the voussoir beam theory) and R_tens(l_i) is the tensile resistance of the block i against the anchor load. Appendix 1 presents a simplified analytical method to calculate the load bearing capacity of the pressure arch. Appendix 2 gives an analytical approach for calculating the tensile resistance of the rock blocks against anchor load; the procedure for determining R(li) is also presented in Appendix 2.

Fig. 9

Block interlocking effect on the anchoring resistance of rock mass: (a) formed voussoir beam and weight of rock mass mobilised by it at depth of l_i, and (b) location of possible deepest voussoir beam that can be used to calculate the anchoring resistance of the rock mass. According to the numerical models, the span of the formed deepest pressure arch is less or equal to the anchor length

Experimental results show that the volume of the rock mass mobilised by an anchor has the approximate shape of a cone (Salim and Schaefer 1968; Brown 1970; Bruce 1978). Moreover, numerical results in Sect. 2 show that the mobilised rock mass by an anchor has a conical frustum shape. Therefore, the span of the pressure arches forming along the anchor should decrease in depth towards the anchor base.

As mentioned above, the load-bearing capacity of the pressure arches can be assessed by the voussoir beam analogy. The load-bearing capacity of the voussoir beams increases with decreasing span (e.g. Brady and Brown 1985; Sofianos 1996; Diederichs and Kaiser 1999). Therefore, the load-bearing capacity of the voussoir beams (or the pressure arches) formed along an anchor increases with depth, since their span decreases. Hence, the deepest possible pressure arch formed close to the anchor base has the largest load-bearing capacity among all the pressure arches formed along the anchor. Moreover, our numerical modelling in Sect. 2 shows that the largest load is transferred to the rock mass close to the anchor base where the last pressure arch along the anchor is formed (Fig. 7). In other words, R(l_N) is the maximum of all R(l_i) for i = 1, 2, 3 …N, where i = 1 corresponds to the first block at the anchor top and i = N represents the last block where anchor will load.

If there is no failure in the anchor–rock mass system (none of the failure modes of A, B, C and D happen), the anchor load and the shear stress distribution at the contact of the anchor-grout and grout-rock mass is exponential (see Farmer 1975; Li and Stillborg 1999). However, if the rock mass anchoring resistance is lower than the anchor load, the main part of the anchor load will be concentrated at the location of the deepest formed pressure arch (as numerical modelling also shows that, see Fig. 7) which has largest load bearing capacity compared to other pressure arches formed above it. In this condition, it can be assumed that the load transferred to the rock blocks along the anchor follows an exponential curve. However, the peak load which is transferred into the rock blocks is at the location of the deepest formed pressure arch (Fig. 9b):

$${R(l}_{i})={R(l}_{N}) {e}^{-k({l}_{N}-{l}_{i})},$$

(3)

where k is the exponentially decreasing coefficient of the loads transferred into the rock blocks along the anchor. If we assume that the anchor load transferred to rock block number 1 located at the anchor collar is R(l₁), then k can be approximated as follows:

$$k\cong -\frac{\mathrm{ln}\left( \frac{R\left({l}_{1}\right)}{R({l}_{N})} \right)}{{l}_{N}-{l}_{1}}$$

(4)

In Sect. 5.3.3 we will show that k ≈ 1 1/m according to the numerical results. Then, the anchoring capacity of the rock mass considering Eqs. (1) and (3) can be obtained as follows:

$${R}_{ult}= \sum_{i=1}^{N}R\left({l}_{N}\right) {e}^{-k({l}_{N}-{l}_{i})}$$

(5a)

In the rock masses with two sub-parallel joint sets to the anchor (rock mass class 90–90-00 in the numerical models in Sect. 2), the anchoring capacity can be similarly calculated as the sum of the loads transferred to the rock blocks along the anchor. In this type of rock masses, the load transferred into the rock blocks along the anchor is almost constant and approximately equal to R(l_N) all along the anchor (see Fig. 7). Hence

$${R}_{ult}= N R({l}_{N})$$

(5b)

Field tests by Bruce (1976) showed that when the failure mode D happens, there is always a small portion of anchor at the base which fails by either mode B or C (sliding along the grout-steel or grout-rock contact). If the anchor length is L and the portion of the anchor which failed by modes either B or C is equal to l_shear, the deepest pressure arch along the anchor which carries the largest portion of the load should be located at the depth of L – l_shear (see Fig. 9b). There are some involved methods to calculate l_shear based on anchor diameter, borehole diameter, stiffnesses of the rock mass and the grout (e.g., Farmer 1975; Li 2018). According to Farmer (1975), in a fully bonded rock bolt, if no debonding and failure in the rock mass happen, the bolt load is distributed in a stretch of approximately 25d where d is the diameter of the bolt. Therefore, in this study we assumed the following:

$${l}_{shear}\le 25 d$$

(6)

To obtain the load bearing capacity of the pressure arches with the voussoir beam analogy, it is required to make assumptions about the span of the deepest formed pressure arch along block N (S_N) and the pressure arch formed along block number 1 (S₁).

Generally, the interlocking of only two neighbouring blocks is sufficient for a pressure arch forming. However, there is the possibility that the anchor passes through a rock block itself. Therefore, two neighbouring blocks of the anchor will also be interlocked with it to form a voussoir beam. In conclusion, the span of the interlocked blocks at the anchor base (deepest formed voussoir beam) always contains at least 2 to 3 blocks. However, assessing the largest possible span of the deepest voussoir beam is not straightforward. Based on laboratory tests, Daidos (1984) showed that the radius of the bulged area at the ground surface is approximately equal to the anchor length when the rock mass contains two discontinuity sets which are sub-parallel with the anchor. Hence, assuming the worst-case scenario of θ = 90 degrees in Fig. 9, the largest span of the voussoir beam formed at the anchor base is always equal to or less than twice the anchor length. Numerical modelling presented in Sect. 2 showed that the span of the pressure arch formed in the anchor base is always shorter or equal to the anchor length. Hence, in this study we assumed that the span of the formed pressure arch in the anchor base is equal to the anchor length.

As it is presented in Appendix 1, to form a voussoir beam which does not fail by shearing between the rock blocks, the voussoir beam should have a span which is equal or larger than 2–3 times of the beam thickness (see Eq. (33)). The voussoir beam thickness is equal to the spacing of the sub-horizontal joints (S_h in Fig. 9). Considering that the span of the deepest formed voussoir beam we assumed to be equal to L, then the developed method in this article is valid if the anchor length equal or larger than 2– 3 S_h dependent on the friction angle of the joints.

In summary to develop the analytical method for calculating the anchoring capacity of the rock masses mentioned above the following assumptions were made:

• Anchor and contacts of the anchor-grout and grout-rock mass are stronger than the rock mass's resistance against the tensile force by the anchor.

• The anchoring capacity of rock mass is accumulation of the loads transferred into rock blocks at which anchor has been embedded in. The anchor load transferred into rock blocks is maximum at the deepest block which has depth of L – l_shear. The transferred load into the rock blocks decreases exponentially along the anchor.

• The anchoring resistance of the rock blocks which anchor passes through is associated with the load bearing capacity of the pressure arch formed around that block or the tensile strength of that rock block. The span of the pressure arch for the deepest formed pressure arch is equal to the anchor length (L) and the span of the pressure arches for the other blocks can be estimated with assuming θ = 45 ̊ (see Fig. 9).

• The anchor length is equal or larger than 2—3 times of S_h, dependent on the friction angle of the rock joints.

4 Implementation

In this section, the procedure and input data required for calculating the anchoring capacity of the rock mass are presented.

The following input data are required from the rock mass and anchors:

• dip/dip-direction of all discontinuity sets.

• spacing of each discontinuity set to estimate the size of the interlocking blocks: S_h, S_v and S_o; where S_h is spacing of discontinuity sets sub-perpendicular to the anchor (thickness of the pressure arch building block), S_v is the spacing of the sub-parallel discontinuities with the anchor and S_o is the spacing of the discontinuities where they are forming the out-of-plane thickness of the pressure arch (for more detail see Appendix 1).

• friction and dilation angles of discontinuities (φ and ψ, respectively).

• uniaxial compressive and tensile strength of the intact rock (σ_ci and σ_ti, respectively).

• Young's modulus of the rock mass (E_rm).

• anchor length (L).

• anchor diameter (d).

• diameter of the borehole (d_g).

To calculate the anchoring capacity of the rock mass, these steps should be followed:

• 1. To have rock block interlocking effect, the rock mass should have at least one discontinuity set which is either parallel to the anchor or has an angle which is less than 1/3 of the discontinuity's friction angle. Moreover, the sub-parallel discontinuity set with the anchor should have a dilation angle equal or greater than 2 degrees. This means that the joints should have a joint roughness coefficient (JRC) equal or larger than 6 (see Sect. 5.2 for more details). In addition, the joints should not have filling materials and joint aperture should be "partly open" meaning aperture ≤ 0.5 mm (according to the ISRM suggested methods, 2007) to guarantee the influences of the joint dilation. Moreover, L ≥ 2 – 3 S_h according to Eq. (33). If these mentioned conditions are valid, then there is the possibility of rock block interlocking, and one can proceed to step 2. If not, then the proposed method in this paper is not applicable.

• 2. The location of the deepest formed voussoir beam at the anchor base is equal to L – l_shear, where l_shear can be determined from Eq. 6.

• 3. Calculate the bearing capacity of the deepest pressure arch that can be formed at depth of L – l_shear with if the span of the beam is S_N = L (use Eq. (2) and see Appendix 1 and 2 for detail of the calculations and considerations). The outcome of this step will be reported as R (l_N).

• 4. If the rock mass contains two perpendicular discontinuity sets which are subparallel with the anchor, the anchoring capacity of rock mass can be calculated by Eq. (5b); else, proceed to step 5.

• 5. Calculate coefficient k by Eq. (4). To be on the safe side for engineering applications it is recommended to utilise Eq. (12) to calculate coefficient k (see Sect. 5.2 for more details). However, assuming k = 1 1/m can be reasonable estimate according to the numerical modelling (see again Sect. 5.2).

• 6. Calculate rock mass anchoring capacity by Eq. (5a).

See Appendix 3 for an illustrative example.

5 Calibration and Discussion

The suggested method is calibrated with the numerical modelling presented in Sect. 2 and field test results by Thomas-Lepine (2014) for the rock mass classes which have the possibility of generating block interlocking. The main objective of the calibration is to show that the developed method can achieve a reasonable estimation of the anchoring capacity of rock masses in comparison to the classical cone model while the real loading and failure mechanism were considered explicitly in the analysis. Then, the correlation between the outcomes of the developed method and the current state-of-the-art anchor design is discussed to further validate the assumptions made in developing of the method, identify its benefits and limitations.

5.1 Calibration of the Developed Analytical Approach with the Numerical Models

The proposed theoretical method is calibrated by the 3D numerical modelling carried out in Sect. 2 for the rock mass classes that exhibited rock block interlocking (classes 90–90–00, 90–60–00 and 90–30–00 in Table 1). In assessing the anchoring capacity of the modelled rock masses, it was assumed that the deepest voussoir beam is located at the anchor base, i.e. the shear length is equal to zero, since in the models the contact of the grout-rock and anchor-grout has very large shear strength to make the failure to be limited to rock mass failure.

To estimate the load bearing capacity of the deepest formed pressure arch we utilise the voussoir beam analogy as demonstrated in Appendices 1 and 2. To do so we need to know the Young's modulus of the rock mass. Based on Goodman (1991), the Young's modulus of the rock mass can be calculated as follows:

$${E}_{rm}= \frac{{E}_{i}{S}_{v}{K}_{n}}{{E}_{i}{+ S}_{v}{K}_{n}},$$

(7)

where E_i is the Young's modulus of the intact rock and K_n is the normal stiffness of the rock joints, and their values can be obtained from Table 1.

Table 3 shows the relevant numerical models, their inputs which were utilised in the numerical models. Table 4 compares the outcomes of the numerical and analytical method. The error between numerical and analytical results were calculated as:

$$Error\left(\%\right)=\frac{{{x}_{num}- x}_{analyt}}{{x}_{num}} \times 100$$

(8)

where x_num is the numerically measured value and x_analyt is the analytical calculated values.

Table 3 Properties rock mass and anchor for the numerical models which are used to calibrate the analytical method*

Table 4 Calibration of the numerical and analytical models

As shown in Table 4, according to the analytical method, in all the numerical models presented in Table 3 the rock blocks should fail in the tensile mode, as it is observed in the numerical models (this can be seen in the Table 4 by the fact that R(l_N) = R_ten(l_N)). In addition, the failure occurs in the deepest formed pressure arch which coincides with the numerical modelling results. Comparison of the results of the analytical and numerical techniques shows that, despite all the simplifications, the developed technique manages to assess the anchoring resistance of the rock mass with error of less than -15% (Table 4). This error margin is much smaller than the extreme overestimation from the traditional cone method (over 600% according to Bruce 1976).

5.2 Calibration of the Developed Analytical Method with the Field Tests

Thomas-Lepine (2014) performed 50 tests on the anchoring capacity of short bolts with diameter of 25 mm installed in boreholes with diameter of 45 mm with lengths of 0.1 to 1 m. Among all the tests, only 21 showed failure in the rock mass. The test site was a dolomite open pit mine, Verdalskalk in Norway. The intact rock has uniaxial compressive strength of 94.5 MPa with standard deviation of 12.41 MPa, the Young's modulus of the intact rock blocks is 61.8 GPa with standard deviation of 4.77 GPa. Thomas-Lepine (2014) together with the test results published photographs of the each test location before and after pull-out test of the rock bolt. In addition, for a number of the test locations, photographs of the cores from the borehole, which used to install the bolt is also provided. As mentioned in the introduction, two different modes of failure were observed by Thomas-Lepine (2014): a pre-existing rock block (wedge) is uplifted by the anchor (wedge uplift) and cracking of the rock blocks due to tensile failure in rock blocks and release of the bolt (tensile failure). In the wedge uplift mode of failure, the anchor was embedded inside only one block, and it is obvious that interlocking has not happened (as we discussed in Sects. 3 and Appendix A relationship between anchor length, voussoir beam span and block sizes in relation to the friction angle of the joints). 11 tests show rock block tensile failure which they are summarised in Table 5. According to the pictures provided for the tests, the rock mass contains 3 joint sets with estimated properties presented in Table 6. It is estimated (with core pictures and pictures from the test sites) that the spacing of the joints should vary between 0.15 to 0.25 m in the tests presented in Table 5.

Table 5 Field tests of fully encapsulated rock anchors by Thomas-Lapin (2014) which represents had block interlocking effect and represented the rock block tensile failure under the tensile force of the anchor

Table 6 Estimated mechanical properties for rock joints for the study site utilised by Thomas-Lapin (2014)

As a rule of thumb, the ratio of the uniaxial compressive strength to the tensile strength for intact rocks is approximately equal to the m_i parameter of the Hoek–Brown strength criterion (Jaeger et al. 2007). For Carbonate rocks according to Hoek and Brown (1997) m_i should be between approximately 10 and 20, meaning that the tensile strength of dolomite at the study site should vary from 4.72 to 9.40 MPa.

Calculations from the developed analytical method indicate that to achieve the anchoring capacities obtained from the field tests (between 15 to 23 tonnes), the joints spacing should be varying between 0.13 and 0.23 m (Table 7). This assessment is in good agreement with the observations for the block sizes in the site. Moreover, the analytical method predicts that the rock blocks should fail by the tensile mode, also confirmed with the field observations.

Table 7 Corresponding joint spacing estimated based on the anchoring capacity measured in the field in comparison to the developed analytical method

5.3 Discussion

5.3.1 Joint Dilation and Friction Angles

As demonstrated in Sect. 4, the anchoring capacity of a rock mass is associated with the load bearing capacity of the deepest formed pressure arch. For block interlocking to form, as demonstrated by the numerical modelling, it is necessary to have a dilation angle of at least 2 degrees in the sub-parallel discontinuities with the anchor. According to Barton and Choubey (1977) and more recently Barton et al. (2023), the initial dilation angle of the joints can be assessed as follows:

$$\psi =\frac{JRC}{3}{\mathrm{log}}_{10}\left(\frac{JCS}{{\sigma }_{n}}\right)$$

(9)

where JRC is the joint roughness coefficient, JCS the joint surface strength and σ_n is the normal stress at the joint surface. Assuming the worst-case scenario where JCS = σ_n, to have at least 2 degree of dilation JRC should be at least 6 which corresponds to planar-rough joint surface or better. Therefore, in rock masses with planar-smooth and planar-slickensides the block interlocking effect cannot be expected even though they might have sub-parallel joints with the anchors.

5.3.2 Rock Mass Classification and Anchoring Capacity

As a general assumption in rock engineering, improving the rock mass quality should lead to an increase in the anchoring capacity of the rock mass. The rock mass quality can be described by rock mass classes based on RMR, Q or GSI methods. The rock mass quality is a combination of weighted factors based on rock block size, shear resistance between blocks, mechanical competences of the blocks, stress state and groundwater condition. Assuming constant intact rock strength, groundwater and stress conditions, increasing the frictional resistance between blocks and increasing the block size, should improve rock mass quality. Hence, by increasing the joint friction angle and block size, while the intact rock's strength remains constant, anchoring capacity of the rock mass is also expected to improve. However, we argued in Fig. 1 that there is not enough published data from anchor tests to validate this assumption. Therefore, in this section, we will discuss how changes in the rock mass quality might affect the anchoring capacity of the rock mass by sensitivity analysis upon the rock block size.

Consider a rock mass with E_i = 40 GPa containing three joint sets, similar to the rock mass classes of 90–90-00, 90–60-00, 90–30-00 in the numerical models. The spacing of all the three joint sets (S_j) varies from 0.2 to 1.0 m. The normal stiffness of the rock joints is 20 GPa/m. Anchors with lengths of 3, 5 and 10 m will be installed vertically in the rock mass. Figure 10 shows the anchoring resistance of the rock mass calculated for different anchor lengths versus the joint spacing in different rock mass classes. It should be noted that for all the rock mass classes and block sizes, the rock block at the anchor base failed by the tensile mode. For the rock mass class 90–90–00 (Fig. 10a), the anchoring resistance of the rock mass increases with the joint spacing. For this rock class, as demonstrated in Sect. 2, the anchor load is distributed evenly in the blocks in which the anchor is embedded. Therefore, the anchoring capacity is also improving by the anchor length.

Fig. 10

Anchoring capacity versus joint spacing for rock mass classes of: (a) 90–90–00, (b) 90–60–00 and (c) 90–30–00

For rock mass classes 90–60–00 and 90–30–00, although anchoring capacity improves by increasing the block size, a larger anchor length does not always lead to a larger anchoring capacity (Fig. 10b, c). In these rock mass classes, increasing the anchor length from 3 to 5 m improves the anchoring capacity but increasing anchor length from 5 to 10 m only slightly changes the anchoring capacity. This can be attributed to the earlier presented reasoning that the anchoring capacity of the rock mass is mostly associated with rock block size and the tensile strength of the rock block which are forming the deepest pressure arch; the load transferred into the rock blocks above the anchor base decreases exponentially. In this case, the ratio of the anchoring capacity to the anchor length should be slightly decreasing if anchor length increases in same quality rock mass. In addition, with improving the rock mass quality the ration of the anchoring capacity to the anchor length should be constant or decreasing if the anchor length also increases, which can also be seen in Fig. 1b–d for field test results. However, according to the traditional cone model the anchoring capacity should increase by the anchor length, which is not supported by the field test data presented in Fig. 1b–d.

Joint spacing is not a single value in reality; the joint spacing in a rock mass can vary in a large range. Considering that a rock mass has several joint sets, finding a representative joint spacing (and the corresponding rock block size) which is a necessary input for the proposed analysis is not a straightforward task. One approach can be utilising statistical methods to calculate a representative joint spacing and the required anchor length which grantee that at least more than one block along the anchor has larger joint spacing (block size) that the representative value. With this technique the length of a fully bonded anchor can be obtained. Investigating this issue is beyond the scope of this paper and is a topic for future research.

5.3.3 Distribution of the Transferred Load to Rock Blocks Along the Anchor

According to the developed analytical method, the anchoring capacity of the rock mass is the sum of the anchoring resistances of the rock blocks along the anchor. The largest portion (over 60%) of the anchoring capacity comes from the anchoring resistance of the base block (rock block located exactly above the shear length at the anchor base, Fig. 7). If the rock mass quality is similar along the anchor (as it is also assumed in developing the analytical method), the anchoring resistance of rock mass is considered to decrease exponentially with coefficient k (Eq. 3). However, numerical models shows that k ≈ 1.0 1/m is valid for all the cases except situations similar to the rock mass class 90–90–00.

In case of elastic contact between anchor and grout and grout and rock, and rock mass anchoring resistance along the anchor larger than the transferred load from the anchor to the blocks, the shear stress distribution along the rock mass and grout interface generated by anchor pull-out can be represented by (Farmer 1975; Li and Stillborg 1999) as follows:

$$\tau = {\tau }_{max}\mathrm{exp}\left(-{k}_{g}l\right),$$

(10)

where τ_max is the maximum shear stress at collar of the anchor for fully grouted anchor and kg is constant which represents the shear stress distribution along the contact of either anchor-grout or grout-rock. In case of elastic rock mass (rock mass much stronger than the anchor load), it can be assumed that k ≈ k_g and hence

$$k=\frac{2}{{d}_{b}} \times \sqrt{\frac{2{G}_{r}{G}_{g}}{{E}_{b}[{G}_{r}\mathrm{ln}\left(\frac{{d}_{g}}{d}\right)+{G}_{g}\mathrm{ln}\left(\frac{{d}_{0}}{{d}_{g}}\right)]}},$$

(11)

where E_b is the Young's modulus of the anchor, G_r is the shear modulus of rock mass, G_g is the shear modulus of grout, d_g is the borehole diameter and d_o is the diameter of an imaginary cylinder around the anchor which is influenced by the anchor load. It can be assumed based on the physical modelling of anchors by Dados (1984) d_o ≈ 2L for a long anchor, and for practical reasons anchors mostly have length which is larger than the shear length (l_shear). Therefore, d₀/d_g ≥ 80 while (d_g/d) ≤ 2. Hence,

$$k\cong \sqrt{\frac{8{G}_{r}}{{d}_{b}^{2}{E}_{b}\mathrm{ln}\left(\frac{2L}{{d}_{g}}\right)}}$$

(12)

Equation (12) can be utilised to estimate the load transferred into the rock blocks along the anchor, if we assume that there is no debonding along the anchor. Figure 11 compares the transferred load to the rock blocks from the anchor obtained from numerical modelling, compared to the assumption of k = 1 and k obtained for the elastic condition by Eq. (12). In the engineering design of the anchors, it is mandatory to guarantee that the rock mass remains elastic, meaning that k should be estimated by Eq. (12); this leads to a conservative estimation of the anchoring capacity (lower bound).

Fig. 11

Load transferred to rock blocks located along the anchor with length of 4 with rock mass classes of: (a) 90–60–00 and (b) 90–30–00. Numerical results are compared with assuming that k = 1 and when k is calculated by Eq. 11

5.3.4 Base Plate Forming and Anchoring Capacity

Numerical modelling shows that at the location of the deepest formed pressure arch close to the anchor base, instead of one pressure arch (voussoir beam) several rows of pressure arches are formed (as demonstrated in Fig. 6) and utilised in Appendix 2 to assess anchoring resistance in a specific depth. The majority of published field tests report that the uplifted rock by an anchor has a cone shape. This might be because in these field tests the authors were more focused on the uplifted mass by the anchors and not the volume of the rock mass interacting with the anchor. The interacting rock mass with an anchor is far larger than the cone volume.

Generating the base plate (as denoted in this paper) leads to a change in the shape of the failed rock mass around anchor: a frustum shape rather than a cone. Base plate forming improves the strength of the pressured arch to be much higher than the tensile strength of the rock block which transfers the anchor load to the rock mass. The tensile failure of the load transferring block can lead to sudden release of the anchor and uplifting the rock mass with it which might have a conical geometry. The base plate forming is an interesting phenomenon which should be considered further in investigating the anchoring capacity of rock masses.

5.3.5 Limitations

The developed method in this paper is for a specific condition in blocky rock masses. It includes simplifications regarding geometry, size, boundary conditions and loading of the formed pressure arches along the anchors.

In addition, according to the voussoir beam mechanic (Appendix 1) the anchor length should be at least 2 –3 times of the average joint spacing (depending on the friction angle of the joints) to avoid shearing failure between the blocks and to generate rock block interlocking (see Eq. (33)). Therefore, the developed method cannot be implemented for such anchor length conditions.

The technique presented in this manuscript does not consider the groundwater in the analysis as it adds more complexity in terms of the weight of the uplifted blocks by the formed pressure arches, decrease in the stiffness of the rock mass, tensile and compressive strength of the rock block. In addition to decreasing the friction angle between the blocks, groundwater can eliminate the rock joint dilations since it can decrease JCS. Moreover, groundwater effect on the friction and dilation angles of weathered joint surfaces can be more dramatic compared to fresh and rough joint surfaces. Addressing these questions requires further numerical modelling in conjunction with field tests of anchors in saturated rock masses.

6 Conclusions

A simplified analytical method was suggested to calculate the anchoring capacity of a rock mass when the rock mass has a joint set which is sub-parallel with the anchor. The analysis shows that in such a situation the rock blocks tend to interlock and generate an arch shaped stress concentrated zone. This zone behaves like an arch and transfers the tensile force of the anchors as a horizontal compressive force into the rock mass. A simplified analytical method was presented to calculate anchoring capacity of the rock mass in this situation, and it was calibrated against numerical models and filed tests.

The method suggested in this paper shows that the traditional rock mass classification techniques are insufficient for selecting sites where anchorage solutions are necessary (e.g., windfarms and suspension bridges). Rock joint orientation relative to the anchor, rock block size, tensile and compressive strength of the intact rock, stiffness of the rock mass and the shearing behaviour of the rock discontinuities are the most important parameters to be considered as well as groundwater table and the ground surface topography.

The major outcome of this study is that the traditional cone weight method can be misleading in determining rock mass capacity against the tensile load from an anchor. For instance, increasing the anchor length does not lead to similar improvements in anchoring capacity in all rock masses, as predicted by the cone method.

Appendices

Appendix 1

Simplified Voussoir Beam Analogy for Rock Block Interlocking

As demonstrated by the numerical modelling in Sect. 2 and physical modelling by Dados (1984), the interlocked blocks help the rock mass to resist the tensile force from the anchor by transferring it as horizontal forces. The stability of interlocked blocks has been investigated by voussoir beam analogy in rock engineering, which will be also utilised here.

For the sake of simplicity, we hereby assume that the anchor is vertical and the rock joints which are sub-parallel with the anchor are sub-vertical. The following assumptions are made to be able to mathematically model the stability of a voussoir beam. The compression arch generated due to the block interlocking has almost the same thickness (n_a) at the abutments of the arch and the centre of the arch. However, the thickness of the pressure arch is larger than n_a in the stretch between the abutments and midspan (Fig. 4d and 12). The stress distribution on the sub-vertical joints at the pressure arch abutments and the midspan of the arch has a triangular shape (Fig. 12). The rock blocks behave elastically. It was assumed by several researchers that the compression arch has a parabolic shape (e.g. Sofianos 1996; Diederichs and Kaiser 1999). However, Shabanimashcool and Li (2015) showed that approximating the parabolic arch with a bilinear shape as shown in Fig. 12 will not lead to a significant error in the results. In this study, the pressure arch is similarly approximated by a truss consisting of two linear elements connected to each other in the midspan of the pressure arch. This assumption allows us to use the techniques used for the stability analysis of two elastic bars hinged together in the midspan subjected to a vertical force, as an example by Maceri (2010). In addition, it was assumed that the magnitude of the horizontal in-situ stress can be neglected.

Fig. 12

Geometry and assumptions used in voussoir beam bearing capacity analysis

As Fig. 12 shows, deflection of the pressure arch under the anchor force (P) generates an axial force F in the truss elements, which has horizontal projection of F_h. The horizontal force (F_h) is offset by the distance of z, denoted as the moment arm. Initially, the moment arm is z₀, but with increase of the anchor force P it decreases to z. z₀ can be calculated as follows:

$${z}_{0}={S}_{h}-\frac{2}{3}{n}_{0},$$

(13)

where S_h is the thickness of the voussoir beam or spacing of the sub-horizontal joints. Due to the pull-up force P, the compression arch shortens, generating force F. Static equilibrium is fulfilled if the vertical force of P is equal to the vertical projection of the force generated in the assumed truss elements as follows:

$$P=\frac{2Fz}{\sqrt{{\left(\frac{S}{2}\right)}^{2}+{z}^{2}}}$$

(14)

The axial force in the truss elements can be calculated as follows:

$$F ={E}_{i}A{\varepsilon }_{c}$$

(15)

where E_i is the Young's modulus of the assembly of the rock blocks, A is the mean cross-section area of the compression arch and ε_c is the Cauchy strain. We know that ε_c = (Γ₀- Γ)/ Γ₀, where Γ₀ is the initial length of the truss element and Γ is the shortened length of the truss element after applying P (the compression strain is positive). To make the calculations simpler in mathematical terms, the Green strain was used instead of the Cauchy strain. The Green strain is defined as follows:

$${\varepsilon }_{G}=\frac{{\Gamma }_{0}^{2}-{\Gamma }^{2}}{{2\Gamma }_{0}^{2}}$$

(16)

We know that

$${\varepsilon }_{G}={\varepsilon }_{c}+\frac{1}{2}{\varepsilon }_{c}^{2}$$

(17)

Considering that the level of strain is very low (always less than 5% before the rock reaches its compressive strength), using the Green strain instead of the Cauchy strain will therefore cause error less than 1.25%, which is acceptable for this analysis.

Considering the Green strain (Eq. 16) in Eq. (14) leads to

$$P=EA\frac{\delta (\delta -1)(\delta -2)}{{(\sqrt{1+{\alpha }^{2}})}^{3}} ,$$

(18)

where δ = (z₀—z)/z₀ and α = S/(2z₀). In the above formulation, α represents the aspect ratio of the pressure arch, δ shows the deflection of the beam, and A is the mean cross-section area of the pressure arch, which is a function of n₀.

It should be noted that if P instead of being concentrated in the middle of the compression arch (as shown in Fig. 12) is uniformly distributed along the arch, then the static equilibrium is governed if the moment generated by P in half of the compression arch (PS/8) is equal to F_h z. In this condition, right-hand side of Eq. (18) and Eq. (14) should be multiplied by 2. In this manuscript for investigating of the anchor and rock mass interaction, we utilised Eq. 18 (concentrated load imposed in the midspan, Fig. 12).

Revisiting Fig. 12, the cross-sectional area of the compression arch in the abutments is n₀ × S_o, where S_o is the out-of-plane spacing of the rock joints or the out-of-plane thickness of the voussoir beam. However, the cross-sectional area of the voussoir beam is not constant along the compression arch (Fig. 4d). Therefore, a mean value for the cross-sectional area of the pressure arch was defined, assuming that the boundary of the compression arch is linear and follows parallel with the bilinear truss elements (Fig. 12). Hence, the mean area of the arch is equal to the following:

$$A=\left({S}_{h}-\frac{{\left({S}_{h}-{n}_{a}\right)}^{2}}{{S}_{h}-\frac{2}{3}{n}_{a}}\right){S}_{o}$$

(19)

Three different modes of failure have been identified for the voussoir beams, namely buckling (snap-through), corner crushing (crushing) and sliding at the abutments and midspan (sliding), according to Brady and Brown (1985). The snap-through type of instability happens when the moment generated by shortening the compression arch is not enough to produce resistance moment against the moment generated by P. The crushing type of failure happens when the maximum stress in the beam abutments reaches the uniaxial compressive strength of the rock blocks and sliding happens when the pull-out force of P is higher than the friction resistance between the rock blocks in the beam.

Assuming a constant value for n_a (meaning that A and α are also constant, indicating that the geometry of the pressure arch is immutable), P can be expressed as the sole function of deflection (δ). In other words, Eq. (18) can be re-written as follows:

$$\frac{P}{EA}{(\sqrt{1+{\alpha }^{2}})}^{3}=\delta (\delta -1)(\delta -2)$$

(20)

Figure 

Fig. 13

(a) Changes in the anchor force (P) versus the beam deflection for a specific n_a. (b) Changes in loading capacity of voussoir beam versus different depths of the pressure arch in the abutments (n_a) for a specific deflection of the beam (constant δ). It shows that when 0.37 ≤ n_a / S_h ≤ 0.48, the load-carrying capacity of the voussoir beams is the maximum. (c) Changes of pressure arch thickness in the abutment versus beam span which leads to maximum load-carrying capacity of the voussoir beams. Both values of n_a and S are normalised to the beam thickness in the vertical direction (S_h)

13a shows the right-hand side of Eq. (20) versus δ. P increases with deflection of the pressure arch until a maximum value, and after that decreases while the deflection increases. The highest amount of P that can be carried by a voussoir beam for a specific value of n_a can be obtained via the following:

$$\frac{\partial (\frac{P{\left(\sqrt{1+{\alpha }^{2}}\right)}^{3}}{EA })}{\partial \delta }=\frac{\partial P}{\partial \delta }=\frac{d(\delta (\delta -1)(\delta -2))}{d\delta }=0$$

(21)

This leads to δ = 0.42, where the load-carrying capacity of the beam is the maximum. However, as soon as the deflection passes beyond 0.42 the beam fails by the snap-through mechanism, since with increase of the deflection the load-carrying capacity decreases. Therefore, the beam load corresponding to δ = 0.42 is the load capacity of the beam in the snap-through failure mechanism. This conclusion is not dependent on the assumed value of n_a. δ = 0.42 for snap through failure coinciding with the detail calculations carried out by Sofiaos (1996) and Yiouta-Mitra and Sofianos (2018).

Several techniques including laboratory tests and numerical modelling were utilised to obtain the value of n_a at which the rock blocks in a voussoir beam start to interlock with each other. However, the majority of researchers utilised numerical modelling to find the value of n_a. For example, Sofianos (1996), through numerical modelling, showed that n_a is between 0.12 and 03 S_h for the voussoir beams consisting of only two rock blocks, assuming rigid abutments and stiff joints in the numerical models. Similarly, Sofianos and Kapenis (1998) showed that n_a varies between 0.12 and 0.3 S_h for a multi-jointed voussoir beam. However, Diederichs and Kaiser (1999) assumed elastic but very stiff abutments and joints, leading to the thickness of the pressure arch from 0.75 to 0.35 S_h for multi-jointed voussoir beams, where snap-through failure happens when n_a = 0.35 S_h. Tsesarsky (2012) argued that, since in nature the rock mass is deformable at the abutments and the rock joints, the approach of Diederichs and Kaiser (1999) should be used for numerical modelling of the voussoir beams. He also showed through sensitivity analysis that when the abutment blocks of the numerical model have a Young's modulus which is 10 times or more larger than the Young's modulus of the beam rock blocks, the abutment stress distribution becomes nonlinear, and the thickness of the compression arch falls below 0.3S_h. The different results by authors were obtained due to different assumptions made for the abutments and joint stiffnesses. However, Talesnick et al. (2007) showed by physical modelling of voussoir beams in the laboratory that the n_a / S_h ≈ 0.5 when the rock blocks interlock. In addition, Shabanimashcool and Li (2015) showed, by the minimum stored potential energy technique, that n_a / S_h varies between 0.45 and 0.375 depending on the S / S_h ratio.

Equation (18) can be re-written as follows:

$$\frac{P}{E\delta (\delta -1)(\delta -2)}=\frac{A}{{(\sqrt{1+{\alpha }^{2}})}^{3}}$$

(22)

In Eq. (22), the right-hand side is a function of n_a, S and S_h; i.e. it is only a function of the n_a / S_h and S / S_h ratios. Figure 13b shows the right-hand side of Eq. (22) for different ratios of S / S_h and n_a/ S_h. It shows that when n_a/ S_h = 0.37‒0.48, depending on the beam S / S_h ratio, the resistance of the beam against the load P is the maximum. The maximum value of the right-hand side of Eq. (22) can be found by the following:

$$\frac{\partial }{\partial {n}_{a}}\left(\frac{A}{{\left(\sqrt{1+{\alpha }^{2}}\right)}^{3}}\right)=0,$$

(23)

where A and α both are a function of n_a, S_h and S. This leads to the following:

$${({S}_{h}-\frac{2}{3}{n}_{a})}^{3}+ {S}^{2}\left({S}_{h}-\frac{2}{3}{n}_{a}\right)-\frac{3}{4} {S}^{2}{S}_{h}=0$$

(24)

The roots of Eq. (24) can be calculated via the Cardano formula (Kurosh 1972), where

$$\Delta = \sqrt{\frac{9}{64}{S}^{4}{{s}_{h}}^{2}+\frac{{S}^{6}}{27}}$$

(25a)

$${n}_{a}=\frac{3}{2} ({s}_{h}- \sqrt[3]{\frac{3}{8}{S}^{2}{S}_{h}+ \Delta }-\sqrt[3]{\frac{3}{8}{S}^{2}{S}_{h}- \Delta } )$$

(25b)

Figure 13 shows n_a obtained from Eq. (24) for different n_a / S_h ratios. It shows that the load-carrying capacity of the beams is the maximum when n_a / S_h varies between 0.435 and 0.37 dependent on S/S_h ratio. This range of n_a variation coincides well with Shabanimashcool and Li (2015). This mathematical observation is similar to the results of the numerical simulations by Nomikos et al. (2002),when the assumed joint normal stiffness of the sub-vertical joints is less than approximately 60 GPa/m, and Tsesarsky (2012), where they showed that 0.3 < n_a / S_h ≤ 0.5. It should be noted that, according to these calculations (Eq. 24), when the beam span compared to the depth of the beam is too large, the compression arch thickness is 0.37 S_h, i.e. when the beam has a very large span and close to experience snap-through failure, the n_a / S_h ratio should be close to 0.37.

The anchor load at which the voussoir beam will undergo the snap-through failure can be obtained via Eq. (18) considering δ = 0.42, while corresponding n_a is calculated by Eq. 24; i.e.

$${P}_{st}\cong 0.385\frac{EA}{{(\sqrt{1+{\alpha }^{2}})}^{3}}$$

(26)

To find out at which stress level the voussoir beam will undergo the corner crushing type of failure, we need to calculate the maximum abutment stress as follows:

$${\sigma }_{m}=\frac{2{F}_{h}}{{n}_{a{S}_{o}}}\cong \frac{4E\delta \left(2-\delta \right)\alpha }{{3\left(1+{\alpha }^{2}\right)}^\frac{3}{2}}$$

(27)

At the moment of corner crushing, σ_m = λ σ_ci, where σ_ci is the uniaxial compressive strength of the rock mass and 0 < λ ≤ 1 is a factor that can be introduced in order to consider the scale effect on the strength of the rock blocks and weathering of rock materials. Corresponding δ which leads to σ_m = λ σ_ci can be calculated as follows:

$${\delta }_{crush}\cong \frac{-2\omega +2\sqrt{{\omega }^{2}-\omega \lambda {\sigma }_{ci}}}{-2\omega }=1-\sqrt{1-\frac{\lambda {\sigma }_{ci}}{\omega }},$$

(28)

where $\omega =\frac{4E\alpha }{3{S}_{o}{\left(1+{\alpha }^{2}\right)}^\frac{3}{2}}$

Later calculated δ_crush can be utilised in Eq. (18) to calculate load carrying capacity of the pressure arch against failure mode of corner crushing, which is denoted as P_cr. Equation (28) is valid when $0<\frac{\lambda {\sigma }_{ci}}{\omega } \le 1$. If $< \lambda {\sigma }_{ci}$, the compressive strength of the rock blocks is very large, and the voussoir beam will never fail by the crushing mode of failure. Hence, in this situation the mode of failure for the beam is only limited to snap through. In addition, due to numerical simplifications δ_crush obtained by Eq. 28 sometimes is slightly larger than 0.42. In this situation, as worst case scenario to calculate Pcr, it should be assumed that δ_crush = 0.42.

For the sliding mode of failure, the rock blocks will slide as follows:

$$P \ge 2F\mathrm{cos}\left(\beta \right)\mathrm{tan}\left(\varphi \right),$$

(29)

where φ is the friction angle of the sub-vertical joints and β is the angle between F and F_h (Fig. 12).

Therefore, sliding happens as follows:

$$\mathrm{tan}\left(\beta \right)>\mathrm{tan}(\varphi )$$

(30)

tan(β) can be calculated as follows:

$$\mathrm{tan}\left(\beta \right)=\frac{2({z}_{0}-z)}{S}$$

(31)

Therefore

$$\mathrm{tan}\left(\varphi \right)\le \frac{2\left({z}_{0}-z\right)}{S}$$

(32)

The above inequality can be checked if we find the value of z₀ and the maximum passible value of z. z₀ = S_h – 2/3 n_a and n_a ≈ 0.48 S_h for short beams, which has the risk of the sliding type of failure. Therefore, z₀ = 0.68 S_h. Knowing that 0 ≤ z ≤ z₀, the maximum possible value of z is 0.42 z₀. Therefore, Eq. (32) can be re-written as follows:

$$\frac{S}{{S}_{h}}\le \frac{0.78}{\mathrm{tan}\left(\varphi \right)}$$

(33)

If S/S_h satisfies Eq. (33), then the voussoir beam will fail due to the sliding of the blocks. For example, assuming that the friction angle of the sub-vertical joints is between 15 to 30 degrees; the voussoir beam will fail by the sliding mode of failure when S/S_h ≤ 1.36 to 2.91. If the beam does not satisfy Eq. (33), then the beam will fail either with snap-through or crushing.

In summery to find load bearing capacity of a voussoir beam (pressure arch) following steps should be considered:

• Obtain S, S_h, S_o and E_rm, σ_ci of intact rock blocks, λ and friction angle of the sub-vertical discontinuities.

• If Eq. (33) does not satisfy by the beam geometry proceed further, unless report that no pressure arch will be generated.

• Use Eq. (26) to calculate P_st.

• Use Eq. (28) to calculate δ_crush and then use it to calculate P_cr utilising Eq. (18).

• Minimum of P_st and P_cr will be the load bearing capacity of the pressure arch or voussoir beam.

The suggested simplified method in Appendix 1 is calibrated with the physical testing of voussoir beams conducted in the laboratory by Talesnick et al. (2007). The objective of the calibration is to show that the simplified method captures the mechanism of loading and deflection of the voussoir beams.

Talesnick et al. (2007) tested two different configurations of the voussoir beams consisting of 6 blocks of gypsum denoted as full beam and half beam under uniformly distributed loading by a centrifuge. In the full beams the gypsum blocks have size of 46, 46 and 46 mm in width, length, and height (respectively) while in the half beam the block size is 46, 46, and 23 mm in width, length and height, respectively. The voussoir beam is equipped with load cell to measure the thrust force generated inside of the beam by the centrifuge rotation. Each block is monitored by two LVDT-s which makes it possible to measure uneven displacement and translation of the blocks. A single block of the beam was instrumented by 3 strain gages, one located at 4 mm from top edge of the block, one at the middle of the block height and the last one is in 4 mm from the lower edge of the block. Strain gages are used only in full-block tests. The strain gages located in middle of the first block from the abutment, second block and third block. Before applying the centrifuge loading, the rock blocks were assembled and a small trust of 50–70 N were applied to hold them together. Table

Table 8 Mechanics and physical properties of gypsum blocks from tests conducted by Talesnick et al. (2007)

8 shows the physical and mechanical properties of the gypsum blocks.

The first outcome of the tests was that regardless of being full-beam or half-beam the trust force increases linearly with increasing of the centrifuge force (or acceleration), Fig. 

Fig. 14

Comparing of the physical modes by Talesnick et al. (2007) with the developed simplified analytical method: (a) developed thrust versus acceleration for full-beam, (b) beam deflection versus acceleration in full-beam, (c) developed thrust versus acceleration for half-beam, and (b) beam deflection versus acceleration in half-beam

14a, c. Extrapolation of the strain gage data toward midspan and abutment of the voussoir beam shows that the thickness of the pressure arch (n_a) along the beam does not change with loading level, and it is almost constant. In the midspan n_a is always approximately 0.46 of the block thickness while in the abutment is approximately 0.76 of the block thickness. The deflection of the beams under the load is nonlinear and half-beam shows larger deflection in comparison to the full beam (Fig. 14b, d).

According to the developed analytical method the thickness of the pressure arch (n_a) is only dependent on the beam span ratio to the beam thickness (S/S_h) and do not dependent on the loading level which can be seen from the tests results as well. According to Eq. 24 for full-beam and half-beam, n_a should be equal to 0.39 S_h and 0.37 S_h in midspan of the beam, which have differences of 17.9% with physical tests for the full beam. Since the laboratory results is extrapolation of the nearest measurement with only 3 strain gages, the differences of 17.9% is acceptable. Moreover, the rock blocks in the tests are pre-tensioned with 50–70 N thrust forces which is affecting the outcomes specially in the thickness of the pressure arch at the abutments.

Comparing the calculated and measured thrust force and deflection for the full-beam and half-beam shows that there are less than 20% differences between them. Analytical method captures the mechanism of developing in the trust and deflections of the voussoir beams similarly to the laboratory measurements.

Appendix 2

Rock Block Interlocking Effect on Rock Mass Anchoring Capacity

In this appendix, we are going to present how to utilise the developed methods for assessing load bearing capacity of the voussoir beams in combination with the tensile strength of the rock blocks to calculate the anchoring capacity in a specific depth along an anchor.

If an anchor embedded in rock mass which contains sub-parallel discontinuities with the anchor, then it has potential to build pressure arches (voussoir beams) along the anchor. Then the anchoring capacity of the rock mass will be dependent on the load bearing capacity of those pressure arches. As demonstrated in Appendix 1, the voussoir beams (pressure arches) fail under one of the mechanisms of block sliding, corner crushing and snap through. However, numerical modelling showed that there is another type of failure which is tensile failure of the block where anchor is grouted in it and the block is transferring the anchor load into the pressure arch. To have tensile mode of failure the contact between anchor-grout and grout -rock is strength enough and they do not go under failure. In addition, the interlocking effect should be strong enough so that the voussoir beams do not fail by any mechanisms mentioned above.

As demonstrated in Fig. 6, at the anchor base (or any point along the anchor) several parallel pressure arches are formed (these group of parallel pressure arches denoted as base plate close to the anchor base). The number of the parallel pressure arch which are generated in minimum is 3 but increases as L/Sj ratio increases (longer anchor and shorter S_j means more rows of parallel pressure arches at the base plate). Considering the frustum shape of the involving rocks with an anchor, the span of the rows of the pressure arches generated along an anchor should increase with decreasing depth.

Figure 

Fig. 15

Free diagram of several group of pressures arches formed in parallel. The possible tensile failure of the block at which the anchor paths through is shown also

15 shows the free diagram of a pressure arch group generated at depth of l_i along an anchor. The load transferred to the block by the portion of the anchor embedded in it is P(l_i), while the resistances of the pressure arches (which are generated in out-of-plane direction in Fig. 15) is R_int(l_i):

$${{R}_{int}\left({l}_{i}\right)= R}_{int,1}\left({l}_{i}\right)+ {R}_{int,2}\left({l}_{i}\right)+ {R}_{int,3}\left({l}_{i}\right)+\dots {R}_{int,n}\left({l}_{i}\right)$$

(34)

n is the total number of the parallel pressure arches generated at depth of l_i. According to the numerical modelling Fig. 6e, at least three rows of the pressure arches are generated in all the models. Hence, the most conservative condition can be to assume to have three rows of the pressure arch. In addition, the span of the first pressure arch is at least equal to the anchor length (see Sect. 3), which decreases in the other parallel formed pressure arches (see Fig. 6). For one specific block depth of l_i, the load bearing capacity of the first voussoir beam is smaller than the second one and second one from the third one, or

$${R}_{int,1}\left({l}_{i}\right)\le {R}_{int,2}\left({l}_{i}\right) \le {R}_{int,3}\left({l}_{i}\right)$$

(35)

Since, their span decreases. However, the portion of the anchor loads carried by beam one, larger than the second and second one larger than third one (three angular distribution of the anchor loads from voussoir beam 1 to 3). Therefore, for a worst-case scenario,

$${R}_{int}\left({l}_{i}\right)\cong 2 {R}_{int,1}$$

(36)

The weight of the total mobilised rock blocks by those parallel pressure arches of 1 to 3 is W(l_i), which is

$${W\left({l}_{i}\right)= W}_{1}\left({l}_{i}\right)+{W}_{2}\left({l}_{i}\right)+{W}_{3}({l}_{i})$$

(37)

With assuming worst case scenario and θ = 90 in Fig. 9, the weight of the mobilised rock masses by each of the voussoir beams follows:

$${W}_{3}\left({l}_{i}\right)\le {W}_{2}\left({l}_{i}\right)\le {W}_{1}\left({l}_{i}\right),$$

(38)

because of the again span of the formed voussoir beams. With assuming that each pressure arch consists of 3 blocks (minimum required number of blocks to form a pressure arch) and 3 parallel voussoir beams are formed, a conservative estimate for the weight of mobilised blocks by the parallel pressure arches will be as follows:

$$W\left({l}_{i}\right)=\left(3{S}_{v}{S}_{o}\gamma {l}_{i}\right)\times 3=9{S}_{v}{S}_{o}\gamma {l}_{i},$$

(39)

where γ is density of the rock blocks.

The rock block at which the anchor embedded in (see Fig. 15) it might also fail by the tensile mode (as discussed above). In this condition, since the pressure arches are strong enough, we can assume that the tensile mode of failure will be similar to concrete cone failure generated by an anchor installed inside it (see ACI 349-85 1985), as shown in Fig. 15. The failure surface is a surface of a cone which is limited when reaches to the boundaries of the rock block and the apex angle of the cone is 90 degrees. The tensile strength of the block against the anchor load can be defined as follows:

$${R}_{tens}\left({l}_{i}\right)= {\sigma }_{ti}{A}_{s}\mathrm{sin}\left(\frac{\pi }{4}\right),$$

(40)

where σ_ti is tensile strength of intact rock and A_s is the surface of the failure cone which can be determined as follows:

$${A}_{s}=\frac{\sqrt{2}{S}_{v}{S}_{o}}{\mathrm{sin}(di{p}_{inc})},$$

(41)

where dip_inc is the dip angle of the inclined joint set, see Fig. 15.

In conclusion, the anchoring capacity of rock mass at depth of l_i, where block i is located, is minimum of the load bearing capacity of the formed voussoir beams plus the weight of mobilised rock mass by them and the tensile load carrying capacity of the block which anchor embedded in, as is presented in Eq. (2).

Appendix 3

Consider a rock mass with 3 joint sets as demonstrated in Table

Table 9 Intact rock and rock mass properties for example

9. The anchor has a length of 3 m, is embedded vertically inside the ground, and the anchor has a nominal diameter of 40 mm which is installed in borehole with diameter of 45 mm. To calculate the anchoring capacity the following steps were followed:

• 1. Since there is a vertical joint set which is parallel with the anchor, block interlocking due to the anchor load will happen. In addition, the rock joint surfaces has dilation angle of larger than 2 degrees.

• 2. The shear length of the anchor considered to be 25 times its diameter (Eq. 6), which is 1 m. The deepest voussoir beam will be formed is between depths of 2 m (Table

  Table 10 Calculations carried out for the example

  10).

• 3. For deepest voussoir beam, R_int(l_N) = 0.2 to 3.11MN, W(l_N) = 0.049 to 0.146 MN and R_tens(l_N) = 0.15 to 1.51 MN. Therefore, the failure mode of the deepest formed pressure arch is due to the tensile failure in the block which anchor embedded in.

• 4. Considering k = 1 1/ m leads to anchoring capacity for the rock mass 0.70 to 2.80 MN.

For design purposes the anchor capacity of rock mass can be assumed to be 0.70 MN. For comparison reason, we can calculate the anchoring capacity with the cone weight method, if the apex of the cone located at depth of L-l_shear = 3 – 1 = 2 m and apex angle of the cone is 90 degrees. The anchoring capacity of the rock mass can be estimated as 0.23 MN.