1 Introduction

A rockfall risk is identified and managed by the identification of the potential instable rock blocks, the prediction of the trajectories of the rock blocks as well as their kinematic attributes. The prediction of block trajectories as well as the energies involved are key to designing protection structures. This is commonly achieved via trajectory models. Due to the complexity of the phenomenon, only a few of these models can predict the occurrence of fragmentation of blocks at impact and its possible outcomes, i.e. number of fragments, size distribution of fragments and trajectory of fragments. As far as the authors are aware, the only two trajectory models possessing a fragmentation capability are HY- STONE (Crosta and Agliardi 2004) and RockGIS (Matas et al. 2017; 2020).

Fragmentation of blocks upon impact has been commonly observed after rockfall events (Crosta et al. 2007; De Blasio et al. 2018; Giacomini et al. 2009; Ruiz-Carulla et al. 2017) and it is recognised as an important phenomenon because it can be a source of energy dissipation and fragments produced at impact may have a very different trajectory (and mass) than the original block they were created from. Both of these points are relevant for the design of protection structures (Jaboyedoff et al. 2005). The probability of occurrence of block fragmentation is also important for the quantitative risk assessment, QRA (Agliardi et al. 2009; Corominas et al. 2005; Scavia et al. 2020).

Fragmentation is a complex phenomenon and it is not fully understood. Indeed, the occurrence of fragmentation can be affected by a variety of factors. Some of these factors are related to the intrinsic nature of the falling rock or rock mass, such as the strength, and presence of discontinuities (or weakness planes) on the impacting block in relation to the potential energy (Giacomini et al. 2009; Haug et al. 2016; Wang and Tonon 2011; Ye et al. 2019b), as well as the characteristics of the impacting ground surface (i.e. the stiffness) (De Blasio and Crosta 2014; Uzi and Levy 2018; Wang and Tonon 2011). Intuitively, other factors that can affect the fragmentation occurrence and outcome are related kinematic and geometry of the block such as the impact velocity, the impact angle and geometry of the collision, or the number of successive impacts (Giacomini et al. 2009; Nocilla et al. 2009; Ruiz-Carulla et al. 2020; Wang and Tonon 2011; Zhang et al. 2000).

A limited number of studies can be found in the literature about the evolution of damage and cracks at impact and the energy dissipation mechanisms during rock fragmentation. Studies with a specific focus on size distribution of fragments can be found in the field of material science and material procession (Carmona et al. 2008; Khanal et al. 2008; Shen et al. 2017; Tomas et al. 1999; Wu et al. 2004). In the field of rock mechanics, quite a few studies were focussed on the effect of cumulative damage under repeated impacts on the rebound characteristics for normal impacts (Chau et al. 2002; Imre et al. 2008; Labous et al. 1997; Seifried et al. 2005; Ye et al. 2019a). In particular, Ye et al. (2019a) conducted drop tests with marble spheres where the trajectory during multiple rebounds was recorded by using a high-speed camera. The results of this study showed the influence of different energy dissipation mechanisms related to the progressive growth of macrocracks as a function of increasing impact energy. Asteriou and Tsiambaos (2018) also observed a reduction of the normal restitution coefficient with impacting velocity (under single impact), which can be explained by damage upon impact.

In situ testing has been widely performed to investigate the rockfall phenomenon and calibrate rockfall models parameters (Bourrier et al. 2009; Dewez et al. 2010; Dorren et al. 2006; Giacomini et al. 2010; Gili et al. 2016; Labiouse and Heidenreich 2009; Ritchie 1963; Spadari et al. 2012; Volkwein and Klette 2014), however, only a few studies focus on experimental analysis of fragmentation in the context of rockfall (Giacomini et al. 2009; Gili et al. 2016; 2022; Prades-Valls et al. 2022; Ruiz-Carulla et al. 2020). In particular, Giacomini et al. (2009) investigated the orientation of the rock discontinuities with respect to the impacted surface (measured from image analysis). The results showed that the angle between the discontinuities and the impacting surface (or impact angle) can significantly influence the outcome of the fragmentation (i.e. the number of fragments after impact). An energy balance analysis was conducted for each test and the results showed that the amount of fragmentation energy dissipated in fragmentation was a constant ratio to the kinetic energy before impact.

Corominas and co-workers (Matas et al. 2017; Ruiz-Carulla and Corominas 2020; Ruiz-Carulla et al. 2015, 2017; 2020) recently developed a fractal-based fragmentation model which can reproduce the volume–frequency distribution of fragments. The model has been validated for several large rockfalls in the Pyrenees mountains. However, their model cannot be used to predict trajectories and likelihood of fragmentation. Guccione et al. (2021a) recently proposed a model to predict the fragmentation survival probability of brittle mortar spheres from the statistical variability of material parameters obtained by quasi-static indirect tensile tests and unconfined compression tests. Even though the current form of the model only applies to homogenous spheres, it is a first step towards predicting the survival probability of blocks at impact in a rockfall context.

Indeed, these studies provide some key information on the phenomenon but, before incorporating fragmentation into predictive trajectory models, more research is required to better understand this complex phenomenon because several questions still remain unanswered. For example, in a given geological setting and for given impact conditions, it is relevant to predict the likelihood of fragmentation. Then, if fragmentation occurs, it is important to predict the outcome of fragmentation, in terms of fragment size distribution, fragment trajectory and fragment energy. Obtaining answers to these questions is complex, even for simplified impact tests.

The experimental campaign presented in this paper is part of a larger ongoing study on rock fragmentation upon impact, which aims at bringing elements of answers to the above-mentioned key questions. Drop tests were conducted with four diameters of mortar spheres (50, 75, 100 and 200 mm) of three different strengths, falling on a horizontal concrete slab, with the objective to gather high-quality fragmentation data. The setup constitutes a very significant simplification compared to real rockfall events. Nevertheless, the current lack of understanding of the fragmentation phenomenon is so that much can be learned from simple tests. This paper focuses on the fragment size distribution, the energy dissipation mechanisms at impact and the distribution of energy amongst fragments after impact. The methodology including two different setups is introduced in Sect. 2. The materials and experimental programme are presented in Sect. 3. Section 4 discusses the results and Sect. 5 provides the conclusions.

2 Methodology

2.1 Primary Setup

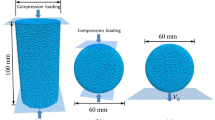
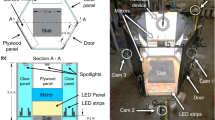
A series of vertical drop tests using mortar spheres was conducted in a specifically designed hexagonal fragmentation cell (see Fig. 1) built at the University of Newcastle’s Civil Engineering Laboratory (Guccione et al. 2019; 2020; 2021b). The facility consists of an enclosed hexagonal container (in the following named cell) including an instrumented concrete slab (three load cells of 100 kN capacity each, two accelerometers of 50 g capacity and an I-scan High Speed VersaTek pressure sensors), a release devise using vacuum, and a system of image recording devices (four synchronised Optronics CR600 × 2 high-speed cameras placed outside the cell and two mirrors, see Fig. 1b). Additional LED strips, LED panels and LED spotlights are also mounted in strategic positions inside the cell to achieve an optimal contrast for the collection of images at 500 fps and 1/3000 s exposure time. The setup has a maximum drop height of 5.1 m which results in a maximum impact velocity of about 10 m/s. A comprehensive description of the experimental apparatus and its validation can be found in Guccione et al. (2021b).

Fig. 1
figure 1

Primary setup: a view of the fragmentation cell designed for the drop tests with the positioning of the high-speed cameras, release device, slab and mirrors; b plan view of the primary setup illustrating the 6 viewpoints obtained from the image recording devices: physical viewpoints V1 to V4 for Cam 1 to Cam 4 and virtual viewpoints V5 and V6 for the mirrored views

Full size image

2.2 Secondary Setup

A secondary setup, inspired by the primary setup, was developed to further investigate fragment size distribution at impact velocities higher than 10 m/s (the maximum impact velocity achievable form the fragmentation cell setup described in Sect. 2.1). It was a temporary setup located in the 6-storey stairwell in a building of the University of Newcastle. The staircase arrangement comprises half-flights of stairs reversing in direction at small landings at either end, to form a central well with a width of 100 mm. To safely drop the spheres from different heights without interference from the adjacent stairs, the spheres were dropped through a 100 mm diameter PVC pipe that was installed through the central well and fixed to the handrail of the stairway (Fig. 2c), in a position so that it could be accessed at any height from the stair flights. The pipe was perforated with pairs of 20 mm holes drilled every metre and positioned diametrically across from each other to reduce the piston effect of the falling sphere.

Fig. 2
figure 2

Secondary setup: a plan view of the secondary setup, b view of the slab, pipe, plastic sheet, lights and Cam 2, c view of pipe within the central well of the staircase, looking down, and d view of Cam 3 and Cam 4

Full size image

The spheres were dropped into the top of the pipe and were delivered from the end of the pipe, 0.8 m above a concrete impact slab (with the same strength as the slab described in Sect. 2.1 but of smaller dimensions 0.8 m × 0.8 m × 0.2 m). Three load cells and an accelerometer were installed on this impact slab. The four Optronics CR600 × 2 high-speed cameras (named Cam 1 to Cam 4) were positioned around the impact point (see Fig. 2a, b, d). Cam 1 was set up perpendicularly to the slab while Cams 2, 3 and 4 were arranged to have three top views of the impact (see Fig. 2a, b, d). A black plastic sheet apron was placed on the floor to increase visibility and contain the fragments.

2.3 Data Analysis

2.3.1 Image and Impact Processing

Images of the impacting blocks and rebounding fragments are collected by the high-speed cameras and processed using the commercial software TEMA3D (Image Systems Motion Analysis 2019) combined with a new algorithm developed by Guccione et al. (2020). Tracking the 3D trajectory of rotating irregular fragments is achieved via an outline tracking algorithm, which is based on the idea of reconstructing the shape of a 3D object from silhouettes captured on different views (Fig. 3). The algorithm can detect the outline of an object from each view and then merge them to create an approximate 3D model, the so-called visual hull. 3D trajectories of the impacting and rebounding objects (spheres and fragments) reconstructed using images obtained from the high-speed cameras are used to infer translational and rotational (if applicable) velocity before and after impact.

Fig. 3
figure 3

The object being tracked is a cube, the 3D reconstructed object is called visual hull. a Concept of silhouette and 3D cone from a viewpoint. b Visual hull (in blue) based on 2 viewpoints

Full size image

Data recorded by load cells and accelerometers installed on the concrete slab are used to indirectly estimate the impact force. This latter accounts for the transmitted force recorded by load cells at the bottom of the slab, the relationship between the impact duration (from the I-scan pressure sensor located on top of the slab) and the transmitted impact duration recorded by the bottom load cells, and the stiffness of the system slab-load cells (composed of the slab and the load cells) (Thorby 2008). A comprehensive description of the impact data processing can be found in Guccione et al. (2021b).

2.3.2 Energy Components

The spheres are released without rotational energy, therefore, the total energy loss associated with the impact \({\Delta E}_{tot}\) can be obtained as:

$${\Delta E}_{tot}={E}_{kt}^{b}-{E}_{kt}^{a}-{E}_{kr}^{a}$$
(1)

where subscript \(k\) stands for kinetic; subscript \(t\) for translational; subscript \(r\) rotational; superscript \(b\) for before the impact; and superscript \(a\) for after the impact. Where impact results in fragmentation, the term \({E}_{k}^{a}\) corresponds to the sum of the total kinetic energy (i.e. translational plus rotational) of all fragments

$$E_{kt}^{a} = \mathop \sum \limits_{i = 1}^{n} E_{kt,i}^{a} = \mathop \sum \limits_{i = 1}^{n} \frac{1}{2} \cdot m_{i} \cdot v_{i}^{2}$$
(2)
$$E_{kr}^{a} = \mathop \sum \limits_{i = 1}^{n} E_{kr,i}^{a} = \mathop \sum \limits_{i = 1}^{n} \frac{1}{2} \cdot \left( {I_{I,i} \cdot \omega_{I,i}^{2} + I_{II,i} \cdot \omega_{II,i}^{2} + I_{III,i} \cdot \omega_{III,i}^{2} } \right)$$
(3)

where \(n\) is the number of fragments; \({E}_{kt,i}^{a}\) is the translational kinetic energy of fragment \(i\); \({m}_{i}\) is the mass of fragment \(i\); \({v}_{i}\) is the absolute translational velocity of fragment \(i\); \({E}_{kr,i}^{a}\) is the rotational kinetic energy of fragment \(i\); \({I}_{I,i}, {I}_{II,i}\) and \({I}_{III,i}\) are the moments of inertia around the principal axes of fragment \(i\); and \({\omega }_{I,i}, {\omega }_{II,i}\) and \({\omega }_{III,i}\) are the rotational velocities around the 3 principal axes of fragment \(i\)

For a normal impact of a mortar sphere on a concrete slab, only three dissipative mechanisms are significant. These are the elastic–plastic deformation of the sphere and slab (\(\Delta {E}_{d}\)), the displacement of the slab as a whole (\(\Delta {E}_{slab}\)) and fracture formation associated with fragmentation (\(\Delta {E}_{fr}\)). The energy loss due to the elastic wave propagation can be considered negligible in these test conditions (Guccione et al. 2021b). Other energy dissipation such as sound and thermal components are also assumed negligible. Consequently, the total energy loss associated with the impact is equal to:

$${\Delta E}_{tot}= {\Delta E}_{slab}+\Delta {E}_{d}+\Delta {E}_{fr}$$
(4)

The energy loss associated with the elastic displacement of the slab \(\Delta {E}_{slab}\) can be estimated as:

$$\Delta E_{slab} = \frac{1}{2} \cdot F_{T} \cdot z_{slab}$$
(5)

where \({F}_{T}\) is the transmitted force recorded by the load cells and \({z}_{slab}\) is the vertical displacement inferred from the accelerometer signal. Equation (5) assumes that the vertical displacement of the centre of the slab, \({z}_{slab}\) does not include a deformation component due to bending of the slab. Given the magnitude of the impact load and the flexural stiffness of the slab, this assumption is considered valid.

The energy loss in local elastic–plastic deformation of both slab and impacting object \(\Delta {E}_{d}\) can be estimated as:

$$\Delta E_{d} = E_{kt}^{b} \cdot \left( {1 - CoR_{d}^{2} } \right)$$
(6)

where \(Co{R}_{d}\) is a theoretical coefficient of restitution based on an elastic-perfectly plastic sphere impacting a plate (Stronge 2000):

$$CoR_{d} = \frac{{v_{y} }}{{v_{imp} }}\left[ {\frac{8}{5} \cdot \left( {\frac{{v_{imp} }}{{v_{y} }}} \right)^{2} - \frac{3}{5}} \right]^{\frac{3}{8}}$$
(7)

In Eq. (7), \({v}_{imp}\) is the impact velocity and \({v}_{y}\) is the yield velocity defined as:

$$v_{y} = \left( {\left( {\frac{4}{5} \cdot \pi } \right)\left( {\frac{3}{4} \cdot \pi } \right)^{4} \left( {\frac{{\vartheta_{y} \sigma_{y} }}{{\tilde{Y}_{mc} }}} \right)^{4} \left( {\frac{{\vartheta_{y} \sigma_{y} \tilde{R}^{3} }}{m}} \right)} \right)^{\frac{1}{2}}$$
(8)

where \(m\) is the mass of the impacting body (the mortar sphere); \({\sigma }_{y}\) is equal to the yield stress of the impacting material (assumed equal to the compressive strength \({\sigma }_{c}\)); and \({\vartheta }_{y}\) is the ratio of mean indentation pressure (assumed fully plastic) to uniaxial yield stress. \({\vartheta }_{y}\) is assumed equal to 1.61 to consider a higher failure stress compared to a uniaxial load case, as per Wang and Zhu (2013). \({\widetilde{Y}}_{mc}\) and \(\widetilde{R}\) are the equivalent Young’s modulus and the equivalent radius, respectively.

The equivalent radius \(\widetilde{R}\) is defined as:

$$\frac{1}{\widetilde{R}}=\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}$$
(9)

where \({R}_{1}\) is the radius of the sphere and \({R}_{2}\) is the radius of the slab. The radius of the slab \({R}_{2}\) is much greater than \({R}_{1}\) so it can be assumed infinite and, hence, Eq. (9) becomes \(\widetilde{R}={R}_{1}\).

The equivalent Young’s modulus \({\widetilde{Y}}_{mc}\) can be determined from Eq. (10):

$$\frac{1}{{\widetilde{Y}}_{mc}}=\frac{1-{\nu }_{m}^{2}}{{Y}_{m}}+\frac{1-{\nu }_{c}^{2}}{{Y}_{c}}$$
(10)

where \({Y}_{m}\) is the Young’s modulus of the mortar, \({\nu }_{m}\) the Poisson’s ratio of the mortar, \({Y}_{\mathrm{c}}\) the Young’s modulus of the system slab (i.e. the combination of the concrete slab plus load cells that support it, see Guccione et al. (2021b), and \({\nu }_{\mathrm{c}}\) is the Poisson’s ratio of the concrete slab.

Hou et al. (2017) suggested that the energy loss to create the fracture surfaces \(\Delta {E}_{fr}\) can be estimated using Eq. (11):

$${\Delta E}_{fr}=\gamma \sum_{j=1}^{n}{A}_{j}$$
(11)

\({A}_{j}\) corresponds to the area of new surfaces generated by fragmentation. This area can be measured after the drop test by scanning each of the fragments. In this study, a high-resolution structured light scanner (EinScan Pro 2X Plus) was used for this purpose. The minimum scannable fragment size was 1 cm3 (mass of about 2 g). The surface energy per unit area of the rock block \(\gamma\) can be determined by the well-known Irwin’s correlation (Zhang and Zhao 2014):

$$\gamma =\frac{{K}_{Ic}^{2}(1-{\nu }_{m}^{2})}{{Y}_{m}}$$
(12)

where \({K}_{Ic}\) is the mode I fracture toughness that can be determined using semi-circular bent specimens (Kuruppu et al. 2014), \({Y}_{m}\) is the Young’s modulus and \({\nu }_{m}\) is the Poisson’s ratio of the material the block is made of (in the case of this work mortar).

Damage and fragmentation are related (i.e. fragmentation is a consequence of damage) so that Eq. (12) can be used to compute the energy consumed in damage and fragmentation. However not all damage causes the formation of discrete fragments, so the difference between the two cases lies in the difficulty to estimate the extent of cracking and new surfaces within fragments, that do not lead to further fragmentation.

2.3.3 Fragmentation Survival Probability

Some of the series used in this study (which will be defined in Sect. 3.2), have been conducted in a specific range of impact energy to establish the fragmentation survival probability of spheres at impact. In this contest, the fragmentation survival probability (or impact survival probability) represents the likelihood that spheres sustain a certain impact energy without breaking (Guccione et al. 2021a). For example, if 20 spheres are dropped all from the same height and 8 break at impact, the fragmentation survival probability (SP) is 60%. The fragmentation survival probability can be determined as:

$$SP\left( \% \right) = \left( {1 - \frac{{N_{f} }}{N}} \right) \cdot 100$$
(13)

where \(N\) is the total number of drop tests and \({N}_{f}\) is the number of tests resulting in fragmentation. The fragmentation survival probability can be expressed in terms of either, impact velocity or impact kinetic energy. The impact velocity (or impact kinetic energy) corresponding to 37% of survival probability is called critical impact velocity (or critical kinetic energy). Experimental evidence obtained by the authors suggests that the survival probability of brittle spheres in drop tests can be approximated as a linear function (Guccione et al. 2021a).

3 Material and Experimental Programme

3.1 Specimen Preparation and Material Characterisation

The drop tests were conducted using mortar spheres to mitigate the issue of shape, material variability and impact variability associated with natural rocks. Spheres of diameter 50, 75, 100 and 200 mm were considered. The mortar was made of silica sand, Portland cement, hydrated lime and water. Three different proportions (by mass) were used to obtain different mortar strengths:

  • For the first mixture (referred to as material M1) the relative proportions were 3 parts of sand for 1 part of cement, 0.25 part of lime and 0.8 part of water. A single batch was used to cast 52 spheres of 100 mm diameter, 5 cylinders (54 mm diameter, 135 mm height), 5 discs (54 mm diameter, 27 mm thickness) and 2 larger cylinders (100 mm diameter, 200 mm height).

  • For the second mixture (referred to as M2), the relative proportions were 3 parts of sand for 1 part of cement, 0.25 part of lime and 1 part of water. A total of 4 batches were made. Each batch was used to cast 30 spheres for each diameter (50, 75 and 100 mm), 30 cylinders (54 mm diameter, 135 mm height), 30 discs (54 mm diameter, 27 mm thickness) and 10 larger cylinders (100 mm diameter, 200 mm height).

  • For the third mixture (referred to as M3), the proportions were 4 parts of sand for 1 part of cement, 1 part of lime and 1 part of water. A single batch was used to create 12 spheres of 200 mm, 24 cylinders (54 mm diameter, 135 mm height) and 12 discs (54 mm diameter, 27 mm thickness).

Spheres of diameter 50, 75 and 100 mm were cast using 3D printed plastic (high-density acrylonitrile butadiene styrene) moulds (see Fig. 4a), while spheres of 200 mm diameter were cast using concrete moulds (see Fig. 4b). The moulds were filled on a vibrating table to expel as many bubbles as possible from the mortar. All specimens (spheres, discs and cylinders) were removed from their mould after 1 day and cured in a water bath at room temperature for 8 weeks, except for the M3 samples that were cured for 12 weeks at room temperature. Following curing, all M1 and M2 specimens were placed in a 40 °C oven for 4 weeks to dry and remove any strength variability caused by differential wetness at the time of testing.

Fig. 4
figure 4

Moulds used to cast the spheres: a 3D printed moulds for the spheres of 50, 75 and 100 mm diameter and b concrete moulds for the spheres of 200 mm diameter

Full size image

Mortar cylinders (54 mm diameter, 135 mm height), discs (54 mm diameter, 27 mm thickness) and larger cylinders (100 mm diameter, 200 mm height) were used to characterise the three mortars via unconfined compression tests, indirect tension tests (i.e. Brazilian tests) and toughness tests (Mode I) on mortar half-discs (diameter 100 mm, thickness 40 mm) notched with a central groove (height 25 mm, thickness 1.7 mm), respectively. The disc specimens for the toughness tests were created by cutting sample slices from the 100 mm diameter, 200 mm height cylinders. Each disc was then separated into two halves and a groove was precisely cut in each half. The properties of the three mortar mixtures are reported in Table 1. It can be seen that mixture M1 is the strongest with an average unconfined compressive strength (UCS) of 34.7 MPa. M2 and M3 have an average UCS of 22.9 and 12.6 MPa respectively.

Table 1 Characteristics of mortar mixture
Full size table

The characteristics of the system slab, which is the combination of the concrete slab plus load cells that support it, are reported in Table 2. The elastic modulus (denoted \({Y}_{c}\)) and the stiffness (\(k\)) of the system slab plus load cells were calibrated using the experimental data of coefficients of restitution, transmitted impact force and displacement of the slab. More detail on these calibrations can be found in Guccione et al. (2021b).

Table 2 Characteristics of system slab
Full size table

3.2 Experimental Programme

Six series of drop tests were conducted, as described below:

  • Series 1 (S1) consists of 24 tests from six different drop heights using the primary setup (Sect. 2.1). For each height, four spheres of 100 mm diameter (using material M1) were used. All energy components were estimated from the tracking and impact data with emphasis on the possible changes in energy partitioned between dissipation mechanisms with increasing impact energy. In this series, only cases with fragmentation were analysed.

  • Series 2 (S2) focussed on fragment size distribution and fracture energy in a range of impact velocities between 6.6 m/s and 21 m/s (drop height between 2.2 m and 22.5 m). This series of tests were performed using the secondary setup (Sect. 2.2). A total of 30 tests were conducted from ten different drop heights. For each height, 3 spheres of 100 mm diameter (using material M1) were used. The fragments produced at each impact were counted, weighed down to a mass of 0.1 g and scanned to calculate the fracture energy (note that the volume of the smallest scannable fragment was 1 cm3, which corresponds to about 2 g). Due to the different dropping device (see Fig. 2), less control on the impact velocity could be applied compared to tests conducted in the primary setup. For this reason, tests with similar measured impact velocities were grouped as per Table 3. Tracking analysis of the fragments was not conducted in this series due to the high number of fragments overlapping each other (i.e. the outline tracking algorithm could not be used).

  • Series 3, 4 and 5 (S3, S4, and S5) correspond to Series #2, #3 and #4 presented in Guccione et al. (2021b) where the data were used to establish the fragmentation survival probability of 50, 75 and 100 mm diameter spheres (using material M2). In the current work, all tests from these series were used to investigate the fragment size distribution and a selection of 16 tests (4 tests per height and 4 heights) per diameter were further analysed to investigate energy dissipated at impact and the partition of the remaining energy among fragments on the range of the fragmentation survival probability.

  • Series 6 (S6) focuses on quantifying the amount of energy dissipated at impact for different values of impact energy (using material M3) for a mortar of different strength, for 200 mm diameter spheres only. In this series, four drop heights were selected and three spheres were dropped at each height using the primary setup.

Table 3 Experimental programme of drop tests
Full size table

Table 3 summarises the specifics of each series of tests conducted.

4 Results and Discussion

4.1 Fragment Size Distribution, Fragmentation Pattern and Fracture Area

In this section, the evolution of the number of fragments as a function of impact velocities is first discussed, with a particular focus on the range of velocity corresponding to an impact survival probability (SP) between 100 and 0% (series S3, S4, S5) and onward (S1, S2 and S6). Then, the cumulative number of fragments is presented as a function of fragment mass, for the series of drop tests at “high velocities” (from 6.6 to 21 m/s, S2). Finally, a relationship between the total fracture area and the number of fragments is proposed.

Figure 5 shows the average number of large and small fragments for all six series: the impact velocity has been normalised by the critical impact velocity (impact velocity corresponding to 37% of survival probability). The latter was determined experimentally for M1 and M2 and theoretically using the model presented in Guccione et al. (2021a) for M3. The values of the critical impact velocity for all series are reported in Table 4. Large and small fragments were arbitrarily defined as those having a mass larger and smaller than 5% of the initial mass of the sphere, respectively. Note that the threshold of 5% is arbitrary but analyses using 1% and 10% indicated no major change in the trend of the results. Fragments equal to and smaller than 0.1 g in mass were not considered. The error bars in Fig. 5 represent the minimum and the maximum number of fragments (large or small) observed at each velocity.

Fig. 5
figure 5

Average number of large (mass > 5% of initial mass) and small (mass < 5% of initial mass) fragments as a function of normalised impact velocity for: 100 mm spheres for M1, for a series S1 with low impact velocities, and b series S2 with higher impact velocities; for spheres of M2 with diameter c 50, d 75 and e 100 mm (Series S3, S4 and S5); f M3 spheres of diameter 200 mm (S6). The error bars on the number of fragments represent the minimum and maximum value recorded at that specific impact velocity. The experimental survival probability (SP) data and its linear fit are also plotted

Full size image
Table 4 Critical impact velocity (impact velocity corresponding to 37% of survival probability) for all series
Full size table

Figure 5a, c, d, e show similar trends in the range of impact velocity corresponding to 0–100% of survival probability, regardless of size, for material M1 and M2. The average number of fragments increases from two, at the onset of fragmentation, to a maximum of five for survival probability of 0% (i.e. all the spheres will break at that impact velocity). The data also suggest that, for the range of velocity considered, the number of small fragments is very low (less than 2).

Results from S1 (Fig. 5a) and S6 (Fig. 5f) show that, for impact velocities of 0% survival probability, the average number of small fragments increases significantly and exceeds the average number of large fragments. This change in trend can be explained by a change in breakage mechanism as the impact velocity increases, with additional crushing and localised damage causing small fragments. The phenomenon was further investigated using Series S2 of material M1 (Figs. 5b and 6). Figures 5b and 6 report the results of drop tests conducted at “high velocity” (S2, impact velocities ranging from 7.3 to 17.3 m/s, see Sect. 3.2) and focus on fragment size distribution. Note that tests of spheres of 100 mm diameter (using material M1) were conducted using the secondary setup.

Fig. 6
figure 6

Cumulative number of fragments as a function of the fragment mass for series S2 (material M1): a all data and b close-up of (a) for fragment masses above 50 g

Full size image

Figure 5b confirms that, for values of impact velocity larger than that corresponding to 0% survival probability (i.e. normalised impact velocity of 1.1 which for this series corresponds to an impact velocity of 7.3 m/s), the average number of small fragments is larger than the average number of large fragments and that the number of small fragments increases with the normalised impact velocity, up to 2.3 (equivalent to 14.8 m/s). Then, between 2.3 (14.8 m/s) and 2.7 (17.3 m/s), the number of fragments, large and small, seems to reach a plateau.

To summarise, mortar spheres were found to fragment into less than five large and a few small fragments for impact velocities within the 0–100% range of survival probability, while for higher values of impact velocities, a higher number of fragments is produced, and the size of the largest fragments progressively decreases with the increasing of the velocity.

Figure 6a shows that the fragment size distributions (FSD) under 7.3 m/s and 17.3 m/s are very different and that progressively increasing the impact velocity leads to a progressive change in the shape of the fragment size distribution. Below 7.3 m/s, the FSD shows three patterns: a steep increase of large fragments (mass > 100 g), a relatively flat central part (0.5 g < mass < 100 g) and a steep accumulation of very small fragments (mass < 0.5 g). Such distribution reflects the presence of 4 to 5 large fragments (mass > 100 g), 1 medium size fragment (usually the bottom cone, mass around 10 g) and some very small fragments. Below 17.3 m/s, the FSD shows a well-graded pattern with three large fragments (mass > 100 g) and many fragments in the 1 to 100 g mass range, leading to a continuous increase in the cumulative number of fragments.

The data in Fig. 5b show a different behaviour. It is possible to see a difference between tests conducted at 14.8 m/s (normalised impact velocity equal to 2.3) and those at 17.3 m/s (normalised impact velocity equal to 2.7). The increase of velocity leads to a steepening of the central part of the FSD (masses below 100 g) and, hence, an upward shift of the curve because the largest fragments (mass > 100 g) produced under 17.3 m/s tend to be of similar size (resulting in a steep start of the FSD) as opposed to three fragments of different sizes (resulting in a flatter start of the FSD).

Interestingly, the FSD obtained are not linear in a logarithmic scale, which accords with in situ observations by Corominas and co-workers (Ruiz-Carulla et al. 2015) but contradicts the idea of a scale-invariant fractal distribution of fragments (Ruiz-Carulla et al. 2017). Ruiz-Carulla and Corominas (2020) updated the fractal fragmentation model using the formulation proposed by Perfect (1997) for scale variant fragmentation, which would result in a better fit of the experimental findings presented in the current study.

Figure 7 reports a typical fragmentation pattern observed in the range of the normalised impact velocity. In the range of survival probability, where the normalised impact velocity increases from 0.8 to 1.1, three fragmentation patterns were typically observed:

  • Meridian crack (Fig. 7a): spheres typically split in tensile mode along a meridian fracture.

  • Three orange slices (Fig. 7b): spheres split in tensile mode along two meridian fractures. The created fragments look like orange slices.

  • Three or four orange slices with cone (Fig. 7c): a cone fragment is created at the impact point due to stress concentration (see Fig. 7h); meridian tension cracks are formed splitting the sphere into three or four parts (slices). Note that it was observed that the cone fragment generally does not move upon impact, instead, it remains located at the point of impact.

Fig. 7
figure 7

Fragmentation pattern observed as a function of the normalised impact velocity. The subfigures a, b, c, d, e, f and g correspond to a top view of the breaking sphere just after the impact. The subfigure (h) shows the bottom cone of a reconstructed sphere associated with the fragmentation pattern illustrate in f. The number of fragments is indicative

Full size image

From the certain occurrence of fragmentation (SP 0%, normalised impact velocity > 1.1) to a normalised impact velocity of 1.8, the creation of a top cone of different sizes was observed (Fig. 7c, d) due to further crack propagation and dispersion with increasing impact velocity. In the range of normalised impact velocity between 1.1 and 1.8, 4 or 5 slices and the bottom cone (sometimes attached as a whole with the top cone) were observed. In the range of normalised impact velocity between 1.8 and 2.3, the top cone generally splits into two parts resulting in 5 to 7 fragment slices as well as a bottom cone. In the higher range of normalised impact velocity tested (between 2.3 and 2.8), a different fragmentation pattern was observed: the top cone splits into 3 to 5 main fragments with an increase of slices formed, between 7 and 12. Also in this range, a bottom cone was recorded.

The last aspect discussed in this section is the relationship between the total fracture of the fragments and the number of fragments. As mentioned in Sect. 3.2, for all series, fragments with a volume higher than 1 cm3 (mass of about 2 g) were scanned to compute the total fracture area needed to compute the amount of energy loss at impact to create the fractures observed at each test (see Eq. (11)). To compare the results obtained in all series (different sizes and strengths), the total fracture area for each test has been normalised by the surface area of the impacting sphere (\(\pi \cdot d^{2}\)) and plotted against the number of fragments (Fig. 8). Note that, theoretically, an intact sphere would have a normalised area of 0, a sphere broken into two halves (as shown in Fig. 7a) would have a normalised area of 0.5 (\(\left( {2 \cdot \left( {\pi \cdot r^{2} } \right)} \right)/\left( {\pi \cdot d^{2} } \right)\)) and sphere broken into four quarters (ignoring the bottom cone, as shown in Fig. 7c) would have a normalised area of 1 (\({{\left( {4 \cdot \left( {\pi \cdot r^{2} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {4 \cdot \left( {\pi \cdot r^{2} } \right)} \right)} {\left( {\pi \cdot d^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\pi \cdot d^{2} } \right)}}\)). Despite some scattering, a clear relationship between the total fracture area and the number of fragments is observed. The higher the impact velocity (or impact energy), the higher the number of fragments (as seen in Figs. 5–7) and the higher the total fracture area and the energy loss at impact to generate these fractures. The proposed fitted power law can be used to obtain an approximative total fracture area by knowing the number of fragments and the diameter of the impacting sphere, without scanning the fracture area of each fragment. Note that this relationship may be valid only for the testing condition considered in this work where homogenous spheres normally impact a perfectly horizontal slab.

Fig. 8
figure 8

Total fracture area normalised by the area of the impacting sphere as a function of the number of fragments for all series S1 (100 mm M1), S2 (100 mm M1), S3 (50 mm M2), S4 (75 mm M2), S5 (100 mm M2), S6 (200 mm M3)

Full size image

4.2 Energy Partition During Impact

In this section, results of energy partition at impact are presented. The components of kinetic energy (before and after impact) and energy dissipation were computed for series S1, S3, S4, S5 and S6 while for S2 (series conducted on the secondary setup at “high” impact velocity) only energy loss to create the fracture surfaces was calculated. Before further discussion, it should be noted that a total of 114 spheres of four diameters of three different strengths were dropped and analysed (Table 3). All drop tests using material M2 (S3, S4 and S5) are limited to the range of impact survival probability between 100 and 0%.

Results obtained for all series are reported in Appendix A, with tests sorted in increasing values of impact velocity. Note that only fragments with significant motion (normalised kinetic energy < 0.01%) were analysed. Figure 9 shows the results for all series in terms of energy components normalised by the kinetic energy before impact as a function of the kinetic energy before impact. Note that only the total fracture energy lost at impact was computed for S2 (tests at “high” velocity for M1 performed using the secondary setup).

Fig. 9
figure 9

Normalised value of energy loss at impact and the total kinetic energy after impact as a function of the kinetic energy before impact for: a S1 (100 mm M1), b S2 (100 mm M1), c S3 (50 mm M2), d S4 (75 mm M2), e S5 (100 mm M2) and f S6 (200 mm M3). Note that only the energy loss to create the fractures has been computed for series S2

Full size image

The results (Fig. 9 and Appendix A) show that the total amount of energy lost at impact slightly increases with increasing impact velocity with different proportions depending on diameter and mortar strength. It is also clearly observed that the proportion of total kinetic energy after impact decreases with increasing impact velocity. Results from series S1 showed that less than 1% of the total kinetic energy at impact is transferred into rotation of fragments, which is largely due to the fact that the spheres impacted without initial rotational velocity. Therefore, it was not computed for the other series.

The analysis of energy components can be summarised as follows:

  • \(\Delta {E}_{slab}\): the energy dissipated by displacing the slab is negligible for all series but for the 200 mm spheres of M3 (S6). It represents less the 0.2% of kinetic energy before impact for spheres of 100 mm diameter or less (about 0.02% for the 50 mm spheres M2) for both material M1 (S1) and M2 (S3, S4 and S5); while it represents about 1–2% for the 200 mm spheres of material M3 (S6).

  • \(\Delta {E}_{d}\): the energy lost in slab/sphere deformation represents the highest energy loss at impact and increases with increasing impact velocity. It accounts for around 80% to 85% of the total kinetic energy at impact for series S1 (100 mm M1), between 87 and 89% in the range of impact survival probability between 100 and 0% for all three diameters of material M2 (S3, S4 and S5) and between 83 and 88% for the series S6 (200 mm M3).

  • \(\Delta {E}_{f}\): the amount of energy loss in fragmentation varies depending on the diameter and the strength of the sphere, however, it seems to be a constant proportion of the kinetic energy before impact, at least in the range tested within this work. It is about 2 to 3% for 100 mm spheres of material M1 (S1), about 4 to 5% for 50 mm and 75 mm spheres of material M2 (S3 and S4), about 3 to 4% for 100 mm spheres of material M2 (S5) and about 6 to 8% for 200 mm spheres of material M3 (S6). The results from the tests at “high” velocity performed on the secondary setup using 100 mm spheres of material M1 (S2) (see Fig. 11b) confirm a slight decrease with increasing impact velocity (or impact energy) from 3 to 1.2%. Note that there is a factor of 10 between the impact energy at lower and higher impact energy.

  • \({E}_{k}^{a}\): the translational kinetic energy after impact decrease with the increase of impact velocity. For the 100 mm spheres of material M1 (S1), the range is between 20 and 7% of the kinetic energy at impact, for 50 mm spheres of material M2 (S3) it is between 18 and 5%, for 75 mm spheres of material M2 (S4) it is between 15 and 3.5%, for 100 mm spheres of material M2 (S5) it is between 10 and 4% and finally for 200 mm spheres of material M3 (S6) it is between 11 and 6% (except for four tests between 5 and 6 m/s which showed less motion after impact compared to the other tests, about 3–4% of the kinetic energy before impact).

Interestingly, although the impact velocity is increasing for all series and covers the full survival probability (from 100 to 0%), the normalised energy components do not vary much with the impact kinetic energy. Figure 5 shows that the number of large fragments increases from 2 to 10 for material M1 (series S1 and S2), for an impact velocity increasing from 5.5 to 17.6 m/s, hence, the amount of fragmentation energy is tripled for series S1 and S2 (see normalised fracture area in Fig. 8 and Tables 5 and 6) but the normalised value of fragmentation energy remains approximately constant. This is consistent with findings from Giacomini et al. (2009) obtained from in situ tests using natural rocks.

Under the conditions of the limited data obtained in this study, it seems that, in the range of energy including 0–100% of the survival probability, the energy consumed in fragmentation can be considered a constant fraction of the total kinetic energy at impact. As the impact energy increases, more fragments are created, leading to more energy dissipated in fragmentation and a constant ratio of fragmentation energy over impact energy. The reason for this ratio being constant is not yet identified. More research is needed to verify whether this observation holds for a wider range of impact velocities and other block sizes and shapes.

4.3 Energy Partition Among Fragments

Accounting for fragmentation in rockfall trajectory models requires knowing how to assign kinetic energy to the fragments after impact. Matas et al. (2020) proposed a fragmentation model which assumes that the kinetic energy is proportionally distributed according to the fragment’s mass. However, as far as the authors are aware, there is no experimental data currently in the literature to support such an assumption. In fact, a numerical study suggests that this correlation might not exist (Ye et al. 2019b).

Figure 10 presents the velocity of fragments normalised by the impact velocity of the sphere they formed from (\({v}_{i}/{v}_{imp}\)) as a function of fragment mass for all series (except S2). Each data point corresponds to one fragment. Figure 10 first shows a large scattering of fragment velocity with different upper and lower bounds depending on the material: for M1 (Fig. 10a) it is between 0.17 and 0.47, for M2 (Fig. 10b–d) between 0.18 and 0.35 and for M3 (Fig. 10e) between 0.12 and 0.33. These figures demonstrate that there is no trend between fragment velocity (normalised by the impact velocity of the sphere) and fragment mass, for all sizes and materials investigated. Small fragments do not seem to possess a higher velocity than large ones or vice-versa.

Fig. 10
figure 10

Fragment velocity over impact velocity (\({v}_{i}/{v}_{imp}\)) as a function of fragment mass: a S1 (100 mm M1), b S3 (50 mm M2), c S4 (75 mm M2), d S5 (100 mm M2) and e S6 (200 mm M3)

Full size image

Figure 11 then presents the fragment kinetic energy normalised by total kinetic energy before impact (\({E}_{k,i}^{a}/{E}_{k}^{b}\)) as a function of fragment mass for all series (except S2). Again, each data point corresponds to one fragment. Because the kinetic energy is a function of the fragment mass, a bias is introduced in the figure, as the two variables (mass and kinetic energy) are not independent. Consequently, the scattering visible in Fig. 10 (velocity) is reduced and some trends emerge in Fig. 11: the heavier the fragment, the higher the kinetic energy. But the trends are a consequence of the dependence of kinetic energy on the mass and the scattering of normalised kinetic energy corresponds to the scattering of normalised velocities (the velocity is squared to compute the energy).

Fig. 11
figure 11

Total kinetic energy of fragments over kinetic energy before impact (\({E}_{k,i}^{a} /{E}_{k}^{b}\)) as a function of fragment mass: a S1 (100 mm M1), b S3 (50 mm M2), c S4 (75 mm M2), d S5 (100 mm M2) and e S6 (200 mm M3)

Full size image

The data clearly suggest that there is no trend between fragment size and fragment velocity, but it is possible to consider a trend between fragment size and kinetic energy, with a large scattering, at least for the present testing conditions. It is anticipated that more realistic impact conditions (with rotational energy, irregular rock block, and irregular slope surface) may lead to even more scattering.

To investigate how the material modulus may affect the velocity of fragments, the normalised velocity has been plotted against the equivalent Young’s modulus (\({\widetilde{Y}}_{mc}\) see Eq. (10)) in Fig. 12. This figure shows that the higher the equivalent Young’s modulus, the higher the average velocity of the fragments after impact, and therefore, its kinetic energy. These findings are in agreement with results obtained by discrete element simulations of impact-induced rock fragmentation presented by Wang and Tonon (2011).

Fig. 12
figure 12

Fragment velocity over impact velocity (\({v}_{i}/{v}_{imp}\)) as a function of the equivalent Young’s modulus \({\widetilde{Y}}_{mc}\) (see Eq. (10)). The error bars indicate the standard deviation

Full size image

The last aspect discussed in this section is the velocity of fragments and, in particular, how the vertical and horizontal components of the trajectory change with increasing impact velocity.

Figure 13 presents the launch angle after impact, defined as the ratio between the vertical component of ejection velocity (\({v}_{z,i}\)) to the horizontal component of ejection velocity (\({v}_{xy,i}\)), as function of the normalised impact velocity (impact velocity over the critical impact velocity) for each fragment for all series. Figure 13a shows all data while Fig. 13b shows the average value at each normalised impact velocity. Increasing the impact velocity also changes the trajectory of fragments post-impact: under low normalised impact velocity (therefore, when fragmentation starts to be observed, i.e. high survival probability), the fragments tend to bounce (launch angle close to 90° from horizontal), at survival probably equal to 0% (therefore, the fragmentation of the sphere is certain) the launch angle of the fragments is about 50° but, as the normalised impact velocity increases, they tend to be ejected sideways (i.e. fragments travel parallel to the impacted surface) (see Fig. 13b). Such observation is very relevant for realistic modelling of the trajectory of fragments.

Fig. 13
figure 13

Launch angle (ratio between vertical (\({v}_{z,i}\)) and horizontal (\({v}_{xy,i}\)) component of velocity) for all fragments as a function of normalised impact velocity: a all data; b average values

Full size image

5 Conclusions

The paper presents results from six series of drop tests using four diameters of mortar spheres (50, 75, 100 and 200 mm) with three different strengths. The objective of the study was to gather high-quality fragmentation data in the contest of rockfall. In this experimental campaign, results of three important aspects have been presented: fragment size distribution, the energy dissipation mechanisms at impact and the distribution of energy amongst fragments after impact.

The main findings of the conducted study can be summarised as follows. In the range of impact velocities corresponding to a 100%–0% range of survival probability, less than five large and a few small fragments can be expected independently by the size and the strength of the mortar sphere, while for higher values of impact velocities, more and more fragments are produced, and the size of the largest fragments progressively decreases with increasing impact velocity. The fragment size distributions (FSD) obtained in this campaign are not linear on a logarithmic scale, hence it is in contrast with the scale-invariant fractal distribution of fragments proposed by some scholars. The total normalised amount of energy loss during the impact increases with impact velocity, consequently the total kinetic energy after impact decreases. Although the quantity of damage and fragments increases with impact velocity, the energy loss to create the fracture surfaces is a constant fraction of the kinetic energy before impact. The experimental data showed that it can be estimated using Eq. (11). There is an absence of a clear relationship between normalised velocity and fragment mass. The trajectories of fragments are related to the impact velocity. At low impact velocity, the fragments tend to bounce but, as the impact velocity increases, they tend to be ejected sideways.

Although testing mortar spheres in normal impact is a simplification of a realistic rockfall event, the series of tests presented in this work has brought some valuable understanding into the fragmentation phenomenon. Indeed, additional tests should be conducted at higher impact energies to confirm these findings. More research is currently ongoing to investigate the effect of more realistic impact conditions on the fragmentation outcomes.