Context-Dependent Parameter Sensitivities in Rock Slope Stability

Abstract

Context-dependent sensitivities of parameters and reliability-based design (RBD) of rock slopes are the subjects of this paper. The similarities and differences between the design points in RBD and those of partial factor design methods are discussed. It is demonstrated that partial factors provided by the design point of the first-order reliability method (FORM) can provide case-specific insights and guidance to partial factor design methods like Eurocode 7 (EC7) and the load and resistance factor design (LRFD). It is suggested that conducting RBD-via-FORM in tandem with partial factor designs is more illuminating and meaningful than calibration of partial factors of parameters which can be sensitive in one case but insensitive in another case. Three cases are analysed probabilistically with respect to plane sliding in rock slopes with one or more discontinuities. In the first two cases, different deterministic solution procedures are used for the single block and two-block mechanisms, for comparison with stereographic projection method and closed form equation, respectively, prior to extending the cases into RBD. The third case involves a failed slope in a limestone quarry, analysed using FORM in this paper, for comparison with Monte Carlo simulation.

Highlights

• Alternative deterministic computations obtain same solutions as Goodman’s deterministic results for single-block slide and two-block slide.

• Extend Goodman’s deterministic single-block and two-block slides to reliability analysis accounting for input uncertainties.

• Reliability-based design (RBD) via the first-order reliability method (FORM) provides enlightening information at the FORM design point on parameter sensitivities.

• RBD-via-FORM automatically reflects context-dependent sensitivities of parameters at the design point of FORM, and can provide insights for Eurocode 7 and LRFD.

• FORM analysis of a failed slope confirms inadequate reliability. Failure probability from reliability index compares well with Monte Carlo simulation.

• An efficient procedure for rapid convergence of RBD-via-FORM using the Excel Forecast function.

1 Introduction

The term context-dependent parameter sensitivities (in the title of this paper) means that it is possible for the variation of the value of a parameter (for example, cohesion c) to have a pivotal influence on slope stability under some circumstances (for example when the cohesive resistance cA is large due to large area A), but a small influence on slope stability under other circumstances (for example when the area A on which cohesion acts is small). Deterministic parametric studies and plots have been used to investigate parametric sensitivities of rock slopes, for example by Hoek and Bray (1981), Goodman (1989), Hudson and Harrison (1997), and Wyllie (2018). These books are valuable because the analytical formulations and mechanics of rock engineering problems in them constitute the deterministic foundation on which one can conduct probabilistic analysis and reliability-based design (RBD). Both the deterministic and probabilistic analyses of slopes require the deterministic formulation of slope stability, in terms of a factor of safety F_s, for example. The difference is that input uncertainties and correlations are not explicitly accounted for in a deterministic analysis which evaluates the F_s using mean values, for example, but are explicitly modelled in a probabilistic approach which evaluates the probability of failure (F_s ≤ 1.0) using mean values, standard deviations, parametric correlations and probability distributions. The formulation of F_s is also needed in the performance function of the probabilistic approach. (The non-intrinsic nature of computed probability of failure and a pragmatic standpoint is discussed in Sect. 5.)

This paper uses the first-order reliability method (FORM) to study context-dependent parameter sensitivities in rock slopes, and extends significantly (with new examples and elaborations) the earlier investigations by Low (2015), Low (2019) and Low and Bathurst (2022). It will be demonstrated that context-dependent parameter sensitivities are revealed more efficiently in reliability analysis and RBD-via-FORM than in deterministic parametric studies.

Research investigations on various aspects of rock slope stability have been conducted by Einstein et al. (1983), Hoek and Bray (1981), Low (1997), Duzgun et al. (2003), Park et al. (2005), Jimenez-Rodriguez and Sitar (2007), Li et al. (2011), Shen et al. (2012), Shen and Abbas (2013), Ahmadabadi and Poisel (2016), Zhao et al. (2016), Dadashzadeh et al. (2017), and Pandit et al. (2019), for example. The investigations cover effect of discontinuity persistence, reliability analysis of 3D wedge mechanisms, probabilistic rock slope analysis, Monte Carlo simulations, system reliability involving multiple failure modes, response surface method, distinct element method and random set theory, determination of Coulomb shear strength parameters from the generalized Hoek–Brown criterion, probabilistic analysis using point estimate methods, Barton-Bandis failure criterion, probabilistic characterization of rock mass from limited data, and other worthy issues. In addition, Vagnon et al. (2020a) applied FORM and RBD for debris flow barriers and demonstrated the applicability and limitations of EC7 for these rock engineering structures, and Vagnon et al. (2020b) investigated the complementarity of the RBD approach within EC7 principles by analyzing the design of a slope subjected to rockfall.

Insights from RBD to complement the load and resistance factor design (LRFD) in soil engineering was presented in Low (2017), using the Low and Tang (2007) spreadsheet-based implementation of FORM which obtains the same solution as the mathematically intricate classical FORM procedure, but in a more lucid and efficient manner than the latter, and with an enlightening intuitive perspective in the original unrotated space of the random variables. The Low and Tang (2007) FORM will be used here.

This paper investigates RBD of 2-dimensional rock slopes containing one or multiple discontinuity planes along which rock blocks may slide. Single failure mode and Coulomb shear resistance are assumed in this study which investigates context-dependent parameter sensitivities. Two originally deterministic cases and one Monte Carlo simulation case from the literature are designed and analysed probabilistically using FORM. The discussions on context-dependent sensitivity information attainable from the design point of RBD-via-FORM, and connections with partial factor design methods, constitute the gist of the paper. The three cases investigated are (i) a single-block mechanism with potential sliding along a discontinuity plane, (ii) a two-block mechanism with potential sliding along two discontinuity planes, and (iii) a failed slope in a limestone quarry. The first two cases were deterministic examples from Goodman (1989), extended probabilistically in this study; the third case was a failed slope analysed by Monte Carlo simulation in Wyllie (2018), which will be compared with reliability analysis using FORM in this paper. The alternative deterministic solution procedures in this paper using practical constrained optimization in spreadsheet will facilitate understanding of the original deterministic solution procedures in the cited sources based on stereographic projection method and derived closed form equation. The extension from deterministic to probabilistic analysis demonstrate the merits and efficiency of FORM-based probabilistic sensitivity analysis and its potential to complement, enhance and enlighten partial factor design methods like EC7 and LRFD.

The context-dependent parameter sensitivities (and insights and information for enhancing partial factor design methods) investigated in this paper is a phenomenon/theme which is pertinent in many disciplines, as elaborated in chapters 2–11 of Low (2021), for about 60 examples in civil, environmental and soil and rock engineering. The three RBD-via-FORM and reliability analysis examples in Sects. 2, 3 and 4 below are based on Chapter 9 (on 2D rock slopes) of the Low (2021) book.

The lucid and transparent Excel-based solution files (54 in total) of all the chapters in Low (2021), including the solutions for the three examples in this paper, are free for download to help understanding FORM and to impart hands-on appreciation, at https:/www.routledge.com/9780367631390 (scroll down to Support Material/Ancillaries, to download Solutions for the book’s examples, 11.7 MB).

2 A Rock Slope with a Single Discontinuity Plane

2.1 Comparing Deterministic Stability Analysis by Stereographic Projection and by Equation

An example problem of a rock slope containing a discontinuity plane is analyzed deterministically in this section, using a procedure different from the cited source, before extending the case to reliability-based design (RBD) in Sects. 2.2–2.4

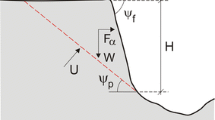
Figure 1 shows a problem from Goodman (1989, problem 8.3), in which a discontinuity plane (Plane 1) daylights into a cut. The orientation of the plane in strike and dip convention is: strike N30° W, dip 50° NE. The weight of a potential sliding mass on the discontinuity plane is 400 metric tons on an area of 200 m². The friction angle is estimated to be 30°. It is required to determine the rock bolt force T that will increase the factor of safety F_s to 1.0 and 1.5 when there is no water pressure, and the water pressure u on the discontinuity plane that will cause slide when the rock bolt force for F_s = 1.5 based on dry slope condition is acting.

Fig. 1

A deterministic plane slide analysis involving rock bolt force T and water pressure on discontinuity plane 1. (After Goodman 1989, problem 8.3)

Some formulas of single-block plane slides were given in Goodman, based on equating the shear force directed down the sliding surface with the shearing resistance along the sliding surface, when the condition for limit equilibrium is reached. For the problem in Fig. 1, Goodman’s solution (1989, pp 530–531) was obtained using the graphical lower hemispherical projection technique and the friction circle concept.

This section solves, deterministically then probabilistically, the same problem using an analytical formulation and the constrained optimization Solver tool of Microsoft Excel spreadsheet.

Force equilibrium along the discontinuity plane leads to the following equation:

$$N^{\prime}\frac{\tan \phi }{{F_{{\text{s}}} }} + T\cos \left( {\delta - \theta } \right) - \left( {W + Q_{{\text{s}}} } \right)\sin \delta = 0,$$

(1)

where

$$N^{\prime} = \left( {W + Q_{{\text{s}}} } \right)\cos \delta + T\sin \left( {\delta - \theta } \right) - uA.$$

(2)

Rearranging, one gets:

$$F_{{\text{s}}} = \frac{{\left[ {\left( {W + Q_{{\text{s}}} } \right)\cos \delta + T\sin \left( {\delta - \theta } \right) - uA} \right]\tan \phi }}{{\left( {W + Q_{{\text{s}}} } \right)\sin \delta - T\cos \left( {\delta - \theta } \right)}}.$$

(3)

Equation (3) means that the traditional global (lumped) factor of safety, F_s, is the ratio of the maximum available upslope resisting force (the numerator) to the downslope sliding force (the denominator).

Another perspective is possible by rearranging Eq. (1) as follows:

$$N^{\prime}\frac{\tan \phi }{{F_{{\text{s}}} }} = \left( {W + Q_{{\text{s}}} } \right)\sin \delta - T\cos \left( {\delta - \theta } \right),$$

(4)

which means mobilized resistance = net sliding force along discontinuity plane. This perspective is useful for EC7 and LRFD, where there are several partial factors instead of a lumped F_s.

Note that Eq. (3) is valid when T is a mobilized force at working condition, of the same nature as the first term in the denominator of Eq. (3) which is the actual downslope sliding force at working condition.

When there is no rock bolt force (i.e. T = 0), and water pressure u is also zero, the above expression reduces to:

$$F_{{\text{s}}} = \frac{{\left[ {\left( {W + Q_{{\text{s}}} } \right)\cos \delta } \right]\tan \phi }}{{\left( {W + Q_{{\text{s}}} } \right)\sin \delta }} = \frac{\tan \phi }{{\tan \delta }} = \frac{\tan 30^\circ }{{\tan 50^\circ }} = 0.48,$$

(5)

which means that the maximum available frictional resistance on the discontinuity plane is only 48% of that needed to maintain equilibrium; the block will slide if not reinforced by rock bolt. The effect of rock bolt force T and water pressure u on the factor of safety is investigated next.

Equations (2) and (3) have been entered in a spreadsheet as shown in Fig. 2, in cells with headings N′ and F_s, respectively. The solution for part (a) of the question in Fig. 1 is obtained easily as follows in Fig. 2a(i), (ii):

Fig. 2

An alternative deterministic analysis of the plane slide example, using force equilibrium equation and the Excel Solver optimization tool, instead of the graphical stereographic projection solution of Fig. 1

Fig. 2a(i): Initially T = 0, and θ = 0. The Solver tool was invoked, to minimize the "T × 1” cell, by changing (automatically) cells T and θ, subject to the constraint F_s = 1.0. The solution obtained by the Solver tool is T = 1340.7 kN = 136.8 tons, and θ = 20.0°, practically the same as those (137 tons and 20°, Fig. 1) obtained by the stereographic projection and friction circle analysis (which involve approximate graphical measurements).

Fig. 2a(ii): Invoke the Solver tool, to minimize the "T × 1” cell, by changing (automatically) cells T and θ, subject to the constraint F_s = 1.5. Get T = 1897.4 kN = 193.6 tons, and θ = 28.9°, again in agreement with those (194 tons, and 29°, Fig. 1) obtained by the graphical stereographic projection and friction circle analysis.

The solution for part (b) of the question in Fig. 1 is obtained easily as follows:

Fig. 2b: With T and θ as found in a(ii) above, invoke Solver to set cell F_s to 1.0, by changing u. Get u = 5.34 kPa = 0.54 ton/m², compared with 0.56 ton/m² obtained approximately in Fig. 1 from scaling the water force U in a force polygon

Note that the weight of 400 tons on an area of 200 m² (mentioned in the question in Fig. 1) means that the potential sliding mass has an average thickness of only about 0.75 m. The average normal stress exerted by the potential sliding mass on the discontinuity plane is about 12.6 kPa. Hence even a seemingly small water pressure of 5.34 kPa can reduce the F_s from 1.5 (dry case, Fig. 2a(ii)) to 1.0, Fig. 2b, where the water force U is 5.34 kPa × 200 m² = 1066 kN. One can already anticipate the context-dependent sensitivity of slope instability to water pressure. The safety of a heavier potential sliding block (or same weight W but smaller area A) will be less sensitive to the same water pressure than a lighter potential sliding block (or same weight W but bigger area A) to the same water pressure. Such context-dependent sensitivities of water pressure and other parameters will be automatically reflected in the outcome of RBD-via-FORM, as demonstrated later.

Goodman (1989) aptly noted that the minimum force direction is not the direction for shortest bolts. The latter is perpendicular to the sliding plane. The optimum direction depends also on the relative costs of steel and drill holes and lies somewhere between these two extremes.

We next consider a case similar to Figs. 1 and 2, but with the aim to determine the mean rock bolt force T which will achieve a reliability index β of 2.5 against sliding of the rock block. The uncertainties of five of the inputs, namely W, A, u, T and ϕ, are accounted for.

2.2 Probabilistic-Based Design: RBD-via-FORM Against Sliding Along a Discontinuity Plane

The random variables are assumed to be the weight of rock W above the discontinuity plane (Fig. 1), the discontinuity surface area A under the potential sliding block, mobilised rock bolt force T at working condition, water pressure u on the discontinuity plane, and friction angle ϕ of the discontinuity plane. Weight W and area A are assumed to be positively correlated with ρ_WA = 0.5, on the ground that larger area A tends to occur with bigger weight. (Weight W is equal to area × thickness × rock unit weight; all else equal, larger weight tends to occur with bigger area, hence it is logical to model positive correlation between W and A).

In Fig. 3, the mean values of W, A and ϕ are 3920 kN, 200 m², and 30°, respectively, the same as the deterministic inputs in Figs. 1 and 2. The mean value of T is the design value to be determined, for a target reliability index β of 2.5, which corresponds to a failure probability of 0.62%. The standard deviations of W, A, T and ϕ are assumed to be 10% of their respective mean values. These four random variables are assumed to obey the normal distribution, which is generally used for probabilistic studies in geotechnical engineering unless there are good reasons for selecting a different distribution (Hoek, 2007). The pore water pressure u is assumed to follow the gamma distribution, Gamma (5, 0.5), for illustrative purpose in this case. The two parametric values (5, 0.5) correspond to a mean μ = 2.5 kPa and a standard deviation σ ≈ 1.12 kPa for the water pressure u. (The probability density function (pdf) curve of Gamma (5, 0.5) can be plotted for visualization, at https://statdist.com/distributions/gamma, for example. It has a mode at around u = 2.0 and is non-symmetric. The pdf curve extends mostly over the domain u = 0 to about u = 7.0, with negligible area under the curve for u > 7. Other pdf of water pressure u can be used in an actual project if data are available, including using the bounded four-parameter beta-general distribution with pdf of diverse shapes, and the three-parameter PERT distribution which is a special case of the beta-general distribution. The use of normal distributions for W, A, T and ϕ in Fig. 3 are also illustrative, and reasonable when the coefficient of variation is smaller than 0.25 and the distribution is judged to be symmetrical.)

Fig. 3

a RBD of mean T for β of 2.5, b reliability index β varies with μ_T and dip angle δ of discontinuity plane, c sensitivities, partial factors, and LF and RF are context-dependent

The two columns labelled “Para1” and “Para2” and the 5-by-5 correlation matrix in Fig. 3 show the statistical inputs described above. The transition from the deterministic set-up of Fig. 2 to the RBD set-up in Fig. 3 is straightforward: replace the numerical values of W, A, u, T and ϕ in the first row by cell addresses so that they read their values from the column labelled “x*”. The five cells under the x* column invoke simple Visual Basic for Applications (VBA) program codes in Microsoft Excel to calculate x* values from the corresponding values under the column labelled “n”, as explained in Low and Tang (2007). The performance function g(x) in Fig. 3a is Eq. (1) with F_s = 1.0:

$$g({\mathbf{x}}) = N^{\prime}\tan \phi + T\cos \left( {\delta - \theta } \right) - \left( {W + Q_{{\text{s}}} } \right)\sin \delta .$$

(6)

The equation for the FORM reliability index β in Fig. 3a is:

$$\beta = \mathop {\min }\limits_{{{\mathbf{x}} \in F}} \sqrt {{\mathbf{n}}^{T} {\mathbf{R}}^{ - 1} {\mathbf{n}}} ,\quad \left( {\text{entered as an array formula}} \right),$$

(7)

where n is the five-cell column and R the 5-by-5 matrix in Fig. 3a.

As explained in Low and Tang (2007) and in Chapter 2 of Low (2021), Eq. (7) literally means finding the smallest equivalent 5D dispersion ellipsoid that just touches the limit state surface (LSS) at the most probable failure point (also called the design point). A 2D illustration is given in the Appendix.

In reliability analysis via FORM, the outcome is the computed reliability index β (as defined by Eq. 7), for a given design, which in this case is a given value of mean rock bolt force T that appears in the performance function g(x) of Eq. (6). In RBD-via-FORM, the objective is to determine the unknown value of a parameter (the mean rock bolt force T) which will achieve a target (or desired) reliability index β, for example a target β of 2.5 or 3.0. The next section provides an efficient procedure for RBD-via-FORM using the Excel Forecast function to estimate the design value of a parameter.

2.3 Rapid RBD-via-FORM Using the Excel Forecast Function

Initially the n column values in Fig. 3a were zeros. Then:

• (a) A trial value (e.g. 1800 kN) was input for the mean value of T (under the “Para1” column), such that the cell labelled g(x) displays a positive value.

• (b) Microsoft Excel built-in routine Solver was invoked, to minimize the cell β, by automatically changing the five values under the column labelled n, subject to the constraint that the performance function cell “g(x)” be equal to 0.0.

• (c) Repeat steps (a) and (b) with another trial mean value of T (e.g. 2300 kN). The two trial values of T and their corresponding computed β values are then used by the Excel forecast.linear function to predict (or estimate) a design value that will achieve the target β value. In most cases only two sequential estimates by the Excel forecast.linear function are needed to obtain the correct design solution, as illustrated in Fig. 12 in the Appendix.

A mean value of T of 2493 kN (under the column labelled “Para1”) achieves the target reliability index β of 2.5. The five values under the x* column represent the design point where the expanding equivalent dispersion ellipsoid first touches the LSS.

The following in Fig. 3a are noteworthy:

• (1) The negative n values of uncorrelated T and ϕ from RBD-via-FORM, − 1.678 and − 1.116, respectively, indicate that these two are resistance parameters, which decrease from their safe mean values (2493 kN, 30°) to smaller design values (2075 kN, 26.65°) under the column labelled x*.

• (2) In contrast, the positive n values of W, A and u, at 1.155, 0.734, and 0.904, respectively, reveal their unfavourable effects on stability (they are “loads”), in having their design values under the x* column (4373 kN, 214.7 m², 3.447 kPa) at higher values than their safe mean values of 3920 kN, 200 m², and 2.50 kPa.

• (3) The unfavourable character of area A arises due to the product uA being a destabilising water force, and also due to A being positively correlated with weight W. However, if shear resistance along discontinuity plane derives from cohesion c apart from friction angle ϕ, the random variable A would have stabilizing-destabilizing duality, in contributing resistance cA and unfavourable load uA. RBD-via-FORM will automatically reveal whether decreasing or increasing the value of area A is more critical in reaching the most probable failure point (i.e., the design point), defined by the values under the x* column.

• (4) In summary, the mean values of W, A, T, u and ϕ constitute the mean-value point in the safe domain if the performance function g(x) is positive when the n column values are initially zeros prior to invoking the Solver tool. The five design values under the x* column represent the design point (the most probable failure point) where the 5-dimensional expanding equivalent dispersion ellipsoid first touches the LSS in the 5D space of W, A, T, u and ϕ, analogous to the 2D illustration in the Appendix.

• (5) It is an important merit of RBD-via-FORM (Fig. 3a) that the context-dependent sensitivities of the random variables are reflected in the probabilistic design outcome, under the column labelled n. Figure 3a reveals that the stability of the rock block, for the adopted statistical inputs and parametric correlations, is most sensitive to the rock bolt force T (a resistance parameter, with the highest absolute value of 1.678 under the n column), followed by weight W (a load parameter), discontinuity friction angle ϕ (a resistance parameter), water pressure u and area A (uA is a load parameter), in decreasing order of sensitivity based on their respective absolute values under the n column.

• (6) The negative sensitivity indicator value of − 1.678 (under the n column, for the rock bolt force T) means that its most probable failure value (2074.7 kN, under the x* column) is at 1.678 times its standard deviation below its mean value of 2493. The positive sensitivity indicator value of 1.1551 (under the n column, for the weight W) means that its most probable failure value (4372.8 kN, under the x* column) is at 1.1551 times its standard deviation above its mean value of 3920. For the nonnormally distributed water pressure u, its positive sensitivity indicator value of 0.9043 means that its most probable failure value of 3.447 kPa (under the x* column) is at 0.9043 times its equivalent normal standard deviation above its equivalent normal mean value.

• (7) The most probable failure values under the x* column are akin to the design values in Eurocode 7, but are obtained as insightful corollary of RBD-via-FORM, not based on code-specified partial factors as in Eurocode 7. This will be further illustrated in the sections below.

• (8) The sensitivities of random variable (in their influence on reliability and the design point) can vary from case to case, depending on the magnitude of their mean values, the level of uncertainty represented by their standard deviations, the correlations among random variables as justified by physical considerations, the probability distributions of the random variables, and the roles played by the random variables in the performance function. RBD-via-FORM will automatically reveal context-dependent and case-specific sensitivities of random variables.

From the perspective of the load and resistance factor design (LRFD), it is possible to back-calculate load factors (LF) and resistance factor (RF) from the outcome of RBD-via-FORM. To do this, one needs to first define loads Q_i and resistance R, and nominal values of loads and resistance.

Based on Eq. (3), one possible way of defining load Q and resistance R is as follows:

$$Q = \left( {W + Q_{{\text{s}}} } \right)\sin \delta - T\cos \left( {\delta - \theta } \right),$$

(8)

$$R = N^{\prime}\tan \phi = \left[ {\left( {W + Q_{{\text{s}}} } \right)\cos \delta + T\sin \left( {\delta - \theta } \right) - uA} \right]\tan \phi .$$

(9)

Partial factors LF and RF can then be back-calculated from:

$${\text{LF }} = \, Q^{*}/Q_{{\text{n}}}$$

(10a)

$$({\text{or mLF }} = \, Q^{*}/\mu_{Q} ),$$

(10b)

and

$${\text{RF }} = \, R^{*}/R_{{\text{n}}}$$

(11a)

$$({\text{or mRF }} = \, R^{*}/\mu_{R} ),$$

(11b)

where Q* and R* are calculated from the design values of the underlying random variables, Q_n is nominal load (typically greater than mean load), and R_n is nominal resistance (typically smaller than mean resistance). Such back-calculated LF and RF will vary from case to case. For example, those for δ = 40° will be different from those for δ = 50°, and those for target β equal to 3.0 will be different from those for target β equal to 2.5.

Figure 3b shows that the required mean value of rock bolt force T depends on the target reliability level and the dip angle δ of the discontinuity plane. Figure 3c shows the context-dependent sensitivity indicators (whether n, or n/β) on the left panel, the back-calculated partial factors of the underlying five parameters in the middle panel, and the LF and RF on the right (based on Eqs. (8) and (9)). The partial factors of the five random variables and the LF and RF are based on mean values (including Eqs. (10b) and (11b)). Other values of partial factors and LF and RF are possible, depending on the level of conservatism in the adopted characteristic values (in Eurocode 7) and nominal values (in LRFD).

Other definitions of Q and R are possible apart from Eqs. (8) and (9). For example, a designer may decide simply to let Q = W, and R = T, and obtain the back-calculated LF and RF as LF = W*/W_n, and RF = T*/T_n, and so on.

It is obvious from Fig. 3 and the above discussions that the values of partial factors and LF and RF back-calculated from the results of RBD-via-FORM are affected by the following:

• (i) The target level of reliability in RBD-via-FORM, whether β = 2.5, 3.0, or 3.5.

• (ii) The level of conservatism in selecting the characteristic or nominal values.

• (iii) The definition of loads and resistance in LRFD.

• (iv) The relative magnitudes of the mean values and COV of the random variables in RBD-via-FORM.

• (v) Other details which may cause the sensitivity of a random variable to vary from case to case. For example, for the case in hand, different dip angle of the discontinuity plane may change the sensitivities (and hence back-calculated partial factors and LF and RF) of W, T, u and ϕ.

2.4 Context-Dependent Sensitivities Manifested by Cohesion c and Water Pressure u

Sensitivity indicators n (or n/β), and back-calculated partial factors and L_F and R_F from RBD-via-FORM, are meaningful for enhancing EC7 and LRFD, in a case-specific (i.e. context-dependent) manner. It is not meaningful to calibrate back-calculated partial factors and LF and RF because the calibrated partial factors do not have general applicability.

To illustrate, Fig. 4a shows a case identical to Fig. 3a except there is an additional cohesive resistance with mean cohesion μ_c = 10 kPa and standard of deviation σ_c = 2 kPa, which means a mean cohesive resistance of 10 kPa × 200 m² = 2 MN. This makes the cohesion by far the most pivotal random variable, with a n_c value of − 1.918, or n_c/β of − 0.77, as shown in the last row of Fig. 4a. The n/β values from Fig. 3a (with no cohesion) is shown in the rightmost column in Fig. 4a, for comparison. In contrast, Fig. 4b shows a case with smaller mean discontinuity area A (μ_A = 60 m²) than Fig. 4a, where mean area μ_A was 200 m². This reduces both the mean cohesive force cA (a resistance) and mean normal water force uA (an unfavourable load) to only 30% of their mean values in Fig. 4a, and greatly diminishes the values of the sensitivity indicators n/β of cohesion c and water pressure u: − 0.07 and 0.12 in Fig. 4b versus − 0.77 and 0.41 in Fig. 4a when the area A was 200 m². The random variables W, T and ϕ in Fig. 4a, with small n/β values of 0.26, − 0.20, and 0.10, respectively, became the three most important players in Fig. 4b, with n/β values of 0.51, − 0.58, and − 0.49, respectively. One may also note that the less-sensitive random variable ϕ in Fig. 4a has its design value (30.76°) slightly above its mean value of 30°, due to its negative correlation with the most-sensitive cohesion c there where discontinuity area was 200 m². This is an example of correlated sensitivities which was explained in Low (2020) in the context of rotational ULS of a spread foundation.

Fig. 4

a With mean cohesion μ_c = 10 kPa, which results in a mean cohesive resistance of 10 × 200 = 2 MN; cohesion becomes by far the most pivotal random variable. b With cohesion, but smaller mean area A of 60 m² instead of 200 m² in a; cohesion no longer a pivotal parameter

In RBD-via-FORM, it is important to distinguish positive from negative reliability index. For example, for the case in Fig. 4b, a mean value of T = 446 kN will also achieve a computed β of 2.50, which must be regarded as the negative root of the equation for β (Eq. 7), because the performance function cell g(x) displayed a negative value when the n values were initially zeros, which means the mean-value point is in the unsafe domain. In contrast, for mean T > 902.1 kN, the g(x) displays a positive value when the n values are initially zeros. For the case in Fig. 4b, a mean value of T = 1540 kN achieves the target β of 2.5 (the positive root of Eq. (7)), or failure probability P_f of 0.62%. For mean T = 902.1 kN, the mean-value point is right on the limit state surface g(x) = 0 (F_s = 1.0), which means a failure probability of about 50%. For mean T = 446 kN, the mean-value point is already inside the unsafe domain, with a β value of − 2.50, or failure probability of 99.38%.

To sum up, the sensitivity indicators (n, or n/β), back-calculated partial factors, and other information in FORM offer valuable perspective and guidance for EC7 and LRFD design in a case-specific and context-dependent way. There is not much point trying to calibrate back-calculated partial factors from FORM for LRFD and EC7, because different cases and changing context can change important random variables in one case to become insignificant random variables in another case, as demonstrated in Fig. 4.

The above examples and figures involve the stability of a single rock block above a discontinuity plane P, as shown in the top sketches of Figs. 1 and 2. We next consider stability analysis involving two-block mechanisms and potential sliding along two discontinuity planes.

3 A Case of Potential Sliding Along Two Frictional Slip Surfaces Which Have Different Dip Angles

A deterministic example of two blocks sliding on two discontinuity planes (Fig. 5) is analysed using simple force equilibrium considerations, to facilitate readers’ understanding of the closed form limit equilibrium equation in the cited source. This is followed by reliability-based design for different scenarios to demonstrate context-dependent sensitivities of the parameters affecting the stability of the rock slope.

Fig. 5

Deterministic two-block stability analysis based on Goodman (1989) closed form equation

3.1 Closed Form Equation for Limiting Equilibrium of a Two-Block Mechanism

The following equation was derived in Goodman (1989, pp 465–468), to calculate the required support force R_b (in the lower passive block of Fig. 5, in a direction θ below horizontal) to achieve limiting equilibrium (i.e. F_s = 1.0):

$$R_{{\text{b}}} = \frac{{W_{1} \sin \left( {\delta_{1} - \phi_{1} } \right)\cos \left( {\delta_{2} - \phi_{2} - \phi_{3} } \right) + W_{2} \sin \left( {\delta_{2} - \phi_{2} } \right)\cos \left( {\delta_{1} - \phi_{1} - \phi_{3} } \right)}}{{\cos \left( {\delta_{2} - \phi_{2} + \theta } \right)\cos \left( {\delta_{1} - \phi_{1} - \phi_{3} } \right)}},$$

(12)

where as shown in the top sketch of Fig. 5a, ϕ₁, ϕ₂, ϕ₃ are the friction angles applicable to sliding along the upper, lower, and vertical slide surfaces, respectively; δ₁ and δ₂ are the inclinations of the upper and lower slide surface, respectively; W₁ and W₂ are the weights of the (upper) active and the (lower) passive blocks per unit of slide width.

Part (a) of the question in Fig. 5 is about back-calculating the available friction angle for a slope with-a two-block mechanism that failed. Since failure occurred without any support force, R_b is set equal to zero on the left of the closed form Eq. (12). Assuming ϕ₁ = ϕ₂ = ϕ_3, the solution of ϕ is obtained by trial and error to be 36.4°.

Part (b) of the question concerns evaluating the factor of safety if the volume V₁ of the upper block is reduced from 10,000 to 6000 m³. Assuming ϕ₁ = ϕ₂ = ϕ₃, the solution is first obtained for the ϕ value that will just maintain equilibrium at the reduced destabilizing weight of the upper block, based on Eq. (12) with R_b = 0. The required ϕ for limiting equilibrium is 33.3°. Knowing from part (a) that the available friction angle is 36.4°, the factor of safety is therefore calculated to be F_s = tan(36.4°)/tan(33.3°) = 1.12.

Part (c) of the question concerns calculating the support force R_b required to achieve the same F_s as the excavation in part (b). Equation (12) for R_b is for limiting equilibrium, i.e. F_s = 1.0. Nevertheless, the required R_b can be calculated by input of ϕ₁ = ϕ₂ = ϕ₃ = 33.3° in Eq. (12), because 33.3° corresponds to an F_s of 1.12 from part (b). Therefore, a support force of 37.1 MN is required to achieve the same F_s as the excavation in Part (b).

Using the same principle as that in the solution of Fig. 5c, the support force R_b to achieve any F_s can be calculated using the above Eq. (12) from Goodman (1989). For example, for the case in hand, based on the original volumes V₁ = 10,000 m³ and V₂ = 14,000 m³, if the desired F_s is 1.20, one can input ϕ₁ = ϕ₂ = ϕ₃ = atan(tan(36.4°)/1.2)) = 31.57° in Eq. (12), and obtain the required support force of R_b = 58.4 MN.

In engineering analysis, if the same solution/s can be obtained by different procedures, it will often enhance understanding to explore and compare the different procedures. The comparison is desirable in this case because the derivation of Eq. (12) involves sixteen intermediate equations and two different coordinate systems. In this spirit, an alternative deterministic solution procedure to the three-part problem of Fig. 5 is presented next, before extending it to reliability-based design.

3.2 An Alternative Deterministic Procedure for Two-Block Stability Analysis

Figure 6 shows the forces acting on the two blocks of the slope, namely weights of the blocks W₁ and W₂, mobilized shear forces Q₁ and Q₂ along the upper and lower sliding planes, total normal forces N₁ and N₂ perpendicular to the sliding planes, external rock anchor force R_b, and internal resultant force Z inclined at an angle α with the normal to the vertical interface. Water forces U₁ and U₂ and cohesion c₁ and c₂ on the discontinuity planes can be readily incorporated if appropriate. In this case, there is no water force, and shear resistances along discontinuity planes are frictional. Hence, U₁, U₂, c₁ and c₂ are zeros. The horizontal and vertical equilibriums of the two blocks are satisfied when the four simple equations of ΣH and ΣV shown in Fig. 6 are equal to zeros.

Fig. 6

An alternative deterministic procedure for two-block stability analysis that obtains the same solution as the Goodman (1989) closed form equation

There are more unknowns than can be solved by the four equilibrium equations. One assumption commonly made to reduce the number of unknowns is that the inclination angle α of the side force Z at the vertical interface is equal to the mobilized friction angle ϕ_m on the discontinuity planes:

$$\alpha = \phi_{{\text{m}}} = \tan^{ - 1} \left( {{{\tan \phi } \mathord{\left/ {\vphantom {{\tan \phi } {F_{{\text{s}}} }}} \right. \kern-\nulldelimiterspace} {F_{{\text{s}}} }}} \right)$$

(13)

as assumed in the Goodman solutions of Fig. 5, where α = ϕ₃, and ϕ₃ = ϕ₁ = ϕ₂, with F_s = 1.0.

For the case in hand, the input parameters for the four equilibrium equations in Fig. 6 are δ₁, δ₂, α, R_b, θ, W₁ and W₂. The mobilized shear force Q₁ and Q₂ can be calculated once the values of N₁, N₂ and F_s are determined, as follows:

$$Q_{1} = N_{1} \frac{{\tan \phi_{1} }}{{F_{{\text{s}}} }},$$

(14a)

$$Q_{2} = N_{2} \frac{{\tan \phi_{2} }}{{F_{{\text{s}}} }}.$$

(14b)

There is no need to derive the factor of safety F_s as a function of the underlying parameters (δ₁, δ₂, R_b, θ, W₁, W₂, ϕ₁, ϕ₂, …). The solution can be obtained easily by solving for four unknowns in the four equilibrium equations using the Excel Solver tool.

For part (a) of the problem in Fig. 5, the solution is obtained in Fig. 7a as follows:

• (i) The value of F_s is 1.0. The unknowns are N₁, N₂, Z, and ϕ (the same for ϕ₁, ϕ₂ and α). Initially ϕ₁ = 30°, F = 1, N₁ = W₁, N₂ = W₂, Z = W₂. These lead to nonzero values in the cells labelled “Eq. (1)”, “Eq. (2)”, “Eq. (3)” and “Eq. (4)” in Fig. 7a, which means the four force equilibrium conditions as specified by the four equations in Fig. 6 are not satisfied.

• (ii) The Solver tool was invoked, to set the “Eq. (1)” cell to 0, by changing the values of cells N₁, N₂, Z and ϕ₁, subject to the constraints that the cell values of Eq. (2), Eq. (3) and Eq. (4) in Fig. 7a be zeros.

• (iii) A solution of ϕ = 36.38° is obtained in the ϕ₁ cell of Fig. 7a, the same as that in Fig. 5a, together with the solution values of N₁, N₂ and Z. All the four “Eq.” cells in Fig. 7a are zeros, indicating satisfaction of force equilibrium conditions.

Fig. 7

Deterministic analysis based on horizontal and vertical equilibrium of the two rock blocks, for comparison with the three solution of Goodman (1989) in Fig. 5

For part (b) of the problem in Fig. 5, the volume V₁ in Fig. 7b is changed to 6000 m³. the solution is obtained in Fig. 7b as follows:

• (i) The unknowns are F_s, N₁, N₂ and Z. Initially F = 1, N₁ = W₁, N₂ = W₂, and Z = W₂.

• (ii) The Solver tool was invoked, to set the “Eq. (1)” cell to 0, by changing the values of cells F_s, N₁, N₂, and Z, subject to the constraints that the values of cells Eq. (2), Eq. (3) and Eq. (4) in Fig. 7b be zeros. (It is good to use the “Automatic Scaling” option in the Solver tool.)

• (iii) A solution of F_s = 1.121was obtained (same as that in Fig. 5b), together with the solution values of N₁, N₂ and Z.

For part (c) of the problem in Fig. 5, the volume V₁ is reset to 10,000 m³. The solution is obtained in Fig. 7c as follows:

• (i) The unknowns are R_b, N₁, N₂ and Z. Initially F = 1.121, R_b = 0, N₁ = W₁, N₂ = W₂, and Z = W₂.

• (ii) The Solver tool was invoked, to set the “Eq. (1)” cell to 0, by changing the values of cells R_b, N₁, N₂, and Z, subject to the constraints that the cell values of Eq. (2), Eq. (3) and Eq. (4) in Fig. 7c be zeros.

• (iii) A solution of R_b = 36.99 MN was obtained (very slight difference with the value 37.1 in Fig. 5c, due to round-off in the latter), together with the solution values of N₁, N₂ and Z.

The deterministic procedure based on simple force equilibrium considerations in Fig. 7 can be extended readily into reliability-based design, as shown next.

3.3 Reliability-Based Design of Rock Bolt Force R _b for a Two-Block Mechanism in Rock Slope

The friction angles ϕ₁ and ϕ₂ on the two discontinuity planes are treated as independent normal random variables, with the same mean value of 36.4°, obtained from the deterministic back-calculations in Figs. 5a and 7a. The standard deviation is 3.5°, as shown in Fig. 8b. In general, the normal or Gaussian distribution can be used for probabilistic studies in geotechnical engineering when the coefficient of variation does not exceed 0.25 and a symmetric distribution is deemed to be acceptable. Different distributions can of course be used if there are good reasons. This is further discussed in Sect. 5. It may be mentioned that Hoek (2007, Chapter 8) also adopted normal distribution for friction angle ϕ and cohesive strength c when estimating the probability of failure of the Sau Mau Ping slope in Hong Kong.

Fig. 8

a Deterministic template as in Fig. 7c; b RBD-via-FORM indicate that a mean support force R_b of 89.45 MN is required to achieve a target β of 2.5; c RBD-via-FORM indicates that the partial factor of ϕ₂ is greater than that of ϕ₁

Other random variables are the volumes V₁ and V₂ of the two blocks, of mean values 10,000 and 14,000 m³, respectively, and a c.o.v. of 0.1, and the external support force R_b with a c.o.v. 0.1. It is assumed that the variables are independent. Suppose that the engineer wants to determine the required mean value of R_b for a target β of 2.5.

The deterministic template of Fig. 8a (similar to the deterministic template of Fig. 7a) can be extended easily into RBD by adding the part shown in Fig. 8b, and replace the five numerical inputs in the V₁, V₂, R_b, ϕ₁ and ϕ₂ cells of Fig. 8a with cell addresses which refer to the five x* cells of Fig. 8b. The performance function in the g(x) is the formula “= F_s − 1”. Initially the values in the n column cells were zeros. For different trial values of the mean support force R_b, the Solver tool was used to set the β cell to minimum, by changing the five cells of the n column and the four numerical values of F_s, N₁, N₂ and Z cells in Fig. 8a, subject to the constraints that the four “Eq. (1)” …, “Eq. (4)” cells in Fig. 8a (containing the four equations of Fig. 6) and the g(x) cells in Fig. 8b be equal to zero. This literally instructs the Solver tool to find the smallest expanding 5D dispersion ellipsoid that just touches the limit state surface defined by g(x) = 0, analogous to the 2D illustration in the Appendix.

A mean value of support force R_b = 89.45 MN (Fig. 8b) is found to achieve the target β of 2.5. The five values in the x* column of Fig. 8b constitute the most probable point of failure (i.e. the design point). This design point lies on the limit state surface defined by g(x) = F_s − 1 = 0, i.e., F_s = 1.0.

3.4 Comparison with Monte Carlo Simulation

Monte Carlo simulation can be done on the Goodman (1989) closed form equation (Eq. (12) above). That equation is for limiting equilibrium condition, which means that it defines the limit state surface where F_s = 1.0. In Monte Carlo simulation, the performance function for the Goodman equation is:

$$g({\mathbf{x}}) = R_{{\text{b,MCarlo}}} - R_{{\text{b,limiting}}} ,$$

(15)

where $R_{{\text{b,MCarlo}}}$ is the random number generated during Monte Carlo simulation, based on a normally distributed R_b of mean value 89.45 MN and standard deviation 8.945 MN, and $R_{{\text{b,limiting}}}$ is the value of R_b required for equilibrium as computed by Eq. (12) which depends on the values of random variables ϕ₁, ϕ₂, V₁ and V₂ generated during Monte Carlo simulation. (V₁ and V₂ determines W₁ and W₂, which appear in Eq. (12) for R_b).

Monte Carlo simulation using the @RISK software with 500,000 realizations of Eq. (15) results in a failure probability of 0.63%, practically the same as the failure probability of P_f = $\Phi \left( { - \beta } \right)$ = 0.62% in the RBD of Fig. 8b where the performance function g(x) is based on satisfying the four force equilibrium equations shown in Fig. 6 with F_s = 1.0. This verifies that the deterministic procedure of Figs. 6 and 7 is equivalent to the closed form equation (Eq. (12)).

Shown in Fig. 8b under the column labelled “− n/β” are the normalized sensitivity indicators from RBD-via-FORM, which are in good agreement with the regression and correlation sensitivity coefficients of the g(x) based on Monte Carlo simulation on Eq. (15), for this case when the random variables are independent and normally distributed.

The design point (i.e. the most probable failure point) is where an expanding dispersion ellipsoid (or equivalent ellipsoid when nonnormal variates are modelled) first touches the limit state surface. Reliability index is the distance, in units of directional standard deviations, from the safe mean-value point to this most probable point of failure, as explained in the Appendix for a 2D case. Monte Carlo simulation is valuable for estimating failure probabilities, but may not explicitly locate the most probable failure point (i.e., the design point).

It is often enlightening to examine the design point (the x* values) and the sensitivity indicators n, as discussed below in the context of Fig. 8.

3.5 Information and Insights at the FORM Design Point, and Implications for Eurocode 7 and LRFD

The partial factors γ_i and load and resistance factors LF and RF, in the discussions below, are with respect to mean values. This is to avoid ambiguity that arises from back-calculated partial factors and LF and RF when different characteristic values (for Eurocode 7) and nominal values (for LRFD) are adopted. RBD-via-FORM needs statistical inputs, but not partial factors. Nevertheless, the partial factors implied at the design point of RBD-via-FORM are back-calculated for discussions with Eurocode 7 and LRFD in the following paragraphs.

• (1) The values of the sensitivity indicators under the column labelled n, with n_ϕ2 = − 2.126 and n_ϕ1 = − 0.901, means that the most probable failure value of ϕ₂ (28.96°, under the x* column) is 2.126 × σ_ϕ2 smaller than its mean value of 36.4°, while the most probable failure value of ϕ₁ (33.25°) is 0.901 × σ_ϕ1 smaller than its mean value of 36.4°. From the Eurocode 7 perspective, the implied partial factors are γ_ϕ2 = 36.4/28.96 ≈ 1.26, and γ_ϕ2 = 36.4/33.25 ≈ 1.10. This suggests that the design is more sensitive to the friction angle ϕ₂ of the lower discontinuity plane than to the friction angle ϕ₁ of the steeper upper discontinuity plane. This conclusion is valid even when partial factors are calculated from γ_ϕ = tanϕ_k/tanϕ*, where ϕ_k is the characteristic value of friction angle.

• (2) That two parameters (ϕ₁ and ϕ₂ in this case) of the same physical nature can have different sensitivity indicators (n₁ = − 0.901, n₂ = − 2.126, Fig. 8b) is a manifestation of context-dependent sensitivity, which is accounted for automatically in RBD-via-FORM, but difficult to deal with in partial factor design approach. Hence, conducting RBD-via-FORM in tandem with partial factor design can throw much light on the latter (e.g. EC7) and provide guidance in its continuing evolvement.

• (3) The plots in Fig. 8c, based on information at the design points of RBD-via-FORM, indicate that the partial factor of ϕ₂ is greater than that of ϕ₁, and that the values of partial factors γ_ϕ1 and γ_ϕ2 increase with the value of the target reliability index β, which is logical, and is another manifestation of context-dependent information.

• (4) From the LRFD and EC7-DA2 perspective, the mobilized resistance for the case in Fig. 8a consists of three components in different directions, namely (i) mobilized frictional resistance Q₁ along the steeper upper discontinuity plane, (ii) mobilized frictional resistance Q₂ along the lower discontinuity plane, and (iii) mobilized support force R_b, which is horizontal when θ = 0 in this case. The prevailing LRFD method allows for multiple loads but only one resistance. Engineers may think differently on how to define a single resistance from the multi-directional three components of resistance. Even the definition of loads for use in LRFD may vary from one designer to another: should it be W₁ and W₂, or their sliding effects along discontinuity planes 1 and 2? If W₁ and W₂ are regarded as loads, the n_V1 value of 0.708 and n_V2 value of − 0.181 in Fig. 8b suggest that W₁ should be factored up, but not W₂. In contrast, if sliding forces along discontinuity planes 1 and 2 are regarded as loads, both should of course be factored up.

It is a significant merit of RBD-via-FORM such as Fig. 8b that it conveys context-dependent information on parameter sensitivities at its most probable failure point. It is likely that conducting RBD-via-FORM in tandem with EC7 and LRFD designs can reveal issues that require attention, and improve design rationale and guide EC7 and LRFD in their continuing evolution.

4 Reliability Analysis of a Failed Slope in a Limestone Quarry

A failed slope of height 30.5 m (Fig. 9) in a limestone quarry was back-analysed in Wyllie (2018, p 137), to obtain the values of shear strength parameters of the discontinuity plane that dips at an angle Ψ_p = 20°, followed by probabilistic analysis using Monte Carlo simulation. The desirability of using probability distributions with bounded lower and upper limits was aptly suggested. The random variables were the shear strength parameters ϕ and c of the discontinuity plane, and the ratio z_w/z where z is the height of the vertical tension crack and z_w is the height of water in the tension crack. Each of the three variables was estimated to have a minimum and a maximum value, and either a mean value or a most likely value, as described below (Wyllie 2018, p 211):

• (a) Friction angle ϕ: maximum and minimum values of 15° and 25°, respectively; the mean value was 19° and the standard deviation was 2.3°. This parameter was modelled in Wyllie (2018) by a skewed beta distribution with the most likely value of 18°.

• (b) Cohesion c: most likely value of 90 kPa, and minimum and maximum values of 80 and 125 kPa, respectively; the mean value was 98 kPa. This parameter was modelled in Wyllie (2018) by a skewed triangular distribution.

• (c) Water pressure: expressed as per cent filling of the 19 m deep tension crack, z_w/z, ranging from 5 m (z_w/z = 26%) to full (z_w/z = 100%), with the most likely value being 15 m (80%); the mean depth was 13 m (68%). This parameter was modelled in Wyllie (2018) by a skewed triangular distribution.

Fig. 9

a A slope that failed in a limestone quarry (after Wyllie 2018); b reliability analysis indicates failure probability on the high side

Probabilistic analysis will be done here using the Low and Tang (2007) FORM procedure for comparison with the Monte Carlo simulation result from Wyllie (2018). The probability distributions follow those in Wyllie (2018). The three parameters defining the triangular distribution are minimum, mode, and maximum. For cohesion c, as described in item (2) above, the inputs are “80, 90, 125”. For the water pressure coefficient z_w/z, as described in item (3) above, the inputs are “0.26, 0.79, 1.0”, where 0.79 is based on 15 m/19 m.

The 4-parameter inputs for the beta distribution was not given in Wyllie (2018). They are estimated here as follows.

In the 4-parameter (λ₁, λ₂, minimum, maximum) beta distribution, the first two parameters (λ₁, λ₂) are shape parameters. The probability density function is symmetrical if λ₁ = λ₂, and non-symmetrical if λ₁ ≠ λ₂. The mean μ and standard deviation σ of a beta distribution with parameters λ₁, λ₂, min and max are (e.g., Evans et al. 2000):

$$\mu = \min + \left( {\max - \min } \right) \times \frac{{\lambda_{1} }}{{\lambda_{1} + \lambda_{2} }},$$

(16)

$$\sigma = \frac{{\left( {\max - \min } \right)}}{{\left( {\lambda_{1} + \lambda_{2} } \right)}}\sqrt {\frac{{\lambda_{1} \lambda_{2} }}{{\lambda_{1} + \lambda_{2} + 1}}} .$$

(17)

Hence, if λ₁ = λ₂ = 4 (not the case here), the mean is at the mid-point between min and max, and the standard deviation is equal to 1/6 of the range (max–min). The mode of the beta distribution is:

$${\text{mode}} = \min + \left( {\max - \min } \right) \times \frac{{\left( {\lambda_{1} - 1} \right)}}{{\left( {\lambda_{1} + \lambda_{2} - 2} \right)}}\quad \lambda_{1} > { 1},\quad \lambda_{2} > {1}.$$

(18)

Item (a) above, on friction angle ϕ, reports a mean value of 19°, a mode of 18°, a standard deviation of 2.3°, minimum of 15°, and maximum of 25°. The two unknowns λ₁ and λ₂ can be determined from two of the three equations (Eqs. (16)–(18)). To satisfy mode = 18 and σ = 2.3°, the solutions are λ₁ = 1.47 and λ₂ = 2.11, for which the mean value is 19.1° by Eq. (16). Hence, the inputs for the beta distribution in Fig. 9b are “1.47, 2.11, 15°, 25°”.

Figure 9b shows the results of FORM analysis, obtaining a reliability index β of 1.85, and a failure probability of $P_{{\text{f}}} = \Phi \left( { - \beta } \right)$ = 3.25%, compared with a failure probability of 3.4% reported in Wyllie (2018) based on Monte Carlo simulation. The sensitivity indicators (n, or − n/β) in the last two columns of Fig. 9b indicate that stability is most sensitive to z_w/z, followed by friction angle ϕ and cohesion c of the discontinuity plane.

Instead of triangular distributions, PERT distributions can be used for cohesion c and z_w/z, as shown in Fig. 10, with the same inputs of “minimum, most likely, maximum” as the triangular distributions in Fig. 9b. A negative correlation between friction angle ϕ and cohesion c of the discontinuity plane is modelled. The reliability index is 1.69, and failure probability is 4.56%.

Fig. 10

a PERT distribution can be considered for a variable with a most likely value (mode) and lower and upper limits; b reliability analysis with PERT distributions for cohesion c and z_w/z, and negatively correlated ϕ and c

The computed reliability index of β = 1.85 (or 1.69 in Fig. 10) is lower than the usual target value of β = 2.5 (for P_f = 0.62%), or β = 3.0 (for P_f = 0.13%), for ultimate limit states. The inadequate level of reliability means that failure could happen, and did happen for the case in hand.

5 Computed Probability of Failure Depends on Inputs

It needs to be emphasized that the results of reliability analysis are only as good as the statistical inputs and reliability method used (e.g., FORM or SORM), in the same way that the results of deterministic analysis are only as good as the deterministic inputs and method used (e.g. inputs for predicting displacement by the finite element method). That different values of probability of failure can be computed for the cases in this study is no ground for doubting the probabilistic approach, in the same way that one should not doubt the method of analysis (e.g. finite element method) when different displacement predictions are obtained depending on the modeled constitutive relationship and input values of parameters.

The same limitations to probabilistic approaches with respect to approximate inputs, idealized formulations, non-exhaustive factors and unknown unknowns also apply to the outputs of deterministic analysis (for both serviceability limit state and ultimate limit state). One is reminded of Terzaghi’s pragmatic approach of aiming at designs such that unsatisfactory performance is not likely, instead of aiming at designs which would behave precisely (e.g. footing settlement of exactly 25 mm). It is in the same spirit that RBD aims to achieve sufficiently safe design, not at a precise probability of failure. For example, in a RBD for a target reliability index of β = 2.5, the resulting design is not to be regarded as having exactly a probability of failure equal to Φ(− β) = 0.6%, but as a design aiming at a sufficiently small probability of failure (e.g. < 1%). One may note that a EC7 design (or LRFD design) via conservative characteristic/nominal values and code-specified partial factors also aims at a sufficiently safe design by implicit considerations of parametric uncertainties. In contrast, the uncertainties, correlations and probability distributions of random variables are open to view in RBD-via-FORM. Instead of shunning probabilistic approaches, case-specific scrutiny and counter-suggestions for more reasonable statistical inputs and related issues in RBD are more likely to result in advancements and improvements of the design approach.

A reliability analysis requires additional statistical input information which is not required in a deterministic analysis, but results in richer information pertaining to the performance function and the design point that is missed in a deterministic analysis.

In short, when faced with a computed probability of failure (P_f) for an engineering case, whether computed by FORM or Monte Carlo simulations, one must not regard it as an invariable intrinsic or endogenous property of the case, but as an outcome that will change if the statistical inputs and probability distributions are changed. The values of reliability analysis via FORM for a particular design (e.g. Fig. 9), and RBD-via-FORM for a target reliability index β (e.g. Figs. 3, 4, 8), are not diminished because even imprecise risk estimate by RBD-via-FORM can help achieve a sufficient level of reliability against failure (similar to the objectives of EC7 and LRFD via implicit probabilistic considerations), or indicate a risky case (e.g. Fig. 9) with insufficient reliability level.

6 Summary and Conclusions

Context-dependent parameter sensitivities were investigated probabilistically in this study via the first-order reliability method (FORM) applied to plane sliding of rock slopes containing discontinuities. Prior to FORM, the alternative deterministic procedures using the Solver constrained optimization tool obtains the same solution (Fig. 2) as the stereographic projection solution (Fig. 1) in the first case of single block on a discontinuity plane, and the same solution (Figs. 6, 7) as the closed form equation (Fig. 5) in the second case of two blocks on two discontinuity planes. Both the single-block sliding on a discontinuity plane and the two-block sliding on two surfaces were extended into RBD-via-FORM to obtain insights on context-dependent parameter sensitivities. A third case involving bounded nonnormal distributions for a failed slope in a limestone quarry showed failure probability estimated by reliability index in good agreement with failure probability based on Monte Carlo simulation.

The following enlightening information provided by the design point of FORM can complement and enhance the evolving partial factor design methods like EC7 and LRFD:

• (1) In the case of RBD of a single block on a plane (Figs. 3, 4), the positive values of the sensitivity indicator (n) of weight W for different scenarios are testament to its being an unfavorable load. However, its sensitivity measure (n value) changes with changing value of its base area A, and with whether the shear resistance along the discontinuity plane is entirely frictional or includes a cohesive component acting on base area A.

• (2) The relative sensitivities of resistance parameters c and ϕ and of load parameter u in case 1 can change significantly depending on the relative mean values and standard deviations of these parameters, and on the area A which affects water force uA and cohesive resistance cA, as shown in Fig. 4. The smaller mean value of A in Fig. 4b reverses the sensitivities of cohesion c and friction angle ϕ, and greatly reduces the sensitivity of water pressure u.

• (3) In contrast to the unambiguous load nature of W mentioned in item 1 above, the RBD of case 2 in Fig. 8 shows the sensitivity indicator (n) of V₁ (from which W₁ = V₁γ_rock) is positive but that of V₂ (the lower passive block) is negative, indicating the destabilizing effect of W₁ and the stabilizing effect of W₂. Also, the design value of ϕ₂ (of the lower passive block) is much smaller than the design value of ϕ₁ (of the upper active block), indicating different sensitivities even though ϕ₁ and ϕ₂ are the same nature and have the same mean value and same standard deviation.

• (4) Mean values and standard deviations are required in RBD, but not partial factors and characteristic (nominal) values. Nevertheless, partial factors can be back-calculated from the design point of RBD-via-FORM. Such back-calculated partial factors (e.g. Fig. 8c) and LF and RF (e.g., Fig. 3c) are illuminating for each case and valuable for comparison with code-specified partial factors and LF and RF, but should not be generalized to other cases.

• (5) It is a significant merit of RBD-via-FORM that its outcome reflects context-dependent parameter sensitivities and resolves load-resistance duality (e.g. base area A of case 1 which affects water force U = uA and cohesive resistance cA).

Because parameter sensitivities can vary from case to case, it is more meaningful to conduct RBD-via-FORM in tandem with limit state design based on partial factors, than to attempt to calibrate partial factors back-calculated from RBD-via-FORM.

The context-dependent parameter sensitivities (and insights and implications for partial factor design) have been investigated in this paper based on the simplifying Coulomb failure criterion and persistent discontinuity plane. The context-dependent phenomenon and insights for partial factor design are pertinent even in other research investigations incorporating more advanced features.

Appendix

1.1 Intuitive Understanding of the Reliability Index of FORM and Its Design Point

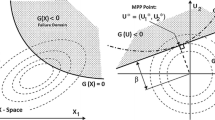
The reliability approach used in this paper is FORM, which can deal with correlated nonnormal (non-Gaussian) random variables. A special case of FORM is the earlier Hasofer–Lind index for correlated normal (Gaussian) random variables. The classical u-space approach for the FORM and the Hasofer and Lind (1974) method requires rotation of coordinate axes if the random variables are correlated, as described by Rackwitz and Fiessler (1978), Ditlevsen (1981), Ang and Tang (1984), Madsen et al. (1986), Haldar and Mahadevan (1999), Melchers (1999), Baecher and Christian (2003), amongst others.

An alternative Excel-automated constrained optimization approach for FORM, without rotation of coordinate axes, was given by Low and Tang (2004), which computes the FORM reliability index β by finding the smallest equivalent hyperellipsoid (centered at the equivalent normal mean-value point μ^N and with equivalent normal standard deviations σ^N, where superscript N denotes normal distribution) that is tangent to the limit state surface (LSS):

$$\beta = \mathop {\min }\limits_{{{\mathbf{x}} \in F}} \sqrt {\left[ {\frac{{x_{i} - \mu_{i}^{N} }}{{\sigma_{i}^{N} }}} \right]^{T} {\mathbf{R}}^{ - 1} \left[ {\frac{{x_{i} - \mu_{i}^{N} }}{{\sigma_{i}^{N} }}} \right]} ,$$

(19)

where x_i denotes the set of random variables, R is the correlation matrix, and F is the failure domain. The notations “T” and “− 1” denote transpose and inverse, respectively. μ_i^N and σ_i^N can be calculated by the Rackwitz and Fiessler (1978) transformation.

Another Excel-based FORM procedure was given by Low and Tang (2007), which uses the following equation for the reliability index β:

$$\beta = \mathop {\min }\limits_{{{\mathbf{x}} \in F}} \sqrt {{\mathbf{n}}^{T} {\mathbf{R}}^{ - 1} {\mathbf{n}}} ,$$

(20a)

where

$$n = \frac{{x_{i} - \mu_{i}^{N} }}{{\sigma_{i}^{N} }}.$$

(20b)

An advantage of the Low and Tang (2007) procedure is that computation of μ_i^N and σ_i^N is not required.

The computational approaches described by Eqs. (19) and (20) and associated ellipsoidal perspectives yield identical results as the classical rotated u-space computational approach, and thus may help reduce the conceptual and language barriers of FORM. The ellipsoidal perspective is shown in Fig. 11, in the space of two shear strength parameters c′ and ϕ′ which obey the normal probability distribution. The mean-value point (μ_ϕ and μ_c) is in the safe domain. The ellipses, tilted due to negative correlation between c′ and ϕ′, are probability density contours that decrease in value as the ellipse expands. Ellipsoid and hyperellipsoid shapes can be visualized in the mind’s eye when the number of random variables is three or greater. The limit state surface (LSS) separates safe from unsafe combinations of parameter values. The point where the expanding elliptical probability contour just touches the LSS is the most probable point (MPP) of failure, also referred to as the design point. The Hasofer and Lind (1974) reliability index can be understood as the distance from the safe mean-value point to the MPP of failure, in units of directional standard deviation. This intuitive ellipsoidal perspective is also valid for FORM (which extends the Hasofer–Lind method to deal with correlated non-normal distributions), if one thinks in terms of ellipsoidal probability contours with equivalent normal standard deviations and centred at the equivalent normal mean-value point, based on the equivalent normal transformation of Rackwitz and Fiessler (1978).

Fig. 11

Illustration of reliability index β in the c′–ϕ′ plane with c′ and ϕ′ negatively correlated. This perspective is also valid for non-normal distributions, when viewed as “equivalent ellipsoids”. Tanϕ′ can be used instead of ϕ′

Readers can enhance their understanding of the reliability index of FORM and its design point (briefly explained in this Appendix) by conducting hands-on implementation on the freely downloadable Excel files from the link given at the end of the Introduction of this paper. More details, including the relationship between the unrotated n vector of this paper and the rotated u vector of the classical approach, are given in Chapter 2 of Low (2021).

1.2 Rapid RBD-via-FORM using the Excel forecast.linear Function

Figure 12 illustrates the efficient RBD-via-FORM procedure for obtaining the value of a design parameter for a target reliability index, for example β = 2.5. The steps are illustrated for the case in Fig. 3a. The same simple steps apply to Figs. 4 and 8, and other RBD-via-FORM problems. More examples can be downloaded for hands-on appreciation, as shown in the author’s YouTube upload at https://www.youtube.com/watch?v=YQ5J2edT6j8, and also at the bottom of the screen at https://www.routledge.com/authors/i21471-bak-kong-low.

Fig. 12

Efficient procedure for RBD-via-FORM using the Excel Forecast.linear function