1 Introduction

Blasting is usually the first step in open-pit mining operation for rock breakage and is widely implemented in mining and civil projects. Although the primary goal of blasting is rock fragmentation, about 80% of the total energy of charged explosives is wasted in other ways. The wasted energy is dissipated in flyrock, air-overpressure (AOp), ground vibration, back break, and dust and fumes emission (Sari et al. 2014; Bakhtavar et al. 2021b; Zhou et al. 2020; Hosseini et al. 2021; Hajihassani et al. 2015; Khandelwal and Monjezi 2013a). Flyrock is determined as the rock fragments propelled beyond the blasting region by the energy of charges. The main reasons for flyrock production in blasting are an inappropriate design of the blasting pattern, inaccurate drilling work, inadequate stemming and burden, and unwarrantable specific charges (Yari et al. 2016). Blasting design parameters such as spacing, sub-drilling, powder factor, charge per delay, hole length, and stiffness factor are the most important controllable factors on flyrock distance (Khandelwal and Monjezi 2013b). On the other hand, rock mass characteristics such as rock density and rock mass rating (RMR) are the uncontrollable parameters in this process (Ghasemi et al. 2012a; b; Khandelwal and Monjezi 2013a, b; Rad et al. 2020).

Accurate flyrock prediction can prevent or minimize blasting-related fatal and nonfatal injuries (Ghasemi et al. 2012a; b). Recently, soft computing techniques have been used to predict flyrock distance in mining and civil engineering projects. The following paragraphs include a concise review of the recent application of different prediction methods with their success measured by R2 values were available.

The least-squares support vector machines (LS-SVM) were used by Rad et al. (2018) to predict flyrock distance in the Gole-E-Gohar surface mine in Iran using data from 90 blastings. Their proposed model predicted the flyrock distance with an R2 of 0.969. Kalaivaani et al. (2020) simulated the flyrock distance caused by bench blasting using an integrated recurrent fuzzy neural network (RFNN) with the Particle Swarm Optimization (PSO) algorithm. They used a dataset of 72 blastings and reached an R2 of 0.933. Yari et al. (2016) predicted flyrock distance using a hybrid multilayer perception neural network (NN) and empirical models. They found the NN model more accurate than empirical models for flyrock distance prediction. An adaptive network-based fuzzy inference system (ANFIS) model was applied by Trivedi et al. (2015) and reported comparable results to the ANN and statistical models for flyrock prediction. In another study, Monjezi et al. (2012) successfully integrated multilayer perceptron NN (MLPNN) and genetic algorithm (GA) to predict blast-induced flyrock by a hybrid ANN-GA technique.

Faradonbeh et al. (2016) proposed genetic programming (GP) and gene expression programming (GEP) models to evaluate flyrock distance. They achieved R2 values of 0.935 and 0.893 for their GP model's training and testing parts, respectively. Their GEP model achieved R2 values of 0.991 and 0.987 for its training and testing, respectively, which suggested the GEP model was more accurate in predicting flyrock distance. Guo et al. (2021a) presented a combination of support vector regression models (SVRs) and Lasso and elastic-net regularized generalized linear model (GLMNET) as the SVRs–GLMNET model to predict flyrock distance in a quarry mine. They developed six SVR models and imported training data into the GLMNET produced the most accurate results for flyrock distance prediction with an R2 of 0.993.

In another recent attempt, Lu et al. (2020) develped an outlier robust ELM (ORELM) model for flyrock distance prediction and compared their results with extreme learning machine (ELM) and ANN models. They collected 82 blasting data by monitoring blasting events in 3 granite quarries for their study. Their ORELM model achieved an R2 value of 0.958, providing higher accuracy than ANN with an R2 value of 0.912 and ELM with an R2 value of 0.955. In another research, Murlidhar et al. (2020) proposed an extreme learning machine (ELM) optimized by biogeography-based optimization (BBO) for flyrock distance prediction and used a particle swarm optimization (PSO)-ELM model for comparison. The R2 values related to testing of PSO-ELM, BBO-ELM and ELM model were obtained as 0.93, 0.94, and 0.79, respectively, which proved the BBO-ELM a more reliable tool for flyrock distance estimation. In a study conducted by Guo et al. (2021b), the deep neural network (DNN) method was used to predict flyrock distance in Ulu Thiram quarry, Malaysia. They optimized the DNN model by whale optimization algorithm (WOA) and obtained the R2 value of 0.9829 and 0.9781 for the training and testing dataset. Fattahi and Hasanipanah (2021) introduced an integrated model based on ANFIS and grasshopper optimization algorithm (GOA) to predict blast-induced flyrock in open-pit mines and obtained an R2 value of 0.974. Hasanipanah et al. (2020a) proposed an adaptive dynamical harmony search (ADHS) algorithm to optimize the ANN architecture. They employed the ANN-ADHS to develop a model to estimate flyrock and predicted the flyrock distance with R2 value of 0.929.

Researchers have also involved theoretical approaches and empirical models to predict the flyrock distance (Lundborg et al. 1975; Siskind and Kopp 1995; Raina et al. 2004; McKenzie 2009). Ghasemi et al. (2012b) proposed a theoretical approach for forecasting flyrock distance in a copper mine; Marto et al. (2014) developed a multivariate linear regression for flyrock prediction in surface mine; and in another study, an empirical model was presented for estimation of flyrock by Armaghani et al. (2016b).

In an attempt to integrate fuzzy systems with optimization techniques, Hasanipanah and Amnieh (2020) developed a fuzzy rock engineering system (FRES) for assessing the risk level of flyrock due to mine blasting. They successfully optimized their model using genetic algorithm (GA), imperialist competitive algorithm (ICA), and particle swarm optimization (PSO) and achieved the R2 values of 0.984, 0.983, and 0.981, respectively. Bakhtavar et al. (2021a) used the fuzzy cognitive map (FCM) technique to analyze the relationship between dust emission parameters due to mine blasting. The FCM method with a fuzzy slack-based efficiency model was also used by Rezaee et al. (2021) to improve auto industry projects. The FCM framework has several primary advantages among other cognitive methods, including as (1) examining the causal-effect relationships between concepts (nodes) of the network, (2) reducing the complexity of decision-making problems, (3) decreasing dependence on experts' views and increasing the accuracy of the calculated weights by applying learning algorithms, and (4) reducing computational time (Bakhtavar et al. 2021a). Therefore, this research involves this method in predicting flyrock distance.

Zadeh (2011) first introduced the Z-number concept, which denotes a fuzzy number pair (A, R). This theory is a new concept in fuzzy logic that has been recently adopted in engineering applications. One of the advantages of Z-number theory is eliminating uncertainty in expert views (Hosseini et al. 2022; Poormirzaee and Hosseini 2021). Ghoushchi et al. (2019) applied reliability of Z-numbers for decreasing complexity of industries and risk assessment of processes. Aboutorab et al. (2018) employed the Z-evaluations to solve the uncertainty of supplier development problem. Stock selection problems were eliminated using Z-numbers by Yaakob and Gegov (2016). In another research, the Z-number theory was used by Tian et al. (2021) to manage uncertain information and for pattern recognition. Jiskani et al. (2022) used Z-number theory to overcome uncertationy of expert views to analyze health and safety risks in surface mines. They integrated Z-numbers with fuzzy fualt tree analysis and concluded that this theory is capable of increasing the results accuracy. Z-number-based fuzzy system has been utilized in predicting food security risk levels by Abiyev et al. (2018). The uncertain environmental conditions in the supplier development problems was solved using an integrated Z-number theory with Best Worst Method proposed by Aboutorab et al. (2018). Yazdi et al. (2019) used Z-numbers for eliminating uncertainty of expert views in probabilistic risk assessment.

A novel soft computing-based model is presented in this research to predict flyrock distance in open-pit mining operations. This model is based on the integration of a multilayer perceptron neural network (MLPNN), fuzzy cognitive maps (FCMs), and Z-number theory. The proposed model is called the artificial causality-weighted neural networks based on reliability (ACWNNsR) and is the first study that simultaneously employs the ANN, FCM, and Z-numbers for flyrock prediction to the best of the authors' knowledge. The proposed model eliminates the uncertainties in the FCM modeling through the use of reliability information of Z-numbers. Notably, the weight of ANN neurons is simulated using the learned FCM by combining nonlinear Hebbian algorithm (NHL) and differential evolution (DE) algorithms, which is an improvement compared to previous models. Implementing the FCM based on Z-number in neurons weighting is expected to help predict the flyrock distance and provide a safer working environment for blasting operation.

2 Research Methodology

2.1 Artificial Neural Networks (ANNs)

Since the 1940s, ANNs have been first pioneered by McCulloch and Pitts (1943). They pointed that ANNs are capable of computing any logical or arithmetic function. The computations of neural signals human-brain inspire the concept of ANNs by translating them into a simple linear mathematical equation to establish an input–output relationship. Simulation of the learning process is one of the prominent characteristics of ANNs (Esmaeili et al. 2014). An original ANNs is structured based on three main components: learning rule, network training architecture, and activation function (Simpson 1990). The recurrent and back-propagation feed-forward neural networks are two major types of ANNs (Armaghani et al. 2015). Besides, the various architectures of ANNs such as radial basis function (RBF), multilayer perceptron neural networks (MLPNN), deep feed-forward neural networks (DFF), recurrent neural networks (RNN), extreme learning machine (ELM), echo state network (ESN), Bayesian regularized neural network (BRNN), generalized feed-forward neural networks (GFNN), etc. have been presented so far. However, optimal constructing of the ANN architecture is a challenge (Nguyen and Bui 2020; Hajihassani et al. 2015). Depending on the different applications of an ANN, various methods are presented to design an ANN.

2.2 Multilayer Perceptron Neural Network (MLPNN)

Multilayer perceptron neural networks (MLPNN) have been employed successfully to overcome different and complex engineering problems through supervised training using the error back-propagation algorithm. The feed-forward back-propagation neural network suggested by Shahin et al. (2002) is one of the most widely used ANNs in prediction aims (Armaghani et al. 2016a; Hoseinian et al. 2017; Alizadeh et al. 2021). An error-correction learning rule is used in this algorithm, in which a backward and a forward pass are performed for error back-propagation learning to take place. In the forward pass, a learning process is initialized in nodes (input vector) of the networks, and conducted calculations propagate from the first layer to the last layer (Hosseini et al. 2021). Then, network outputs (actual response) are determined based on a set of inputs. In this process, the generated synaptic weights remain unchanged. However, the error-correction rule has been used to adjust the synaptic weights in the backward pass. In addition, an error signal is produced by subtracting network output from a desirable target. Synaptic connections are reversible as this error propagates backward (Esmaeili et al., 2014; Bakhtavar et al., 2021a).

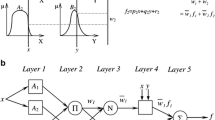
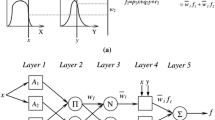
A multilayer perception (MLP) is the famous and most well-known structure of ANN. This network is structured from three primary input, hidden, and output layers, each considering several neurons (nodes). As the simple form of a biological neuron, the nodes are connected to other nodes by an exclusive weight. The MLPNN receives the input data and propagates in a forward path. It should be noted that the weight value is initialized to make connections among input, hidden, and also output nodes, which are randomly assigned. The general architecture of an MLP is shown in Fig. 1.

Fig. 1
figure 1

General MLP architecture

Full size image

MLP simulates the output value by Eq. (1):

$$y = f_{i} \left( {\sum\limits_{i = 1}^{n} {w_{ij} x_{j} + b_{i} } } \right),$$
(1)

where x and y indicate the input matrix and output value, respectively. w represents the weight vector, and b shows the bias value of each neuron. f indicates the activation (transfer) function. According to the various usage, the number of hidden layers and the number of hidden neurons in each hidden layer, learning algorithm, and activation function, can be different.

The created error during MLP training is calculated as follows:

$$e\left( w \right) = \frac{1}{n}\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{I} {\left( {s_{i} - o_{i} } \right)} } ,$$
(2)

where e(w) is the MLP network error, w indicates tth iteration weight, si denotes output node, oi represents output value of the ith output node, I signify output nodes number, and n stands patterns number. The main disadvantages of MLP are getting trapped in local minima and a slow learning rate. Researchers solve these difficulties by applying metaheuristic algorithms to optimize the weight of neurons and increase ANN performance (Taheri et al. 2017; Moosazadeh et al. 2019).

2.3 Bayesian Regularized Neural Network (BRNN)

An ANN can be designed with various hidden nodes, so it is difficult to be determined precisely. Once overfitting occurs, the results will be unreliable if too many hidden neurons are considered. Inversely, an ANN with inadequate neurons has difficulty in the learning process. The Bayesian regularized neural network (BRNN) is proposed to overcome these problems by combining Bayes’ theory into the regularization system. The learning process of the Bayesian scheme considers the uncertainty in the weight vector.

BRNN can be used for solving nonlinear problems effectively. BRNN was first basically presented by MacKay (1992), which focuses on the probabilistic learning operation of ANNs. The outstanding feature of BRNN is to determine the number of effective weights of the network. Based on this fact, an optimal network size is automatically determined based on the number of training cases needed for the learning process. BRNN, as one of the AI methods, employs the propagation algorithm which computes the amount of the least-squares error function as in Eq. (3) (Nguyen et al. 2020):

$$S\left( w \right) = \beta \sum\limits_{i = 1}^{n} {\left( {y_{i} - t_{i} } \right)^{2} } + \alpha \sum\limits_{i = 1}^{m} {w_{i}^{2} } ,$$
(3)

where α and β indicate the hyperparameters (regularization parameters). n indicates the number of data, w denotes the weight of inputs value, y signify the weight of output values, and t is the weight of target values.

BRNN performs best when the regularization parameters are set at their optimum. Based on a Bayesian model, the weights in the network can be operated as random elements. The weights are represented in the form of a density function, which is determined using Bayes' theorem (Kurnaz and Kaya, 2018):

$$P\left( {w|\alpha ,\beta ,D} \right) = \frac{{P\left( {D|w,\beta } \right) \cdot P\left( {w|\alpha } \right)}}{{P\left( {D|\alpha ,\beta } \right)}},$$
(4)

where P(w|α) denotes the prior density.

Before collecting databases, the degree to which the weights are known is signified by P(w|α). Furthermore, P(D|w,β) indicates the possibilities function determined the probability of the error, and P(D|α,β) denotes model evidence or normalization parameter. Maximizing the posterior probability of the model can lead to optimal weights in the training process; thus, the error function of BRNN is obtained. Suppose the priority data and the probability distribution of weights be Gauss; weights are assigned a priority probability function with the following:

$$P\left( {w|\alpha } \right) = \frac{1}{{Z_{w} \left( \alpha \right)}} \cdot \left( {e^{{ - \alpha E_{w} }} } \right).$$
(5)

The probability of errors, possibility, is formulated as:

$$P\left( {D|w,\beta } \right) = \frac{1}{{Z_{D} \left( \beta \right)}} \cdot \left( {e^{{ - \beta E_{w} }} } \right).$$
(6)

The posterior distribution is achieved as Eq. (7):

$$P\left( {w|\alpha ,\beta ,D} \right) = \frac{1}{{Z_{S} \left( {\alpha ,\beta } \right)}} \cdot \left( {e^{ - S(w)} } \right).$$
(7)

The optimal Regularization parameters α, β are calculated through the Bayes theorem as follows:

$$P\left( {\alpha ,\beta |D} \right) = \frac{{P\left( {D|\alpha ,\beta } \right) \cdot P\left( {\alpha ,\beta } \right)}}{P\left( D \right)},$$
(8)

where P(α, β) and P(D| α, β) are the prior probabilities for the normalized parameters α, β, and the term of possibility, respectively. The optimum values of α, β are determined as Eqs. (9)–(11):

$$\alpha = \gamma /2E_{w}$$
(9)
$$\beta = \left( {n - \gamma } \right)/2E_{D}$$
(10)
$$\gamma = \sum\limits_{i = 1}^{m} {m - \alpha \cdot {\text{trace}}^{ - 1} \left( A \right)} .$$
(11)

In which γ indicate the effective parameter, m is the number of parameters, and A denotes the objective function (Hessian matrix of S(w)).

2.4 Fuzzy Cognitive Maps (FCMs)

The cognitive map (CM) approach is widely employed in engineering since it can examine and obtain the complicated cause-and-effect interactions between several parameters (variables). Various parameters communicate complex relations with the other parameters supporting a cause-and-effect status in actual issues. A CM is structured to connect knots through organized arcs consisting of signs on the bow. In a precise scheme of a cognitive map, nodes denote unique theories which represent a system. In addition, arcs indicate cause-and-effect relations (weights) among the nodes.

The fuzzy CM (FCM) is a powerful method applied to specific problems in which the cost of collecting data is high or inaccessible. An FCM uses fuzzy numbers in the interval [− 1,1] or [0,1] to explain intellectual opinion, which indicates the strength of attraction of causal relationships. The mental perspective of experts is crucial to design the map of FCM and predict concept weights and relationships between factors using neural network logic (Rezaee et al. 2017, 2018). A view of the cognitive map is presented in Fig. 2.

Fig. 2
figure 2

A view of the cognitive map

Full size image

As illustrated in Fig. 2, Ci shows concepts (nodes) that are connected with weighted arcs. Wij represents cause-and-effect relationships between Ci and Cj. Wij > 0 and Wij < 0 denote a positive and negative causal relationship, respectively. In addition, Wij = 0 indicates no relationship among connected concepts.

It should be noted the weight of factors should not depend on expert opinions. However, the combination of Hebbian and metaheuristic algorithms is appropriate for adjusting map concept weights. This problem is solved by proposing learning algorithms that decrease dependency on expert views and simultaneously improve the weights and map convergence accuracy. Learning algorithms such as the Hebbian, hybrid, and population-based algorithms are used to apply the FCM (Papageorgiou and Kannappan 2012). This study integrates the nonlinear Hebbian algorithm (NHL) with the differential evolution (DE) algorithm to apply in FCM. The proposed hybrid algorithm is known as the NLH-DE algorithm, which can update non-dimensional weights in various simulations and maintain connections among nodes in a general map.

Different type of relationships between concepts shows the state vector A = [A1, A2, …, An]. The state vector A must continually transfer through the weight vector to develop a system. Hence, Eq. (12) is introduced to estimate the state vector A for each concept of Ci at repetition t:

$$A_{i}^{t} = f\left( {A_{i}^{t - 1} + \sum\limits_{\begin{subarray}{l} j \ne i \\ j = 1 \end{subarray} }^{N} {A_{j}^{t - 1} \cdot W_{ij} } } \right),$$
(12)

where At and At−1 are the values of concept Ci at iteration t and t−1, respectively. Wij denotes the connection weight through concept Cj to concept Ci. In addition, f(x) indicates a threshold function. The unipolar sigmoid function (Eq. 13) is the best function to convert the result in the interval of [0, 1] or [− 1, 1] compared among other threshold functions, where λ represents the function slope. State vector A is simulated using Eqs. (12) and (13), and the new value of A is updated, and this proceeds until convergence is achieved (Onari et al. 2020).

$$f\left( x \right) = \frac{1}{{1 + e^{{\left( { - \lambda x} \right)}} }}.$$
(13)

2.5 Z-Number Concept

This theory was presented to overcome the numbers that are not reliable at all (Onari et al. 2020). Pair of Z-number (A, R) denotes restrictions to representing the behavior of the Z-numbers. Components of A and R describe a fuzzy set and degree of reliability, respectively. The degree of certainty can be denoted as a probability density function or a fuzzy set. For example, the production rate is announced as follows:

"daily blasted rocks in a large scale mine is about 1500 tons", low.

This announcement can be expressed as "X is Z = (A, R)." In contrast, X is the "daily blasted rocks" variable, A is a fuzzy set that expresses the daily blasted rocks "about 1500 tones", and R is the degree of certainty of A in the event that is "low" (Eq. 14).

$$R\left( X \right) \, = X {\text{is}}\;A.$$
(14)

Equation (14) describes probability constraint and A expressed probability distribution X. In this regard, it can be stated that:

$$R\left( X \right):X\;{\text{is}}\;A \to {\text{Poss}}\left( {X = u} \right) \, = \mu_{A} \left( u \right),$$
(15)

where u is the general value of X and µA is the membership function of A, and set of A can be indicated as a restriction that is related to R(X):

$$R\left( X \right):X\;{\text{is}}\;p,$$
(16)

whereas p is the probability density function of X (Zadeh 2011):

$$R\left( X \right):X\;{\text{is}}\;p \to {\text{Prob}}(u \le X \le u + {\text{d}}u) \, = p\left( u \right){\text{d}}u.$$
(17)

The problem description by Z-numbers is clear; nevertheless, performing problem calculations by Z-numbers are comparatively difficult (Zadeh 2011). Z-numbers are disposed of accurately with their operations to overcome this problem, and transforming them into crisp numbers is investigated (Song et al. 2020). The complicated computational procedures of Z-number are solved by transforming Z-value to the fuzzy number or crisp value; however, this method significantly loses some information and decreases the advantages of using Z-information during information transformation (Onari et al. 2020). Therefore, triangular fuzzy numbers (TFNs) convert Z-number into fuzzy numbers. These conversion rules were first proposed for reliable linguistic variables. In this research, the first way is applied to Z-number conversion. The opinions of the team of experts require linguistic variables to explain each estimation (Table 1), which its membership function is illustrated in Fig. 3 schematically.

Table 1 Expressed Z-numbers as linguistic values
Full size table
Fig. 3
figure 3

Linguistic term sets of Z-number

Full size image

Figure 3 illustrates the reliability level of Z-number in the ranges 0–100%. The value of 100% is used for strong reliability, while 0% represents unreliability. In other words, experts used this scale to express their judgments confidence. Notably, the reliability level has hugely improved the obtained results; therefore, experts' judgments are modified based on reliability, and reliable results are presented.

Suppose \(Z = (\tilde{A},\tilde{R})\):

$$\left\{ {\tilde{A} = \left( {x,u_{{\tilde{A}}} } \right)|x \in [0,1]} \right\}$$
(18)
$$\left\{ {\tilde{R} = \left( {x,u_{{\tilde{R}}} } \right)|x \in [0,1]} \right\}.$$
(19)

The Z-numbers reliability is calculated as follows:

$$\alpha = \frac{{\int {x\mu_{{\tilde{B}}} (x)\,\,{\text{d}}x} }}{{\int {\mu_{{\tilde{B}}} (x)\,\,{\text{d}}x} }}.$$
(20)

Finally, crisp numbers of reliability are applied to the restriction:

$$\tilde{Z}^{\alpha } = \left\{ {\left( {x,u_{{\tilde{A}}} } \right)|u_{{\tilde{A}^{\alpha } }} \left( x \right) = \alpha u_{{\tilde{A}}} \left( x \right),\,x \in [0,1]} \right\}.$$
(21)

For example, Let a Z-number \(Z = (\tilde{A},\tilde{R})\) for the constraint. There is a linguistic variable 'High (H)' (A = H) with a reliability' 0.95% sure' (R = 0.95% sure). This is explained as follows:

$$Z = \left[ {\left( {{5},{ 7},{ 9};{ 7}} \right), \, \left( {0.{9}, \, 0.{95},{ 1}} \right)} \right].$$

First, the reliability part is transformed to a crisp value as follows:

$$\alpha = \frac{{\int {x\mu_{{\tilde{B}}} (x)\,\,{\text{d}}x} }}{{\int {\mu_{{\tilde{B}}} (x)\,\,{\text{d}}x} }} = 0.95.$$

Second, the reliability weight is added to the restriction by:

$$\tilde{Z}^{\alpha } = ({5},{ 7},{ 9}; \, 0.{95}).$$

Finally, the weighted Z-number is changed into the regular fuzzy number.

$$\tilde{Z}^{\prime} = (\sqrt {0.95} \times 5,\sqrt {0.95} \times 7,\sqrt {0.95} \times 9) = (4.87,6.82,8.77).$$

Figure 4 represented Z values after affecting the reliability, and the fuzzy number transformed from Z-number. Similarly, other Z-numbers are translated into TFNs.

Fig. 4
figure 4

Converting of Z-number to fuzzy number

Full size image

2.6 Artificial Causality-Weighted Neural Networks Based on Reliability (ACWNNsR) Model

Figure 5 indicates the framework of the proposed ACWNNsR Model. As shown in the methodology framework, the effective parameters were first specified by literature investigations. Generally, the weight of each parameter is randomly calculated in the learning process of ANN. However, determining weights based on a learning rule is of particular importance. Therefore, the FCM technique simulated and updated parameter weights in different iterations. In addition, Z-number theory was applied to improve the expert's opinions in the matrix corresponding to causal-effect weights. Hence, the causal-effect weights were used in the ANN learning process. The results of the reliability FCM were finally utilized in the proposed ACWNNsR model. Finally, the sensitivity of flyrock to each input parameter was evaluated in two different methods.

Fig. 5
figure 5

The framework of the proposed ACWNNsR model

Full size image

3 Reference Case and Data Analysis

The required dataset for the study was collected from Anguran mine in Iran. This mine is one the large-scale and oldest lead–zinc mine in the Middle East, with an annual extraction rate of one million tons. According to Fig. 6, this mine is placed in Zanjan province at the west of Iran, at 47° 82′ 00″ E longitude and 36° 84′ 00″ N latitude, at an altitude of approximately 2935 m above sea level.

Fig. 6
figure 6

The geographical location of Anguran mine and blasting rounds

Full size image

Figure 6 illustrates the location of the Anguran based on satellite imagery and a snapshot of blasting round. Blasting works are operated through 76, 114, and 127 mm blast holes. Blasting operations are principally conducted using ANFO (combine fuel oil and ammonium nitrate with a specific gravity of 0.85–0.95 g/cm3). In this mine, flyrock distances were recorded from a total number of 416 blasting works. It should be noted that 416 blasting datasets were recorded during 4 years. Table 2 summarizes descriptive statistics of the collected data and their ranges. The frequency histogram of the flyrock distance is shown in Fig. 7. As shown in Fig. 7, 209 blasting events are accompanied by a flyrock distance of 100 m, while a flyrock distance of 340 m is observed in 7 blasting rounds. Notably, 204 blasting events caused 120 m long flyrock.

Table 2 Descriptive statistics of the recorded blasting parameters
Full size table
Fig. 7
figure 7

Frequency distributions of the flyrock distances

Full size image

The B, St, S, Pf, MC, and flyrock factors measured in Anguran mine are variated in the range of 3–5 m, 0.9–0.8 m, 3–6 m, 0.01–1.67 kg/m3, 5.54–697.72 kg and 46.42–389.03 m, respectively. The parameters were immediately measured after performing the blasting pattern. This study defines the flyrock as the maximum distance to which rocks are impelled outside the blast location. Due to the difficulty in measurement of flyrock distance, part of the bench was painted before operating each blast rounds, and blasting was recorded on video. The maximum distance related to fragment rocks was measured using tracking fragment rocks. Note that the Pf and CD were calculated using other measured parameters.

4 Flyrock Prediction

In this research, MLPNN, BRNN, and the proposed ACWNNsR models were employed to predict the flyrock distance due to mine blasting. First, 416 collected datasets were randomly divided into two main parts; training and testing datasets. Subsequently, the normalized values of inputs and outputs variables were calculated using the following equation:

$$x_{n} = \frac{{x_{i} - x_{\min } }}{{x_{\max } - x_{\min } }}.$$
(22)

In which xn is the normalized value, xi indicates the measured data, and xmin, and xmax are the minimum and maximum values of data, respectively. The performance of the proposed models was evaluated employing three statistical criteria, including coefficient of determination (R2), root-mean-squared error (RMSE), and value account for (VAF) (Keshtegar et al. 2021; Hasanipanah et al. 2020b), which are determined as follows:

$$R^{2} = 1 - \left( {\frac{{\sum\nolimits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } }}{{\sum\nolimits_{i = 1}^{n} {(P_{i} - \overline{P}_{i} )^{2} } }}} \right)$$
(23)
$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } }$$
(24)
$${\text{VAF}} = 100 \cdot \left( {1 - \frac{{{\text{var}}(O_{i} - P_{i} )}}{{{\text{var}}(O_{i} )}}} \right),$$
(25)

where Oi and Pi are measured and predicted amounts, respectively; \(\overline{P}_{i}\) is the average of the predicted values, and n is the number of datasets.

4.1 Prediction of Flyrock by MLPNN

In this study, MLP neural network is employed to flyrock prediction Anguran lead–zinc mine. In this regard, five effective parameters and flyrock are considered inputs and outputs of the modeling process. The maximum number of the hidden layer(s) is considered two layers, and the number of hidden nodes is determined based on the trial-and-error procedure. The MLP architectures are structured based on 3–23 hidden nodes; 100 training epochs are fixed. The statistical indicators formulated in Eqs. (23) to (25) are calculated for each trained structure. Then the best optimal architecture with high performance on both test and train phase is selected using the scoring system presented by Zorlu (Zorlu et al. 2008). In this technique, a score is assigned for each training and testing dataset and the highest score is considered to be the best model. The MLP modeling with different numbers of the hidden layer(s) and node(s) along with the rating of indices are presented in Table 3. As a result, the MLP4 with a total rate of 57 from 60 predicts the flyrock better than other architecture. Therefore, the best model with the optimal structure is the MLP4 model with a 5-10-1 structure.

Table 3 Obtained performance indices to detect the optimum MLPNN model
Full size table

4.2 Prediction of Flyrock by BRNN

In this section, the flyrock distance is predicted using BRNN predictive model. The number of hidden nodes causes complexity in the BRNN modeling process. Therefore, stopping criteria is determined based on the number of hidden neurons. A range between 1 and 8 was considered for the number of hidden neurons to prevent overfitting and learning problems. Several trained BRNN models were achieved using the trial–error procedure and evaluated using performance indices to select the best BRNN structure capable of predicting flyrock distance with a high degree of accuracy.

The obtained results from BRNN modeling are tabulated in Table 4. The best model is selected by Zorlu scoring system. As it can be seen, BRNN, with the total rate value of 45 from 48, attained the highest value among eight architectures. Hence, it was concluded that the BRNN with a 5-5-1 structure is the best to predict blast-induced flyrock in the reference case.

Table 4 Obtained performance indices to detect the optimum BRNN model
Full size table

4.3 Prediction of Flyrock by ACWNNsR

A learned FCM based on the NHL and DE hybrid learning algorithm was developed to calculate the weight linked to the hidden layers of ANN. In this regard, the cause-and-effect relationships between concepts (effective parameters and flyrock distance) were initialized using an expert team's opinion. It should be noted that experts expressed their opinions at all stages by applying the Z-number reliability in the interval 0–100%. An example of expert opinions and the reliability of opinions are tabulated in Table 5. The effect of Z value in their opinions is tabulated in Table 6.

Table 5 Example of expert opinion
Full size table
Table 6 Final value of one of the expert opinions
Full size table

The final matrix resulting from integrating an expert team of six-member opinions is reported in Table 7, which indicates the cause-and-effect relationships between the inputs and output variables.

Table 7 The causal-and-effect relationship between inputs and output variables
Full size table

This obtained matrix is used in the proposed FCM method as an initial matrix. Subsequently, an initial matrix was trained by applying hybrid NHL-DE algorithms to reduce the expert opinion and weighting errors dependency. Dynamic FCM solved this matrix and resulted in concept weight as a final point. The weighting outcomes by the proposed FCM model based on the hybrid NHL-DE algorithms are shown in Fig. 8.

Fig. 8
figure 8

Weighting outcomes by the proposed FCM model

Full size image

The weighting effective parameters using the proposed FCM provides more realistic results than the weighting method based on random numbers in a usual ANN. As illustrated in Fig. 8, the trained FCM shows weights among intervals [0, 1] and the sensitivity level of each parameter on the target node, which can be interpreted. According to the concept of cause-and-effect, burden and charge per delay with weights of 0.707 and 0.648 denote the highest sensitivity and effect weights on flyrock distance.

The weightings of effective parameters are imported into an ANN architecture. Figure 9 shows the employed weights in the MLP process. Ten trained ACWNNsR models were achieved by means of the trial-and-error method and evaluated using R2, RMSE, and VAF, to select the best architecture. The obtained results are reported in Table 8. The ACWNNsR7 is the best structure that can be used to predict flyrock distance accurately.

Fig. 9
figure 9

Designing the ACWNNsR architecture with causal-and-effect relationships

Full size image
Table 8 Performance indices for ACWNNsR models
Full size table

5 Result and Discussion

The current paper developed the MLP, BRNN, and ACWNNsR models to estimate flyrock distance in surface mines. The comparative analyses related to calculating statistical indices (R2, RMSE, and VAF) are tabulated in Table 9. The results show that the ACWNNsR model (with R2 (0.996,0.991), RMSE (1.404,2.535), and VAF (99.867, 99.136)) performed better in estimating blast-induced flyrock distance compared to the BRNN model with R2 (0.949,0.921), RMSE (4.605, 4.350), and VAF (94.226, 92.267) and also MLP model with R2 (0.932, 0.909), RMSE (5.000, 6.618), and VAF (93.849, 92.188). Furthermore, measured flyrock compared to predicted values by MLP, BRNN, and ACWNNsR models for 416 blasting rounds is plotted in Figs. 10, 11, 12, respectively. The correlation of the ACWNNsR model shows a significant relationship between the actual and estimated flyrock. Figure 13 shows the error in flyrock distance predicted by the ACWNNsR, BRNN, and MLP models for all 83 blasting events (testing dataset), comparing them with the recorded flyrock. These results show that the ACWNNsR model can predict the flyrock diatance more accurately than the MLP and BRNN models in training and testing datasets.

Table 9 Performance indexes for the three developed models
Full size table
Fig. 10
figure 10

Correlations of flyrock estimated by modeling MLP with actual values

Full size image
Fig. 11
figure 11

Correlations of flyrock estimated by modeling BRNN with actual values

Full size image
Fig. 12
figure 12

Correlations of flyrock estimated by modeling ACWNNsR with actual values

Full size image
Fig. 13
figure 13

Errors of flyrock prediction for testing datasets using MLP, BRNN, and ACWNNsR

Full size image

6 Sensitivity Analysis

The effectiveness and relative significance of the controllable parameters burden (B), stemming (St), spacing (S), powder factor (Pf), and charge per delay (CD) on the flyrock distance was evaluated using a sensitivity analysis. The cosine amplitude method (CAM) (Jong and Lee 2004) and partial derivatives (PaD) method (Gevrey et al. 2003) were used in this sensitivity analysis as shown in Eqs. (26) and (27). The sensitivity analysis results are shown in Fig. 14, which shows the spacing as the most influential parameter on flyrock distance, whereas the charge per delay indicates minor importance.

$$r_{ij} = \frac{{\sum\nolimits_{k = 1}^{m} {x_{ik} \cdot x_{jk} } }}{{\sqrt {\left( {\sum\nolimits_{k = 1}^{m} {x_{ik}^{2} } } \right) \cdot \left( {\sum\nolimits_{k = 1}^{m} {x_{jk}^{2} } } \right)} }}$$
(26)
$$E = \frac{{{\text{SSD}}_{i} }}{{\sum\nolimits_{i} {{\text{SSD}}_{i} } }},\,\,\,{\text{SSD}}_{i} = \sum\limits_{p} {\left( {\frac{{\partial O_{k}^{p} }}{{\partial O_{i}^{p} }}} \right)}^{2} .$$
(27)
Fig. 14
figure 14

The importance of effective parameters on flyrock distance

Full size image

In which yik and yjk are the input and output parameters. m denotes the number of datasets, E is elements of data pairs participation of ith variable, \(O_{k}^{p}\) is output values for pattern P, \(O_{i}^{p}\) indicates input values for pattern P, and SSDi the sum of the squares of the partial derivatives. Notably, the highest E and rij value demonstrates the most influential inputs.

7 Conclusion

A new hybrid model based on the integration of multilayer perceptron neural networks (MLPNN) and fuzzy cognitive map (FCM) with the reliability of the Z-number concept was developed to predict flyrock distance induced by blasting operations. The developed model called artificial causality-weighted neural networks based on reliability (ACWNNsR) uses five effective, controllable parameters, including burden, stemming, spacing, powder factor, and charge per delay, to predict the flyrock distance. Performance indices of RMSE, VAF, and R2 were determined to estimate the superiority of the predictive models. The ACWNNsR model resulted in R2 of (0.996, 0.991), RMSE of (1.404, 2.535), and VAF of (99.867, 99.136) for train and test, respectively. The higher R2 and VAF values and lower RMSE achieved by the ACWNNsR model than the conventional ANN and BRNN models show its success in providing a more accurate prediction flyrock distance. Notably, the proposed approach resulted in 62% and 42% improvement in the RMSE of the testing model in comparison to the MLP and BRNN models.

The effectiveness and relative significance of the effective parameters on flyrock distance was evaluated using a sensitivity analysis by Cosine Amplitude Method (CAM) and PaD method. The sensitivity analysis results showed the spacing has the most significant impact on flyrock distance, while charge per delay is the least important.

The presented approach is recommended for flyrock distance prediction in surface mines where buildings are close to the blasting site. Since the datasets used in this study were specific to the Anguran mine, applying the developed model in other projects would demand adjustments based on the employed blasting and mining operations. In addition, some limitations existed in the scope of this study that should be removed in future studies to increase the accuracy of the prediction. The applied dataset should be more comprehensive by including more controllable blasting parameters. The uncontrollable blasting parameters such as geomechanical properties of rock masses could also be monitored, measured, and involved for more accurate and reliable predictions.