1 Introduction

Borehole breakouts, defined as diametrically opposed elongations of an initially circular wellbore along a preferred direction, resulting from stress-induced rock failure, have been studied for over 3 decades. This phenomenon is often encountered in mine tunnels and petroleum wellbores, in areas of high in situ stress. Observations of breakouts were reported by Leeman (1964) at a gold mine in South Africa, and also by Carr (1974), who observed consistency between the breakout orientation with the least in situ stress in Yucca Flat, Nevada. Later, Bell and Gough (1979) observed a strong correlation between breakout orientation and the direction of the minimum horizontal stress in Alberta, Canada. To substantiate their observation, Gough and Bell (1982) proposed a breakout model using the Mohr–Coulomb failure criterion and the Kirsch equations. Since then, numerous researchers have verified that the concentrated stress around the wellbore is responsible for the development of the breakout, and that the orientation of the breakout is parallel to the least principal stress direction. This phenomenon has attracted practitioners and researchers to try to use breakout geometry as a tool to estimate in situ stress orientation and magnitude, due to the abundant availability of such inexpensive datasets.

Extensive efforts have been made to verify the relation between breakout formations with in situ stress and whether, in an inverse manner, in situ stress can be inferred from the breakout geometry. For instance, Plumb and Hickman (1985) concluded that the direction of the minimum principal stress can be inferred from the elongation detected by the dipmeter and borehole televiewer. Independently, Zoback et al. (1985) also used an ultrasonic borehole televiewer, and concluded that the failure around the wellbore is strongly controlled by the magnitude and orientation of the in situ stress field. Plumb (1989) later concluded that breakout may be used to infer the relative magnitude and orientation of the near-wellbore stress. Similarly, Mastin (1988) studied the rotation of breakout orientation in deviated wellbores, which depends on the relative magnitude of the near-wellbore stress. At the Underground Research Laboratory (URL) in Canada, Read et al. (1995) observed non-symmetrical breakouts in a borehole that was not aligned with the principal axis. In conjunction with numerical modeling and microseismic monitoring, they concluded that the asymmetric breakout appearance is caused by the influence of an anti-plane shear stress.

Several attempts have been made to understand the mechanism of breakout formation through laboratory experiments. Lee and Haimson (1993) used cubical specimens of Lac du Bonnet granite to investigate the micro-mechanism of a ‘dog-eared’ shaped breakout. They observed a progressive detachment of thin long flakes due to extensile cracking in two zones aligned with the minimum principal stress direction. A comprehensive review of breakout micromechanisms in a variety of rock types, e.g. granites, limestones, and sandstones, was given by Haimson (2007). He concluded that, depending on the rock type, the microcracks leading to breakout could fail in tensile or shear openings, extending inter- or intra-granularly, producing a dog-eared shape of breakout. An exception was a high-porosity quartz-rich sandstone, which develops a fracture-like breakout due to grain debonding and compaction aligned with the direction of least principal stress.

Several researchers have also attempted to model breakout development using numerical and analytical modeling. The first breakout model was proposed by Gough and Bell (1982), based on the hypothesis that shear fractures occur at the points of the highest tangential stress. They adopted the Mohr–Coulomb failure criterion to predict the two conjugate shear fractures tangent to the borehole wall. Their model, however, is independent of the in situ stress magnitude, and only depends on the internal friction angle of the rocks. The model was later improved by Zoback et al. (1985) by calculating the stress around the borehole using the Kirsch equations, and assessing the zone within which shear fractures occur, according to the Mohr–Coulomb failure criterion. Although their work was an improvement from that of Gough and Bell (1982), by accounting for the stress, their predicted breakout geometry is rather shallow and flat-bottomed; it seems that they were only calculating the initial breakout geometry.

Ever since, numerous researchers have proposed numerical models for a successive breakout initiation, growth, and stabilization. To capture the episodic breakout development, it is necessary to compute the stress state to assess its stability at each episode. Such studies have been carried out by Zheng et al. (1989), who used the boundary element method to model the progressive spalling of thin slabs near the hole wall by extensile splitting; see also Ewy et al. (1987) and Zheng et al. (1988). Herrick and Haimson (1994) compared breakout geometries obtained from prismatic specimens of Alabama limestone under a true-triaxial stress state with numerical simulations considering the scaling effect due to the hole size. Their numerical model was used to simulate a vertically drilled borehole under constant in situ stress based on the plane strain linear elastic boundary element method. The extent of the breakout zone at each step was obtained by comparing the stress around the wellbore with the Mohr–Coulomb failure criterion. The experimental data of Herrick and Haimson (1994) are used in the present paper for verification purposes. Du and Kemeny (1993) considered heterogeneous and discontinuous rocks containing a random distribution of microcracks to simulate breakout formation as a result of the interaction and coalescence of microcracks in Westerly granite. Duan and Kwok (2016) studied the effect of elastic and strength anisotropy on the initiation, propagation, and pattern of borehole breakout in shale, using discrete element modeling. Sahara et al. (2017) modeled the evolution and stabilization of borehole breakouts using continuum damage mechanics (CDM) by considering the changes of the elastic moduli as a result of failure around the hole.

Zhang et al. (2018) numerically modeled the successive spalling leading to a stable breakout, and then inverted the knowledge of the final geometry to obtain the in situ stress. They concluded that the in situ stress can be effectively obtained from breakout geometry. Later, Zhang et al. (2019) also investigated the potential misinterpretation of breakdown pressure from hydraulic fracturing in a borehole with breakout, and concluded that the difference with that of a perfectly circular wellbore could be as large as 82%. Recently, Tan et al. (2019) developed a workflow, which they referred to as Failure Geometry Stabilization (FGS), to simulate the drilling and breakout development, progression, and stabilization of shale rocks. Their method was validated using polyaxial block tests on Wellington shale and Pierre II shale. Although numerical models such as finite-elements and boundary-elements have been implemented extensively for such a problem, analytical solutions can provide the advantage to allow for a parametric investigation. Recently, Gerolymatou (2019) proposed a method to analytically model breakout evolution in isotropic materials using conformal mapping. The same method was then used by Gerolymatou and Petalas (2020) to estimate the magnitude of in situ stress based on the width and depth of brittle borehole breakouts. A comprehensive review of the mechanisms and experimental and modeling results of breakouts was provided by Germanovich and Dyskin (2000).

The present paper discusses the episodic development of a stable breakout, and attempts to find a relationship between in situ stress and breakout geometry. Although the failure process discussed here reflects an evolution of a successive process, this evolution cannot be associated with an actual time scale clock. The change in each successive process is only related to the change in the hole’s cross-sectional shape from circular to non-circular. As the modeling of the breakout development requires a method that allows the stress components to be computed around non-circular holes and irregular hole geometries, the semi-analytical solution procedure developed by Setiawan and Zimmerman (2020) is used. With this method, it is possible to track the development of the breakout and examine the stability of the breakout geometry at each episode and, hence, its development can be tracked. Finally, the possibility is examined of using the breakout geometry, along with the Mogi–Coulomb or Mohr–Coulomb failure functions, to estimate the minimum in situ stress, and some remaining difficulties are discussed.

2 Stresses Around an Arbitrarily-Shaped Hole in Isotropic or Anisotropic Rocks

Recently, Setiawan and Zimmerman (2020) presented a semi-analytical method to calculate the stress components around an arbitrary hole contour in an isotropic or anisotropic medium, based on Melentiev’s graphical conformal mapping procedure and Muskhelishvili’s complex stress potentials method. The solution is essentially exact, and in closed-form, in the sense that the stresses can be explicitly expressed in terms of the mapping coefficients and parameters that depend only on the elastic moduli of the materials. The detailed derivation of the method is available in Setiawan and Zimmerman (2020), and only a few key equations will be shown here.

The procedure ensures that the unit circle is conformally mapped onto a simply connected region by an analytic function of the form

$$z = \omega (\xi ) = \sum\limits_{k = 0}^{N} {m_{k} } \xi^{1 - k} ,$$
(1)

in which \(z = x + iy\) is the physical coordinate of the actual hole boundary, \(\xi\) is the coordinate in a plane that contains a circular hole, \(\omega (\xi )\) is the function that maps the region outside this unit circle in the \(\xi\)-plane into the region outside the physical hole in the z-plane, and \(m_{k} = \alpha_{k} + i\beta_{k}\) are the complex conformal mapping coefficients. An iterative process is required to obtain the most appropriate values of \(m_{k}\) to conformally map the boundary of the physical hole in the z-plane into a unit circle in the \(\xi\)-plane, according to Eq. (1). In principle, an infinite number of terms may be needed, but in practice the summation can be truncated at about 30 terms.

To facilitate the stress computation around an arbitrary cross-sectional hole in an anisotropic material using Melentiev’s conformal mapping and complex stress potentials, the two stress potentials \(\phi_{0} (\xi )\) and \(\psi_{0} (\xi )\) have been derived and can be expressed as (Setiawan and Zimmerman 2020):

$$\phi_{0} (\xi ) = A_{1} \alpha_{0} \xi^{ - 1} + A_{2} \beta_{0} \xi^{ - 1} + A_{3} \sum\limits_{k = 2}^{N} {\alpha_{k} } \xi^{1 - k} + A_{4} \sum\limits_{k = 2}^{N} {\beta_{k} } \xi^{1 - k} ,$$
(2)
$$\psi_{0} (\xi ) = A_{5} \alpha_{0} \xi^{ - 1} + A_{6} \beta_{0} \xi^{ - 1} + A_{7} \sum\limits_{k = 2}^{N} {\alpha_{k} } \xi^{1 - k} + A_{8} \sum\limits_{k = 2}^{N} {\beta_{k} } \xi^{1 - k} ,$$
(3)

where the \(A_{i}\) (i = 1, 2, …, 8) are related to the elastic properties of the rock, and the far-field stresses. The explicit expressions for the \(A_{i}\) are given by Setiawan and Zimmerman (2020).

The in-plane stress components can be obtained from the following equations:

$$\sigma_{xx} = \sigma_{xx}^{\infty } + 2{\text{Re}} [\mu_{1}^{2} \phi^{\prime}_{0} (z_{1} ) + \mu_{2}^{2} \psi^{\prime}_{0} (z_{2} )],$$
(4)
$$\sigma_{yy} = \sigma_{yy}^{\infty } + 2{\text{Re}} [\phi^{\prime}_{0} (z_{1} ) + \psi^{\prime}_{0} (z_{2} )],$$
(5)
$$\tau_{xy} = \tau_{xy}^{\infty } - 2{\text{Re}} [\mu_{1} \phi^{\prime}_{0} (z_{1} ) + \mu_{2} \psi^{\prime}_{0} (z_{2} )],$$
(6)

in which \(\phi^{\prime}_{0} (z_{1} )\) and \(\psi^{\prime}_{0} (z_{2} )\) are the derivatives of the two potentials, which can be obtained from Eqs. (1) to (3) as follows:

$$\phi^{\prime}_{0} (z_{1} ) = \frac{{{\text{d}}\phi_{0} (\xi )}}{{{\text{d}}\xi }}\frac{{{\text{d}}\xi }}{{{\text{d}}z_{1} }} = \frac{{\phi^{\prime}_{0} (\xi )}}{{\omega^{\prime}_{1} (\xi )}},$$
(7)
$$\psi^{\prime}_{0} (z_{1} ) = \frac{{{\text{d}}\psi_{0} (\xi )}}{{{\text{d}}\xi }}\frac{{{\text{d}}\xi }}{{{\text{d}}z_{2} }} = \frac{{\psi^{\prime}_{0} (\xi )}}{{\omega^{\prime}_{2} (\xi )}}.$$
(8)

The material properties of the rock are represented by the roots of the material characteristic equation, \(\mu_{1}\) and \(\mu_{2}\), whereas \(\{ \sigma_{xx}^{\infty } ,\sigma_{yy}^{\infty } ,\tau_{xy}^{\infty } \}\) are the far-field stresses. The tangential and radial stress components can be calculated using the following transformation:

$$\sigma_{\theta \theta } - \sigma_{rr} + 2\tau_{r\theta } = (\sigma_{xx} - \sigma_{yy} + 2\tau_{xy} )e^{2i\delta } ,$$
(9)
$$\sigma_{\theta \theta } + \sigma_{rr} = \sigma_{xx} + \sigma_{yy} ,$$
(10)

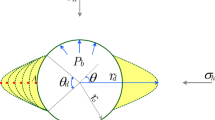
where \(\delta\) is the rotational angle made by the radial axis r with respect to the x-axis (Fig. 1).

Fig. 1
figure 1

Conformal mapping of a wellbore with breakouts in the z plane, into a unit circle in the ξ plane

Full size image

The principle of superposition can be used for cases of biaxial tension or compression. Setiawan and Zimmerman (2020) validated the method against numerous analytical and numerical results, using various hole shapes, including elliptical, rectangular, oval, and triangular, in both isotropic and anisotropic materials. The advantage of this method is that it only requires knowledge of the coordinates of the hole, the elastic moduli of the material, and the magnitude and direction of the far-field stresses. This method is, therefore, suitable for the purpose of tracking the evolution of wellbore breakouts, as long as the coordinates of the hole contour are known (or calculated) at each step. However, in principle, the stresses could be computed by a boundary element or finite element code, if the simulations were shown to be sufficiently accurate.

3 Modeling an Episodic Borehole Breakout

To model the successive formation of the breakout, it is necessary for the stress components to be computed as the boundary changes at each episode. In the following examples, the initial hole is assumed to be a circle in a linearly elastic, homogeneous, and isotropic infinite plate. The body is subjected to a far-field in situ stress state \(\{ \sigma_{{\text{v}}} ,\sigma_{{\text{H}}} ,\sigma_{{\text{h}}} \} = \{ 4100,8500,3050\} {\text{ psi}}\) (Fig. 2a). The rock is assumed to have a compressive strength of \(C_{o}\) = 16,800 psi, and a friction angle of \(\varphi = 20^{ \circ }\).

Fig. 2
figure 2

a Problem definition, and b the episodic breakout development of a rock with UCS = 16,800 psi and \(\varphi\)\(= 20^\circ\), under a stress state of \(\{ \sigma_{{\text{v}}} ,\sigma_{{\text{H}}} ,\sigma_{{\text{h}}} \} = \{ 4100,8500,3050\}\) \(\mathrm{psi}.\)

Full size image

To initiate the simulation, the stress components around the circular wellbore are calculated using Eqs. (4–10). The in situ stresses \(\{ \sigma_{{\text{v}}} ,\sigma_{{\text{H}}} ,\sigma_{{\text{h}}} \}\) are applied instantaneously, i.e. their magnitudes are not ramped up during the simulation. The rock strength parameter is kept constant throughout the simulation—in contrast the approach of Herrick and Haimson (1994), who applied an evolving scaling factor to their rock strength, as the breakout progressed. The stress components, i.e. the tangential stress, radial stress, and axial stress calculated at each point around the wellbore, are then inserted into the failure criterion, e.g. Mohr–Coulomb or Mogi–Coulomb, to examine the stability of the surrounding rock. The zone within which the stress state satisfies the failure criterion is then removed, and the new outline of the cross-sectional shape is captured. An iterative Melentiev conformal mapping procedure is then performed to determine the appropriate conformal mapping coefficients for the new shape, after which the stresses are again computed. This procedure is repeated until the latest incremental breakout depth is insignificant compared with the preceding step; in this work, this convergence criterion is taken to be 10–5. At this point, the breakout is said to have reached its stable state. The procedure is illustrated in Fig. 3.

Fig. 3
figure 3

Modeling of episodic development of borehole breakouts

Full size image

At each step, the geometry of the forming breakout, i.e. the width of the breakout, \(\theta_{{{\text{bo}}}}\), and the tip of the breakout, \(r_{{{\text{bo}}}}\), are captured, as shown in Fig. 2b. The relationship between the final breakout geometry and the in situ stress can then be examined.

The procedure developed in this work is capable of handling any stress-based failure criterion. The two failure criteria that have been used in the present work are the classic Mohr–Coulomb criterion, and its extension into true-triaxial stress space, which is known as the Mogi–Coulomb criterion (Al-Ajmi and Zimmerman 2005). The Mohr–Coulomb states that when the shear stress \(\tau\) on a plane exceeds the shear strength of the rock, as represented by its strength parameters cohesion, (\(S_{o}\)), and friction angle, (\(\varphi\)), failure will occur along that plane. According to the criterion, the maximum shear stress that the rock can withstand is linearly correlated with the normal stress \(\sigma_{n}\) acting on the plane. This can be expressed mathematically as

$$\tau = S_{o} + \mu \sigma_{n} ,$$
(11)

or, in terms of principal stresses (Jaeger et al. 2007),

$$\sigma_{1} = C_{o} + \sigma_{3} \tan^{2} \left( {\frac{\pi }{4} + \frac{\varphi }{2}} \right).$$
(12)

To account for the effect of intermediate principal stress, \(\sigma_{2}\), Al-Ajmi and Zimmerman (2005) proposed the Mogi–Coulomb criterion, which they showed to reduce to the Mohr–Coulomb criterion if two of the three principal stresses are equal, but which is more accurate than Mohr–Coulomb if the stress state is fully triaxial. An advantage of the Mogi–Coulomb criterion is that the strength parameters that appear in it can be obtained from traditional triaxial \((\sigma_{2} = \sigma_{3} )\) datasets. The Mogi–Coulomb criterion relates the critical octahedral shear stress, \(\tau_{{{\text{oct}}}}\), with the effective mean stress, \(\sigma_{m,2}\):

$$\tau_{{{\text{oct}}}} = a + b\sigma_{m,2} ,$$
(13)

where

$$\sigma_{m,2} = \frac{1}{2}(\sigma_{1} + \sigma_{3} ),$$
(14)
$$\tau_{{{\text{oct}}}} = \frac{1}{3}\sqrt {(\sigma_{1} - \sigma_{2} )^{2} + (\sigma_{2} - \sigma_{3} )^{2} + (\sigma_{3} - \sigma_{1} )^{2} } .$$
(15)

The parameters a and b can be obtained directly from the Coulomb strength parameters as follows (Al-Ajmi and Zimmerman, 2005):

$$a = \frac{2\sqrt 2 }{3}S_{0} \cos \varphi , \, b = \frac{2\sqrt 2 }{3}\sin \varphi$$
(16)

4 Examples and Comparison to Experimental Data

4.1 Comparison with Measurements of Herrick and Haimson (1994)

The parameters used in this paper are taken from Herrick and Haimson (1994), who conducted a breakout initiation experiment on Alabama limestone, under true-triaxial stress conditions; comparison with their experimental results will also be presented here. The compressive strength of the Alabama limestone was reported as 16,800 psi, after taking into account the scale effect of the hole (discussed in more detail in the next paragraph), and the friction angle was reported as 18°(± 2°). In the present work, \(\varphi\) was taken to be 20°, to honour the reported value, while acknowledging that a somewhat higher value might be more plausible. The magnitude of the vertical stress, \(\sigma_{{\text{v}}}\), was 1015 psi higher than the minimum horizontal stress, \(\sigma_{{\text{h}}}\). The experimental result of Herrick and Haimson (1994) resembling the “cusp” or “dog-eared” shaped of the breakout geometry, as shown in Fig. 4a, was created under a stress state of \(\sigma_{{\text{h}}} = 4060\) psi, and \(\sigma_{{\text{H}}}\) = 12,050 psi.

Fig. 4
figure 4

a The experimental breakout shape observed by Herrick and Haimson (1994); the modeled breakout geometry using the b Mohr–Coulomb and c Mogi–Coulomb failure criteria, respectively

Full size image

The “scale effect” observed by Herrick and Haimson (1994) has also been noted by other researchers; see, for example, Martin (1997). Herrick and Haimson reported the breakout stress at the borehole wall, for a set of prismatic specimens containing holes of different radii. They found that as the radius increases, the breakout stress converges (roughly) to the UCS that would be measured on a solid cylinder. The compressive strength of 16,800 psi corresponds to a borehole radius of 1.1 cm, as was used in their breakout geometry tests. Attempts to explain and model this hole effect include the recent work by Lin et al. (2020). Nevertheless, it is reassuring that the size effect seems to essentially disappear for borehole diameters greater than about 10 cm, and so this effect may not be of much relevance in the field.

The final breakout shape obtained using the semi-analytical method used in this paper is shown in Fig. 4b, when the Mohr–Coulomb failure criterion is considered. The breakout tip extends deep into the formation to a stable position at \(r_{{{\text{bo}}}} /r_{{\text{w}}}\) = 1.84, with a breakout width \(\theta_{{{\text{bo}}}}\) = 88°. If the Mogi–Coulomb failure criterion is used, the final breakout geometry is relatively narrower and shallower: \(r_{{{\text{bo}}}} /r_{{\text{w}}}\) = 1.54 and \(\theta_{{{\text{bo}}}}\) = 76°, as shown in Fig. 4c. The strengthening effect introduced by the intermediate principal stress in the Mogi–Coulomb failure criterion is responsible for the less severe breakout geometry. In Fig. 4, the final breakout geometries of the laboratory experiment and numerical modeling are deep and sharp, with pointed edges resembling “cusp” or “dog-eared” shapes. The azimuth of the breakout propagation is also parallel to the direction of the least principal stress.

4.2 Evolution of Wellbore Shape and the Stress Around the Hole

Several authors, including Zheng et al. (1989), Zoback et al. (1985), Herrick and Haimson (1994), and Zoback et al. (2003), observed that the width of the breakout remains constant throughout its initiation, progression, and stabilization. The breakout width of each growth episode is relatively smaller than that of the preceding steps, leading to an overall sharp, pointed-end breakout (Figs. 4b, c). Shown in Fig. 5 is the evolution of the near-wellbore stress during breakout development of the same rock properties under a stress state of \(\{ \sigma_{{\text{v}}} ,\sigma_{{\text{H}}} ,\sigma_{{\text{h}}} \} = \{ 4060,7500,3045\} \, \;{\text{psi}}\). Although the stress state in this example is different than the one used in Fig. 4, the stress regime remains the same, i.e. \(\sigma_{{\text{H}}} > \sigma_{{\text{v}}} > \sigma_{{\text{h}}}\). Thus, the final breakout width from this example is not as wide as that shown in Fig. 4, and the breakout depth is also shallower; but the overall breakout geometry still resemble a “dog-eared” shape.

Fig. 5
figure 5

An episodic breakout development showing the major principal stress around the breakout normalized by the vertical in situ stress (\(\sigma_{{\text{v}}}\)). The far-field stress state is \(\{ \sigma_{{\text{v}}} ,\sigma_{{\text{H}}} ,\sigma_{{\text{h}}} \} = \{ 4060,7500,3045\}\) psi

Full size image

The normalized major principal stress, (\(\sigma_{1} /\sigma_{{\text{v}}}\)), around the failed zone increases as the breakout develops. A detailed examination suggests that, as the breakout tip sharpens and deepens, the stress concentration becomes more localized around the tip with increasing magnitude. In the case considered here, the major principal stress is more than ten times the vertical stress near the tip of the final breakout geometry.

There is a strong indication that the stress relaxation around the flank of the breakout, particularly near the intersection of the failing zone with the circular hole boundary, is responsible for the relatively constant breakout width throughout the process. As shown in Fig. 6, at the flank of the breakout during this intermediate breakout formation, particularly near the intersection of the initial hole with the boundary of the breakouts, the stress becomes less compressive. Around the tip of the progressing breakout, the major principal stress magnitude is about seven-times of the applied vertical in situ stress, \(\sigma_{{\text{v}}}\), whereas, around the relaxation zone, the magnitude is only about 2.5-times the applied in situ vertical stress, and it is enclosed by zones of relatively higher stress. Consequently, the reduction of the stress concentration causes the Mohr circle to shrink and, hence, move away from the failure line, which leads to a more stable structure around the flank. The point indicated by the black circle in Fig. 6 corresponds to the purple Mohr circle in the inset at the top right of the figure. The direct consequences of these phenomena are: (1) although the shear failure propensity near the tip of the breakout increases, the affected area becomes smaller, and (2) the stress relaxation around the flank improves the stability of the structure, hence, responsible for the relatively constant width as the breakout develops. This observation is consistent with the observations of Zheng et al. (1989), who concluded that breakout will not widen, but instead will deepen into the formation.

Fig. 6
figure 6

Main figure: Major principal stress (\(\sigma_{1}\)) around the breakout, normalized by the vertical in situ stress (\(\sigma_{{\text{v}}}\)). Inset: Large black Mohr circle represents the stress state at location × , where the rock is in a state of failure. Small purple Mohr circle represents the stress state at location Ο, where the rock is now in a stable state

Full size image

It is now obvious that breakout development has a strong dependence on the stress state around the hole. Therefore, it is tempting to investigate the relation with the magnitude of the in situ stress. In practice, estimating the magnitude of the minimum horizontal stress, \(\sigma_{{\text{h}}}\), can be achieved from a micro-fracturing test or extended leak-off test (see, for example, White et al. (2002) and Addis et al. (1998)) and the task is arguably more straightforward than estimating the magnitude of the maximum horizontal stress, \(\sigma_{{\text{H}}}\). Many efforts have been directed towards finding the relationship between maximum horizontal stress and breakout geometry, particularly its width.

5 Estimating the In Situ Stress from Breakout Geometry

Perhaps the most interesting question to ask at this stage is whether or not the breakout geometry can be used to infer the magnitude of the in situ maximum horizontal stress, \(\sigma_{{\text{H}}}\). The data set of Herrick and Haimson (1994) will now be used to quantitatively test this possibility.

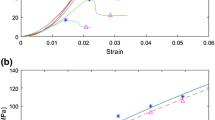
Simulations using the semi-analytical method proposed by Setiawan and Zimmerman (2020) have been conducted for three different values of the minimum horizontal stress: \(\sigma_{{\text{h}}}\) = 3045, 4060, 5075 psi, in each case assuming the same rock strength properties. The vertical stress, \(\sigma_{{\text{v}}}\), was set to be 1015 psi higher than the minimum horizontal stress, \(\sigma_{{\text{h}}}\), while the maximum horizontal stress, \(\sigma_{{\text{H}}}\), was varied over a wide range, leading to a borehole breakout for the given rock properties. The correlation between the breakout width \(\theta_{{{\text{bo}}}}\) and breakout depth \(r_{{{\text{bo}}}}\) is shown in Fig. 7, for two different failure criteria. The experimental results of Herrick and Haimson (1994) are plotted as the black squares in the same figure.

Fig. 7
figure 7

The correlation between the breakout width \((\theta_{{{\text{bo}}}} )\) and breakout depth \((r_{{{\text{bo}}}} )\). The breakout depth is normalized against the initial borehole radius, \(r_{{\text{w}}}\); the breakout width is shown in degrees. The experimental results of Herrick and Haimson (1994) are shown as black squares

Full size image

As shown in Fig. 7, the model predicts the correct trend, but not quite the right slope, compared with the experimental results of Herrick and Haimson (1994). Figure 7 is useful for a consistency check of the method proposed in this research. A more interesting plot for in situ stress estimation is the relation between breakout geometry and in situ stress. For the case considered here, the correlation of maximum horizontal stress with breakout depth and width from the numerical simulation is encouraging, as shown in Fig. 8a, b, respectively. As seen, however, the experimental data are more scattered than the numerical simulations. The slight scatter of the numerical simulations is inevitable, and is related to the conformal mapping procedure that involves numerical calculations to approximate the actual shape of the hole boundary.

Fig. 8
figure 8

Relationship a between maximum horizontal stress and breakout depth \((r_{{{\text{bo}}}} )\), normalized against the initial borehole radius, \(r_{{\text{w}}}\), and b between maximum horizontal stress and breakout width \((\theta_{{{\text{bo}}}} )\), for all minimum horizontal stress variations. The experimental results from Herrick and Haimson (1994) are also shown, as black squares

Full size image

The following exercise can now be done to investigate the possibility of estimating \(\sigma_{{\text{H}}}\) from the observed breakout geometry. Consider the left-most point from the Herrick and Haimson (1994) experimental data in Fig. 8a. This data point corresponds to a normalized breakout depth of \(r_{{{\text{bo}}}} /r_{{\text{w}}}\) = 1.2, with an actual maximum horizontal stress of \(\sigma_{{\text{H}}}\) = 7240 psi. If this data point is fitted to the best-fit trendline of the actual experimental data (black line), the estimated maximum horizontal stress \(\sigma_{{\text{H}}}\) would be 8654 psi; this estimate corresponds to an error of 16%. If the same data point is now fitted to the Mohr–Coulomb (blue) and Mogi–Coulomb (red) trendlines, the estimated values are 6635 psi (9.1% error) and 8430 psi (14.1% error), respectively. This exercise can be repeated for all the data points from Herrick and Haimson, so that the overall RMS error can be estimated. The RMS error of the entire experimental data set with respect to the actual best-fit trendline in Fig. 8a is 1059 psi, while the RMS error of the experimental data, as compared to the Mohr–Coulomb and Mogi–Coulomb trendlines, are 1939 psi and 1480 psi, respectively. A lower RMS error is produced by the Mogi–Coulomb trendline than by Mohr–Coulomb, as one can also visually see from Fig. 8a. Note that using the trendline of the actual data to estimate \(\sigma_{{\text{H}}}\) gives errors that are more than half as large as those that occur using the two proposed inversion procedures (Mohr–Coulomb and Mogi–Coulomb).

The same exercise can also be done for breakout width, as shown in Fig. 8b. The RMS error for the entire dataset based on the actual trendline (black) is 1068 psi. The Mohr–Coulomb and Mogi–Coulomb trendlines will give an RMS error of 1264 psi and 1605 psi, respectively. Therefore, for the case of breakout width, it seems that Mohr–Coulomb produces less error than Mogi–Coulomb. Hence, although it is known that Mogi–Coulomb provides a better fit to true-triaxial data obtained on solid cylinders, it is not clear that Mogi–Coulomb is generally more accurate than Mohr–Coulomb, for this borehole breakout data set.

Now, it is tempting, and seems logical, to expect that a much better estimation, i.e. less RMS error, can be obtained using the average values of the predicted stress using breakout depth and breakout width. For each data point, if one then takes the average value of the predicted maximum horizontal stress from breakout width and breakout depth, then the RMS error of the actual trendline is 1053 psi. The RMS errors of the Mohr–Coulomb and Mogi–Coulomb trendlines using this hybrid method are 1536 psi and 1362 psi, respectively. The errors incurred by estimating \(\sigma_{{\text{H}}}\) using the methodology described above are, therefore, not much larger than the errors that would be incurred using the actual trendline derived from the data themselves. It can, therefore, be concluded that most of the “error” of the proposed method is actually due to the inherent variability from one sample to another, and to the experimental uncertainties in measuring the breakout width and depth, and is, therefore, unavoidable.

If the same results are grouped according to the three levels of minimum horizontal stress \((\sigma_{{\text{h}}} )\) considered here, a better relationship between breakout width and depth and maximum horizontal stress is obtained (Fig. 9). Again, although both the Mohr–Coulomb and Mogi–Coulomb failure criterion led to the correct trends, it is not possible to draw a definitive conclusion as to their relative merits for this borehole breakout problem.

Fig. 9
figure 9

Correlation a–c between the maximum horizontal stress, \((\sigma_{{\text{H}}} )\), and breakout depth, \((r_{{{\text{bo}}}} )\), normalized against the initial borehole radius, \(r_{{\text{w}}}\), and d–f between the maximum horizontal stress, \((\sigma_{{\text{H}}} )\), and breakout width, \((\theta_{{{\text{bo}}}} )\), at several minimum horizontal stress magnitudes

Full size image

6 Conclusion and Discussion

Episodic breakout initiation, progression, and stabilization have been modeled using the semi-analytical method based on Melentiev’s graphical conformal mapping and Kolosov–Muskhelishvili complex stress potentials. The method allows the geometry stabilization and the stress evolution throughout the process to be tracked. The simulation performed in the current study produced a cusp or dog-eared shaped breakout, as observed by several researchers. The orientation of the breakout propagation is consistent with the direction of the least principal stress. It is observed that the stress at the flank of the breakout, particularly near the intersection of the initial hole with the boundary of the breakouts, becomes less compressive as the breakout progresses. This stress relaxation around the flank improves the stability of the surrounding rock, and hence is responsible for the relatively constant width as the breakout deepens. Moreover, although the shear failure propensity near the tip of the breakout increases, the affected area becomes smaller as the breakout tip sharpens and deepens; the stress concentration becomes more localized around the tip with increasing magnitude.

The proposed modeling method was then used to estimate the maximum horizontal stress, based on knowledge of the vertical stress, the minimum horizontal stress, the Coulomb strength parameters, and the observed width and depth of the breakouts. When applied to the laboratory data set of Herrick and Haimson (1994), the RMS error in the estimates of \(\sigma_{{\text{H}}}\) based on the Mohr–Coulomb and Mogi–Coulomb failure criteria were 1536 psi and 1362 psi, respectively. These errors were not much larger than the errors that would be incurred using the trendline derived from the actual data themselves, which was 1053 psi. This latter error reflects natural sample-to-sample variability, as well as errors in estimating the breakout depth and width, and, therefore, sets a lower bound on the error that could be expected from any modeling-based method. Clearly, however, the method would need to be tested against a much larger data set before its accuracy could be confirmed.

Despite the fact that the results are encouraging, it is important to note that the simulations discussed above are based on the assumption of a constant in situ stress, but ignore other factors that might also influence the geometry of breakouts, such as drill pipe, erosion, etc. (Frydman and Ramirez 2006). Unlike in the laboratory, the subsurface is more dynamic, and having a fully controlled downhole condition will be challenging, if not impossible. It has been seen that the stress state around the hole greatly influences the final breakout geometry. The latest downhole imaging technology, for instance by means of ultrasonic waves or resistivity impedance, enables practitioners to capture the detailed wellbore features, including wellbore elongation and enlargement. The final breakout geometry tested under controlled parameters in the laboratory seems to be very ideal, and is rarely observed in actual downhole conditions. The actual hole geometry can be extremely irregular (see for example the breakout shapes presented by Plumb and Hickman (1985), Zoback et al. (1985), and Huber et al. (1997)) and an ideal cusp or dog-eared shaped breakout is extremely rare. Fluctuations of wellbore pressure, as well as thermal and chemical factors, will perturb the stress state near the wellbore wall and, hence, will influence the final breakout geometry; see, for example, Valley et al. (2018) and Moore et al. (2011). Therefore, the breakout that is used for estimating the in situ stress is only that produced by the stress-induced phenomena, e.g. one must exclude hole enlargement due to drill-string vibration or erosion.

In a review that covered, among other issues, rock damage around tunnels, Martin (1997) observed that “the numerical two-dimensional models that utilized an iterative slab removal scheme to simulate progressive failure overpredicted the depth of failure by a factor of 2 to 3.” The present paper, on the other hand, has shown that an iteration of the process of an elastic stress calculation, followed by “removal of failed material”, leads to quite realistic predictions of the ultimate stable breakout geometry. This discrepancy may point to a size effect, since the tunnel diameters in the cases highlighted by Martin (1997) were two orders of magnitude larger than the boreholes in the experiments of Herrick and Haimson (1994). Another possible, albeit speculative, explanation for the failure of these previous approaches is that the numerical stress computations might not have been accurate enough to capture the localized stress concentrations around the tip of the breakout. This may point to the advantage of using as essentially analytical stress calculation, which does not suffer from mesh artifacts.

It was mentioned in Sect. 4.2 that many authors have observed that the width of the breakout remains constant throughout its initiation, progression, and stabilization. This implies that the breakout width can be estimated from the Kirsch solution for the stresses around the initially circular borehole, in conjunction with a failure criterion. Indeed, Shen (2008) derived an expression for the initial breakout angle as a function of the in situ stresses and the UCS of the rock. It would be interesting exercise to compare the use of the method proposed in the present paper, and Shen’s equation, against a larger data set of breakout cases.

With regards to the concept that the breakout “deepens but does not widen”, it is worth mentioning the work of Azzola et al. (2019). They used ultrasonic borehole imaging to monitor the long-term evolution of the borehole geometry in open-hole sections of two deep geothermal wells drilled in the Rhine Graben. They concluded that the breakouts widen, but do not deepen, and attributed the widening to coupled thermo-mechanical effects due to wellbore thermal equilibration. Such effects, which occurred over a period of several years, clearly cannot be modeled with the type of elastic/brittle failure model suggested in the present paper, which has no actual “time clock” associated with the breakout development.

The computational methodology outlined above always yields a dog-eared breakout shape. As pointed out by one of the reviewers, dog-eared breakouts are plausible in very brittle rocks, where the assumption that failed rock is immediately removed is likely to be valid. In rocks with less steep strain softening, other breakout shapes may occur (Detournay and Roegiers 1986; Wu et al. 2016). This raises the possibility of using the observed breakout shape, which may depart from a dog-ear, to estimate the field-scale strain softening properties of the rock.

Another issue that is relevant in the field, and which is not accounted for in the analysis presented above, are three-dimensional effects associated with changes in the stress path to which the rock is subjected, as the borehole advances in the axial direction. These effects have been investigated and discussed by Bahrani et al. (2015), among others. Finally, it should be noted that the preceding analysis was applicable only to vertical wells. The possibility of using breakouts in deviated wells to estimate the stress state has been investigated by, among others, Qian and Pedersen (1991), Zajac and Stock (1997), and Etchecopar et al. (2013).