Investigation of Parent-Well Production Induced Stress Interference in Multilayer Unconventional Reservoirs

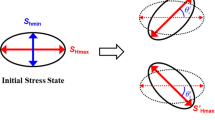
Abstract

A 3D explicitly coupled geomechanics and multiphase compositional model is developed with an embedded discrete fracture model (EDFM) and finite element method (FEM) to simulate the spatiotemporal stress evolution in a multilayer unconventional reservoir with complex fracture geometry. Different scenarios with and without interlayer geomechanical heterogeneity are studied to provide rules of thumb for infill drilling under the impacts of reservoir permeability, fracture penetration, differential stress, and rock stiffness. With a five-layer reservoir model setup—two parent wells located in the middle layer and the top and bottom layers being potential targets, numerical results show that (a) higher reservoir permeability aggravates the stress reorientation and reduces the magnitude of minimum horizontal stress (S_hmin) in both the production and potential targets; (b) fracture penetration has negligible influence on the stress evolution in the top and middle layers but speeds up the stress reversal in the bottom layer; (c) larger differential stress retards the orientation change of maximum horizontal stress (S_Hmax) more significantly in the bottom layer than in the top layer; (d) increasing rock stiffness of the top and bottom layers accelerates the stress reversal in these layers while an opposite response is observed in the middle layer.

Highlights

• A novel 3D coupled geomechanics and multiphase compositional model is developed to investigate multilayer stress interference.

• The complex fracture geometry is characterized by an embedded discrete fracture model (EDFM), and solid deformation is captured by the finite element method (FEM).

• The mechanisms of stress reorientation or stress redistribution spreading towards the top and bottom potential pay zones of stacked formations are proposed.

• Different scenarios with and without interlayer geomechanical heterogeneity are investigated to provide rules of thumb for the multilayer infill operations.

Appendix A

The McNamee–Gibson problem is solved using Laplace and Fourier transformations (1960a, b). The analytical solutions for excess pore pressure and consolidation settlement are provided as follows.

• Excess pore press ($p$)

$$p(x,z) = 2G\left( {\frac{\partial S}{{\partial z}} - \eta e} \right),$$

(34)

where

$$2G\frac{\partial S}{{\partial z}} = \frac{\eta }{2\eta - 1}\mathop \smallint \limits_{0}^{\infty } K\left( {x,\xi } \right)e^{ - \xi z} \left[ {1 + erf\left( {\xi \sqrt t } \right) + \frac{\eta - 1}{\eta }e^{{ - \frac{2\eta - 1}{{\eta^{2} }}\xi^{2} t}} erfc\left( {\frac{\eta - 1}{\eta }\xi \sqrt t } \right)} \right]{\text{d}}\xi ,$$

(35)

$$2G\eta e = \frac{\eta }{2\eta - 1}\mathop \smallint \limits_{0}^{\infty } K\left( {x,\xi } \right)e^{ - \xi z} \left[ {e^{ - \xi z} erfc\left( {\frac{z}{2\sqrt t } - \xi \sqrt t } \right) + \frac{\eta - 1}{\eta }e^{{ - \frac{2\eta - 1}{{\eta^{2} }}\xi^{2} t + \frac{\eta - 1}{\eta }\xi z}} erfc\left( {\frac{\eta - 1}{\eta }\xi \sqrt t + \frac{z}{2\sqrt t }} \right)} \right]{\text{d}}\xi ,$$

(36)

$$K\left( {x,\xi } \right) = \frac{2}{\pi \xi }{\text{cos}}\left( {x\xi } \right){\text{sin}}\xi ,$$

(37)

where G is the shear modulus, $G = E/2\left( {1 + \nu } \right)$; $\eta$ is an auxiliary elastic constant, $\eta = \left( {1 - \nu } \right)/\left( {1 - 2\nu } \right)$; e is the dilation of the soil skeleton, $e = - \left( {\partial u_{x} /\partial x + \partial u_{z} /\partial z} \right)$; and $u_{x}$, $u_{z}$ are the horizontal and vertical displacement, respectively.

• Consolidation settlement $\left( {\left[ {u_{z} - u_{z,t = 0} } \right]_{z = 0} } \right)$

$$\left[ {u_{z} \left( x \right) - u_{z} \left( x \right)_{t = 0} } \right]_{z = 0} = \frac{1}{2G}\frac{\eta }{2\eta - 1}\mathop \smallint \limits_{0}^{\infty } \frac{1}{\xi }K\left( {x,\xi } \right)\left\{ {erf\left( {\xi \sqrt t } \right) - \frac{\eta - 1}{\eta }\left[ {1 - e^{{ - \frac{2\eta - 1}{{\eta^{2} }}\xi^{2} t}} erfc\left( {\frac{\eta - 1}{\eta }\xi \sqrt t } \right)} \right]} \right\}{\text{d}}\xi ,$$

(38)

For special case $\eta = 1$, i.e., the Poisson’s ratio of the medium is equal to zero, the consolidation settlement can be simplified as

$$\left[ {u_{z} \left( x \right) - u_{z} \left( x \right)_{t = 0} } \right]_{z = 0} = \frac{1}{2G}\sqrt {\frac{t}{\pi }} \left[ {erf\left( {\frac{1 + x}{{2\sqrt t }}} \right) + erf\left( {\frac{1 - x}{{2\sqrt t }}} \right)} \right] + \frac{1}{2\pi }\left[ \begin{gathered} \left( {1 + x} \right)Ei\left\{ { - \frac{{\left( {1 + x} \right)^{2} }}{4t}} \right\} \hfill \\ + \left( {1 - x} \right)Ei\left\{ { - \frac{{\left( {1 - x} \right)^{2} }}{4t}} \right\} \hfill \\ \end{gathered} \right],$$

(39)

We choose $a$ as the characteristic length and ${{a^{2} } \mathord{\left/ {\vphantom {{a^{2} } c}} \right. \kern-\nulldelimiterspace} c}$ as the characteristic time to convert the pressure and displacement formulations into dimensionless form, where $c$ is the coefficient of consolidation defined as $c = {{2G\eta k} \mathord{\left/ {\vphantom {{2G\eta k} \mu }} \right. \kern-\nulldelimiterspace} \mu }$.