1 Introduction

Fractures provide preferential flow paths that define the rock mass internal “plumbing”, especially in low matrix-permeability rocks. Therefore, the rock mass hydraulic response results from the fracture density, orientation, and the stress-sensitive fracture transmissivity (Barton et al. 1995; Zimmerman and Bodvarsson 1996). In turn, fluid conduction in fractured rock masses affects the pore pressure distribution and effective stress field, flow rates, and immiscible fluid invasion (Aydin 2000; Shin and Santamarina 2019). Consequently, fracture transmissivity is critical to the engineering design of geotechnical structures, resource recovery, contaminant transport, and the geological storage of nuclear waste or CO2.

The void space between two rough fracture surfaces governs fracture transmissivity (Hakami and Larsson 1996; Olsson and Barton 2001), controls the fracture deformation during normal loading (Tsang and Witherspoon 1981; Brown and Scholz 1986), and determines fracture dilation during shear displacement (Patton 1966; Saeb and Amadei 1992; Lee and Cho 2002).

This study explores the effects of surface roughness on geometric aperture and hydraulic transmissivity as a function of normal stress and shear displacement. The manuscript is organized into three complementary sections: geometric aperture, contact mechanics, and flow. Each section includes an overview of previous research, provides new laboratory data, and advances analyses toward the enhanced understanding and modeling of fracture transmissivity. Altogether, the different sections provide new physical insight into fracture transmissivity and the effects of normal stress and shear displacement. The concise presentation is complemented by seminal references for further details.

2 Geometric Aperture: Fracture Roughness and Matedness

Rock characteristics and fracture genesis define surface roughness and the matedness or geometric correlation between fracture surfaces. For example, fresh tensile fractures exhibit higher degrees of matedness than shear fractures (Odling 1994; Al-Fahmi et al. 2018). Either cross-grain or inter-granular fracture propagation and frictional wear dominate roughness at the sub-meter scale, while kinematics, fracture convergence and the coalescence of secondary fractures control roughness at larger scales (Lee and Bruhn 1996; Candela et al. 2012; Brodsky et al. 2016). Furthermore, post-genesis stress changes and associated displacements, asperity crushing, cataclasis, creep and ploughing, fines generation, chemical dissolution and precipitation alter the void space and lead to complex hydro-thermo-chemo-mechanically coupled phenomena (Berkowitz 2002; Rutqvist et al. 2002; Taron et al. 2009).

The “geometric aperture” hG (m) reflects both the roughness of the two rock surfaces in contact and the matedness between them (Barton et al. 1985). The direct measurement of aperture in the laboratory relies on resin injection and casting, or tomographic imaging based on X-rays or nuclear magnetic resonance NMR. However, limitations in these techniques such as specimen size, partial fluid invasion, volume changes during curing, and low resolution limited by specimen size hinder the accuracy of casting and imaging methods (Pyrak-Nolte et al. 1987; Sharifzadeh et al. 2008; Keller 1998; Dijk et al. 1999; Bertels et al. 2001). On the other hand, indirect methods measure the roughness of the two fracture surfaces and infer geometric aperture numerically for a given relative positioning of the two surfaces (Brown and Kranz 1986; Lanaro 2000; Vogler et al. 2018).

The following sub-sections introduce the tested materials and roughness measurements, present analyses based on power spectra either compiled from the literature or computed from the measurements and digitized JRC profiles, and advance a protocol to create synthetic fracture surfaces using power spectra information. These synthetic surfaces, combined with fracture matedness define the fracture aperture.

2.1 Fracture Surface Roughness—Measurement

Empirical approaches simplify the characterization of surface roughness for engineering analyses, however, they are not adequate for quantitative aperture studies. The qualitative joint roughness coefficient JRC is a salient example (Barton 1973; Beer et al. 2002).

Detailed fracture roughness measurement techniques use either contact probes or optical techniques (Leach 2011; Tarolli 2014). In particular, optical methods from field devices such as LIDAR to laboratory electron microscopy span 8–10 orders of magnitude in scale, and often involve laser scanning or light interferometry.

We measured the surface roughness of natural and artificially fractured limestones using a table-top chromatic confocal interferometer (Nanovea ST400). Smooth surfaces were produced using a polishing device (Kent KGS618), whereas sandblasted surfaces used a water–sand jet (MBA Wet Blaster). We also measured the roughness of a natural fracture present in a limestone core. Insets in Fig. 1 present the scans obtained for 15 × 15 mm polished and sandblasted limestone surfaces and a 10 × 10 mm natural fracture surface. The height resolution is 0.2 μm. The peak-to-valley distance ranges from 60 µm for the polished surface to 600 µm for the sandblasted and natural surfaces.

Fig. 1
figure 1

Roughness power spectral density G(λ) derived from 1D fractures and faults profiles. The wavelength λ scale spans eight orders of magnitude. As the legend on the right indicates, empty markers correspond to published data (references below) filled markers are data from digitized JRC-profiles, and solid lines correspond to the average power spectrum of the three carbonate specimens profiles tested in this study. Insets correspond to interferometer surface scans of three tested specimens: a 15 × 15 mm sandblasted specimen (color-bar indicates surface roughness and varies from 0 to 600 μm); b 15 × 15 mm polished specimen (roughness color-bar varies from 0 to 60 μm); c 10 × 10 mm natural fracture (color-bar varies from 0 to 600 μm). Empty red markers indicate profiles of exhumed faults surfaces parallel to slip and blue markers show profiles perpendicular to the slip direction. Squares: Magnola, Diamonds: Corona Heights; Triangles: Vuache-Sillingly; Circles: Dixie Valley; Star: Bolu (after Candela et al. 2012). Green empty squares are a natural surface in Harcourt Granite (after Power and Durham 1997). Orange empty squares correspond to a granodiorite from Fenton Hill, New Mexico (after Brown and Kranz 1986)

Full size image

2.2 Fracture Surface Roughness—Analysis

The analysis of roughness data involves amplitude and texture descriptors. Amplitude refers to elevation normal to the mean fracture plane, while texture considers patterns on the plane. Table 1 summarizes statistical parameters that are used to evaluate amplitude and texture. These parameters readily reveal the challenges in roughness characterization; for example, slope and curvature values are not unique but depend on the sampling interval and computation method, and amplitude distributions depend on specimen length and suggest nonstationary randomness (Majumdar and Bhushan 1990; Sayles and Thomas 1978). In fact, roughness studies highlight the inherent link between roughness values, the measurement scale, and resolution.

Table 1 Amplitude and texture descriptors for fracture roughness (Thomas 1998; Magsipoc et al. 2020)
Full size table

The surface roughness power spectral density provides unbiased amplitude and texture information (Power and Tullis 1991; Jacobs et al. 2017). We followed a five-step procedure to compute the surface roughness power spectrum: (1) measure 500 parallel roughness profiles on the specimen surface (lateral spacing between linear scans = 20 μm), (2) remove the linear trend for each profile, (3) window the detrended signal with a 3% cosine taper to reduce leakage, (4) compute the normalized power spectral density G (m3) using the Fast Fourier Transform and (5) average the spectra for the 500 parallel profiles to obtain an equivalent 1D representation. Inherently, this procedure imposes a high-pass filter whereby wavelengths longer than the specimen size are filtered out. Figure 1 shows the roughness power spectral densities for three limestone surfaces: polished, sandblasted and a natural fracture.

2.3 Fracture Surface Roughness—Database

We compiled an extensive database of power spectra for rock surfaces in various lithologies including carbonates and granites. Surfaces involved exhumed faults parallel and perpendicular to slip (i.e., meter scale), laboratory specimens (i.e., centimeter scale), and digitized JRC fracture profiles. Laboratory specimens included fractures recovered from cores, created during strength testing, or sawed-polished, and sandblasted surfaces (measured in this study—Sect. 2.1). Figure 1 presents spectral densities as a function of wavelength λ (m) for the complete dataset. The various datasets involved different devices (i.e., LiDAR, profilometers, and interferometers) and spectral data analyses, yet, most of the data collapses onto a narrow trend. In fact, the roughness power spectrum of laboratory and natural fractures and faults follows a power law with respect to wavelength:

$$G\left( \lambda \right) = \alpha \left( {\frac{\lambda }{{\left[ m \right]}}} \right)^{\beta } .$$
(1)

The power law implies a fractal surface topography (Mandelbrot et al. 1984; Katz and Thompson 1985; Power and Durham 1997). The parameters for the overall trend are α = 6 × 10–7 m3 and β = 2.8, where the α-factor is the spectral density for λ = 1 m, and the β-exponent is related to the fractal dimension (Brown 1995).

The fractal nature of surface roughness extends from geological features (e.g., strata in sedimentary rocks and faults) to the grain/crystal scale. Indeed, data in Fig. 1 suggest that this power law relationship remains valid over six orders of magnitude, and provides a convenient framework to relate laboratory measurements to the field scale.

We analyzed the individual roughness trends for all specimens in the database. In all cases, spectral densities fall along the main power trend in Fig. 1, but exhibit a range of α-factors [2 × 10–10 to 7 × 10–4 m3] and β-exponents [1.9–3.0]. The α-factor and β-exponent increase with JRC roughness (for example: α = 2 × 10–8 m3 and β = 2.1 for JRC 0–2, while α = 4 × 10–7 m3 and β = 2.4 for JRC 18–20). Deviations from the global trend occur at large wavelengths for “smooth” profiles, e.g., λ > 10–3 m for our polished limestone surface and λ > 10–2 m for the JRC 0–2. These results indicate non-natural smoothness and suggest inherent limitations in the use of artificially roughened specimens to study fracture processes. Similar studies refer to this transition as corner frequency (Chen and Spetzler 1993).

The following sub-section uses this power–law relationship and proposes a methodology to create synthetic fracture surfaces.

2.4 Numerical Generation of Rough Surfaces

The power spectral density G(λ) for a given wavelength λ is a function of the corresponding sinusoid amplitude X(λ) (m):

$$G\left( \lambda \right) = \frac{{N{{\Delta }}x}}{4}\left[ {X\left( \lambda \right)} \right]^{2} ,$$
(2)

where N is the number of digital values in a given profile and Δx (m) the sampling interval. Note that the scaling factor (NΔx/4) in Eq. 2 depends on the selected Fourier pair and transform definition (i.e., one-sided vs. two-sided). Nevertheless, Eqs. 1 and 2 relate amplitudes Xu and Xv to their corresponding wavelengths λu and λv regardless of the scaling factor

$$\frac{{X_{u} }}{{X_{v} }} = \left( {\frac{{\lambda _{u} }}{{\lambda _{v} }}} \right)^{{\beta /2}} .$$
(3)

Alternatively, given a signal length N·Δx, the sinusoid amplitude X(λ) for a given wavelength can be computed in terms of the fitted α and β parameters

$$X\left( \lambda \right) = 2\sqrt {\frac{1}{{N{{\Delta }}x}}\alpha \left( {\frac{\lambda }{{\left[ m \right]}}} \right)^{\beta } } .$$
(4)

The power spectrum lacks phase information, thus we assumed a uniformly distributed random phase ϕ(λ). Together X(λ) and ϕ(λ) define the fracture roughness in the frequency domain. We imposed a wavelength cutoff of one-fifth of the fracture length to avoid the lower order periodicity in computed profiles (i.e., high-pass filtering): this cutoff value is the longest wavelength that does not generate preferentially oriented ridges and valleys (Matsuki et al. 2006; Briggs et al. 2017). Finally, we computed the Inverse Fast Fourier Transform to determine roughness profiles in space. This methodology can be readily extended to 2D surfaces, and both the linear 1D and surface 2D algorithms satisfy Parseval’s identity.

2.5 Matedness

We created fractures by bringing two rough surfaces together. Perfectly mated fractures have zero geometric aperture, thus null hydraulic transmissivity. Power spectral analyses help assess the characteristic length for surfaces matching, i.e., a mismatched length scale (Glover et al. 1997; Ogilvie et al. 2006). However, the lack of phase information in power spectra means that two surfaces with identical spectra can result in mismatched topography and non-zero apertures. Other matedness descriptors rely on contact area or joint matching coefficient JMC but disregard the wavelength-dependent correlation between the surfaces (Zhao 1997; Grasselli 2001).

3 Contact Mechanics

This section combines numerical realizations of fracture surfaces (Sect. 2.4), contact mechanics, and kinematic deformation to anticipate fracture deformation and the resulting aperture during normal loading and shear displacement. The simple yet robust approach proposed herein is physics-based and further validated against experimental data.

3.1 Normal Stress

The fracture contact area and stiffness increase and the mean aperture decreases with increasing normal stress (Iwano and Einstein 1995; Nemoto et al. 2009). Some analyses adopt a non-linear elastic contact model whereby the fracture roughness is an assembly of spheres or cylinders (Greenwood et al. 1966; Hopkins et al. 1987). Other analyses assume that fracture surfaces interpenetrate and overlap each other to reach a prescribed displacement, contact area, or fluid transmissivity (Watanabe et al. 2008; Li et al. 2015; Souley et al. 2015). These are inherently non-elastic fracture models and often involve numerical algorithms that incorporate elasto-plastic behavior of the contacts (Walsh et al. 2008; Kling et al. 2018).

We adopted the interpenetration model and assumed a perfectly rigid-plastic rock response. Since the true contact area Ac(σ) (m2) is minimal compared to the fracture apparent area Af (m2), we assumed that all contact points reached the yield stress of the material σyield (MPa); then, equilibrium with the far field normal stress σ (MPa) implies:

$$\frac{\sigma }{{\sigma _{{{\text{yield}}}} }} = \frac{{A_{c} \left( \sigma \right)}}{{A_{f} }}.$$
(5)

The algorithm brings fracture surfaces together by imposing a displacement δv until the interpenetration contact area Ac(σ) is sufficient to resist the applied stress σ. Figure 2 compares experimental and numerical results for the sandblasted limestone specimen. The fitted yield stress σyield = 200 MPa exceeds the measured unconfined compressive strength UCS = 70–90 MPa by a factor of three; this reflects differences in mono-crystal asperities vs. poly-crystal specimens, boundary conditions, and the low aspect ratio of the asperities compared to the 2:1 ratio used for cylindrical specimens during UCS testing (ASTM 2014; Tuncay and Hasancebi 2009). The insets in Fig. 2 illustrate the apertures computed at 0 MPa (δv = 0 mm) and 12 MPa (δv ≈ 0.2 mm). The preferential deformation around edges reflects the global convex geometry observed in sandblasted specimens.

Fig. 2
figure 2

Fracture normal displacement data due to applied normal stress. Sandblasted limestone specimen (yellow markers). Predicted response (continuous line): the rigid-plastic contact model assumes a yield stress of 200 MPa. Insets reflect aperture maps computed at 0 MPa (δv = 0 mm) and 12 MPa (δv ≈ 0.2 mm), respectively

Full size image

We explore the effect of normal stress on aperture size distribution using numerically generated surfaces. Figure 3a shows the distribution of local aperture for a normally compressed fracture; Fig. 3b shows mean trends computed from 1000 unmated synthetic fracture realizations (following the approach described in Sect. 2.4). Increments in normal stress shift the aperture size distribution toward smaller values; the cutoff at zero aperture corresponds to the true contact area Ac(σ). Truncated Gaussian distributions properly represent the computed histograms in all cases tested as part of this study (see also Barr and Sherrill 1999; Xiong et al. 2018).

Fig. 3
figure 3

Evolution of aperture size distribution during normal loading for numerically generated surfaces. A Aperture field estimated using the contact yield model at 1 MPa for a fracture composed of two unmated synthetic surfaces. B Evolution of the aperture size distribution with normal stress (mean of 1000 realizations—σyield = 200 MPa). 1D profiles are 100 mm long, and wavelengths range between λmin = 0.02 mm and λmax = 20 mm

Full size image

3.2 Shear Displacement

Shear-induced dilation and contraction are a consequence of surface roughness and initial matedness, asperity overriding, roughness wear, and degradation, and the consequent progressive generation of gouge material. The normal stress on the fracture surface determines the tradeoff between dilation during asperity overriding and asperity breakage (Barton 1973; Gutierrez et al. 2000). Typical normal versus shear displacement behavior exhibits some initial contraction followed by dilation toward an asymptotic aperture. The dilatancy rate is maximum at peak shear strength. Existing models attempt to capture these effects through geometrical descriptors, spectral information, or JRC-based qualifiers (Grasselli et al. 2002; Asadollahi and Tonon 2010).

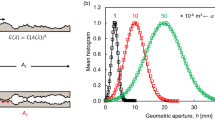
Initial matedness is particularly relevant to the evolution of aperture size distributions during the early stages of shear displacement. In the following analysis, we used synthetically generated 1D roughness profiles to explore two matedness cases: (1) an initially “perfectly mated” fracture composed of two mirror surfaces, and (2) an initially “unmated” fracture composed of two distinct surfaces each created with the amplitude power law X(λ) and random phase ϕ(λ) for each wavelength. Figure 4 illustrates the mean aperture size distribution obtained using 1000 realizations for unmated fractures. These results suggest that shear displacement does not affect the aperture size distribution of initially unmated fractures. By contrast, the mean and standard deviation increase with shear displacement in initially mated fractures, and reach a maximum mean aperture value when the shear displacement δs is half of the longest roughness wavelength, δs ~ λmax/2 (Fig. 5a).

Fig. 4
figure 4

Aperture size distributions during shear displacement for initially unmated fractured surfaces. Mean aperture histograms for 1000 roughness realizations. Numerically generated surfaces are 100 mm long and have a maximum wavelength λmax = 20 mm. The shear displacement δs is normalized by λmax shows the lateral offset. Note: the roughness profile shown has an exaggerated vertical scale for clarity

Full size image
Fig. 5
figure 5

Evolution of aperture size distribution during shear displacement for initially mated fractures. Mean aperture histograms for 1000 realizations. A σ = 0 MPa, B Normal stress σ = 10 MPa imposed after shear displacement. Dashed lines relate histograms before and after normal load. Note: the roughness profile shown has an exaggerated vertical scale for clarity

Full size image

We extended the previous analysis to include the combined effects of shear displacement (imposed first) and normal stress (Eq. 5). Figure 5a displays the mean aperture size distribution obtained from 1000 realizations at normal stress σ = 0 MPa for initially mated fracture surfaces after four different shear displacements. Figure 5b shows aperture histograms after normal loading to σ = 10 MPa. The effects of normal loading and asperity yield after shear displacement on aperture size distribution are more pronounced as matedness decreases with increased shear displacement. Note that the adopted contact model does not consider asperity shear.

4 Flow: Hydraulic Aperture

Flow follows the path of least drag in a variable aperture field. Thus, flow trajectories deviate from linear streamlines. A fracture’s “hydraulic aperture” hH is the equivalent aperture between two parallel flat plates that allow the same flow for the same pressure gradient assuming the cubic law (Witherspoon et al. 1980). Estimates of the hydraulic aperture are based on statistics (Table 2). Interestingly, most models anticipate that the hydraulic aperture decreases as the aperture coefficient of variation sG/μG increases where sG is the aperture standard deviation and μG its mean. Analogous conclusions using network models for a wide range of pore size distributions can be found in Jang et al. (2011). Numerical studies, new experimental data, and data compiled from published studies are used herein to extend previous fracture flow analyses.

Table 2 Hydraulic aperture models
Full size table

4.1 Numerical Study: Evolution of Transmissivity with Normal Stress and Shear Displacement

We assumed the cubic law to be locally valid. Then, Stokes flow and continuity requirements result in the following expression, similar to the seepage flow equation for a heterogeneous medium (Oron and Berkowitz 1998):

$$\frac{\partial }{{\partial x}}\left( {h_{G}^{3} \frac{{\partial P}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {h_{G}^{3} \frac{{\partial P}}{{\partial y}}} \right) = 0,$$
(6)

where hG is geometric aperture.

This equation assumes that (1) roughness amplitudes X are much smaller than the roughness wavelength λ (λ/X ≫ 1), and (2) the wavelength is much greater than the aperture (λ/hG ≫ 1). The power function between roughness and wavelength automatically satisfies the first assumption (Fig. 1 and Eqs. 1 and 3). The second assumption is valid taking into consideration the wavelength that controls the aperture. Note that two sinusoidal surfaces in contact create a hG = 4X aperture when the shear displacement is λ/2, i.e., a π-shift.

We solved Eq. 6 using finite differences and explored the implications of changes in geometrical aperture on flow due to changes in effective normal stress. Numerical results in Fig. 6 show the decrease in fracture transmissivity as the effective normal stress increases for different yield stress values σyield. Besides the reduction in aperture, the increase in contact area leaves a smaller available fracture cross section for flow. Figure 6a shows flow rate magnitudes at different stress levels for a synthetic unmated fracture: flow trajectories redistribute and flow channeling becomes more pronounced at later stages of loading because larger aperture channels remain open and control flow. In fact, the fracture area responsible for 90% of the flow reduces during loading (Fig. 6b).

Fig. 6
figure 6

Transmissivity changes due to normal load. A Estimated flow rates through an unmated fracture using the contact yield and local cubic law approximations for different normal stresses (σ’ = 0, 1, 5, and 15 MPa—Eq. 5 for an assumed yield stress of 200 MPa). B The fraction of the fracture area that carries 90% of the total flow for 1000 realizations. Vertical bars indicate the 25th and 75th percentiles. The inset shows the assumed pressure gradient (top to bottom) and the no-flow side boundaries

Full size image

Transmissivity data gathered in the field suggest that shear dilation in critically stressed natural fractures enhances fluid flow, predominantly in crystalline rocks (Barton et al. 1995). Shear displacement induces aperture anisotropy. Contact points increase in the direction of shear, detach transversely to the shear direction, and therefore, aperture ridges emerge on the fracture aperture field (Gentier et al. 1997; Yeo et al. 1998; Auradou et al. 2005; Matsuki et al. 2010). Consider a synthetic initially mated rough fracture (i.e., zero aperture) subjected to shear displacement in the y-direction (Fig. 7a). The geometric aperture field at different levels of shear displacement in Fig. 7a displays a clear alignment of apertures transverse to the shear direction at early stages of shear as discussed above. The ensuing transmissivity anisotropy is most pronounced soon after shear displacements starts δs/λmax < 0.1, and gradually decreases toward isotropic conditions at large shear displacements when all surface correlations are lost (Fig. 7b). Datapoints in Fig. 7b are averages of 1000 realizations, and error bars show that the anisotropy variability increases with shear displacement due to the higher probability of dominant flow paths.

Fig. 7
figure 7

Transmissivity changes during shear displacement. A Geometric apertures for different levels of shear displacement at 0 MPa of normal stress and initially perfectly mated fracture. B Evolution in transmissivity anisotropy for shear displacement along x and y directions (1000 realizations). Vertical bars indicate the 25th and 75th percentiles

Full size image

4.2 Experimental Study: Torsional Ring Shear Device

Numerical results highlight profound differences in the evolution of geometric aperture and flow during normal loading and shear displacement, and the impact on natural fracture surface roughness and matedness. A focused experimental study complements this numerical study.

We designed and manufactured a torsional ring shear device to subject a pre-fractured cylindrical specimen to normal stresses up to 30 MPa, to independently apply a torsional shear displacement, and to impose radial flow through the annular fracture plane (Fig. 8). This device benefits from accurate normal stress and shear displacement control, imposes precise flow boundaries without the need for jacketed specimens, maintains a constant nominal fracture area throughout the test, and reduces stress localization (for comparison, see: linear shear in Esaki et al. 1999; biaxial tests in Makurat et al. 1990; triaxial configuration in Teufel 1987; and torsional shear in Olsson 1992).

Fig. 8
figure 8

Torsional shear device to assess fracture transmissivity as a function of normal stress and shear displacement. A Reaction frame, hydraulic cylinder for vertical load, lever arm and specimen. B Instrumentation: LVDT to monitor the fracture normal displacement and strain gages SG to measure the applied torque. C Ball bearings in the annular space between the cap and the plunger preserve the coaxility

Full size image

The reaction load frame houses a pressure-controlled hydraulic jack to impose the vertical load, and two horizontal screw positioners to exert the torsional moment via diametrically opposite lever arms. Fluid is injected into the fracture plane through a small central hole drilled into the specimen’s lower half. The instrumentation includes a LVDT to record the normal displacement, strain-gages mounted on the lever arms to measure torque, and two pressure transducers to monitor the fluid pressure at low and high pressure ranges.

The limestone specimen preparation method involved five steps: (1) core two 56 mm diameter cylindrical plugs, (2) modify the fracture surface by either sandblasting or polishing, (3) cut a cross-shaped groove on the other side of each plug to accommodate the torque transmission cap, (4) drill the central hole and chamber in one of the two plugs for fluid injection (hole diameter = 3.5 mm, chamber diameter = 18 mm), and (5) attach with epoxy the two steel caps onto the rock cylinders. For natural fractures, we cored across the fracture and implemented steps 3, 4, and 5 detailed above.

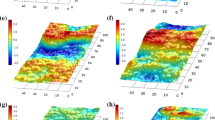
Figure 9 shows typical experimental results where transmissivity decreases with effective normal stress. The smooth and rough limestone specimens start with distinct geometrical aperture fields, yet their transmissivities converge as the effective normal stress exceeds ~ 1 MPa (Fig. 9a). On the other hand, the high roughness variability in a natural fracture plane, with longer asperity wavelength, localizes contact yield at few asperities; there is a reduced effect on the governing large flow channels and transmissivity exhibits lower sensitivity to normal stress (Fig. 9b). A set of five tests conducted with limestone plugs confirmed these observations.

Fig. 9
figure 9

Evolution of transmissivity with normal stress—Experimental data. A Limestone specimen with two different surface roughness. Insets correspond to roughness scans for the smooth (2.3 × 2.3 mm) and rough (6 × 6 mm) fracture surfaces. Color bar values range from 0 to 0.06 mm and from 0 to 0.1 mm, respectively. B Natural specimen. The inset corresponds to the roughness of a 10 × 10 mm specimen

Full size image

Results in Fig. 7 call for the analysis of hydro-mechanical boundary conditions in experimental and numerical studies, relative to field conditions. For example, radial flow in our ring shear device is normal to the shear direction; on the other hand, most numerical and experimental studies impose flow collinear with shear. In addition, radial flow and torsional shear imply a radial gradient in fluid velocity and shear displacement; we minimize radial effects by limiting the ratio between the external specimen diameter and the internal chamber size (56 mm/18 mm in this study).

4.3 Transmissivity Models: Normal Stress and Shear Displacement

We compiled a database of fracture transmissivity evolution with normal stress and shear displacement for various rock types. Data sources cover a wide range of measurement techniques (e.g., linear, biaxial, and torsional shear) and boundary conditions (i.e., linear and radial flow). This database, which includes published results and our experimental results, allow us to advance new physics-inspired yet data-driven transmissivity models.

4.3.1 Normal Stress

Earlier fracture transmissivity models as a function of normal stress recognized non-linear contact behavior and asperity yield, flow channeling, and the influence of fracture roughness (e.g., Pyrak-Nolte and Nolte 2016). These phenomenological models involve power, logarithmic, or exponential decay functions for transmissivity as a function of normal stress. However, these models fail to capture the asymptotic behavior of fracture transmissivity T (cm2/s) at very low effective normal stress (Tσ0 as σ′ → 0) and very high effective normal stress (Tσ∞ as σ′ → ∞) and may be unreliable for general applications.

We modified a selection of published models to satisfy asymptotic behavior so that transmissivity reaches prescribed values when the effective stress approaches zero or infinity (see Table 3). Then, we fitted trends in the database with the various models. The following power–law expression provides the best fit for all cases analyzed in this study:

$$\frac{{T\left( {\sigma ^{\prime } } \right) - T_{{\sigma _{\infty } }} }}{{T_{{\sigma _{0} }} - T_{{\sigma _{\infty } }} }} = \left( {\frac{{\sigma ^{\prime } + \sigma _{c} }}{{\sigma _{c} }}} \right)^{{ - \gamma }} .$$
(7)
Table 3 Fracture transmissivity models as a function of effective normal stress. Notes models are modified to satisfy asymptotic behavior
Full size table

This four parameter model indicates that transmissivity T(σ′) at a given effective normal stress σ′ normalized by the asymptotic values Tσ0 and Tσ∞ is a function of the normalized effective normal stress with respect to the characteristic stress σc, where the γ-exponent captures the transmissivity stress-sensitivity (Fig. 10). Note that the normalized transmissivity is 2−γ when the normal stress is equal to the characteristic stress σ′ = σc. Complementary numerical simulations not shown here indicate that (1) fracture roughness and matedness control the transmissivity asymptotes Tσ0 and Tσ∞, and (2) σc is a function of the rock yield stress σyield.

Fig. 10
figure 10

Transmissivity as a function of normal stress—Experimental data and fitted power model (Eq. 7). Transmissivity normalized with respect to the transmissivity at zero and infinite normal stress Tσ0 and Tσ∞. Empty markers: published data. Filled markers: experimental data for limestone specimens (this study). Rock type: square-granites, diamond-granodiorites, cross-sandstones, 4 point star-marbles, triangle-shales, circle-gneiss, and 6 point star-amphibolites. Data sources: Witherspoon et al. (1980) (gray); Gale (1982) (black); Raven and Gale (1985) (blue); Brown and Kranz (1986) (purple); Makurat (1990) (olive); Wilbur and Amadei (1990) (yellow); Boulon et al. (1993) (maroon); Durham (1997) (brown); Indraratna et al. (1999) (green); Gutierrez et al. (2000) (orange); Pyrak-Nolte and Morris (2000) (magenta); Lee and Cho (2002) (lavender); Watanabe et al. (2008) (cyan); Cuss et al. (2011) (lime); Chen et al. (2017) (red)

Full size image

Figure 10 illustrates data clustering according to rock type: fractures in sandstones are more sensitive to stress (γ = 3-to-20), whereas the transmissivity in igneous and metamorphic rocks exhibits a lower stress-sensitivity (γ = 0.4-to-2). The exponent γ for limestone specimens tested in this study ranges from γ = 3-to-8.

4.3.2 Shear Displacement

Previous empirical models for transmissivity during shear displacement relate shear dilation to the joint roughness coefficient JRC or an empirical fitting factor (Table 4). Some models recognize cataclasis during shear displacement, but are complex and require shear stress information (Plesha 1987; Nguyen and Selvadurai 1998). Furthermore, available empirical and theoretical models are asymptotically incorrect, thus, unreliable for general applications.

Table 4 Fracture transmissivity models as a function of shear displacement
Full size table

We adopted the following logistic function with a distinct S-shaped trend in log–log scale to capture the evolution of the normalized transmissivity during shear displacement:

$$\frac{{T\left( {\delta _{s} } \right) - T_{{\delta _{0} }} }}{{T_{{\delta _{\infty } }} - T_{{\delta _{0} }} }} = \frac{{e^{{\left( {\frac{1}{{1 + e^{{\eta \left( {1 - \delta _{s} /\delta _{{sc}} } \right)}} }} - 1} \right)}} - T_{c} }}{{1 - T_{c} }}~\quad {\text{where}}\;T_{c} = e^{{\left( {\frac{1}{{1 + e^{\eta } }} - 1} \right)}} .$$
(8)

The four parameters model capture: the sensitivity of the fracture transmissivity to shear displacement in the η-exponent, the displacement at maximum dilatancy or contractive rate in the characteristic shear displacement δsc, and the transmissivity asymptotes Tδ0 as δs → 0 and Tδ∞ as δs → ∞. This model can accommodate data that exhibits either monotonic dilation or contraction during shear; in fact, Zhou et al. (2018) proposed a similar mathematical expression for dilation.

Figure 11 presents normalized transmissivity data plotted against the normalized shear displacement δs/δsc for studies reported in the literature and new data gathered in this study. The limited clustering by rock type suggests that changes in aperture are most sensitive to initial fracture roughness and matedness. In fact, complementary numerical simulations with synthetic fractures not shown in this manuscript demonstrate that roughness, matedness, and normal stress determine the transmissivity asymptotes Tδ0 and Tδ∞, and the characteristic shear displacement δsc. The η-exponent reflects the dilative tendency which is a function of surface roughness and initial matedness for a given normal stress.

Fig. 11
figure 11

Transmissivity as a function of shear displacement—Experimental data and fitted logistic model (Eq. 8). Transmissivity normalized with respect to the transmissivity at zero and infinite shear displacement Tδ0 and Tδ∞. Empty markers: published data. Filled markers: experimental data for limestone specimens (this study). Rock type: square-granites, diamond-plaster, cross-mortar, 4 point star-sandstone, triangle-marbles, welded tuff-gneiss, and 6 point star-chalk. Data sources: Makurat 1990 (cyan); Esaki et al. 1991 (black); Olsson 1992 (brown); Ahola et al. 1996 (green); Gentier et al. 1996 (gray); Cheon et al. 2002 (magenta); Li et al. 2008 (blue); Nishiyama et al. 2014 (red)

Full size image

4.4 Hydro-Chemo–Mechanical Coupling: Dissolution

Carbonate rocks exhibit high solubility and high reaction rates (Plummer et al. 1978). Consequently, mineral dissolution, and precipitation play a significant role in the evolution of both geometric and hydraulic apertures. The Damkhöler number compares reaction kinetics and advective transport, while the transverse Peclet number contrasts longitudinal advective transport to diffusive transport across the fracture (Fredd and Fogler 1998; Golfier et al. 2002). These two dimensionless ratios help anticipate the type of transport regime: homogeneous dissolution, near-inlet dissolution, or channeling (Elkhoury et al. 2013; Deng et al. 2015).

Mineral dissolution impacts the aperture evolution for a given normal stresses. We explored the evolution of fracture transmissivity due to reactive fluid flow across a limestone specimen with an initially polished fracture surface using our annular fracture flow device. Figure 12 presents the fracture transmissivity and normal displacement data during loading and unloading before acid treatment. The initial transmissivity-stress trends obtained with water follow a typical compaction behavior, where transmissivity decreases as effective normal stress increases. We injected 5 cm3 of a pH = 2 HCl-solution at 1 cm3/min under constant normal stress σz = 0.55 MPa. For a diffusion coefficient D = 2 × 10–9 m2/s, mean fracture aperture hH = 25 μm, and kinetic rate k = 3.2 s−1, the Damkhöler and Peclet numbers are Da = 9.1 and Pe = 2.7 × 10–2 respectively (see Kim and Santamarina 2016 for detailed Da and Pe definitions). These high Damkhöler and Peclet numbers imply fast reaction and seepage which cause near-inlet dissolution. Then, we measured transmissivity and normal displacement during a second loading–unloading cycle. There is a marked increment in fracture transmissivity during acid injection and insignificant changes in normal displacement. Thereafter, gains in transmissivity remain during loading even at high stress. This observation suggests the formation of dissolution channels during the acid treatment while the true contact area between fracture planes remains unaltered (see inset in Fig. 12).

Fig. 12
figure 12

Fracture transmissivity changes due to dissolution. Limestone subjected to the injection of HCl solution-pH 2 at 1 cm3/min. (A) Fracture transmissivity versus effective normal stress and (B) normal displacement versus effective normal stress before (black) and after (yellow) acidizing treatment. The inset sketch illustrates the hypothesized aperture evolution following dissolution (dashed lines: surface before acidization)

Full size image

5 Conclusions

Fluid flow in fractured rock masses is a common phenomenon in natural and engineered systems, from infrastructure applications to resource recovery and CO2 geological storage. Fracture transmissivity along fractures defines the prevalent flow paths and controls all forms of hydro-thermo-chemo-bio-mechanically coupled processes. This study combined data compilation, new experimental data, and numerical studies to advance the understanding of fracture roughness, aperture, and transmissivity.

The fracture roughness reflects mineralogy and fabric at small scales compounded by kinematics at large scales. The power spectral density captures the inherent interplay between surface roughness amplitude and wavelength: (Xu/Xv) = (λu/λv)β/2 where β ranges from β = 1.9 to 3. When plotted against wavelength, roughness power spectral density data cluster along a single trend for more than eight orders of magnitude in roughness wavelength with a global β ≈ 2.8. Deviations from this trend at large wavelengths in artificially roughened specimens suggest non-natural smoothness and highlight experimental limitations to study large scale fracture processes. Nevertheless, the fractal nature of surface roughness provides a convenient framework for analytical and numerical studies.

Specimen size limitations and fractal characteristics limit physical experiments. Statistical numerical experimentation appear as a valuable approach to study fracture transmissivity. Our normal contact and kinematically based shear models provide first-order insight on fracture deformation. The power function between fracture roughness and wavelength automatically guarantees the validity of the simplified Navier–Stokes model (i.e., local cubic law).

Surface roughness and matedness define fracture aperture and its evolution during normal loading and shear displacement. Normal stress increments cause contact yield, fracture closure, and changes in the fracture void space. The closure of small local apertures increases the relative contribution of larger interconnected voids and promotes flow channeling. Rougher unmated surfaces preserve channels during loading, and transmissivity exhibits lower stress sensitivity. An asymptotically correct power function accurately captures the evolution of transmissivity with normal stress. Model parameters reflect initial roughness, matedness, and mineralogy.

The shear displacement of unmated fractures results in statistically identical aperture fields. By contrast, shear displacement increases both the aperture mean and standard deviation in initially mated fractures; in this case, contacts align along ridges transversely to the shear direction and lead to anisotropy in transmissivity during early stages of shear displacement. However, anisotropy decreases as the shear displacement increases (relative to the largest wavelength present in the fracture). A logistic function represents transmissivity changes with shear displacement. The fracture roughness, initial matedness, and normal stress relative to yield determine the transmissivity asymptotes.

Reactive flow modifies the void space. The impact of dissolution on fracture transmissivity depends on the rates of reaction, diffusion, and advection. In high advective regimes, transmissivity increases due to positive advective-reactive feedback and channeled erosion, even at minimal normal fracture displacement.