1 Introduction

The overall cost of a tunnel project is significantly affected by tunnel completion time. TBM performance prediction is therefore a key issue in the early stage of the project, when the profitability of the mechanised method is evaluated. In this regard, several prediction methods were developed, including semi-theoretical models (e.g., Roxborough and Phillips 1975; Snowdon et al. 1982; Sanio 1985; Wijk 1992; Rostami and Ozdemir 1993), empirical models (e.g., Bruland 1998; Barton 1999; Bieniawski et al. 2006; Gong and Zhao 2009; Khademi Hamidi et al. 2010; Hassanpour et al. 2011; Farrokh et al. 2012; Delisio and Zhao 2014; Zare Naghadehi and Ramezanzadeh 2017), computer-aided models (e.g., Alvarez Grima et al. 2000; Zhao et al. 2007; Mahdevari et al. 2014; Salimi et al. 2016; Armaghani et al. 2017) and full-scale laboratory tests (e.g., Bilgin et al. 1999; Chang et al. 2006; Gertsch et al. 2007; Cho et al. 2010; Copur et al. 2014). Among them, no one may be effectively used in every case; each model, with a certain degree of reliability, works better than others in some contexts, but is unreliable in others. Semi-theoretical and empirical models present considerable advantages in terms of ease of use, cost and execution time, but they are sometimes unable to provide accurate results. Computer-aided models may provide reliable results when applied in context with characteristics similar to their original database. Full-scale tests are usually the best solution in massive rock conditions, provided that appropriate equipment and samples are available. In special cases, a prototype machine in laboratory or a real machine on-site is tested. This solution is the more precise method but is very expensive and time-consuming (Bilgin et al. 2014). In this regard, there is a growing tendency to realise exploratory tunnels in the preliminary stage of very long tunnel projects (tens of kilometres), which generally consist of double tubes. These tunnels, whose length is typically within a few kilometres, are usually realised in the same rock mass context as the main tunnel, with a similar excavation method and a little smaller diameter, providing very detailed information for the machine performance prediction and the cutterhead design in the early stage of the main project.

The models discussed above often involve deterministic approaches, which are easy to use, but are not able to take into account the variability of the predictors. Such variability is particularly relevant in TBM performance prediction, considering the nature of the parameters involved and the effects of their unpredictability. In particular, according to Bilgin et al. (2014), the factors influencing TBM performance can be divided into three main groups: mechanical factors (related to the machine), geological-geomechanical factors (related to the rock) and operational factors. Mechanical factors are often constant during the tunnel excavation (guaranteed by proper machine maintenance), whereas geological-geomechanical and operational factors may vary, resulting in a significant variability of the machine performance (Rispoli et al. 2018). In this regard, TBM performance is usually defined as overall performance and net performance. Overall performance includes parameters such as advance rate (AR), in meters of advancement per working day, and machine utilization factor (UF), in percentage. Net performance is normally expressed as rates of penetration in meters of advancement per boring hour (PR) or in millimetres of penetration per cutterhead revolution (ROP).

The unpredictability of a phenomenon is the result of the contribution of two main factors: epistemic uncertainty and aleatory variability (Bedi 2013). Epistemic uncertainty is related to the lack of knowledge of the phenomenon analysed and can be reduced by additional information (Guo and Du 2007). The aleatory variability is instead caused by the inherent randomness of the physical system and cannot be reduced by increasing the amount of information (Bedi 2013). According to Bedi and Harrison (2013), the optimal modelling approach can be selected on the basis of the level of information available (Fig. 1). In particular, in presence of unpredictability that essentially consists of aleatory variability, the use of stochastic models may produce accurate results, which are provided in probabilistic terms, allowing the evaluation of the probability of occurrence of a certain outcome.

Fig. 1
figure 1

Modelling approach depending on the degree of knowledge (from Bedi and Harrison 2013)

Full size image

In view of these advantages, some literature studies for TBM performance prediction were developed by stochastic approaches, though their number is quite limited due to the high degree of knowledge required on the input parameters. Among them, Einstein (1996) adopted stochastic approaches in the planning of tunnel projects. Alber (2000) evaluated the probability distribution of AR on the basis of nine classes of tunnelling conditions. Isaksson and Stille (2005) used the Monte Carlo technique to estimate time and costs of completion of TBM tunnel projects. Frenzel (2012) provided a comparison between deterministic and stochastic approach, to determine PR and cutters wear on the basis of input parameters such as uniaxial compressive strength (UCS), Brazilian tensile strength and the Cerchar abrasivity index (CAI). Piaggio et al. (2013) used the Monte Carlo method together with CSM model (Rostami and Ozdemir 1993), to estimate the probability distribution of PR and AR for the safety gallery of the Fréjus Tunnel. Copur et al. (2014) implemented a stochastic model into a deterministic model, to assess the performance of two EPB TBMs, by defining the input variables on the basis of the results obtained from full-scale rock cutting tests. Maji and Theja (2017) provided a model for estimating PR through a stochastic approach, which incorporates the unpredictability of input parameters such as UCS, RMR, cutter life index and CAI.

This paper is devoted to the TBM performance prediction for a specific section of the Mont Cenis base tunnel (MCBT) planned to be parallel to a portion of the completed Maddalena exploratory tunnel. The observations made during the excavation of the exploratory tunnel, together with those obtained from similar projects reported in the literature, provided a high degree of knowledge of the input parameters involved in the machine performance prediction for the section of the MCBT analysed, thus allowing the use of a stochastic approach. Moreover, a preliminary design of the cutterhead was provided, according to the requirements of the design documents.

2 Mont Cenis Base Tunnel

2.1 General Overview of the Project

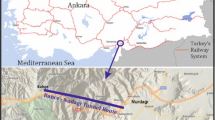
The MCTB will cross the route between Susa (Italy) and Saint-Jean-de-Maurienne (France), representing the core element in the construction of the new Lyon-Turin line (NLTL), which will be an essential component of the Mediterranean corridor of the trans-European transport network from Algeciras to Budapest. The MCBT final design currently involves a total tunnel length of 57.5 km (45 km in France and 12.5 km in Italy), consisting of two parallel tubes at a distance ranging from 25 to 40 m, with a final diameter of 8.4 m (Bufalini et al. 2017). Four access tunnels are planned (Fig. 2). One of them, the Maddalena exploratory tunnel, extends into Italy, with the portal located at La Maddalena, in the municipality of Chiomonte (Turin). It was completed in February 2017, with a final length of 7 km, and was driven by a 6.3 m diameter gripper TBM.

Fig. 2
figure 2

Scheme of the Mont Cenis base tunnel alignment (TELT Company)

Full size image

2.2 Section of the MCBT under Study

The TBM performance prediction provided in this paper concerns a particular section of the Italian side of the MCBT between pk 48 + 68 (close to the state border) and pk 51 + 64 (before the safety area). The alignment of this MCBT section (hereafter referred to as MCBTgripper) is planned to be parallel to the axis of the portion of the Maddalena exploratory tunnel between pk 3 + 955 and pk 6 + 915 (hereafter referred to as METpar). This condition allows for the extraction of critical information regarding the MCBTgripper, including geological features, rock mass properties and excavation conditions expected.

2.3 Information from Maddalena Exploratory Tunnel

2.3.1 Geological Features

The geological profile expected for the MCBTgripper is shown in Fig. 3. The MCBTgripper alignment crosses the Clarea complex, which is basically characterized by mica-schist. The main schistosity is on average oriented NE-SW and tends to incline at nearly horizontal angles. The most prevalent joint sets are substantially arranged on the schistosity or parallel to the tunnel axis. High-angle fault systems are also present, usually oriented along NE-SW directions, with a maximum thickness of a decimetre (Parisi et al. 2017).

Fig. 3
figure 3

Geological profile of the MCBTgripper, according to the observations made during the excavation of the METpar (TELT company)

Full size image

2.3.2 Rock Mass Properties

On the basis of the observations made during the METpar excavation, the rock mass properties expected in MCBTgripper are summarised in Table 1. Average RMR and GSI are 59 and 64, respectively. The rock is strongly anisotropic due to the schistosity, shown by the significant difference in UCS obtained for different test directions. The joint spacing usually ranges from 0.5 to 1.2 m. The water inflows are very limited. The extremely low values of the RMR partial rating related to joint orientation (P6RMR) are due to the joint sets arranged parallel to the tunnel axis.

Table 1 Summary of the distribution of rock mass parameters obtained from the geo-structural surveys performed during the excavation of the METpar
Full size table

2.3.3 Excavation Conditions

The rock mass conditions encountered in METpar involved a systematic rock blocks detachment from the crown and at the face of the tunnel, affecting the TBM performance. The blocks detachment from the tunnel crown involved a longer time to ensure the tunnel stability. The blocks release at the face of the tunnel resulted in frequent conveyor belt breakages, due to overly coarse rock fragments directly conveyed onto the belt. To deal with these issues, two main operational measures were taken during the excavation of the METpar: a vibrating sieve and a crusher were introduced to avoid the belt breakages, and a special support was adopted, consisting of steel ribs connected by steel rebars in the upper arch, to limit instability issues (Rispoli et al. 2018).

These conditions would suggest the use of a Shield TBM; however, the adoption of the above-mentioned measures allowed a significant improvement of the excavation conditions, resulting in an increase of the overall machine performance. On this basis, NLTL design documents (2017a) have planned that the MCBTgripper will be driven by a Gripper TBM, together with technical measures similar to those employed in METpar. Nonetheless, the TBM design for the MCBTgripper excavation has not yet been included in the design documents.

3 Cutterhead Preliminary Design

The cutterhead design was performed according to the requirements of the design documents (e.g., machine type and diameter), the observations made during the METpar excavation (e.g., rock mass boreability and excavation condition) and literature studies.

A nominal TBM diameter of 10 m with 63 cutters was selected for this study. On the basis of the characteristics of 262 TBMs, including 72 Gripper TBMs, Ates et al. (2014) provided relationships among several TBM parameters, such as machine diameter and weight, cutterhead thrust, torque and rotational speed, and number of cutters. Although a specific value of the MCBTgripper diameter is not currently included in the design documents, information is provided about the Single Shield Multi-mode TBM planned for the excavation of the other section on the Italian side of MCBT, with a diameter of 9.95 m and an additional 0.02 m for overcutting (NLTL design documents 2017b). On this basis, a nominal diameter of 10 m was chosen, with an average value of 63 cutters, based on a range of cutters between 60 and 65 (except those for overcutting) in Ates et al. (2014).

A disc cutter size of 19″ was chosen. Although an average normal cutter force lower than 200 kN was recorded during the excavation of the METpar, suggesting the use of 17″ disc cutters, further aspects should be taken into account. First, the use of larger cutters would allow for a higher limit of cutterhead rotational speed, which will be significantly lower than that of METpar, because of its higher cutterhead diameter. Second, the thrust level of the TBM recorded during the METpar excavation was also affected by the explorative nature of the tunnel, which sometimes led to a reduction of the operating level. However, in the excavation of MCBTgripper, reaching the maximum advance rate is a primary aim and consequently a thrust level higher than in METpar excavation may be necessary. Moreover, assuming that the TBM designed for the MCBTgripper could also be used in other sections of MCBT, different possible rock mass contexts should also be considered; e.g., Rispoli et al. (2018) showed that the load capacity of 17″ disc cutters was definitely not sufficient for an efficient rock chipping in the massive rock formation encountered in the first portion of the Maddalena exploratory tunnel, which lead to dramatic reductions of the net performance. Thus, 19″ discs were selected, allowing a longer cutter life as well (Ozdemir 1992; Roby et al. 2008).

A maximum thrust force of 25.5 MN was chosen, based on the total number of cutters and the load capacity of the 19″ disc cutters, namely 311 kN (Zou 2017). Moreover, according to Concilia (2003), a coefficient of 1.3 was adopted to take account of the friction losses in extraordinary excavation conditions (i.e., advancement axis adjustment).

According to Bilgin et al. (2008), the average cutter spacing was calculated as:

$$s=\frac{{\varnothing }_{\mathrm{TBM}}}{2\cdot {N}_{\mathrm{cutter}}}= \frac{10}{2\cdot 63}=0.0794\,\mathrm{ m},$$
(1)

where \(s\) is the average cutter spacing in m, \({\varnothing }_{\mathrm{TBM}}\) is the nominal diameter of the TBM in m and \({N}_{\mathrm{cutter}}\) is the number of cutters (except those for overcutting).

Assuming a 19″ disc cutter velocity limit of 200 m/min (Rostami 2008; Rostami and Chang 2017), the maximum cutterhead speed was obtained as:

$${\mathrm{RPM}}_{\mathrm{max}}=\frac{{V}_{\mathrm{max}}}{{\varnothing}_{\mathrm{TBM}}\cdot\uppi }= \frac{200}{10\cdot\uppi }=6.37\,\mathrm{ rev}/\mathrm{min},$$
(2)

where \({\mathrm{RPM}}_{\mathrm{max}}\) is the maximum cutterhead speed and \({V}_{\mathrm{max}}\) is the cutter velocity limit for 19″ cutters in m/min.

A maximum cutterhead torque of 9855 kN m was conservatively chosen, based on Ates et al. (2014), who, for a TBM diameter of 10 m, provided a torque around 6700 kN m with an additional 47% as upper limit.

The maximum cutterhead power was obtained as:

$$P=\frac{2\cdot \pi \cdot T\cdot {\mathrm{RPM}}_{\mathrm{max}}}{60}= \frac{2\cdot \pi \cdot 9855\cdot 6.3}{60}=6501.6\,\mathrm{ kW,}$$
(3)

where \(P\) is the maximum power in kW, \(T\) is the maximum torque kN m and \({\mathrm{RPM}}_{\mathrm{max}}\) is the maximum cutterhead speed in rev/min.

Since the MCBTgripper will cross quite fractured rock masses, using a cutterhead provided with a roof shield, similarly to the machine employed in METpar, is advisable, to protect the crew immediately behind the cutterhead from rock falls. Moreover, the cutterhead should be properly designed in order to reduce the wear that typically affects cutterhead and cutters in jointed rock mass conditions. In particular, as suggested by Delisio and Zhao (2014), it is advisable to build a flat-profile cutterhead for minimizing any protrusion to the tunnel face, to insert a cutter protection for preventing cutter breakages due to the impacts against the rock blocks detached from the tunnel face, and to reinforce the cutter housing structures.

Based on the above, the characteristics of the Gripper TBM preliminary designed for the MCBTgripper are summarised in Table 2.

Table 2 Technical characteristics of the Gripper TBM designed for the MCBTgripper excavation
Full size table

4 Stochastic Approach

According to Bedi and Harrison (2013), the best modelling approach should be selected on the basis of the degree of knowledge of the phenomenon analysed. In the case under study, the level of information provided from METpar, together with similar projects reported in the literature, appears to be suitable for an effective use of the stochastic approach. However, the reliability of the results obtained is highly dependent on the correctness of the assumptions reported in Table 3.

Table 3 Assumptions that are the basis of the stochastic approach used for TBM performance prediction in the MCBTgripper
Full size table

The stochastic modelling was carried out by means of a series of custom MATLAB (MathWorks) scripts and is based on the Monte Carlo technique (James 1980). Monte Carlo method involves the definition of the input variables by means of random sequences of numbers, which follow the probability distributions assigned to the variables involved. Starting from the generated random samples, a deterministic calculation is then applied to estimate the distribution of the output variables, according to the prediction model selected.

4.1 Prediction Model

The prediction model adopted is based on the following equations:

$$\mathrm{ROP}=\frac{{F}_{\mathrm{Nnet}}}{\mathrm{FPI}},$$
(4)
$$\mathrm{PR}=\frac{\mathrm{ROP}\cdot \mathrm{RPM}\cdot 60}{1000},$$
(5)
$$\mathrm{AR}=\frac{\mathrm{PR}\cdot \mathrm{UF}\cdot 24}{100},$$
(6)

where \(\mathrm{ROP}\) is the rate of penetration in mm/rev, \({F}_{\mathrm{Nnet}}\) is the net normal cutter force in kN, \(\mathrm{FPI}\) is the field penetration index in kN/mm, \(\mathrm{PR}\) is the penetration rate in m/h, \(\mathrm{RPM}\) is the cutterhead rotational speed in rev/min, \(\mathrm{AR}\) is the advance rate in m/d, and \(\mathrm{UF}\) is the machine utilization factor in %.

The input variables are FPI, excavation parameters (FNnet and RPM) and UF. ROP and PR, which are outputs of Eqs. (4) and (5), are inputs in Eqs. (5) and (6), respectively. Each input variable represents a risk variable of the phenomenon to be assessed, since a small deviation from its expected value may involve potentially misleading results (Copur et al. 2014).

FPI is an effective parameter for TBM performance prediction in geological contexts already excavated. It is defined as the ratio of net normal cutter force (FNnet) to ROP, resulting in an indication of the rock mass boreability. In general, high values of FPI are indicative of low boreability and vice versa. FPI was employed by several researchers for performance prediction modelling (e.g., Khademi Hamidi et al. 2010; Hassanpour et al. 2011; Delisio et al. 2013; Salimi et al. 2016; Zare Naghadehi and Ramezanzadeh 2017). However, FPI may produce misleading results if the new project involves significant differences in terms of thrust levels applied (Farrokh et al. 2012). Moreover, considerable differences in cutterhead and cutter characteristics may also involve a variation of FPI (Rispoli 2018). In the case under study, the variations in terms of mechanical factors that may affect FPI, passing from METpar to MCBTgripper, are related to an increase of the average cutter spacing and cutter diameters. Nevertheless, both the increase of cutter spacing (< 3 mm) and that of cutter diameter (2″) are quite limited. On the other hand, a different operating level is expected in MCBTgripper compared to METpar. Thus, in this study the value of FPI was selected on the basis of the thrust levels applied, according to the data from METpar.

The excavation parameters define the machine operating level, one of the most sensitive aspects in TBM performance prediction. In this regard, the basic philosophy in hard rock TBM excavation is to provide the highest advance rate, which however is not always achieved by the same driving choices. In particular, hard rock TBMs usually operate close to their limits of thrust and rotational speed in massive rock contexts (Rostami 2016), whereas an excessively high level of thrust in jointed rock mass implies a significant increase of wear and breakages on the cutterhead and cutters, resulting in a decrease of the utilization factors and hence of the advance rate (Delisio and Zhao 2014). In the case under study, as noted above, the operating level observed in METpar may differ from the one that will be kept in MCBTgripper, mainly due to the different characteristics of the TBMs employed. However, a similar driving philosophy is expected in MCBTgripper, in view of the same rock mass context excavated. On this basis, several scenarios of the operating level were considered, on the basis of the data from METpar and from similar projects from the literature.

To define ROP on the basis of FPI, reference was made to FNnet, namely the normal cutter force excluding the friction losses. In this regard, several factors, such as machine type and size, should be considered to assess the friction losses (Frenzel et al. 2012). For the same machine weight, Shield TBMs generally involve greater friction losses than Gripper TBMs, because of the friction between the shield and the rock mass. In Gripper TBMs without a partial shield (Open TBM), the friction losses depend basically on the resistance force generated by the front shoes of the cutterhead (Wittke 2007). On this basis, a proper assessment of the friction losses would require the execution of on-site TBM penetration tests (e.g., Bruland 1998; Gong et al. 2007; Balci and Tumac 2012; Bilgin et al. 2012; Frenzel et al. 2012; Yin et al. 2014; Macias 2016; Villeneuve 2017). In lack of such tests, several studies in literature assessed the friction losses as a proportion of the thrust applied or of the machine weight, respectively for Shield TBM or Open TBM (e.g., Wittke 2007; Bilgin et al. 2008; Delisio et al. 2014; Bilgin et al. 2014; Copur et al. 2014).

UF represents the parameter that allows the transition from net performance to overall performance. It is affected by operational factors (Bilgin et al. 2014), making an accurate prediction of AR quite complex. Nevertheless, useful information about UF can be once again obtained from METpar, considering that a same machine type and similar tunnel supports are planned for MCBTgripper.

4.2 Selection of the Input Variable Probability Distributions

The distribution of the selected input variables aims to define the aleatory variability caused by some factors affecting the TBM performance (Fig. 4). In particular, FPI was employed to define the variability of the rock mass boreability; FNnet and RPM define the variability of the machine operating level; UF accounts for the variability of the operational factors. An important issue to consider is the possible influence that each one of these factors exerts on the others. For this purpose, the analysis of the correlation between the input variables was performed (Sect. 4.3).

Fig. 4
figure 4

Factors variability defined by the input variables distribution (after Rispoli 2018)

Full size image

The input variable distributions were selected in accordance with the assumptions reported in Table 3, the results from METpar, literature studies, and technical characteristics of the TBM designed.

The reference datasets used for the analysis are the results of a further elaboration of data presented in Rispoli et al. (2018).

4.2.1 F Nnet

As noted in Sect. 4.1, the operating level in MCBTgripper may differ from that observed in METpar. As for the thrust level, a similar shape of the distribution is expected, considering the assumption No.5 of Table 3 (i.e., similar driving philosophy); on the other hand, an increase of the thrust applied is also likely, with the aim of the maximization of the penetration rate. This increase is however expected to be rather low, to avoid consequences in terms of utilization factor and therefore advance rate. On this basis, three main different scenarios of thrust level were considered starting from data of METpar:

\({F}_{\mathrm{Nnet}}={F}_{\mathrm{Nnet }({\mathrm{MET}}_{\mathrm{par}})}\)

\({F}_{\mathrm{Nnet}}={F}_{\mathrm{Nnet }({\mathrm{MET}}_{\mathrm{par}})}+10\mathrm{ kN}\)

\({F}_{\mathrm{Nnet}}={F}_{\mathrm{Nnet }({\mathrm{MET}}_{\mathrm{par}})}+20\mathrm{ kN}\)

An estimation was made to take into account the friction losses. As reported earlier, the friction losses of Open TBMs are generally estimated as a proportion of the machine weigh. However, the Gripper TBM employed in MCBTgripper will likely include a roof shield and this may involve additional thrust losses due to the friction with the rock blocks detached from the tunnel crown. Thus, since a frequent rock blocks detachment is expected during the excavation of the MCBTgripper, the friction losses were defined as a proportion of the thrust applied and, according to Bilgin et al. (2008), a coefficient of 1.2 was applied.

4.2.2 FPI

Since a similar thrust level between METpar and MCBTgripper is not guaranteed (e.g., scenarios no. 2 and no. 3), same values of FPI cannot be assumed, considering that FPI tends to decreases with increasing FNnet (Hamilton and Dollinger 1979). However, on the basis of the assumptions reported in Table 3 and the TBM characteristics selected, METpar and MCBTgripper show comparable mechanical and geological-geotechnical factors. Thus, it can be assumed that these two tunnels present the same relationship between FPI and ROP. Such a relationship, for a given rock mass context, is usually well fitted by a power function (e.g., Gong et al. 2007; Balci 2009; Yin et al. 2014; Villeneuve 2017) that can be expressed as follows:

$$\mathrm{FPI}=\mathrm{SRMBI}\cdot {\mathrm{ROP}}^{-c},$$
(7)

where \(\mathrm{SRMBI}\) is the specific rock mass boreability index proposed by Gong et al. (2007) and c is a fitting parameter.

Basis on the above, the FPI sample was selected by means of a detailed analysis of the FPI–ROP relationship observed in each tunnel portions of METpar with a uniform rock mass context. For this purpose, the datasets were developed according to the “survey” level of analysis. In such level of analysis each dataset is related to a tunnel section that showed the same overall rock mass properties (Rispoli et al. 2019). In Fig. 5 an example of the relationship between FPI and ROP for a tunnel section analysed is showed. FPI value was define for each tunnel section and thrust level by means of a specific Matlab code, which is able to:

  • define the equation of the power function (7) with the best fit with the data points;

  • define the FPI value for each scenario of FNnet according to the equation obtained.

Fig. 5
figure 5

Relation between FPI and ROP in the tunnel section within pk 4 + 090 – 4 + 108. Scenario no. 1: FNnet = 196.2 kN, FPI = 72.6 kN/mm, ROP = 2.7 mm. Scenario no. 2: FNnet = 206.2 kN, FPI = 51.2 kN/mm, ROP = 4.0 mm. Scenario no. 3: FNnet = 216.2 kN, FPI = 36.7 kN/mm, ROP = 5.9 mm

Full size image

4.2.3 RPM

A triangular distribution, which is commonly used for modelling the expert opinion (Copur et al. 2014), was selected for RPM, based on TBM characteristics together with the need of maximising PR. In this regard, an increase of RPM involves an increase of PR, but it may also result in extremely high rates of torque together with negative effects on cutters and cutterhead in fractured rock masses. The triangular distribution selected for all the scenarios is included in the range 5–6.3 rev/min, with the more frequent value around 6 rev/min, which was chosen by applying a reduction coefficient of 0.95 to the maximum rotational speed, according to Delisio et al. (2013), to consider the reduction of the RPM that is typically carried out in this rock mass context.

4.2.4 UF

A normal distribution with a mean value of 29.3% was chosen for UF, on the basis of data from METpar. In particular, Rispoli et al. (2018) showed that the introduction of the sieve/crusher system, as well as of the tunnel support with rebars, significantly affected the value of UF in the excavation of Maddalena exploratory tunnel. Since such measures are planned for MCBTgripper, the UF distribution was selected by considering only the portion of METpar after their introduction. Furthermore, it should be noted that an increase of the thrust level may sometimes involve a decrease of the UF due to cutterhead/cutter wear. However, the preventive measures in the cutterhead construction recommended in Sect. 3 should limit the negative effects caused by the increase of the thrust level. On this basis, the same UF distribution was considered for all the thrust level scenarios. In any case, the more the thrust levels of MCBTgripper and METpar are similar, the more UF distributions will be close.

4.3 Analysis of the Correlation Between the Input Variables

The correlation between input variables is one of the most sensitive and complex aspects in stochastic modelling. Disregarding it may produce quite misleading results (Smith et al. 1992; Wall 1997), because of modelling unrealistic scenarios, especially in presence of high values of correlation. However, taking account of it involves two main issues:

  • how to evaluate the correlation between the input variables involved;

  • how to take account of the correlation in the generation of data samples.

As for the first issue, an effective assessment of the correlation between input variables requires a deep knowledge of the variables involved, together with a comprehensive reference database, where a quantitative measure of the correlation can be obtained.

With regard to the second issue, numerous studies in the literature were focused on methods able to take account of the correlation in the random samples generation (e.g., Smith et al. 1992; Touran and Wiser 1992; Helton et al. 2006). Many of them refer to the Cholesky decomposition (e.g., Iman and Conover 1982; Haas 1999; Huang et al. 2013), which allows the factorization of a Hermitian and positive definite matrix into a lower triangular matrix and its conjugate transpose. By applying Cholesky decomposition to the correlation matrix assigned to the input variables involved, correlated samples can be obtained starting from the generated random samples. Briefly, a simple form of this procedure can be summarised as follows:

  • Generation of the random sequences of numbers related to the input variables involved (e.g., two input variables) and inclusion in a matrix (A):

    $$A=\left(\begin{array}{cc}{X}_{1}& {Y}_{1}\\ {X}_{2}& {Y}_{2}\\ .& .\\ .& .\\ {X}_{n}& {Y}_{n}\end{array}\right)$$
    (8)

    where \(X\) and \(Y\) are the two random samples generated, and \(n\) is their size.

  • Calculation of the matrix (C) through the Cholesky decomposition:

    $$R={C}^{T}\cdot C$$
    (9)

    where \(R\) is the correlation matrix assigned to the input variables, \(C\) and \({C}^{\mathrm{T}}\) are, respectively, an upper triangular matrix and its transpose.

  • Calculation of the new correlated samples:

    $${A}_{n}=A\cdot C$$
    (10)

    where \({A}_{n}\) is the matrix that includes the correlated samples.

In the case under study, the input variables are involved in the Eqs. (4), (5) and (6) of the prediction model. According to the assumptions reported in Table 3, the correlation conditions between the input variables can be evaluated on the basis of the datasets obtained from METpar, which present the correlation matrixes reported in Table 4. In particular, FPI and FNnet show a quite strong positive correlation, whereas ROP and RPM present a significant negative correlation. These conditions are due to the driving choices made during the excavation of METpar: the thrust tends to increase with decreasing rock mass boreability (i.e., increasing FPI); the rotational speed tends to decrease with increasing rate of penetration, to limit the torque consumption, as well as the cutters and cutterhead wear. The above-mentioned driving choices are quite common in TBM tunnelling when jointed rock mass are involved (Delisio and Zhao 2014). On the other hand, PR and UF show a very limited correlation.

Table 4 Correlation matrixes related to the input variables, on the basis of the results obtained from METpar
Full size table

On this basis, the correlation between FPI and FNnet, and between ROP and RPM was taken into account in the sample generation, whereas that one between PR and UF was disregarded. The correlation conditions between FPI and FNnet were directly ensured by the procedure used to define the FPI sample, described in Sect. 4.2.2. The correlation between ROP and RPM samples was obtain by means of the Cholesky decomposition.

4.4 Generation of Data Samples

The distribution of the data samples generated for each scenario of thrust level is shown in Fig. 6.

Fig. 6
figure 6

Distribution of the data samples generated. CDF is cumulative distribution function

Full size image

With regard to the samples related to Eq. (4), one data point of FNnet and FPI was defined for each tunnel section of METpar, according to the “survey” level of analysis described in Sect. 4.2.2, with a total of 106 tunnel sections considered. The FNnet sample was obtained on the basis of the data observed in METpar and the thrust level scenarios assumed. The FPI sample was developed by the analysis of the FPI–ROP relationship in METpar, using the process described in Sect. 4.2.2. Basically, data samples with a size of only 106 data points were used for the assessment of ROP by the Eq. (4). This is quite unusual in stochastic modelling by Monte Carlo technique, where data samples with a very large size are normally used. However, in this case the high level of knowledge available in terms of aleatory variability of the rock mass boreability, together with the strong relationship between FPI, FNnet and ROP, have recommended the use of this approach to avoid dramatic consequences in terms of reliability in the ROP assessment.

On the other hand, for the samples related to Eq. (5) and (6), each data sample was created by generating a set of 100,000 random numbers. The ROP sample was produced on the basis of the distribution with best fit with the “raw” sample of ROP obtained by applying Eq. (4) to the FPI and FNnet samples. The RPM sample was defined starting from an initial set of random numbers based on the triangular distribution described in Sect. 4.2.3, which was then adjusted by means of the Cholesky decomposition, applying the Eqs. (8), (9) and (10). The final RPM sample generated was able to be consistent both with the initial triangular distribution and with the correlation conditions considered, since a correlation coefficient of − 0.73 was obtained between ROP and RPM samples generated. Finally, the PR sample was created on the basis of ROP and RPM samples generated, using Eq. (5). In view of the observations made in Sect. 4.3, UF sample was not adjusted and refers to a normal distribution (Sect. 4.2.4).

4.5 Output Variables Assessment

Output variables were obtained by applying a deterministic calculation to the samples generated, according to Eqs. (4), (5) and (6). Before generating the output variables, the presence of unrealistic scenarios in the data samples was checked, on the basis of the characteristics of the TBM designed. In particular, FNnet should be consistent with the machine thrust capacity, RPM should not exceed the cutterhead rotational speed limit, and PR should be lower than 6 m/h, which is the maximum penetration rate allowed by the haulage system capacity.

The distribution of the output variables predicted by the stochastic approach for each thrust level scenario is shown in Fig. 7. As noted in the previous section, a ROP sample with a size of 106 data points was obtained as output variable of Eq. (4); then, a sample of 100,000 random numbers was generated as input variable of Eq. (5), on the basis of the distribution with the best fit with the original ROP sample, which is consistent with a lognormal distribution. The PR and AR samples obtained are also consistent with a lognormal distribution.

Fig. 7
figure 7

Distribution of the output variables predicted for the MCBTgripper by the stochastic approach. PDF is probability density function. CDF is cumulative distribution function. Scenario no. 1—ROP: PDF = lognormal (μ = 1.0191, σ = 0.2567); PR: PDF = lognormal (μ = − 0.0410, σ = 0.2264); AR: PDF = lognormal (μ = 1.8844, σ = 0.3229). Scenario no. 2—ROP: PDF = lognormal (μ = 1.3949, σ = 0.3352); PR: PDF = lognormal (μ = 0.3324, σ = 0.2993); AR: PDF = lognormal (μ = 2.2587, σ = 0.3771). Scenario no. 3—ROP: PDF = lognormal (μ = 1.7449, σ = 0.4077); PR: PDF = lognormal (μ = 0.6908, σ = 0.3751); AR: PDF = lognormal (μ = 2.6155, σ = 0.4420)

Full size image

5 Comparison Between the Parameters observed in METpar and Those Predicted for MCBTgripper

The average values of the parameters predicted for each thrust level scenario are reported in Table 5, together with the average values of the parameters observed in METpar.

Table 5 Comparison between the average values of the parameters observed in METpar and predicted by the stochastic approach for the three thrust level scenarios of MCBTgripper
Full size table

As for the input variables, the same values of FPI were considered between METpar and the scenario no. 1 of MCBTgripper, in view of the equivalent thrust level and rock mass context, whereas a decrease of the FPI values is found in the scenarios no. 2 and no. 3 due to the increase of the thrust level. A reduction in terms of RPM is observed from METpar to MCBTgripper, where the same average values are obtained in all the scenarios; in this regard, slight differences in the RPM distribution are found due to the adjustment of the RPM initial sample performed by the Cholesky decomposition, which is dependent on the different ROP samples generated. The UF of MCBTgripper was chosen on the basis of the data from METpar, according to the assumptions reported in Table 3; however, only the portion of METpar after the introduction of the operational improvements described in Sect. 4.2.4 was considered, resulting in the slight difference of the average values of UF observed between METpar and MCBTgripper.

The same ROP is observed in METpar and scenario No.1 due to the same values of FPI and FNnet. On the other hand, a dramatic increase of the ROP is found with increasing the thrust level, as shown in the scenarios no. 2 and no. 3; this increase is more than proportional, on the basis of the not linear relationship between FNnet and ROP for the same rock mass context.

Despite the same ROP, the reduction of RPM results in a decrease of PR passing from METpar to the scenario no. 1. The significant increase of ROP in the scenarios no. 2 and no. 3 however involves a PR higher than that of METpar. The same considerations can be extended to the values of AR, in view of the analogous values of UF.

Assuming an excavation length of 2.96 km, the total excavation time expected for a single tube of MCBTgripper can be assessed for the three scenarios considered. Moreover, according to the distribution provided for AR, the probability of occurrence of a certain outcome can also be estimated. In particular, in the scenario no. 1 the total excavation time is expected to be on average around 428 days and between 361 and 553 days with 50% chance. An average of around 288 excavation days is expected for the scenario no. 2, with a 50% chance that the total excavation time is between 238 and 396 days. For the last thrust level scenario, a total excavation time is expected to be around 197 days on average, and between 159 and 288 with 50% chance.

According to the results obtained by the stochastic approach, it can be concluded that an excavation time higher than METpar will be required in MCBTgripper if the same thrust level will be applied. An overall increase of 10 kN of FNnet will results in an advance rate that is on average around 1 m/day higher than that of METpar. A significant reduction of the excavation time is however expected if an overall increase of 20 kN of the FNnet will be performed during the excavation of MCBTgripper, with an average increase of more than 6 m/d in terms of advance rate compared than METpar. In this last scenario, it should be noted that the reliability of the assumptions made in terms of UF could be affected, due to the impact produced on the cutterhead and cutters wear by the increase of the thrust level, resulting in a reduction of the overall advance rate; nonetheless, these negative effects could be limited or avoided by the use of the preventive measures in the construction of the cutterhead described in Sect. 3.

6 Discussion and Conclusions

This study provided the TBM performance prediction for a specific section of the Mont Cenis base tunnel that is parallel to the last portion of the Maddalena exploratory tunnel. The observations made during the excavation of the exploratory tunnel supplied a high degree of knowledge about some of the key factors involved, including the rock mass boreability and the excavation conditions expected.

After designing the cutterhead according to the characteristics required by the design documents, the machine performance prediction was carried out by means of a stochastic approach based on a prediction model that includes FPI, FNnet, RPM and UF as input variables, and ROP, PR and AR as output variables. The impact of the driving choices on the TBM performance was investigated by considering three main different scenarios of thrust level. The values of FPI were selected by means of a detailed analysis of the FPI-ROP relationship. The correlation between the input variables was also taken into account in the generation of the data samples. The distribution of the output variables was provided, allowing the assessment of the probability of occurrence of the outcomes whose reliability is highly dependent on the accuracy of the initial assumptions made.

In conclusion, the use of stochastic approaches is recommended for TBM performance prediction when a high degree of knowledge about the input variables distribution is available, as in the case of the tunnel section analysed in this study. This solution is particularly valuable in the early stage of a tunnel project, considering that the probability of occurrence of a certain excavation time range can be assessed. In the other cases, the aleatory variability of the parameters involved cannot be properly addressed, and the use of other approaches is preferred.