Fracture Frequency and Block Volume Distribution in Rock Masses

Abstract

There are important potential engineering applications of a prediction model for rock mass block size distribution from linear fracture frequency measurements along scanlines on exposed rock walls along diamond drill cores, or along digitized borehole walls. These pertain to the characterization of rock masses in mining and geotechnical engineering projects either using rock mass classification systems or empirical equations for the reduction of rock mass parameters or numerical simulation codes. Another application is the resource estimation of decorative stone deposits using diamond drill coring or image analysis of borehole walls. In these cases, the resources are derived from the distribution of rock block volumes greater than a certain cut-off volume. It could be realized that such a prediction could lead apart from the evaluation of the measured decorative stone resources, also to the optimization of pit limits and the final estimation of proven reserves. Further, it could lead to optimization of block volume diamond wire cuts at the later stage of squaring of block volumes by comparing the final distribution after squaring with the original in situ block size distribution. Towards this aim and based on the results of a previous paper, we further elaborate: (a) on the composition of the method to characterize the fracture frequencies observed along diamond drill cores and (b) on the analytical prediction of the block volume distribution. Analytical model predictions are finally validated against actual production data from a white dolomitic marble quarry and they are compared with predictions of a more rigorous numerical simulation model based on a non-homogeneous Poisson process.

Appendices

Appendix A

Correction of Joint Orientation Bias

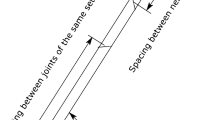
The true spacing $d$ between two adjacent joints of the same set assumed to be parallel to each other could be found from the apparent spacing $\hat{d}$ using the acute angle $\theta$ subtended between the normal to the joint planes and the borehole axis (Fig. 

Fig. 9

Apparent spacing between neighboring joints of the same set measured along the axis of a borehole and the true spacing measured along the normal line to the traces of joints on the vertical plane normal to the strike

9)

$$d = \hat{d}\cos \theta .$$

(A.1)

If the borehole is vertical, then the angle $\theta$ is simply the dip angle of discontinuity, otherwise $\cos \theta$ is determined from the scalar product of the unit vector ${\text{n}}$ directed normal to the joint planes of a set and of the vector ${\text{m}}$ directed along the borehole in the following manner:

$${\text{n}} \cdot {\text{m}} = \left| {\text{n}} \right| \cdot \left| {\text{m}} \right| \cdot \cos \theta ,$$

(A.2)

wherein bold small case letters denote vectors and $\left| {\; \cdot \;} \right|$ denotes the length of the vector it encloses. It is recalled that the unit normal vector of a plane of the i-th joint set with dip angle $\alpha_{i}$ and dip direction angle $\beta_{i}$ is defined as an 1 × 3 array as follows:

$${\text{n}} = \left[ {\sin \alpha_{i} \sin \beta_{i} \quad \sin \alpha_{i} \cos \beta_{i} \quad \cos \alpha_{i} } \right].$$

(A.3)

From the above expression and assuming a right-handed Cartesian coordinate system Oxyz the cosine factor may be derived as follows:

$$\cos \theta = \frac{{n_{x} m_{x} + n_{y} m_{y} + n_{z} m_{z} }}{{\sqrt {n_{x}^{2} + n_{y}^{2} + n_{z}^{2} } \sqrt {m_{x}^{2} + m_{y}^{2} + m_{z}^{2} } }}.$$

(A.4)

The unit vector of the borehole axis with trend $\beta$ and plunge $\alpha$ is defined as

$${\text{m}} = \left[ { - \sin \beta \cos \alpha \quad - \cos \beta \cos \alpha \quad \sin \alpha } \right].$$

(A.5)

Substituting Eqs. (A.3) and (A.5) into Eq. (A.2) it is found

$$\cos \theta = \cos \alpha_{i} \sin \alpha - \sin \alpha_{i} \cos \alpha \cos \left( {\beta_{i} - \beta } \right).$$

(A.6)

Block Face Area and Block Volume Calculation

The two parallel sides of the six-sided parallelepiped rock block shown in Fig. 

Fig. 10

Angles and edge lengths of a six-sided parallelepiped formed between three joint planes 1, 2, and 3

10 belong to the joint set 3 and they are formed by the intersection of the two parallel planes of discontinuity set 1 with true spacing $d_{1}$ and the two planes of discontinuity 2 with true spacing $d_{2}$. Then the area of each face of the same block corresponding to joint set 3 could be found as follows:

$$\begin{gathered} A_{3} = d_{23} d_{13} \sin \theta_{12} = \frac{{d_{1} }}{{\cos \theta_{23} }}\frac{{d_{2} }}{{\cos \theta_{13} }}\sin \theta_{12}^{{}} \hfill \\ = \frac{{\hat{d}_{1} \cos \theta_{1} }}{{\cos \theta_{23} }}\frac{{\hat{d}_{2} \cos \theta_{2} }}{{\cos \theta_{13} }}\sin \theta_{12}^{{}} , \hfill \\ \end{gathered}$$

(A.7)

where $d_{23} ,\;d_{13}$ denote the lengths of the edges formed by the intersections of planes 2,3 and 1,3, respectively, $\hat{d}_{1} ,\;\hat{d}_{2}$ are the apparent spacings of consecutive joints of sets 1,2, respectively, measured along the borehole, and $\theta_{1}^{{}} ,\;\theta_{2}$ are the acute angles subtended between the normal vectors to the joint planes 1, 2, respectively and the borehole axis.

The apparent frequencies $\hat{\lambda }_{i} ,\;i = 1,2,3$ of the pdf’s of each joint set inferred along a set of boreholes may be used to find the product of the basic joint frequencies that is used in the volume distribution function [i.e. Eq. (4)], as follows:

$$\lambda_{1} \lambda_{2} = \left( {\hat{\lambda }_{1} \frac{{\cos \theta_{23} }}{{\cos \theta_{1} }}} \right)\left( {\hat{\lambda }_{2} \frac{{\cos \theta_{13} }}{{\cos \theta_{2} }}\frac{1}{{\sin \theta_{12} }}} \right).$$

(A.8)

The angle $\theta_{12}$ formed between joint planes 1 and 2 is found from the vector product of the vectors of the edges formed by the intersection of planes 1 and 3 and of planes 2 and 3 in the following fashion:

$${\text{n}}_{{{13}}} \times {\text{n}}_{{{23}}} = \left| {{\text{n}}_{{{13}}} } \right| \cdot \left| {{\text{n}}_{{{23}}} } \right| \cdot \sin \theta_{12} \cdot {\text{n}}_{{3}} ,$$

(A.9)

with ${\text{n}}_{{{13}}}$, ${\text{n}}_{{{23}}}$ denoting the vectors of parallelogram edges and ${\text{n}}_{{3}}$ the unit normal vector of plane 3 defined by Eq. (A.3).The edge vectors ${\text{n}}_{{{13}}}$,${\text{n}}_{{{23}}}$ may be found from the vector product of the respective unit normal vectors of three joint planes (side 13 belongs to plane 1 and 3 and side 23 belongs to 2 and 3) in the following manner:

$${\text{n}}_{{{13}}} = {\text{n}}_{{1}} \times {\text{n}}_{{3}} ,\quad {\text{n}}_{{{23}}} = {\text{n}}_{{2}} \times {\text{n}}_{{3}} ,$$

(A.10)

where the normal unit vectors on the joint planes are found by recourse to Eq. (A.3).

Also the angles $\theta_{13}$ and $\theta_{23}$ can be found from the following scalar products:

$${\text{n}}_{{1}} \cdot {\text{n}}_{{{13}}} = \left| {{\text{n}}_{{1}} } \right| \cdot \left| {{\text{n}}_{{{13}}} } \right| \cdot \cos \theta_{13} {\text{, n}}_{{2}} \cdot {\text{n}}_{{{23}}} = \left| {{\text{n}}_{{2}} } \right| \cdot \left| {{\text{n}}_{{{23}}} } \right| \cdot \cos \theta_{23} .$$

(A.11)

In a final step of calculations performed in the Excel worksheet “Volume”, the volume of a block created from three repeated discontinuity sets is found by multiplying the area of the face given by Eq. (A.7) with the true distance (or spacing) between consecutive joints of the set 3, i.e.

$$V = A_{3} d_{3} = cf\hat{d}_{1} \hat{d}_{2} \hat{d}_{3} ,$$

(A.12)

where here the orientation correction factor denoted with the symbol cf is defined as follows:

$$cf = \frac{{\cos \theta_{1} \cos \theta_{2} \cos \theta_{3} \sin \theta_{12} }}{{\cos \theta_{23} \cos \theta_{13} }}.$$

(A.13)

By virtue of Eqs. (A.12) and (A.13), the apparent frequencies $\hat{\lambda }_{i} ,\;i = 1,2,3$ of the pdf’s of each joint set inferred along the boreholes may be employed for the calculation of the product of the basic joint frequencies, as follows:

$$\lambda_{1} \lambda_{2} \lambda_{3} = \left( {\hat{\lambda }_{1} \frac{{\cos \theta_{23} }}{{\cos \theta_{1} }}} \right)\left( {\hat{\lambda }_{2} \frac{{\cos \theta_{13} }}{{\cos \theta_{2} }}\frac{1}{{\sin \theta_{12} }}} \right)\left( {\frac{{\hat{\lambda }_{3} }}{{\cos \theta_{3} }}} \right).$$

(A.14)