1 Introduction

The Austrian Guideline ONR 24810 (On 2021) regulates the design of rockfall protection nets, embankments, and galleries. The design is based on the kinetic energy and bounce height of a so-called design block. The design block is specified as a percentile (P95-P98) of a recorded block size distribution (BSD), depending on the event frequency. BSDs may be determined from the detachment area (in the following referred to as in situ block size distribution—IBSD) and/or from the deposition area (in the following referred to as rockfall block size distribution—RBSD). The ONR 24810 proposes various methods to determine BSDs. In the detachment area, these include estimation by visual assessment, statistical IBSD and discrete explicit block measurement. In the deposition area, these include estimation, random axis measurements, the line-counting method, the area method, sieve analysis or photosieving by software (Gaich and Pötsch 2022).

Deposition areas, if available, are generally accessible and measurable without technical aids. However, most measuring methods are subjective, uncertain, not verifiable, or inaccurate. Blocks smaller than a fist are usually not measured. Often, (very) small block volumes are underrepresented, unnoticed or considered minor events and not included in rockfall inventories (De Biagi et al. 2017; Laimer 2019). This affects the percentiles of the BSD. Neglecting many small blocks in a BSD results in bigger P95–P98 blocks. In hazard analyses, smaller blocks may play an important role, depending on the protection target. For most realistic distributions of kinetic energy, bounce height and runout, the entire BSD should be considered in rockfall models (Illeditsch and Preh 2020). Also, rockfall blocks are often fragmented due to the preceding fall process. RBSDs determined from a few dozen blocks (or defined design blocks thereof) do not seem to be sufficient for meaningful rockfall modelling. If possible, IBSDs should (also) be considered. Visual assessment of rock faces seems subjective and not verifiable. Discrete explicit block measurements with rope access require intensive resources and time and are often unfeasible. The statistical method seems the most efficient and cost-effective method to determine IBSDs with many blocks within the full range of block sizes.

The distribution of in situ block sizes (IBSDs) is based on the knowledge that bedding, foliation and joints are commonly closely spaced and have low persistence. Wide spacing and high persistence joints are less common. Consequently, for rock blocks formed by joints, small blocks are more common than large blocks (Wyllie 2014). In a case study, Wyllie (2014), Chapter 8.3.1, estimates the means and standard deviations of lognormal distributions for the rockfall diameter [m] and thickness [m] of discoid-shaped blocks. Based on these distributions, he determines an IBSD [m3]. Priest and Hudson (1981) show a histogram of measured joint sizes [m] (i.e., persistence) in a Cambrian sandstone. They fit both exponential and lognormal curves to this data, for which the correlation coefficients r are 0.69 and 0.89, respectively. While the lognormal curve has a higher correlation coefficient, the exponential curve has a better fit at longer joint sizes. Hudson and Harrison (1997), Chapter 7.2.1, show that, when a sufficient large sample of individual joint spacings [m] (more than 200) is plotted in histogram form, a negative exponential distribution is often evident. Palmström (2000) measures the orientation and spacing of three joint sets on a horizontal and vertical surface. He cuts a cube of 10 m edge length by these joint sets and plots the distribution curve of the resulting blocks [m3] in logarithmic scale. The s-shaped curve reminds of a sieve curve. He suggests characterizing the curve with representative volumes, e.g., with the minimum, 25th, 50th and 75th and maximum percentile. Moos et al. (2021) sample eight RBSDs [m3] of different rockfall sites and fit them to a power law distribution of the form f(x, a, b) = ax−b. Generally, the calculated block volumes of certain return periods are significantly larger than the expert-based maximum block volumes. The fitted power law only corresponds well to the empirical data for block volumes ≥ 0.05 m3. There is a strong influence of parameter b on the modelled frequency.

Today, Palmström’s method of creating an IBSD by cutting a cube by joint sets can be applied in a more advanced way using synthetic rock mass (SRM) models. We asked whether IBSDs derived from SRM models can be described by probability distribution functions and if yes, how well. Because IBSDs are depending on the joint properties and they are often described by the lognormal and exponential distribution functions, we asked how well those functions describe IBSDs. Describing IBSDs by probability distribution functions could allow for more certain, accurate, verifiable, holistic, and objective results. For this purpose, we calculate different synthetic rock mass (SRM) models based on photogrammetric surveys by UAV (unmanned aerial vehicle). We carry out exact rock mass block surveys with the help of these models and determine IBSDs. We fit the lognormal, exponential, and various other distribution functions to the determined IBSDs. Finally, we compare the correlations between the IBSDs and the distribution functions using the KS test and the MSE method.

2 Method

We determine block size distributions from detachment areas (IBSDs) using synthetic rock mass (SRM) models, fit them to various distribution functions and check their correlations.

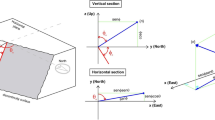
In SRM models, a discrete joint network (DFN) is intersected with a volume model to simulate the rock mass (Fig. 1). The central element here is the DFN. It statistically describes the geometric properties of the joint sets. For this purpose, we consider the distribution of the joint orientation, the joint density (e.g., number of joints per m; reciprocal of joint spacing) and the joint size distribution (persistence) for each individual joint set. A DFN results in a collection of disk-shaped joints whose geometric properties, such as location, orientation, density/intensity, and joint size distribution, are subject to a probability distribution. Thus, the joints created in this way do not represent the actual joints in the rock mass. Nevertheless, in this way it is possible to model the joint system very realistically.

Fig. 1
figure 1

Intersection of a volume model with a discrete fracture network (DFN) creates a synthetic rock mass (SRM) model

Full size image

In detail, the procedure starts with a survey of the rock face by unmanned aerial vehicle (UAV). We took several high-resolution photos of the rock face from different angles and distances with respect to the rock face. Thanks to integrated GPS within the UAV, we know the positions of where the photographs are taken. To create a 3D model by photogrammetry, it is necessary to clearly assign each point of the rock face from at least three different perspectives. From the overlapping photos, the software Agisoft Metashape (Agisoft 2021) creates a point cloud and triangulates it into a mesh. This results in a 3D digital elevation model (DEM) of the rock face. We analysed the point cloud regarding the orientation and distance of the joint sets using the CloudCompare software (Cloudcompare 2020). Joint orientations can be measured at the visible outcrops of the rock face. To measure orientations, CloudCompare creates a flat surface for a certain area if the correspondence of its containing points is large enough. The orientation of the created surface is specified with dip angle and dip direction. We can group the measured joints into joint sets. It is not possible to measure the joint spacings in CloudCompare directly. These are defined as normal distances between two joints of the same joint set, which are generally neither parallel nor at right angles to the rock face. However, by back-calculating to normal distances and averaging the measurements, we can derive joint spacings. Joint size (persistence) is another very important rock mass parameter. It can have a significant influence on the strength and stability of the rock slope. Pahl (1981) has developed a method and equations to calculate the approximate average joint size of a joint set. His method requires a cut-off of small joint sizes and provides an exact solution, if the joint size distribution can be assumed to be exponential. There has been considerable discussion in the literature as to whether the distribution of joint sizes is a negative exponential or a lognormal distribution (Hudson and Harrison 1997). However, in this case we are interested in block sizes of future rockfall events. They require full detachment from the rock face. Thus, we assume that the blocks are completely cut free by the intersecting joint sets. In other words, we assume 100% persistence for all joints.

Based on the above survey information, we can develop a discrete joint network (DFN). A DFN artificially reproduces the existing joint structure as realistically as possible. The joint orientations are created by the bootstrapping method. This method assumes that the available random sample is ‘representative’ of the population from which it is drawn. The bootstrap replaces the theoretical distribution function of a random variable by the empirical distribution function of the sample. So, it is obvious that bootstrapping only works well if the empirical distribution function can approximate the actual distribution function sufficiently well. This requires a certain size of the original sample. Bootstrapping can be understood as a Monte Carlo method, since it repeatedly draws random samples of a distribution. 3DEC offers the possibility to generate the joint spacings indirectly via the joint density or joint intensity. The joint density is defined as the area of joints per unit volume [m2/m3] (P32), or the length of joints per unit area [m/m2] (P21), or the number of joints per unit length [m−1] (P10). One square meter of joint in one cubic meter of the rock mass would correspond to a joint density of 1 [m2/m3]. The joint density depends only on the joint area per volume. So, several small joint areas can have the same density as a few large joint areas within the same volume. 3DEC models joint sizes as disks. The joint length, or generally the joint size, refers to the diameter of this disk. We can set the limits of the smallest and largest disk (lmin and lmax) in the software (Itasca 2020). In our case, we model disks that go through the entire model domain (100% persistence).

We simplified the determination of the joint density by counting the number of joints per length normal to the joints (P10), for each joint set. Assuming a persistence of 100%, the number of joints per unit length corresponds to the area of joints per unit volume, i.e., P10 = P21 = P32.

By intersecting the DEM with the DFN, we calculate the SRM model. We are not setting any strength parameters for the rock mass. We are only interested in the volume of the blocks. So, we can rather speak of a synthetic rock block model than a synthetic rock mass model. With the help of this model, we perform an exact rock mass block survey and determine a holistic IBSD.

The derived IBSDs represent block volumes [m3]. We want to check their correlations to various fitted continuous distributions by the Kolmogorov–Smirnov (KS) test and the mean-squared error (MSE) method. We are not interested in properties like density or porosity, which would be affected by cubic dimensions. In our case, it seems more appropriate to work with size distributions in linear dimensions [m] rather than in cubic dimensions [m3]. Furthermore, fitting distribution functions to linear dimensions can provide a more intuitive visual representation of the size distribution (e.g., grain sizes in a sieve curve). For these reasons, we are transferring the derived IBSDs from cubic meters to meters by taking the cube root.

We use Python to check our derived IBSDs against 79Footnote 1 distribution functions (Christopher 2017). Among them are also the lognormal and exponential distribution functions.

The probability density function (pdf) for lognorm is:

$$f\left( {x,s} \right) = \frac{1}{{sx\sqrt {2\pi } }} exp\left( { - \frac{{log^{2} \left( x \right)}}{{2s^{2} }}} \right)$$
(1)

for \(x > 0, s > 0\), where x is the random variable and s is the standard deviation. Lognorm takes \(s\) as a shape parameter. The probability density above is defined in the ‘standardized’ form. To shift and/or scale the distribution, the loc and scale parameters are used. Specifically, \({\text{lognorm}}.{\text{pdf}} \left({x,s,{\text{loc}},{\text{scale}}} \right)\) is identically equivalent to \(\frac{{{\text{lognorm}}.{\text{pdf}}\left( {y, s} \right)}}{{{\text{scale}}}}\) with \(y = \frac{{x - {\text{loc}}}}{{{\text{scale}}}}\). In case of a normally distributed random variable x with mean m and standard deviation s, y = exp(x) is normally distributed with standard deviation s and scale = exp(m).

The probability density function (pdf) for expon is:

$$f\left( x \right) = \exp \left( { - x} \right)$$
(2)

for \(x \ge 0\). The probability density above is defined in the ‘standardized’ form. To shift and/or scale the distribution, the loc and scale parameters are used. Specifically, \({\text{expon}}.{\text{pdf}}\left( {x,{\text{loc}},{\text{scale}}} \right)\) is identically equivalent to \(\frac{{{\text{expon}}.{\text{pdf}}\left( y \right)}}{{{\text{scale}}}}\) with \(y = \frac{{x - {\text{loc}}}}{{{\text{scale}}}}\). A common parametrization for expon is in terms of the rate parameter λ, such that \({\text{pdf}} = \lambda \cdot \exp \left( { - \lambda \cdot x} \right)\). This parametrization corresponds to using \({\text{scale}} = \frac{1}{\lambda }\).

The Kolmogorov–Smirnov test, also known as the KS test, is a nonparametric statistical test. It assesses whether a sample comes from a specific distribution. In other words, the test compares the observed data with the predicted data (also known as the one-sample KS test) under the null hypothesis that the two distributions are identical. It is sensitive to both location and shape differences between the sample and reference distributions. The KS test results in the test statistic (D) and the p value. These two components are essential in interpreting the outcome of the KS test. The test statistic (D) is a numerical value that compares the sum of vertical distances of all data points (supremum) of the cumulative distribution function (cdf) of the sample to the sum of vertical distances of all data points of the cdf of the reference distribution. The D value ranges between 0 and 1. A value of 0 means a perfect match between the sample and reference distribution. The p value is a probability that measures the strength of evidence against the null hypothesis. It determines whether the observed difference (D) is meaningful and reliable or can be attributed to random chance. If the p value is smaller than the chosen significance level (e.g., p ≤ 0.05), we can consider the result statistically significant. We can reject the null hypothesis in favour of concluding that the sample does not follow the reference distribution. If the p value is greater than the significance level, the result is not statistically significant. We cannot reject the null hypothesis. There is no sufficient evidence to claim a difference between the sample and the reference distribution. We choose a confidence level of 95%; that is, we reject the null hypothesis in favour of the alternative if the p value is less than 0.05 (i.e., 5%).

The mean-squared error (MSE) is a statistical metric, also known as the mean-squared deviation. It measures the average squared differences between the observed values and the predicted values in a dataset. It quantifies the accuracy of a prediction by assessing how well it fits the observed data points. For each data point, the squared difference between the observed value and the predicted value is calculated. Squaring the differences ensures that negative differences do not cancel out positive differences. All squared differences are summed up and divided by the total number of data points. This results in the average squared difference, which is the MSE. Lower MSE values indicate a better fit of the model to the data (Hedderich and Sachs 2020).

3 Results

We applied the described method to three different rock faces in three different areas within Lower Austria: Tiefenbach, Spitz and Greifenstein, as shown in Fig. 2.

Fig. 2
figure 2

Project areas (from West to East) Tiefenbach, Spitz and Greifenstein (black) within Lower Austria (Gba 2002)

Full size image

3.1 Tiefenbach

The rock face in Tiefenbach is in the West of Lower Austria, along the state road Greiner Straße (B 119) next to and along the Danube, which represents the border to Upper Austria there. The rock face is about 25 m high. The geological unit (Fig. 3) is the so-called Weinsberger Granite (38): coarse-grained biotite granite with porphyritic large potassium feldspar (Mississipium) next to metablastic to dialectic paragneiss (53), relics of biotite-rich paragneiss (‘pearl gneiss’) (Moser and Linner 2019).

Fig. 3
figure 3

Geological map (1:50 000) of the project area Tiefenbach. The red star marks the location of the rock face. The geological unit is the so-called Weinsberger Granite (38): coarse-grained biotite granite with porphyritic large potassium feldspar (Mississipium). The pink Xs mark fine-grained granitic dikes (Moser and Linner 2019)

Full size image

The 3D photogrammetry model of the Tiefenbach rock face is shown in Fig. 4left. We limited the structural geological analysis of the Tiefenbach rock face to the marked area in Red, because of the low vegetation outcrop. The investigated rock face has a length of about 38 m, a slope height of 20–25 m and an average inclination of 73°. Figure 4right shows the 3D point cloud model of the selected Tiefenbach rock face coloured according to the dip direction.

Fig. 4
figure 4

Left: 3D photogrammetry model (Agisoft 2021) of the Tiefenbach rock face. The structural geological analysis was limited to the marked area (red); Right: 3D point cloud model (Cloudcompare 2020) of the selected Tiefenbach rock face, coloured according to the dip direction (degrees): k1 (red), k2 (blue/yellow), k3 (green)

Full size image

The analysis via CloudCompare resulted in 102 joint orientations (Helm 2023). We grouped them into three joint sets: k1 (red), k2 (blue and yellow) and k3 (green) with 30, 58 and 14 measured orientations, respectively (Fig. 5). We used all measured joint orientation to generate the DFN. They provide a sufficiently large sample for bootstrapping. Table 1 lists the mean dip direction and dip, and the determined joint densities for each joint set.

Fig. 5
figure 5

Equal-area lower hemisphere plot of the 102 measured joints (great circles) and the slope (black) in Tiefenbach, using OpenStereo (Grohmann and Companha 2017); for the density plot, refer to Fig. 7(left)

Full size image
Table 1 Tiefenbach DFN data: joint directions and joint density
Full size table

The dimensions (x y z) of the model domain are approx. 230 × 500 × 100 m. We cut the model domain by two planes parallel to the slope (289/73) with a 50-m distance. The resulting 3D volume model of the slope is approx. 500 m long, 50 m deep (into the rock mass) and 100 m high. Figure 6 shows the joint sets of the rock mass slope in Tiefenbach, with the y axis pointing north. Figure 7 compares the equal-area lower hemisphere density plots of the 102 measured joint poles [left; using OpenStereo (Grohmann and Companha 2017)] and the 94 created joint poles in the SRM model (right) for Tiefenbach.

Fig. 6
figure 6

3DEC SRM model of Tiefenbach showing the block joint sets (y axis = north)

Full size image
Fig. 7
figure 7

Equal-area lower hemisphere density plots of the 102 measured joint poles (left; using OpenStereo; max ~ 337/76 and ~ 069/87) and the 407 created joint poles in the SRM model (right; using 3DEC; max. ~ 162/77) for Tiefenbach

Full size image

We derived 60,503 block volumes from the Tiefenbach SRM model. Assuming the block shape cuboid, we calculated their edge lengths by taking the cube root. The IBSD [m] of the Tiefenbach slope is plotted in Fig. 8. Our check against 79 different distribution functions with Python found that neither the exponential nor the lognormal distribution fits well. Rather, the generalized exponential distribution function fits best. We show this both graphically in Fig. 9 and numerically using the KS test and the mean-squared error (MSE) method (as described above).

Fig. 8
figure 8

IBSD of the Tiefenbach slope with 60,503 blocks (edge length a in [m])

Full size image
Fig. 9
figure 9

IBSD of the Tiefenbach slope [m] (blue bars) with the fitted exponential (maroon), lognormal (blue) and generalized exponential (green) probability density functions (left: pdfs, right: cdfs)

Full size image

The fitted parameters of the three tested continuous distribution functions and the KS test and MSE results are listed in Table 2. With a p value near 0.00, we reject the null hypothesis in favour of concluding that the sample does not follow the reference distributions. This is the case for the exponential (expon) and the lognormal (lognorm) distribution. With a p value of 0.58 (> 0.05), we cannot reject the null hypothesis. This indicates that there is no sufficient evidence to claim a difference between the sample and the generalized exponential (genexpon) reference distribution. Comparing the MSE values for the expon, lognorm and genexpon distribution functions, the genexpon distribution function has the lowest MSE value, indicating its best fit. A comparison of the quantiles is listed in Table 3.

Table 2 Fitting parameters of the fitted distribution functions and computational test results of the KS tests and MSE method; SRM Tiefenbach
Full size table
Table 3 Comparison of quantiles for the SRM Tiefenbach
Full size table

3.2 Spitz

The rock face in Spitz (Fig. 10) is a former marble quarry in the middle of Lower Austria, West of the state road Donau Straße (B 3) next to and along the Danube. The geological unit (Fig. 10) is marble, ribbon marble and silicate marble (46) (Fuchs et al. 1983). The 3D photogrammetry model of the Spitz rock face is shown in Fig. 11top. The investigated rock face has a length of about 70 m, a slope height of up to 30 m and an average inclination of 84°. Figure 11bottom shows the 3D point cloud model of the selected Spitz rock face coloured according to the dip direction.

Fig. 10
figure 10

Geological map (1:50 000) of the project area Spitz. The red star marks the location of the rock face. The geological unit is marble, ribbon marble and silicate marble (46) (Fuchs et al. 1983)

Full size image
Fig. 11
figure 11

Top: 3D photogrammetry model (Agisoft 2021) of the Spitz rock face; bottom: 3D point cloud model of the selected Spitz rock face, coloured according to the dip direction (degrees): SE (green), N/S (red/cyan), NW (purple)

Full size image

The analysis via CloudCompare resulted in three main joint sets forming the rock face: SE, N and NW with 132, 55 and 21 (total 208) measured orientations, respectively (Fig. 12). To generate the DFN, all measured joint orientations are used to provide a sufficient large sample for bootstrapping. Table 4 lists the mean dip direction and dip, as well as the determined mass densities and joint size for each joint set.

Fig. 12
figure 12

Equal-area lower hemisphere plot of the 208 measured joints (great circles) and the slope (black) in Spitz, using OpenStereo; for the density plot, refer to Fig. 14 (left)

Full size image
Table 4 Spitz DFN data: joint directions and joint density
Full size table

The dimensions (x y z) of the model domain are approx. 500 × 100 × 100 m. We cut the model domain by two planes parallel to the slope (356/84) with a 50-m distance. The resulting 3D volume model of the slope is approx. 500 m long, 50 m deep (into the rock mass) and 100 m high. Figure 13 shows the joint sets of the rock mass slope in Spitz, with the y axis pointing north. Figure 14 compares the equal-area lower hemisphere density plots of the 208 measured joint poles (left) and the 174 created joint poles in the SRM model (right) for Spitz.

Fig. 13
figure 13

3DEC SRM model of Spitz showing the block joint sets (y axis = north)

Full size image
Fig. 14
figure 14

Equal-area lower hemisphere density plots of the 208 measured joint poles (left; using OpenStereo; max ~ 356/85 and ~ 135/40) and the 185 created joint poles in the SRM model (right; using 3DEC; max. ~ 303/80) for Spitz

Full size image

We derived 26,253 block volumes from the Spitz SRM model. Assuming the block shape cuboid, we calculated their edge lengths by taking the cube root. The IBSD [m] of the Spitz slope is plotted in Fig. 15. Our check against 79 different distribution functions with Python found that neither the exponential nor the lognormal distribution fits well. Rather, the generalized exponential distribution function fits best. We show this both graphically in Fig. 16 and numerically using the KS test and the mean-squared error (MSE) method (as described above).

Fig. 15
figure 15

IBSD of the Spitz slope with 26,253 blocks (edge length a in [m])

Full size image
Fig. 16
figure 16

IBSD of the Spitz slope [m] (blue bars) with the fitted exponential (maroon), lognormal (blue) and generalized exponential (green) probability density functions (left: pdfs, right: cdfs)

Full size image

The fitted parameters of the three tested continuous distribution functions and the KS test and MSE results are listed in Table 5. With a p value near 0.00, we reject the null hypothesis in favour of concluding that the sample does not follow the reference distributions. This is the case for the exponential (expon) and the lognormal (lognorm) distribution. With a p value of 0.16 (> 0.05), we cannot reject the null hypothesis. This indicates that there is no sufficient evidence to claim a difference between the sample and the generalized exponential (genexpon) reference distribution. Comparing the MSE values for the expon, lognorm and genexpon distribution functions, the genexpon distribution function has the lowest MSE value, indicating its best fit. A comparison of the quantiles is listed in Table 6.

Table 5 Fitting parameters of the fitted distribution functions and computational test results of the KS tests and MSE method; SRM Spitz
Full size table
Table 6 Comparison of quantiles for the SRM Spitz
Full size table

3.3 Greifenstein

The rock face in Greifenstein is within a former quarry (until 1993) and landfill North of Vienna, also close to the Danube, located within the Rhenodanubian flysch zone (Figs. 17, 18). This zone extends from Vienna to Vorarlberg north of the northern Limestone Alps. Basically, the flysch zone was formed by sedimentary depositional processes of rivers in the sea of that time. Due to the different flow velocities, sedimentary layers of different thickness were formed. About 42 million years ago, the ‘Eurasian Plate’ and the ‘Adriatic Plate’ collided and the flysch zone came to the surface (Egger and Coric 2017). The easternmost part of this Rhenodanubian flysch zone is called the Greifenstein Formation (58): fine- to coarse-grained, medium- to thick-bedded, siliciclastic sandstone and clay shale (Ypresium) (Kreuss 2020).

Fig. 17
figure 17

Top: 3D photogrammetry model (Agisoft 2021) of the Greifenstein rock face; Bottom: 3D point cloud model of the selected Greifenstein rock face, coloured according to the dip direction (degrees): bedding (light blue), N (red), SW/NE (blue/yellow)

Full size image
Fig. 18
figure 18

Geological map (1:50 000) of the project area Greifenstein. The red star marks the location of the rock face. The geological unit is the so-called Greifenstein Formation (58): fine- to coarse-grained, medium- to thick-bedded, siliciclastic sandstone and clay shale (Ypresium) (Kreuss 2020)

Full size image

The 3D photogrammetry model of the Greifenstein rock face is shown in Fig. 17top. The investigated rock face has a length of about 80 m, a slope height of 20–27 m and an average inclination of 70° (Wiesinger 2023). Figure 17bottom shows the 3D point cloud model of the selected Greifenstein rock face coloured according to the dip direction.

The structural geological analysis of the Greifenstein 3D rock face model resulted in 143 joint orientations, which could be grouped into three joint sets: the bedding, the Northeast-Southwest joint set and the North joint set (Fig. 19) (Wiesinger 2023). To generate the DFN, all measured joint orientations are used to provide a sufficient large sample for bootstrapping. Table 7 lists the mean dip direction and dip, as well as the determined mass densities and joint size for each joint set.

Fig. 19
figure 19

Equal-area lower hemisphere plot of the measured joints (great circles) and the slope (black) in Greifenstein, using OpenStereo; for the density plot refer to Fig. 21 (left)

Full size image
Table 7 Greifenstein DFN data: joint directions and joint density
Full size table

The dimensions (x y z) of the model domain are approx. 200 × 160 × 40 m. We cut the model domain by two planes parallel to the slope (011/70) with a 20-m distance. The resulting 3D volume model of the slope is approx. 200 m long, 20 m deep (into the rock mass) and 40 m high. Figure 20 shows the joint sets of the rock mass slope in Greifenstein, with the y axis pointing north. Figure 21 compares the equal-area lower hemisphere density plots of the 143 measured joint poles (left) and the 381 created joint poles in the SRM model (right) for Greifenstein.

Fig. 20
figure 20

3DEC SRM model of Greifenstein showing the block joint sets (y axis = north)

Full size image
Fig. 21
figure 21

Equal-area lower hemisphere density plots for Greifenstein; of the 143 measured joint poles (left; using OpenStereo; max. ~ 357/65); and the 381 created joint poles in the SRM model (right; using 3DEC; max. ~ 135/23)

Full size image

We derived 143,029 block volumes from the Greifenstein SRM model. Assuming the block shape cuboid, we calculated their edge lengths by taking the cube root. The IBSD [m] of the Greifenstein slope is plotted in Fig. 22. Our check against 79 different distribution functions with Python found that neither the exponential nor the lognormal distribution fits well. Rather, the generalized exponential distribution function fits best. We show this both graphically in Fig. 23 and numerically using the KS test and the mean-squared error (MSE) method (as described above).

Fig. 22
figure 22

IBSD of the Greifenstein slope with 143,029 blocks (edge length a in [m])

Full size image
Fig. 23
figure 23

IBSD of the Greifenstein slope [m] (blue bars) with the fitted exponential (maroon), lognormal (blue) and generalized exponential (green) probability density functions (left: pdfs, right: cdfs)

Full size image

The fitted parameters of the three tested continuous distribution functions and the KS test and MSE results are listed in Table 8. With a p value near 0.00, we reject the null hypothesis in favour of concluding that the sample does not follow the reference distributions. This is the case for the exponential (expon) and the lognormal (lognorm) distribution. With a p value of 0.58 (> 0.71), we cannot reject the null hypothesis. This indicates that there is no sufficient evidence to claim a difference between the sample and the generalized exponential (genexpon) reference distribution. Comparing the MSE values for the expon, lognorm and genexpon distribution functions, the genexpon distribution function has the lowest MSE value, indicating its best fit. A comparison of the quantiles is listed in Table 9.

Table 8 Fitting parameters of the fitted distribution functions and computational test results of the KS tests and MSE method; SRM Greifenstein
Full size table
Table 9 Comparison of quantiles for the SRM Greifenstein
Full size table

Additionally, we have examined whether there is a difference between the block size distribution derived from a rock slope and a block size distribution derived from the rock mass (i.e., a cube) in the example of Greifenstein. The dimensions (x y z) of the model domain are approx. 60 × 60 × 60 m. Figure 24 shows the joint sets of the rock mass cube in Greifenstein, with the y-axis pointing north. 134,711 block volumes were derived from the SRM model, and assuming the block shape cuboid, their edge lengths were calculated taking the cube root. The distributions of the block sizes are plotted in Fig. 25. Again, neither the exponential nor lognormal distributions fit well. Rather, the generalized exponential distribution function fits best. We show this both graphically in Fig. 26 and numerically using the KS test and the mean-squared error (MSE) method (as described above).

Fig. 24
figure 24

3DEC SRM model of the Greifenstein 60 m cube showing the block joint sets (y axis = north)

Full size image
Fig. 25
figure 25

IBSD of Greifenstein 60 m cube with 134,711 blocks (edge length a in [m])

Full size image
Fig. 26
figure 26

IBSD of the Greifenstein 60 m cube [m] (blue bars) with the fitted exponential (maroon), lognormal (blue) and generalized exponential (green) probability density functions (left: pdfs, right: cdfs)

Full size image

The fitted parameters of the three tested continuous distribution functions and the KS test and MSE results are listed in Table 10. With a p value near 0.00, we reject the null hypothesis in favour of concluding that the sample does not follow the reference distributions. This is the case for the exponential (expon) and the lognormal (lognorm) distribution. With a p value of 0.09 (> 0.05) we cannot reject the null hypothesis. This indicates that there is no sufficient evidence to claim a difference between the sample and the generalized exponential (genexpon) reference distribution. Comparing the MSE values for the expon, lognorm and genexpon distribution functions, the genexpon distribution function has the lowest MSE value, indicating its best fit. A comparison of the quantiles is listed in Table 11.

Table 10 Fitting parameters of the fitted distribution functions and computational test results of the KS tests and MSE method; SRM Greifenstein 60 m cube
Full size table
Table 11 Comparison of quantiles for the SRM Greifenstein cube 60 m
Full size table

4 Discussion

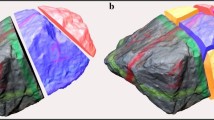
The equal-area density plots proof that it is possible to represent joint systems using a DFN. The joint orientations of the left and right density plots correspond very well (see Figs. 7, 14, 21). The pole densities of the measured joint planes (left plots) represent joints exposed on the rock face. So, wall-building joints may be measured more frequently than other joints. This can lead to a situation where joint surfaces of lower joint density (with greater joint distances) are measured more frequently on the rock face, and vice versa. Thus, measurements from the rock face may be distorted. The SRM density plots (on the right) reflect the ‘true’ joint densities of the joint sets (relative to each other). For example, in Greifenstein (Fig. 21, left) the joint set N (357/65, red) is dominating on the rock face and measured more frequently than the bedding (135/23, light blue). The surface areas (outcrops) of the bedding are very small. Yet, the bedding has a much higher joint density than the other two joint sets. This is reflected in the density plot in Fig. 21 on the right. We can conclude that the density plot of the SRM is more realistic and more meaningful than the density plot of the measured joints on the rock face.

We chose the slope and cube dimensions of the SRM models to create many blocks for our investigations. In Tiefenbach, a slope size of approximately 500 × 50 × 100 m generated 60,503 block volumes. In Spitz, a similar slope size generated 26,253 block volumes. In Greifenstein, with a bedding of relatively high joint density, a slope size of approximately 200 × 20 × 40 m generated 143,029 block volumes, and the Greifenstein 60 m cube generated 134,711 block volumes. The size of the model should correspond to the homogeneous area investigated.

We show that neither the lognormal nor the exponential distribution functions describe IBSDs [m] well. To fit best, the lognormal is shifted with a negative loc parameter. This results in negative block volumes. Both, the lognorm and expon have relatively long tails. This results in much larger blocks compared to the IBSDs. We also tried to fit Python’s power law distribution in the form f(x, a) = axa−1 to our derived IBSDs (both in [m3] and in [m]). No correlations could be found. The generalized exponential distribution function best describes block size distributions [m] across three various lithologies when compared to 78 other distribution functions via the one-sample KS test and the MSE method.

The probability density function (pdf) for genexpon is:

$$f\left( {x,a,b,c} \right) = \left( {a + b\left( {1 - \exp \left( { - cx} \right)} \right)} \right)\exp \left( { - ax - bx + \frac{b}{c}\left( {1 - \exp \left( { - cx} \right)} \right)} \right)$$
(3)

for \(x \ge 0, a,b,c > 0\), where x is the random variable and a, b, and c are shape parameters. The probability density above is defined in the ‘standardized’ form. To shift and/or scale the distribution, the loc and scale parameters are used. Specifically, \({\text{genexpon}}.{\text{pdf}}\left( {x,a,b,c,{\text{loc}},{\text{scale}}} \right)\) is identically equivalent to \(\frac{{{\text{genexpon}}.{\text{pdf}}\left( {y,a,b,c} \right)}}{{{\text{scale}}}}\) with \(y = \frac{{x - {\text{loc}}}}{{{\text{scale}}}}\). Above generalized exponential distribution is an extension of Marshall and Olkin’s bivariate exponential distribution (Ryu 1993). The three shape parameters provide quite a bit of flexibility for analysing any skewed dataset. Table 12 lists the genexpon fitting parameters for the different investigated slope and cube sizes. The location parameters are essentially zero.

Table 12 Genexpon fitting parameters for the investigated locations Tiefenbach (slope size 500 × 50 × 100 m), Spitz (slope size 500 × 50 × 100 m) and Greifenstein (slope size 200 × 20 × 40 m and 60 m cube)
Full size table

For the Greifenstein slope and the Greifenstein cube calculations, we used the same DFN data (Table 7). The models differ in their dimensions and orientation. We cut the slope model parallel to the mean rock face orientation. The cube model is north–south oriented, independent of the observed rock face orientation. Comparing the results (Table 12), the genexpon fitting parameters, especially b and c, do vary. It is unclear how these differences affect rockfall modelling results. Modelling a cube, independent of the slope direction, would be much more practicable when investigating a quarry, for example. Further investigations on the sensitivity of the scale and shape parameters are required. Comparing the quantiles of the Greifenstein slope and the Greifenstein cube models (Table 13), the blocks of the cube model are generally slightly bigger. Due to the bigger dimensions of the cube in the y direction (20 m vs. 60 m), bigger blocks are built. The maximum block volumes depend on the size of the homogeneous area, as also recognized by Laimer (2019) and Moos et al. (2021).

Table 13 Comparison of quantiles [m] for different SRM models
Full size table

The DFN- and genexpon-quantiles correspond very well (see Table 13). Comparing the P98 of the genexpon cdfs, the block sizes seem plausible, considering the different lithologies and joint systems. In Spitz, where we could observe huge marble blocks in the deposition area (Fig. 27left), the P98 block edge length in the genexpon cdf is 8 m (512 m3). In Greifenstein, where we could observe a sandstone bedding of relatively high joint density (Fig. 27right), the P98 block edge length in the genexpon cdf is approximately 2 m (8 m3). The P98 block edge length in the genexpon cdf of the Tiefenbach granite lies in between, with approximately 6 m (216 m3).

Fig. 27
figure 27

Photographs of the deposition areas; left: Spitz with huge marble blocks versus right: Greifenstein with smaller sandstone blocks due to rather dense bedding

Full size image

As already criticized by Laimer (2019), the use of P95–P98 appears too high for rock formations, which form very large rockfall blocks (> 10 m3). He had sufficient data from the Dachstein Formation (limestones and dolomites) to show that the return periods of P95 to P96 blocks (0.15–2.25 m3) range from 23.5 to 56.5 years for this formation. This corresponds to the service life of a conventional rockfall protection barrier. P97 and P98 limestone blocks have return periods of more than 100 years.

In our holistic rock mass block investigations of relatively large rock masses (homogeneous areas), the problem of very large (P95–P98) blocks becomes even more apparent. Our SRM approach does not consider whether blocks are kinematically capable of failure. IBSDs can include blocks with very high return periods. One approach to deal with this problem could be a kinematic analysis of the blocks using block theory (Goodman and Shi 1985). However, this approach does not consider return periods. In the design of rockfall protection measures and hazard analyses, rockfall frequencies (magnitude to frequency relations M/F (Corominas et al. 2018)) and return periods play an important role. This requires knowledge of the events on the one hand and the definition of a worst-case scenario (depending on the protection target) on the other. Our IBSD provides knowledge of all possible events within a homogenous area, including their frequencies (i.e., magnitude to frequency relations). Based on a defined worst-case scenario, events/block sizes of higher return periods may be neglected (cut off). This could be achieved based on (limited) available information, such as silent witnesses with estimated ages, reports from residents or records of past events.

5 Conclusion and outlook

We were able to find a probability distribution function that describes in situ block size distributions (IBSDs) very well. It could be generally applicable for block size distributions (BSDs). Further investigations on the sensitivity of the scale and shape parameters are required. We show that both the lognormal and the exponential distribution functions do not describe IBSDs well enough. Describing IBSDs by probability distribution functions could provide more certain, accurate, verifiable, holistic, and objective results. With the presented method, it is possible to determine IBSDs based on photogrammetry and SRM models. The investigation of many more sites of different lithologies with this method could lead to a catalogue that recommends a range of scale and shape parameters for specific lithologies in the future. This requires locations of sufficiently large outcrops with low vegetation. The implications on rockfall modelling should be further investigated, for example, by comparing runout, kinetic energies, and bounce heights when modelling whole IBSDs versus genexpon pdfs and design blocks. The use of a distribution function together with a catalogue of suitable fitting parameters can offer the advantage that the determination of an IBSD, and thus, a meaningful evaluation of a design block is also possible with a limited number of block size measurements (silent witnesses).