1 Introduction

In view of ongoing urban expansions worldwide, underground space of fractured rock is increasingly used, the most common uses being related to infrastructure such as transportation, electricity cables or fresh/wastewater facilities. Examples of future, more challenging uses of rock are repositories for highly radioactive waste, or mercury, planned for instance in deep crystalline formations. For such facilities, not only is the constructability important, but even more so the long-term performance and safety. A key to a successful construction and realistic safety assessment of any facility is a well-characterised rock, where flow and transport properties are accurately inferred. The more common rock constructions may accept larger uncertainties, using simpler tools. It is, though, still important to have an estimate of the uncertainty magnitudes in order to be able to make a good interpretation of the rock mass.

Together with size, intensity and spatial correlation, information about orientation of geological structures such as fractures and rock contacts and lineated objects such as foliations and rock stresses is important for stability, flow and transport modelling. Prior to any excavated tunnel, the only possibility to obtain highly detailed information at great depths on this is through boreholes drilled from the surface. The orientation of the object is hence dependent on the orientation of the borehole.

Due to the uncertainties arising during the measurements, the inferred orientation differs from the true orientation. Hence, using these measured orientations values, neglecting the uncertainties, will result in an erroneously inferred orientation model of the rock mass.

Despite the importance of correctly characterising the fracture population, limited number of attempts to estimate the magnitudes of the uncertainties is found in the literature. According to Orpen (2007), there has historically been little interest in evaluating the orientation uncertainty of borehole directions. However, lately there has been made some attempts to measure the spatial uncertainty of the borehole (Wolmarans 2005; Devico 2015; Nilsson 2015). Unfortunately for the present application, all of these attempts are made in subhorizontal boreholes with focus on the spatial uncertainty rather than the angular uncertainty. An exception is the test facility in Spring Creek Mine (Solid Energy New Zealand Ltd 2015) where the overall inclination is around −30°, with more focus on the angular uncertainty.

Any attempt to quantify the uncertainty of the objects measured in a borehole dates back to the late eighties. At that time, the petroleum industry reported several advancements (Bleakly et al. 1985a, b; Nelson et al. 1987) where the magnitude of the orientation uncertainty for fractures was estimated using a mechanical goniometer on oriented cores. The uncertainty was stated as a rough estimation by simply adding scalar values to a one-parameter uncertainty.

Except for the initial work carried out at the Swedish Nuclear Fuel and Waste Management Co., SKB (Stigsson et al 2014; Stigsson and Munier 2012, 2013; Munier and Stigsson 2007), no attempts to comprehensively evaluate the uncertainty space of objects measured in cored boreholes are available in the literature. The present work, hence, aims to fill this gap by: (1) defining the different sources that may affect the orientation uncertainty; (2) proposing evaluation methods and deriving equations for the inference of the magnitudes of the uncertainties; and (3) briefly pointing out problems arising due to the uncertainties but also noting potential benefits when one more fully understands and quantifies the uncertainty space.

The paper is organised as follows. In the next section, all conceivable sources of uncertainty are addressed individually, using the comprehensive data from 70 boreholes, acquired in Swedish rock by SKB. Next, aggregated uncertainty from all these sources and its potential effects are discussed followed by a summary and, lastly, some concluding remarks.

2 Sources of Uncertainty

During the investigations for siting a repository for spent nuclear fuel, at Laxemar or Forsmark, in Sweden (SKB 2008, 2009) more than 70 cored boreholes were drilled to a maximum length of 1000 m. Almost 200,000 fracture intercepts were characterised along the more than 34 km of mapped core. These fracture intercepts and borehole orientation measurements together with the experience gained during the site investigations are used to develop and quantify the uncertainty models.

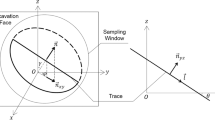
There are different ways to calculate the orientation of a fracture mapped in a borehole. In this work, a method where the bearing (or azimuth) and inclination (sometimes referred to as pitch) of the borehole are used, together with two angles, α and β, relative to the borehole (the acute dihedral angle between the fracture plane and local trajectory of the borehole, and the rotation angle from the crown of the borehole profile to the lower inflexion point of the fracture trace on the borehole wall, respectively; for details, see Stigsson and Munier 2013), to calculate the trend and plunge of the fracture normal pole. The trend, plunge, bearing and inclination are thus angles related to a global coordinate system, whilst the α and β angles are relative to a local coordinate system along the core. According to e.g. Stigsson and Munier (2013) the fracture normal pole orientation can be calculated according to Eq. (1).

$${\mathbf{n}}_{\text{G}} = {\mathbf{Z}}_{\text{rot}} \cdot {\mathbf{Y}}_{\text{rot}} \cdot{\mathbf{n}}_{\text{BH}}$$
(1)

where n denotes the fracture normal pole vector in global, G, and borehole, BH, coordinate system, and Y rot and Z rot are two rotation matrices.

The method of inferring the orientation includes six steps: (1) the diameter of the borehole is measured along the borehole; (2) the orientation of the borehole is measured along the borehole; (3) the inside of the borehole is filmed using borehole TV; (4) the borehole imagery is semiautomatically oriented; (5) the α and β angles are measured on the borehole TV image or directly on the core; and (6) Eq. (1) is used to calculate the orientation of the fracture. All of the measurements introduce some degree of uncertainty that adds up to a total uncertainty of the orientation, denoted as the aggregated uncertainty, χ (see further Sect. 3).

2.1 Inherent Uncertainty of the Tools

The uncertainty that originates from the measuring device itself, given by the manufacturer under ideal conditions, is often negligible. This uncertainty serves as the minimum uncertainty which can not be avoided. Despite that the stated uncertainty often is small, it can, under unfavourable condition, result in an unexpectedly large uncertainty for the total uncertainty of the measured structure (see further Sect. 2.6). Different brands using the same or different techniques to measure a quantity may be available which may affect the uncertainty. For example, Sindle et al (2006) evaluated the uncertainties or errors for a few devices measuring the borehole orientation.

The uncertainty of a measurement contains both the inherent uncertainty, and the uncertainty due to usage. There is, hence, no need to quantify inherent uncertainty alone but the total uncertainty for the parameter measured, unless there is a bias of the tool.

2.2 Solar Flares and Space Weather Effects

Solar flares and space weather disturb the magnetic field around the earth and consequently tools using magnetic compasses to measure orientations are affected. This disturbance is measured at several places around the world (INTERMAGNET 2015). Figure 1 shows two 24-h periods of the magnetic field at Uppsala, Sweden (INTERMAGNET 2015). One period when the magnetic activity is high, resulting in a large difference between maximum and minimum value in the magnetic field, >2°, and another period when the activity is low resulting in a small maximum difference, c. 0.07°, and hence, the magnetic field is more stable. Provided the measurement is done using a stable period, the uncertainty due to solar activity, expressed as the standard deviation from the mean value, can be assumed to be insignificant, σ solar < 0.02°.

Fig. 1
figure 1

Plots of the magnetic field at Uppsala observatory Sweden (INTERMAGNET 2015) during two different 24-h periods. To the left a period of large variations in the magnetic field (noon 24 October 2011 to noon 25 October 2011), and to the right a period of stable magnetic field (19 January 2014). The zero lines correspond to declination 5° and inclination 73.0° of the magnetic field lines

Full size image

There are other organisations, e.g. (NOAA 2015 or TESIS 2015), that do space weather forecasts that can be used for planning measurements using devices relying on the magnetic field.

2.3 High-Voltage Direct Current, HVDC, Cables

Cables for transmitting high-voltage direct current affect the magnetic field locally and thereby tools using magnetic compasses for orientation. If it is not possible to synchronise measurements in boreholes with periods of no amperage through the cables, the influence has to be calculated. The influence of the magnetic field can be calculated if the geometry of the borehole and the cable is known together with the amperage through the cable using the Biot–Savart law (see e.g. Griffiths (1998)). Hence, if all parameters are known, the measurements can be corrected accordingly. However, it is usually not possible to get the information about the amperage, and hence, the uncertainty has to be inferred from the uncertainty in the input parameters for the calculation.

2.4 Minerals with High Magnetic Susceptibility

Along the core there may be sections containing minerals with high magnetic susceptibility influencing devices that use magnetic compasses to keep track of its orientation. If areas with high magnetic susceptibility are found, and there is no possibility to use a tool not sensitive to magnetism, the values from these sections have to be omitted, orientation values within them interpolated, and the uncertainty estimated using information from other parts of the borehole.

2.5 Borehole Diameter Variation

When calculating the orientation of a fracture visible in the BIPS, Borehole Image Processing System by RaaX (2015), SKB uses a software called Boremap developed by ErgoData (2015). The software assumes that the diameter of the borehole is constant despite that there is variation along the core (see Fig. 2c). This discrepancy between the theoretical diameter, used in the software, and the actual real diameter of the borehole renders an error of the inferred α angle.

Fig. 2
figure 2

a Relationship between the theoretical alpha angle, α T, the real alpha angle, α R, and the difference between the two angles, δ α . b The difference, δ α , becomes larger for a constant error, δ h, when alpha angle increases, c the calliper measurement along borehole KFM01A; the fine jagged red line shows the measured values, whilst the thick vertical straight line indicates the assumed theoretical diameter, 76.3 mm, used in Boremap for the actual borehole

Full size image

The theoretical α angle, α T, is calculated by measuring the distance, h, on the BIPS image assuming a theoretical borehole diameter, D T (see Fig. 2a). The real α angle, α R, is calculated using the real borehole diameter, D R. The interpretation of the α R angle is, hence, dependent on the accuracy of the measured real borehole diameter. The difference, δ α , between the two angles α T and α R can be calculated according to Eq. (2).

$$\delta_{\alpha } = 90 - \alpha_{\text{T}} - \arctan \left( {\frac{{\tan \left( {90 - \alpha_{\text{T}} } \right) \cdot D_{\text{T}} }}{{D_{\text{R}} }}} \right)$$
(2)

where α T is the theoretical alpha angle, measured in Boremap, D T is the theoretical diameter of the borehole and D R is the real diameter of the borehole.

The difference has its maximum value when α is close to 45° as long as the ratio between D T and D R is within 0.7–1.4.

Ideally, the alpha angle should be corrected for the real borehole diameter for each fracture to eliminate the error δ α . However, this is not possible due to uncertainty in the length correction that is only constrained every 50th metre in the investigated holes.

To evaluate the uncertainty of the borehole diameter, 63 cored boreholes with 311,266 calliper measurements were analysed. The standard deviation, together with the 95 % confidence interval, for each integer of α between 0° and 90° is shown in Fig. 3. Due to the vast amount of data, the confidence interval of the standard deviation is extremely small. An uncertainty model that manages to be within the confidence interval is shown in Eq. (3a). However, if a discrepancy of 0.005° is acceptable a simpler model, proposed in Eq. (3b), can be used.

$$\sigma_{{\alpha_{{{\text{Borehole}}\phi ,{\text{measure}}}} }} = 0.4 \cdot \sin \left( {2\alpha_{\text{T}} } \right) + \sin \left( {5.53\alpha_{\text{T}} - 0.017 \cdot \alpha_{\text{T}}^{2} } \right) \cdot \left( {0.0049 - 1.2 \cdot 10^{ - 5} \alpha_{\text{T}} } \right)$$
(3a)
$$\sigma_{{\alpha_{{{\text{Borehole}}\phi ,{\text{measure}}}} }} = 0.4 \cdot \sin \left( {2\alpha_{\text{T}} } \right).$$
(3b)
Fig. 3
figure 3

Standard deviation of the α uncertainty due to borehole diameter variation as a function of the measured α T angle. The 95 % confidence interval is extremely narrow due to the large amount of data, 311,266. The uncertainty model shown is the symmetry-simplified approximation, Eq. (3b), which is suggested as input to the aggregated uncertainty calculations

Full size image

2.6 Measuring Bearing and Inclination of the Borehole

The uncertainty in the bearing, B, and inclination, I, is a mix of uncertainties. It includes the handling of the tool, which can be seen as a human factor, the inherent uncertainty of the tool itself and the external uncertainty that is related to the fact that the tool does not actually measure the orientation of the borehole, but the orientation of the tool itself.

Performing full scale tests to calculate the uncertainty in orientation of boreholes is not trivial. It requires several boreholes in different directions and rock types with known start and end points. There are, however, facilities using plastic tubes instead of rock, for example, De Beer’s facility in Voorspoed Mine (Orpen 2007), Devico’s test facility in Trondheim (Devico 2015) and SKB’s test facility at Äspö (Nilsson 2015). Unfortunately, all these facilities have a much larger horizontal extension than vertical. There is, however, a test facility for nonmagnetic tools constructed at Solid Energy’s Spring Creek mine (Solid Energy New Zealand Ltd 2015) where the inclination is between −17° and −37°. A small number of tests have been run, but unfortunately none were publically reported, but kindly shared to the author to be used as a comparison to the SKB site investigation data.

In lack of proper test facilities, the uncertainty can be inferred by multiple measurements using different tools to minimise any systematic error. During the investigations for siting a waste facility for high-level nuclear waste, SKB mainly used four tools for the evaluation of the borehole orientation; (1) Flexit Multi Smart (magnetometer/accelerometer); (2) Reflex EZ-AQ/EMS (magnetometer/accelerometer); (3) Maxibor I, and (4) Maxibor II (optical). A few other tools, e.g. borehole radar and televiewer, were used, but the results were judged to give data of lower quality due to less accuracy or oscillating results. No gyro tools were used.

During the SKB site investigation programme, the orientation was measured every third metre along the boreholes and each series of measurement was evaluated regarding quality. By this procedure, multiple measurements of quality-assured reliable values of orientation at each measuring depth were obtained from most boreholes. The true orientation still remains unknown, but a best estimate of the orientation can be calculated using the median value of all reliable data at the actual depth. This method is further explained in Munier and Stigsson (2007).

The uncertainty of the bearing and inclination can then be inferred by evaluating the standard deviation of all angle differences between the expected orientation and all reliable measurements at each 3-m interval. This results in an individual bearing and inclination uncertainty for each borehole.

However, there are several boreholes with only one reliable orientation measurement at each depth, and hence, the uncertainty has to be inferred from other boreholes with similar properties. To investigate what properties that are important for inferring the uncertainty, the 30,592 uncertainty data from all 3-m intervals with multiple reliable measurements are lumped into a database together with information about; device type (mag/acc or optical); inclination of the borehole at the current 3-m interval; length coordinate in the hole; rock type; curvature of the borehole together with; min, max and difference in borehole diameter at the 3-m interval. This database is analysed using ANOVA, ANalysis Of Variance, (e.g. Fisher 1925), a method to analyse differences between groups of data. Full-effects ANOVAs are not possible to perform due to that the boreholes does not cover all directions, and some rock types only occur in one single borehole. Hence, the main-effects ANOVA is used, neglecting any dependence between the studied parameters.

The analysis of the bearing uncertainty shows that the device type and inclination of the borehole are the two parameters that significantly deviate from the null hypothesis that no parameter has any impact on the magnitude of the uncertainty. For the inclination uncertainty, there is no clear pattern, but both device type and inclination deviate from the null hypothesis, together with most other parameters such as rock type and curvature.

Based on the ANOVA, it is judged that both the bearing and inclination uncertainties are dependent on both the device type and the inclination of the borehole, but no other parameter (see Fig. 4).

Fig. 4
figure 4

Average, blue, and standard deviation, red, of the bearing and inclination uncertainties including the 95 % confidence interval. The interpreted uncertainty models, in grey, according to Eqs. (4a) and (4b). a Inclination uncertainty for mag/acc device, b inclination uncertainty for optical device, c bearing uncertainty for mag/acc device, d bearing uncertainty for optical device

Full size image

The extreme increase in uncertainty when the boreholes are close to vertical is interpreted as the tool not measuring the actual borehole trajectory for steep boreholes. The tool measures the orientation of itself, and when the borehole is steep enough, the tool might not align properly with the invert of the borehole. At the extreme, the tool might start to dangle in the hole.

Given the scattered data, the uncertainty models are based on judgement using data in intervals where the average is close to zero and the number of measurements is large. The analysis suggests the following equations to infer the bearing and inclination uncertainty from measuring the orientation of the boreholes

$$\sigma_{{{\text{bear}}_{\text{Borehole,Measure}} }} = \left\{ {\begin{array}{*{20}l} {\text{mag/acc}} \hfill & {0.2 + \frac{0.1}{{\cos \left( {\text{inclination}} \right)}}} \hfill & { - 90 < {\text{incl}} \le - 35} \hfill \\ {\text{optical}} \hfill & {0.4 + \frac{0.1}{{\cos \left( {\text{inclination}} \right)}}} \hfill & { - 90 < {\text{incl}} \le - 35} \hfill \\ \end{array} } \right.$$
(4a)
$$\sigma_{{{\text{incl}}_{\text{Borehole,Measure}} }} = \left\{ {\begin{array}{*{20}l} {\text{mag/acc}} \hfill & {0.05 + \frac{0.0003}{{\cos \left( {\text{inclination}} \right)}}} \hfill & { - 90 < {\text{incl}} \le - 35} \hfill \\ {\text{optical}} \hfill & {0.5 + \frac{0.003}{{\cos \left( {\text{inclination}} \right)}}} \hfill & { - 90 < {\text{incl}} \le - 35} \hfill \\ \end{array} } \right.$$
(4b)

An evaluation of the data provided from gyro tools tested in the Spring Creek Mine facility (Solid Energy New Zealand Ltd 2015) results in a standard deviation of the inclination of about 0.15°, and a standard deviation of the bearing of about 0.35°. These values are in the good agreement to Eqs. (4a) and (4b), developed from SKB data.

Unfortunately, the database does not contain any boreholes with inclination values less steep than −34.87°, and hence, no information exists about the uncertainty for subhorizontal boreholes. It is, however, not expected that the constant terms in Eqs. (4a) and (4b) will solely accurately describe the uncertainty for subhorizontal holes. Instead, there is, presumably, a need for an additional, for the moment unknown, term describing the increased uncertainty due to the pushing of the tool into the borehole when close to horizontal.

2.7 Manual Adjustment of Borehole TV Image

During the Site investigations, the inside of the borehole was filmed using the BIPS 1500 tool by RaaX (2015). When filming the borehole wall, the camera device rotates around its own axis. This rotation is manually corrected during the time of the recording by an operator, who turns a knob to keep two markers aligned, either an air bubble pointing at the crown of the borehole, a steel ball pointing at the invert, or a compass pointing towards north. The uncertainty that arises from this manual activity affects the β angle and the uncertainty magnitude is estimated separately after running the correction. The uncertainty varies along the core due to visibility, the rapidness of rotation of the device, and if there are sudden jumps of the markers. The uncertainty is also dependent on the device used where a small air bubble to orient the device will give smaller uncertainty than using a steel ball due to the difference in inertia. The orientation of the borehole will also affect the magnitude of the uncertainty where a steeper borehole will render larger uncertainty. Each borehole will hence have a unique uncertainty value due to this manual adjustment.

The operator him/herself estimates the uncertainty by expert judgement, and hence, the uncertainty is qualitatively inferred. The uncertainties for 50 boreholes are plotted in Fig. 5. Only four boreholes were logged using a steel ball, due to the inertia problem. Two boreholes were logged with compass, but only one has data for most of the borehole length; hence, the other is excluded. Provided that the best method is used, i.e. air bubble technique in inclined boreholes and compass in almost vertical boreholes, a linear uncertainty model may be used to describe the β uncertainty according to Eq. (5). If air bubble or steel ball is used, the uncertainty is expected to increase rapidly after about −85° inclination and be undefined at −90° inclination.

Fig. 5
figure 5

Uncertainty stemming from the correction of the BIPS image together with the inferred uncertainty model

Full size image
$$\sigma_{{\beta_{\text{BIPS,Human}} }} = \begin{array}{*{20}c} {2 - 0.04 \cdot {\text{incl}}} & { - 90 \le {\text{incl}} \le } \\ \end{array} {-}40.$$
(5)

2.8 Mapping of α and β Angles

Uncertainties arising when mapping α and β angles are subjected to human factors. The α angle is the acute dihedral angle between the fracture plane and the local trajectory of the borehole. The angle is restricted to be between 0° and 90°, where 90° corresponds to a fracture perpendicular to the borehole, i.e. the fracture normal and borehole trajectory are parallel. The β angle is the rotation angle from the crown of the borehole profile to the lower inflexion point of the fracture trace on the borehole wall, i.e. where the perimeter of the borehole is the tangent of the fracture trace. The angle is measured clockwise looking in the direction of the borehole trajectory and can be between 0° and 360°. The uncertainty can be inferred using multiple teams of geologists mapping the same piece of core. Hence, an experiment was set up where two experienced teams of geologists, GS and SP, mapped the same parts of two different cores each (see Table 1).

Table 1 Mapped borehole intervals and number of mapped fractures in the two boreholes by the two teams
Full size table

The two teams did not only map the α and β angles, but also other parameters such as mineralisation and roughness (Glamheden and Curtis 2006) which makes it possible to investigate if there are certain factors increasing the uncertainty. As shown in Table 1, the two teams did not always recognise the same fractures on the core, where a fracture is defined as a “general term that refers to all kinds of mechanical breaks in a rock mass” according to Glamheden and Curtis (2006) (Appendix D). Actually only 993 of the 1281–1314 fractures were judged to be the same.

There are hence 993 fractures available to analyse. However, when the α angle is 90°, the β angle becomes undefined. There are 26 such data where either one or both teams have mapped the α angle to 90°, and hence, only 967 β angle pairs can be analysed.

Using ANOVA, it was concluded that the α angle and the visibility in BIPS were the two parameters that significantly steered the magnitude of the uncertainty. In Fig. 6, the data are divided regarding visibility in borehole imagery and the uncertainty is plotted versus the average α angle, α average, of the two teams. The data are plotted as 10° moving average for fractures visible in BIPS. For fractures not visible in BIPS, the moving average is 20° due to a smaller amount of data.

Fig. 6
figure 6

Evaluated uncertainties and inferred uncertainty models for the α and β angles stemming from the fracture mapping. Observe that the uncertainty scale for c and d is four times the scale of a and b. a α Uncertainty for fractures visible in BIPS, b α uncertainty for fractures not visible in BIPS, c β uncertainty for fractures visible in BIPS, d β uncertainty for fractures not visible in BIPS

Full size image

The standard deviation of the difference between the two teams is, naturally, smaller if the fracture is visible in the borehole imagery compared to those fractures whose orientation has to be measured on the core relative to a nearby visible feature (see Fig. 6). The standard deviation of the α angle increases as the α average angle increases, which is natural since the angle difference increases for a constant height difference on the borehole imagery picture, as the α angle becomes closer to 90° (see Fig. 2b). It is also natural that the standard deviation of the β angle becomes larger when α average approaches 90° due to the less pronounced peak of the trace. On the other hand, the impact of the standard deviation of the β angle becomes smaller as α average approaches 90° (Stigsson and Munier 2013).

The uncertainty models, Eqs. (6a) and (6b), are manually optimised to have as few points as possible outside the 95 % confidence interval and can be expressed as:

$$\sigma_{{\alpha_{\text{Map,Human}} }} = \left\{ {\begin{array}{*{20}l} {\text{VIB}} \hfill & {1.2 + 0.055 \cdot \alpha } \hfill & {0 \le \alpha \le 90} \hfill \\ {\text{notVIB}} \hfill & {1.9 + 0.11 \cdot \alpha } \hfill & {0 \le \alpha \le 90} \hfill \\ \end{array} } \right.$$
(6a)
$$\sigma_{{\beta_{\text{Map,Human}} }} = \left\{ {\begin{array}{*{20}l} {\text{VIB}} \hfill & {\hbox{min} \left( {\begin{array}{*{20}c} {\frac{9 - 0.06 \cdot \alpha }{\cos \left( \alpha \right)};} & {180} \\ \end{array} } \right)} \hfill & {0 \le \alpha < 90} \hfill \\ {\text{notVIB}} \hfill & {\hbox{min} \left( {\begin{array}{*{20}c} {\frac{32 - 0.3 \cdot \alpha }{\cos \left( \alpha \right)};} & {180} \\ \end{array} } \right)} \hfill & {0 \le \alpha < 90} \hfill \\ \end{array} } \right. .$$
(6b)

2.9 Fracture Undulation

The most obvious uncertainty might be the uncertainty due to the undulation of the fracture, i.e. how well does a small borehole intercept represent the overall orientation of the fracture. This uncertainty is as most other uncertainties difficult to measure in situ.

Fracture surfaces can be described as self-affine fractal surfaces according to Mandelbrot and Van Ness (1968), Fournier et al. (1982), Mandelbrot (1985) and Saupe (1988). A self-affine fractal line, or surface, has the measure axis decoupled from the extension axis, or axes, and usually scales differently in the measure direction compared to the extension directions. In contrast, a self-similar line, or surface, scales equally along all axes, and hence, the axes are coupled. More detailed explanations are found in, e.g. Stigsson (2015). As the fractures are supposed to be self-affine, rather than self-similar, they need both an amplitude measure and a fractal dimension to be fully constrained. One such method is the standard deviation of the correlation function (RMS–COR) method that has been successfully used by Renard et al (2006), Candela et al. (2009) and Stigsson (2015). The outcome of the method is a scaling relationship described by Eq. (7).

$$\sigma \delta h_{{\left( {\Delta L} \right)}} = \sigma \delta h_{{\left( { 1\;{\text{unit}}} \right)}} \cdot\Delta L^{{2 - D_{\text{line}} }}$$
(7)

where σδh (1 unit) is the standard deviation when ΔL = 1 unit, ΔL is the length of the studied interval, and D line is the fractal dimension along the direction of a line across a fracture surface (1 < D line < 2).

Using the assumption that the radius distribution of fractures in a rock mass follows a pareto distribution with shape parameter <4, the contribution to the α and β uncertainties can be described according to Eqs. (8a) and (8b).

$$\sigma_{{\alpha_{\text{Und,External}} }} = \arctan \left( {\sigma \delta h_{{\left( {\Delta L} \right)}} \cdot \left( {\frac{{{\o}_{BH} }}{\sin \left( \alpha \right)}} \right)^{{\left( {1 - D_{\text{Line}} } \right)}} } \right)$$
(8a)
$$\sigma_{{\beta_{\text{Und,External}} }} = \arctan \left( {\sigma \delta h_{{\left( {\Delta L} \right)}} \cdot {\o}_{\text{BH}}^{{\left( {1 - D_{\text{Line}} } \right)}} } \right)$$
(8b)

where σδh (ΔL) is the intercept from the RMS–COR evaluation, in the same unit as øBH, øBH is the diameter of the borehole, in the same unit as σδh (ΔL), α is the acute angle between the borehole trajectory and the fracture surface, D Line is the fractal dimension along the direction of a line on the fracture surface.

Stigsson (2015) investigated several fracture traces and surfaces from the Kamaichi mine in Japan, the ONKALO facility in Finland and the Äspö Hard Rock laboratory in Sweden. These traces and surfaces spanned from about 5 cm to about 10 m in extension with corresponding resolutions from about 0.1 mm to 10 dm. According to Stigsson (2015), fractures that are judged to have had no shear movement have the fractal parameters, D line = 1.17 and σδh (1 mm) = 0.17 mm. Using these parameter values, the uncertainty model becomes as shown in Fig. 7.

Fig. 7
figure 7

Uncertainty model of the fracture undulation for a joint-like fracture and the 95 % confidence interval according to Stigsson (2015)

Full size image

3 Consequences of the Aggregated Orientation Uncertainty

The expected orientation of a fracture can be calculated using Eq. (1). Adding the uncertainties from the measurements will result in the aggregated uncertainty, χ, stated in Eq. (9).

$$\begin{aligned} & \chi_{\text{conf}} = \left[ {\begin{array}{*{20}c} {n_{\sigma x} } \\ {n_{\sigma y} } \\ {n_{\sigma z} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\sin \left( {N\left( {B,\sigma_{{B,{\text{BH}}}} } \right)} \right)} \hfill & { - \cos \left( {N\left( {B,\sigma_{{B,{\text{BH}}}} } \right)} \right)} \hfill & 0 \hfill \\ {\cos \left( {N\left( {B,\sigma_{{B,{\text{BH}}}} } \right)} \right)} \hfill & {\sin \left( {N\left( {B,\sigma_{{B,{\text{BH}}}} } \right)} \right)} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {\sin \left( {N\left( {I,\sigma_{{I,{\text{BH}}}} } \right)} \right)} \hfill & 0 \hfill & {\cos \left( {N\left( {I,\sigma_{{I,{\text{BH}}}} } \right)} \right)} \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill \\ { - \cos \left( {N\left( {I,\sigma_{{I,{\text{BH}}}} } \right)} \right)} \hfill & 0 \hfill & {\sin \left( {N\left( {I,\sigma_{{I,{\text{BH}}}} } \right)} \right)} \hfill \\ \end{array} } \right] \\ & \quad \left[ {\begin{array}{*{20}l} {\cos \left( {N\left( {\beta ,\sqrt {\sigma_{{\beta ,{\text{BIPS}}}}^{2} + \sigma_{{\beta ,{\text{Map}}}}^{2} + \sigma_{{\beta ,{\text{Und}}}}^{2} } } \right)} \right) \cdot \cos \left( {N\left( {\alpha ,\sqrt {\sigma_{{\alpha ,{\text{BH}}\varphi }}^{2} + \sigma_{{\alpha ,{\text{Map}}}}^{2} + \sigma_{{\alpha ,{\text{Und}}}}^{2} } } \right)} \right)} \hfill \\ {\sin \left( {N\left( {\beta ,\sqrt {\sigma_{{\beta ,{\text{BIPS}}}}^{2} + \sigma_{{\beta ,{\text{Map}}}}^{2} + \sigma_{{\beta ,{\text{Und}}}}^{2} } } \right)} \right) \cdot \cos \left( {N\left( {\alpha ,\sqrt {\sigma_{{\alpha ,{\text{BH}}\varphi }}^{2} + \sigma_{{\alpha ,{\text{Map}}}}^{2} + \sigma_{{\alpha ,{\text{Und}}}}^{2} } } \right)} \right)} \hfill \\ {\sin \left( {N\left( {\alpha ,\sqrt {\sigma_{{\alpha ,{\text{BH}}\varphi }}^{2} + \sigma_{{\alpha ,{\text{Map}}}}^{2} + \sigma_{{\alpha ,{\text{Und}}}}^{2} } } \right)} \right)} \hfill \\ \end{array} } \right] \\ \end{aligned}$$
(9)

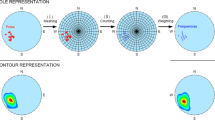
χ is space filling but different levels of confidence will show as different areas on a stereonet. For example χ 95 will show the 95 % confidence area of the fracture orientation. One way to visualise χ conf is thoroughly described in Stigsson and Munier (2013), and only briefly recapitulated below.

The uncertainty space for each of the four parameters, B, I, α and β follows lines on a lower hemisphere projection. Adding these line sample spaces for a specific confidence interval will render a surface, χ conf, on the stereonet. Another measure, Ω conf, is defined as the minimum dihedral angle from the expected fracture orientation that fully encircles χ conf. As an example, the sample spaces of the four uncertainty parameters are shown in Fig. 8 together with χ 95 and Ω 95.

Fig. 8
figure 8

Visualisation of χ 95 constructed from the B, I, α and β line uncertainties. The minimum dihedral angle, Ω 95, is the smallest angle from the expected orientation of the fracture that entirely circumferences χ 95

Full size image

The χs will affect the interpretation of the orientation model as well as parameters coupled to the fracture sets. It is not possible to ubiquitously correct this distortion of the data for a single fracture, but it can be estimated on a global level for a fracture set. To examine some of these aspects, a small study is carried out and presented in Online Resource 1. The study covers four topics: change in distribution shape; usage of low uncertainty data; effects on parameters coupled to fracture sets; and possibility to explain outliers. The interested reader is encouraged to download and read Online Resource 1, but for convenience a summary of the results is given below.

First, the uncertainty will change the shape of the fracture set distribution and lower the concentration parameter. In the example shown in Online Resource 1, section A1.1, the shape of the distribution is inferred as elliptical Fisher despite the correct distribution should be uniform Fisher. Further, the Fisher concentration parameter, κ, is inferred to be around 12 instead of the correct value of 25. However, the mean orientations of the fracture sets will not be affected to any greater extent. In the example, in Online Resource 1 the dihedral angle between the correct mean pole and the inferred mean pole of the set is <0.1°.

Second, the effect of the uncertainty may be less by only using data with low uncertainty. This procedure, however, requires that the kept data constitute a representative sample of all fractures in the borehole, including all conceivable parameters. The smaller part of the borehole that can be used, the larger the risk of the fractures not being a representative sample. In the example borehole, shown in section A1.2 in Online Resource 1, about 20 % of the borehole length is judged to be good enough for evaluation.

Third, the uncertainty may bias the interpretation of parameters coupled to the different sets. In section A1.1 in Online Resource 1, it is shown that the uncertainty may result in erroneous set affiliation for fractures. This will lead to an erroneous inference of any parameter coupled to the sets, e.g. flow capacity of fractures, as shown in section A1.3 in Online Resource 1. In the example, the difference in log mean flow capacity between the two fracture sets is more than halved, whilst the standard deviation is increased for both the sets.

Fourth, if the uncertainty is known for a fracture, the information can be used to explain outliers that do not fit the prevailing conceptual model. In Online Resource 1, section A1.4, an example is shown of two fractures that contradicts the conceptual understanding of rock stress and fracture flow capacity. However, both fractures have very large uncertainties and, hence, large possibility to have alternative interpreted orientations that conforms to the conceptual understanding.

The uncertainties are, hence, not solely detrimental, but can be valuable provided the reason for their presence is properly understood and the magnitudes correctly inferred.

4 Summary

Despite that orientation data are a cornerstone for characterisation of a discrete fracture network, DFN, and, ultimately, the construction of DFN models, limited attempts have been reported to identify and evaluate all the different uncertainties related to measurements. By neglecting the uncertainty, there is a considerable risk that the orientation model, and thereby the inference of parameters coupled to the fractures, will become erroneous.

The current work fills a knowledge gap by taking advantage of the extensive drilling, more than 34 km of core, performed by SKB during the investigations for siting a repository for spent nuclear fuel at the Forsmark or Laxemar sites in Sweden. The current work identifies nine sources of uncertainty together with techniques to infer the magnitude models of these uncertainties. The different uncertainties are combined to construct the aggregated uncertainty space, χ conf, using Eq. (9) for different levels of confidence.

The orientation uncertainty can have a large impact on the inference of parameter settings that are input to numerical models relying on DFNs, e.g. the inference of transmissivity distribution to different fracture sets. This will consequently affect the results from any downstream model using DFNs and have impact on decisions made that are based on the model results.

Knowledge of the uncertainty of the four parameters, B, I, α and β, is necessary to be able to correctly infer the orientation model of a DFN and how the uncertainty affects the inference of parameters coupled to different fracture sets. Consequently, it is essential that the orientation uncertainty is recognised and exploited carefully.

5 Conclusions

The work presented uses orientation of fractures to show how orientation uncertainty can be inferred. However, the techniques to infer the magnitude of orientation uncertainty presented in this paper may be applied to all types of structures and lineated objects in boreholes, such as foliation, rock contact, and rock stress. It also opens a new area in investigating the effects of the uncertainties, not only to the inference of parameters coupled to fracture sets but also to the connectivity, flow and transport, rock mechanics, etc. in fractured media.

The main conclusions from this work are as follows:

  1. 1.

    knowledge of the orientation uncertainty is crucial in order to be able to infer correct orientation model and parameters coupled to the fracture sets;

  2. 2.

    it is important to perform multiple measurements to be able to infer the actual uncertainty instead of relying on the theoretical uncertainty provided by the manufacturers;

  3. 3.

    it is important to use the most appropriate tool for the prevailing circumstances; and

  4. 4.

    using the tools and methods presented in this paper, the single most important parameter to decrease the size of the uncertainty space for objects measured in inclined boreholes is to avoid drilling steeper than about −80°.

The uncertainty is not solely detrimental, but can be valuable, provided that the reasons for its presence are properly understood and the magnitude correctly inferred. It blurs and skews orientation models towards less concentrated and erroneously spread sets, but can also be used to explain and correct outliers that do not fit a prevailing conceptual model. Hence, the uncertainty should be exploited carefully and neither be underestimated nor overestimated.