Baryon Anticorrelations in PYTHIA

Abstract

We present a computational investigation of a problem of hadron collisions from recent years, that of baryon anticorrelations. This is an experimental dearth of baryons near other baryons in phase space, not seen upon examining numerical Monte Carlo simulations. We have addressed one of the best known Monte Carlo codes, PYTHIA, to see what baryon (anti)correlations it produces, where they are originated at the string-fragmentation level in the underlying Lund model, and what simple modifications could lead to better agreement with data. We propose two ad-hoc alterations of the fragmentation code, a “one-baryon” and an “always-baryon” policies that qualitatively reproduce the data behaviour, i.e anticorrelation, and suggest that lacking Pauli-principle induced corrections at the quark level could be the culprit behind the current disagreement between computations and experiment.

1 Introduction

1.1 Baryon Anticorrelations

The baryon anticorrelation problem was exposed in a series of works by the ALICE collaboration [1, 2], investigations derived therefrom [3], and further corroborated by the STAR collaboration [4]. Basically it is a severe disagreement about the probability of two baryons exiting a high-energy collision closely in phase-space (similar momenta). Computational simulations using event generators fail to see an anticorrelation clearly present in the data. To understand it, let us first define the appropriate two-particle correlations that are measured.

Let us begin with the definition of the single and pair densities of species $\alpha$ and $\beta$ as

$$\begin{aligned} \rho _1^{\alpha }(\eta _1,\varphi _1)&\equiv \frac{\textrm{d}^2N_1^{\alpha }}{\textrm{d}\eta _1\textrm{d}\varphi _1}, \end{aligned}$$

(1)

$$\begin{aligned} \rho _2^{\alpha \beta }(\eta _1,\varphi _1,\eta _2,\varphi _2)&\equiv \frac{\textrm{d}^4N_2^{\alpha \beta }}{\textrm{d}\eta _1\textrm{d}\varphi _1\textrm{d}\eta _2\textrm{d}\varphi _2} \end{aligned}$$

(2)

where $N_1^{\alpha }$ represents the number of particles of species $\alpha$, $N_2^{\alpha \beta }$ represents the number of pairs of particles of species $\alpha$ and $\beta$, and $\eta _\textrm{i}$ and $\varphi _\textrm{i}$ represent the corresponding pseudorrapidity, $\eta$, and azimuthal angle, $\varphi$, of the involved particle. Clearly the magnitude

$$\begin{aligned} \rho _2^{\alpha \beta }(\eta _1,\varphi _1,\eta _2,\varphi _2) - \rho _1^{\alpha }(\eta _1,\varphi _1)\rho _1^{\beta }(\eta _2,\varphi _2) \end{aligned}$$

(3)

measures the degree of correlation between particles of species $\alpha$ in the phase–space bin $(\eta _1,\varphi _1)$ and particles of species $\beta$ in the phase–space bin $(\eta _2,\varphi _2)$. Two-particle correlations are usually reported, normalizing the Eq. (3) magnitude, as normalized second order cumulants, and in relative separation in pseudorapidity, $\Delta \eta = \eta _1-\eta _2$, and azimuth, $\Delta \varphi =\varphi _1-\varphi _2$

$$\begin{aligned} R_2^{\alpha \beta }(\Delta \eta ,\Delta \varphi ) = \frac{\rho _2^{\alpha \beta }}{\rho _1^{\alpha }\rho _1^{\beta }} - 1\text {.} \end{aligned}$$

(4)

Experimentally, the expression in the denominator is usually obtained directly in $\Delta \eta$, $\Delta \varphi$ by using the mixed events technique which builds the $\rho _2$ distribution considering one pair component from one event and the second pair component from a different event. By using this technique, the expression (3) is identically zero, because particle from different events are not correlated, and

$$\begin{aligned}{}[\rho _1\cdot \rho _1] (\Delta \eta ,\Delta \varphi ) = \rho _2^\textrm{mixed} (\Delta \eta ,\Delta \varphi ) \end{aligned}$$

(5)

is obtained. Then, what is usually reported as measured two-particle correlation function is

$$\begin{aligned} C^{\alpha \beta }(\Delta \eta ,\Delta \varphi ) = R_2^{\alpha \beta }(\Delta \eta ,\Delta \varphi ) + 1 = \frac{S^{\alpha \beta }(\Delta \eta ,\Delta \varphi )}{B^{\alpha \beta }(\Delta \eta ,\Delta \varphi )} \end{aligned}$$

(6)

where S is the ratio of the distribution density in relative rapidity $\Delta \eta$ and azimutal angle $\Delta \varphi$ of presumably correlated pairs (because they are taken from the same event), to the total number of pairs,

$$\begin{aligned} S(\Delta \eta ,\Delta \varphi )=\frac{1}{N^\textrm{signal}_{2}}\frac{\textrm{d}^2N_{2}^\textrm{signal}}{\textrm{d}\Delta \eta \, \textrm{d}\Delta \varphi }\ , \end{aligned}$$

(7)

and B is the equivalent distribution of uncorrelated pairs (stemming from separate events, or “mixed” in the field’s jargon)

$$\begin{aligned} B(\Delta \eta ,\Delta \varphi )=\frac{1}{N^\textrm{mixed}_{2}}\frac{\textrm{d}^2N^\textrm{mixed}_{2}}{\textrm{d}\Delta \eta \, \textrm{d}\Delta \varphi } \end{aligned}$$

(8)

The mixed event distribution in Eq. (8) corrects for the effects of limited acceptance in pseudorapidity on S but, apart from a scale factor, it does not affect its azimuthal shape. For this reason, S may be studied alone to investigate the behaviour in $\Delta \varphi$ of the correlation function C.

Now let us describe the baryon anticorrelation problem. Contrasting experimental data for baryon correlation with simulations from three tunes of the PYTHIA Monte Carlo event generator (two Perugia and the Monash one), the outcome was rather disappointing [1]. The disagreement is not particularly due to PYTHIA because its substitution by PHOJET, an alternative Monte Carlo event generator, did not bring improvement. Figure 1, taken from [2], shows the two-particle correlation functions. There, the correlation functions are integrated over $\Delta \eta$ (and normalized), which is a more convenient way to compare several results.

Fig. 1

Left: Typical meson-meson correlation function from ALICE data [2] as a function of $\Delta \varphi$, showing a large forward peak (two Kaons are more likely to be detected with $\Delta \varphi =\varphi _2-\varphi _1\simeq 0$) and a sizeable backward peak at $\Delta \varphi =\pi$. Simulation and experimental data are in reasonable qualitative agreement. Center and right: Experimental baryon–baryon$+$anti-baryon–anti-baryon correlation functions become smaller than 1, corresponding to negative $R_2$ (data, grey squares) when $\Delta \varphi \simeq 0$, showing a forward anticorrelation. Monte Carlo simulations seem unable to reproduce that behaviour. Note that this happens not only for identical baryons such as ${\textrm{pp}}$ (center) but also for distinguishable ones such as $\textrm{p}\Lambda$ (right). Not shown here, but also available from [2], are the baryon–anti-baryon correlation functions which show the same behaviour as the meson–meson correlations in both, data and simulations. Reproduced from [2] by the ALICE collaboration under the terms of the Creative Commons License 4.0 (http://creativecommons.org/licenses/by/4.0/); no changes have been effected. (The red and green lines correspond to PYTHIA 6 with two Perugia tunes, and play no further role in our discussion)

Looking back to earlier work, the OPAL collaboration discussed in [5] what was known on baryon correlations at the time of wrapping up the LEP experimental program. Their conclusion was that, due to limited statistics and insensitivity to dynamics by lacking rapidity in the analysis, the correlations due to discrete quantum number (flavor, charge, baryon number conservation) were clearly visible, but not much beyond that: quark/fragmentation-level correlations were not clearly established. The situation has now changed due to the impressive statistics and tracking capabilities of more modern devices, and dynamical effects will need to be addressed.

1.2 Common Use of the PYTHIA Software to Predict Correlations

PYTHIA is a Monte Carlo event-generator software program, widely used to simulate possible outcomes of experiments (like collisions between two objects, be it fundamental particles or nuclei) and help understand detector responses. Through various physical model mechanisms, PYTHIA evolves the initial input state into a number of output particles. These are listed by their flavor, spin and momentum in its original format described in [6].

Such simulation packages are popular because of their convenience to explore possible experimental outcomes when designing a measurement or during its later analysis. Moreover, PYTHIA allows one to quickly test theoretical ideas, for example, adding some Beyond the Standard Model feature, to start assessing its impact on the data, even to guess physics at energies that current colliders cannot reach. Finally, finding a way to simulate a process can help understand it, so the shortcomings of PYTHIA can sometimes reveal shortcomings in current knowledge.

PYTHIA addresses those goals by quickly generating a great number of simulated events. The main requirements on the software are speed of execution and fidelity of the data produced at the end of the simulation compared to the data from experiment. On the contrary, fidelity to physical behaviour in the intermediates steps is secondary: the description of physical mechanisms used by PYTHIA can be highly phenomenological, notwithstanding its inspiration in the ideas of flux tubes forming among color sources and breaking in Quantum Chromodynamics [7]. It is therefore more descriptive than predictive, and can disagree with experiment when confronted with a new type of data. The phenomenological parametrizations deployed tend to use many parameters not set by any fundamental theory, but in order to fit the data. There are several possible ensembles of their values, called “tunes”.

Returning to the left plot of Fig. 1 for meson-meson correlations, we see that the results of the PYTHIA simulation are not far from experiment. The usual features are a strong correlation at small phase-space separation ($\Delta \varphi \simeq 0 \simeq \Delta \eta$) for particles that exit the collision together, perhaps from the same jet; a positive correlation for back-to-back particles with opposite azimuthal angles (a peak at $\Delta \varphi =\pi$ from two-jet events) and often (not visible in this flat depiction of the $\Delta \varphi$ dependence alone) a ridge-shaped correlation extending in $\Delta \eta$ often attributed to string-like flux tubes stretched by the separating nuclei. The same relative behaviour as for meson–meson correlation functions, although not shown, is obtained for baryon–anti-baryon correlation functions for both data and simulations (see Ref [2]).

For baryon–baryon and anti-baryon–anti-baryon correlations, shown in the center and right panels of Fig. 1, however, the Monte Carlo simulation is unable to obtain a satisfactory description. The worst agreement is for baryon–baryon correlations, where PYTHIA does not even produce the right qualitative behaviour. At around $\Delta \varphi =0$, all the tunes considered predict a peak instead of the salient depression (negative correlation, that is, anticorrelation) shown by the experiment. We would like to understand what modification of PYTHIA would suppress that peak in baryon-baryon correlations and produce an anticorrelation instead.

Changing the “tune” (particular parameter set) of the simulation does not really improve the predicted correlations. Tunes can balance the influence of the different mechanisms inside PYTHIA, but cannot change them drastically. Whatever reason for the failure of PYTHIA in reproducing the data, it has to be deeper. Therefore we will limit ourselves to using the Monash tune in this work.

1.3 Recent Attempts: The Afterburners Method

To correct the results of the simulation, a postprocessing procedure of the data has been proposed [3]. In the following, it will be named the “afterburners” procedure (in analogy to motor technology). This correction to the PYTHIA output produces encouraging results for generic kinematics, but in this work we will only evaluate the very specific problem of proton-proton anticorrelation at $\Delta \varphi =0$, only one of several physical situations [3] but a problematic one: the correction to the ${\textrm{pp}}$ correlation (see Fig. 2 in that article) is insufficient to account for the anticorrelation.

The idea behind this procedure is to write an additional code that from the output of PYTHIA associates to each pair of particles a weight. The same-event correlation function S is computed and binned as an histogram, which allows to weight each pair. In the simplest situation (no coupled channels, non identical particles), the weight is equal to the square modulus of the following wave function

$$\begin{aligned}{} & {} \psi (\mathbf{k^*},\mathbf{r^*})=e^{i\arg \Gamma (1+i\eta )}\sqrt{A_C}\,\times \nonumber \\{} & {} \quad \left( 1+\sum _{n=1}^\infty \frac{\zeta ^n\prod _{m=0}^{n-1} (-i\eta +m)}{n!^2}+\frac{e^{i\mathbf{k^*}\cdot \mathbf{r^*}}\sqrt{A_C} \left( G_0(\rho ,\eta )+iF_0(\rho ,\eta )\right) /r^*}{f_0^{-1}+\frac{d_0{k^*}^2}{2}-ik^*A_C- \frac{2}{a}\left( \sum _{n=1}^\infty \frac{\eta ^2}{n(n^2+\eta ^2)}- \gamma -\ln |\eta |\right) }\right) \end{aligned}$$

(9)

with

$$\begin{aligned} \eta =\frac{1}{ak^*} \qquad \rho =k^*r^* \qquad \zeta =\mathbf{k^*}\mathbf{r^*}+k^*r^* \qquad A_C=\frac{2\pi \eta }{e^{2\pi \eta }-1} \end{aligned}$$

(10)

The variables $\mathbf{k^*}$ and $\mathbf{r^*}$ are the momentum and position vectors in the pair rest frame, $\gamma$ is Euler’s constant and $f_0$, $d_0$ and a are parameters given for each pair. Further, $F_0$ and $G_0$ are the regular and singular s-wave Coulomb functions. For further explanations, see [3] and [8].

The implementation of this final-state wavefunction allows to correct the correlation function C to account for the antisymmetry upon exchanging the final-state baryons, unlike in the raw PYTHIA output. That computation of the weights is thus grounded both on quantum statistics and on final-state interactions due to Coulomb and nuclear forces. The exact formula giving the weight of a pair from the experiment, from the momentum and position of each particle (classically treated by PYTHIA, as explained below in Sect. 2) is quite complex.

We have attempted to redeploy that proposed method in our computations: the resulting modified correlation functions are shown in Fig. 2. One can see at first glance that the data behaviour is not fully reproduced: the ridge at $\Delta \varphi =0$ present in the panel labeled as (a) is not totally suppressed in (b); and further, the correlation now strongly peaks at $(\Delta \eta ,\Delta \varphi )=(0,0)$.

Fig. 2

Changes to the prediction of the proton-proton $R_{2}$ correlation function induced by the “afterburners” correction. (a) Proton-proton correlation predicted directly from the PYTHIA Monte Carlo program, without correction. (b) Predicted proton-proton correlation corrected by the afterburners method. Note that the positive correlation at the surroundings of $\Delta \varphi \simeq 0$ has not been erased

Though this method does not seem to alleviate the baryon-anticorrelation problem in our pedestrian simulation, the existence of this new peak is not completely problematic. The middle plot of Fig. 1 shows a tiny peak in the middle of the anticorrelation valley (probably not a statistical blip, it is also clearly visible in three-dimensional renderings where it stands out for $\Delta \eta =0$). It appears that the afterburners correction might be predicting such peak. But (at least in our implementation) it does not produce the wide depression surrounding it.

Anyway, the afterburners procedure corrects the simulation output for all possible correlation functions: both ${\textrm{pp}}$ and $\pi \pi$ are affected (in this case, the wavefunction is of course symmetrized).

Given this quick calculation, and the more extensive one [3] reported by the Warsaw Technical University investigators, we think an additional way to correct the PYTHIA output needs to be found.

2 Fragmentation in PYTHIA

To motivate to the reader the modification that we are going to effect, we briefly expose our understanding of the PYTHIA algorithms to produce final–state hadrons. Then in the next Sect. 3 we will show the correlations that PYTHIA produces before modification.

2.1 Simplified Working Method

A wise initial focus to minimize intervention in a time-tested code is to try to solve the problem at one single step of the algorithm. Since the afterburner postprocessing in Sect. 1.3 proved insufficient, this step would probably be at a previous level inside PYTHIA (the earlier a modification is applied, the larger its effect upon cascading over the rest of the simulation.)

On the one hand, unstable-hadron decays cannot be the source of the problem, for they are simple processes in the code mimicking experimentally measured decays, so a disagreement with experiment is hard to expect.

On the other hand, computed meson-meson correlations broadly agree with experiment, hinting that we should modify only the baryon-production algorithm.

Additionally, QCD amplitudes are also well understood so the perturbative matrix elements affecting the initial stages of the process are unlikely to be the culprit.

So we adopt the point of view that if there is one single mechanism to be corrected in order to obtain the experimental behaviour of the correlation function C for proton pairs in Fig. 1, it must occur at the step of the formation of hadrons.

Because of the reported $\textrm{p}\Lambda$ anticorrelation (right panel of Fig. 1), the wanted mechanism has to be generic, not tied to the nucleon.

We then proceed in the next subsection to summarize the way [9] PYTHIA obtains prompt hadrons given initial partons.

2.2 Lund String Model

The PYTHIA level just before the formation of hadrons handles quarks and gluons organized into color singlets. Any interactions involving different such singlet clusters had been taken into account earlier during the parton level computations and can probably be ignored for hadronization. At the stage of hadron formation, the code takes as input a set of partons and returns hadrons, modelling low-energy QCD interactions. Due to its complexity and for speed of algorithm execution, PYTHIA uses a phenomenological model called the Lund string model. Being far from perfect, this is convenient to treat hadron formation with sufficient richness of detail while maintaining acceptable turnout.

Summarizing the next few paragraphs, PYTHIA views the input color singlet made of quarks and gluons as a string that fragments into pieces (the hadrons). The simplest possible string is made of one quark, one antiquark and no gluons. For brevity, we will describe the process of fragmentation only in that case. For a complete description, we refer to the literature [9].

In the internal machinery of PYTHIA, each particle is modelled semiclassically, with exactly defined position and momentum, at odds with Heisenberg’s uncertainty. The Lund model thus makes sense on average; this is convenient if a great number of fragmentations are performed, as is the regular usage of PYTHIA, at the cost of microscopic interpretability.

A model string stretches between a quark and an antiquark of opposite color, called “ends”; their flavor is not significant for the QCD interaction. Due to our understanding of QCD, the binding energy is taken as proportional to the distance that separates the ends.

If a quark-antiquark pair of the right color appeared at some point of the string (a tunnel-like effect), each parton of the pair could bind with an end to form its color singlet. Thus, the system would become two strings. If the total length of these two new strings was lower than the length of the original one, the situation would be energetically favorable.

The momentum of these partons emerging from the vacuum is chosen such that one of the daughter strings turns into a physical hadron of a certain flavour and invariant mass. This constitutes “an iteration”. During the next iteration, the remaining daughter string becomes the mother one. This loop stops when all of the string’s energy has been taken away by hadrons.

Instead of creating a $\textrm{q}\bar{\textrm{q}}$ pair, PYTHIA can also opt to produce a diquark-antidiquark one. PYTHIA views the diquark made of two quarks as a single particle. Such diquark can form a color singlet with a quark, just like an antiquark would. The only difference is that the hadron produced is a baryon instead of a meson.¹

The hadrons that have been produced by this process can be of any flavour, for example containing charm or other types of spatial or spin excitations. Most of them are going to decay in the next step of PYTHIA, to finally give particles stable against strong-force mediated decays, such as pions, nucleons, kaons, Lambdas etc.

3 Correlations Among Strings and Among Baryons in PYTHIA Fragmentation

In Sect. 2 we described the passage from a string to prompt hadrons in terms of the color flow. Flavour is of lesser interest because at the end, most heavy-flavoured quarks later disappear following weak decays and are often not detected.

More determining is the momentum of the objects implied in the fragmentation. It so happens that the theoretical study of the hadrons’ momentum distribution function is burdensome (so that how to apply some level of Pauli suppression depending on the momentum distributions is not obvious to us). Earlier work [9] addresses momentum distributions at the level of one iteration, but extracting the momentum distributions from the full fragmentation loop is not trivial.

Because theoretical computation of the momentum distributions (both string input and hadron output to the fragmentation process) is unassailable, plotting the output data from simulations is the only way to understand their global behaviour.

3.1 Hadron Distributions

To qualitatively understand the proton-proton two-particle correlation function (6) in $\Delta \varphi$, we put aside the denominator B, to focus on the numerator S, which is basically a two-particle distribution affected by the limited longitudinal, $\eta$, acceptance which introduces the characteristic triangular shape in $\Delta \eta$. We expect the protons present in the final state to have been produced during the fragmentation of some string or by the decay of a heavier baryon, itself due to the fragmentation. Roughly, half of the baryons are supposed to decay into protons, half into neutrons and some into $\Lambda$ hyperons. Thus, the distribution of protons in the final step should be comparable to the distribution of baryons just after the fragmentation step (respectively antiprotons to anti-baryons).

What we want to extract is the distribution S of the pairs of baryons coming from the same event. Such same-event distribution will receive contributions from baryons ejected from the same string as well as baryons coming each from a separate string within the same event. S is then equal to the sum of the same-string baryon correlation plus the different-string baryon correlations.

Fig. 3

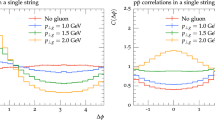
Various two-particle baryon and/or antibaryon correlations extracted at the level of strings in PYTHIA. By meson string we mean one with zero baryon number, while a baryon string contains baryon number one (and thus, one net baryon is produced in the fragmentation). By $S_\textrm{frag}$ we mean that the two particles in each term of the correlation comes from the same string within the same event

Because we seek to understand whether/why there are not suppressed correlations of baryons near to each other in phase space we will focus on baryons stemming from the same string, denoting the corresponding correlation with $S_\textrm{frag}$. For later comparability with data, the study is carried out in the laboratory frame.

The resulting numerical data is shown in Fig. 3. Among the plots there, (a), (c), (d) and (f) will contribute to the proton-proton or antiproton-antiproton S (if they were followed to the very end of the fragmentation).

Independently of the baryon number combination, all pairs are positively correlated. The only structure that seems to break the isotropy in $\Delta \varphi$ is the peak at around $(\Delta \eta , \Delta \varphi )=(0,0)$. Such peak accepts an easy interpretation: when a string fragments, baryons are preferentially produced along the same direction of the string, due to momentum conservation. Apart from that peak, (anti-)baryons from the pair are emitted with random $\varphi$ in the laboratory frame.

This strong forward peak at zero relative angle and pseudorapidity is precisely what seems to be suppressed in experimental data for $\mathrm{B\, B}$ and $\overline{\textrm{B}}\, \overline{\textrm{B}}$ correlation functions, and we thus see the unwanted feature is already present at the level of individual string fragmentation.

The baryon string (bottom row panels) also produces two curious ridges most visible in panel (d) around $\Delta \eta = \pm 4$ for 13 TeV, which are outside ALICE’s acceptance.

3.2 Internal String Distribution

To ascertain whether the “wrong” baryon correlations in PYTHIA are produced already at the string level, before the actual production of final-state particles, we have computed string-string correlations and report them in this section. As advanced in Fig. 3, we distinguish two types of string, defined by their baryon number. If the initial two ends of a string are a quark and an anti-quark, the global baryon number is equal to 0, and we call it a meson string. If the ends hold a quark and a diquark, the baryon number is 1, and we call it a baryon string. Other cases happen to be so rare in PYTHIA that they do not affect statistical distributions and are not further considered.

Fig. 4

String-string $S_\textrm{str}$ correlations in $\textrm{pp}$ collisions from PYTHIA showing clear $\Delta \varphi =\pi$ peaks that would eventually evolve to back-to-back jets. No kinematic cuts have been applied. As the strings carry a lot of energy, the pseudorapidity scale is not comparable to measured hadrons. Because high-$\eta$ hadrons escape ALICE’s acceptance, the contribution of the beams remnant from the original collided nuclei are erased in experimental data, but are clearly visible here in the uncut simulation, as a pair of ridges at $|\Delta \eta |>10$

Each string is viewed as a particle whose momentum (and thus its pseudorapidity $\eta$ and azimuth $\varphi$) is the sum over the string’s constituents. The angular dependence of the two-string correlation (6) (unlike the absolute normalization) can be inferred from the same-event correlation $S_\textrm{str}$, which we plot in Fig. 4. In it we find that in the azimuthal dimension the distribution is mostly isotropic, except around $\Delta \varphi =\pi$, where we find a sizable peak. The relative importance of the isotropic and the peaking contributions varies with the participating strings. For meson-meson strings (a), the peak is tiny and the isotropic background offset is large. For baryon-baryon strings (c), it is the structure at $\Delta \varphi =\pi$ (now separated in two peaks at large relative pseudorapidity) that dominates the graph, and the azimuthal isotropic offset is negligible in comparison. In (b), for meson-baryon strings, the situation is intermediate.

The pair of twin peaks at large relative pseudorapidity of order 10 or more in (c) is somewhat surprising. It must be that the simulated collision between two protons produces, not only isotropically emitted baryons, but also two opposite beams. Whether a program artifact or an effect of the parent colliding protons remains to be seen, but in any case it is not currently comparable to the experimental data due to the limited rapidity coverage of the ALICE detector.

3.3 Interpretation

To summarize, the picture in $\Delta \varphi$ is the following: strings are quite uncorrelated except that they are likely to appear with opposite momenta (Sect. 3.2).

Baryons and anti-baryons from the same string (Sect. 3.1) are likewise often randomly distributed, though also with a colinear component. A part of the explanation is that between every baryon pair an antibaryon needs to be produced (to balance quark number) and this erases azimuthal baryon-baryon correlations, for example. Baryons from the same string tend to be emitted in separate directions in the string’s reference frame, but the Lorentz boost given to the string upon passing to the laboratory frame appears to overcome this effect, so that baryons stemming from the same string are actually strongly collimated and yield a forward peak in the final correlation.

The part of the hadrons that is uniformly distributed along $\Delta \varphi$ either from the same or from different strings are not supposed to provide any particular correlation in the final output. They only contribute to the isotropic offset, that influences the height of each peak or depth of each valley. As they do not change the qualitative behaviour, we do not discuss them any further in the following.

The fraction of baryons and anti-baryons from the same string, colinearly emitted, will cause a peak around $\Delta \varphi =0$ in the final picture. The baryons and anti-baryons from different strings will contribute to the isotropic offset if their strings are uncorrelated and to a peak at around $\Delta \varphi =\pi$ if their strings are anti-colinear.

Given that the number of uncorrelated strings is much larger than that of opposite-momentum strings, providing a large combinatorial background, it appears that the balance of the peaks at around $\Delta \varphi =0$, both for proton-proton and for proton-antiproton, are made of the correlations between the (anti-)baryons emitted by the same string .²

This suggests to us that a modification to bring the Monte Carlo in better agreement with experimental data would be most efficient if applied to the production of baryons from the same string (that are naturally more affected by Fermi statistics, even starting at the quark level).

4 Example Modifications to PYTHIA That Seem to Reproduce Baryon Anticorrelations As Seen in Data

4.1 First Modification: One-Baryon Policy

Following the explanation in Sect. 3.3, the existence of the peak at around $\Delta \varphi =0$ in $\mathrm{p\, p}+\overline{\textrm{p}}\, \overline{\textrm{p}}$ correlation functions might be linked to strings giving birth to more than one hadron.

To test this idea, we completely forbid it in the program with a Von Neumann rejection step: anytime that a string fragments into more than one baryon (idem for anti-baryons), the fragmentation is recalculated.

4.1.1 Physical Justification

One can see this procedure as a way to impose the Pauli principle to baryons (which are fermions). The algorithm is not influenced by the nature of the baryons nor their spin. Instead, it could be influenced by the Fermi statistics of the quarks themselves. The similarity of the center ($\textrm{pp}$) and right ($\textrm{p}\Lambda$) plots in Fig. 1 hints that no difference should be made among species of baryons. At the baryon level this may sound strange since $\textrm{p}$ and $\Lambda$ are distinguishable, but at the quark level, since both contain $\textrm{u}$ and $\textrm{d}$ valence quarks, it may be more understandable.

In the current PYTHIA 8.3 version, Fermi-Dirac statistics does not seem to be implemented in any way. It would have been surprising that the absence of such an important principle was not falsified at some point by contrasting the generated data against experiment: it so has happened that multiple-baryon final states have not been thoroughly analyzed until this last decade.

The appropriate theoretical procedure would be to anti-symmetrize an appropriate multi-fermion wavefunction or quantum amplitude, so we write down some formalism that could serve as illustration to fix ideas, although our computer-algorithm modifications will be much cruder. A possible output of a fragmentation [11] is associated with such an amplitude, derived from the wavefunctions of the involved entities through

$$\begin{aligned} M(A\rightarrow BC)=\int d^3r\int d^3w \, \psi _B^* (\textbf{r}/2+\textbf{w}) \psi _C^* (\textbf{r}/2-\textbf{w}) \mathbf{\alpha }\cdot (i\mathbf{\nabla _B}+i\mathbf{\nabla _C}+\textbf{q}) \psi _A(\textbf{r}) e^{\frac{1}{2}i\textbf{q}\cdot \textbf{r}} \gamma ^a_{bc}(\textbf{r},\textbf{w})\nonumber \\ \end{aligned}$$

(11)

Were A, B and C are strings or hadrons, which are equivalent in this description. $\gamma ^a_{bc}(r,w)$ is a function that can be computed with methods discussed in the literature [11].

It is easy to write a (perhaps long) expression for the semi-inclusive two-baryon production amplitude of the form

$$\begin{aligned} M(A\rightarrow B_1+B_2+X)=\int \; \cdots \quad \psi _{B_1}^*(\cdots ) \psi _{B_2}^*(\cdots ) \quad \cdots \end{aligned}$$

(12)

That allows to anti-symmetrize the baryon part of the wavefunction as in an atomic Slater determinant

$$\begin{aligned} \tilde{M}(A\rightarrow B_1+B_2+X)=\int \; \cdots \quad \left( \psi _{B_1}^*\psi _{B_2}^*-\psi _{B_2}^*\psi _{B_1}^*\right) \quad \cdots \end{aligned}$$

(13)

and we expect $|\tilde{M}|<|M|$.

Taking the perhaps drastic but much simplifying approximation $\frac{|\tilde{M}|}{|M|} \rightarrow 0$ leads us to forbid the production of two baryons from the same string. This is the content of the first “one-baryon only” correction.

If one wanted to apply less dramatic simplification, one would have to redevelop parts of the Lund string model formalism to make it compatible with, for example, the formalism of [11].

4.1.2 Results

Fig. 5

$\textrm{pp}$ correlation function C in pp collisions from standard PYTHIA 8 (top left) shows clear forward and backward ridges for $\Delta \varphi =0,\pi$ and all relative pseudorapidities. The one-baryon policy modification (top right) forbids two baryons from the same string, erasing the forward correlation but depressing the total number of baryons. The additional modification of the always-baryon policy (lower left) solves this problem by increasing the overall number of baryons. The backward correlation is still there; the forward correlation has now been turned into an anticorrelation; and the number of baryons produced is more adequate

Fig. 6

Correlation functions C (top row) for $\textrm{pp}$, $\Lambda \Lambda$, $\Lambda \textrm{p}$, and $\Lambda {\bar{\textrm{p}}}$ in pp PYTHIA8 collisions applying the one-baryon policy. Azimuthal projection (bottom row) of the correlation function C for $\textrm{pp}$, $\Lambda \Lambda$, $\Lambda \textrm{p}$, and $\Lambda {\bar{\textrm{p}}}$ compared to ALICE data [2]

That simplest procedure of imposing a one-baryon per string policy can be very time consuming. Combining it with the afterburners correction worsens this and additionally leads to technical difficulties that makes it unpractical to gather sufficient Monte Carlo statistics in a limited university departmental cluster.

In the afterburners procedure, the lengthy code, together with the number of pairs increasing with the square of the number of events, can be a drawback. It brings about a rise of the whole time of execution, increases the frequency of software crashes and produces random pairs that occasionally give nonsense results (like negative weights) and must be discarded. If the afterburners method is used alone this is not dramatic and can be handled. But the difficulties compound if this addition to PYTHIA is combined with another.

As it is, we renounce to deploy the two methods together. It would be interesting to find a time-economic implementation, but we have not managed to design one in a reasonably small time. Our one-baryon policy correction gives results that are sufficiently encouraging to confirm the relevance of our method and suggest that further work will be interesting.

Figure 5 (right top plot marked as b) shows that the first demand on the output is fulfilled: the peak at $\Delta \varphi =0$ has been suppressed by imposing to each string the one-baryon policy. Indeed, that peak seems to be produced by baryons coming from the same string. Still, this policy has a major side effect, which is to strongly reduce the number of protons in the final state (and also of $\Lambda$ hyperons and generically all baryon species). This was predictable because the method flatly reduces the average number of baryons produced by each string.

More detail is presented in Fig. 6 that shows, in the top row, the correlation function C from PYTHIA8 pp collisions, after applying the one-baryon policy, for $\textrm{pp}$, $\Lambda \Lambda$, $\Lambda \textrm{p}$, and $\Lambda {\bar{\textrm{p}}}$ particle pairs. The bottom row shows the correlation function azimuthal projections compared to ALICE data [2]. Observe the excellent agreement between data and simulation for baryon-baryon correlations where the anticorrelation observed in data is perfectly reproduced by the simulation. But because the spectrum is not well reproduced (see Fig. 8), we need a bit more thought presented in the next subsection. The appreciable discrepancy in the baryon-antibaryon correlation function compared to data shown in Fig. 6 is not produced by the application of the one-baryon policy: the discrepancy is already observed from PYTHIA8 without introducing any modification as was also realized by the ALICE collaboration [2].

4.2 Second, Balancing Correction: No Baryonless Fragmentation or “Always Baryons” Policy

To repurpose PYTHIA to correct for the dearth of protons in the final state, following the one-baryon policy, a second correction is tried.

Recognizing that the overall baryon number has been reduced because each fragmentation is now constrained to produce one baryon at most, a simple way to rebalance it is to force each meson string to fragment into exactly one baryon and one anti-baryon (two baryons and one anti-baryon for baryon strings).

This second “always baryons” correction is a purely practical expedient that no physical explanation seems to justify within the string model. And yet, the results are satisfactory. Figure 5 (lower-left plot marked c) shows that the relative features (ridges, valleys, absence of peaks) are equivalent to those of the one-baryon policy (upper right plot marked b), and it is only the overall number of baryons and anti-baryons which is increased. Any small remaining differences can probably be solved by a change of PYTHIA tune: indeed, each change to PYTHIA must induce a new calibration of its tune, but we leave this for future investigators and comment on it only briefly.

Among the parameters to be tuned, one should be carefully considered: $P_{Q\rightarrow QQ}$, the probability to engender diquark/anti-diquark pairs emerging from the vacuum during the string fragmentation, instead of quark/anti-quark ones. Changing this relative ratio is not independent of restraining the number of baryons emitted during the fragmentation. With our second always-baryons modification, this number of baryons is imposed so this parameter has no impact on the final output.

Nevertheless, an unwise choice of this $P_{Q\rightarrow QQ}$ parameter has an unwelcome consequence. If one fragmentation iteration is unlikely to give exactly one baryon, it will be relaunched multiple times until it branches into a solution that satisfies the one-baryon policy. This may affect dramatically the length of execution of each fragmentation program loop.

But if only the first “one-baryon policy” correction is imposed, during fragmentation of meson strings the number of baryon–anti-baryon pairs produced can be either one or none, and that control parameter affects the relative probability of the two outcomes, becoming relevant to the output and not only to the execution time.

Choosing a high value for this $P_{Q\rightarrow QQ}$ parameter can be viewed as getting closer to the second correction “always-baryon policy” even without imposing it. But increasing it causes the mean number of baryons in a string-fragmentation iteration to rise, and with it the possibility of discarding the fragmentation and having to rerun it due to exceeding the one-baryon policy. The effect on the global execution time could then be dramatic. Hence, the “always-baryon policy” can be viewed as an effective way of achieving the same effect without having to increase this parameter nor pay the extra execution time.

On the downside, this always-baryon policy is far from perfect from a computing implementation point of view. Compared to the one-baryon policy alone, it makes the code slower and more likely to crash. As it is, this implementation makes a combination with the afterburners method impractical.

Fig. 7

Correlation functions C (top row) for $\textrm{pp}$, $\Lambda \Lambda$, $\Lambda \textrm{p}$, and $\Lambda {\bar{\textrm{p}}}$ in pp PYTHIA8 collisions applying the always-baryon policy. As in figure 6, we show the azimuthal projection (bottom row) of the correlation function C for $\textrm{pp}$, $\Lambda \Lambda$, $\Lambda \textrm{p}$, and $\Lambda {\bar{\textrm{p}}}$ compared to ALICE data [2]

For completeness Fig. 7 shows, in the top row, the correlation function C from PYTHIA8 pp collisions, after applying the always-baryon policy, for $\textrm{pp}$, $\Lambda \Lambda$, $\Lambda \textrm{p}$, and $\Lambda {\bar{\textrm{p}}}$ particle pairs. The bottom row shows the correlation function azimuthal projections compared to ALICE data [2].

We see that the agreement with the data has deteriorated a bit respect to Fig. 6. It is interesting to highlight that the agreement of the baryon-antibaryon correlation function with data instead improves. With both one-baryon and all-baryon policies the result for the correlations is reasonable. And the “always baryon” policy correctly reproduces the baryon spectrum, indicating that the overall number of baryons is now accounted for. This can be seen in Fig. 8.

Fig. 8

Transverse particle spectra in unmodified (“Ref”) and modified (“one B”, “always B”) PYTHIA simulations. The “One baryon policy” (open squares) are seen to undershoot production of both protons and $\Lambda$ baryons respect to standard PYTHIA. On the other hand, additionally implementing the “Always baryon policy” (open circles) basically restores the original prediction. As expected none of both policies modify the meson spectra

5 Conclusion and Perspectives

We have examined the problem of baryon anticorrelations, a severe current disagreement between experimental data from the ALICE collaboration (lately also from the STAR collaboration) and theoretical Monte Carlo simulations of hadron collisions. Such anticorrelations are typical of lower-energy nuclear physics, for example in two-proton radiactivity (see [12], right panel of Fig. 18, that shows a decrease at $\cos \theta _Y=-1$ when the protons are emitted back to back, respect to $\cos \theta _Y>-1$, an effect ascribed to Coulomb repulsion and the Pauli principle) but are now also routinely obtained in high-energy collisions, due to the improved particle identification; they should, and are not, reproduced by current event generators.

We believe that the “fault” lies on the theory side and that we have made a contribution to the discussion by exposing that modification of the Monte Carlo event generator package PYTHIA 8 at the fragmentation level can qualitatively account for anticorrelation. In our not very refined approach, this has been achieved by means of a “one-baryon policy” applied to each string. Because, with standard PYTHIA parameters, this depresses the baryon to meson ratio (the total number of baryons produced is naturally smaller), a temporary correcting “all-baryon policy” has also been adopted, so that in our implementation given in the appendix, each string fragments into exactly one baryon (plus an unspecified number of mesons).

If this problem was to be reassessed in future work, one could try, instead of suppressing baryons from the same string, to give them a natal kick to separate them (or more selectively suppress them depending on their produced momentum). Another interesting theoretical extension would entail an extended probability distribution along the string, in order to mimic baryon or quark wave functions therealong.

Implementing a mechanism to take into account Fermi statistics in some way in PYTHIA is really difficult if we want to keep its computer efficiency, reasonably fit the data and give a convincing physical explanation. This is largely due to the fact that the Lund string model is mostly classical with point like particles while Fermi statistics is a quantum phenomenon based on wavefunctions. These two description are both essential, the first one for speed of execution and the second one for physical meaning. Thus, for the problem to be solved in a cleaner way, a translation between the two formalisms is necessary. For this, one must perhaps wait for a deeper understanding of the soft QCD processes that string fragmentation approximates. Conversely, finding a convenient procedure explaining major data features can give hints towards understanding of those deeper processes.

As for the extant LEP baryon correlation data, it could be reasonably fit by PYTHIA as is, given that the color string did form linking a back-to-back primary quark-antiquark pair; this means that baryons from the same string did not form positive correlations near $\Delta \eta \simeq 0 \simeq \Delta \varphi$ in OPAL data, as they were somewhat randomized, with the string frame not too far from the laboratory frame.

At the LHC strings are however formed at various rapidities and azimuths, with a natal Lorentz boost. Because of that string boost, two baryons formed from the same string will create that positive correlation in the laboratory frame. Therefore, to avoid it and bring about the anticorrelation seen in the data, two-baryon production from the same string should be suppressed: our way of achieving it is the very rough pair of policies (one-baryon and all-baryon) that certainly need to be improved in future work.

Appendix A: Specific Modification to PYTHIA

The most important modifications that we have described in the article are specified here. We act on line 663 of the PYTHIA 8 version 307 package file

         /src/StringFragmentation.cc,

in the function

         StringFragmentation::fragment.

The only other file that needs to be modified is

         /src/PYTHIA.cc,

to adapt the validity checks accordingly.

We here provide the code of StringFragmentation::fragment with the modifications highlighted.

(These flags and modes are the interface with the user to configure the hadron policy.)

(This part makes PYTHIA return the strings together with the remaining intermediates particles of the event. It is needed to plot Figs. 3 and 4.)

(If that condition is not fulfilled, the whole function is executed again. This corresponds to the one-baryon policy if $(n_{min},n_{max})=(0,2)$, and to the always-baryon policy if $(n_{min},n_{max})=(2,3)$.)