1 Introduction

The large charge symmetry breaking (CSB), manifested in the differences of the \({\varLambda }\)-separation energies of the mirror nuclei \({^4_\varLambda \mathrm{He}}\) and \({^4_\varLambda \mathrm{H}}\), is one of the mysteries of hypernuclear physics. Already experimentally established in the early 1960s [1, 2], for the ground (\(0^+\)) state, there is still no plausible and generally accepted explanation of it despite of numerous investigations [3,4,5,6,7,8,9,10]. Indeed, the separation-energy difference \(\varDelta E(0^+)\) of 340 keV [11], benchmark for many decades, is about half of the corresponding difference in the mirror nuclei \({^3\mathrm H}\) and \({^3\mathrm He}\) which amounts to 764 keV [12]. However, while in the latter case about 90 % of the difference is due to the Coulomb force, its effect is rather small for the \(A=4\) hypernuclei and, moreover, it goes into the wrong direction [5, 7]. Thus, most of the CSB seen in the \(A=4\) hypernuclei must come from the strong interaction.

The separation-energy difference for the excited \((1^+)\) state was established with a measurement from 1979 [13] and found to be \(\varDelta E(1^+) = 240\) keV. Thus, at that time, it looked as if CSB effects are practically spin (state) independent. The situation changed considerably around 2015-2016 when new and more refined data from experiments at J-PARC [14] and Mainz [15, 16] became available. These led to the presently accepted values of \(\varDelta E(0^+) = 233\pm 92\) keV and \(\varDelta E(1^+) = -83\pm 94\) keV [10].

As already indicated above, initial calculations of the \({^4_\varLambda \mathrm He}\)-\({^4_\varLambda \mathrm{H}}\) binding energy difference based on a two-body model [1, 4] failed to describe the data. The principle CSB mechanism considered in those studies consisted of \({\varLambda }-{\Sigma }^0\) mixing. It facilitates pion exchange between the \({\varLambda }\) and the nucleons [1], which is otherwise forbidden by isospin conservation. In addition, contributions from \(\eta -\pi ^0\), \(\omega -\rho ^0\), etc., mixing were taken into account. The situation did not improve with first more elaborate studies that employed four-body wave functions from variational Monte Carlo calculations [6]. And it remained also unchanged when the first full-fledged four-body calculations based on the Faddeev-Yakubovsky approach became available [7]. The coupled-channel \({\varLambda }N\)-\({\Sigma }N\) interactions employed in the latter study, constructed by the Nijmegen group [17, 18], all include \({\varLambda }-{\Sigma }^0\) mixing as essential source of CSB. In addition, further sources of CSB such as the Coulomb interaction in the NN and \({\Sigma }N\) subsystems and the mass differences between \({\Sigma }^-\), \({\Sigma }^0\) and \({\Sigma }^+\) were taken into account in Ref. [7]. But these calculations could only explain a fraction of the experimentally found CSB in \(A=4\) hypernuclei. Very recently four-body calculations within the no-core shell model were presented by Gal and Gazda [9, 10] which promised, finally, a solution to the CSB “puzzle”. However, the CSB mechanism is somewhat unorthodox and rests on the assumption that the CSB part of the \({\varLambda }N\) interaction can be entirely and uniquely fixed by the \({\varLambda }N\rightarrow {\Sigma }N\) transition potential [8].

In the present work, we study CSB in the hyperon-nucleon (YN) interaction within SU(3) chiral effective field theory (EFT) [19,20,21,22], which is an extension of Weinberg’s idea suggested for nuclear forces [23] to systems involving baryons with strangeness. In this approach, the long-range part of the interaction (due to exchange of pseudoscalar mesons) is fixed by chiral symmetry. The short-distance part is not resolved and effectively described by contact terms whose strengths, encoded in low-energy constants (LECs), need to be determined by a fit to data [23,24,25]. This notion applies to the charge-symmetry conserving as well as to the charge-symmetry breaking part of the interaction [26,27,28]. Accordingly, in our investigation, we do not follow the aforementioned procedure applied by Gal and Gazda. Rather, we fix the CSB part of the \({\varLambda }N\) potential from the \(A=4\) separation energies and then predict CSB effects for the elementary \({\varLambda }p\) and \({\varLambda }n\) interactions. We do not share the view of Gazda and Gal who consider this procedure basically as a tautology [10] but actually as an excellent tool to pin down the \({\varLambda }n\) interaction, relying on and being consistent with available hypernuclear data.

The paper is structured in the following way: in the subsequent section, we give a detailed account of the CSB part of the \({\varLambda }N\) interaction. Here we follow closely the arguments from analogous studies of the nucleon-nucleon (NN) system. Technical details of the treatment of the three- and four-body systems are summarized in Sec. 3. In Sec. 4, we explain how the CSB part is determined from the separation-energy differences in the \(0^+\) and \(1^+\) states of the \(A=4\) hypernuclei. Specifically, considering those differences allows us to fix the low-energy constants of corresponding CSB contact terms that arise at next-to-leading order in the chiral expansion [28]. Once those are established, predictions for \({\varLambda }p\) and \({\varLambda }n\) scattering lengths are presented. The paper ends with some concluding remarks.

2 Hyperon-Nucleon Interaction

2.1 YN Interaction in Chiral EFT

For the present study, we utilize the YN interactions from Refs. [20, 21], derived within SU(3) chiral EFT up to next-to-leading order (NLO). At that order of the chiral expansion, the YN potential consists of contributions from one- and two-pseudoscalar-meson exchange diagrams (involving the Goldstone boson octet \(\pi \), \(\eta \), K) and from four-baryon contact terms without and with two derivatives. The two YN interactions are the result of pursuing different strategies for fixing the low-energy constants (LECs) that determine the strength of the contact interactions. In the YN interaction from 2013 [20], denoted by NLO13 in the following, all LECs have been fixed exclusively by a fit to the available \(\varLambda N\) and \(\Sigma N\) data. The other potential [21] (NLO19) has been guided by the objective to reduce the number of LECs that need to be fixed from the YN data by inferring some of them from the NN sector via the underlying (though broken) SU(3) flavor symmetry. A thorough comparison of the two versions for a range of cutoffs can be found in Ref. [21], where one can see that the two YN interactions yield essentially equivalent results in the two-body sector. Note that there is no explicit CSB in the \({\varLambda }N\) potential of the published YN interactions. However, since the scattering amplitude in Refs. [20, 21] is obtained from solving a coupled-channel Lippmann-Schwinger equation in the particle basis, the mass differences between \({\Sigma }^-\), \({\Sigma }^0\), and \({\Sigma }^+\) enter and likewise the Coulomb interaction in the \({\Sigma }^- p\) channel. Because of that isospin symmetry is broken and the results for \({\varLambda }p\) and \({\varLambda }n\) scattering are (slightly) different.

2.2 CSB in Chiral EFT

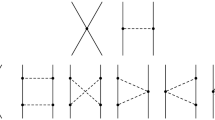
As noted by Dalitz and von Hippel many decades ago [1], \({\varLambda }- {\Sigma }^0\) mixing leads to a long-ranged CSB contribution to the \({\varLambda }N\) interaction due to pion exchange, see Fig. 1. The strength of the potential can be estimated from the electromagnetic mass matrices,

$$\begin{aligned} \langle {\Sigma }^0|\delta m|{\varLambda }\rangle= & {} [m_{{\Sigma }^0}-m_{{\Sigma }^+}+m_p-m_n]/\sqrt{3}, \nonumber \\ \langle \pi ^0|\delta M^2|\eta \rangle= & {} [M^2_{\pi ^0}-M^2_{\pi ^+}+M^2_{K^+}-M^2_{K^0}]/\sqrt{3} \end{aligned}$$
(1)

and subsumed in terms of an effective \({\varLambda }{\varLambda }\pi \) coupling constant

$$\begin{aligned} f_{{\varLambda }{\varLambda }\pi } = \left[ -2 \frac{\langle {\Sigma }^0|\delta m|{\varLambda }\rangle }{m_{{\Sigma }^0}-m_{{\varLambda }}}+ \frac{\langle \pi ^0|\delta M^2|\eta \rangle }{M^2_{\eta }-M^2_{\pi ^0}} \right] \, f_{{\varLambda }{\Sigma }\pi } \ . \end{aligned}$$
(2)

Based on the latest PDG mass values [29], one obtains

$$\begin{aligned} f_{{\varLambda }{\varLambda }\pi }=f^{({\varLambda }- {\Sigma }^0)}_{{\varLambda }{\varLambda }\pi }+f^{(\eta -\pi ^0)}_{{\varLambda }{\varLambda }\pi } \approx (-0.0297 - 0.0106)\, f_{{\varLambda }{\Sigma }\pi } \ . \end{aligned}$$
(3)

In this context, let us mention that there are also lattice QCD calculations of \({\varLambda }-{\Sigma }^0\) mixing [30,31,32,33].

Fig. 2
figure 1

CSB contributions involving pion exchange, according to Dalitz and von Hippel [1], due to \({\varLambda }-{\Sigma }^0\) mixing (left two diagrams) and \(\pi ^0-\eta \) mixing (right diagram).

Full size image
Fig. 3
figure 2

CSB contributions from \(K^{\pm }\)/\(K^0\) exchange (left) and from contact terms (right)

Full size image

In our implementation of CSB within chiral EFT, we follow closely the arguments given in pertinent studies of isospin-breaking effects in the nucleon-nucleon (NN) system, see Refs. [26,27,28]. According to Ref. [27], the CSB contributions at leading order are characterized by the parameter \(\epsilon M^2_\pi / \varLambda ^2 \sim 10^{-2}\), where \(\epsilon \equiv \frac{m_d-m_u}{m_d+m_u} \sim 0.3\) and \(\varLambda \sim M_\rho \). In particular, one expects a potential strength of \(V^{\mathrm{CSB}}_{BB} \sim (\epsilon M^2_\pi / \varLambda ^2)\, V_{BB}\). At order \(n=2\) (NLØ in the notation of Ref. [28]), there are contributions from isospin violation in the pion-baryon coupling constant, which in the \({\varLambda }N\) case arise from the aforementioned \(\Sigma ^0-\varLambda \) mixing as well as from \(\pi ^0-\eta \) mixing. In addition, there are contributions from short range forces (arising from \(\rho ^0-\omega \) mixing, etc.). In chiral EFT, such forces are simply represented by contact terms involving LECs (Fig. 2 right) that need to be fixed by a fit to data. Contributions at \(n=1\) (LØ) are due to a possible Coulomb interaction between the baryons in question and due to mass differences between \(M_{\pi ^\pm }\) and \(M_{\pi ^0}\). Such contributions do not arise in the \(\varLambda N\) system. However, in the extension to SU(3), there is CSB induced by the \(M_{K^\pm }\)-\(M_{K^0}\) mass difference, see left side of Fig. 2. We take that into account in our calculation, since it is formally at leading order. But because the kaon mass is rather large compared to the mass difference, its effect is actually very small. For a general overview, we refer the reader to Table 1 in Ref. [28].

The CSB part of the \({\varLambda }N\) potential at NLØ is given by

$$\begin{aligned} V^{CSB}_{{\varLambda }N\rightarrow {\varLambda }N}= & {} \Bigg [ -f^{({\varLambda }-{\Sigma }^0)}_{{\varLambda }{\varLambda }\pi } f_{NN\pi }\frac{\left( \varvec{\sigma }_1\cdot \mathbf{q}\right) \left( \varvec{\sigma }_2\cdot \mathbf{q}\right) }{\mathbf{q}^2+M^2_{\pi ^0}} \nonumber \\&- f^{(\eta -\pi ^0)}_{{\varLambda }{\varLambda }\pi } f_{NN\pi }\left( \varvec{\sigma }_1\cdot \mathbf{q}\right) \left( \varvec{\sigma }_2\cdot \mathbf{q}\right) \left( \frac{1}{\mathbf{q}^2+M^2_{\pi ^0}}-\frac{1}{\mathbf{q}^2+M^2_{\eta }} \right) \nonumber \\&+\frac{1}{4}(1-\varvec{\sigma }_1\cdot \varvec{\sigma }_2)\, C^{CSB}_{s} \,+\,\frac{1}{4}(3+\varvec{\sigma }_1\cdot \varvec{\sigma }_2)\, C^{CSB}_{t} \Bigg ] \ \tau _N \ , \end{aligned}$$
(4)

where \(C^{CSB}_{s}\) and \(C^{CSB}_{t}\) are charge-symmetry breaking contact terms in the spin-singlet (\(^1S_0\)) and triplet (\(^3S_1\)) partial waves, respectively, and \(\tau _p = 1\) and \(\tau _n =-1\). In the treatment of the contribution from \(\pi ^0-\eta \) mixing, we follow Ref. [4].

Besides the CSB in the \({\varLambda }N\) potential, there is also some effect due to the coupling to the \({\Sigma }N\) channel. Specifically, the coupled-channel Lippmann-Schwinger (LS) equation is solved in the particle basis and the physical masses of the \({\Sigma }\)’s and p, n are used. In addition, the Coulomb interaction in the \({\Sigma }^-p\) channel that couples to \({\varLambda }n\) is taken into account. As mentioned above, these effects are already considered in our standard calculation [20, 21] and lead to a small but noticeable CSB breaking in the \({\varLambda }N\) results but also in case of \({^4_\varLambda \mathrm{He}}\) / \({^4_\varLambda \mathrm{H}}\) [34,35,36]. CSB contributions to the \({\varLambda }N\) potential from (irreducible) two-pion exchange, which in our case not only involves the p-n mass difference but also the one for \({\Sigma }^+\)-\({\Sigma }^0\)-\({\Sigma }^-\), are expected to be small [27] and, therefore, omitted in the present study. Note that the corresponding two-pion exchange diagrams involve either \(\pi ^{\pm }\) or \(\pi ^0\) so that the pion-mass difference does not enter.

We note already now that the value for \(f_{{\varLambda }{\varLambda }\pi }\) given in Eq. (3) as well as the CSB LECs used in the actual calculation are in line with the aforementioned order-of-magnitude estimate by Friar et al. [27].

3 Faddeev-Yakubovsky Equations

Our predictions for \(A=3\) and \(A=4\) systems are based on solutions of Faddeev-Yakubovsky equations in momentum space [7, 37, 38]. Here, we just briefly summarize our way of solving the Yakubovsky equations for \(A=4\) hypernuclei. For one hyperon and three identical nucleons, the Schrödinger equation can be rewritten in a set of five coupled Yakubovsky equations

$$\begin{aligned} | \psi _{1A} \rangle= & {} G_0 t_{12} (P_{13}P_{23}+P_{12}P_{23}) \left[ | \psi _{1A}\rangle + | \psi _{1B}\rangle + | \psi _{2A}\rangle \right] \nonumber \\ | \psi _{1B} \rangle= & {} G_0 t_{12} \left[ (1-P_{12}) (1-P_{23}) | \psi _{1C}\rangle + (P_{13}P_{23}+P_{12}P_{23}) | \psi _{2B}\rangle \right] \nonumber \\ | \psi _{1C} \rangle= & {} G_0 t_{14} \left[ | \psi _{1A}\rangle + | \psi _{1B}\rangle + | \psi _{2A}\rangle -P_{12} | \psi _{1C}\rangle +P_{13}P_{23} | \psi _{1C}\rangle +P_{12}P_{23} | \psi _{2B}\rangle \right] \nonumber \\ | \psi _{2A} \rangle= & {} G_0 t_{12} \left[ (P_{12}-1)P_{13} | \psi _{1C}\rangle + | \psi _{2B}\rangle \right] \nonumber \\ | \psi _{2B} \rangle= & {} G_0 t_{34} \left[ | \psi _{1A}\rangle + | \psi _{1B}\rangle + | \psi _{2A}\rangle \right] \ . \end{aligned}$$
(5)

For the solution of this problem, we distinguish the proton and neutron and the \(\Sigma \) masses in the free propagator \(G_0\) and for the solution of the Lippmann-Schwinger equations for the t-matrices \(t_{ij}\) that are embedded into the four-baryon system. The reduction to only five Yakubovsky equations is possible because of the identity of the nucleons which allows to relate different Yakubovsky components to each other using permutation operators \(P_{ij}\) that interchange the quantum numbers of nucleon i and j.

Table 1 \(^3_\varLambda \)H, \(^4_\varLambda \)He and \(^4_\varLambda \)H separation energies for NLO13 and NLO19 for various cutoffs in combination with SMS \(\hbox {N}^4\)LO+ (450) [40] and different cutoffs for NLO13 and/or NLO19
Full size table

The five remaining Yakobovsky components \(| \psi _{1A}\rangle \), \(| \psi _{1B}\rangle \), \(| \psi _{1C}\rangle \), \(| \psi _{2A}\rangle \) and \(| \psi _{2B}\rangle \) are expanded in terms of their natural Jacobi coordinate

$$\begin{aligned} | p_{12} p_3 q_4 \alpha _A \rangle= & {} \left| p_{12} p_3 q_4 \left[ \left[ (l_{12}s_{12})j_{12} \left( l_3 \frac{1}{2} \right) I_3 \right] j_{123} \left( l_4 \frac{1}{2} \right) I_4 \right] J \left[ (t_{12} \frac{1}{2}) \tau _{123} t_Y \right] T M_T \right\rangle \ \nonumber \\ | p_{12} p_4 q_3 \alpha _B \rangle= & {} \left| p_{12} p_4 q_3 \left[ \left[ (l_{12}s_{12})j_{12} \left( l_4 \frac{1}{2} \right) I_4 \right] j_{124} \left( l_3 \frac{1}{2} \right) I_3 \right] J \left[ (t_{12} t_Y ) \tau _{124} \frac{1}{2} \right] T M_T \right\rangle \ \nonumber \\ | p_{14} p_2 q_3 \alpha _C \rangle= & {} \left| p_{14} p_3 q_4 \left[ \left[ (l_{14}s_{14})j_{14} \left( l_2 \frac{1}{2} \right) I_2 \right] j_{124} \left( l_3 \frac{1}{2} \right) I_3 \right] J \left[ (t_{14} \frac{1}{2}) \tau _{124} \frac{1}{2} \right] T M_T \right\rangle \ \nonumber \\ | p_{12} p_{34} q \beta _A \rangle= & {} \left| p_{12} p_{34} q \left[ \left[ (l_{12}s_{12})j_{12} \lambda \right] I \ (l_{34}s_{34})j_{34} \right] J \ (t_{12} t_{34}) T M_T \right\rangle \ \nonumber \\ | p_{34} p_{12} q \beta _B \rangle= & {} \left| p_{34} p_{12} q \left[ \left[ (l_{34}s_{34})j_{34} \lambda \right] I \ (l_{12}s_{12})j_{12} \right] J \ (t_{34} t_{12}) T M_T \right\rangle \ . \end{aligned}$$
(6)

There are two types of Jacobi coordinates required. The first three basis sets are of the “3+1” type. Here, three momenta \(p_{ij}\), \(p_k\) and \(q_l\) are required that are relative momenta within the pair ij, of particle k with respect to pair ij and of particle l with respect to the three-body subsytem ijk. Corresponding orbital angular momenta \(l_{ij}\), \(l_j\) and \(l_k\) are used to expand angular dependencies. \(s_{ij}\) and \(j_{ij}\) are the spin and total angular momentum of the two-body subsystem. We also introduce \(j_{ijk}\) and \(\tau _{ijk}\) for the total angular momentum and isospin of the three-body subsystem. J, T and \(M_T\) are the total angular momentum, isospin and third component of isospin of the four-baryon system. We have omitted the spins and isospins of the two baryons in the inner most subsystem since only \(t_4=t_Y\) differs from 1/2. The last two basis sets are of the “2+2” type. Here, relative momenta of two two-body subsytems \(p_{ij}\) and \(p_{kl}\) are introduced together with angular momenta and isospins for these subsystems. Additionally, the relative momentum of the two pairs q and its angular momentum \(\lambda \) is required. In order to finally define the total four-body angular momentum in this case, an additional intermediate angular momentum I is required and coupled to the other angular momenta as shown in Eq. (6).

Once the Yakubovsky components are found, we obtain the wave function by

$$\begin{aligned} | \varPsi \rangle= & {} (1+P_{13}P_{23}+P_{12}P_{23}) | \psi _{1A} \rangle \nonumber \\&+ (1+P_{13}P_{23}+P_{12}P_{23}) | \psi _{1B} \rangle \rangle \nonumber \\&+ (1-P_{12}) (1+ P_{13}P_{23}+P_{12}P_{23}) | \psi _{1C} \rangle \nonumber \\&+(1+P_{13}P_{23}+P_{12}P_{23}) | \psi _{2A} \rangle \rangle \nonumber \\&+(1+P_{13}P_{23}+P_{12}P_{23}) | \psi _{2B} \rangle \ . \end{aligned}$$
(7)

For the solution of the Yakubovsky equations, the permutation operators \(P_{ij}\) and transformations between different Jacobi coordinates Eq. (6) need to be evaluated. For these parts of the code, we use averages of the nucleon and \(\Sigma \) masses. A comparison of the resulting energies and expectation values of the Hamiltonian shows that this approximation does not alter the results.

For the numerical solution, the partial wave states have to be constrained. Here, we choose \(j_{ij}\le 4\), \(l_i\le 4\), \(\lambda \le 4 \). Additionally, we restrict \(l_{ij}+l_k+l_l \le 10\) and \(l_{ij}+l_{kl}+\lambda \le 10\). We also only take the dominant isospin state \(T=1/2\) into account.

We checked carefully that, for the chiral interactions employed here, these constraints ensure that the numerical accuracy is better than 10 keV for the energies entering the Yakubovsky equations (5) and 20 keV for expectation values of the energy. It turns out that the additional isospin components with \(T=3/2\) and \(T=5/2\) induced by isospin breaking effects which we do not take into account here lead to changes of the energy in this order and contribute most to this uncertainty.

For the solution of this bound state problem, the Coulomb interaction in YN and NN is included. As discussed above, the Coulomb interactions only contribute a few keV to the separation energies. The same is true for the n-p mass difference as has been shown in Ref. [39] for \(^3\)H-\(^3\)He. We therefore do not distinguish between contributions due to the n-p mass difference and the one of the \(\Sigma \)’s in our results. In fact, the n-p mass difference also contributes to the CSB of the core nucleus which we also do not separate from the other CSB contributions of the core.

As shown in previous calculations, the \({\varLambda }\) separation energies of light hypernuclei are only mildly dependent on the underlying NN interaction [7, 21]. Therefore, we employ in all of the calculations presented here the same chiral semi-local momentum-space-regularized (SMS) NN interaction of Ref. [40] at order \(\hbox {N}^4\)LO+ for a cutoff of \({\varLambda }=450\) MeV. We have also used the Idaho interaction [41] for these calculations and have not found any significant changes of the CSB predictions. We note that at LO, we find somewhat larger separation energies for \(A=4\) hypernuclei for \(\hbox {N}^4\)LO+ compared to Idaho. Apparently, the missing repulsion at short distances at LO increases the sensitivity to configuration of the nucleons in the core. At NLO, the NN force dependence of the separation energies is of the order of 100 keV and within the range expected from calculations based on phenomenological interactions [7]. To define a baseline, we summarize our results for the separation energies of \(A=3\) and 4 hypernuclei for the original NLO13 and NLO19 interactions in Table 1.

Below we will present two kinds of results for the CSB. First, we will perform complete calculations for \(^4_\varLambda \)He and \(^4_\varLambda \)H. This will allow us to obtain the CSB of the separation energies directly. But it does not allow for an easy separation of the different contributions to CSB. Second, we will use the wave function and Yakubovsky components for \(^4_\varLambda \)He of the original interactions to evaluate CSB perturbatively. For this, we calculate the expectation values of the differences of the kinetic energy and the NN and YN potentials when n and p and \(\Sigma ^+\) and \(\Sigma ^-\) are interchanged. The total CSB of both calculations agrees to better than 10 % for our standard calculations.

4 Results

As argued in Refs. [21, 42], the contribution of three-body forces (3BFs) is probably negligible for \(A=3\), but very likely becomes relevant for the more strongly bound \(A=4\) system. The dependence of the separation energies on the regulator (cutoff) is an effect of next-to-next-to-leading order (\(\hbox {N}^2\)LO) which includes also 3BFs [43]. As can be seen from the results in Table 1, the variation is negligible for the hypertriton but can be as large as 200–300 keV for \(A=4\). Even larger is the difference between the two different realizations of YN interactions: NLO19 and NLO13. For the \(1^+\) state, the predictions of these two essentially equivalent realizations of the YN interaction can differ by as much as 500 keV. These variations in the predicted \(A=4\) separation energies have to be kept in mind and, ultimately, should be explained by similarly large 3BF contributions.

However, such 3BFs should have only a minor influence on the observed splittings between the \({^4_\varLambda \mathrm{He}}\) and \({^4_\varLambda \mathrm{H}}\) states, which are primarily due to CSB two-baryon forces. This is the basic assumption in the strategy pursued below.

4.1 CSB in \(A=4\) Hypernuclei

To start with, we need to fix the CSB-breaking LECs \(C^{CSB}_{s}\) and \(C^{CSB}_{t}\) in the \({\varLambda }N\) interaction, cf. Eq. (4). We do this by considering the observed CSB splittings in the \(A=4\) hypernuclei, defined in the usual way in terms of the separation energies

$$\begin{aligned} \varDelta E(0^+)= & {} E^{0^+}_{{\varLambda }}({^4_\varLambda \mathrm{He}}) -E^{0^+}_{{\varLambda }}({^4_\varLambda \mathrm{H}}), \nonumber \\ \varDelta E(1^+)= & {} E^{1^+}_{{\varLambda }}({^4_\varLambda \mathrm{He}}) -E^{1^+}_{{\varLambda }}({^4_\varLambda \mathrm{H}}) \ . \end{aligned}$$
(8)

In our principal results, we aim at a reproduction of the present experimental situation, based on the recent measurements of the \({^4_\varLambda \mathrm{H}}\) \(0^+\) state in Mainz [16] and the one of the \({^4_\varLambda \mathrm{He}}\) \(1^+\)-\(0^+\) splitting at J-PARC [14], i.e. \(\varDelta E(0^+) = 233\pm 92\) keV and \(\varDelta E(1^+) = -83\pm 94\) keV. It is the same scenario as considered by Gazda and Gal in Ref. [10]. Below, we will refer to this choice as CSB1. In order to illustrate the effect of CSB in the \(A=4\) hypernuclei on the underlying \({\varLambda }N\) interaction, we consider also two other scenarios. One (CSB3) corresponds to the situation after the publication of the J-PARC experiment [14] but before the final results from Mainz became available: \(\varDelta E(0^+) = 350\pm 50\) keV and \(\varDelta E(1^+) = 30\pm 50\) keV. It is the status considered by Gazda and Gal in Ref. [9] and discussed in the review [44]. In addition, we look at the situation up to 2014 (which will be labeled CSB2), namely \(\varDelta E(0^+) = 350\pm 50\) keV and \(\varDelta E(1^+) = 240\pm 80\) keV [13]. It is the one discussed by Gal in Ref. [8] and, of course, in all pre-2014 studies of CSB in the \(A=4\) hypernuclei. Note that the CSB splitting in the \(1^+\) states in the scenarios CSB1 and CSB3 is compatible with zero, given the experimental uncertainty.

Table 2 Comparison of different CSB scenarios, based on the YN interactions NLO13 and NLO19 with cutoff \(\varLambda = 600\) MeV
Full size table
Table 3 Singlet (s) and triplet (t) S-wave scattering lengths and \(\chi ^2\) values for the fits to the present experimental CSB splittings of \(\varDelta E(0^+)=233\) keV and \(\varDelta E(1^+)=-83\) keV (CSB1), based on the YN interactions NLO13 and NLO19
Full size table

We determine the CSB LECs from perturbative calculations of the CSB contribution to the \(^4_\varLambda \)H-\(^4_\varLambda \)He splittings for the three scenarios CSB1-3. Table 2 provides a comparison of the results for the different scenarios with those of the original (NLO13 and NLO19) YN potentials, for a regulator with cutoff \({\varLambda }= 600\) MeV, cf. Ref. [20] for details. The total \(\chi ^2\) for the NLO13 and NLO19 potentials is from a global fit to 36 \({\varLambda }N\) and \({\Sigma }N\) data points [21] while the \(\chi ^2\) for \({\varLambda }p\) includes 12 data points [45, 46]. In case of the scenarios CSB1 and CSB3, the CSB contributions are just added to the NLO13 and NLO19 potentials as published in Refs. [20] and [21], respectively. However, for CSB2 the required CSB changes the overall YN results considerably and the total \(\chi ^2\) increases to values around \(40-50\). Here we had to re-fit the charge-symmetry conserving part in order to achieve a description of the YN data that is comparable to those in the other scenarios, cf. the \(\chi ^2\) values in Table 2. After that for CSB2 the scattering length of the singlet state produced by the charge-symmetric part amounts to \(a_{s}= -3.3\) fm, as compared to \(-2.9\) fm for the other two scenarios. We want to emphasize that the predicted binding energies of the hypertriton remain practically unchanged for the different considered scenarios for CSB. The variations are in the order of at most 30 keV, and thus remain well within the experimental uncertainty. This is expected for a \(T=0\) \(\varLambda np\) state where the \(\varLambda p\) and \(\varLambda n\) interactions are basically averaged.

Results for the principal scenario CSB1 are summarized in Table 3, based on NLO13 and NLO19 and for the standard range of cutoffs \(\varLambda =500-650\) MeV [20, 21]. Finally, the actual values for the short range CSB counter terms for that principal scenario are listed in Table 4. As one can see, those LECs are indeed much smaller than the ones of the regular (charge-symmetry conserving) contact terms (cf. Table 3 in [20]) and in line with the expectations from power counting, see Sect. 2.2.

Table 4 CSB contact terms for the \(^1S_0\) (s) and \(^3S_1\) (t) partial waves, cf. Eq. (4), fixed from the present experimental splittings \(\varDelta E(0^+) = 233\) keV and \(\varDelta E(1^+) = -83\) keV (CSB1)
Full size table

Let us start with the comparison of the various scenarios based on the calculations for the cutoff 600 MeV, listed in Table 2, and focus first on the \(\varLambda n\) scattering lengths, Obviously there is a sizable splitting between the \(\varLambda n\) and \(\varLambda p\) results, depending on the CSB scenario for \(A=4\) hypernuclei. In particular, for CSB2 the \({\varLambda }n\) interaction becomes significantly less attractive as compared to \(\varLambda p\) and, in the triplet state, also as compared to the case without CSB forces. In the other two scenarios, the singlet interaction in \(\varLambda n\) is more attractive than that in \(\varLambda p\). Furthermore, there are noticeably smaller changes for the triplet \({\varLambda }n\) scattering length in those two scenarios. In particular, for CSB1 the values for \(\varLambda n\) and \(\varLambda p\) are fairly close to that without CSB.

Table 2 also provides the results of the full (non-perturbative) calculation of the CSB splittings of the \(0^+\) and \(1^+\) states for \(A=4\) hypernuclei for all three CSB scenarios. In addition, the predictions for the original YN potentials, without any explicit CSB force, and for the case where only the one-boson-exchange CSB contributions (CSB-OBE) (\({\varLambda }-{\Sigma }^0\) mixing, \(\eta -\pi ^0\) mixing, \(K^\pm /K^0\) exchange) are added. For CSB1 and CSB3, the CSB of the separation energy agrees within experimental uncertainties with the values mentioned above. For CSB2, there are some deviations to the pre-2014 situation. Given that this is an outdated scenario anyway and that CSB2 required a complete refit of the YN interaction, we refrained from further improving the description of CSB. The obtained splittings without CSB contact terms confirm the conclusion from earlier studies [7, 34, 35] that the standard mechanisms can only explain a very small fraction of the experimentally found CSB in \(A=4\) hypernuclei. In particular, because of cancellations between the OBE contributions, once \(\eta -\pi ^0\) mixing is treated properly [4], the overall results do not really improve when including those. In addition, the large variation between the NLO13 and NLO19 results is a clear signal for the missing CSB contact terms.

Now we analyze in more detail the results for scenario CSB1, the one which is in line with the present experimental situation. Corresponding results are summarized in Table 3. There is a clear and universal trend for a sizable splitting between the \({\varLambda }p\) and \({\varLambda }n\) scattering length in the singlet state, once we impose the reproduction of \(\varDelta E(0^+)\) and \(\varDelta E(1^+)\). The splitting in the triplet state is much smaller and actually goes into the opposite direction. In particular, for reproducing the experimentally observed CSB splitting in the \(A=4\) hypernuclei, in the \(^1S_0\) state the \({\varLambda }n\) interaction is required to be more attractive than for \({\varLambda }p\), whereas for \(^3S_1\) the \({\varLambda }n\) interaction is slightly less attractive than that for \({\varLambda }p\).

With regard to the \(\varLambda n\) scattering lengths the results for the singlet channel are quite robust. The predictions are in the narrow range of \(-3.2\) to \(-3.3\) fm and practically independent of the cutoff and whether NLO13 or NLO19 is used. There is more variation in case of the triplet state which, however, is simply a reflection of the situation observed already in the calculation without CSB forces. One very interesting aspect is that, adding the CSB interaction to our NLO potentials established in Refs. [20, 21], improves also the overall description of the \(\varLambda p\) data as quantified by the \(\chi ^2\) value – without any refit, see Table 2. It is due to the noticeable reduction of the strength of the \(\varLambda p\) interaction in the singlet channel by the needed CSB force, cf. the pertinent scattering lengths in the table. In fact, one could interpret this as sign for a consistency of the available \(\varLambda p\) data with the present values of the CSB level splittings in the \(A=4\) hypernuclei. In this context we want to mention that a recent measurement of the \(\varLambda p\) momentum correlation function in pp collisions at 13 TeV [47] likewise indicates that a slightly less attractive \(\varLambda p\) interaction is favored by the data.

Finally, note that \(\varDelta a_{1S0}^{CSB} \equiv a_{{\varLambda }p} - a_{{\varLambda }n}\) is \(\approx 0.62\pm 0.08\) fm for the \(^1S_0\) partial wave, which is comparable to but noticeably smaller than the CSB effects in the pp and nn scattering lengths where it amounts to \(\varDelta a^{CSB} = a_{pp} - a_{nn} = 1.5\pm 0.5\) fm [12]. On the other hand, in case of the triplet state, the prediction is with \(\varDelta a_{3S1}^{CSB} \approx -0.10\pm 0.02\) fm significantly smaller and of opposite sign. Here, in the \(\varLambda N\) case, the uncertainty is estimated solely from the differences between NLO13 and NLO19 and the cutoff variations. A precise experimental determination of the CSB in \(A=4\) hypernuclei will allow one to obtain the scattering length with the accuracy estimated here. As can be seen in Table 2, different scenarios for CSB lead to rather different values of the scattering length. This is the main lesson from this work. Obviously, for reliable values one needs a confirmation of the presently available experimental data, with best possible accuracy.

4.2 Relation of CSB in the Separation Energies to the Expectation Values

Table 5 \(^3_\varLambda \)H, \(^4_\varLambda \)He and \(^4_\varLambda \)H separation energies for scenario CSB1 for NLO13 and NLO19 for various cutoffs in combination with SMS \(\hbox {N}^4\)LO+ (450) [40] and different different cutoffs for NLO13 and/or NLO19
Full size table

This section is a short summary of the relation between the expectation values obtained and the CSB in the separation energies of \(^4_\varLambda \)He-\(^4_\varLambda \)H for CSB1. We start with a summary of the \(A=3\) and \(A=4\) results for the separation energies in Table 5. These results are qualitatively quite similar to the ones of Table 1. We will discuss the CSB contributions for \(A=4\) in more detail below. Here, we just remark that we observed small changes of the separation energy of \(^3_\varLambda \)H of the order of 3 keV since we take isospin \(T=1\) and \(T=2\) components into account. The effect of CSB is calculated perturbatively based on the wave function for \(^4_\varLambda \)He for the orginal interaction. The results are given as differences of expectation values

$$\begin{aligned} \langle H \rangle _{\mathrm{CSB}} \equiv \langle H \rangle _{^4_\varLambda \mathrm{He}} - \langle H \rangle _{^4_\varLambda \mathrm{H}} \ . \end{aligned}$$
(9)

For the separation energies, one therefore finds

$$\begin{aligned} \varDelta E_\varLambda= & {} E_\varLambda (^4_\varLambda \mathrm{He}) - E_\varLambda (^4_\varLambda \mathrm{H}) \nonumber \\= & {} E(^3\mathrm{He}) - E(^3\mathrm{H}) - \left( \, E(^4_\varLambda \mathrm{He}) - E(^4_\varLambda \mathrm{H}) \, \right) \ \, \end{aligned}$$
(10)

where then the last contribution is approximated by the expectation values. We separate

$$\begin{aligned}&E(^4_\varLambda \mathrm{He}) - E(^4_\varLambda \mathrm{H}) \approx \langle H \rangle _{\mathrm{CSB}} \nonumber \\&\quad = \langle T \rangle _{\mathrm{CSB}} + \langle V_{NN} \rangle _{\mathrm{CSB}} + \langle V_{YN} \rangle _{\mathrm{CSB}} \nonumber \\. \end{aligned}$$
(11)

It turns out that \(E(^3\mathrm{He}) - E(^3\mathrm{H})\) is similar to \(\langle V_{NN} \rangle _{\mathrm{CSB}}\). Therefore, the contributions largely cancel. For example, one finds for the SMS NN interaction at order \(\hbox {N}^4\)LO+ [40] with cutoff 450 MeV \(E(^3\mathrm{He}) - E(^3\mathrm{H}) = 751\) keV. Based on the scenario CSB1 for NLO19 (600), \(\langle V_{NN} \rangle _{\mathrm{CSB}} = 740\) keV. Thereby, \(E(^3\mathrm{He}) - E(^3\mathrm{H})\) contains approximately 10 keV due to the mass difference of proton and neutron. The remaining 741 keV are mostly due to the point proton Coulomb interaction but also include CSB of the NN interaction. We note that this combined effect in most cases contribute positively to the CSB whereas the Coulomb interaction alone is expected to give a negative contribution [5, 7].

Table 6 Perturbative estimate of different contributions to the CSB of \(^4_\varLambda \)He and \(^4_\varLambda \)H for the \(0^+\) state based on \(^4_\varLambda \)He wave functions for scenario CSB1
Full size table
Table 7 Perturbative estimate of different contributions to the CSB of \(^4_\varLambda \)He and \(^4_\varLambda \)H for the \(1^+\) state based on \(^4_\varLambda \)He wave functions for scenario CSB1
Full size table

In Tables 6 and 7 , we summarize the different contributions to CSB for the scenario CSB1 for different YN potentials. It can be seen that the contribution of the kinetic energy (mostly due to the mass difference within the \(\Sigma \) multiplet) is strongly dependent on the chosen interaction. After properly including the CSB LECs, the YN potential provides the by far largest contribution to the CSB. The total CSB is by construction fairly independent of the YN interaction. The comparison of the perturbative estimate to the direct result for the CSB \(\varDelta E_\varLambda \) shows that both calculations agree well with each other. In the tables, we assumed an uncertainty of \(\varDelta E_\varLambda \) of 14 keV estimated by adding the uncertainty for \(^4_\varLambda \)H and \(^4_\varLambda \)He in quadrature. We note that the agreement is slightly less good when performing the estimate using the \(^4_\varLambda \)H wave functions instead of the \(^4_\varLambda \)He ones for the evaluation of the expectation values.

Fig. 4
figure 3

CSB of \(^4_\varLambda \)He/\(^4_\varLambda \)H in the \(0^+\) (top, red circles) and \(1^+\) (bottom,blue circles) state compared to the currently best experimental values (red and blue bands). The error bars reflect the numerical uncertainty

Full size image

Finally, in Fig. 3, we plot a comparison of the obtained CSB to the currently best experimental values including the uncertainties. Clearly, the dependence on the interaction and the numerical error are smaller than the experimental uncertainty.

As already seen in Table 3, the predictions for the \(\varLambda p\) and \(\varLambda n\) scattering lengths are largely independent of the interaction. The latter property is not trivial and suggests that the CSB of the scattering lengths can be indeed determined using \(A=4\) data.

4.3 The Prescription of CSB Employed by Gazda and Gal

In the calculations by Gazda and Gal [9, 10], a global prescription for the CSB potential was employed, suggested in Ref. [8]:

$$\begin{aligned} \langle N{\varLambda }|V^{CSB}_{{\varLambda }N} |N{\varLambda }\rangle = -0.0297 \tau _N \frac{1}{\sqrt{3}}\langle N{\Sigma }|V|N{\varLambda }\rangle \ . \end{aligned}$$
(12)

Obviously here the CSB contribution to the \({\varLambda }N\) interaction is equated with the full \({\varLambda }N\rightarrow {\Sigma }N\) transition potential, appropriately scaled with the \({\varLambda }-{\Sigma }^0\) mixing matrix element. Indeed, this is appropriate for isovector mesons whose direct contribution to the \({\varLambda }N\) potential is forbidden when isospin is conserved, but becomes non-zero via \(\varLambda -\Sigma ^0\) mixing. For example, in the Nijmegen YN potentials such as NSC97 [18] this aspect is implemented and \({\varLambda }-{\Sigma }^0\) mixing is taken into account for all isovector mesons (\(\pi \), \(\rho \), \(a_0\), \(a_2\)) that contribute to the \({\varLambda }N \rightarrow {\Sigma }N\) transition potential. However, with such a global prescription CSB contributions are also attributed to K and/or \(K^*\) exchange - though strange mesons contribute anyway directly to the charge-symmetry conserving part of the \({\varLambda }N\) potential. If there is CSB from say K exchange it should arise directly from the \({\varLambda }N\rightarrow {\varLambda }N\) potential, cf. Sect. 2.

Apart from that, the prescription Eq. (12) dismisses other CSB contributions not related to \({\varLambda }-{\Sigma }^0\) mixing, e.g. the ones from \(\eta -\pi ^0\), \(\rho ^0-\omega \), etc. mixing. According to the literature, \(\rho ^0-\omega \) mixing provides the main contribution to the CSB observed between the pp and nn systems [12]. Though pertinent studies for \(^{\,4}_{\varLambda }\mathrm{He}\) and \(^{\,4}_{\varLambda }\mathrm{H}\) are inconclusive [4, 6], they certainly reveal a strong model dependence. This is a clear signal that corresponding contact terms representing short-range physics should be and have to be included. In fact, also in case of Gazda and Gal, the result for the CSB splitting of the \(0^+\) state based on the LO interaction exhibits a large cutoff dependence [10]. For the \(1^+\) state, the energy levels themselves show a sizable cutoff dependence, while the CSB splitting itself appears to be too large as compared to the present experimental value. In order to quantify the uncertainty of the prescription in Eq. (12) by ourselves, we have performed calculations for the \(0^+\) state using the LO, NLO13 and NLO19 interactions. We reproduce the CSB of Ref. [10] for LO fairly well (36-309 keV). Using the same prescription, we find 461-2266 keV for NLO13 and 86-458 keV for NLO19. Evidently, the results at NLO are likewise strongly cutoff dependent and there are also strong variations between the two variants NLO13 and NLO19, which otherwise yield practically identical results for \({\varLambda }N\) and \({\Sigma }N\) scattering. The discussion in Sect. 4 of Ref. [10] suggests that the cutoff dependence and the interplay between contact terms and (unregularized) pion exchange was indeed a concern for the authors and an attempt was made to stabilize the outcome within an ad hoc procedure. However, adding genuine CSB contact terms as done in the present work is the appropriate remedy – and anyway required in a consistent application of chiral EFT. Finally, we note that this again stresses that the strength of the \(\varLambda N\)-\(\Sigma N\) transition potential is not observable and intimately correlated with consistently defined three-baryon interactions [21, 48].

5 Conclusions

In the present work, we have studied effects from CSB in the YN interaction. Specifically, we have utilized the experimentally known difference of the \(\varLambda \) separation energies in the mirror nuclei \({^4_\varLambda \mathrm{He}}\) and \({^4_\varLambda \mathrm{H}}\) to constrain the \(\varLambda \)-neutron interaction. For that purpose, we derived the contributions of the leading CSB interaction within chiral effective field theory and added them to our NLO chiral hyperon-nucleon interactions [20, 21]. CSB contributions arise from a non-zero \({\varLambda }{\varLambda }\pi \) coupling constant which is estimated from \(\varLambda -\Sigma ^0\) mixing, the mass difference between \(K^{\pm }\) and \(K^0\), and from two contact terms that represent short-ranged CSB forces. In the actual calculation, the two arising CSB low-energy constants are fixed by considering the known differences in the energy levels of the \(0^+\) and \(1^+\) states of the aforementioned \(A=4\) hypernuclei. Then, by construction, the resulting interaction describes all low energy hyperon-nucleon scattering data, the hypertriton and the CSB in \({^4_\varLambda \mathrm{He}}\) and \({^4_\varLambda \mathrm{H}}\) accurately.

It turned out that the reproduction of the presently established splittings of \(\varDelta E(0^+) = 233\pm 92\) keV and \(\varDelta E(1^+) = -83\pm 94\) keV requires a sizable difference between the strength of the \({\varLambda }p\) and \({\varLambda }n\) interactions in the \(^1S_0\) state, whereas the modifications in the \(^3S_1\) partial wave are much smaller. The effects go also in opposite directions, i.e. while for \(^1S_0\) the \({\varLambda }p\) interaction is found to be noticeably less attractive than \({\varLambda }n\), in case of \(^3S_1\) it is slightly more attractive. In terms of the pertinent scattering lengths we predict for \(\varDelta a^{CSB} = a_{{\varLambda }p} - a_{{\varLambda }n}\) a value of \(0.62\pm 0.08\) fm for the \(^1S_0\) partial wave and \(-0.10\pm 0.02\) fm for \(^3S_1\).

The required CSB implies a significantly stronger \({\varLambda }n\) interaction in the \(^1S_0\) partial wave and the pertinent scattering length of our NLO potentials [20, 21] increases from \(-2.9\) fm to around \(a^{\varLambda n}_s=-3.2\) fm. Therefore, it is worthwhile to explore in how far this has consequences for the possible existence of \({\varLambda }nn\) resonances [49,50,51,52,53,54,55,56,57,58,59]. It will be also interesting to utilize the CSB forces established in the present work in calculations of p-shell hypernuclei. Indeed, there are several experimentally established mirror hypernuclei in the p-shell region with \(A=7-10\) [60,61,62] which have been already studied within phenomenological approaches in the past [63,64,65]. However, now those systems can be also explored by more systematic microscopic approaches such as ab-initio calculations based on the no-core shell model [66,67,68].

Interestingly, adding the CSB interaction to our NLO potentials established in Refs. [20, 21], improves slightly the overall description of the YN data as quantified by the \(\chi ^2\) value – without any refit. This could be interpreted as sign for a consistency of the available YN data with the present values of the CSB level splittings in the \(A=4\) hypernuclei. In any case, with regard to the latter new but still preliminary results by FINUDA for the ground-state binding energy of \(^{\,4}_{\varLambda }\mathrm{H}\) have been reported already [62]. Also the STAR and ALICE collaborations have presented new results and plans for further experiments (see e.g. [69]). Further measurements of the splitting of the \(0^+\) and \(1^+\) states of \(^{\,4}_{\varLambda }\mathrm{H}\) are envisaged at J-PARC [70, 71]. Therefore, it can be expected that improved experimental constraints on the CSB of \(A=4\) hypernuclei will become available soon. Then a more careful analysis should be performed so that the uncertainty of the experimental CSB input is reflected in the uncertainty of the \(\varLambda \)n scattering length.