1 Introduction

In 2013 the Jülich-Bonn-Munich group presented a study of \(\varLambda N\) and \(\varSigma N\) scattering up to next-to-leading order (NLO) in SU(3) chiral effective field theory (EFT) [1], following closely earlier analogous investigations of the NN interaction [2,3,4,5]. It demonstrated that one can achieve a satisfactory description of the available low-energy \(\varLambda N\) and \(\varSigma N\) data within such an approach. First applications of the underlying hyperon–nucleon (YN) potential in calculations of binding energies for light hypernuclei were encouraging [6, 7]. In addition, and maybe most remarkable, it was found that the resulting in-medium interaction for the \({\varLambda }\) hyperon exhibits quite unusual properties. Contrary to most phenomenological YN potentials [8, 9], it becomes already repulsive at fairly low nuclear densities \(\rho \), i.e. for \(\rho \) in the order of two-to-three times that of normal nuclear matter [10]. For such an interaction the onset for hyperon formation in neutron stars could be shifted to rather high densities, a feature that appears to be promising as a possible explanation for the so-called hyperon puzzle [11]. The latter refers to the still unsolved question how one can reconcile the softening of the equation-of-state due to the appearance of hyperons with the observed large size (mass) of neutron stars [11,12,13,14].

The YN potential up to NLO in SU(3) chiral EFT consists of contributions from one- and two-pseudoscalar-meson exchange diagrams (involving the Goldstone boson octet \(\pi \), \(\eta \), K) and from four-baryon contact terms without and with two derivatives. In deriving such an YN potential in Ref. [1] the SU(3) flavor symmetry was considered primarily as a working hypothesis and not so much as a fundamental prerequisite, as emphasized in that work. Accordingly, the baryon-baryon-meson coupling constants for the pseudoscaler mesons were fixed in line with SU(3) symmetry and the symmetry was also exploited to derive relations between the various low-energy constants (LECs) that characterize the strength of the contact interactions. At the same time, in the actual calculation the SU(3) symmetry is broken, first by the mass differences between the pseudoscalar mesons entering the potential, and second by those of the baryons (N, \(\varLambda \), \(\varSigma \)) in the evaluation of the reaction amplitudes when solving a coupled-channel (\({\varLambda }N\)-\({\varSigma }N\)) scattering equation. For these masses the known physical values were already utilized in the leading-order (LO) study [15].

In addition, and contrary to past studies of the YN interaction within phenomenological approaches [8, 16], no use of SU(3) symmetry was made to constrain the (strangeness \(S=-1\)) YN potential by information from (\(S=0\)) NN scattering. One reason for this was the observation that a combined (and realistic) description of the YN and NN systems with contact terms that fulfil strict SU(3) symmetry turned out to be intractable. Specifically, the friction between the strengths needed for reproducing the pp (or np) \(^1S_0\) phase shifts and the \(\varSigma ^+ p\) cross section could not be reconciled in a scenario which maintained SU(3) symmetry for the contact terms [17]. Another and equally important reason was the goal to explore in how far the YN data themselves already allow one to pin down the interaction in the \(S=-1\) sector. It should be emphasized that the aspects discussed above apply only to the interaction in the S waves. Since there are practically no data for differential observables, it is impossible to fix the YN contact terms in the P-waves. In this case, implementing constraints from the NN sector provided by SU(3) symmetry is essential, cf. the corresponding discussion in Ref. [1].

Evidently, under the premises described above, an excellent reproduction of the available YN data is possible, as shown in Ref. [1]. Indeed, for the commonly considered set of 36 low-energy \({\varLambda }N\) and \({\varSigma }N\) data points a \(\chi ^2\) of around 16 could be achieved. This value is comparable or even better than the results obtained with elaborate phenomenological models derived in the traditional meson-exchange picture [8, 16]. Interestingly, it turned out that the fit to the YN data allowed one to fix the majority of the S-wave LECs. Nonetheless, some correlations between the values of the S-wave LECs at LO and NLO persisted, as already pointed out in that work. Those were attributed to the fact that the fitted \({\varSigma }^- p\) and \({\varSigma }^+ p\) cross sections lie all within a rather narrow energy interval near threshold so that there is only a fairly weak sensitivity to the momentum-dependent terms that involve the NLO LECs, see the appendix for explicit expressions of the contact interaction. The correlations found for the S-wave LECs suggest that alternative realizations of the \(\varLambda N\) and \(\varSigma N\) contact interaction should be possible. However, in view of the excellent \(\chi ^2\) obtained in the initial study [1], at that stage, it seemed unnecessary to explore these correlations further.

In the present work, we want to catch up on this issue and consider variations of the YN potential due to the aforementioned ambiguities in the LECs. The questions that can be addressed in this way are: (1) is it possible to achieve a description of \(\varLambda N\) and \(\varSigma N\) scattering for an alternative set of LECs that is comparable or even better than the one in Ref. [1], i.e. with comparable or even lower \(\chi ^2\)? (2) Do the resulting \({\varLambda }N\) and \({\varSigma }N\) potentials have different properties? In particular, do they lead to qualitatively different results when employed in studies of few- and many-body systems involving hyperons?

One possibility to reduce the aforementioned correlations between the LECs consists in implementing additional constraints to simply reduce the number of contact terms that need to be fitted to the YN data. A sensible choice is to impose SU(3) symmetry more strictly than in Ref. [1] and to take into account the symmetry relations between YN and NN also for the S-waves, and not only for the P-waves. How this can be done in practice was demonstrated in Ref. [17] for a specific case, namely the \(^1S_0\) partial wave in the NN, \({\varSigma }N\), and \({\varSigma }{\varSigma }\) systems. This work exploited the fact that at NLO in the perturbative expansion of the baryon-baryon potentials genuine SU(3) symmetry-breaking contact terms arise [18]. Accordingly, the LO LECs for NN and YNS-waves are no longer completely constrained by SU(3) symmetry, only those at NLO. This allows one to remedy the friction between the pp and \({\varSigma }^+ p\) results mentioned above and, at the same time, stay in line with the underlying power counting of SU(3) chiral EFT. In the present work, we now apply this scheme to all S-waves of the NN, \({\varLambda }N\), and \({\varSigma }N\) systems.

Anticipating our results, it turns out that an equally convincing description of \(\varLambda N\) and \(\varSigma N\) scattering data can be achieved based on such an alternative choice of the LECs. Indeed, the cross sections (actually all considered two-body observables) are practically indistinguishable from those in Ref. [1]. Small variations are observed for the predicted binding energies for the hypertriton \(^3_{\varLambda }{{\mathrm{H}}}\) and the \(^4_{\varLambda }{{\mathrm{H}}}\) and \(^4_{\varLambda }{\mathrm{He}}\) hypernuclei. However, in case of the properties of the hyperons in nuclear matter, the differences are much more sizable. Specifically, the in-medium interaction of the \(\varLambda \) predicted by the new potential is now considerably more attractive and becomes repulsive at much higher nuclear densities as compared to the EFT interaction published in [1].

The paper is structured in the following way: In the next section, a summary of the formalism is provided. Since a thorough description of the approach for treating YN scattering within SU(3) chiral EFT is available in Ref. [1], we will be brief here. Details that are needed to understand in how far the EFT interaction proposed in the present work differs from that in [1] are summarized in an appendix. The coverage of the Brueckner reaction-matrix formalism that is employed for evaluating the in-medium properties of the \({\varLambda }\) and \({\varSigma }\) is likewise kept short. Here, we refer the reader to Refs. [19] and [20] for details. In Sect. 3, the results for the alternative potential are presented and compared to the ones published in 2013 (for \({\varLambda }N\), \({\varSigma }N\) scattering) and 2015 (for nuclear matter). Implications of our results are discussed in Sect. 4. The paper ends with concluding remarks.

2 Formalism

2.1 \({\varLambda }N\) and \({\varSigma }N\) scattering

The derivation of the chiral baryon-baryon potentials for the strangeness sector using the Weinberg power counting is outlined in Refs. [1, 15, 18]. The LO potential consists of four-baryon contact terms without derivatives and of one-pseudoscalar-meson exchanges while at NLO contact terms with two derivatives arise, together with contributions from (irreducible) two-pseudoscalar-meson exchanges. The contributions from pseudoscalar-meson exchanges (the Goldstone bosons \(\pi \), \(\eta \), K of the spontaneously broken chiral symmetry of QCD) are completely fixed by the assumed SU(3) flavor symmetry. On the other hand, the strength parameters associated with the contact terms, the low-energy constants (LECs), need to be determined in a fit to data. How this is done is described in detail in Ref. [1]. With regard to the alternative version considered in the present work, the strategy followed is described in the beginning of Sect. 3. Note that, in general, SU(3) symmetry is also imposed for the contact terms which reduces the number of independent LECs that can contribute.

After a partial-wave projection [15], the potential V is inserted into a regularized coupled-channels Lippmann–Schwinger (LS) equation for the YNT-matrix T,

$$\begin{aligned} T^{\kappa ''\kappa ',J}_{\nu ''\nu '}(p'',p';\sqrt{s})= & {} V^{\kappa ''\kappa ',J}_{\nu ''\nu '}(p'',p') \nonumber \\&+\sum _{\kappa ,\nu }\int _0^\infty \frac{dp \, p^2}{(2\pi )^3} \, V^{\kappa ''\kappa ,J}_{\nu ''\nu }(p'',p)\nonumber \\&\times \frac{2\mu _{\nu }}{q_{\nu }^2-p^2{+}i\eta }T^{\kappa \kappa ',J}_{\nu \nu '}(p,p';\sqrt{s})\ . \nonumber \\ \end{aligned}$$
(1)

and its solution provides us the reaction amplitudes. The labels \(\nu \), \(\nu '\), and \(\nu ''\) in Eq. (1) indicate the particle channels and the label \(\kappa \), \(\kappa '\), and \(\kappa ''\) the partial wave ones where J is the total angular momentum [15]. \(\mu _\nu \) is the pertinent reduced mass. The on-shell momentum in the intermediate state, \(q_{\nu }\), is defined by \(\sqrt{s}=(m^2_{B_{1,\nu }}+q_{\nu }^2)^{1/2}+(m^2_{B_{2,\nu }}+q_{\nu }^2)^{1/2}\). Relativistic kinematics is used for relating the laboratory energy \(T_{\mathrm{lab}}\) of the hyperons to the c.m. momentum. Otherwise, we use non-relativistic kinematics for the solution of the two- and more-baryon equations.

We solve the LS equation in the particle basis in order to incorporate the correct physical thresholds. The Coulomb interaction is taken into account appropriately via the Vincent–Phatak method [21]. Regularization is done in the same way as in our initial work [1], see also Ref. [2]. This means that the potentials in the LS equation are cut off with an exponential regulator function, \(f_R(\varLambda ) = \exp \left[ -\left( p'^4+p^4\right) /\varLambda ^4\right] \), so that high-momentum components are removed [2]. We consider cutoff values in the range \(\varLambda =500\) – 650 MeV where the best \(\chi ^2\) values were achieved in the 2013 study [1]. As before, we present our results as bands which reflect the variation with the cutoff and, thus, indicate a lower bound for the uncertainty due to truncation of the chiral expansion. A more sensible way for estimating this uncertainty, that does not rely on cutoff variation, has been proposed in Refs. [22, 23] and we will show selected results based on that method, too. However, one should keep in mind that the present YN interactions are still only on the level of NLO which possibily leads to an underestimation of the uncertainty (as explained in more detail below).

Finally, let us note that the question how regularization should be performed and how ultimately cutoff independence can be achieved is still controversially discussed in the literature, see, e.g. [24,25,26,27,28]. In the context of YN scattering at LO this issue was touched in Ref. [29] where one can also find further references.

2.2 \({\varLambda }\) and \({\varSigma }\) in nuclear matter

The nuclear matter properties of the \({\varLambda }\) and \({\varSigma }\) hyperons are evaluated within the conventional Brueckner theory. We summarize below only the essential elements. A detailed description of the formalism can be found in Refs. [19, 20], see also Ref. [30]. We consider a \({\varLambda }\) or \({\varSigma }\) hyperon with momentum \({{\varvec{p}}}_Y\) in nuclear matter at density \(\rho \). In order to determine the in-medium properties of the hyperon, we employ the Brueckner reaction-matrix formalism and calculate the YN reaction matrix \(G_{Y N}\), defined by the Bethe–Goldstone equation

$$\begin{aligned}&\langle Y N | G(\zeta ) | Y N \rangle = \langle Y N | V | Y N \rangle \nonumber \\&\quad + \sum _{Y'N} \ \langle Y N | V | {Y'N} \rangle \, \nonumber \\&\quad \times \left\langle {Y'N} | \frac{Q}{\zeta - H_0}|{Y'N} \rangle \, \langle {Y'N} | G(\zeta ) | Y N \right\rangle , \nonumber \\ \end{aligned}$$
(2)

with \(Y,Y' = {\varLambda }\), \({\varSigma }\). Here, Q denotes the Pauli projection operator which excludes intermediate YN-states with the nucleon inside the Fermi sea. \(H_0\) is the kinetic energy of the YN system. The starting energy \(\zeta \) for an initial YN-state with momenta \({{\varvec{p}}}_Y \) and \({{\varvec{p}}}_N\) is given by

$$\begin{aligned} \zeta = E_Y (p_Y) + E_N (p_N), \end{aligned}$$
(3)

where the single-particle energy \(E_\alpha (p_\alpha )\) (\(\alpha = {\varLambda }, {\varSigma }, N\)) includes not only the (non-relativistic) kinetic energy and the baryon mass but in addition the single-particle (s.p.) potential \(U_\alpha (p_\alpha , \rho )\):

$$\begin{aligned} E_\alpha (p_\alpha ) = m_\alpha + \frac{{\varvec{p}}^{\,2}_\alpha }{2m_\alpha } + U_\alpha (p_\alpha , \rho )\, . \end{aligned}$$
(4)

The so-called gap-choice [19] for the intermediate-state spectrum is adopted. The Y single-particle potential \(U_Y(p_Y,\rho )\) is given by the following integral and sum over diagonal YNG-matrix elements:

$$\begin{aligned} U_Y(p_Y, \rho ) = \int \limits _{|{\varvec{p}}_N|< k_F} \frac{d^3p_N}{(2\pi )^3}\, {\mathrm{Tr}} \langle {{\varvec{p}}}_Y ,{{\varvec{p}}}_N | G_{Y N}(\zeta ) | {{\varvec{p}}}_Y, {{\varvec{p}}}_N \rangle ,\nonumber \\ \end{aligned}$$
(5)

where \({\mathrm{Tr}}\) denotes the trace in spin- and isospin-space. Note that \(\rho = 2k^3_F/3\pi ^2\) for symmetric nuclear matter and \(\rho = k^3_F/3\pi ^2\) for neutron matter, where \(k_F\) denotes the Fermi momentum.

Equations (2) and (5) are solved self-consistently in a standard way, with \(U_Y(p_Y, \rho )\) appearing also in the starting energy \(\zeta \). Like in Ref. [10], the nucleon single-particle potential \(U_N(p_N,\rho )\) is taken from a calculation of nuclear matter employing a phenomenological NN potential. Specifically, we resort to results for the Argonne \(v_{18}\) potential published in Ref.  [31]. As pointed out in Ref. [19], calculations of hyperon potentials in nuclear matter using the gap-choice are not too sensitive to the details of \(U_N(p_N,\rho )\). Indeed, the difference for, e.g., \(U_{\varLambda }(0,\rho )\) using \(U_N(p_N,\rho )\) from Ref. [31] or the parameterization utilized in Ref. [20] amounts to around 1 MeV at nuclear matter saturation density \(\rho = 0.17\) \(\hbox {fm}^{-3}\) (\(k_F=1.35\) \(\hbox {fm}^{-1}\)).

Since, at this stage, we are primarily interested in comparing the results for the two YN interactions, we refrain from a much more time-consuming calculation necessitated by the so-called continuous choice [32].

2.3 Faddeev and Yakubovsky equations

Binding energies of light \(A=3\) and 4 hypernuclei can be obtained by solving Faddeev or Yakubovsky equations in momentum space [33,34,35,36]. The method is well suited for chiral YN interactions since it allows one to employ non-local interactions including particle and partial wave channel couplings. Indeed, the works by Miyagawa et al. [33, 34] constitute the first successful attempt to use realistic meson-exchange potentials (including tensor forces and the \(\varLambda N\)-\(\varSigma N\) coupling) directly in a hypertriton calculation within the Faddeev framework. In Ref. [33], an overview of earlier calculations of the hypertriton is provided.

The few-body results given in this work have been obtained solving the three- and four-body non-relativistic Schrödinger equation in momentum space by rewriting them into Faddeev or Yakubovsky equations, respectively. For a bound state of one hyperon and two nucleons, one finds two coupled Faddeev equations

$$\begin{aligned} \psi _1= & {} G_0 T_{NN} (1-P_{12}) \psi _2 \nonumber \\ \psi _2= & {} G_0 T_{YN} (\psi _1-P_{12}\psi _2) \ , \end{aligned}$$
(6)

for the two independent Faddeev components \(\psi _{1}\) and \(\psi _{2}\) [33, 35]. \(P_{12}\) is the operator permuting the coordinates of nucleon 1 and 2. The NN and YN interactions enter via the corresponding T-matrices \(T_{NN}\) and \(T_{YN}\). They are obtained by solving LS equations embedded in the three- or four-body Hilbert space and which are therefore fully off-shell. The free propagator is denoted by \(G_0\). We are only considering bound states. Therefore, directly using the Schrödinger equation is in principle possible. However, using two different kinds of Jacobi coordinates for \(\psi _1\) and \(\psi _2\) that single out either an NN or a YN subsystem leads to an improved convergence with respect to partial waves. Therefore, the rewriting in Faddeev equations is advisable also for a bound state calculation. The two basis sets used for the calculation are then denoted by

$$\begin{aligned}&| p_{12} p_3 \alpha _1 \rangle \nonumber \\&\quad = \left| p_{12} p_3 ((l_{12} s_{12}) j_{12} \left( l_3 \frac{1}{2}\right) I_3) J; (t_{12} t_Y)T \right\rangle \nonumber \\&| p_{23} p_1 \alpha _2 \rangle \nonumber \\&\quad = \left| p_{23} p_1 ((l_{23} s_{23}) j_{23} \left( l_1 \frac{1}{2}\right) I_1) J; (t_{23} \frac{1}{2})T \right\rangle , \end{aligned}$$
(7)

where \(p_{ij}\) are the magnitudes of the pair momenta and \(p_k\) is the magnitude of the spectator momentum. Their angular dependence is expanded in orbital angular momenta \(l_{ij}\) and \(l_k\), respectively. The orbital angular momenta are coupled with the spin of the pair \(s_{ij}\) and the spin of the spectator baryon to the intermediate angular momentum \(j_{ij}\) and \(I_k\). These are then coupled to the total angular momentum of the hypertriton \(J=\frac{1}{2}\). Since we work in the isospin basis, the pair isospin \(t_{ij}\) is either coupled with the isospin \(t_Y\) of the spectator hyperon or the isospin \(\frac{1}{2}\) of the spectator nucleon to total isospin \(T=0\). For a more complete description of the basis states see Ref. [35]. The number of partial waves is finite, if one restricts \(j_{ij} \le j_{\mathrm{max}}\). For the calculations shown here, we chose \(j_{\mathrm{max}}=6\). The binding energies are then converged to better than 1 keV. The momenta are typically discretized using a grid of 44 or 58 points for \(p_{ij}\) and \(p_k\), respectively.

In the four-body case, we find a set of five Yakubovsky equations for five independent Yakubovsky components \(\psi _{1A}\)\(\psi _{1B}\), \(\psi _{1C}\), \(\psi _{2A}\), and \(\psi _{2B}\)

$$\begin{aligned} \psi _{1A}= & {} G_0 T_{NN} P (\psi _{1A}+\psi _{1B}+\psi _{2A}) \nonumber \\ \psi _{1B}= & {} G_0 T_{NN} ((1-P_{12})(1-P_{23})\psi _{1C}+ P \psi _{2B}) \nonumber \\ \psi _{1C}= & {} G_0 T_{YN} (\psi _{1A}+\psi _{1B}+\psi _{2A} \nonumber \\&-P_{12}\psi _{1C}+P_{12}P_{23}\psi _{1C} + P_{13}P_{23}\psi _{2B}) \nonumber \\ \psi _{2A}= & {} G_0 T_{NN} ((P_{12}-1)P_{13})\psi _{1C}+\psi _{2B}) \nonumber \\ \psi _{2B}= & {} G_0 T_{YN} (\psi _{1A}+\psi _{1B}+\psi _{2A}) \ . \end{aligned}$$
(8)

\(P = P_{12}P_{23}+P_{13}P_{23}\) is the sum of a cyclic and anti-cyclic permutation of the three nucleons. Again, all five components are expanded in a different set of Jacobi basis states. The first three components use so-called \(3+1\) coordinates, which single out one pair momentum \(p_{ij}\), one baryon moving relative to the pair with momentum \(p_{k}\) and the spectator moving relative to the other three baryons with momentum \(q_l\). The other two components use \(2+2\) coordinates which single out two pair momenta \(p_{ij}\) and \(p_{kl}\) and a momentum q describing the relative motion of the two pairs. The angular dependence is expanded in terms of corresponding orbital angular momenta. These are coupled with spins to a total angular momentum J. Similarly, the isospins are finally coupled to total isospin T. More details are given in [35]. In the case of the four-body system, restricting pair angular momenta \(j_{ij} \le j_{\mathrm{max}}\) is not sufficient to get a finite set of equations. We therefore impose two more constraints: all orbital angular momenta \(l \le 4\) and the sum of all three orbital angular momentum quantum numbers is less than \(l_{\mathrm{sum}}=8\). We carefully checked that the energies are converged to better than 10 keV for the chiral NN and YN interactions. For the three different momenta, a discretization using 52, 56 and 48 grid points is typically sufficient to get an accuracy better than a few keV. Since phenomenological interactions are less soft, we use more partial waves in this case in order to get a similar accuracy. We note that the number of partial wave and isospin channels are especially larger for the excited \(J^\pi =1^+\) state. With the restrictions defined above, we had to take more than 13,000 partial wave combinations into account. The discretized set of linear equations is then more than \(10^9\) dimensional. However, the accuracy of 10 keV that we obtain for the four-body system is sufficient to discuss the NN and YN interaction dependence of our results.

3 Results

In the following subsections, we present results for \({\varLambda }N\) and \({\varSigma }N\) scattering, for binding energies of light hypernuclei, and for the \({\varLambda }\) and \({\varSigma }\) s.p. potentials in nuclear matter for our NLO chiral EFT interactions. Thereby, we will show results for two different fits. We refer to the original NLO fit [1] by NLO13. Additionally, we devised a new version in the way described below which we will label NLO19 in the following. Occasionally, also results for YN potentials based on the traditional meson-exchange approach [8, 9] will be shown for illustration.

Let us first describe in more detail how the contact terms for the new YN interaction NLO19 were fixed. The total number of independent LECs up to NLO amounts to 13 for the \(^1S_0\) and \(^3S_1\)-\(^3D_1\)YN partial waves, with 4 (6) for the singlet (triplet) S-states and 3 for the \(^3S_1\leftrightarrow ^3D_1\) transition, see the appendix. In Ref. [1], their values have been fixed by a fit to the usually considered [1, 8, 9, 15] set of low-energy \({\varLambda }p\), \({\varSigma }^- p\), and \({\varSigma }^+ p\) data [37,38,39,40,41]. Based on SU(3) symmetry, three of those can be inferred from the NN interaction, namely \(C^{27}_{^1S_0}\), \(C^{10^*}_{^3S_1}\), and \(C^{10^*}_{^3S_1-^3D_1}\), so that there are only 10 LECs left to be fitted. For the refit NLO19 of the present work, we utilize the NN LECs of Ref. [32]. There, an NN potential has been established within the same framework and the same regularization scheme. The pertinent LECs were determined by a fit to np phase shifts. pp phase shifts could be used instead for \(^1S_0\) partial wave. The difference in the corresponding LEC \(C^{27}\) is, however, tiny, see Ref. [17], so that we ignore this for the time being.

We use the NLO potential from 2013 [1] as starting point for our new fit, of course, with substituting the LECs that are fixed from the NN sector. Remarkably, in case of the \(^1S_0\), there is only a small difference in the actual values for the \(C^{27}\)’s found in the fit to the YN data (cf. Table 3 in Ref. [1]) and the ones from the NN results (cf. the appendix). These coincide within 5–10%, despite of being fitted independently. One could interpret this as a sign that, beyond corrections at leading order, SU(3) symmetry is fairly well realized.

In case of the \(^3S_1\), the situation is different. Here the values for \(C^{10^*}\) from the fit to the np phase shifts are more than a factor 5 smaller than those determined in the YN study. Indeed, the LECs for the new fits are now well in line with being of “natural size” [3]. Note that the LECs for the 10 and \({10^*}\) representations have been erroneously interchanged in Table 3 of Ref. [1]! We view these large variations primarily as a sign of the correlations between the LO and NLO LECs discussed already in the introduction.

The best description of YN data was obtained for the range 500–650 MeV for the cutoff \(\varLambda \) in the regulator function in Ref. [1]. Therefore, we consider again this range in the present work. For smaller values, there is a rapid deterioration in the \(\chi ^2\), cf. Table 5 in [1], and likewise (though less dramatic) for larger values.

All LECs in the P-waves are taken over from Ref. [1]. No readjustment is done in this case. Thus, all differences in the results for the two interactions reported below stem from the differences in the S-waves.

Table 1 Scattering lengths (a) and effective ranges (r) for singlet (s) and triplet (t) S waves, for \(\varLambda p\), \({\varSigma }N\) with isospin \(I=1/2\), and \({\varSigma }^+ p \) (\(I=3/2\)). In addition, the achieved \(\chi ^2\) for the 36 data points is listed. \(^*\)In case of the Jülich ’04 potential, the capture ratio was not included in the fit and the evaluation of the \(\chi ^2\)
Full size table

3.1 \({\varLambda }N\) and \({\varSigma }N\) scattering

In this section, we present results for \({\varLambda }N\) and \({\varSigma }N\) scattering. In particular, we compare the results obtained with the new procedure to those from 2013. A summary of the \(\varLambda p\) effective range parameters is given in Table 1 together with information about the achieved overall \(\chi ^2\). The latter, listed at the bottom, provides clear evidence that the quality of description of the YN data by the two interactions is identical. The differences in the \(\chi ^2\) are marginal considering the inherent residual regulator dependence in both cases. We observe though that the dependence of the \(\chi ^2\) on the cutoff is slightly different for the two interactions. The effective range parameters in the singlet state are practically identical. Noticeable variations occur only in the effective range at the lower end of the considered cutoff range. In the triplet S-wave, the scattering lengths differ in average by 7%.

Fig. 1
figure 1

Cross section for \({\varLambda }p\) scattering as a function of \(p_{lab}\). The red (dark) band represents the result for NLO13 [1] including cutoff variations, the cyan (light) band that for the alternative version NLO19. The dashed curve is the result of the Jülich ’04 meson-exchange model [9], the dotted curve that of the Nijmegen NSC97f potential [8]. The experimental cross sections are taken from Refs. [37] (filled circles), [38] (filled squares), [42, 43] (open triangles), [44] (open squares), and [45] (open circles). The dotted vertical lines labeled with \({\varSigma }^{+}\)n and \({\varSigma }^0\)p indicate the thresholds of the pertinent \({\varSigma }\)N channels

Full size image

Results for the \(\varLambda p\) cross section are displayed in Fig. 1, where the region around the \({\varSigma }N\) thresholds is shown separately so that one can see the details. As usual, the results are presented as bands that reflect the variation with the cutoff \(\varLambda \). The results for NLO13 are shown as red (dark) bands while the new results are shown as cyan (light) bands. In this figure and the following ones, YN data included in the fitting procedure [37,38,39,40] are displayed by filled symbols, while for additional data at higher energies [42,43,44,45,46,47,48] open symbols are used.

Fig. 2
figure 2

Different \({\varSigma }\)N and \({\varSigma }\)N \(\rightarrow \)\({\varLambda }\)N cross sections. Same description of curves as in Fig. 1. The experimental cross sections are taken from Refs. [39] (\(\varSigma ^-p \rightarrow \varLambda n\), \(\varSigma ^-p \rightarrow \varSigma ^0 n\)) and [40] (\(\varSigma ^-p \rightarrow \varSigma ^- p\), \(\varSigma ^+p \rightarrow \varSigma ^+ p\))

Full size image
Fig. 3
figure 3

Different \({\varSigma }\)N and \({\varSigma }\)N \(\rightarrow \)\({\varLambda }\)N cross sections for higher energy. Same description of curves as in Fig. 1. The experimental cross sections are taken from Refs. [39, 46] (\(\varSigma ^-p \rightarrow \varLambda n\), \(\varSigma ^-p \rightarrow \varSigma ^0 n\)) and [40, 47] (\(\varSigma ^-p \rightarrow \varSigma ^- p\)), and [40, 48] (\({\varSigma }^+ p \rightarrow {\varSigma }^+p\)). Note that the data at higher energy are not included in the fit

Full size image
Fig. 4
figure 4

Differential cross section for \({\varLambda }p\) scattering at 500 MeV/c and at 633 MeV/c. Same description of curves as in Fig. 1

Full size image
Fig. 5
figure 5

\(^3S_1\)\({\varLambda }N\) phase shift with (left) and without (right) \({\varSigma }N\) coupling. Same description of curves as in Fig. 1

Full size image
Fig. 6
figure 6

\(^1S_0\)\({\varLambda }N\) phase shift with (left) and without (right) \({\varSigma }N\) coupling. Same description of curves as in Fig. 1

Full size image

Obviously, the \(\varLambda p\) cross sections produced by the two interactions are practically identical over the whole considered momentum range and hard to distinguish in the plot. Visible differences occur only at higher momenta near to the \({\varSigma }N\) thresholds where the NLO19 interaction predicts somewhat larger cross sections. There is also a more noticeable dependence of the results on the cutoff in the region below and above the thresholds. The latter is not too surprising because some LECs are fixed from NN in the NLO19 interaction so that there is less flexibility to absorb the regulator dependence than in NLO13. Consequently, in general, a somewhat stronger variation of the cross sections with the cutoff has to be expected.

Results for the various \({\varSigma }N\) channels are summarized in Fig. 2. Also here, there is practically no difference between the results of the NLO13 and NLO19 interactions, except maybe for the already mentioned slightly increased dependence on the cutoff in case of the latter. Even at higher energies, the cross sections for the two interactions are difficult to distinguish, see Fig. 3. Note that these results have to be considered as genuine predictions because none of the \({\varSigma }N\) data at momenta above 170 MeV/c have been included in the fitting procedure. The similarity of the predictions is particularly surprising in view of the mentioned correlations between the LO and NLO LECs. One would have expected variations at higher momenta because the different values for the LO and NLO LECs in the interactions NLO13 and NLO19 should yield a different energy dependence, at least when a larger energy region is considered.

The predictions for differential cross sections, for \({\varSigma }^-p\rightarrow {\varSigma }^-p\), \({\varSigma }^-p \rightarrow {\varLambda }n\), and \({\varSigma }^+p \rightarrow {\varSigma }^+p\), at the few momenta were data are available [1], remain basically unchanged and, therefore, we refrain from showing them. Instead, for illustrative purposes, we present results for the \({\varLambda }p\) differential cross section at two selected laboratory momenta, see Fig. 4. The momenta correspond to \(T_{lab} = 107\) and 167.3 MeV, respectively, where the latter is just below the \({\varSigma }^+ n\) threshold. Again, the variations with the cutoff aside, there is hardly any difference between the predictions of the NLO13 and NLO19 interactions. One can see that for both potentials, at the lower energy, the cross section is dominated by the S-waves whereas, at the \({\varSigma }^+ n\) threshold, there is a pronounced angular dependence that is actually induced by an interference of the \(^3S_1\)-\(^3D_1\) with the \(^3P_2\) partial wave. More striking are the differences to the predictions by the phenomenological potentials. In case of the Jülich ’04 potential [9], there is already a stronger angular dependence at the lower energy, indicating a sizable contribution from P-waves. On the other hand, in the NSC97f potential [8], there is a large contribution from the \(^3D_1\) which is most obvious from the result at the \({\varSigma }^+ n\) threshold. Evidently, experimental information would be very valuable here, but is, of course, rather difficult to obtain.

Finally, the low-energy parameters for the \({\varSigma }N\) channels can be found in Table 1, too. Besides the \({\varSigma }^+ p\) effective range parameters which include the distortion from the Coulomb interaction, we list also the \({\varSigma }N\) scattering length for the isospin \(I=1/2\) channel calculated with an isospin-averaged \({\varSigma }\) mass. Obviously, the variations in the predictions by the NLO13 and NLO19 potentials are small, especially in case of the \(^1S_0\) partial wave. Only in the \(^3S_1\) partial wave with \(I=1/2\), there is a more sizable difference, at least for the lower cutoff values. Here, the magnitude of the real and imaginary parts are noticeably different. There are also differences to the predictions of the phenomenological potentials. Note that for some effective-range parameters the dependence on the cutoff is not completely smooth, for NLO13 but also for NLO19. This is caused by the correlations between the LECs, which obviously are still present in the NLO19 interaction, in combination with the fact that we fit to cross sections at finite energies and not to scattering lengths (i.e. at zero energy).

This brings us to the question, whether there is any significant difference between the \({\varLambda }N\) and \({\varSigma }N\) scattering results of the NLO13 and NLO19 potentials. And the simple answer is that there is none, at least not in terms of observable quantities. That said, the just discussed \(I=1/2\)\({\varSigma }N\) scattering length gives us a clue that there is a subtle difference and it concerns the strength of the \({\varLambda }N\)-\({\varSigma }N\) transition potential. The simplest way to see that is to perform an “academic” calculation. It consists in simply switching off the coupling potential between the two channels [10]. The outcome of such an exercise for the \({\varLambda }N\)\(^3S_1\) phase shift is presented in Fig. 5. The results on the left side are for the full (coupled-channel) calculation and it is obvious that the phase shifts for the NLO13 and NLO19 potentials lie basically on top of each other, at least up to momenta of \(p_{lab}\approx 400\) MeV/c. On the right hand side are the results without channel coupling. Here, one can see that NLO13 (i.e. the \({\varLambda }N\) potential alone) leads to mostly negative phase shifts that are a sign for a repulsive potential, the Jülich ’04 potential leads to a positive (attractive) phase, and the NLO19 potential yields results somewhat in between. While such differences are not visible in two-body observables, once evaluated for the full (coupled-channel) potential (cf. the results presented above), they do have an influence in applications to few- and many-body systems, to be discussed in the next subsections, even when the full \({\varLambda }N\)-\({\varSigma }N\) potential is used.

For completeness, we show also the corresponding results for the \(^1S_0\) partial wave, cf. Fig. 6. Here, NLO13 and NLO19 behave alike. In both cases, there is a moderate reduction of the attraction when the coupling to \({\varSigma }N\) is switched off. Differences occur only for the two phenomenological potentials where the result for the \(^1S_0\) phase shift remains practically unchanged (NSC97f) or even increases (Jülich ’04) without \({\varSigma }N\) coupling.

Note that the cutoff dependence increases when the coupling is switched off. This happens because we use the (diagonal) \({\varLambda }N\) potential as established in the full coupled-channel calculation. No re-adjustment of the contact terms is done and, thus, there is no proper absorption of the regulator dependence in this ”academic” calculation.

Finally, for illustration, we present an estimate for the theoretical uncertainty following the method proposed in Ref. [22]. In Fig. 7, selected results for the NLO19 potential for the cutoff \(\varLambda =600\) MeV are shown. This value is also used as breakdown scale [22]. The difference of the LO results [15] and the NLO13 result is used for the estimation. Certainly, for addressing the question of convergence, orders beyond NLO are needed. Higher orders are also required to avoid that accidentally close results lead to an under estimation of the uncertainty. For the YN interaction, this uncertainty estimate is especially difficult since the data is not sufficient to unambiguously determine all LECs. For this reason, it is also not useful to quantify the uncertainty of phase shifts of individual partial waves in this manner. Nonetheless, we want to emphasize that the estimated uncertainty appears sensible and also plausible. In particular, it encases the variations due to the regulator dependence and, thus, is consistent with the expectation that cutoff variations provide a lower bound for the theoretical uncertainty. For details of the method and a thorough discussion of the underlying concept, we refer the reader to [23].

Fig. 7
figure 7

Uncertainty estimate for the YN interaction in the \({\varLambda }p\) and \({\varSigma }^+ p\) channels employing the method suggested in Ref. [22]. As basis the LO [15] and NLO13 interactions with cutoff \(\varLambda =600\) MeV are used. We only show the NLO result and its uncertainty

Full size image
Table 2 \({\varLambda }\) and \({\varSigma }\) single-particle potentials \(U_Y(p_Y=0)\) (in MeV) at nuclear matter saturation density (\(k_F = 1.35\)\(\hbox {fm}^{-1}\)). The contributions from the S waves and the total result including all partial waves up to \(J=5\) are given
Full size table

3.2 \({\varLambda }\) and \({\varSigma }\) in nuclear matter

Let us now compare the in-medium properties of the YN interactions NLO13 and NLO19. Table 2 summarizes the values for the \(\varLambda \) and \(\varSigma \) potential depths, \(U_\varLambda (p_\varLambda = 0)\) and \(U_\varSigma (p_\varSigma = 0)\), evaluated at the saturation point of nuclear matter, i.e. for \(k_F=1.35\)\(\hbox {fm}^{-1}\). Note that the results for NLO13 slightly differ from those given in [20] because a different and more up to date nucleon s.p. potential is used, see Sect. 2.2. Corresponding results obtained for the Jülich’04 meson-exchange potential [9] and the Nijmegen NSC97f potential [8] are also included. The dependence of the hyperon potential depths on the Fermi momentum is displayed in Figs. 8 and 9.

Fig. 8
figure 8

The \({\varLambda }\) single-particle potential \(U_{\varLambda }(p_{\varLambda }= 0)\) as a function of the Fermi momentum \(k_F\) in symmetric nuclear matter (a) and in neutron matter (b). Same description of curves as in Fig. 1. The dotted curve is the result of the Nijmegen NSC97f potential [8], taken from Ref. [49]. The vertical bar indicates the ”empirical” value [60]

Full size image

It is quite obvious from Fig. 8 that the EFT potential NLO19 is much more attractive in the medium than NLO13. The difference is primarily due to the contribution of the \(^3S_1\)-\(^3D_1\) partial wave which is enhanced by more or less a factor 2 for the new interaction, see Table 2. Actually, the density dependence predicted by NLO19 is similar to the one of the NSC97f potential, cf. the dotted line in Fig. 8. It is instructive to compare the figure for \(U_{\varLambda }\) with the one for the \(^3S_1\) phase shifts with the \({\varLambda }N\)-\({\varSigma }N\) coupling switched off (right-hand side of Fig. 5). One can easily see that the strength of the conversion is inversely correlated with the strength of the single-particle potential. It is well-known that the outcome for the single-particle potential of the \(\varLambda \) is strongly influenced by the strength of the \({\varLambda }N\)-\({\varSigma }N\) coupling potential [50,51,52]. For the NLO13 interaction, the influence of the strength of the transition potential on the in-medium properties of the \({\varLambda }\) was already discussed in detail by some of us in Ref. [10] and subsequently by Kohno [53].

Figure 8 also reveals that there is a sizable and certainly unsettling cutoff dependence of the predictions. However, this is not too surprising given that a likewise strong regulator dependence has already been detected in applications of the approach that we follow here to studies of nuclear matter properties in the NN sector [54,55,56]. Since the Pauli operator in Eq. (2) suppresses the contributions from low momenta, the G-matrix results are more sensitive to higher momenta and, thus, to intermediate and short-distance physics [56]. In the mentioned applications to the NN case, indications for a convergence and a reduced regulator dependence were only found after going to much higher order - \(\hbox {N}^3\)LO in Refs. [54, 55] and \(\hbox {N}^4\)LO in [56] - and after including three-body forces. Indeed, as argued in Ref. [56], the cutoff dependence could allow one to draw indirect conclusions on the size of such many body forces.

Fig. 9
figure 9

The \({\varSigma }\) single-particle potential \(U_{\varSigma }(p_{\varSigma }= 0)\) as a function of the Fermi momentum \(k_F\) in symmetric nuclear matter. Same description of curves as in Fig. 1. The vertical bar indicates the ”empirical” value [60]

Full size image

For completeness, we also show results for a \(\varLambda \) in neutron matter (right-hand side of Fig. 8). Also in this case the \({\varLambda }\) s.p. potential predicted by NLO19 is much more attractive than the one by NLO13. Though there is a trend to repulsion with increasing density, similar to NLO13 and the NSC97f potential, it is clear that the actual change of sign will take place at significantly higher densities.

Table 3 Dependence of the separation energies of \(^3_\varLambda {{\mathrm{H}}}\), \(^4_\varLambda {\mathrm{He}(0^+)}\) and \(^4_\varLambda {\mathrm{He}(1^+)}\) for NLO19(650) on the NN interaction. The \(\varSigma \) probabilities are shown, too. Energies are given in MeV, probabilities in %. The semilocal momentum-space (SMS) chiral NN interaction from Ref. [63] is employed
Full size table

Investigations of (finite) \({\varLambda }\) hypernuclei utilizing the EFT interactions can be found in Ref. [57], based on the formalism described in Ref. [58]. For even lighter hypernuclei, the interactions are also currently studied [59].

Results for the \({\varSigma }\) s.p. potential in symmetric nuclear matter are presented in Fig. 9. It is predicted to be repulsive by NLO13 as well as by NLO19, in agreement with evidence from the analysis of level shifts and widths of \(\varSigma ^-\) atoms and from measurements of \((\pi ^-,K^+)\) inclusive spectra related to \(\varSigma ^-\)-formation in heavy nuclei [60]. As discussed in detail in Ref. [20], a repulsive \(\varSigma \) s. p. potential is achieved because the EFT interactions in the \(^3S_1\) partial wave of the \({\varSigma }^+ p\) channel (which provides the dominant contribution, cf. Table 2) are repulsive. Note that a repulsive \(^3S_1\) interaction is in accordance with results from lattice QCD calculations [61, 62]. The NLO19 interaction provides slightly more repulsion. But overall, with regard to the \(\varSigma \) in-medium properties, there is very little difference to NLO13. This is also true on the level of the partial-wave contributions, as can be seen by comparing the corresponding values in Table 2.

As exemplified by the predictions of the Jülich ’04 and NSC97f potentials, typically phenomenological potentials fail to produce a repulsive \(\varSigma \)-nuclear potential, cf. the corresponding results in Table 2. Because of that we refrain from showing the pertinent curves in Fig. 9.

3.3 Three- and four-body systems

In this section, we present results for the \(^{\,3}_{\varLambda }{\mathrm{H}}\) and \(^{\,4}_{\varLambda }{{\mathrm{He}}}\) binding energies based on the NLO13 and NLO19 YN potentials and for the phenomenological Nijmegen (NSC97f) [8] and Jülich ’04 [9] YN interactions. We want to emphasize that the binding energies of the hypernuclei also depend on the employed NN interaction and are affected by three-nucleon forces (3NFs). However, detailed calculations show that this dependence enters through the binding of the 3N core nucleus. It is therefore useful to present the results in terms of the difference of the core nucleus binding energy and the hypernuclear binding energy, the \({\varLambda }\) separation energies, which are denoted by \(E_{\varLambda }\) in the following. This fact is exemplified in Table 3 for the YN interaction NLO19 with cutoff \({\varLambda }=650\) MeV in combination with the high-order semilocal momentum-space regularized chiral NN potential (SMS) [63] with different cutoffs. One can see that the \({\varLambda }\) separation energy for \(^{\,3}_{\varLambda }{\mathrm{H}}\) varies only by 10 keV. In case of \(^{\,4}_{\varLambda }{\mathrm{He}}\) the variations are in the order of 80 and 40 keV for the \(0^+\) and \(1^+\) states, respectively. Similarly, small variations have been found in calculations where phenomenological NN potentials were employed [6]. The addition of a 3NF changes the binding energy by approximately 800 keV (depending on the chosen NN interaction) but the separation energy only by 20–50 keV [36]. In the following, we can therefore discuss the predictions for the separation energies independently from the NN and 3N interactions.

In former studies of hyperonic few-body systems, the role of the spin-dependence of the \(\varLambda N\) potential for the binding energies of s-shell hypernuclei has been discussed in terms of the appropriately averaged effective \({\varLambda }N\) interaction [64,65,66]. We will do the same here. It is rather instructive and allows for a good qualitative understanding of the corresponding bound-state properties, though one should certainly not forget that this is a simplification. The relations in question are [64, 66]

$$\begin{aligned}&{^{\,3}_{\varLambda }{\mathrm{H}}:} \quad {{\tilde{V}}}_{{\varLambda }N} \approx \frac{3}{4} V^s_{{\varLambda }N} + \frac{1}{4} V^t_{{\varLambda }N} \end{aligned}$$
(9)
$$\begin{aligned}&{^{\,4}_{\varLambda }{\mathrm{He}}} \ (0^+): \quad {{\tilde{V}}}_{{\varLambda }N} \approx \frac{1}{2} V^s_{{\varLambda }N} + \frac{1}{2} V^t_{{\varLambda }N} \end{aligned}$$
(10)
$$\begin{aligned}&{^{\,4}_{\varLambda }{\mathrm{He}}} \ (1^+): \quad {{\tilde{V}}}_{{\varLambda }N} \approx \frac{1}{6} V^s_{{\varLambda }N} + \frac{5}{6} V^t_{{\varLambda }N} \end{aligned}$$
(11)
$$\begin{aligned}&{^{\,5}_{\varLambda }{\mathrm{He}}:} \quad {{\tilde{V}}}_{{\varLambda }N} \approx \frac{1}{4} V^s_{{\varLambda }N} + \frac{3}{4} V^t_{{\varLambda }N} \end{aligned}$$
(12)

From these the well-known fact follows that the hypertriton is dominated by the \({\varLambda }N\) singlet interaction while the \({^{\, 4}_{\varLambda }{\mathrm{He}}} \ (1^+)\) and \({^{\,5}_{\varLambda }{\mathrm{He}}}\) states are dominated by the triplet interaction.

Table 4 Dependence of the separation energies \(E_\varLambda \) of \(^3_\varLambda {{\mathrm{H}}}\), \(^4_\varLambda {{\mathrm{He}}(0^+)}\) and \(^4_\varLambda {{\mathrm{He}}(1^+)}\) on the YN interaction.The \(\varSigma \) probabilities \(P_\varSigma \) are also shown. For the chiral YN forces, the SMS NN interaction [63] at order \(\hbox {N}^4\)LO+ with cutoff of 450 MeV has been used. For Jülich’04 and NSC97f, the CD-Bonn NN interaction [67] has been employed. Energies are given in MeV, probabilities in %. Experimental values are taken from Refs. [68] (\(^3_\varLambda {{\mathrm{H}}}\), \(^4_\varLambda {\mathrm{He}(0^+)}\)) and [69] (\(^4_\varLambda {\mathrm{He}(1^+)}\))
Full size table

Our results for the binding (separation) energies for the hypertriton and the \(^{\,4}_{\varLambda }{\mathrm{He}}\) hypernucleus are listed in Table 4. (Preliminary results for the NLO19 interaction were reported in [70, 71] based on a different NN interaction.) The hypertriton binding energies for the two NLO interactions are identical within the uncertainty caused by the regulator dependence. The overall variations are of the order of 50 keV. As noted just above, in this case, the binding energy is dominated by the \({\varLambda }N\) interaction in the \(^1S_0\) (singlet) interaction, see Eq. (9). That partial wave is less influenced by the \({\varLambda }-{\varSigma }\) conversion as can be read off from the fact that the imaginary part of the \({\varSigma }N\) (\(I=1/2\)) \(^1S_0\) scattering length is zero for basically all considered potentials, cf. Table 1, see also Fig. 6.

There is somewhat stronger variation in the predictions for the \({^{\,4}_{\varLambda }{\mathrm{He}}}\) binding energies, cf. Table 4. However, at least for the \(0^+\) state, we are reluctant to see a clear tendency in the results. Recall that this state should receive contributions from the \(^1S_0\) and \(^3S_1\)\({\varLambda }N\) interactions with equal weight, according to the simple estimate Eq. (10). Here, the regulator dependence of the binding energy is of the order of 210 and 180 keV for NLO13 and NLO19, respectively, and, thus, larger than the average difference between the two EFT interactions. Interestingly, the predictions of the two considered phenomenological YN models for the \(0^+\) bound state are almost the same, despite of the large differences in the \({\varLambda }N\)-\({\varSigma }N\) transition potentials. Note that all considered interactions under-predict the experimental separation energy of the \(0^+\) state.

For the \(1^+\) state of \({^{\,4}_{\varLambda }{\mathrm{He}}}\), the \(^3S_1\) partial wave of the \({\varLambda }N\) interaction should dominate, according to Eq. (11). This partial wave is strongly affected by the \({\varLambda }-{\varSigma }\) conversion and the effects are different for NLO13 and NLO19 as discussed in Sect. 3.1. Here, we observe a more pronounced regulator dependence of the binding energy. Specifically, for the NLO19 interaction, it is in the order of 300 keV and around 200 keV for the NLO13 potential. Despite those variations, there is clearly a trend towards larger binding energies for NLO19, i.e. for the interaction with a weaker \({\varLambda }N\)-\({\varSigma }N\) transition potential. This conjecture is also supported by the result for the Jülich ’04 potential. Here the transition potential in the \(^3S_1-^3D_1\) partial wave is extremely weak and, corresponding to that, the \(1^+\) binding energy is very large. The prediction for the NSC97f interaction, on the other hand, with its moderately strong transition potential, matches well with those of the chiral EFT potentials. Comparing with the empirical information, one can say that the NLO19 prediction is compatible with the experiment within the uncertainty, whereas the NLO13 and NSC97f interactions underestimate the separation energy for the \(1^+\) state. On the other hand, the Jülich ’04 potential leads to over-binding and, as a matter of fact, to a wrong level ordering of the \(0^+\) and \(1^+\) states.

Similar to the \({^{\,4}_{\varLambda }{\mathrm{He}}}\)\(1^+\) state, the \({^{\,5}_{\varLambda }{\mathrm{He}}}\) bound state is likewise dominated by the \({\varLambda }N\) triplet component, cf. Eq. (12). Thus, it will be interesting to see corresponding results based on the NLO13 and NLO19 interactions [59]. The anomalously small binding energy of this state has been notoriously difficult to describe in past calculations [72]. Among other things, a strong suppression of the \({\varLambda }N\)-\({\varSigma }N\) coupling is seen as one possible explanation [66, 73]. Thus, one would expect noticeable differences between the predictions of the two EFT interactions.

We refrain from addressing the long-standing and still unsettled issue of the large charge symmetry breaking (CSB) [60, 74,75,76] observed in the binding energies of the \({^{\, 4}_{\varLambda }\mathrm{He}}\) and \({^{\, 4}_{\varLambda }\mathrm{H}}\) systems  [69, 77] here in detail. Indeed, there is no explicit CSB in the \({\varLambda }N\) EFT potentials employed in the present study. Corresponding contributions that would arise, e.g., from \(\pi ^0\) exchange in conjunction with \({\varLambda }-{\varSigma }^0\) mixing [78] are ignored. Additional CSB effects that enter into the four-body calculations like the Coulomb interaction and the mass difference of the \({\varSigma }^+\) and \({\varSigma }^-\) hyperons are small [6]. In Refs. [75, 76], the CSB part of the \({\varLambda }N\) interaction was constructed from the \({\varLambda }N \rightarrow {\varSigma }N\) transition potential via an appropriate scaling with the \({\varLambda }-{\varSigma }^0\) mixing matrix element. However, one has to be cautious in doing so. Specifically, one cannot turn that around and use CSB effects to fix the \({\varLambda }N \rightarrow {\varSigma }N\) transition potential in a quantitative way. Besides the aforementioned \({\varLambda }-{\varSigma }^0\) mixing, there should be CSB contributions from, say, \(\eta -\pi ^0\) mixing or \(\omega -\rho ^0\) mixing [74] that are definitely not proportional to the transition potential and, thus, demand the explicit introduction of pertinent CSB contact interactions in the \(^1S_0\) and \(^3S_1\)\({\varLambda }N\) partial waves in the framework of EFT.

That said, on a qualitative level there is definitely a relation between the CSB, the strength of the \(\varLambda \)-\(\varSigma \) conversion, and the \({\varSigma }\) component of the four-body bound-state wave function [6, 36]. Therefore, we include in Table 4 the probability \(P_{\varSigma }\) to find a \(\varSigma \) in the hypernuclear wave function. However, one should always keep in mind that this quantity is not an observable and, thus, provides an instructive but not a real measure for the strength of the \(\varLambda \)-\(\varSigma \) conversion. As expected, \(P_{\varSigma }\) is smaller for the NLO19 interactions. There is, however, a visible cutoff dependence of this quantity. For NLO13 and NSC97f, \(P_{\varSigma }\) is smaller for the \(1^+\) state. This is somewhat surprising since Eq. (11) indicates that the triplet interaction should dominate and since \(\varLambda \)-\(\varSigma \) conversion is stronger for the triplet in most interactions. For NLO19 and Jülich ’04, the \(1^+\) state has a larger \(\varSigma \)-probability which is more in line with naive expectations. As stated above, the \(0^+\) separation energies are rather independent from the version of the chiral interaction but the \(1^+\) state is more dependent on this choice. For the \(\varSigma \) probability, the dependence is exactly opposite. Therefore, it is clear that both properties of the interactions are not directly linked to each other.

Finally, let us mention that a new measurement by the STAR collaboration suggests that the \({^{\, 3}_{\varLambda }\mathrm{H}}\) binding energy could be significantly larger [79]. We ignore this in the present work where the focus is on a comparison of our EFT interactions from 2013 and 2019. Nonetheless, we performed some exploratory calculations which indicate that a larger binding energy can indeed be achieved. Moreover, the excellent description of the \({\varLambda }N\) and \({\varSigma }N\) data can be maintained, by an appropriate re-adjustment of the potential strengths in the \({\varLambda }N\)\(^1S_0\) and \(^3S_1\) partial waves – though at the expense of giving up the strict SU(3) constraints on the (S-wave) LECs between the \({\varLambda }N\) and \({\varSigma }N\) channels. Details are reported elsewhere [80].

4 Discussion

The \({\varLambda }\)-\({\varSigma }\) conversion and its impact on hyperonic few- and many-body systems has been discussed in numerous works in the past [50,51,52, 65, 66, 73, 81,82,83,84]. However, in basically all studies so far simplified potential models for the YN interactions have been employed and usually only the extreme scenarios of “coupled or not-coupled” were compared. The present study is on a much more subtle level. First, the full complexity of the YN interaction is taken into account. Second, the coupling of the \({\varLambda }N\) and \({\varSigma }N\) is always considered and a simultaneous description of the available low-energy \({\varLambda }p\) and \({\varSigma }N\) data is achieved by both YN potentials compared in this work.

Nevertheless, the effects due to the \({\varLambda }\)-\({\varSigma }\) conversion revealed by the present study are qualitatively rather similar to those reported in earlier calculations. This is true for three- and four-body systems [66, 81, 82] but also for the in-medium properties of the \({\varLambda }\) hyperon [50,51,52]. Perhaps surprising at first sight, it is an indication that most interactions used in the former works captured reasonably well the bulk properties of the YN interaction.

There is one aspect, however, that has not been really in the focus of past discussions and, thus, we want to elaborate on it in more detail. It concerns the situation embodied by the two EFT interactions: These yield practically identical results for \({\varLambda }p\) as well as \({\varSigma }N\) observables in the low-energy region, as demonstrated in Sect. 3.1, but are characterized by a noticeably different strength of the \({\varLambda }N \rightarrow {\varSigma }N\) transition potential. One might think that additional and/or more accurate scattering data could facilitate a discrimination. But this is unlikely, because one has to realize that the transition potential itself is not an observable quantity. The situation is analogous to that of the deuteron. It is well-known that its D-state probability is not a measurable quantity [85]. Yet it cannot be zero (because of the quadrupole moment of the deuteron) and not too large either. Similarly, the measured \({\varSigma }^- p \rightarrow {\varLambda }n\) (and \({\varLambda }p \rightarrow {\varSigma }^0 p\)) cross section requires a non-zero transition potential, but it fixes its actual strength only within certain limits.

In few- and many-body calculations involving hyperons, differences in the elementary \({\varLambda }N \rightarrow {\varSigma }N\) transition potential are to be balanced by corresponding three-body forces (3BFs). In chiral EFT, the latter appear naturally and automatically in a consistent implementation of the framework [3, 4, 86]. In the power counting followed in Ref. [1] and in the present work, such 3BFs arise first at next-to-next-to-leading order (\(\hbox {N}^2\)LO) in the chiral expansion [3, 87]. For the specific case of the \({\varLambda }\)-\({\varSigma }\) conversion, the necessity for 3BFs is illustrated in a pedagogical way by the similarity renormalization group (SRG) transformation, a tool that is nowadays commonly applied in studies of few-nucleon systems but also of hypernuclei [59, 88,89,90,91,92]. It amounts to a prediagonalization of the Hamiltonian in momentum space in order to improve the convergence of calculations using various many-body methods. One specific feature of this diagonalization is the occurrence of so-called induced three- and higher many-body forces of moderate size. In applications to hypernuclei, such a prediagonalization also involves a decoupling of the \({\varLambda }N\) and \({\varSigma }N\) systems, i.e. leads to a strong reduction of the \({\varLambda }N \rightarrow {\varSigma }N\) transition potential in the Hamiltonian. In this case, induced YNN 3BFs appear, however, they have a more sizable effect as discussed in detail in Ref. [90]. This clearly demonstrates that, in few- and many-body applications, the actual strength of the \({\varLambda }N \rightarrow {\varSigma }N\) transition potential is correlated with and has to be supplemented by corresponding (\({\varLambda }NN\), \({\varSigma }NN\)) 3BFs.

Fig. 10
figure 10

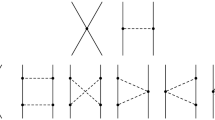
Illustration of three-body dynamics: a standard contribution in the \({\varLambda }NN\) three-body equations. b effective three-body force arising from the \({\varLambda }N\)-\({\varSigma }N\) coupling. c\({\varLambda }N\)-\({\varSigma }N\) transition in the presence of a spectator, leading to a dispersive effect. d three-body force due to the excitation of the \({\varSigma }^*\)(1385) baryon

Full size image

Let us further expand on the role of 3BFs in few-body systems. To begin with, we want to remind the reader that 3BFs are strongly scheme dependent, as discussed extensively in, e.g., Ref. [86]. Specifically, the actual physics represented by a 3BF depends crucially on the degrees of freedom taken into account in the EFT and/or in the specific calculation. For example, in the SU(3) chiral EFT applied by us, the \({\varLambda }\) and \({\varSigma }\) hyperons are treated on equal footing. This is also done in the three- and four-body calculations within the conventional Faddeev–Yakubovsky approach presented in Sect. 3.3. Then contributions represented schematically by the diagrams (a)–(c) in Fig. 10 are all automatically included by solving the corresponding Eqs. (6) and (8). As discussed thoroughly in Ref. [33], the inclusion of the \({\varSigma }\) leads to two types of effects in the three-body dynamics. One is the so-called dispersive effect. It arises when the \({\varLambda }N\) interaction takes place in the presence of one or two spectator nucleons, cf. Fig. 10c. Then the contribution of, say, the transition \({\varLambda }N \rightarrow {\varSigma }N \rightarrow {\varLambda }N\) to the effective two-body potential is reduced as compared to the situation in free space because the propagator includes now the kinetic energy of the spectator nucleons and, as a consequence, the effective interaction is less attractive [33, 66]. At the same time, the equal treatment of the \({\varLambda }\) and \({\varSigma }\) hyperons in the two- and few-body equations generates contributions of the form shown in Fig. 10b. In SU(3) chiral EFT, this contribution is not a 3BF [87] but a result of two-body dynamics. The corresponding contributions can be attractive and then they can compensate or even exceed the dispersive effects. Note that a smaller (larger) \({\varLambda }N \rightarrow {\varSigma }N\) transition potential leads to smaller (larger) dispersive effects but at the same time also to smaller (larger) “3BFs”, so that the net result might be not too sensitive to the actual strength of the transition potential, provided that a consistent and complete calculation has been performed as in the present study. Of course, in general, the properties of the 3BF-type contributions generated in this way depend crucially on the considered state and hypernucleus so that there will be a delicate and distinct interplay between the two three-body effects. The diagram in Fig. 10d is not generated by the dynamical equations since decuplet baryons are not explicitly included. Thus, it constitutes a proper contribution to the 3BF in SU(3) chiral EFT [87, 93].

The situation is different for pionless EFT which has been likewise employed in studies of the properties of the hypertriton and of other light hypernuclei [72, 94,95,96]. In that framework, only the \({\varLambda }\) and the nucleons are kept as active degrees of freedom while pions but also the \({\varSigma }\) are “frozen out”. As a consequence, proper 3BFs appear already at LO in this approach. And these 3BFs represent effectively the dynamics illustrated in Fig. 10b–d, among other things. Recall that the virtual elimination of the \({\varSigma }\) degrees of freedom is also one of the reasons for the induced 3BFs in the discussed SRG transformation [90].

Studies of the nuclear matter properties are usually based on the G-matrix calculated from the Bethe–Goldstone equation, as it is done here. Then only the dispersive effect is taken into account and, thus, a stronger \({\varLambda }N\rightarrow {\varSigma }N\) potential leads unavoidably to a less attractive \({\varLambda }\) nuclear potential. It is the prime reason why we see a sizable difference in the nuclear matter results for the NLO13 and NLO19 potentials, cf. Sect. 3.2. But it is also the main reason for the differences in nuclear matter calculations observed for phenomenological YN potentials. A proper way to deal with this would be to solve the corresponding Bethe–Faddeev equation [97] where three-body correlations are taken into account consistently. It is, however, technically rather challenging and therefore generally avoided.

Should one give preference to either the NLO13 or the NLO19 interaction? In our opinion there are no stringent reasons that would make one superior over the other. That said, a YN potential where SU(3) symmetry is fulfilled by the NLO LECs in combination with the NN interaction and which is, therefore, more in line with the underlying power counting, is certainly more favorable from a fundamental point of view. Note, however, that the symmetry is anyway broken by the corresponding NLO contributions from two-meson exchange [1]. Certainly a positive aspect in favor of the new fit is that the corresponding LECs are somewhat smaller and, therefore, more in line with the requirement of natural size [3].

Another aspect is, whether it would be sensible to “optimize” the YN potential so that the 3BFs become small. As argued in Ref. [86], such a strategy is doomed to fail on the level of accuracy of the last order of the EFT where 3BFs do not contribute. For a 3BF that only depends on one adjustable parameter, it is obviously advantageous to choose the YN interaction such that this parameter is minimal. This will simultaneously minimize the effect of the 3BF in all observables. Once several parameters are involved, as is certainly the case for the chiral YNN interaction at \(\hbox {N}^2\)LO, the optimal set of parameters will depend on the observable chosen and will not be universal. A good example of this aspect shown in this work is the observation that we can improve the description of the \(1^+\) state for specific choices of the cutoff or by choosing NLO19. This, however, will not improve the description of the \(0^+\) state. State-of-the-art calculations of few-nucleon systems based on chiral NN potentials commonly include 3BFs. The arising additional LECs in the 3BF are fixed by considering few- or many body observables, for example the triton binding energy or the minimum of the differential pd cross section [98]. Their actual values depend on the specific features of the employed EFT and, in particular, on the adopted regularization scheme [86]. With regard to few-body systems involving hyperons, the LECs corresponding to \({\varLambda }NN\) (or \({\varSigma }NN\)) forces will be necessarily interrelated with the strength of the \({\varLambda }N \rightarrow {\varSigma }N\) transition potential. Since such 3BFs arise only at \(\hbox {N}^2\)LO in the power counting, as mentioned above, we do not consider them in the present work which is at the NLO level. Anyway, given the present experimental situation it remains unclear in how far the various LECs that arise in the lowest-order \({\varLambda }NN\) 3BF [87] could be fixed by considering few-body observables such as the \({^{\, 3}_{\varLambda }{\mathrm{H}}}\) and/or \({^{\, 4}_{\varLambda }{\mathrm{H}}}\) (\({^{\, 4}_{\varLambda }{\mathrm{He}}}\)) binding energies. One possible solution would be the explicit inclusion of decuplet baryons in the EFT as discussed in Ref. [93]. Assuming that the YNN 3BF can be saturated by the excitation of decuplet baryons reduces the number of pertinent LECs considerably. As a byproduct, this framework would also promote the corresponding contributions to NLO [4] which is consistent with the assumption that these contributiuons are the dominant 3BFs to be expected in chiral EFT.

Either way, including 3BFs into our codes for solving the Faddeev-Yakubovsky equations for the YNN and YNNN systems is technically rather demanding. It requires considerable additional work which we postpone to the future. Thus, at present, we cannot give reliable estimates for the size of 3BFs. However, since the effect of the \({\varLambda }\)-\({\varSigma }\) conversion is explicitly included in our few-body calculation, we expect only moderate contributions from such 3BFs for light hypernuclei and, specifically for the hypertriton. This is in contrast with the aforementioned studies within pionless EFT [72, 94] or with phenomenological approaches [99] where an effective \({\varLambda }N\) interaction is employed and the coupling to \({\varSigma }N\) is not taken into account. Here the effect of 3BFs is significant and without including them explicitly, no realistic results can be achieved, as testified by past calculations. It is argued in Refs. [6, 86] that the dependence of the predictions on the regulator should provide a lower bound for the magnitude of the contributions from three- and higher-body forces. Based on that measure, one expects a rather small influence in case of the hypertriton. This is in line with other arguments that consider the fact that the bound state is very shallow and, accordingly, the \({\varLambda }\) is on average far from the two nucleons [34]. Then the likelihood that all three particles are close to each other and feel a 3BF is very small. For the \({^{\, 4}_{\varLambda }\mathrm{He}}\) system, the cutoff dependence of the separation energies is larger and, thus, one would expect larger effects from 3BFs here, specifically for the \(1^+\) state.

Table 5 Comparison of the separation energies \(E_\varLambda \) of \(^3_\varLambda {\mathrm{H}}\), \(^4_\varLambda {\mathrm{He}(0^+)}\) and \(^4_\varLambda {\mathrm{He}(1^+)}\) including and excluding explicit \(\varSigma \)s for different YN interactions. See text for more details. For the chiral YN forces, the SMS NN interaction [63] at order \(\hbox {N}^4\)LO+ with cutoff of 450 MeV has been used. For Jülich’04 and NSC97f, the CD-Bonn interaction [67] has been employed. Energies are given in MeV
Full size table

A rough indication for the magnitude of possible effects of 3BFs can be obtained by switching off the \({\varSigma }\) in the three- and four-body systems as discussed in Refs. [6, 36]. Corresponding results are summarized in Table 5. Clearly, this procedure provides primarily a measure for the effective 3BFs coming from the \({\varSigma }\) excitation, cf. Fig. 10b. But one might speculate that the magnitude of an actual 3BF represented, e.g., by the excitation of the \({\varSigma }^*\)(1385) [93] see Fig. 10c, should be smaller given that the \({\varSigma }^*\) mass is significantly larger and that the power counting suggests first contributions at a higher order. The actual change in the \(^3_\varLambda \)H separation energy for the hypertriton amounts to less than 10 keV for the NLO interactions when the \({\varSigma }\) component is switched off. There is an increase in the binding which means that the effective 3BFs coming from the \({\varSigma }\) excitation are overall repulsive. Interestingly, the opposite is the case for the NSC97f potential, and also for other Nijmegen YN interactions considered in the past [6, 36]. Obviously, there is a delicate interplay reflecting the actual strength of the \({\varLambda }\)-\({\varSigma }\) conversion as well as its realization in the \(^1S_0\) and \(^3S_1\) partial waves. In the four-body system, there is a reduction of the binding energy by around 340 (230) keV for the \(0^+\) state and by 150 (180) keV for \(1^+\), for NLO13 (NLO19), when the \({\varSigma }N\) component is switched off in the few-body calculations. For results with the NLO13 interaction with other cutoffs, see Ref. [6]. Also for \(^4_\varLambda {\mathrm{He}}\), the trend exhibited by the phenomenological potentials differs in part. Nonetheless, at least for the chiral interactions, the variations in the separation energies when the \(\varSigma \) component is removed is even slightly smaller than the cutoff dependence, discussed above. Since these variations provide a measure for the diagram of Fig. 10b, the results support that 3BFs in our approach [87] are likely smaller than the uncertainty at order NLO.

Finally, note that, for nuclear matter calculations, one possibility to circumvent the computational challenges of many-body equations consists in the use of density-dependent effective \({\varLambda }N\) (and \({\varSigma }N\)) interactions that can be derived from chiral three-body forces [87]. Assuming furthermore that the 3BFs are dominated by the excitation of decuplet baryons (decuplet saturation), the number of independent LECs in the three-baryon interactions can be considerably reduced. A first application of that formalism in studies of the in-medium properties of the \({\varLambda }\) has been reported in Ref. [10]. In this context, let us mention that adding a density-dependent effective \({\varLambda }N\) force to the NLO19 interaction, with the strength considered in the aforementioned reference, would bring the single-particle potential \(U_{\varLambda }\) for NLO13 and NLO19 roughly in agreement with each other, up to the highest considered Fermi momentum of \(k_F = 1.7\) \(\hbox {fm}^{-1}\), corresponding to a density of twice the nuclear matter saturation density.

5 Conclusions

In the present work, we have investigated the \(\varLambda N\) and \(\varSigma N\) interactions at next-to-leading order in SU(3) chiral effective field theory. In particular, we have explored different options for the low-energy constants that determine the strength of the contact interactions. One YN interaction considered is the initial NLO potential published in 2013 [1]. The other potential has been established in the present paper. It is guided by the objective to reduce the number of LECs that need to be fixed in a fit to the \(\varLambda N\) and \(\varSigma N\) data by inferring some of them from the NN sector via the underlying SU(3) symmetry. Correlations between the LO and NLO LECs of the S-waves had been observed already in our initial YN study [1] and indicated that a unique determination of them by considering the existing \(\varLambda N\) and \(\varSigma N\) data alone is not possible.

As demonstrated in the present work, the two variants considered yield equivalent results for \(\varLambda N\) and \(\varSigma N\) scattering observables. However, they differ in the strength of the \(\varLambda N \rightarrow \varSigma N\) transition potential and that becomes manifest in applications to few- and many-body systems. The influence of this difference on predictions for light hypernuclei and for the properties of the \(\varLambda \) and \(\varSigma \) hyperons in nuclear matter has been shown and discussed in detail. It turned out that the effect of the variation in the strength of the \(\varLambda N\)-\(\varSigma N\) coupling (\({\varLambda }-{\varSigma }\) conversion) is moderate for the considered hypernuclei but sizable in case of the matter properties.

Since the YN scattering data alone cannot fully constrain the \(\varLambda N\)-\(\varSigma N\) transition potential, arguably as a matter of principle, consistent three-body forces are needed to compensate for the differences in few- and many-body systems. Such 3BFs arise only at \(\hbox {N}^2\)LO in the power counting that we follow, and therefore, we did not consider them in the present work which is at the NLO level. However, we speculate that the effect of such 3BFs should be fairly small, at least for light hypernuclei, once the \({\varLambda }-{\varSigma }\) conversion is taken into account consistently in the corresponding calculations. In such a case, important aspects of three-body dynamics such as dispersive effects but also effective three-body forces that arise from the coupling of \(\varLambda N\) to \(\varSigma N\) are taken into account rigorously.

In this work, the influence of the \(\varLambda -\varSigma \) conversion strength on light hypernuclei and nuclear matter has been investigated. For further insight, but also for addressing other aspects, more and/or more accurate data are essential. A new measurement of the hypertriton bound state has been presented which points to a noticeably larger binding energy [79]. Measurements of \(^{\,4}_{\varLambda }{\mathrm{H}}\) and \(^{\,4}_{\varLambda }\mathrm{He}\) with improved accuracy in order to determine the amount of charge-symmetry breaking more precisely have been performed [69, 77] or are on the way [100]. There are also attempts to shed more light on the elementary YN interaction directly via studies of the \({\varLambda }p\) correlation function measured in heavy-ion collisions or high-energy pp collisions [101,102,103]. Moreover, there are plans for a future measurement of \({\varSigma }^-p\) scattering at J-PARC [104]. Depending on the outcome of those experiments, one might have to readjust the YN interaction. In particular, this concerns the relative strength of the \({\varLambda }p\) interaction in the \(^1S_0\) and \(^3S_1\) channels. Efforts at the COSY accelerator in Jülich to determine the strength of the spin-triplet \({\varLambda }p\) interaction from the final-state interaction in the reaction \(pp\rightarrow K^+\varLambda p\) [105] suffered from low statistics and, unfortunately, could not provide the desired and urgently needed stringent constraint. Given the lack of appropriate spin-dependent observables, it is fixed in our studies by considering the hypertriton separation energy [1, 9, 15]. A larger hypertriton separation energy would certainly require a more attractive \(^1S_0\)\({\varLambda }p\) interaction. That, in turn, would influence the predictions of an appropriately modified chiral YN interaction for the \(^{\,4}_{\varLambda }{\mathrm{H}}\) and \(^{\,4}_{\varLambda }\mathrm{He}\) states [80].