A simple method for perfect packing of squares of sidelengths $n^{-1/2-\epsilon}$

Abstract

A simple method for perfect packing a square by squares of sidelengths $1$, $2^{-t}$, $3^{-t}$, $4^{-t},\ldots$ is presented for $1/2<t\leq 17/32$.

1 Definitions

There are many questions about packing. In this note, we will describe one problem of perfect packing.

Let $Q_{n}$ be a square, for $n=1,2,\ldots$, and let $R$ be a rectangle. We say that the squares $Q_{1},Q_{2},\ldots$ can be packed into $R$ if it is possible to apply translations and rotations to the sets $Q_{n}$ so that the resulting translated and rotated squares are contained in $R$ and have mutually disjoint interiors. If the area of $R$ is equal to the sum of areas of the squares, then the packing is perfect.

Example 1

Three squares of sidelength $1/2$, three squares of sidelength $1/4$, three squares of sidelength $1/8$, $\ldots$ (i.e., three squares of sidelength $2^{-n}$ for $n=1,2,3,\ldots$), of the sum of areas equal to $\frac{3}{4}+\frac{3}{16}+\frac{3}{64}+\ldots=3\cdot\sum_{n=1}^{\infty}\frac{1}{4^{n}}=1$, can be packed into the square $I$ of sidelength 1 (see Fig. 1). The sum of areas of squares equals the area of $I$, so the packing is perfect.

 

Fig. 1

Example 1, perfect packing

Example 2

One square of sidelength 1, one square of sidelength $1/2$, one square of sidelength $1/4$, $\ldots$ (i.e., squares of sidelength $2^{-n}$ for $n=0,1,2,\ldots$), of the sum of areas equal to $1+\frac{1}{4}+\frac{1}{16}+\ldots=\frac{4}{3}$, cannot be packed into the square of sidelength $\frac{2\sqrt{3}}{3}$; the reason is that $1+\frac{1}{2}> \frac{2\sqrt{3}}{3}$ (see Fig. 2). Moreover, the squares cannot be packed into any rectangle of area 4/3; the smallest rectangle ($1\times 3/2$) into which a square of sidelength 1 can be packed together with a square of sidelength 1/2 is of area greater than 4/3. Consequently, the squares cannot be perfectly packed into any rectangle.

 

Fig. 2

Example 2

Given a rectangle $R$, by the width $w(R)$ we mean the smaller of the two sidelengths; the other sidelength $h(R)$ of $R$ is called the height. We will write $R=w(R)\times h(R)$. Clearly, if $R$ is a square, then $w(R)=h(R)$.

2 Packing of squares of harmonic sidelengths

In 1966 Moser [9] posed the following well known problem (see also problem LM6 in [10]): find the smallest $\varepsilon\geq 0$ such that the squares of sidelengths $1/2,1/3,1/4,\ldots$ (see Fig. 3) can be packed into a rectangle of area $\frac{1}{6}\pi^{2}-1+\varepsilon$ (the sum of areas of the squares equals $\frac{1}{6}\pi^{2}-1$). Obviously, if $\varepsilon=0$, then we get the perfect packing.

Fig. 3

Squares of harmonic sidelengths

This problem is still open. Only some upper bounds are known for $\varepsilon$:

• Meir and Moser [8] showed that the squares can be packed into a square of sidelength 5/6 (consequently, $\varepsilon<1/20$). Obviously, this is the smallest possible square; to pack a square of sidelength 1/2 together with a square of sidelength 1/3, a square of sidelength at least 1/2+1/3=5/6 is needed.

• Jennings ([5]) proved that $\varepsilon<1/127$.

• Ball [1] showed that $\varepsilon<1/198$.

• Paulhus [11] obtained the very impressive bound $\varepsilon\leq 1/1244918662$. However, Joós (see [6]) pointed out that the proof given in the article is incorrect. In [3] it is showed that the Paulhus’ lemma can be refolmulated so that the the upper bound $\varepsilon\leq 1/1244918662$ remains valid.

The packing method presented in [11] is very easy. Squares of sidelengths $1/2,1/3,1/4,\dots$ are packed into a rectangle $R_{1}=1/2\times(\pi^{2}/3-2)$. Difficulties arise only in estimating the effectiveness of this method.

Paulhus’ method [11].

• 1. The first square is packed into a corner of $R_{1}$. After packing, the rectangle $V_{2}=1/2\times(\pi^{2}/3-2-1/2)$ remains uncovered. We take $\mathcal{R}_{2}=\{V_{2}\}$.

• 2. The square of sidelength 1/3 is packed into a corner of $V_{2}$. After packing, the uncovered part of $V_{2}$ is divided into $U_{3}\cup V_{3}$, where $U_{3}=(1/2-1/3)\times 1/3$ and $V_{3}=(h(V_{2})-1/3)\times 1/2$; we take $\mathcal{R}_{3}=\{U_{3},V_{3}\}$.

• 3. Assume that $n> 3$, that the squares of sidelength $1/2,1/3,\ldots,1/(n-1)$ are packed into $R_{1}$ and that the family $\mathcal{R}_{n-1}$ is defined. We choose the rectangle with the smallest width from $\mathcal{R}_{n-1}$ into which the square of sidelength $1/n$ can be packed. Denote this rectangle by $R$. We pack the square into a corner of $R$. After packing, we divide the uncovered part of $R$ into $U_{n}\cup V_{n}$, where $U_{n}$ is the rectangle of sidelengths $1/n$ and $w(R)-1/n$ and where $V_{n}$ is the rectangle of sidelengths $w(R)$ and $h(R)-1/n$; it is possible that $U_{n}$ is an empty set. We take $\mathcal{R}_{n}=\bigl(\mathcal{R}_{n-1}\setminus\{R\}\bigr)\cup\{U_{n},V_{n}\}$.

Fig. 4 illustrates the initial stage of the packing process. The first square is packed into a corner of $R_{1}$. The second square (of sidelength 1/3) is packed into a corner of the uncovered area. The family $\mathcal{R}_{3}$ consists of two rectangles: $U_{3}$ and $V_{3}$. Since $1/4> 1/2-1/3$, the square of sidelength 1/4 cannot be packed into $U_{3}$ (the width $w(U_{3})=1/6$). It is packed into a corner of $V_{3}$ of width $w(V_{3})=\pi^{2}/3-2-1/2-1/3<1/2$ and height $h(V_{3})=1/2$. After packing, the uncovered part of $V_{3}$ is divided into rectangles $V_{4}$ and $U_{4}$. Now the family $\mathcal{R}_{3}$ consists of three rectangles: $U_{3}$, $U_{4}$ and $V_{4}$. Since $w(U_{3})<1/5<w(U_{4})<w(V_{4})$, the square of sidelength 1/5 is packed into $U_{4}$. From among four rectangles in $\mathcal{R}_{5}$, the rectangle $U_{3}$ is the one with the smallest width ($w(U_{3})=1/6$) into which the square of sidelength 1/6 can be packed.

Fig. 4

Paulhus’ method

Paulhus used computer calculations and checked that at least $10^{9}$ squares can be packed into $R_{1}$. It is highly unlikely that this method would produce a perfect packing. However, it is not known how many squares can be packed, i.e., which square stops the packing process with this method.

3 Generalization

Let $S_{n}^{t}$ be a square of sidelength $n^{-t}$ for $n=1,2,\ldots$ If $t\leq 1/2$, then the total area of the squares is equal to $\sum_{n=1}^{\infty}\frac{1}{n^{2t}}$ and the series is divergent. However, if $t> 1/2$, then the sum of areas of the squares is finite. Therefore, one can ask whether $S_{1}^{t},S_{2}^{t},\ldots$ (for $t> 1/2$) can be packed perfectly into a rectangle. Obviously, for $t=1$ we get Moser’s original question.

Note that $\sum_{n=1}^{\infty}\frac{1}{n^{2t}}=\zeta(2t)$, where $\zeta(s)$ is the Riemann zeta function.

Some results for packing are known for $t<1$. Chalcraft [2] showed that $S_{1}^{t},S_{2}^{t},S_{3}^{t},\ldots$ can be packed perfectly into a square for all $t$ in the range $[0.5964,0.6]$. Joos [7] checked that these squares can be also packed perfectly for all $t$ in the range $[\log_{3}2,2/3]$ ($\log_{3}2\approx 0.63$). Wästlund [13] proved that $S_{1}^{t},S_{2}^{t},S_{3}^{t},\ldots$ can be packed into a finite collection of squares of the same area as the sum of areas of the squares, provided $1/2<t<2/3$. In [4] it is showed that for all $t$ in the range $(1/2,2/3]$, the squares $S_{1}^{t},S_{2}^{t},S_{3}^{t},\ldots$ can be packed perfectly into a single square. Tao [12] proved that for any $1/2<t<1$, and any $n_{0}$ that is sufficiently large depending on $t$, the squares $S_{n_{0}}^{t},S_{n_{0}+1}^{t},\ldots$ can be packed perfectly into a square. Unfortunately, existing packing methods and proofs are not very easy. This note presents a simple method for perfect packing, but only for $t$ slightly greater than $1/2$. In particular, the packing method is not effective for $t=1$ (for packing of squares of harmonic sidelength).

4 Perfect packing of squares

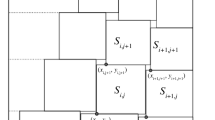
Let $t$ be a fixed number from the interval $(1/2,17/32]$ and let $S$ be a square of area $\sum_{n=1}^{\infty}\frac{1}{n^{2t}}$. We will write $S_{m}$ instead of $S_{m}^{t}$. The idea of the packing method is as follows. For each $n\geq 2$, the empty space in $S$, i.e., the part of $S$ not covered by packed squares $S_{1},\ldots,S_{n-1}$, will be divided into $2n-1$ rectangles. Then, as in the Paulhus’ method, $S_{n}$ will be packed into a corner of one of these rectangles.

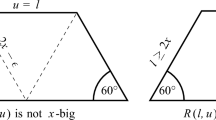
A rectangle $R$ is $m$-big, provided that $w(R)\geq 2m^{-t}$.

A rectangle $R$ is basic, provided that $w(R)\leq h(R)\leq 2w(R)$.

Obviously, each $m$-big rectangle is also $n$-big for $n> m$. Moreover, each basic rectangle is $n$-big for sufficiently large value of $n$.

Lemma 1

Let $m$ be a positive integer and let $R$ be an $m$ -big rectangle. Then $R$ can be divided into four parts: $S_{m}$ and three rectangles that are either basic or $m$ -big.

Proof

Case 1, when $w(R)> 5m^{-t}$. The rectangle $R$ is divided into: $S_{m}$, $B_{m}$, $L_{m}$ and $T_{m}$ (see Fig. 5, left), where $B_{m}=m^{-t}\times m^{-t}$, $L_{m}=(2m^{-t})\times(h(R)-m^{-t})$ and $T_{m}=(w(R)-2m^{-t})\times h(R)$. Clearly, $B_{m}$ is basic. Moreover, $L_{m}$ and $T_{m}$ are $m$-big. It is possible that $T_{m}$ is $m$-big and basic at the same time.

Case 2, when $w(R)\leq 5m^{-t}$. Let $B_{m}$ and $L_{m}$ be rectangles of sidelengths $m^{-t}$ and $(w(R)-m^{-t})/2$. Obviously, $B_{m}$ and $L_{m}$ are basic.

By $h(R)\geq w(R)\geq 2m^{-t}$ we get $h(R)-m^{-t}\geq w(R)-m^{-t}\geq\frac{1}{2}w(R)$. Let $T_{m}$ be a rectangle of sidelengths $w(R)$ and $h(R)-m^{-t}$. Observe that $T_{m}$ is either $m$-big (provided $h(R)-m^{-t}\geq 2m^{-t}$) or basic (provided $h(R)-m^{-t}\leq 2w(R)$). It is possible that $T_{m}$ is $m$-big and basic at the same time. The rectangle $R$ is divided into $S_{m}$, $L_{m}$, $B_{m}$ and $T_{m}$ (see Fig. 5, middle and right).

 

Fig. 5

$w(R)\geq 2m^{-t}$, $R=S_{m}\cup L_{m}\cup B_{m}\cup T_{m}$

Packing method.

• 1. The first square is packed into a corner of $S$. After packing $S_{1}$, the uncovered part of $S$ is divided into $L_{1}\cup B_{1}\cup T_{1}$ (as in the proof of Lemma 1) and we take $\mathcal{R}_{1}=\{L_{1},B_{1},T_{1}\}$.

• 2. Assume that $n> 1$, that the squares $S_{1},\ldots,S_{n-1}$ are packed into $S$ and that the family $\mathcal{R}_{n-1}$ is defined. We choose one of $n$-big rectangles from $\mathcal{R}_{n-1}$ in any way. Denote this rectangle by $R$. We pack $S_{n}$ into a corner of $R$. After packing $S_{n}$ we divide the uncovered part of $R$ into $L_{n}\cup B_{n}\cup T_{n}$ (as in the proof of Lemma 1) and we take $\mathcal{R}_{n}=\bigl(\mathcal{R}_{n-1}\setminus\{R\}\bigr)\cup\{L_{n},B_{n},T_{n}\}$.

Fig. 6 illustrates the initial stage of the packing process. The first square is packed into a corner of $S$. We have four possibilities; for example, we pack $S_{1}$ into the lower left corner. Since $w(L_{1})\geq 2\cdot 2^{-t}$ as well as $w(T_{1})\geq 2\cdot 2^{-t}$, both rectangles $L_{1}$ and $T_{1}$ are 2‑big. We have eight possibilities for packing $S_{2}$: either in one of the corners of $L_{1}$ or in one of the corners of $T_{1}$. We choose one of them.

Fig. 6

Packing method

Clearly, $\mathcal{R}_{n-1}$ contains $2n-1$ rectangles with mutually disjoint interiors, for any $n\geq 2$. Each rectangle from $\mathcal{R}_{n-1}$ is either $n$-big or basic.

Theorem 1

For each $t$ in the range $1/2<t\leq 17/32$, the squares $S_{n}^{t}$ can be packed perfectly into the square $S$.

Proof

Let $t$ be a fixed number from the interval $(1/2,17/32]$. The area of $S$ is equal to $\sum_{i=1}^{\infty}\frac{1}{i^{2t}}=\zeta(2t)\geq\zeta(17/16)> 16$. Consequently, $w(S)> 2\cdot\frac{1}{1^{t}}$, i.e., $S$ is 1‑big. We pack $S_{1}^{t},S_{2}^{t},{\ldots}$ into $S$ by our method. To prove Theorem 1 it suffices to show that for any $n$ there is an $n$-big rectangle in $\mathcal{R}_{n-1}$ (into which $S_{n}^{t}$ can be packed).

First we estimate the sum of areas of rectangles in $\mathcal{R}_{n-1}$, i.e., the area of the uncovered part of $S$ after packing $S_{n-1}^{t}$. This value is equal to the sum of areas of unpacked squares $S_{n}^{t},S_{n+1}^{t},\ldots$ (which is equal to the sum of areas of rectangles of sidelengths 1 and $\frac{1}{i^{2t}}$, for $i=n,n+1,n+2,\ldots$), i.e., is equal to (see Fig. 7)

$$\frac{1}{n^{2t}}+\frac{1}{(n+1)^{2t}}+\ldots> \int_{n}^{+\infty}\frac{1}{x^{2t}}{\text{d}}x=\frac{1}{2t-1}n^{1-2t}\geq\frac{1}{2\cdot\frac{17}{32}-1}n^{1-2t}=16n^{1-2t}{.}$$

Assume that there is an integer $n$ such that $S_{n}^{t}$ cannot be packed into $S$ by our method. This implies that there is no $n$-big rectangle in $\mathcal{R}_{n-1}$. Then all rectangles in $\mathcal{R}_{n-1}$ are basic and the width of each such rectangle is smaller than $2n^{-t}$. The area of each such rectangle is smaller than $(2n^{-t})\cdot 2(2n^{-t})=8n^{-2t}$. Since $2n-1$ rectangles are in $\mathcal{R}_{n-1}$, it follows that the total area of rectangles in $\mathcal{R}_{n-1}$ is smaller than $(2n-1)\cdot 8n^{-2t}<16n^{1-2t}$, which is a contradiction.

Consequently, $S_{1}^{t},S_{2}^{t},\ldots$ can be packed into $S$.

 

Fig. 7

Sum of areas of rectangles

Remark 1

The same packing method permits a perfect packing of $S_{1}^{t},S_{2}^{t},\ldots$ into any rectangle $R$ of area $\zeta(2t)$, provided $w(R)\geq 2$ and $1/2<t\leq 17/32$.