Lights Out on graphs

Abstract

We model the Lights Out game on general simple graphs in the framework of linear algebra over the field $\mathbb{F}_{2}$. Based upon a version of the Fredholm alternative, we introduce a separating invariant of the game, i.e., an initial state can be transformed into a final state if and only if the values of the invariant of both states agree. We also investigate certain states with particularly interesting properties. Apart from the classical version of the game, we propose several variants, in particular a version with more than only two states (light on, light off), where the analysis relies on systems of linear equations over the ring $\mathbb{Z}_{n}$. Although it is easy to find a concrete solution of the Lights Out problem, we show that it is NP-hard to find a minimal solution. We also propose electric circuit diagrams to actually realize the Lights Out game.

1 Introduction

The game Lights Out exists in several versions. The classical edition, issued by Tiger Electronics in 1995, consists of a $5\times 5$ grid of lights which are switches at the same time. Pressing a light will toggle the state of this light and its adjacent neighbors between off and on. Initially a random set of lights are on and the aim is to turn all lights off, if possible with a minimum number of operations. More generally, a given initial state has to be transformed into a prescribed final state.

This game and some variants of it have been studied several times in the literature: The classical problem as described above was modeled in the language of linear algebra in [1]. In [16] the puzzle on a $2^{k}\times 2^{k}$ torus is investigated, and a criterion for the solvability of the $5^{k}\times 5^{k}$ torus is derived. In [19] the solvability of the Lights Out game with respect to varying board size and with more than one color (see Sect. 4.4 below) is studied by methods from algebraic number theory. The game has first been studied under the name Garden of Eden (configuration with no predecessor) in [24] and [25] in the context of cellular automata. The Lights Out game may also be described in the framework of graph theory where the set of buttons to be pushed in order to invert a given state corresponds to an odd dominating set (see [11, 13,14,15]). Sutner was the first to show that the “all-on” configuration is universal. This means that on any $n$-vertex graph it is possible in finitely many steps to turn off all lights when you started with all lights on. Different proofs regarding this problem were later given in [5], [7], [13], and [12]. Other results regarding universally solvable graphs were for instance considered in [13] and [12]. In [8] the authors were looking for universal configurations also for similar games like “Orbix”.

Another modification can be found in [3] where the Lights Out game was investigated on a grid $\{1,\dots,m\}\times\{1,\dots,n\}$. In [22] the Lights Out game for cartesians products of graphs has been investigated. In particular, conditions are formulated for this particular situation which imply that every initial configuration of lights can be turned off. For a wide historical review of the game and its variants we refer to [9] and the references therein.

In the present paper we investigate some new variants of the Lights Out game and add some new elements to the theory of such games: Based upon a version of the Fredholm alternative, we introduce a separating invariant of the game and several of its variants, i.e., an initial state can be transformed into a final state if and only if the values of the invariant of both states agree (see Theorems 4, 11 and 13). We also investigate certain states with particularly interesting properties and their relations (see Theorem 5 and Propositions 7, 8, 9 and 10). Apart from the classical version of the game, we propose several variants of it, in particular a version with more than only two states (light on, light off), where the analysis relies on systems of linear equations over the ring $\mathbb{Z}_{n}$ (see Theorem 17). Although it is easy to find a concrete solution of the Lights Out problem, we show that it is NP-hard to find a minimal solution (see Proposition 18 and Theorem 21). We also propose electric circuit diagrams to actually realize the Lights Out game in Sect. 6.

We can play the game with the rules described above on an arbitrary simple graph $G$ (see Sect. 2 for some basic definitions of graph theory) with vertex set $V:=\{v_{1},\ldots,v_{n}\}$. Each vertex is a light and at the same time a switch. The status of the lights is modeled by a map $V\to\mathbb{F}_{2}=\{0,1\}$, represented by a vector $(x_{1},\ldots,x_{n})^{\top}$, where $x_{i}=1$ means that the light in vertex $v_{i}$ is on, and off if $x_{i}=0$. Let $A\in\mathbb{F}_{2}^{n\times n}$ be the adjacency matrix of $G$. Then $N:=A+\mathbb{I}$, where $\mathbb{I}$ is the $n\times n$ identity matrix, encodes the information about which lights are toggled when pushing a certain button: If $x\in\mathbb{F}_{2}^{n}$ represents a state of lights and we press switch $v_{j}$, then the resulting state will be

$$x+Ne_{j},$$

(1)

where $e_{j}$ is the $j$-th column of $\mathbb{I}$, and where the operations in (1) are carried out in the field $\mathbb{F}_{2}$. Hence, pressing a sequence of switches, say $v_{j_{1}},v_{j_{2}},\ldots,v_{j_{k}}$, will lead an initial state $x\in\mathbb{F}_{2}^{n}$ to the resulting state

$$x+Ne_{j_{1}}+Ne_{j_{2}}+\ldots+Ne_{j_{k}}=x+N(e_{j_{1}}+e_{j_{2}}+\ldots+e_{j_{k}}).$$

In particular,

• the order in which switches are pushed does not play a role, and

• pressing a switch an even number of times is equivalent to not pressing it at all.

Hence, for an initial state $i\in\mathbb{F}_{2}^{n}$ of lights, a given final state $f\in\mathbb{F}_{2}^{n}$ can be reached in the Lights Out game if and only if there exists $a\in\mathbb{F}_{2}^{n}$ such that $f=i+Na$. Here, $a=(a_{1},a_{2},\ldots,a_{n})^{\top}$ encodes the concrete solution: To get from $i$ to $f$ we push all switches $v_{j}$ for which $a_{j}=1$.

2 A separating invariant for the Lights Out game on graphs

Since we will use several notions from graph theory, we first recall some basic concepts:

• A graph $G=(V,E)$ is a mathematical structure consisting of a set $V$ of points called vertices and a (possibly empty) set $E$ of edges. Each edge connects a pair of vertices.

• A loop is an edge that connects a vertex to itself.

• A simple graph is a graph which does not have more than one edge between any two vertices and which has no loops.

• Two vertices are said to be adjacent if there is an edge connecting them.

• A vertex is incident to an edge if the vertex is one of the two vertices the edge connects.

• The degree of a vertex of a graph is the number of edges that are incident to the vertex.

• A directed graph is a graph in which edges have an orientation.

• A complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.

• The adjacency matrix $A$ is a square matrix used to represent a finite graph. The element $A_{ij}$ is equal to $1$ if the vertices $v_{i}$ and $v_{j}$ are adjacent, and $0$ otherwise.

As we have seen in the introduction, a final state $f\in\mathbb{F}_{2}^{n}$ can be reached from an initial state $i\in\mathbb{F}_{2}^{n}$ if and only if $i+f$ belongs to the column space of $N:=A+\mathbb{I}$. This observation can conveniently be expressed by introducing the following equivalence relation:

Definition 1

Two elements $x,y\in\mathbb{F}_{2}^{n}$ are called equivalent with respect to the matrix $N\in\mathbb{F}_{2}^{n\times n}$ (or just equivalent) if $x+y$ lies in the column space of $N$. In this case we write $x\sim y$.

Hence, an initial state $i\in\mathbb{F}_{2}^{n}$ can be transformed into a final state $f\in\mathbb{F}_{2}^{n}$ if and only if $i\sim f$. In principle, it is now easy to check, if $i$ and $f$ belong to the same equivalence class by applying Gauss elimination in $\mathbb{F}_{2}$ for the linear system $Na=i+f$. However, if we want to see at a glance whether $i\sim f$, we need a handy separating invariant. In order to formulate such an invariant, we first define a bilinear form on $\mathbb{F}_{2}^{n}$:

Definition 2

$\langle\cdot,\cdot\rangle:\mathbb{F}_{2}^{n}\times\mathbb{F}_{2}^{n}\to\mathbb{F}_{2},(x,y)\mapsto\sum_{i=1}^{n}x_{i}y_{i}$ .

Two vectors $x,y\in\mathbb{F}_{2}^{n}$ with $\langle x,y\rangle=0$ are called orthogonal. If $M$ is an arbitrary subset of $\mathbb{F}_{2}^{n}$, $M^{\bot}:=\{x\in\mathbb{F}_{2}^{n}\mid\langle x,m\rangle=0$ for all $m\in M\}$ is a vector space. However, note that the bilinear form $\langle\cdot,\cdot\rangle$ is not positive definite: Every $x\in\mathbb{F}_{2}^{n}$ with an even number of ones satisfies $\langle x,x\rangle=0$ (such vectors are called isotropic). Nonetheless, the Fredholm alternative holds in the following sense:

Proposition 3

Let $N\in\mathbb{F}_{2}^{m\times n}$ be an $m\times n$ matrix. Then the linear system $Nx=b$ has a solution $x\in\mathbb{F}_{2}^{n}$ if and only if $b\in\mathbb{F}_{2}^{m}$ is orthogonal to all solutions of the adjoint system $N^{\top}y=0$ . I.e., we have

$$\operatorname{im}N=(\operatorname{ker}N^{\top})^{\bot}.$$

Proof

Let $C:=\operatorname{im}N$. Then $\operatorname{dim}C=\operatorname{rank}N=:r$. Observe that $\operatorname{ker}N^{\top}=C^{\bot}$ and that $\operatorname{dim}C^{\bot}=m-\operatorname{dim}C=m-r$. Clearly, we have

$$C\subset C^{\bot}{}^{\bot}.$$

(2)

On the other hand, as above, we get for the dimension of $C^{\bot}{}^{\bot}$:

$$\operatorname{dim}C^{\bot}{}^{\bot}=m-\operatorname{dim}C^{\bot}=m-(m-r)=r.$$

(3)

Thus, by (2) and (3) the two vector spaces $\operatorname{im}N$ and $(\operatorname{ker}N^{\top})^{\bot}$ agree. $\square$

In the theory of linear codes, Proposition 3 is formulated as $C^{\bot}{}^{\bot}=C$: a code $C$ coincides with its double-dual code.

Now we apply Proposition 3 in our case to the symmetric matrix $N=N^{\top}\in\mathbb{F}_{2}^{n\times n}$ and get:

Theorem 4

Let $A\in\mathbb{F}_{2}^{n\times n}$ be the adjacency matrix of a simple graph $G$ and $N:=A+\mathbb{I}$ with rank $r$ . Let $v_{1},\ldots,v_{n-r}$ be a basis of $\operatorname{ker}N$ and $J\in\mathbb{F}_{2}^{(n-r)\times n}$ be the matrix with rows $v_{1}^{\top},\ldots,v_{n-r}^{\top}$ . Then $x\mapsto Jx$ is a separating invariant for the Lights Out game on $G$ : An initial state $i$ can be transformed into a final state $f$ if and only if $Ji=Jf$ . In particular, all lights can be turned off if and only if $Ji=0$ .

Proof

As we have seen above, $i$ can be transformed into $f$ if and only if $i+f\in\operatorname{im}N$. According to Proposition 3 this is equivalent to the fact that $i+f$ is orthogonal to $\operatorname{ker}N$, which in turn means that $J(i+f)=0$. And over $\mathbb{F}_{2}$ this is equivalent to $Ji=Jf$. $\square$

In the case where the final state is given by $f=(0,\dots,0)$, an illustrative survey regarding the question which problems are completely solvable is given by [18].

Remarks.

We conclude this section by a simple consideration how to count the number of equivalence classes of states for a given graph: Since the rank of $J$ is equal to $n-r$ we know that the linear system $J(i+f)=0$ has $r$ parameters which can be freely chosen. Therefore the system has $2^{r}$ solutions. Hence we have $2^{n-r}$ equivalence classes for a given graph.

In [17] the authors gave a result regarding the number of equivalence classes for a generalisation of the Lights Out game in the sense that every vertex can have a state given by a number out of $\{0,\dots,p-1\}$ where $p$ is an arbitrary given positive number.

3 Special states

3.1 Inverting a state

Let $x\in\mathbb{F}_{2}^{n}$ describe a state in the Lights Out game. Then we say that $\bar{x}:=x+(1,1,\ldots,1)^{\top}$ is the inverse state: Lights which are on in $x$ are off in $\bar{x}$ and vice versa. It turns out that in the Lights Out game every state can be inverted:

Theorem 5

Let $G$ be an arbitrary simple graph and $x$ an initial state. Then, $x$ can be transformed into its inverse state $\bar{x}$ .

Theorem 5 is also called Sutner’s theorem (see [24]). For completeness we provide a short proof of it based on the following Lemma which is also interesting in itself:

Lemma 6

Let $N\in\mathbb{F}_{2}^{n\times n}$ be symmetric with all diagonal elements $N_{ii}=1$ . Then, each $x\in\operatorname{ker}N$ is isotropic.

Proof

Let $x\in\operatorname{ker}N$. We have to show that the number of components $x_{i}$ of $x$ which are equal to 1 is even. Let $\Omega=\{j\mid x_{j}=1\}$ and $N^{(i)}$ denote the $i$-th column of $N$. Then

$$0=\langle N^{(i)},x\rangle=\sum_{j\in\Omega}N_{ij}.$$

(4)

Taking the sum over $i\in\Omega$ in (4) we get, by the symmetry of $N$,

$$0=\sum_{i,j\in\Omega}N_{ij}=\sum_{i\in\Omega}N_{ii}+2\sum_{i<j\in\Omega}N_{ij}.$$

(5)

The first term on the right hand side of (5) is $\operatorname{card}(\Omega)\operatorname{mod}2$ because all diagonal elements of $N$ equal 1, the second term is zero in $\mathbb{F}_{2}$. Hence $x$ is isotropic. $\square$

Proof of Theorem  5

Let $A\in\mathbb{F}_{2}^{n\times n}$ be the adjacency matrix of $G$ and $N:=A+\mathbb{I}$. We have to show that $x+\bar{x}=(1,1,\ldots,1)^{\top}\in\operatorname{im}N=(\operatorname{ker}N)^{\bot}$. In fact, according to Lemma 6, all elements $y\in\operatorname{ker}N$ have an even number of ones. Hence, $\langle(1,1,\ldots,1)^{\top},y\rangle=0$. $\square$

Let $\Theta=\{v_{j_{1}},\ldots,v_{j_{k}}\}$ be a set of buttons which, when pressed, invert a state. Such a set will be called inverting set. Hence, if $x\in\mathbb{F}_{2}^{n}$ is a vector with ones at the coordinates $j_{1},\ldots,j_{k}$ and zeros at all other coordinates, then we have $Nx=(1,\ldots,1)^{\top}$. Such a vector will be called inverting.

Remarks.

Theorem 5 is optimal in the sense that for the complete graph $K_{n}$, we have $\operatorname{dim}(\operatorname{im}N)=1$. Indeed, on $K_{n}$ inverting a state is the only possible operation. In [5] the question whether a state can be inverted has been treated in connection with the existence of an odd-parity cover of a graph (see also Theorem 15 below).

3.2 Self-reproducing, self-avoiding and neutral vectors

Is it possible, starting from all lights off, to press a certain set of buttons such that exactly those lights are turned on? Such a self-reproducing set $\Theta=\{v_{j_{1}},\ldots,v_{j_{k}}\}$ corresponds to a self-reproducing vector $x\in\mathbb{F}_{2}^{n}$ having ones exactly at the coordinates $j_{\ell}$, $\ell=1,\ldots,k$, and zeros in all other coordinates, such that $Nx=(A+\mathbb{I})x=x$. Hence we have the following:

Proposition 7

A vector $x\in\mathbb{F}_{2}^{n}$ is self-reproducing on the graph $G$ with adjacency matrix $A$ if and only if $Ax=0$ .

Is it possible, starting from all lights off, to press a certain set of buttons such that exactly all other lights are turned on? Such a self-avoiding set $\Theta=\{v_{j_{1}},\ldots,v_{j_{k}}\}$ corresponds to a self-avoiding vector $x\in\mathbb{F}_{2}^{n}$ having ones exactly at the coordinates $j_{\ell}$, $\ell=1,\ldots,k$, and zeros in all other coordinates, such that $Nx=(A+\mathbb{I})x=\bar{x}=x+(1,\ldots,1)^{\top}$. Hence we have:

Proposition 8

A vector $x\in\mathbb{F}_{2}^{n}$ is self-avoiding on the graph $G$ with adjacency matrix $A$ if and only if $Ax=(1,\ldots,1)^{\top}$ .

Next we are looking for a set of lights $\Theta=\{v_{j_{1}},\ldots,v_{j_{k}}\}$ with the following property: If the lights in $\Theta$ are on and all others are off, and if then all buttons in $\Theta$ are pushed, then again exactly the lights in $\Theta$ are supposed to be on. Such a neutral set $\Theta=\{v_{j_{1}},\ldots,v_{j_{k}}\}$ corresponds to a neutral vector $x\in\mathbb{F}_{2}^{n}$ having ones exactly at the coordinates $j_{\ell}$, $\ell=1,\ldots,k$, and zeros in all other coordinates, such that $x=x+Nx=x+(A+\mathbb{I})x$, i.e. $Nx=0$ or equivalently $Ax=x$.

Proposition 9

A vector $x\in\mathbb{F}_{2}^{n}$ is neutral on the graph $G$ with adjacency matrix $A$ if and only if $Ax=x$ .

In other words, pressing the buttons which correspond to a neutral vector $x$ has no effect since $x=x+0=x+Nx$. From these considerations we conclude immediately:

Proposition 10

• The sum of an even number of self-avoiding vectors is self-reproducing.

• The sum of an arbitrary number of self-reproducing vectors is self-reproducing.

• The sum of an arbitrary number of neutral vectors is neutral.

• The sum of a self-avoiding vector and an arbitrary number of self-reproducing vectors is self-avoiding.

• The sum of a neutral vector and a sum of an even number of inverting vectors is neutral.

4 Variants of the game

4.1 The Second Neighbors Lights Out game

Here, we change the rules of the game a little bit to create a new challenge. Let $G$ be a simple graph with the property that either every vertex has even degree or zero degree, or every vertex has odd degree. In the first case every row of the adjacency matrix $A$ is isotropic. On this graph, we play the Lights Out game as follows: If we push a button $v_{i}$, the corresponding light is inverted and also the second neighbors. However, if a vertex $v_{k}$ is connected with $v_{i}$ by an even number of paths of length 2, then $v_{k}$ keeps its status. We call this game the Second Neighbors Lights Out game. We find:

Theorem 11

Let $A\in\mathbb{F}_{2}^{n\times n}$ be the adjacency matrix of a simple graph $G$ such that

• (a) all vertices have even degree or zero degree, and $r$ is the rank of $\bar{N}:=A^{2}+\mathbb{I}$ , or

• (b) all vertices have odd degree, and $r$ is the rank of $\bar{N}:=A^{2}$ .

Let $v_{1},\ldots,v_{n-r}$ be a basis of $\operatorname{ker}\bar{N}$ and $J\in\mathbb{F}_{2}^{(n-r)\times n}$ be the matrix with rows $v_{1}^{\top},\ldots,v_{n-r}^{\top}$ . Then $x\mapsto Jx$ is a separating invariant for the Second Neighbors Lights Out game on $G$ : An initial state $i$ can be transformed into a final state $f$ if and only if $Ji=Jf$ .

Proof

Observe that the Second Neighbors Lights Out game is equivalent to the original Lights Out game, but on a new simple graph $\bar{G}$ with adjacency matrix $\bar{A}:=A^{2}$ in case (a). It is at this point where we need the fact that all rows of $A$ are isotropic: This implies that all elements on the diagonal of $A^{2}$ are 0, which means that indeed $\bar{G}$ has no loops. Let $\bar{N}=\bar{A}+\mathbb{I}=A^{2}+\mathbb{I}$. Then, the claim follows from Theorem 4 applied to $\bar{G}$. Similarly in case (b) $\bar{A}=A^{2}+\mathbb{I}$ is the adjacency matrix of a simple graph $\bar{G}$. Hence, if we put $\bar{N}=\bar{A}+\mathbb{I}=A^{2}$, then the claim follows from Theorem 4 applied to $\bar{G}$ as above. $\square$

Moreover, we have

Theorem 12

• (a) Every state in the Second Neighbors Lights Out game on $G$ can be inverted.

• (b) If all vertices of $G$ have even degree or zero degree, then the following is true: If an initial state $i$ can be transformed into a final state $f$ in the Second Neighbors Lights Out game on $G$ , then this is also possible for the original Lights Out game on $G$ .

Proof

Part (a) follows from Theorem 5 applied to the graph $\bar{G}$ in the proof of Theorem 11.

To prove part (b) we argue as follows: Let again $A$ be the adjacency matrix of $G$, and $N:=A+\mathbb{I}$. If, as in the proof of Theorem 11, $\bar{A}=A^{2}$ denotes the adjacency matrix of $\bar{G}$, we have $\bar{N}:=\bar{A}+\mathbb{I}=A^{2}+\mathbb{I}=N^{2}$. Recall that the Second Neighbors Lights Out game on $G$ is equivalent to the original Lights Out game on $\bar{G}$. Thus, an initial state $i$ can be transformed into a final state $f$ in the Second Neighbors Lights Out game on $G$ if and only if $i+f$ belongs to the column space of $\bar{N}$. But $\operatorname{im}N^{2}\subset\operatorname{im}N$, and hence $i$ can be transformed into $f$ in the original Lights Out game on $G$ if this is possible on $\bar{G}$. $\square$

4.2 The Neighborhood Lights Out game

Here, we mix the original and the Second Neighbors Lights Out game: Let $G$ be a simple graph such that either every vertex has odd degree, or every vertex has even degree or zero degree. On this graph, we play the game as follows: If we push a button $v_{i}$, the corresponding light is inverted, its direct neighbors and also the second neighbors. As before, if a vertex $v_{k}$ is connected with $v_{i}$ by an even number of paths of lengths 1 or 2, then $v_{k}$ keeps its status. We call this game the Neighborhood Lights Out game. For this game we have:

Theorem 13

Let $A\in\mathbb{F}_{2}^{n\times n}$ be the adjacency matrix of a simple graph $G$ such that

• all vertices have odd degree, and $r$ is the rank of $\bar{N}:=A+A^{2}$ , or

• all vertices have even degree or zero degree, and $r$ is the rank of $\bar{N}:=A+A^{2}+\mathbb{I}$ .

Let $v_{1},\ldots,v_{n-r}$ be a basis of $\operatorname{ker}\bar{N}$ and $J\in\mathbb{F}_{2}^{(n-r)\times n}$ be the matrix with rows $v_{1}^{\top},\ldots,v_{n-r}^{\top}$ . Then $x\mapsto Jx$ is a separating invariant for the Neighborhood Lights Out game on $G$ : An initial state $i$ can be transformed into a final state $f$ if and only if $Ji=Jf$ .

Proof

In case (a) the Neighborhood Lights Out game is equivalent to the original Lights Out game, but on a new simple graph $\bar{G}$ with adjacency matrix $\bar{A}:=A+A^{2}+\mathbb{I}$. Since all vertices of $G$ have odd degree the elements on the diagonal of $\bar{A}$ are 0, and hence $\bar{G}$ has no loops. Let $\bar{N}=\bar{A}+\mathbb{I}=A+A^{2}$. Then, the claim follows from Theorem 4 applied to $\bar{G}$. Similarly in case (b), $\bar{A}=A+A^{2}$ is the adjacency matrix of a simple graph $\bar{G}$. Hence, with $\bar{N}=\bar{A}+\mathbb{I}=A+A^{2}+\mathbb{I}$, the claim follows from Theorem 4 applied to $\bar{G}$. $\square$

Moreover, we have

Theorem 14

• (a) Every state in the Neighborhood Lights Out game on $G$ can be inverted.

• (b) If every vertex of $G$ has odd degree, then the following ist true: If an initial state $i$ can be transformed into a final state $f$ in the Neighborhood Lights Out game on $G$ , then this is also possible for the original Lights Out game on $G$ .

Proof

Part (a) follows from Theorem 5 applied to the graph $\bar{G}$ in the proof of Theorem 13.

For part (b) let again $A$ be the adjacency matrix of $G$ and $N:=A+\mathbb{I}$. Then $\bar{A}=A+A^{2}+\mathbb{I}$ is the adjacency matrix of $\bar{G}$, and $\bar{N}:=\bar{A}+\mathbb{I}=A+A^{2}=N+N^{2}$. The Neighborhood Lights Out game on $G$ is equivalent to the original Lights Out game on $\bar{G}$. Thus, an initial state $i$ can be transformed into a final state $f$ in the Neighborhood Lights Out game on $G$ if and only if $i+f$ belongs to the column space of $\bar{N}$. But $\operatorname{im}(N+N^{2})\subset\operatorname{im}N$, and hence $i$ can be transformed into $f$ in the original Lights Out game on $G$ if this is possible on $\bar{G}$. $\square$

4.3 The Non-reflexive Lights Out game

Suppose, your Lights Out game device does not function properly anymore: You notice that some of the buttons $v_{i}$ (maybe all) invert only their direct neighbors but no longer the light in $v_{i}$. This means that on the diagonal of the original matrix $N=A+\mathbb{I}$, some places turned from 1 to 0. Hence the game is described by a new matrix $\bar{N}=A+\bar{\mathbb{I}}$, where $\bar{\mathbb{I}}\in\mathbb{F}_{2}^{n\times n}$ is a given diagonal matrix.

It is clear that Theorem 4 with $N$ replaced by $\bar{N}$ remains true for this version of the game. However, Theorem 5 turns into the following:

Theorem 15

Let $G$ be a simple graph with adjacency matrix $A$ , and $\bar{N}=A+\bar{\mathbb{I}}$ , where $\bar{\mathbb{I}}\in\mathbb{F}_{2}^{n\times n}$ is diagonal. Then, $\bar{\mathbb{I}}(1,1,\ldots,1)^{\top}$ belongs to the column space of $\bar{N}$ . I.e., if $i,f\in\mathbb{F}_{2}^{n}$ are such that $i+f=\bar{\mathbb{I}}(1,1,\ldots,1)^{\top}$ , then the initial state $i$ can be transformed into the final state $f$ . In particular, if all lights are turned off initially, the state $\bar{\mathbb{I}}(1,1,\ldots,1)^{\top}$ can be reached.

Proof

Let $d=(\bar{N}_{11},\bar{N}_{22},\ldots,\bar{N}_{nn})^{\top}=\bar{\mathbb{I}}(1,\dots,1)^{\top}$ be the vector consisting of the diagonal entries of $\bar{N}$ and $x\in\ker\bar{N}$ be an element of the kernel of $\bar{N}$. Then, we have

$$0=x^{\mathrm{T}}\bar{N}x=\sum_{i,j=1}^{n}\bar{N}_{ij}x_{i}x_{j}=2\sum_{i<j}\bar{N}_{ij}x_{i}x_{j}+\sum_{i=1}^{n}\bar{N}_{ii}x_{i}^{2}=\left<d,x\right> .$$

Thus, $d$ is orthogonal to all elements $x\in\ker\bar{N}$, which is, according to Proposition 3 and in view of the symmetry of the matrix $\bar{N}$, equivalent to $d\in\operatorname{im}(\bar{N})$. $\square$

The same theorem has been obtained independently by Igor Minevich (see [20]).

4.4 The Colored Lights Out game

We consider again a simple graph $G$ with $n$ vertices and with adjacency matrix $A$. Instead of toggling between on and off, we may consider a cycle

$$\text{off}\to\text{color }1\to\text{color }2\to\ldots\to\text{color }k-1\to\text{off}.$$

We encode the colors by their numbers, and off by $0$. Hence a state of colored lights on $G$ corresponds to a vector $(x_{1},\ldots,x_{n})^{\top}\in\mathbb{Z}_{k}^{n}$, where $x_{i}$ indicates the color of the light in vertex $v_{i}$. Pushing a button in vertex $v_{i}$ will increment the color in $v_{i}$ and its neighbors by one, modulo $k$. Suppose we push $a_{i}$-times the button in $v_{i}$, $i=1,\ldots,n$, then an initial state $i\in\mathbb{Z}_{k}^{n}$ of colored lights on the graph will end up in the final state $f=i+Na$, where $a=(a_{1},\dots,a_{n})^{\top}$ and the operations are carried out in $\mathbb{Z}_{k}$, and where $N=A+\mathbb{I}$. This means, we have to solve the linear system

$$Na\equiv c\mod k$$

(6)

where $c=f-i$. We first treat the simpler case where $k$ is squarefree.

Proposition 16

If $k$ is a product of different prime numbers $p_{1},p_{2},\ldots,p_{\ell}$ , then a solution of ( 6 ) can be found as follows:

• 1. Solve ( 6 ) modulo $p_{i}$ for $i=1,2,\ldots,\ell$ by Gauss elimination, i.e., find $b_{i}\in\mathbb{Z}^{n}$ such that $Nb_{i}\equiv c\mod p_{i}$ for $i=1,2,\ldots,\ell$ .

• 2. Let $k_{i}:=k/p_{i}$ and use the extended Euclidean algorithm to find $r_{i},s_{i}\in\mathbb{Z}$ such that $r_{i}p_{i}+s_{i}k_{i}=1$ for each $i$ . Then a solution of ( 6 ) is given by

  $$a=\sum_{i=1}^{\ell}b_{i}s_{i}k_{i}.$$

In particular, a solution of ( 6 ) exists if and only if $\operatorname{det}N\not\equiv 0\mod p_{i}$ for all $i\in\{1,\ldots,\ell\}$ .

Proof

Observe that $s_{i}k_{i}\equiv 1\mod p_{i}$ and $s_{i}k_{i}\equiv 0\mod p_{j}$ for all $j\neq i$. Therefore we have modulo $p_{j}$

$$Na=\sum_{i=1}^{\ell}Nb_{i}s_{i}k_{i}\equiv\sum_{i=1}^{\ell}(c+q_{i}p_{i})s_{i}k_{i}\equiv c$$

for all $j\in\{1,\ldots,\ell\}$, and the claim follows by the Chinese Remainder theorem. $\square$

For the general case of an arbitrary $k\in\mathbb{N}$, we first observe that (6) can equivalently be written as

$$M\bar{a}=c$$

(7)

where $M:=(N\mid k\mathbb{I})$ is the $n\times 2n$-matrix with $N$ in the left block and $k\mathbb{I}$ in the right block, and where $\bar{a}$ is the vector with first $n$ components $a$ and $n$ additional (unknown) integer components below. Then (7), and hence (6), can be solved as follows:

Theorem 17

Let $UMV=B$ be the Smith decomposition of $M$ , i.e., $U\in\mathbb{Z}^{n\times n}$ and $V\in\mathbb{Z}^{2n\times 2n}$ are unimodular matrices, and $B\in\mathbb{Z}^{n\times 2m}$ is the Smith normal form of $M$ . Let $y$ be an integer solution of $By=Uc$ . Then, $\bar{a}=Vy$ solves ( 7 ), and in particular, the first $n$ components of $\bar{a}$ solve ( 6 ). Moreover, ( 7 ) has a solution if and only if $B_{ii}$ divides the $i$ -th component of $Uc$ for all $i$ .

Proof

The proof follows immediately from the properties of the Smith decomposition. $\square$

Remark.

The Colored Lights Out game on a particular class of graphs, so called subdivided caterpillars, has been treated in [21]. In [2] harmonic functions on graphs are used to formulate the Colored Lights out game. In [17] they observed the number of equivalence classes of this problem. Furthermore, in [10] they give a complete list of graphs for which this generalized Lights Out game is solvable in the sense that from any initial state one can reach the state where all lights are turned off.

4.5 The asymmetric Lights Out game

Here we play the game on a directed graph $G$: If a certain button is pressed the corresponding light toggles and also the lights in all of its out-neighbors. The adjacency matrix $A\in\mathbb{F}_{2}^{n\times n}$ of $G$ is in this case in general not symmetric:

$$A_{jk}=\begin{cases}1&\text{if }j\text{ is the foot and }k\text{ is the head of a directed edge,}\\ 0&\text{otherwise.}\end{cases}$$

We put again $N=A+\mathbb{I}$. If $i\in\mathbb{F}_{2}^{n}$ is an initial state and $f\in\mathbb{F}_{2}^{n}$ a final state, then $i$ can be transformed into $f$ if and only if $f=i+N^{\top}a$ for some $a\in\mathbb{F}_{2}^{n}$, i.e., if $i+f$ belongs to the column space of $N^{\top}$. But then, according to Proposition 3, $\operatorname{im}N^{\top}=(\operatorname{ker}N)^{\bot}$, and therefore Theorem 4 remains true for the Lights Out game on the directed graph $G$.

5 The problem of finding minimal solutions

The questions we encountered so far could easily be answered by standard tools of linear algebra: E.g. to determine whether an initial state $i$ can be transformed into a final state $f$ for the Lights Out game is answered by the separating invariant from Theorem 4: This requires only to compute a matrix multiplication $J(i+f)$ and to check if the result is the zero vector. Similarly, to actually compute a solution for this problem, we just apply Gauss elimination to solve the linear system $Na=i+f$ for $a$ over $\mathbb{F}_{2}$. However, it turns out that finding minimal solutions is computationally much more difficult. We recall the following concepts from computational complexity theory:

• A decision problem $H$ is NP-complete if $H$ is in NP and if every problem in NP is reducible to $H$ in polynomial time.

• A decision problem $H$ is called NP-hard if there is a polynomial-time reduction from an NP-complete problem $G$ to $H$.

We have:

Proposition 18

The problem of finding a self-reproducing vector $x\neq 0$ in Proposition  7 of minimal Hamming weight is NP-hard.

Proof

Recall that a self-reproducing vector $x$ is characterized by the equation $Ax=0$, where $A$ is the adjacency matrix of the graph $G$. Such a vector $x$ corresponds to a vertex set $V^{\prime}=\{v_{j_{1}},\ldots,v_{j_{\ell}}\}\subset V$ with $v_{j_{k}}\in V^{\prime}\iff x_{j_{k}}=1$ which has the property that every vertex $v\in V$ has an even number of vertices of $V^{\prime}$ (or none of them) among its neighbors. This translates into the following decision problem:

Even Vertex Set

Instance::

A graph $G=(V,E)$ and an integer $w> 0$.

Question::

Is there a nonempty subset $V^{\prime}\subset V$ of at most $w$ vertices, such that every vertex $v\in V$ has an even number of vertices of $V^{\prime}$ among its neighbors?

It has been shown by Vardy [26] that the Even Vertex Set problem is NP-complete. To find a vector $x$ with $Ax=0$ and minimal Hamming weight is therefore NP-hard. $\square$

As a second example, we take a closer look at the problem of finding a minimal solution to the Non-reflexive Lights Out game with $N=A$ (see Sect. 4.3), i.e., a solution with a minimum buttons pressed. Suppose our graph has $n$ vertices. As we have seen above, to transform an initial state $i\in\mathbb{F}_{2}^{n}$ into a final state $f\in\mathbb{F}_{2}^{n}$ we need to solve the linear system $Aa=i+f$ over $\mathbb{F}_{2}$ for $a\in\mathbb{F}_{2}^{n}$. If the matrix rank of $A$ over $\mathbb{F}_{2}$ is $n$, the solution $a$ is unique. However, in general, $r:=\operatorname{rank}A<n$ and the set of solutions (if non-empty) forms an affine space $\mathcal{A}$ of dimension $n-r> 0$ in $\mathbb{F}_{2}^{n}$. To find a solution with a minimum number of buttons to push means to find a vector in $\mathcal{A}$ with minimum Hamming weight. We will show that this problem is NP-hard. The reasoning is based upon the result of Berlekamp, McEliece and van Tilborg who showed in [4] that the nearest codeword problem is NP-complete:

Nearest Codeword Problem

Instance::

A binary $m\times n$ matrix $A$, a binary vector $y\in\mathbb{F}_{2}^{m}$, and an integer $w> 0$.

Question::

Is there a vector $x\in\mathbb{F}_{2}^{n}$ of Hamming weight $\leq w$ such that $Ax=y$?

We first show that the special case of a square matrix $A$ is not easier than the general problem:

Balanced Nearest Codeword Problem

Instance::

A binary $n\times n$ matrix $A$, a binary vector $y\in\mathbb{F}_{2}^{n}$, and an integer $w> 0$.

Question::

Is there a vector $x\in\mathbb{F}_{2}^{n}$ of Hamming weight $\leq w$ such that $Ax=y$?

Lemma 19

The Balanced Nearest Codeword Problem is NP-complete.

Proof

It is easy to see that the Balanced Nearest Codeword Problem is in NP. We will now show that the General Nearest Codeword Problem can be reduced to the Balanced Nearest Codeword Problem: Let $A\in\mathbb{F}_{2}^{m\times n}$ and $y\in\mathbb{F}_{2}^{m}$. Consider first the case $n<m$ and let

$$\bar{A}:=(A\mid 0)\in\mathbb{F}_{2}^{m\times m},\quad\bar{y}:=y.$$

If $x$ is a solution of $Ax=y$ with Hamming weight $w$, then

$$\bar{x}=\left(\begin{array}[]{c}x\\ \hline 0\end{array}\right)\in\mathbb{F}_{2}^{m}$$

is a solution of $\bar{A}\bar{x}=\bar{y}$ with Hamming weight $w$. Vice versa, if $\bar{x}\in\mathbb{F}_{2}^{m}$ is a solution of $\bar{A}\bar{x}=\bar{y}$, then

$$x=\begin{pmatrix}\bar{x}_{1}\\ \vdots\\ \bar{x}_{n}\end{pmatrix}\in\mathbb{F}_{2}^{n}$$

is a solution of $Ax=y$ with Hamming weight $\leq w$.

If $n> m$ we define similarly

$$\bar{A}:=\left(\begin{array}[]{c}A\\ \hline 0\end{array}\right)\in\mathbb{F}_{2}^{n\times n},\quad\bar{y}:=\left(\begin{array}[]{c}y\\ \hline 0\end{array}\right)\in\mathbb{F}_{2}^{n}.$$

If $x$ is a solution of $Ax=y$ with Hamming weight $w$, then $\bar{x}=x$ is a solution of $\bar{A}\bar{x}=\bar{y}$ with Hamming weight $w$ and vice versa. $\square$

Next, we show that the symmetric case is not easier than the general problem:

Symmetric Nearest Codeword Problem

Instance::

A symmetric binary $n\times n$ matrix $A$, a binary vector $y\in\mathbb{F}_{2}^{n}$, and an integer $w> 0$.

Question::

Is there a vector $x\in\mathbb{F}_{2}^{n}$ of Hamming weight $\leq w$ such that $Ax=y$?

Lemma 20

The Symmetric Nearest Codeword Problem is NP-complete.

Proof

Obviously the Symmetric Nearest Codeword Problem is in NP, and we have to show that the Balanced Nearest Codeword Problem can be reduced to the Symmetric Nearest Codeword Problem. To this end, let $A\in\mathbb{F}_{2}^{n\times n}$ and $y\in\mathbb{F}_{2}^{n}$, and consider

$$\bar{A}=\left(\begin{array}[]{c|c}0&A^{\top}\\ \hline A&0\end{array}\right)=\bar{A}^{\top}\in\mathbb{F}_{2}^{2n\times 2n},\quad\bar{y}=\left(\begin{array}[]{c}0\\ \hline y\end{array}\right)\in\mathbb{F}_{2}^{2n}.$$

If $x$ is a solution of $Ax=y$ with Hamming weight $w$, then

$$\bar{x}=\left(\begin{array}[]{c}x\\ \hline 0\end{array}\right)\in\mathbb{F}_{2}^{2n}$$

is a solution of $\bar{A}\bar{x}=\bar{y}$ with the same Hamming weight $w$. Vice versa, if $\bar{x}\in\mathbb{F}_{2}^{2n}$ is a solution of $\bar{A}\bar{x}=\bar{y}$ with Hamming weight $w$, then

$$x=\begin{pmatrix}\bar{x}_{1}\\ \vdots\\ \bar{x}_{n}\end{pmatrix}\in\mathbb{F}_{2}^{n}$$

is a solution of $Ax=y$ with Hamming weight $\leq w$. $\square$

The corresponding computational problem for the Non-reflexive Lights Out game is the following:

Non-reflexive Lights Out game Problem

Instance::

A simple graph $G$ with $n$ vertices, an initial state $i\in\mathbb{F}_{2}^{n}$, a final state $f\in\mathbb{F}_{2}^{n}$, and an integer $w> 0$.

Question::

Is there a solution $a$ in $\mathbb{F}_{2}^{n}$ of Hamming weight $\leq w$ such that $i+Ax=f$?

From Lemma 20 it follows now immediately:

Theorem 21

The Non-reflexive Lights Out game Problem is NP-complete. Hence, to find a solution of the Non-reflexive Lights Out game Problem with a minimal number of pressed buttons is NP-hard.

If the rank of $A$ is $r<n$, this indicates that one has to go over all of the $2^{n-r}$ points in the affine space defined by $Ax=i+f$ to determine a minimal solution of the Non-reflexive Lights Out game.

A related question has been treated in [11]. There an initial state of the Lights Out game is given, and the problem is to determine the maximum number of vertices with light off. This problem also turned out to be NP-hard.

Another problem which was shown in [6] and [9] (and the references therein) to be NP-hard is to determine the minimal number of steps to turn off all lights when you start with all lights on.

Other similar results regarding the complexity of coding problems were done by Barg in [23, p. 733ff]. For instance he showed that the following problem is NP-complete:

Weight of error

Instance::

A matrix $H$, a vector $s$, and a nonnegative integer $w$.

Question::

Is there a vector $y$ of weight $\text{wt}(y)\leq w$ such that $Hy^{T}=s^{T}$?

6 Circuit diagrams of the Lights Out game

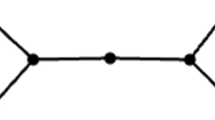
It is far from obvious how a classical electric circuit with voltage source, lamps and switches can be built which realizes the Lights Out game. We propose such a circuit diagram for the cycle graph $\mathcal{C}_{n}$ with $n\geq 3$ vertices. To this end, consider the building block $\mathcal{B}_{k}$ in Fig. 1.

Fig. 1

Quadrupole changeover switch for the Lights Out game on a cycle graph

Then, combine blocks $\mathcal{B}_{1},\ldots,\mathcal{B}_{n}$ such that $A_{k}$ is connected to $a_{k+1}$, $B_{k}$ to $b_{k+1}$, $C_{k}$ to $c_{k+1}$, and $D_{k}$ to $d_{k+1}$, for $k=1,\ldots,n-1$, and close the cycle by connecting $A_{n}$ and $a_{1}$, $B_{n}$ and $b_{1}$, $C_{n}$ and $c_{1}$, and $D_{n}$ and $d_{1}$. Then, the quadrupole changeover switch in block $\mathcal{B}_{k}$ will invert the lamps $\ell_{k},\ell_{k+1}$ and $\ell_{k+2}$ cyclically. An initial state can be arranged by changing, if necessary, the contacts of the switch next to each lamp.

Using a circuit diagram with boolean gates gives more flexibility. In this case, the building blocks are T flip-flops (Fig. 2).

Fig. 2

T flip-flop for the Lights Out game on general simple graphs

Whenever a clock pulse at $C$ arrives, the output state $Q,\bar{Q}=\neg Q$ toggles. To build the Lights Out game, we are going to use only the $Q$ output which will represent the lamp: $Q=1$ corresponds to light on, $Q=0$ corresponds to light off. To implement the Lights Out game on an arbitrary graph, we represent every vertex $v_{i}$ by the circuit element in Fig. 3.

Fig. 3

Circuit element in vertex $v_{i}$

The output of the or-gate is connected to the clock input of the T flip-flop T${}_{i}$. The button $B_{i}$ of vertex $v_{i}$ is then connected to

• an input pin of the corresponding or-gate (see Fig. 3), and

• an input pin of the or-gate of every neighboring vertex of $v_{i}$.

In this way, pushing the button $B_{i}$ toggles the outputs $Q_{i}$ and the outputs of all neighboring vertices.

7 Lights Out on graphs with symmetries

Let $G=(V,E)$ be a graph with vertex set $V=\{v_{1},\ldots,v_{n}\}$ and edge set $E=\{e_{1},\ldots,e_{k}\}$, where each edge $e_{\ell}$ is the set $\{v_{i},v_{j}\}$ of the two vertices which are incident with it. An automorphism of $G$ is a bijective map

$$\phi:V\to V\text{ such that }\{\phi(v_{i}),\phi(v_{j})\}\in E\iff\{v_{i},v_{j}\}\in E.$$

The bijection $\phi:(v_{1},\ldots,v_{n})\mapsto(v_{\sigma(1)},\ldots,v_{\sigma(n)})$ corresponds to a permutation $\sigma$ of the index set $\{i,\ldots,n\}$ which in turn can be expressed by a permutation matrix $P\in\mathbb{F}_{2}^{n\times n}:(1,\ldots,n)^{\top}\mapsto P(1,\ldots,n)^{\top}=(\sigma(1),\ldots,\sigma(n))^{\top}$ with the property that $P^{\top}AP=A$.

Prominent examples of graphs with a nontrivial automorphism group are Cayley graphs: Let $\mathcal{G}$ be a finite group and $S\subset\mathcal{G}$ be a symmetric subset, i.e., with each $s\in S$, also the inverse $s^{-1}\in S$. The Cayley graph $\Gamma(\mathcal{G},S)$ has as vertices the elements $g\in\mathcal{G}$ and the edges are $\{\{g,gs\}:g\in\mathcal{G},s\in S\}$. If we assume in addition that $S$ does not contain the unit element of $\mathcal{G}$, then the resulting graph has no loops, and is therefore suitable for the Lights Out game. Observe that $\mathcal{G}$ is a subgroup of the automorphism group of the Cayley graph $\Gamma(\mathcal{G},S)$. In fact, each $h\in\mathcal{G}$ induces an automorphism of $\Gamma(\mathcal{G},S)$ by $\mathcal{G}\to\mathcal{G},g\mapsto hg$. Indeed, the edge $\{g,gs\}$ is mapped to the edge $\{(hg),(hg)s\}$.

The symmetries of a graph allow mapping a special state of the Lights Out game from Sect. 3 into a similar one by applying an automorphism of the graph:

Proposition 22

Let $\phi$ be an automorphism of a graph. Then:

• (a) If $J$ is an inverting set, then $\phi(J)$ is an inverting set.

• (b) If $J$ is a self-avoiding set, then $\phi(J)$ is a self-avoiding set.

• (c) If $J$ is a self-reproducing set, then $\phi(J)$ is a self-reproducing set.

• (d) If $J$ is a neutral set, then $\phi(J)$ is a neutral set.

Proof

(a) Let $x\in\mathbb{F}_{2}^{n}$ be the vector with ones at the coordinates which correspond to elements of $J$, and $y=P^{\top}x$ the vector with ones at the coordinates which correspond to elements of $\phi(J)$. The set $J$ is inverting if and only if $Nx=(1,\ldots,1)^{\top}$. Letting $x=PP^{\top}x$ gives, after multiplying the previous equation from the left by $P^{\top}$, the identity

$$(1,\ldots,1)^{\top}=P^{\top}(1,\ldots,1)^{\top}=P^{\top}Nx=P^{\top}(A+\mathbb{I})PP^{\top}x=P^{\top}(A+\mathbb{I})Py=(A+\mathbb{I})y=Ny$$

and hence $\phi(J)$ is inverting.

The proofs of (b), (c) and (d) are analogous. $\square$