Quantifying state transfer strength on graphs with involution

Abstract

This paper discusses continuous-time quantum walks and asymptotic state transfer in graphs with an involution. By providing quantitative bounds on the components of the eigenvectors of the Hamiltonian, it provides an approach to achieving high-fidelity state transfer by strategically selecting energy potentials based on the maximum degrees of the graphs. The study also involves an analysis of the time necessary for quantum transfer to occur.

1 Introduction

We study quantum transport phenomena in a network of spin-1/2 particles with local XX coupling and transverse magnetic fields in the Z direction applied to the nodes. This protocol of using a spin chain for quantum information communication was initially proposed by Bose [1] and later extended to spin networks by Christandl et al. [2]. To describe this spin network using a graph, we define a connected and finite graph with vertices representing qubits and edges associated with local interactions. The network is given as a simple and connected graph G(V, E) with a vertex set V and an edge set E. The XX-Hamiltonian is given by

$$\begin{aligned} \tilde{H} = \sum _{v\in V}Q_v Z_v + \frac{1}{2}\sum _{(uv)\in E} w_{uv} (X_u X_v + Y_u Y_v ) \end{aligned}$$

where X, Y, Z are the standard Pauli matrices, $w: E \rightarrow \mathbb {R}$ are coupling strengths, and $Q: V \rightarrow \mathbb {R}$ describes the strength of the transverse magnetic field (see [3,4,5,6]) applied at each node. This transmission protocol was studied in [4,5,6] where numerical simulations showed strong transfer in the presence of large magnetic fields at the endpoints of a spin chain. Meanwhile, [7] provided rigorous mathematical proof of exactly in which general spin network does state transfer fidelity converge to 1 as the strength of the magnetic field applied at the source and target node goes to infinity. However, the relationship between the strength of the magnetic field and the strength of the state transfer was not studied in [7]. Recently, van Bommel and Kirkland [8] were the first to mathematically prove a quantitative relationship. They achieved this only in the case of a spin chain with uniform couplings, relying on explicit formulas for the eigenstates of the Hamiltonian.

Our main contribution is a generalization of the estimates of van Bommel and Kirkland [8] to arbitrary spin networks with mirror symmetry. These includes spin chains with non-uniform coupling as long as the coupling strength are symmetric around the middle of the chain, but our method can handle spin networks that aren’t one-dimensional as long as they admit an order-2 symmetry.

1.1 Main result

It is well known (see, e.g., [9]) that node-to-node quantum transportation can be analyzed by restricting the system to its single-excitation subspace, where the solution of the Schrödinger equation becomes what is known as the continuous-time quantum walk:

$$\begin{aligned} \psi (t)= e^{i t H} \psi (0). \end{aligned}$$

(1.1)

Here, the Hamiltonian $H = A_\mathrm{{G}} + D_Q$ where $A_\mathrm{{G}}$ is the adjacency matrix of the graph G, while $D_\mathrm{{Q}}$ is a diagonal matrix containing the values of the function Q. The function $\psi (t): V \rightarrow \mathbb {C}$ described the state of the system at time t. The probability of the quantum walk getting from node u to node v at time t is given by $p(t) = |\langle u|e^{itH}|v\rangle |^2$.

In the ideal scenario, if $p(t)=1$ at some time t, then we say there is a perfect state transfer between vertices u and v. However, achieving perfect state transfer demands strict conditions. Notably, Godsil demonstrated that ratio condition is necessary for the existence of such vertex pairs [10].

Relaxations have been introduced due to the rarity of perfect state transfer. It has been observed before that large, equal, magnetic fields applied to u and v can lead to transfer strength close to 1 [11]. In physics, this phenomenon is referred to as quantum tunneling. Let us define the transfer fidelity of the network from u to v by

$$\begin{aligned} F(Q) = F(G,u,v,Q) = \sup _{t\ge 0} p(t). \end{aligned}$$

(1.2)

In the rest of the paper, we assume that $Q(u)=Q(v)$ and $Q(x) = 0$ for all nodes $x \ne u,v$. By a slight abuse of notation, we will refer to the value $Q(u)=Q(v)$ simply as Q.

Lin et al. Yau [7] showed that $\lim _{Q \rightarrow \infty } F(G,u,v,Q) = 1$ provided that the graph exhibits certain local symmetries around u and v. While they provide a complete characterization of when $F(Q) \rightarrow 1$, their result is not quantitative. The first—and so far only—rigorous quantitative result on F(Q) was published recently by van Bommel and Kirkland [8] who quantified the convergence in (1.2) for the case of the two endpoints of a path graph.

Theorem 1.1

[8] Let G be the path graph on at least 3 nodes and u, v be its two endpoints. Then for $Q \ge \sqrt{2}$

$$\begin{aligned} F(Q) > \left( \frac{Q^2-2}{Q^2}\right) ^2 \approx 1 - \frac{4}{Q^2} \end{aligned}$$

(1.3)

Furthermore, this fidelity is reached within time $O(Q^{n-2})$

These bounds are derived from a careful asymptotic analysis of the difference between the two largest eigenvalues $\lambda _1-\lambda _2$ and their corresponding eigenvectors.

An important feature of (1.3) is that it doesn’t depend on the length of the path, n. In this paper, we prove, in the same spirit, a general lower bound that holds for any graph with an involution, along with an assessment of the time required for quantum transfer to occur.

Theorem 1.2

Let G be a graph with an involution $\tau : V(G) \rightarrow V(G)$ and let $u = \tau (v) \in V(G)$ and maximum degree m. Then for $Q \ge m$

$$\begin{aligned} F(Q) > 1- \frac{16 \sqrt{m+1}}{\sqrt{Q}} \end{aligned}$$

and this fidelity is achieved within time $O(Q^{d(u,v)-1})$ where $d(v _i,v_j)$ denotes the distance between two vertices in the graph.

It turns out that to achieve the quantum state transfer from a vertex to its image with fidelity $1-\epsilon$, it is sufficient to choose the energy potential based on the maximum degree of the graph, and the potential is of order $O(\epsilon ^{-2})$. This is in contrast to the energy level of $O(\epsilon ^{-0.5})$ required on a path, as derived from the lower bound on fidelity given in [8]. While the order of Q is higher, this approach extends the application to any graph that has an involution. This result is valuable in determining the minimal energy consumption necessary to achieve a specific probability level. Remarkably, these bounds depend on the maximum degree of the graph and are independent of its size.

Remark 1.3

Unfortunately, the transfer time required to reach high fidelity with this protocol is exponential in the distance of the two nodes. There are other protocols which achieve faster transfer, see [12, 13] for examples of “ballistic” transfer. This is achieved at the cost of having to tune certain coupling strength to very specific, very small (eg $N^{-1/3}$) values depending on the size of the network, leading to poor error tolerance. In contrast, the situation studied in this paper uses uniform couplings and a magnetic field of bounded strength, which yields a much more robust protocol.

We are not aware of any setup that uses quasi-uniform couplings and bounded magnetic fields and guarantees high-fidelity state transfer in sub-exponential time.

The paper is structured as follows: in Sect. 2 we introduce the basic setup and all relevant notation for graphs with an involution and the corresponding Hamiltonians. In Sect. 3 we prove the main result modulo estimates of the eigenvalues and eigenvectors. We provide these in Sects. 3.1 and 3.2, respectively. Finally, in Sect. 3.3 we analyze the time required to achieve strong state transfer.

2 Preliminaries

2.1 Spectral decomposition

In the current setup, the Hamiltonian H governing the continuous-time quantum walk is the sum of the adjacency matrix of the graph and a diagonal matrix. This concept of using an adjacency matrix as the Hamiltonian was initially introduced by Christandl et al. [2]. We say two vertices are adjacent, denoted by $v_i\sim v_j$, if the edge $v_iv_j$ is in the edge set E(G). In the matrix presented below, $Q: V \rightarrow \mathbb {R}$ represents the energy potential at the vertices and the off-diagonal entry $H_{ij}=1$ if there is an edge between $v_i$ and $v_j$:

$$\begin{aligned} H=\begin{bmatrix} Q(v_1) &{} \mathbb {1}(v_1\sim v_2) &{}... &{} \mathbb {1}(v_1\sim v_n)\\ \mathbb {1}(v_1\sim v_2) &{} Q(v_2) &{}... &{} \mathbb {1}(v_2\sim v_n)\\ \vdots \\ \mathbb {1}(v_1\sim v_n)&{}...&{}...&{} Q(v_n) \end{bmatrix}. \end{aligned}$$

Since H is a real symmetric $n\times n$ matrix, it has n real eigenvalues, $\lambda _1\ge \lambda _2\ge ...\ge \lambda _n$ and their corresponding eigenvectors $\varphi _1, \varphi _2,...,\varphi _n$ which together form an orthonormal basis. This spectral decomposition of H helps us to compute the solution to the Schrödinger equation. Given a vector representing the initial state $\psi (0)$, it can be written as a linear combination of the orthonormal basis $\psi (0)=\sum _{j=1}^n c_j\varphi _j$. In the context of this problem, $\psi (0)$ is usually the characteristic vector of the starting vertex u, meaning the system starts at vertex u with probability 1. It immediately follows that

$$\begin{aligned} \psi (t)=\sum _{j=1}^n c_j e^{it\lambda _j}\varphi _j. \end{aligned}$$

(2.1)

If our objective is to achieve strong state transfer between vertices u and v, we primarily aim to find a system such that $\psi (t)\cdot e_v$ has a significantly large squared norm

$$\begin{aligned} p(t)=|\sum _{j=1}^n\varphi _j(u) \varphi _j(v) e^{it\lambda _j}|^2 .\end{aligned}$$

(2.2)

Here, we consider the eigenvector $\varphi _j$ as a function $\varphi _j: V\rightarrow \mathbb {R}$ that returns the corresponding entry of an vertex. Therefore, the main focus of our study revolves around investigating how the structure of the graph and the energy potential assigned to its vertices influence the eigenvalues and eigenvectors at the endpoints. For instance, if the energy potential Q on vertices u and v is relatively large compared to the potential on other vertices, and $Q\gg \max _{x\in V}\deg (x)$, then there are two eigenvalues that are significantly larger than the rest $\lambda _1\ge \lambda _2 \gg \lambda _3\ge ...\ge \lambda _n$.

2.2 Graphs with involution

Definition 2.1

Vertices u and w are strongly cospectral if for any eigenvector $\varphi$ of H, $\varphi (u)=\pm \varphi (w)$. They are cospectral if this holds for at least a given orthonormal basis of eigenvectors $\varphi _1,\dots , \varphi _n$.

In many quantum walk studies, a common aspect explored is the presence of strong cospectrality [14] or, to some extent, cospectrality [7], since strong cospectrality is a necessary condition for two vertices to have perfect state transfer. Consequently, if the graph structure already exhibits cospectrality, it becomes easier for us to show strong state transfer. A notable example of such a graph is one with involution.

Definition 2.2

G is a graph with involution if there is a bijection from the set of vertices to itself $\sigma : V (G)\rightarrow V (G)$ which satisfies the following conditions,

• $\sigma \circ \sigma (u)=u$

• if $u\sim v$ then $\sigma (u) \sim \sigma (v)$

• $\sigma$ preserves the potential on V, that is $Q(v)=Q(\sigma (v))$

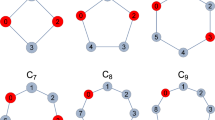
For simplicity, we denote $\sigma (v)$ by $v'$ in the rest of this paper. Noticeably, many families of graphs possess involution functions, including paths, cycles, hypercubes, complete graphs, and so on (Fig. 1).

Fig. 1

An example graph with involution

Let $S=\{ v\in V| v=v'\}$ be the set of fixed vertices. Select a vertex from each pair of $\{v,v'\}$ that are not fixed by $\sigma$, then we get a partition of the vertex set $V=N \cup \sigma N \cup S$. Denote the sizes of the subsets by $s=|S|$ and $k=|N|$. This divides the Hamiltonian into a block matrix

$$\begin{aligned} H= \begin{bmatrix} H' &{} A_\sigma &{} A_S\\ A_\sigma &{} H' &{} A_S\\ A_S^T &{} A_S^T &{} H_S \end{bmatrix}. \end{aligned}$$

(2.3)

The $k\times k$ matrix $H'$ and the $s\times s$ matrix $H_S$ are the Hamiltonians of the subgraphs induced by N and S, respectively. The $k\times k$ matrix $A_\sigma$ contains all the edges between N and $\sigma N$. The $k\times s$ matrix $A_S$ contains all the edges between N and S.

Lemma 2.3

[15] Let graph G be a graph with involution $\sigma$, and Q be its potential function. The Hamiltonian of G has eigenvalues $\lambda _1\ge \lambda _2\ge ...\ge \lambda _n$ and corresponding eigenvectors $\varphi _1$, $\varphi _2$... $\varphi _n$. Then every $\lambda _j$ is either the eigenvalue of

$$\begin{aligned} H^+=\begin{bmatrix} H' + A_\sigma &{} A_S\\ 2A_S^T &{} H_S \end{bmatrix} \end{aligned}$$

(2.4)

or the eigenvalue of $H^-=H'-A_\sigma$.

It can be easily verified that given an eigenvector of the reduced matrix $H^+ a=\lambda _j a$, $\varphi _j$ is in the form $\begin{bmatrix} a&a&b \end{bmatrix}^T$. On the other hand, if $H^-c=\lambda _jc$, then $\lambda _j$ has corresponding eigenvector $\begin{bmatrix} c&-c&0 \end{bmatrix}^T$. Here a and c represents vectors in $\mathbb {R}^k$, and b and 0 are vectors in $\mathbb {R}^s$.

Lemma 2.4

Denote the set of eigenvalues of $H^+$ by $\pi ^+$ and the set of eigenvalues of $H^-$ by $\pi ^-$, then $\max _{\lambda _i}\pi ^+>\max _{\lambda _i}\pi ^-$. In the double-well case, that is when $Q(v)=Q(v')\gg Q(v_i)$ for the rest of vertices, $\lambda _1$ and $\lambda _2$ are the largest numbers inside $\pi ^+$ and $\pi ^-$, respectively, as long as Q(v) is significantly greater than the maximum degree of the graph.

Proof

Since the graph is connected, H is an irreducible nonnegative symmetric matrix. By the Perron–Frobenius theorem, $\lambda _1$ is strictly greater than $\lambda _2$, and the components of its corresponding eigenvector are all positive. This implies $\varphi _1$ is symmetric and $\lambda _1\in \pi ^+$.

Gershgorin’s Circle Theorem tells us that every eigenvalue is bounded by a disk centered at some $Q(v_i)$ with radius $\deg (v_i)$. When Q(v) is large enough such that there is no intersection between $[Q(v)-m, Q(v)+m]$ and $[Q(v_i)-m, Q(v_i)+m]$, both $H^+$ and $H^-$ have a large eigenvalue close to Q(v). Therefore, the second largest eigenvalue $\lambda _2$ is in $\pi ^-$. $\square$

By applying these lemmas to the spectral decomposition (2.2), we conclude that if $u=\sigma (v)$, then

$$\begin{aligned} \sum _{\lambda _j}\varphi _j(u) \varphi _j(v) e^{it\lambda _j}=\sum _{\lambda _j\in \pi ^+} \varphi _j(u)^2 e^{it\lambda _j}- \sum _{\lambda _j\in \pi ^-} \varphi _j(u)^2 e^{it\lambda _j}. \end{aligned}$$

(2.5)

Therefore, when the two largest eigenvalues are differed by $\frac{\pi +2k\pi }{t}$, the sum of the leading terms reaches its maximum $\varphi _1(u)^2+\varphi _2(u)^2$. In this scenario, we can ensure the probability is close to 1 by showing both $\varphi _1(u)^2$ and $\varphi _2(u)^2$ are close to $\frac{1}{2}$.

3 Achieving state transfer with high probability

As before, we assume that only the endpoints v and $v'$ possess a large potential $Q(v)=Q(v')=Q$, while the remaining vertices have zero potential $Q(v_i)=0$ going forward. Theorem 1.2 is a direct corollary of the following statement.

Theorem 3.1

Let G be a graph with involution and maximum degree m. For every small real number $\epsilon >0$, if the potential Q on v and $v'$ satisfies

$$\begin{aligned} Q\ge \frac{256\cdot (m+1)}{\epsilon ^2} \end{aligned}$$

(3.1)

then there exists time $t<\frac{\pi }{2}(Q+m)^{d(v,v')-1}$ such that the probability of state transfer from v to $v'$ is no less than $1-\epsilon$.

Proof

When $t=\frac{\pi }{\lambda _1-\lambda _2}$, then $|\varphi _1(v)^2 e^{it\lambda _1}+\varphi _2(v)^2 e^{it\lambda _2}|=\varphi _1(v)^2+\varphi _2(v)^2$. The bound on time t is further discussed in Sect. 3.3. In Theorem 3.4, we will prove that both $\varphi _1(v)$ and $\varphi _2(v)$ have lower bound $\sqrt{\frac{1}{2}-\frac{m}{2Q^2}}-\sqrt{\frac{m+1}{Q-m-1}}$. Certainly, Q should be large enough such that the bound is greater than $\frac{1}{2}$. Thus, the probability has a lower bound depending on Q and the maximum degree m,

$$\begin{aligned} p(t)&=|\varphi _1(v)^2+\varphi _2(v)^2+\sum _{j=3}\varphi _j(v) \varphi _j(v') e^{it\lambda _j}|^2\\&\quad \ge (\varphi _1(v)^2+\varphi _2(v)^2-(1-\varphi _1(v)^2-\varphi _2(v)^2))^2\\&\quad \ge (2\varphi _1(v)^2+2\varphi _2(v)^2-1)^2, \end{aligned}$$

and so

$$\begin{aligned} p(t)\ge \left( 4\cdot \left( \sqrt{\frac{1}{2}-\frac{m}{2Q^2}}-\sqrt{\frac{m+1}{Q-m-1}}\right) ^2-1\right) ^2. \end{aligned}$$

(3.2)

To guarantee the probability exceeds $1-\epsilon$, a simple computation shows it is sufficient for Q to satisfy

$$\begin{aligned} Q\ge \frac{(m+1)(c+1)}{c},\quad \text {where } c=\frac{1}{2}\cdot \left( \frac{1}{2}-\frac{1+\sqrt{1-\epsilon }}{4}\right) ^2 \end{aligned}$$

(3.3)

$\square$

3.1 Lower bounds on $\lambda _1$ and $\lambda _2$

The purpose of this section is to derive new lower bounds on the two largest eigenvalues that improve upon the ones given by the Gershgorin Circle Theorem.

Theorem 3.2

Label the vertices in N as $v_1$, $v_2$,...,$v_{k}$ and S’s vertices as $v_{k+1}$,...,$v_{k+s}$. Denote the degree of a vertex in $N\cup S$ by $\text {deg}_{N\cup S}(v_i)$. Let y be a vector in $\mathbb {R}^{k+s}$ and $y_i=Q^{-\text {min}\{\text {dist}(v_1,v_i),\text {dist}(v_1,v_i')\}}$. Then

$$\begin{aligned} \lambda _1 \ge Q + Q^{-1} \cdot \frac{1+\sum _i (\text {deg}_{N\cup S}(v_i)-1)y_i^2}{\sum _i y_i^2} .\end{aligned}$$

(3.4)

Proof

According to Lemma 2.3, $\lambda _1$ is also the largest eigenvalue of $H^+$. The vector y is a good approximation of the eigenvector because its entries decrease as the vertex moves further away from $v_1$. Therefore, by calculating the Rayleigh quotient on $H^+$ and y, one can expect to obtain a reasonably close lower bound on $\lambda _1$. Without loss of generality, we make $H^+$ symmetric by conjugation

$$\begin{aligned} H^+=\begin{bmatrix} H' + A_\sigma &{} \sqrt{2}A_S\\ \sqrt{2}A_S^T &{} H_S \end{bmatrix} .\end{aligned}$$

(3.5)

Notice that summing the nonzero entries $H^+_{ij}y_j$ in the numerator of the quotient is equivalent to counting the edges connected to vertex $v_i$. Therefore, the question becomes finding the number of vertices adjacent to $v_i$ and is closer, further away, or of equal distance to $v_1$.

When $i=1$,

$$\begin{aligned} y_1\sum _{i,j} H_{ij}^{+} y_j \ge Q + Q^{-1}\text {deg} (v_1). \end{aligned}$$

(3.6)

This is because any vertex $v_j$ adjacent to $v_1$ has $y_j=Q^{-1}$; counting all the nonzero coefficients in front of $y_j$ gives the degree of $v_1$.

When $i=2,3,..., k+s$,

$$\begin{aligned} y_i\sum _{i,j} H_{ij}^{+} y_j \ge (Q+(\text {deg}_{N\cup S}(v_i)-1)Q^{-1})y_i^2. \end{aligned}$$

(3.7)

The coefficient in front of $y_iy_j$ is nonzero if and only if $y_j=y_i$, $y_j=Qy_i$, or $y_j=Q^{-1}y_i$. Moreover, since the graph is connected, for every vertex $v_i$, one can find a vertex adjacent to it and is in one of the shortest paths from $v_1$ to $v_i$. Hence, there must exist $y_j=Qy_i$.

Every term contains $Qy_i^2$ and $(\text {deg}_{N\cup S}(v_i)-1)Q^{-1}y_i^2$ which immediately implies the result. $\square$

Noticeably, the lower bound given in [8] for a path of length n is $Q+Q^{-1}+O(Q^{2-n})$, close to our result $Q+Q^{-1}+O(Q^{-1})$ for graphs with involution.

The calculation for $\lambda _2$’s lower bound follows a similar approach. Recall that $\lambda _2$ is the largest eigenvalue of $H^-=H'-A_\sigma$. Due to the possibility of negative numbers in the matrix, some adjustments need to be made. Consider the vertex set excluding all fixed vertices $V \backslash S = N \cup \sigma N$. Fix an endpoint $v_1$ in N and assign vertex $v_i$ to N if $v_i$ is closer to $v_1$ than to $v_1'$. In case the distances are equal, $v_i$ can belong to either N or $\sigma N$. Next, define a new vector y in $\mathbb {R}^{k}$

$$\begin{aligned} y_i = {\left\{ \begin{array}{ll} Q^{-\text {dist}(v_1,v_i)} &{} \text { if } \text {dist}(v_1,v_i)<\text {dist}(v_1',v_i)\\ 0 &{} \text { if }\text {dist}(v_1,v_i)=\text {dist}(v_1,v_i') \end{array}\right. } . \end{aligned}$$

(3.8)

Theorem 3.3

Let $\text {deg}_{N\cup \sigma N}(v_i)$ denote the degree of vertex $v_i$ in $N\cup \sigma N$. Use the same setting in Theorem 3.2 and the vector y defined above. The lower bound on $\lambda _2$ is given by

$$\begin{aligned} \lambda _2&\ge Q - \frac{1+\sum _{i\ne 1} (\text {deg}_{N\cup \sigma N}(v_i)-1)y_i^2}{\sum _{i} y_i^2}. \end{aligned}$$

(3.9)

Proof

Again by Rayleigh’s inequality,

$$\begin{aligned} \lambda _2\ge \frac{\sum _{i} y_i \sum _{i,j} H_{ij}^{-} y_j}{\sum _{i} y_i^2}. \end{aligned}$$

(3.10)

When $i=1$,

$$\begin{aligned} y_1\sum _{j} H_{1j}^{-} y_j \ge Q - 1 .\end{aligned}$$

(3.11)

This is because starting from $j=2$, $\mathbb {1}(v_1\sim v_j) - \mathbb {1}(v_1\sim v_j')$ has to be nonnegative. If that was not the case, then $v_j$ would be closer to $v_1'$ instead of $v_1$, which would contradict the assumption.

When $i= 2,3,...,k$, similar to the proof of the previous theorem, there exists a vertex in $N\cup \sigma N$ that is adjacent to $v_i$ and is in one of the shortest paths from $v_1$ to $v_i$. Consequently, there must exist a $y_j=Qy_i$. There are three cases for the coefficient in front of $y_iy_j$. If $[\mathbb {1}(v_1\sim v_j) - \mathbb {1}(v_1\sim v_j')]$ takes the form $(1-1)$ or $(0-1)$, it is easy to verify that $\text {dist}(v_1,v_i)=\text {dist}(v_1,v_i')$, which implies $y_iy_j$ is zero.

Sum over $y_iy_j$ only when its coefficient is $(1-0)$, and it follows that

$$\begin{aligned} y_i\sum _{j} H_{i,j}^{-} y_j \ge Qy^2_i - (\text {deg}_{N\cup \sigma N}(v_i)-1)y_i^2 .\end{aligned}$$

(3.12)

$\square$

Notice that this lower bound is greater than $Q-\max _{v_i\in V}{\text {deg}(v_i)}$, which is an improved bound compared to the one given by the Circle Theorem.

3.2 Lower Bounds on $\varphi _1(v_1)$ and $\varphi _2(v_1)$

Recall the probability of quantum state transfer from vertex $v_1$ to vertex $v_1'$ at time t can be written as the following expression

$$\begin{aligned} p(t)=\left| \sum _{\lambda _j\in \pi ^+} \varphi _j(v_1)^2 e^{it\lambda _j}- \sum _{\lambda _j\in \pi ^-} \varphi _j(v_1)^2 e^{it\lambda _j}\right| ^2 \end{aligned}$$

(3.13)

where eigenvectors $\varphi _j$ form an orthonormal basis. To demonstrate that this probability can be close to 1 at some time t, it suffices to prove that both $\varphi _1(v_1)$ and $\varphi _2(v_1)$ are close to $\frac{1}{\sqrt{2}}$.

Theorem 3.4

Let m be the maximum degree of the graph. If Q is greater than 2m, then the corresponding normalized eigenvectors of $\lambda _1$ and $\lambda _2$ satisfy

$$\begin{aligned} \varphi _1(v_1)&\ge \sqrt{0.5-\frac{m}{2Q^2}}-\sqrt{\frac{m}{Q-m}} \end{aligned}$$

(3.14)

$$\begin{aligned} \varphi _2(v_1)&\ge \sqrt{0.5-\frac{m}{2Q^2}}-\sqrt{\frac{m+1}{Q-m-1}}. \end{aligned}$$

(3.15)

Proof

Consider the vector y we constructed earlier in Sect. 3.1, but this time in $\mathbb {R}^{2k+s}$. It can be expressed as $y=\sum ^{2k+s}c_i \varphi _i$, a linear combination of the eigenvectors. Denote the squared Euclidean norm of y by D. Due to the involution, $y(v)=y(v')$ is true for every vertex. If $\lambda _i$ is in $\pi ^-$, then its corresponding eigenvector alternates, meaning $\varphi _i(v)=-\varphi _i(v')$. On the other hand, $\varphi _i(v)=\varphi _i(v')$ if $\lambda _i$ is in $\pi ^+$. This implies $c_i$ is 0 for every $\lambda _i\in \pi ^-$. By Cauchy–Schwartz inequality,

$$\begin{aligned} \varphi _1 (v_1)\ge \frac{1-\sqrt{D-c_1^2}}{\sqrt{D}}. \end{aligned}$$

(3.16)

Denote the difference between $\lambda _1$ and the Rayleigh quotient on $H^+$ and y by $\epsilon$,

$$\begin{aligned} \epsilon =\lambda _1-\frac{\sum \lambda _i c_i^2}{\sum c_i^2} \end{aligned}$$

(3.17)

Now the expression is left with only the eigenvalues in $\pi ^+$. Assume k is the second smallest index of the eigenvalues in $\pi ^+$, then

$$\begin{aligned} D-c_1^2&\le \frac{\epsilon D}{\lambda _1-\lambda _k}. \end{aligned}$$

(3.18)

According to Gershgorin’s Circle Theorem, $\lambda _1$ and $\lambda _2$ lie in the interval $[Q-m, Q+m]$, whereas the other eigenvalues are bounded by $[-m,m]$. The gap between the Rayleigh quotient and $\lambda _1$ now satisfies $\epsilon \le Q+m- R(H,y)$. It is easy to verify that the lower bound in Theorem 3.2 also applies to $R(H, \begin{bmatrix} a&a&0 \end{bmatrix}^T)= R(H^+,\begin{bmatrix} a&0 \end{bmatrix}^T)$.

When all the inequalities are combined, expression (3.18) transforms into

$$\begin{aligned} D-c_1^2\le D \cdot \frac{m}{Q-m}. \end{aligned}$$

(3.19)

Let $F_l$ be the set of vertices with minimum distance to either $v_1$ or $v_1'$ equals to l. Then the maximum possible value of the size of $F_l$ is $m^l$. This partition of the vertex set gives an upper bound on $D=2(1 + Q^{-2}|F_1|+Q^{-4}|F_2|+...+Q^{-2d}|F_d|)\le \frac{2}{1-\frac{m}{Q^2}}$. Naturally, this requires Q to be at least $\sqrt{m}$ to ensure that the series converges. By replacing the upper bound on D in inequality (3.16), we obtain the lower bound on $\varphi _1(v_1)$ as stated in the theorem.

To determine the lower bound on $\varphi _2(v_1)^2$, we need a similar vector $\tilde{y}$, but with alternating signs between vertex sets N and $\sigma N$. Let

$$\begin{aligned} \tilde{y}_i = {\left\{ \begin{array}{ll} Q^{-\min {\{\text {dist}(v_1,v_i)},{\text {dist}(v_1,v_i')}\}} &{} \text { if }v_i\in N \text { and } \text {dist}(v_1,v_i)\ne \text {dist}(v_1,v_i')\\ -Q^{-\min {\{\text {dist}(v_1,v_i)},{\text {dist}(v_1,v_i')}\}} &{} \text { if }v_i\in \sigma N \text { and } \text {dist}(v_1,v_i)\ne \text {dist}(v_1,v_i')\\ 0 &{} \text { if }\text {dist}(v_1,v_i)=\text {dist}(v_1,v_i') \end{array}\right. }. \end{aligned}$$

(3.20)

And if it is written as a linear combination of the eigenvectors, then coefficients $\tilde{c}_i=0$ for eigenvalues $\lambda _i$ in set $\pi ^+$. Similarly, it follows that

$$\begin{aligned} \varphi _2(v_1)\ge \frac{1-\sqrt{D}\cdot \sqrt{\frac{m+1}{Q-m-1}}}{\sqrt{D}}\ge \sqrt{0.5-\frac{m}{2Q^2}}-\sqrt{\frac{m+1}{Q-m-1}} \end{aligned}$$

(3.21)

$\square$

Remark

These lower bounds depend solely on the ratio between Q and the maximum degree of the graph. Regardless of the number of vertices, as long as Q is significantly larger than the maximum degree, then the probability is close to 1.

3.3 Time t of achieving strong state transfer

So far, we have demonstrated that given the maximum degree of the graph, one can ensure the probability of quantum state transfer between v and $v'$ to be arbitrarily close to 1 by selecting a sufficiently large Q. For practical purposes, we also need to ensure that the time $t = \frac{\pi }{\lambda _1-\lambda _2}$, when $|\varphi _1(v_1)e^{it\lambda _1}+\varphi _2(v_1)e^{it\lambda _2}|$ is at its maximum, is not too large. To find a lower bound on $\lambda _1-\lambda _2$, we will first take a detour and study the eigenvectors using the reduced $2\times 2$ matrix first introduced in [7].

Lemma 3.5

[7] H is the adjacency matrix of a simple connected graph with potential Q on vertices u, v. Let $\lambda$ be an eigenvalue of H with corresponding eigenvector $\varphi$. If $\varphi (u)=\mu$ and $\varphi (v)=\nu$, then $\mu$ and $\nu$ satisfy

$$\begin{aligned} \begin{bmatrix} Z_{uu}(\lambda ) &{} Z_{uv}(\lambda )\\ Z_{uv}(\lambda ) &{} Z_{vv}(\lambda ) \end{bmatrix} \begin{bmatrix} \mu \\ \nu \end{bmatrix}=(1-\frac{Q}{\lambda }) \begin{bmatrix} \mu \\ \nu \end{bmatrix} \end{aligned}$$

(3.22)

where $Z_{xy}(\lambda )=\sum _{P:x\rightarrow y} \frac{1}{\lambda ^{|P|}}$ denotes the sum of $\frac{1}{\lambda ^{|P|}}$ over all walks from x to y; |P| is the length of the walk.

Proof

To construct a function $f: V(G)\rightarrow \mathbb {R}$ which we claim to be an eigenvector of H, let $f(u)=\mu$, $f(v)=\nu$, and $Hf(x)=\lambda f(x)$ for all $x\in V(G)\backslash \{u,v\}$. Since $f(x)=\frac{Af(x)}{\lambda }$ sums over all vertices y adjacent to x and divides f(y) by $\lambda$, we can compute f(x) by summing over all possible walks from the endpoints u and v to x. In particular,

$$\begin{aligned} f(x)=\mu \cdot \sum _{P:x\rightarrow u} \frac{1}{\lambda ^{|P|}} +\nu \cdot \sum _{P':x\rightarrow v} \frac{1}{\lambda ^{|P'|}}. \end{aligned}$$

(3.23)

In order for f to be the actual eigenvector of H, $\lambda f(x) = Hf(x)$ should also be true at the endpoints:

$$\begin{aligned} \lambda f(u)=Qf(u)+\sum _{x\sim u}f(x) \text { ; } \lambda f(v)=Qf(v)+\sum _{x\sim v}f(x). \end{aligned}$$

(3.24)

Dividing both sides of Eqs. (3.24) by $\lambda$, we get the following equality when x is one of the endpoints

$$\begin{aligned} f(x)=\frac{Q}{\lambda } f(x) + \mu \cdot \sum _{P:x\rightarrow x} \frac{1}{\lambda ^{|P|}} +\nu \cdot \sum _{P':x\rightarrow v} \frac{1}{\lambda ^{|P'|}} , \end{aligned}$$

(3.25)

which is exactly what the $2\times 2$ linear system in the lemma describes. $\square$

Theorem 3.6

Given a graph with an involution and potential Q on v and $v'$. If the maximum degree is m and the distance from v to $v'$ is d, then

$$\begin{aligned} \lambda _1-\lambda _2 >\frac{2}{(Q+m)^{d-1}}. \end{aligned}$$

(3.26)

Proof

When the graph has an involution $\sigma$ and $u=\sigma (v)$, taking a walk from u to itself is equivalent to taking a walk from v to v. Thus, the matrix in Lemma 3.5 has eigenvectors $\begin{bmatrix} 1&1 \end{bmatrix}^T$ and $\begin{bmatrix} 1&-1 \end{bmatrix}^T$. According to Lemma 2.3$, \mu =\nu$ if $\lambda \in \pi ^+$ and $\mu =-\nu$ if $\lambda \in \pi ^-$. Therefore, $\lambda _1$ and $\lambda _2$ satisfy

$$\begin{aligned} \lambda _1(Z_{vv}+ Z_{vv'})=\lambda _1-Q \text { and } \lambda _2(Z_{vv}- Z_{vv'})=\lambda _2-Q. \end{aligned}$$

(3.27)

After comparing these two equations, we obtain

$$\begin{aligned} \lambda _1-\lambda _2= \sum _{P:v\rightarrow v} \left( \frac{1}{\lambda _1^{|P|-1}} -\frac{1}{\lambda _2^{|P|-1}} \right) +\sum _{P:v\rightarrow v'} \left( \frac{1}{\lambda _1^{|P|-1}} +\frac{1}{\lambda _2^{|P|-1}}\right) . \end{aligned}$$

(3.28)

Moving the first summation to the left-hand side, it becomes

$$\begin{aligned} (\lambda _1-\lambda _2)\left( 1+\frac{n_2}{\lambda _1\lambda _2}+\frac{n_3(\lambda _1+\lambda _2)}{\lambda _1\lambda _2}+...\right) >\lambda _1-\lambda _2. \end{aligned}$$

(3.29)

Here $n_k$ is the number of walks from v to itself of length k. The right-hand side contains $\frac{1}{\lambda _1^{d-1}}$ and $\frac{1}{\lambda _2^{d-1}}$. Therefore,

$$\begin{aligned} \lambda _1-\lambda _2> \frac{1}{\lambda _1^{d-1}}+\frac{1}{\lambda _2^{d-1}}>\frac{2}{(Q+m)^{d(v,v')-1}}. \end{aligned}$$

(3.30)

Consequently, the time it takes for p(t) to be arbitrarily close to 1 is less than $\frac{\pi }{2}(Q+m)^{d-1}$. $\square$