Modeling, analysis and design of centrifugal force driven transient filling flow into rectangular microchannel

Abstract

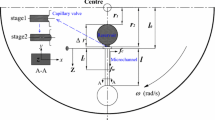
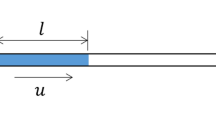
Recently, centrifugal pumping has been discovered to be an excellent alternative method for controlling the fluid flow inside microchannels. In this paper, we have developed the physical modeling and carried out the analysis for the centrifugal force driven transient filling flow into a rectangular microchannel. Two types of analytic solutions for the transient flow were obtained: (1) a pseudo-static approximate solution, and (2) an exact solution. Analytic solutions include expressions for flow front advancement, detailed velocity profile and pressure distribution. The obtained analytical results show that the filling flow driven by centrifugal force is affected by three dimensionless parameters which combine fluid properties, rectangular channel geometry and processing condition of rotational speed. Effects of inertia, viscous and centrifugal forces were also discussed based on the parametric study. Furthermore, we have also successfully provided a simple and convenient analytical design tool for such rectangular microchannels, demonstrating two design application examples.

Appendices

Appendix 1: Detailed solution procedures for dimensionless exact filling flow front advancement, l*(t*), and dimensionless exact velocity profile, w*(x*, y*, t*)

The governing equation for w*(x*, y*, t*) and the corresponding boundary conditions are stated in Eqs. 13 and 14a, b, respectively. The governing equation for l*(t*) and the corresponding initial condition are written in Eqs. 15 and 16, respectively. Equations 13 and 15 are coupled with each other.

For this particular problem, the separation of variable technique turns out to be successful to lead to an exact solution with the following form

$$w^{*} (x^{*}, y^{*}, t^{*}) = W^{*} (x^{*}, y^{*})T^{*} (t^{*}),$$

(34)

where W* and T* are spatial and temporal velocity components which are the functions of x* and y* only and t* only, respectively. With the solution form of Eq. 34, Eq. 13 can be rewritten by

$$Re\,G_{{\rm A}} W^{*} \frac{{{\rm d}T^{*} }}{{{\rm d}t^{*} }} - {\left[ {C_{{\rm A}}^{2} \frac{{\partial^{2} W^{*} }}{{\partial x^{*2} }} + \frac{{\partial^{2} W^{*} }}{{\partial y^{*2} }}} \right]}T^{*} = \frac{1}{2}Re\,G_{{\rm A}} \overline{V}^{2} \omega^{*2} {\left( {l^{*} (t^{*}) + L_{0}^{*} } \right)}.$$

(35)

Observing that the right-hand side in Eq. 35 is the function of t* only, i.e., independent of x* and y*, one can decompose the left-hand side of Eq. 35 by functions of spatial variables, x* and y*, and temporal variable, t*, so that the part of the function of x* and y* only could set to be constant. With this in mind, the following relation is assumed

$$\frac{{{\rm d}T^{*} }}{{{\rm d}t^{*} }} = A\,T^{*} (t^{*}),$$

(36)

where A is constant. Then from Eqs. 35 and 36, one can obtain the following equations

$$ - C_{{\rm A}}^{2} \frac{{\partial^{2} W^{*} }}{{\partial x^{*2} }} - \frac{{\partial^{2} W^{*} }}{{\partial y^{*2} }} + Re\,\, G_{{\rm A}} AW^{*} = B$$

(37)

$$B\,T^{*} (t^{*}) = \frac{1}{2}Re\,G_{{\rm A}} \,\bar{V}^{2} \omega^{*2} {\left( {l^{*} (t^{*}) + L_{0}^{*} } \right),}$$

(38)

where B is constant.

By substituting Eqs. 34 and 38 to the governing equation for l*(t*), Eq. 15, one can obtain the following equation:

$$\frac{{{\rm d}l^{*} }}{{{\rm d}t^{*} }} = Re\,G_{{\rm A}} \, \bar{V}^{2} \omega^{*2} {\left( {l^{*} (t^{*}) + L_{0}^{*} } \right)}\,{\int \limits_0^1 {{\int \limits_0^1 {\;\frac{{W^{*} (x^{*}, y^{*})}}{B}\,{\rm d}x^{*} {\rm d}y^{*} } }} }.$$

(39)

We define the constant part in the right-hand side of Eq. 39 by D as follows

$$D \equiv Re\,G_{{\rm A}} \, \bar {V}^{2} \omega^{*2} \,{\int\limits_0^1 {{\int\limits_0^1 {\;\frac{{W^{*} (x^{*}, y^{*})}}{B}\,{\rm d}x^{*} {\rm d}y^{*} } }} }.$$

(40)

Then Eq. 39 is rewritten as

$$\frac{{{\rm d}l^{*} }}{{{\rm d}t^{*} }} = D{\left( {l^{*} (t^{*}) + L_{0}^{*} } \right)}.$$

(41)

By applying the initial condition of Eq. 16, one attains a final form of the dimensionless exact filling flow front advancement

$$l^{*} (t^{*}) = L_{0}^{*} {\left[ {2e^{{D\,t^{*} }} - 1} \right]}$$

(42)

which corresponds to Eq. 25.

From Eqs. 38 and 42, one can find T*(t*) as

$$T^{*} (t^{*}) = \frac{1}{B}Re\,G_{{\rm A}} \, \bar{V}^{2} \omega^{*2} L_{0}^{*} e^{{D\,t^{*} }} $$

(43)

Since Eq. 43 holds, one can recognize that Eq. 36 is satisfied if A appearing in Eq. 36 is no more than D defined in Eq. 40, i.e.:

$$A = D.$$

(44)

Reflecting Eq. 44, one can rewrite Eq. 37 as

$$ - C_{{\rm A}}^{2} \frac{{\partial^{2} W^{*} }}{{\partial x^{*2} }} - \frac{{\partial^{2} W^{*} }}{{\partial y^{*2} }} + Re\,\, G_{{\rm A}} DW^{*} = B$$

(45)

which is the differential equation for the geometrical velocity component to be solved along with the no-slip boundary conditions,

$$W^{*} (x^{*} = 0,y^{*}) = 0,\,W^{*} (x^{*} = 1,y^{*}) = 0$$

(46)

$$W^{*} (x^{*}, y^{*} = 0) = 0,\,W^{*} (x^{*}, y^{*} = 1) = 0.$$

(47)

It may be mentioned that Eq. 45 becomes an integro-differential equation for W* if D defined in Eq. 40 is explicitly substituted to Eq. 45. This integro-differential equation is difficult to be solved analytically. Thus, in the present approach, we regard Eq. 45 as a differential equation just for W* considering D as a parameter given, even if D could be determined only after W* is solved. And then, it is rather straightforward to solve Eq. 45 with the boundary condition, Eqs. 46, 47 based on the eigenfunction expansion method to obtain the spatial velocity component, W*(x*, y*),

$$W^{*} (x^{*}, y^{*}) = {\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{{16B}}{{\lambda_{{mn}} mn\pi^{2} }}\sin m\pi x^{*} \sin n\pi y^{*} } }} },$$

(48)

where the eigenvalues of the exact flow, λ _mn are

$$\lambda_{{mn}} = Re\,G_{{\rm A}} D + C_{{\rm A}}^{2} m^{2} \pi ^{2} + n^{2} \pi^{2} \quad \hbox{for} \enspace m = 1, 3, 5, \ldots \hbox{and} \enspace n = 1, 3, 5,\ldots .$$

(49)

which corresponds to Eq. 27.

Finally, from Eqs. 34, 43 and 48, the dimensionless exact velocity field is expressed as

$$w^{*} (x^{*}, y^{*}, t^{*}) = 16Re\,G_{{\rm A}} \overline{V} ^{2} \omega^{*2} L_{0}^{*} {\left[ {{\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda _{{mn}} mn\pi^{2} }}\sin m\pi x^{*} \sin n\pi y^{*} } }} }} \right]}\,e^{{Dt^{*} }} $$

(50)

which corresponds to Eq. 29.

Now to complete the solution, one needs an expression for D. By substituting Eq. 48 to Eq. 40, one can obtain the following relation for D,

$$D = 32Re\,G_{{\rm A}} \overline{V}^{2} \omega^{*2} {\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{mn}} m^{2} n^{2} \pi^{4} }}} }} }$$

(51)

which corresponds to Eq. 26.

Appendix 2: Solutions in dimensional form

Dimensional forms of the pseudo-static solutions are expressed below.

A pseudo-static filling flow front advancement, l(t), corresponding to Eq. 22:

$$l(t) = L_{0} {\left[ {2\exp {\left( {\frac{{32\rho \omega^{2} }}{\mu }{\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{mn,{\rm static}}} m^{2} n^{2} \pi^{4} }}} }} }\;t} \right)} - 1} \right]}.$$

(52)

A pseudo-static velocity profile, corresponding to Eq. 23:

$$\begin{aligned} w(x,y,t) = \frac{{16\rho \omega^{2} L_{0} }}{\mu } {\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{mn,{\rm static}}} mn\pi^{2} }}\sin \frac{{m\pi }}{W}x \sin \frac{{n\pi }}{H}y} }} } \\ \exp {\left[ {\frac{{32\rho \omega^{2} }}{\mu }{\sum\limits_{m^{\prime} = 1,3,5, \ldots }^\infty {{\sum\limits_{n^{\prime} = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{m^{\prime}n^{\prime},{\rm static}}} m^{\prime 2} n^{\prime 2} \pi^{4} }}\;t} }} }} \right]. } \\ \end{aligned} $$

(53)

A pseudo-static pressure distribution, corresponding to Eq. 24:

$$p(z,t) = \frac{{\rho \omega^{2} }}{2}{\left( {z - L_{0} } \right)}{\left[ {z + L_{0} - 2L_{0} \times \exp {\left( {\frac{{32\rho \omega ^{2} }}{\mu }{\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{mn,{\rm static}}} m^{2} n^{2} \pi ^{4} }}} }} }\;t} \right)}} \right]}.$$

(54)

A dimensional form of D _static, corresponding to Eq. 28:

$$D_{{{\rm static}}} = \frac{{32\rho \omega^{2} }}{\mu }{\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{mn,{\rm static}}} m^{2} n^{2} \pi^{4} }}} }} }.$$

(55)

A dimensional form of λ _mn,static , corresponding to Eq. 20:

$$\lambda_{{mn,{\rm static}}} = {\left( {\frac{{m\pi }}{W}} \right)}^{2} + {\left( {\frac{{n\pi }}{H}} \right)}^{2} \quad \hbox{for} \enspace m = 1, 3, 5, \ldots \hbox{and} \enspace n = 1, 3, 5,\ldots .$$

(56)

Dimensional forms of the exact solutions are expressed below.

An exact filling flow front advancement, l(t), corresponding to Eq. 25:

$$l(t) = L_{0} {\left[ {2e^{{Dt}} - 1} \right]}.$$

(57)

An exact velocity profile, corresponding to Eq. 29:

$$w(x,y,t) = \frac{{16\rho \omega^{2} L_{0} }}{\mu }{\left[ {{\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda_{{mn}} mn\pi^{2} }}\sin \frac{{m\pi }}{W}x \sin \frac{{n\pi }}{H}y} }} }} \right]}\;e^{{Dt}} .$$

(58)

An exact pressure distribution, corresponding to Eq. 31:

$$p(z,t) = \frac{{\rho \omega^{2} }}{2}{\left( {z - L_{0} } \right)}\,{\left[ {z + L_{0} - 2L_{0} e^{{Dt}} } \right]}.$$

(59)

A dimensional form of D, corresponding to Eq. 26:

$$D = \frac{{32\rho \omega^{2} }}{\mu }{\sum\limits_{m = 1,3,5, \ldots }^\infty {{\sum\limits_{n = 1,3,5, \ldots }^\infty {\frac{1}{{\lambda _{{mn}} m^{2} n^{2} \pi^{4} }}} }} }.$$

(60)

A dimensional form of λ _mn , corresponding to Eq. 27:

$$\lambda_{{mn}} = \frac{{D\rho }}{\mu } + {\left[ {{\left( {\frac{{m\pi }}{W}} \right)}^{2} + {\left( {\frac{{n\pi }}{H}} \right)}^{2} } \right]}.$$

(61)