Abstract
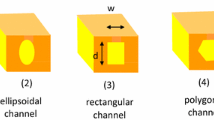
This paper studies the efficiency of capillary pump analytically in circular, square and rectangular channels with results verified by experiment. The effect of liquid momentum is analyzed with respect to channel size and equations are developed to enable most efficient fluid pumping. It is found that the momentum term is negligible at channel cross-cut area < 0.1 mm2 while it has a significant contribution at > 0.3 mm2 region. The optimized equations show that the most efficient pumping and thereby the quickest liquid filling is accomplished in square shaped channel when compared with rectangular and circular channels. Generally, the longer the filling distance, or the longer the filling time, the larger the channel size is required after optimization, and vice versa. For the rectangular channel with channel height fixed, the channel width requirement to maximize the ability of capillary pump is obtained and discussed. Experimental verifications are conducted based on the measurement of filling distance versus time, and the simulation results are well correlated with the testing results. The equations developed in the paper provide a reference for the microfluidic channel design, such that the channel filling speed can be maximized.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Capillary components are widely used in microfluidic chips for various applications, such as polymerase chain reaction (PCR), biomedical reagent assay and molecular diagnostics. Unlike the traditional fluidics in which the inertia, the external pressure, the potential energy and even the turbulence usually dominate the liquid behavior, the liquid flowing in microfluidic chip is dominated by capillary effects [1,2,3], which is negligible in traditional fluidics. In order to control and manipulate the micro fluid in chip, capillary effects must be well studied and fully manipulated.
There are many capillary components used in the microfluidic chips, such as various capillary pumps [4,5,6], capillary valves [7, 8], bubble trapping and removing [2, 9], capillary chambers and network circuits [10,11,12]. Recently, a critical review by Olanrewaju et al. [13] provide a comprehensive introduction of the capillary components and circuits as well as the fabrication techniques employed in microfluidic chips. It divides the development of microfluidics over the past 40 years into three waves, dictated by the fabrication technology as mechanical micromaching, cleanroom fabrication and rapid prototyping [14]. In order to further understand the processes of liquid flows, powerful commercial software, such as CFD-ACE + , ANSYS Fluent and COMSOL Multiphysics, are usually employed to the study of details of liquid motion in the microfluidic channels [15,16,17,18]. However, due to the long time involved in simulation of micro fluid motion using the commercial software, mixed methodology simulations have been developed and are being employed for the integrated system with very fast speed and acceptable accuracy [18, 19]. In addition, external forces, such as magnetic force and electrostatic force, are also used in microfluidic chips to help control and manipulate the liquid flowing behavior, [20,21,22,23] and centrifugal force controlled by rotation speed is employed to drive the liquid flowing in channel [7, 24, 25]. Analytical methods have also been employed to study the capillary phenomenon [21, 26], such as the liquid filling process in the height direction generated by the capillary pump.
In a microfluidic chip, sometimes it is necessary to transport liquid from one position to another position quickly using a capillary pump. This motion of liquid depends not only on liquid properties such as the liquid density, viscosity, contact angle and surface tension between the liquid and the channel, but also on the channel shape and size. In addition to the above-mentioned criteria, analytical expressions that dictate the channel filling speed to the design parameters, are essential for designing channels and will be the main target of this paper.
This paper first develops an extended Bosanquet equation which is suitable for not only the circular channel, but also any channel shape including the square and rectangular channels. Based on the extended equation, the cross-cut sizes of channels are optimized such that the liquid can fill the channels with the fastest speed. To check the maximum value analytically obtained, we plot the curve of the extended Bosanquet equation and compare the analytical result of optimization with the curve around the maximum value. It is observed that the analytical results match with the curves exactly, proving the analytical development and the optimization in this paper are correct.
In order to verify the simulation results of the present paper, we measure the liquid filling distance versus time in capillary tubing with different diameters and lengths, and the experimental results are well correlated with the simulation results.
2 Evaluation of the contribution of momentum term
Suppose a type of liquid is filling horizontally from the inlet to the outlet through a channel by the capillary force and the peripheral pressure, as illustrated in Fig. 1. The transient filling process is governed by the following differential equation,
where \(\rho \), \(\sigma \) and \(\theta \) are the liquid density, the surface tension and the advancing contact angle, respectively, and \(p\) and \(A\) are the channel’s cross-cut perimeter and area, respectively. Here the advancing contact angle is used because the liquid is moving, and the advancing contact angle is usually larger than the static contact angle in hydrophilic channel. The inlet and outlet pressures are expressed as \(P_{in}\) and \(P_{out}\) respectively, and \(l\) and \(u\) are the liquid filling distance and speed, respectively. The hydraulic resistance of the channel is \(Rl\), and is linearly proportional to the filling distance. Here \(R\) is defined as the normalized hydraulic resistance, and it is independent to the filling distance. The flow rate of the channel is \(Q\), and it can also be expressed as \(A dl/dt\). In Eq. (1) the term \(\rho Alu\) is the liquid momentum in the channel, and the right hand side is the total force acting on the liquid.
In order to evaluate the contribution of the momentum term on the left hand side, we first neglect it and then Eq. (1) is simplified as
By solving Eq. (2) with the boundary condition \(l = 0\) when \(t = 0\), it gives
in which \(\Delta P = P_{in} - P_{out}\). For the circular channel, substitute \(p = \pi d\), \(A = \left( {\pi d^2} \right)/4\) and \(R = 128\mu /\left( {\pi d^4 } \right)\) into Eq. (3), and denote \(\mu\) and \(d\) as the liquid dynamic viscosity and channel diameters, respectively, and suppose that \(\Delta P\) is 0, we can obtain
It is the well-known Washburn equation, and by conducting differential on Eq. (4), the liquid filling speed can be expressed as
Equation (5) means that as \(t \to 0\), \(u \to \infty\). To clarify this singularity, and also to evaluate the contribution of the liquid momentum term, we solve Eq. (1) directly. Equation (1) can be rewritten as
Solving Eq. (6) using boundary conditions \(l = 0\) and \(u = 0\) when \(t = 0\), gives
In which \(c_{1} = \rho /2\), \(c_{2} = 1/2 RA\) and \(c_{3} = \sigma \cos \theta p/A + \Delta P\). Let \(y = c_{3} t - c_{2} l^2\), then \(c_{2} l^2 = c_{3} t - y\) and \(\left( {dl^2} \right)/dt = 1/c_{2} \left( {c_{3} - dy/dt} \right)\). Substituting them into Eq. (7), and solving further with boundary conditions \(y = 0\) when \(t = 0\), gives
Substituting \(y = c_{3} t - c_{2} l^{2}\) in Eq. (8) and rearranging leads to
where \(c_{4} = \sqrt {\frac{{c_{3} }}{{c_{2} }}}\) and \(c_{5} = - \frac{{c_{1} }}{{c_{2} }}\). On inserting the circular channel’s perimeter \(p\), area \(A\) and normalized hydraulic resistance \(R\) into Eq. (9) and assuming \(\Delta P = 0\), leads to
Equation (10) is known as Bosanquet equation. When the liquid density \(\rho\) is 0, Bosanquet equation is reduced to Washburn equation. So both Bosanquet equation and Washburn equation are the special cases of Eq. (9).
From Eq. (9) the filling speed can be expressed as
As \(t \to 0\), the initial speed \(u\left( 0 \right)\) is calculated to be
It has a finite value, hence showing that the speed singularity is caused by neglecting the liquid momentum term.
Now we evaluate the contribution of the liquid momentum term in the filling process. We use water as the liquid for simplicity. The advancing contact angle between water and the channel is supposed to be 85°, or the channel is hydrophilic to water. The water’s properties include that the dynamic viscosity µ of 0.00089 Pa s, the density ρ of 997 kg/m3, and the surface tension σ of 0.0725 N/m. Suppose that \(\Delta P = 0\).
Figure 2 illustrates the results with and without consideration of the momentum term, based on Eq. (9) and Eq. (3), respectively. We address a rectangular channel with width and height of 200 µm and 100 µm, respectively. It is observed that there is no significant contribution of the momentum term on the filling process generally, as illustrated in Fig. 2a and b. The difference of filling distances between with and without momentum term is 0.65% approximately at the time of 50 ms. However, in the beginning range where the time value is within 4 ms, as marked by the red circles, the differences are significant, as shown in Fig. 2c and d. Note that in Fig. 2d the filling speed is approximately 436 mm/s at \(t = 0\) for the case with momentum term, but for the case without momentum term the time cannot be zero, as discussed before. The dot is plotted to the time of 5 µs only.
Comparison of the results with and without liquid momentum term when channel width and height are 200 and 100 µm, respectively. The sub-figures (c) and (d) are the zoom-in sections highlighted by red circles in (a) and (b), respectively, for clarity. Generally, the contribution of liquid momentum term is not significant, as shown in (a) and (b). The difference of filling distances between with and without momentum term is approximately 0.65% at 50 ms. But in the beginning range of filling shown in (c) and (d), the differences are significant. Note that in (d), the smallest time value of dots is 5 µs for the case without momentum term, while for the case with momentum term, the smallest time value is 0
When the channel size increases, the contribution of the momentum term grows rapidly. Figure 3 plots the difference of filling distances between with and without momentum term at the time of 50 ms, and also gives out the filling distance with momentum term at that time. Generally, it is observed that when the channel cross-cut area is under 0.1 mm2, the contribution of the momentum term is limited and the term can be neglected. However, when the cross-cut area is large, especially above 0.3 mm2, the difference is significant. It is also noticed that if the height is half of the width, the longest filling distance is obtained when the width is 1200 µm approximately at the time of 50 ms. While for the square channel, the longest filling distance is achieved when the size is 800 µm approximately. It means that the efficiency of the capillary pump is maximized for these sizes.
Comparison of the results with and without consideration of the momentum term for different channel sizes (a). Here “Error %” is the filling distance difference between with and without momentum term in percentage at the time of 50 ms, and “Distance filled” is the result with momentum term at 50 ms. For the rectangular channel, if the height is half of the width, the liquid will get the longest filling distance when the width is 1200 µm approximately. While for the square channel, the longest filling distance is obtained at the size of 770 µm approximately. It is reasonable to neglect the momentum term when the channel cross-cut area is under 0.1 mm2. However, when the area is above 0.3 mm2, the contribution of the momentum term is significant and should be considered. Zoom in the filled distance around the maximum values of the square channel (b) and the rectangular channel (c). From (b) and (c), it is observed that the maximum value of filled distance is 6.7223 mm when the square size is 768.67 µm, while for the rectangular channel, the maximum value is 6.5745 mm when the width is 1205.4 µm. The data will be used to compare with the analytic results later
3 Methodology of optimization
Here we address obtaining the analytic expressions of the most efficient capillary pump such that we can get the maximum filling distance in a certain time, or the minimum time for a certain filling distance. Three types of channel shape are investigated. They are the circular channel, the square channel and the rectangular channel. According to the aforementioned results, the liquid momentum term will be considered in the following study.
We shall start with the circular channel. From Eq. (10), we have
Let \(y = 4\frac{\mu }{\sigma cos\theta }l^{2}\), \(\eta = \frac{\rho }{32\mu }\), \(x = d\), then
Taking derivative on Eq. (13) gives
Let \(z = \eta x^{2}\). To get the maximum value of \(y\), we have
Let \(\xi = \frac{t}{z}\), then
It is a nonlinear equation, in which the solution \(\xi = 0\) is meaningless. By solving the equation numerically, we can obtain that \(\xi = 2.1491\), and hence \(z = 0.46531t\).
As \(z = \eta x^{2}\), \(x = d\), \(\eta = \frac{\rho }{32\mu }\), so
In order to check whether it is the maximum value, we differentiate Eq. (14) further to get
Substitute \(\eta x^{2} = 0.46531t\), \(\eta x = \sqrt {0.46531t\eta }\) and \(\eta x^{3} = \left( {0.46531t} \right)^{\frac{3}{2}} \eta^{{ - \frac{1}{2}}}\) into the above equation, we have
So it is the maximum value. Note that both \(t\) and \(\eta\) are positive numbers.
From Eq. (17), it is interesting to find that the optimized diameter is not related to the contact angle and the surface tension of liquid, but related to the viscosity and the density only if the filling time is fixed. It is also observed that the longer the filling time, the larger the channel diameter is required in order to get the maximum filling speed.
On substituting Eq. (17) into Eq. (10), we can obtain the longest filling distance \(l\) in a certain time \(t\),
For water, suppose the filling time is 0.05 s, and substitute the water parameters aforementioned into Eq. (17) and (19), we can get that the maximum possible filling distance is 6.53 mm with the channel diameter of 815 µm approximately. For the filling time of 0.02 s, the maximum possible filling distance is 3.28 mm with the channel diameter of 516 µm approximately.
From Eq. (19), for a certain distance \(l\), the shortest filling time is
And the diameter for the shortest time to fill a distance \(l\) can be obtained by substituting Eq. (20) into Eq. (17),
It means that when the filling distance is longer, the diameter should also be larger for getting maximum filling speed. For examples, to deliver water through a circular channel of 2 mm in length with the fastest speed, the shortest time is 10.3 ms and its correspondent diameter is 0.371 mm; while the channel length is 4 mm, the shortest time is 26.0 ms with its correspondent diameter of 0.588 mm. As comparisons, if a circular channel with diameter of 0.1 mm is used, the times to reach 2 mm and 4 mm are 22.9 ms and 90.5 ms, respectively, larger than the optimized values above significantly. Moreover, for the channel with diameter of 0.05 mm, the times to reach 2 mm and 4 mm is further increased to 45.2 ms and 180 ms, respectively. It shows that the optimization can help to improve the delivery speed significantly.
In Eq. (21) we notice that the optimized diameter is related to the surface tension and the contact angle. It is caused by the involvement of the filling distance. Since the filling distance is definitely related to the surface tension and the contact angle, as expressed by Eq. (19), in order to let the diameter be independent to the surface tension and the contact angle, they have to be involved to counteract that effect of filling distance on the diameter. As a result, Eq. (21) is not contradicted to Eq. (17).
Now we study the case of square channel. Suppose the width or height of the square channel is \(a\), then \(R = \frac{12\mu }{{0.4218a^{4} }}\), \(A = a^{2}\), \(p = 4a\). We can further get \(c_{1} = \frac{\rho }{2}\), \(c_{2} = \frac{1}{2}RA = \frac{6\mu }{{0.4218a^{2} }}\), \(c_{3} = \frac{\sigma cos\theta p}{A} = \frac{4\sigma cos\theta }{a}\) (assuming that the external pressure difference is negligible), \(c_{4} = \sqrt {\frac{{c_{3} }}{{c_{2} }}} = \sqrt {\frac{2*0.4218\sigma cos\theta a}{{3\mu }}}\), \(c_{5} = - \frac{{c_{1} }}{{c_{2} }} = - \frac{{0.4218\rho a^{2} }}{12\mu }\), then Eq. (9) can be expressed as
It is quite similar to Eq. (10), Bosanquet equation. By using the same method as before, we can obtain for a certain time \(t\), when
the liquid can get the longest filling distance, which is expressed as
For a certain distance \(l\), the shortest filling time is
And the width or height for the shortest time to fill a distance \(l\) can be obtained as
Substitute water’s property parameters and time 0.05 s into Eq. (23), we get \(a = 768.67\) µm. From Eq. (24) we have the maximum filling distance of 6.7223 mm. By zooming in Fig. 3a on the range with the maximum value, it is observed that the analytical results, both the square size and the maximum filling distance, are exactly the same as those shown in Fig. 3b. It means that the analytical equations developed, as well as the maximum value obtained, are correct.
Finally we address the rectangular channel. Suppose \(w\) and \(h\) are the width and height of the rectangular channel, respectively, and here we define \(w \ge h\). If the height is larger than the width, then the definition of the height and the width can be reversed, as the contribution of the potential energy is negligible in this microfluidic case. The normalized hydraulic resistance can be expressed as \(R = \frac{12\mu }{{wh^{3} \left( {1 - \alpha \left( {h/w} \right)} \right)}}\). Suppose the ratio of the height to the width is fixed, or \(\gamma = \frac{h}{w}\) is a constant, then \(R = \frac{12\mu }{{w^{4} \gamma^{3} \left( {1 - \alpha \gamma } \right)}}\), where \(\alpha\) is an infinite series [18] but can be expressed approximately as \(0.1293\gamma^{4} - 0.3519\gamma^{3} + 0.2124\gamma^{2} - 0.0446\gamma + 0.633\) by the polynomial interpolation method.
Now we substitute the coefficients \(c_{1} = \frac{\rho }{2}\), \(c_{2} = \frac{1}{2}RA = \frac{6\mu }{{w^{2} \gamma^{2} \left( {1 - \alpha \gamma } \right)}}\), \(c_{3} = \frac{\sigma cos\theta p}{A} = \frac{{2\sigma cos\theta \left( {1 + \gamma } \right)}}{w\gamma }\), \(c_{4} = \sqrt {\frac{{c_{3} }}{{c_{2} }}} = \sqrt {\frac{{\sigma cos\theta w\gamma \left( {1 + \gamma } \right)\left( {1 - \alpha \gamma } \right)}}{3\mu }}\), \(c_{5} = - \frac{{c_{1} }}{{c_{2} }} = - \frac{{\rho w^{2} \gamma^{2} \left( {1 - \alpha \gamma } \right)}}{12\mu }\) into Eq. (9), and it leads to
Equation (27) is similar to Eq. (10) too, and we can also use the aforementioned method to deal with it. For a certain time \(t\), when
it will get the longest filling distance which is expressed as
For a certain distance \(l\), the shortest filling time is
And the width for the shortest filling time can be obtained as
Suppose \(\gamma\) = 0.5, then \(\alpha\) = 0.62789. Put them into Eq. (28), and together with the water’s property parameters, then we can get \(w\) = 1205.4 µm. From Eq. (29), we can get the longest filling distance is 6.5745 mm. By zooming in Fig. 3a on the range with the maximum value, as shown in Fig. 3c, it is found that the analytical results obtained by Eqs. (28) and (29) are exactly the same as those of Fig. 3c, proving that the analytical equations on the rectangular channel are also correct.
Moreover, let \(\gamma\) = 1, then \(\alpha\) = 0.5782. Substitute them into Eq. (31), the coefficient \(3.0525\gamma^{ - 1} \left( {1 + \gamma } \right)^{{ - \frac{1}{3}}} \left( {1 - \alpha \gamma } \right)^{{ - \frac{2}{3}}}\) is \(4.3077\), the same as the coefficient of the square channel expressed by Eq. (26). Substituting \(\gamma\) = 1 and \(\alpha\) = 0.5782 into Eq. (30), the coefficient \(1.6688\left( {1 + \gamma } \right)^{{ - \frac{2}{3}}} \left( {1 - \alpha \gamma } \right)^{{ - \frac{1}{3}}}\) becomes 1.4017, also the same as that of the square channel expressed by Eq. (25).
From Eq. (30), in order to make the filling time as short as possible, the term \(\left( {1 + \gamma } \right)^{\frac{2}{3}} \left( {1 - \alpha \gamma } \right)^{\frac{1}{3}}\) should be as large as possible. Put the expression of \(\alpha\) into the term, and let the term be denoted as \(y\), it gives
Figure 4 illustrates the case for \(\gamma\) between 0 and 1. It is shown that when \(\gamma = 1\), \(y\) gets its maximum value. In other words, Eq. (30) will get its minimum value, or the shortest filling time when \(\gamma = 1\). In such a case, the rectangular channel converges to the square channel. When \(\gamma\) is approaching to 0, \(y\) will get its minimum value of 1, and thus Eq. (30) will get its maximum value, or the longest filling time.
4 Discussion
In the paper we discuss three types of channel shape, and they have similar equations for maximizing the efficiencies of their capillary pumps. Therefore, we can compare the abilities of their capillary pumps directly.
We focus on the time \(t\) needed for the liquid filling a certain distance \(l\). From Eqs. (20), (25) and (30), it is observed that all of them have the same term \(\left( {\sigma cos\theta } \right)^{{ - \frac{2}{3}}} \left( {\rho \mu } \right)^{\frac{1}{3}} l^{\frac{4}{3}}\), so we just compare their coefficients, which are listed in Table 1.
Since the coefficient of rectangular channel is not less than that of square, as analyzed before, the square channel has the smallest coefficient among the three types of channel. Compared with the circular channel, the coefficient of the square channel is 3.84% less approximately. In other words, the filling time is 3.84% less approximately for the square channel, if both the square and the circular channels are optimized. For the rectangular channel, when the height/width ratio is approaching zero, the coefficient approaches 1.6688, which is the maximum value as aforementioned in Fig. 6. This value is 19% larger than that of the square channel approximately. So the rectangular channel has a filling time 0%–19% longer than that of the square channel, if their sizes are both optimized.
From Eq. (12), we notice that if \(\Delta P = 0\), the initial filling speed is \(\sqrt {\frac{{c_{3} }}{{2c_{1} }}} = \sqrt {\frac{\sigma Cos\left( \theta \right)p}{{A\rho }}}\). It means that the smaller the channel size, the faster the initial filling speed, because \(\frac{p}{A}\) is inversely proportional to the channel size. However, since the normalized hydraulic resistance is inversely proportional to the fourth power of the channel size, the filling speed drop in the small channel is much faster during the filling process, when compared with that of the large channel. After the filling distance reaches a certain level, the filling speed of the small channel will be slower than that of the large channel. That is why for a certain filling distance \(l\), if the distance is short, the optimized channel size should be small, and vice versa.
In a practical microfluidic chip, the channel’s height is usually fixed, while the channel’s width is adjustable. This leads to another relevant question: What is the requirement for the channel width if the channel height is fixed in order to maximize the ability of the capillary pump? Fig. 5 illustrates the results when the filling time is 50 ms, and aforementioned water properties are used. It is observed that when the channel height is fixed at 25 µm, the optimized channel width is 85.25 µm approximately, and the ratio of height to width is 0.293 approximately. As the height increases, the width also increases, and reaches its local maximum value of 815 µm approximately when the height is 500 µm. After that the optimized width decreases as the height increases, which makes the ratio of height to width increases rapidly, as plotted in Fig. 5a. Finally, the rectangular channel converges to the square channel with width of 768.7 µm and gets its longest filling distance of 6.722 mm, as aforementioned on the square channel. It is the global maximum filling distance for the rectangular channel. This point is also the local minimum value of channel width, as shown in Fig. 5a. When the channel height continues to increase after 768.7 µm, the optimized channel width always equals the channel height, and the filling distance drops gradually as the channel height increases, as illustrated in Fig. 5b.
The optimized channel width, as well as the ratio of height to width when the channel height is fixed (a), and their corresponding filling distance (b) when the filling time is 50 ms. When the channel height is small, the ratio of height to width will be also small, such as a little smaller than 0.3. However, as the height increases, the ratio also increases, and finally converges 1, which is the square channel with size of 768.7 µm and corresponding to the global maximum filling distance of 6.722 mm for the rectangular channel. When the channel height continues to increase, the optimized width always equals the height, and the filling distance drops gradually
In some practical operations circular channels with diameters less than 0.1 mm are frequently used. From Eq. (21), if water is used, the correspondent filling distance is 0.280 mm for diameter of 0.1 mm. It means that if the filling distance is 0.280 mm, the fastest delivery speed is achieved by using diameter of 0.1 mm channel. If the filling distance is longer, larger diameter should be used, and vice versa. Therefore, in the viewpoint of the fastest delivery speed, the circular channels with diameters less than 0.1 mm are suitable for filling distances less than 0.280 mm. However, it other liquids are used, the distance needs to recalculate based on Eq. (21) due to the physical properties of the liquids are changed.
5 Experimental verification
In order to verify the simulation aforementioned, experimental measurement is conducted. We choose water as the testing liquid as it is convenient to obtain and its properties are well known. The water is dyed red for easy observation. Two types of circular capillary tubing are employed for the experiment, and the outside of the tubing is marked evenly with interval of 5 mm. When the dyed water passes through each mark, the time is recorded by video. The tubing is put on a support frame horizontally, and one end can be inserted into a mini centrifugal tube containing up to 2 mL dyed water. The tube is hydrophobic to water, and can hold the dyed water in horizontal state without flowing out, as shown in Fig. 6. When the tubing is insert to the dyed water in tube, the water will flow faster at the beginning, and then slows down gradually due to the increasing hydraulic resistance, which is proportional to the filling distance. The whole filling process is recorded by a hand-phone in a video. The video is separated into individual pictures by software, and thus each picture’s shooting time is known. The time interval between two continual pictures is 1/30 s. From the pictures the times to reach all the marks are obtained accordingly. Since both the inlet and the outlet are exposed to the ambient environment, there is no pressure difference between them. The water is driven by the capillary pressure solely.
The glass tubing filling experiment. The tubing is put on a rack horizontally, and is marked with a fixed interval of 5 mm. A mini centrifugal tube containing up to 2 ml water is dyed red color for easy observation. The mini tube is hydrophobic to water, and can hold the dyed water in the horizontal state without leaking. The mini tube is being pushed to the glass tubing (a), and when the water touches with the glass tubing, the filling process begins. b shows the half-filled tubing. When the water reaches the end of the tubing, the filling process stops (c). The whole filling process is recorded by a hand phone. From the video, the curve of filling distance versus time can be plotted out, as illustrated in Fig. 7
The first experiment is on the tubing of 0.5 mm in inner diameter, and its length is 90 mm. Figure 7a illustrates the simulation results by curve and the experimental data by dot. It is observed that the simulation results and the experimental data are well correlated generally. Although the filling distance of experiment is smaller than that of simulation, their trends are the same. The inner wall roughness of the tubing may be one of the reasons that causes the testing speed slower than that of the simulation. The second experiment is on the tubing of 1.15 mm in inner diameter and 75 mm in length, as shown by Fig. 7b. It is observed again that the simulation results and the experimental data are well correlated. It is interesting to notice that in the second experiment the filling speed is significantly faster than that in the first one. At the filling distance of 75 mm, the filling times for the simulation and the experiment are 6.35 s and 7.87 s, respectively, in Fig. 7a. While in Fig. 7b, the filling times are 2.02 s and 2.40 s, respectively. The main reason is caused by the inner diameter, and the reason can be explained Eq. (10).
Comparison between simulation result and experimental observation. The inner diameters of tubing are 0.5 mm (Fig. 7a) and 1.15 mm (Fig. 7b), respectively. The filling distance of experiment is somewhat smaller than that of the simulation. However, the trends are the same, and generally the simulation results are well correlated with the experimental data. The roughness of the tubing inner wall may be one of the reasons that causes the experimental observation speed lower
The experiment confirms that the channel size has significant influence on the filling speed, and it is meaningful and important to optimize the channel size for maximization of the capillary pump efficiency.
6 Conclusions
This paper investigates the efficiency of the capillary pump transferring liquid in the microfluidic channel. First, the contribution of the liquid momentum term is evaluated, and it is found that if the channel cross-cut area is below 0.1 mm2, the liquid momentum term is negligible. However, if the channel size is large, especially above 0.3 mm2, the contribution of the momentum term is significant. Secondly, the capillary pump efficiency for three types of channel shape are studied, and their maximum filling distances within a certain time as well as their minimum filling time for a certain filling distance, are deduced analytically. It is found that the square channel can fill liquid faster than the circular channel and the rectangular channel, if their sizes of channels are all optimized. The longer the filling distance, the larger the channel size required in order to get the fastest filling speed, and vice versa. The optimized channel size is independent to the surface tension and the contact angle if the filling time is fixed. Thirdly, for the rectangular channel, if the channel height is fixed, the channel width can be optimized to get the longest filling distance in a certain time. As the channel height increases, the rectangular channel converges to the square channel at last, which will get the global maximum filling distance. After that, the filling distance will decrease gradually as the channel size increases. Finally, experimental measurements are employed to verify the simulation results. It is observed that the experimental data are well correlated with the simulation results.
The analytical equations developed in the present paper can be taken as the references while designing microfluidic channel for the fastest liquid filling speed.
References
Guo W, Hansson J, Wijngaart W (2018) Capillary pumping independent of the liquid surface energy and viscosity. Microsys Nanoeng 4:2
Lochovsky C, Yasotharan S, Gunther A (2012) Bubbles no more: in-plane trapping and removal of bubbles in microfluidic devices. Lab Chip 12:595–601
Olanrewaju AO, Robillard A, Dagher MD (2016) Juncker, autonomous microfluidic capillaric circuits replicated from 3D-printed molds. Lab Chip 16:3804–3814
Majhy B, Iqbal R, Gaikwad R et al (2018) Dynamics of capillary flow in an open superoleophilic microchannel and its application to sensing of oil. Microfluid Nanofluid 22:116
Safavieh R, Tamayol A, Juncker D (2015) Serpentine and leading-edge capillary pumps for microfluidic capillary systems. Microfluid Nanofluid 18(3):357–366
Vasilakis N, Papadimitriou KI, Morgan H et al (2017) High-performance PCB-based capillary pumps for affordable point-of-care diagnostics. Microfluid Nanofluid 21:103
Chen JM, Huang PC, Lin MG (2008) Analysis and experiment of capillary valves for microfluidics on a rotating disk. Microfluid Nanofluid 4(5):427–437
Papadimitriou VA, Segerink LI, Berg A et al (2018) 3D capillary stop valves for versatile patterning inside microfluidicchips. Anal Chim Acta 1000:232–238
Karlsson JM, Gazin M, Laakso S et al (2013) Active liquid degassing in microfluidic systems. Lab Chip 13:4366–4373
Hagmeyer B, Zechnall F, Stelzle M (2014) Towards plug and play filling of microfluidic devices by utilizing networks of capillary stop valves. Biomicrofluidics 8(5):056501
Novo P, Chu V, Conde JP (2014) Integrated optical detection of autonomous capillary microfluidic immunoassays: a hand-held point-of-care prototype. Biosens Bioelectron 57:284–291
Safavieh R, Juncker D (2013) Capillarics: pre-programmed, self-powered microfluidic circuits built from capillary elements. Lab Chip 13:4180–4189
Olanrewaju AO, Beaugrand M, Yafia M et al (2018) Capillary microfluidics in microchannels: from microfluidic networks to capillaric circuits. Lab Chip 18:2323–2347
Martin A, Teychené S, Camy S et al (2016) Fast and inexpensive method for the fabrication of transparent pressure-resistant microfluidic chips. Microfluid Nanofluid 20:92
Phan VN, Nguyen NT, Yang C et al (2010) Capillary filling in closed end nanochannels. Langmuir 26:13251–13255
Ramalingam N, Warkiani ME, Ramalingam N et al (2016) Numerical and experimental study of capillary-driven flow of PCR solution in hybrid hydrophobic microfluidic networks. Biomed Microdevices 18(4):68
Salih NM, Hashim U, Nafarizal N et al (2014) Numerical simulation of water flow velocity for microfluidic application using COMSOL multiphysics. Adv Mater Res 925:651–655
Song H, Wang Y, Pant K (2011) System-level simulation of liquid filling in microfluidic chips. Biomicrofluidics 5:024107
Krishnamoorthy S, Bedekars A, Slddhaye S et al (2008) Integrated microfluidic system design using mixed methodology simulations. US Patent/0177518 A1
Li M, Li D (2018) Microvalve using electrokinetic motion of electrically induced janus droplet. Anal Chim Acta 1021:85–94
Shen T, Huang L, Wang J (2016) Analysis and experiment of transient filling flow into a rectangular microchannel on a rotating disk. Microfluid Nanofluid 20:52
Wang Y, Wu R, Varma VB et al (2018) Flowing label-free bacteria trapped by small magnetic fields. Sens Actuators B: Chem 260:657–665
Wang ZM, Wu RG, Wang ZP et al (2016) Magnetic trapping of bacteria at low magnetic fields. Sci Rep 6:26945
Clime L, Daoud J, Brassard D et al (2019) Active pumping and control of flows in centrifugal microfluidics. Microfluid Nanofluid 23:29
Moore JL, McCuiston A, Mittendorf I et al (2011) Behavior of capillary valves in centrifugal microfluidic devices prepared by three-dimensional printing. Microfluid Nanofluid 10:877–888
Wu P, Zhang H, Nikolov A et al (2016) Rise of the main meniscus in rectangular capillaries: experiments and modeling. J Colloid Interf Sci 461:195–202
Acknowledgements
We would like to express our deep thanks to Dr. Suhanya Duraiswamy for her great effort on revising this paper and providing good suggestions for us.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hua, W., Zhou, W., Wang, W. et al. Maximization of the capillary pump efficiency in microfluidics. SN Appl. Sci. 3, 315 (2021). https://doi.org/10.1007/s42452-021-04293-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-021-04293-1