Introduction

Dome-shaped structures, characterised by a core of high-grade metamorphic or granitic rocks surrounded by low-grade rocks, are important tectonic features in orogens (Burg et al. 2004; Whitney et al. 2004, 2013; Platt et al. 2015; Cao et al. 2022). Their origin and tectonic setting are still debated, and several mechanisms have been proposed for their formation, tectonic regime, and exhumation (Coney et al. 1980; Whitney et al. 2004). During the 1980s and 1990s, these dome-shaped structures were interpreted as metamorphic core complexes (MCCs; Coney et al. 1980; Coney and Harms 1984; Lister and Davis 1989) as inferred in the Basin and Range province (western North America). The formation of MCCs has been attributed to both extensional and compressional tectonic regimes (e.g., Searle and Lamont 2020; Cao et al. 2022). Recent studies have highlighted the importance of strike-slip movement, i.e., transcurrent, transtensional or transpressional tectonics all as a general concept for exhumation processes (e.g., Nabavi et al. 2020) and in the formation of dome-shaped structures (Druguet 2001; Denèle et al. 2007, 2009; Gébelin et al. 2009; Zhang et al. 2017). Transtension or transpression involves km-scale, high-temperature (HT) ductile shear zones, which contribute to the exhumation and the possible emplacement of igneous intrusions (Druguet 2001; Rosenberg and Handy 2005). For this reason, a multidisciplinary approach combining structural investigations with petrochronology is required to better constrain the formation of dome-shaped structures (e.g., Aguilar et al. 2015; Broussolle et al. 2015; Zhang et al. 2017; Cao et al. 2022; Chen et al. 2022; Fu et al. 2022; Spencer et al. 2022).

The Variscan orogeny in Europe comprises numerous dome-shaped structures that developed between the collisional stage at ca. 360–350 Ma and the collapse of the orogen at ca. 300–290 Ma (Vanderhaeghe and Teyssier 2001; Faure et al. 2009; Gapais et al. 2015; Cochelin et al. 2021; Vanderhaeghe et al. 2020; Vanardois et al. 2022a, b). The development of the Variscan chain was also widely affected by the activity of crustal-scale strike-slip shear zones during the late-Carboniferous ca. 340–300 Ma (Arthaud and Matte 1977; Matte 2001; Carosi and Palmeri 2002; Di Vincenzo et al. 2004; Carreras and Druguet 2014; Franke et al. 2017; Simonetti 2021; Schulmann et al. 2022; Franke and Żelaźniewicz 2023).

The Monte Grighini dome, exposed in the Variscan belt in central Sardinia, is a NW–SE elongated dome within the Nappe Zone (Musumeci 1992). Elter et al. (1990) interpreted the Monte Grighini dome to have resulted from late-Carboniferous strike-slip movement in a shear zone. In contrast, Cruciani et al. (2016) interpreted this area to have developed in a transtensional regime at ca. 305–295 Ma, where exhumation was driven by the Monte Grighini shear zone (MGSZ). Owing to several similarities between the MGSZ and the transpressive Posada-Asinara shear zone (PASZ) in northern Sardinia and within the framework of the southern European Variscan belt (Matte 2001; Corsini and Rolland 2009; Carosi et al. 2020, 2022; Simonetti 2021 for a review), a re-investigation of the tectonic regime associated with the MGSZ has been performed. Here we present an updated view on the tectono-metamorphic history of the Monte Grighini dome and its non-coaxial deformation, by integrating field observations, meso- and microstructural data, vorticity analysis, P–T estimates and in situ U–(Th)–Pb (texturally- and chemically-controlled) geochronology of monazite.

Geological overview of the Variscan belt in Sardinia

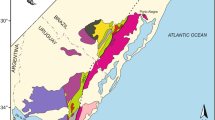
Due to the lack of a strong subsequent Alpine age overprint, the segment of the Variscan orogen exposed in Sardinia, Italy, represents a key locality for investigating the southern European Variscan belt (Carosi et al. 2020). Carmignani et al. (1994, 2001, 2015) divided the Variscan basement of Sardinia into three main tectono-metamorphic zones (Fig. 1a). These include: (i) the External Zone or the foreland; (ii) the Axial Zone or the hinterland; and (iii) the Nappe Zone or the hinterland–foreland transition zone.

Fig. 1
figure 1

a Tectonic sketch map of Sardinia (modified after Carosi et al. 2020). The blue box marks the location of the investigated area; b Simplified geological map of the Monte Grighini dome (modified after Musumeci et al. 2015; Cruciani et al. 2016, 2017). Previous radiometric ages, the method used for dating, and the studied mineralogical phase are shown in the inset (b). The dashed blue line indicates the perimeter of the investigated area (Fig. 2a)

Full size image

The Nappe Zone, which comprises most of the metamorphic basement, is subdivided into External and Internal Nappes Zones (Fig. 1a). The boundary between these zones is marked by the Barbagia Thrust, a regional-scale, top-to-the S–SW, thrust-sense, ductile to brittle shear zone (Carosi and Malfatti 1995; Conti et al. 1998; Montomoli et al. 2018; Petroccia et al. 2022a, b).

The External Nappe Zone comprises five tectonic units. From the structurally deepest to shallowest, these are: (i) the Monte Grighini Unit, (ii) the Riu Gruppa/Castello Medusa Unit, (iii) the Gerrei Unit, (iv) the Meana Sardo Unit, and (v) the Sarrabus Unit (Carmignani and Pertusati 1977; Carmignani et al. 1982, 1994, 2012; Carosi and Pertusati 1990; Carosi et al. 1991; Loi et al. 1992, 2023; Conti et al. 1999, 2001; Barca et al. 2003; Funedda et al. 2011, 2015; Cocco et al. 2018, 2022). The Gerrei, Meana Sardo, and Sarrabus units underwent regional greenschist-facies metamorphism, as constrained by illite and chlorite crystallinity (Franceschelli et al. 1992; Carosi et al. 2010; Montomoli et al. 2018) and recently confirmed, by Raman spectroscopy on carbonaceous material (RSCM) on samples from the Meana Sardo Unit (Petroccia et al. 2022a,c). The deepest unit of the External Nappe Zone, i.e., the Monte Grighini Unit, reached medium-grade metamorphic conditions (i.e., amphibolite-facies; Musumeci 1992; Carmignani et al. 1994; Cruciani et al. 2016), within the core of the largest tectonic culmination, i.e., the Flumendosa Antiform. In a more external position (i.e., the External Zone or Foreland), Cruciani et al. (2022a, b) interpreted the Mt. Filau orthogneiss to be a similar example of a LP–HT metamorphic complex, like the Monte Grighini dome.

Geology of the Monte Grighini dome

The Monte Grighini dome (Musumeci 1992; Musumeci et al. 2015; Fig. 1b) consists of three tectonic units that, structurally from the bottom to the top, are (i) the Monte Grighini Unit (MGU), (ii) the Castello Medusa Unit, and (iii) the Gerrei Unit. The MGU comprises amphibolite-facies felsic metavolcanics (i.e., the Truzzulla Formation), metasediments (i.e., the Toccori Formation), and intrusive granitic rocks (Musumeci et al. 2015). The Truzzulla Formation (Fm.) consists of Upper Ordovician (447 ± 4.3 Ma) metavolcanics, metarkoses, and arkosic metasandstones (Cruciani et al. 2013). The Toccori Formation comprises metapelitic phyllites passing into hornfels adjacent to granitic intrusions (Cruciani et al. 2013, 2017) of the Intrusive Complex (IC; Cruciani et al. 2016). The IC is a NW–SE trending, sub-vertical intrusive body characterized by ages of 303 ± 18 Ma and 305 ± 16 Ma (Rb/Sr isochron) for a two-mica leucogranite and monzogranite, respectively (Carmignani et al. 1987; Fig. 1b). K/Ar, Ar/Ar, and Rb/Sr dating of igneous biotite and muscovite yielded cooling ages ranging between 305 and 295 Ma (Del Moro et al. 1991; Musumeci 1992; Fig. 1b).

The MGU records a polyphase deformation history (Musumeci 1992; Cruciani et al. 2016). The main foliation (S2) is a NW–SE striking continuous schistosity that dips steeply both to the NE and SW. The S2 foliation is characterised by syn-metamorphic pervasive ductile shearing (Cruciani et al. 2016). According to Musumeci (1992) and Cruciani et al. (2016), the D1 and D2 phases are associated with deformation that occurred during nappe stacking. D3 folds are represented by large-scale NW–SE trending upright antiforms and synforms, related to the development of a late, regional-scale folding event. The D3 phase is associated with syn-kinematic blastesis of chlorite, indicating deformation under lower grade metamorphic conditions (Cruciani et al. 2016). The D4 phase corresponds to a kilometre-wide NW–SE trending dextral transtensional shear zone located in the western sector of the MGU (Musumeci 1992; Columbu et al. 2015; Cruciani et al. 2016, 2017; Musumeci et al. 2015; Fig. 1b). This shear zone, i.e., the MGSZ (Elter et al. 1990; Fig. 1b), is associated with a steeply SW dipping foliation and subhorizontal to gently plunging object and mineral lineations (Musumeci et al. 2015). The MGSZ is marked by syn-kinematic sub-vertical emplacement of the IC, with a dextral sense of movement (Musumeci 1992). Along the westernmost and the south-westernmost sector of the Monte Grighini dome, a NW-trending fault containing cataclastic rocks (Fig. 1b) marks the contact between the MGU and the overlying Gerrei Unit (Musumeci et al. 2015). A thrust contact in the northeastern sector of the Monte Grighini dome (Fig. 1b) marks the boundary between the dome and the Castello Medusa Unit.

Field data and mesoscale observations

In order to describe the structural architecture of the studied area without bias from the previous investigations, the sequence of deformation events and structural elements are numbered relative to the principal event (e.g., Sp, Sp − 1), where the subscript ‘p’ denotes ‘principal’. Abbreviations are: (S) for foliation surfaces or axial plane foliation; (A) for fold axes; (L) for object stretching lineations; (F) for folds; and (D) for deformation phases. Four ductile deformation phases were observed. Figure 2a and b shows the geological map and the cross-section based on fieldwork performed as part of this study, integrated with the existing cartographic data (Musumeci et al. 2015). Figure 2c displays stereoplots of the main structural elements.

Fig. 2
figure 2

a Simplified geological map of the investigated sector of the dome (modified after Musumeci et al. 2015; see Fig. 1b for its location). See the geological map from Musumeci et al. (2015) for a complete overview of the structural elements of the Monte Grighini dome. Samples selected for study and the corresponding types of analysis are shown; b SW–NE oriented geological cross-section; c Stereoplots (equal area, lower hemisphere projections) of the main structural elements

Full size image

The oldest detectable deformation phase (Dp − 1) is denoted by a relict foliation (Sp − 1), observed only in the hinges of Dp folds (Fig. 3a). The Dp tectonic phase is characterised by deformation that is partitioned into low- and high-strain zones. Low-strain zones are domains associated with tight to isoclinal folding (Fig. 3a), where the Ap fold axes are scattered with general W–E to NW–SE plunges (Fig. 2c) and by the occurrence of an anastomosing pattern of deformation with centimetre to metre thick milonitic domains separating unsheared or weakly deformed domains. In contrast, mylonitic high-strain zones are characterized by LS tectonites containing well-developed kinematic indicators, with the occurrence of rootless folds. The Fp folds are associated with an Sp an axial planar foliation, representing the main structural elements in the study area (Fig. 3a). The sub-vertical Sp foliation (Fig. 2c) generally strikes NW–SE and dips moderately to steeply to the N–NE and to S–SW (Fig. 3b). Sp changes from a disjunctive cleavage in the northeastern part of the area, to a continuous mylonitic foliation (Fig. 3c) toward the westernmost sector. Thus, moving toward the MGSZ, the strain increases progressively and is characterised by an increase of the degree of non-coaxial deformation (i.e., the high-strain zone). The Lp object lineation is defined by elongated biotite, sillimanite and muscovite crystals and by millimetre to centimetre-scale quartz rods. Lp generally plunges gently to sub-horizontal (~ 0°–30°) to the NW and SE (Figs. 2c, 3b). The presence of a sub-vertical or moderate dipping angle Sp foliation, parallel to the mylonitic foliation in the high-strain zone, and Fp fold axes, parallel to the sub-horizontal Lp mineral lineation, is compatible with the simultaneous development of Dp high-strain and Fp fold domains linked to the MGSZ activity. Shear sense indicators were observed within the high-strain zones on sections parallel to the XZ plane of the finite strain ellipsoid (the X axis is defined by the orientation of Lp) and are coeval with Dp. They are mainly represented by S–C and S–C′ fabrics (Fig. 3d) and rotated porphyroclasts. Kinematic indicators, both at the meso- and microscale, point to a dextral displacement in agreement with the previous interpretations (Elter et al. 1990; Musumeci 1992). Fp + 1 folds affect the Sp foliation and commonly show gentle to slightly asymmetric upright geometry (Fig. 3e), with metre to decametre-scale wavelengths. Locally, kink and/or chevron-type Fp + 1 folds are observed. Ap + 1 fold axes trends are similar to the Ap fold axes and Lp object lineations but their plunges are greater (Fig. 2c). The Fp–Fp + 1 fold interference pattern shows parallel axes and sub-orthogonal axial planes (Fig. 3e). A Dp + 1 crenulation cleavage (Sp + 1) is locally recognisable. Dp + 2 produced gentle to open Fp + 2 folds with sub-horizontal axes and axial planes (Fig. 3f). The trend of shallowly plunging Ap + 2 axes varies from E–W to NW–SE with a very high degree of dispersion (Fig. 2c). The Dp + 2 deformation phase is not associated with the development of foliations and lineations.

Fig. 3
figure 3

a Outcrop view of Fp folds in the Toccori Formation deforming an older relict foliation (Sp − 1); b Lp sub-horizontal object lineation along the moderately dipping Sp is displayed; c Sub-vertical Sp foliation. The contact between the intrusive rock belonging to the IC (on the left) and the Toccori Formation schist (on the right) is parallel to the Sp (the yellow card indicating the scale is 5 cm in length). The white dashed line indicates the boundary between the intrusive rock and the schist; d Mylonite from the Toccori Formation at the mesoscale: C′–S fabric is indicative of a dextral sense of shear; e upright Fp − 1 fold, deforming the Sp attitude (the yellow card indicating the scale is 5 cm in length). The inset shows an enlarged view of the Fp fold and the Sp − 1 foliation located in the NE limb of the Fp + 1 fold is displayed; f Outcrop showing late open folds (Fp + 2) with sub-horizontal axes and axial planes, deforming the Sp foliation

Full size image

The late Fp + 2 gentle folds modified the steeply dipping attitude of the main Sp causing a different dip that alternate between the SW and NE. Kinematic indicators, on the different dipping limbs of the Fp + 2 folds, indicate top-to-the-NW or to-the-SE sense of shear respectively (see Supplementary Material S6).

Microstructures

We performed microstructural investigations on 24 samples (see Fig. 2a for sample locations). Foliations have been classified according to Passchier and Trouw (2005). Quartz dynamic recrystallisation microstructures are defined according to Stipp et al. (2002a, b) and Law (2014). Mineral abbreviations are after Warr (2021).

Porphyroids (metamorphosed volcanic felsic rocks or tuffs) and metavolcanic rocks of the Truzulla Formation are deformed and characterised by a porphyroclastic microstructure (Fig. 4a) with millimetre-sized K-feldspar (Fig. 4b) and subordinate plagioclase porphyroclasts. The Sp cleavage is marked by white mica, biotite, and rare chlorite. Quartz and phyllosilicate grains are oriented parallel to the main schistosity (Sp) wrapping around feldspar porphyroclasts (Fig. 4b). Sigma- and delta-type asymmetric K-feldspar porphyroclasts (Fig. 4b) and asymmetric strain shadows around clasts, indicate a dextral sense of shear. Quartz shows lobate grain boundaries suggesting dynamic recrystallisation by grain boundary migration (GBM), indicative of temperatures > 500 °C (Law 2014). In some samples, overprinting by subgrain rotation (SGR) recrystallisation indicates lower temperatures.

Fig. 4
figure 4

a, b Sheared metavolcanic rock belonging to the Truzulla Formation showing a dextral sense of shear. σ-type porphyroclast shows a dextral sense of shear; c garnet porphyroclast showing an internal foliation Sp − 1 (blue line) both discordant and locally concordant with the Sp foliation. Garnet is wrapped by the main foliation Sp (violet line) defined by white mica + biotite; d mica-fish in Truzulla Formation rock showing a dextral movement; e C′–S fabric in sillimanite-bearing schist, indicating a dextral sense of shear; f dynamically recrystallised quartz showing lobate and irregular grain boundaries indicative of GBM recrystallization

Full size image

Metasediments belonging to the Truzulla Formation are characterised by a disjunctive foliation (Sp; Fig. 4c), sub-parallel cleavage domains, and a continuous schistosity mainly defined by biotite, white mica, and quartz. The Sp foliation wraps around garnet and staurolite (Fig. 4c). A sporadic internal foliation (Sp − 1), consisting of oriented quartz, white mica, ilmenite, and graphite, varies from discordant to concordant with the external foliation (Fig. 4b). This suggests that garnet and staurolite may be inter- to early syn-tectonic (syn-Sp) with respect to Sp (i.e., their growth either occurred between Dp-1 and Dp or during the early stage of Dp). Quartz has irregular, lobate, and ameboid grain boundaries compatible with GBM recrystallisation. Samples collected within the high-strain zone display a dextral sense of shear, marked by mica-fish (Fig. 4d), S–C and S–C′ fabrics, and asymmetric strain shadows around porphyroclasts.

Schists and paragneisses from the Toccori Formation are characterised by a continuous foliation defined by the alternating quartzo-feldspathic and muscovite–biotite–sillimanite-rich layers (Fig. 4e). Prismatic sillimanite, biotite, and white mica define the Sp schistosity (Fig. 4e). Fine-grained fibrolite (Fig. 4e), kinematic indicators, such as S–C and S–C′ fabrics (Fig. 4e) and mica-fish, are also present. Quartz shows evidence of GBM and, more rarely, chessboard extinction (Fig. 4f).

Methods

Kinematic vorticity analysis

The non-coaxiality of flow in shear zones is commonly expressed by the kinematic vorticity number, Wk (Xypolias 2010), which can be estimated using several kinematic vorticity analysis techniques. Wk describes instantaneous deformation and is the ratio between the magnitude of the vorticity vector and the difference between the intermediate and minimum principal stretching rates, whereas the mean kinematic vorticity number Wm is used when referring to finite deformation (Xypolias 2010). Vorticity analysis is based on information about progressive deformation or flow parameters, such as the incremental strain, instantaneous stretching axes (ISA), and flow apophysis, and the relative rotation of line and plane structures during deformation. In any type of two-dimensional flow, it is possible to recognize two lines, defined as the flow apophyses (A1 and A2), that do not undergo rotation. The component of simple shear decreases as the angle between A1 and A2 increases, such that: the flow apophyses are orthogonal in pure shear flow and coincide with each other in simple shear flow. For general shear flow, A1 and A2 define an acute angle in the direction of the flow.

One of the most common assumptions when carrying out kinematic vorticity analysis is that of simple shear, i.e. plane strain and the deformation is monoclinic (Passchier 1998). The other important assumption is of steady-state deformation, or that the estimated Wk value represents an average Wk over the deformation interval during which the applied structure or fabric formed. In addition, constant volume is commonly assumed, which will, for simplicity, also be assumed here. The nominal error for kinematic vorticity analysis is ± 0.1 (Tikoff and Fossen 1995). A comparison of different possible systematic error sources indicates that for medium to low mean kinematic vorticity numbers (Wm < 0.8), the vorticity data minimum systematic error is ± 0.2 (Iacopini et al. 2011).

Progressive pure and simple shear are described by Wk = 0 and Wk = 1, respectively. The progressive simple and pure shear components contribute equally to the deformation when Wk = 0.71 (Law et al. 2004; Passchier and Trouw 2005; Xypolias 2010). The consequence of having a pure shear component within a shear zone is that the shear zone material is extruded in the X direction parallel to the measured object lineation. The kinematics of flow, namely, the components of pure and simple shear acting simultaneously during deformation (see Fossen and Cavalcante 2017; Xypolias 2010, for reviews) expressed by the kinematic vorticity number Wm, were estimated using two independent kinematic vorticity gauges: the C′ shear band method (Kurz and Northrup 2008; Gillam et al. 2013) and two different porphyroclast-based methods: (a) the porphyroclast aspect ratio method (PAR; Passchier 1987; Wallis et al. 1993) and (b) the rigid grain net method (RGN; Jessup et al. 2007).

The C′ shear band method is based on measurements of the orientation of C′ planes with respect to the boundaries of the MGSZ (ν angle). Theoretically, C′ planes nucleate as the bisector of the angle between the two flow apophyses (Platt and Vissers 1980; Kurz and Northrup 2008; Xypolias 2010). Based on this assumption, the kinematic vorticity number is given by Wm = cos2ν (Kurz and Northrup 2008). As each element in a flow tends to rotate, including C′ planes, it is necessary to consider the spread of ν value measurements to estimate the initial amplitude of the angle during the formation of the C′ planes. Gillam et al. (2013) proposed to use an average ν value for low-strain rocks or in cases where C′ planes developed at a late stage of the deformation history and nucleated in a stable orientation; in such cases, C′ planes undergo little or no rotation after inception. For highly strained rocks, deformed in long-lasting shear zones, as in the present study case, the maximum value of ν is preferable since it better approximates the nucleation angle of C′ planes (see Kurz and Northrup 2008).

Porphyroclast-based methods have proved to be extremely useful for quantifying vorticity in ductile shear zones, but their accuracy is affected by several factors (see Xypolias 2010 for a review): (i) rigid clasts should be embedded in a homogeneously deforming matrix; (ii) the shape of clasts should not change during deformation due to recrystallisation or fracturing; (iii) the sample should consist of a population of clasts with a range of aspect ratios (Law et al. 2004); (iv) the strain must be sufficient to allow clasts to reach a stable sink position. If these conditions are not met, porphyroclast-based methods tend to overestimate Wm values (e.g. Bailey et al. 2004). For both porphyroclasts-based methods, measurements were conducted using the EllipseFit 3.8.0 software (Vollmer 2015). The results were plotted on both PAR (Passchier 1987; Wallis et al. 1993) and RGN (Jessup et al. 2007) graphs. In detail, both the PAR and RGN methods require measurement of the axial ratio of porphyroclasts (R) and the angle (ф) between the long axis of the rigid grain and the mylonitic foliation (Passchier 1987; Wallis et al. 1993). For simple shear, particles will rotate permanently for all realistic porphyroclast shapes, but for subsimple shear, particles with an aspect ratio above a critical aspect value (Rc) will rotate into a stable position and then stay fixed (Jeffery 1922). To find Rc we plot the porphyroclast aspect ratio against the angle between the clast's long axis and the foliation as observed in the XZ plane. This method is commonly referred to as the PAR method (Passchier 1987). For high-strain rocks, the flow plane is considered to be parallel to the straight tails of porphyroclasts; although most published studies take the trace of macroscopic mylonitic foliation as the reference frame (Xypolias 2010). Theoretically, on such graphs, two fields of behaviour for rotated clasts can be distinguished: (a) a field where the clasts with low shape factor rotate infinitely and hence display a wide range in their long axis orientations; and (b) a field where the clasts rotate slowly (forward or backward). To minimise the uncertainties, two Rc values have been chosen (Rc min and Rc max) and an average vorticity has been calculated using the relation Wm = ( Rc2 − 1)/(Rc2 + 1). Graphs for natural porphyroclast systems, however, often exhibit a gradual transition rather than an abrupt change between these two fields (e.g. Jessup et al. 2007). The Rigid Grain Net (RGN) is an alternative graphical method for estimating mean kinematic vorticity number (Wm) from the shape and orientation of porphyroclasts that are inferred to represent variably rotating rigid objects in a flowing matrix (Jeffery 1922). proposed by Jessup et al. (2007). The RGN method uses a modification of the original plot proposed by Passchier (1987) for PAR analysis and includes a set of semi-hyperbolas plotted in both positive and negative space at 0.025 intervals of Wm that are mathematically equivalent to a hyperbolic net (Xypolias 2010). Each clast is plotted on the rigid grain net according to its shape factor (B*) and the angle made between its long axis and foliation (θ). These semi-hyperbolas transition into vertical lines to define the maximum B* as the critical threshold (Rc) between grains that rotate infinitely and those that reach a stable-sink position. In other words, grains with B* values below Rc rotate freely (i.e., they define a vertical boundary outside of the semi-hyperbola) and do not develop a preferred orientation, while grains with B* values above Rc have limited rotation (i.e., they lie within the semi-hyperbola). Wm is estimated directly from the RGN based on where the critical shape factor (B*) equals the aspect ratio of the porphyroclast at the critical threshold (Rc). Therefore, each sample’s estimated Rc is equal to its estimated Wm. The validity of RGN analysis relies on two assumptions (e.g. Xypolias 2010): (i) the plane of reference for measurement is parallel to lineation and the pole to foliation; and (ii) the plane of reference for measurement is normal to the vorticity vector. These assumptions define a monoclinic shear zone and, therefore, require that the shear zone to which the methods are applied have a history dominated by monoclinic deformation. It is important to note that we assume that Wk = Wn = Wm for samples dominated by monoclinic deformation.

About the fifteen analysed samples (see Fig. 2a for sample location), twelve have been investigated by the C′ shear band method, due to the presence of C′ planes, whereas only 3 samples have been analysed using porphyroclast-based methods. Only samples with a considerable number of freely rotating clasts (> 50), lacking internal deformation, were chosen.

Phase equilibrium modelling

Pressure–temperature (P–T) conditions were estimated using phase equilibrium modelling. The investigated sample (GR19) was selected because it shows a well-developed equilibrium mineral assemblage, fundamental for constraining P–T conditions, and also contains both white mica and biotite. The construction of equilibrium phase diagrams depends on the choice of a bulk composition representative of the sample or a specific stage in its metamorphic history (reactive bulk composition), the use of an appropriate chemical system, and the selected thermodynamic dataset and solution models.

The bulk composition used for modelling can influence the topology and phase proportions predicted in a P–T phase diagram (e.g., Stüwe and Powell 1995; Palin et al. 2016). In this study, a local bulk composition was determined using an X-ray map of a representative area of the thin section (~ 45 × 30 mm), chosen based on the size of the smallest grains. X-ray compositional maps and quantitative chemical analyses were performed using the electron probe microanalyser (EPMA) JEOL JXA-8200 superprobe at the Institute of Geological Sciences (University of Bern). X-ray maps of Al, Fe, K, Mg, and Na were acquired in a single scan by wavelength-dispersive spectrometry (WDS), whereas Ca, P, Si, and Ti were measured simultaneously by energy-dispersive spectroscopy (EDS). The program XMapTools v4 (Lanari et al. 2014) was used to process compositional maps, including (i) classification, (ii) analytical standardisation, (iii) structural formulae calculation and (iv) distinction of compositional groups. Mineral structural formulae have been calculated based on 11 oxygens for white mica and biotite and 8 oxygens for plagioclase. Local bulk compositions were generated from the oxide weight-percentage maps by averaging pixels with a density correction (Lanari and Engi 2017).

Pseudosection (or forward) modelling was conducted in the 10-component NCKFMASHTO (Na2O–CaO–K2O–FeO–MgO–Al2O3–SiO2–H2O–TiO2–Fe2O3) system. MnO was not considered because all phases contained negligible manganese concentrations. Only total Fe is determined by EPMA, while Fe oxidation states (Fe2+ and Fe3+) are not measured. XMapTools considers all Fe in muscovite and biotite to be Fe2+ and thus the bulk composition calculated for sample GR19 assumed total Fe as Fe2+. However, biotite and muscovite in pelitic rocks contain appreciable amounts of Fe3+ (Forshaw and Pattison 2021 and references therein). To account for this and to model in the NCKFMASHTO system, a bulk XFe3+ (= Fe3+/(Fe3+ + Fe2+) in moles) for sample GR19 was determined by combining estimates of XFe3+ in minerals with modal abundances (e.g., Forshaw et al. 2019). Modal abundances of biotite and muscovite were extracted from XMapTools. Ilmenite is the main Fe-oxide in sample GR19, therefore XFe3+ was estimated to be 0.11 in biotite and 0.49 in muscovite (Forshaw and Pattison 2021). Bulk XFe3+ was calculated to be 0.10, which is lower than the whole-rock XFe3+ = 0.23 of the worldwide median pelite (Forshaw and Pattison 2023). However, the latter is based on XFe3+ measurements from titration which should be considered a maximum due to pre-analysis oxidation during grinding (Fitton and Gill 1970). An XFe3+ = 0.10 is consistent with the chosen thermodynamic dataset and solution models that give a Fe-oxide assemblage (ilmenite) that is matched by the phase diagrams (see results below and discussion in Forshaw and Pattison 2021).

Phase diagrams were computed using Theriak–Domino (De Capitani and Brown 1987; De Capitani and Petrakakis 2010), the internally consistent dataset of Holland and Powell (2011; update ds62; February 2012), and associated solution models of White et al. (2014), except for the plagioclase model where the model of Holland et al. (2021) was used. The thermodynamic dataset and solution models were chosen because the solution models incorporate enough Fe3+ end members to simulate Fe3+-bearing phase equilibria (Forshaw and Pattison 2021).

The results of phase equilibrium modelling were compared with those of the conventional Ti-in-Bt geothermometer (Henry et al. 2005). The calibration of Henry et al. (2005) is applicable in peraluminous rocks containing graphite and a Ti reservoir, such as rutile or ilmenite, at low-to-medium pressures (P = 0.4–0.6 GPa) and a T range of 480–800 °C. This geothermometer has an estimated precision of ± 24 °C.

In situ monazite U–(Th)–Pb geochronology

In situ U–(Th)–Pb dating of monazite, integrated with its chemical and microstructural characterisation, was used to constrain the timing of metamorphism (see Kohn et al. 2017 for a detailed review of this technique). Using a scanning electron microscope at the University of Turin (Italy), we investigated the locations of grains, their internal features (e.g., inclusions), and their textural position. Each monazite crystal was then analysed using the JEOL 8200 Super Probe electron microprobe hosted at the Department of Earth Sciences “A. Desio” of the University of Milan (Italy) to elucidate their chemical composition and test for the presence of compositional zoning. This step was necessary in order to correctly interpret monazite grains and their relative ages. Isotopic monazite dating was conducted in situ, on 30 μm-thick thin sections, using Laser Ablation Inductively Coupled Plasma-Mass Spectrometry (LA-ICP-MS) at the Università degli Studi di Perugia (Italy). This facility consisted of a Teledyne/Photon Machine G2 LA device equipped with a HelEx2 two-volumes cell and coupled with a Thermo-Fisher Scientific quadrupole-based iCAP-Q ICP-MS. Monazite crystals were analysed using a circular laser beam of 8–10 μm diameter, a frequency of 10 Hz and a laser fluence on the sample surface of ~ 3.5 J/cm2. Oxides were checked on the NIST SRM 612 standard by monitoring and maintaining the ThO/Th ratio below 0.005. The Delaware standard (424.9 ± 0.8 Ma; Aleinikoff et al. 2006) was used as a calibrator (Supplementary Information S1). The Moacir (or Moacyr, 507.7 ± 1.3 Ma (207Pb/235U) and 513.6 ± 1.2 Ma (206Pb/238U); Gonçalves et al. 2016) and Manangotry (555 ± 2 Ma, Horstwood et al. 2003; 537 ± 14 Ma, Montel et al. 2018) monazite standards were used as quality controls. Data reduction was performed in Iolite4 (Paton et al. 2011) utilising the VizualAge_UcomPbine data reduction scheme (Chew et al. 2014). All subsequent data processing and plotting was done using the software ISOPLOT (Ludwig 2003).

Results

Kinematics of ductile flow

The results of the kinematic vorticity analysis are reported in Table 1. Twelve samples (see Fig. 2a for sample location) analysed with the C′ shear band method gave kinematic vorticity numbers (Wm) ranging from 0.41 to 0.50, with a mean of 0.46. Vorticity analysis using the porphyroclasts-based methods on three samples (GR22-5, L-GRIGHINI and M-GRIGHINI) gave Wm values between 0.37–0.47 and 0.37–0.53 for RGN and PAR, respectively. The datasets collected by the two porphyroclast-based methods are comparable with results using the C′ shear bands approach. Taking into account all results obtained by different methods, the Wm values range between 0.3 and 7–0.53 (Fig. 5).

Table 1 Results of kinematic vorticity investigations: number of data (N), angle between C′ planes and the shear zone boundary (ν), Wm value (Wm), mean value of Wm in a range (Wm) and the average of its range (Wm mid); minimum critical axial ratio (Rc min), maximum critical axial ratio (Rc max), minimum value of Wm (Wm min), maximum value of Wm (Wm max), mean value of Wm (Wm mid)
Full size table
Fig. 5
figure 5

Relationship between kinematic vorticity number Wm and the percentage of pure shear (PS) and simple shear (SS) (modified after Law et al. 2004)

Full size image

Although we used different methods, the resulting kinematic vorticity number values are relatively homogeneous and do not show a significant variation with the degree of strain. The obtained kinematic vorticity number values indicate that the MGSZ experienced general shear (Forte and Bailey 2007) during deformation, which involved 77–64% pure shear and 23–36% simple shear components (Fig. 5). Green bar represents the range of Wm values obtained in this study for the MGSZ.

Mineral composition

Sample GR19 is a sillimanite-bearing mylonitic schist (Fig. 6a) from the Toccori Formation (see Fig. 2a for the sample location) showing syn-kinematic growth of micas and sillimanite. GR19 contains (Fig. 6b; area% = vol%, estimated from XMapTools): quartz (36%), white mica (26%), biotite (22%), sillimanite (14%), with plagioclase and ilmenite as the main accessory minerals (2% in total). Selected mineral compositions for biotite and white mica in sample GR19, derived both from the XMapTools and WDS spot analysis, are reported in Table 2. Representative analyses of plagioclase are provided in Supplementary Material S2.

Fig. 6
figure 6

a Thin section scan of sample GR19. The area mapped using EPMA is indicated in yellow; b Processed X-ray map of sample GR19 showing the distribution of different minerals. The inset pie-chart depicts the volume % for each phase; c/d P–T equilibrium phase diagrams for the high-temperature mylonitic sample GR19. The inferred equilibrium assemblage is highlighted in grey; c Yellow and blue lines mark the staurolite-out and sillimanite-in reactions, respectively; d The intersection of compositional isopleths of biotite and white mica. The temperature obtained from the conventional Ti-in-Bt thermometer is shown by isotemperate purple lines

Full size image
Table 2 Mean XMapTools map analyses and representative WDS spot analyses for white mica and biotite. Position denotes the representative micro-structural domain from which analyses were taken. Structural formulae were calculated for biotite and white mica based on 11 oxygens per formula unit
Full size table

White mica is a muscovite with minor pyrophyllite content. It is homogeneous in composition, with mean Si contents of 3.04 ± 0.03 a.p.f.u. and XMg (= Mg/(Mg + Fetot)) of 0.42 ± 0.04. Whilst two generations of biotite can be distinguished using microstructural criteria (Fig. 6a), these different generations are compositionally similar. Using the Rieder et al. (1999) classification, biotite is classified mainly as biotite with high Al, plotting on the siderophyllite-eastonite solid solution vector with intermediate XMg. Biotite parallel to the Sp shows XMg of 0.39 ± 0.01, whereas the post-kinematic (i.e., post-Dp) biotite displays XMg of 0.35 ± 0.02. The Ti a.p.f.u. in biotite does not change with its structural position and has a mean value of 0.14 ± 0.03. Plagioclase is albitic in composition (XAn = 0.04–0.07).

P–T constraints

Figure 6c and d shows the P–T equilibrium phase diagram for sample GR19, calculated for 0.1–1.0 GPa and 500–700 °C. The sillimanite-in curve is located in the pressure range of ~ 0.3–0.7 GPa and between ~ 560–700 °C. Rutile is stable above the upper sillimanite-in line, while ilmenite is predicted in the sillimanite stability field. The observed mineral assemblage (labelled as Pl–Ms–Bt–Ilm–Sil; Fig. 6c) is represented by a field restricted by a P–T range of 0.3–0.7 GPa and 560–670 °C, delimited by the disappearance of staurolite, the stability boundary of sillimanite, and by the melt-in reaction (Fig. 6c). Predicted compositional isopleths for syn-Sp biotite (XMg = 0.39–0.40) and white mica (Si = 3.03–3.05 a.p.f.u.; XMg = 0.41–0.43) occur within the observed mineral assemblage stability field. The P–T condition has been inferred with compositional isopleths thermobarometry.

Similar temperature results (T = 625 ± 25 °C) have been obtained using Ti-in-Bt conventional geothermometry (Henry et al. 2005), consistent with the phase diagram results (Fig. 6d).

Monazite textural position and chemistry

Two samples, inside and outside MGSZ (GR19 and G49X, respectively; see Fig. 2a for the sample position), were chosen for in situ geochronology of monazite. Cruciani et al. (2016) have previously investigated the P–T conditions of sample G49X. A total of seven monazite grains, two for sample GR19 and five for sample G49X were analysed. Selected analyses of monazite and the spot analysis position are available in Supplementary Material S3 and Fig. 7, respectively.

Fig. 7
figure 7

Textural position, back-scattered electron images and Th, Y chemical maps of selected monazites. Red dots represent the spots of quantitative chemical analyses. Compositional maps of Th and Y made by electron microprobe with spot location and the corresponding 208Pb/232Th (Th) and 206Pb/238U (U) ages are shown; color bar scale qualitatively points lower (L) to higher (H) Y–Th concentration

Full size image

Monazites from sample G49X are between ~ 40 and ~ 120 μm in length. We analysed three monazites from the quartz, biotite, and white mica-dominated foliation and two monazites (Mnz 6a and Mnz 7b) that occur as inclusions within garnet. The monazites from GR19 are between ~ 20 and ~ 60 μm in length. Most of the monazites in this mylonite are very small and difficult to analyse. The crystals located along the Sp foliation are generally within biotite- or sillimanite-rich domains. One monazite (Mnz 11) has an inclusion of sillimanite (Fig. 7). This crystal is particularly interesting because the sillimanite grew during the high-strain shearing event. Backscattered electron (BSE) images show clear zoning in most grains with domains of different grey tones (Fig. 7). X-ray compositional maps reveal that such zoning is controlled by the different distributions of X(HREE + Y) and X(LREE) + Th (Fig. 7). X(HREE + Y) is defined as (HREE + Y)/REE, whereas X(LREE) is LREE/REE. The Electron microprobe analysis revealed two chemical domains (I and II), based on Y, Th, and REE content. In sample G49X, Domain I (Fig. 8a, b) is characterised by cores with medium-Y content ranging from 0.022 to 0.035 (a.p.f.u.), low-Th values from 0.01 to 0.026 (a.p.f.u), and X(HREE + Y) low amounts varying from 0.044 to 0.067. Domain II (Fig. 8a, b) is characterized by medium–high Y rims/grains, 0.028 < Y < 0.057 (a.p.f.u.), low-medium Th values from 0.05 to 0.055 (a.p.f.u) and 0.071 < X(HREE + Y) < 0.094. The monazites enclosed in garnet crystals follow the same zoning pattern of many matrix crystals and are chemically similar, in which the cores show medium/low-Y and X(HREE + Y), and the rims are enriched in these same elements. In sample GR19, Domain I (Fig. 8a, b), as documented by X-ray maps (Fig. 7), occurs only in Mnz 11, where a medium-Y (Y = 0.033) and low-medium-Th (Th = 0.013) core is recognisable. Medium- to high-Y values (0.042 < Y < 0.061 a.p.f.u.), medium-Th values from 0.018 to 0.041 (a.p.f.u) and X(HREE + Y) between 0.069 < X(HREE + Y) < 0.095 are well preserved and represent the main features of Domain II (Fig. 8a, b). This domain has been observed both as a continuous rim around cores or as a homogeneous medium–high-Y content grain. The sillimanite inclusion is inside the Y-rich rim correlated with Domain II.

Fig. 8
figure 8

Chemical monazite variations in sample G49X and GR19: a X(HREE + Y) vs. X(LREE) plot and in b X(Y + HREE) vs. Th plot. X(HREE + Y) is defined as (HREE + Y)/REE, whereas X(LREE) is LREE/REE. In both diagrams, monazite compositional domains (I and II) and the microstructural position of the analysed grains are highlighted; c and d 206Pb/238U versus 207Pb/235U concordia diagrams for sample G49X and GR19. In sample G49X the dashed ellipse indicates a spot not aligned along the concordia line

Full size image

In summary, based on the previously described textural and chemical arguments, monazite, in both samples, shows two main growth domains/generations: (i) Domain I, representing the core of the grains both in garnet and along the mylonitic foliation, with low-medium-Y contents; and (ii) Domain II, forming continuous to rarely discontinuous high X(HREE + Y) rims or homogeneous grains, mainly occurring in the matrix. Considering the resolution of the applied method, we did not detect any significant differences between the monazite chemistry and obtained ages.

In situ U–(Th)–Pb geochronology and ages

The measured isotopic data are reported in Supplementary Material S4 (see Fig. 7 for the laser spot analysis position). A total of seven monazite grains covering the whole textural–chemical variability were selected for in situ dating, and analyses were collected from a total of 13 spots (10 for sample G49X and 3 for sample GR19). Results are plotted on a 206Pb/238U versus 207Pb/235U concordia diagram (Fig. 8c, d). The concordia calculation gives ages of 321 ± 3.3 and 311 ± 7.3 Ma for G49X and GR19, respectively (Fig. 8c, d). The monazite grain within a sillimanite inclusion (Sample GR19 in Mnz 11) produced similar ages of 315–310 Ma. Results are similar for the two samples, with no variation in ages between different chemical domains within the analytical error.

Discussion

P–T–D–t tectono-metamorphic evolution

The combination of structural investigations at different scales (from meso- to microscale), with the P–T estimations from pseudosection (or forward) modelling integrated with conventional Ti-in-biotite geothermometry, have elucidated the tectono-metamorphic evolution of four ductile deformation phases in the study area. Correlations between the deformation phases identified in this work, indicated with the subscript “p” and those previously proposed in the area (Musumeci et al. 2015; Cruciani et al. 2016) are reported in Supplementary Material S5.

Dp − 1 structures are associated with a relict Sp − 1 foliation both in the hinges of Fp folds or as an internal foliation in porphyroblasts. The dominant structural architecture of the study area is controlled by the Dp phase, where the deformation is partitioned into low- and high-strain zones. Moving toward the MGSZ, strain increases progressively and is characterised by an increase in the degree of non-coaxial deformation. Dp folds become smaller and less frequent in the high-strain zones, while the mylonitic foliation becomes more penetrative and continuous (strain partitioning; e.g., Jones and Tanner 1995). Our data highlight, in agreement with previous authors (Columbu et al. 2015), an increase in strain and in the abundance of kinematic indicators towards the MGSZ, with mylonites observable in both the IC and the MGC. The mylonitic foliation in the MGSZ is from moderate to sub-vertical and the lineation is from gently plunging to sub-horizontal.

The kinematics of ductile Dp deformation in terms of the percentages of progressive pure and simple shear components were determined using two independent methods. Although different lithologies (i.e., gneiss vs micaschist) with different rheologies and possibly strain memory were analysed along the studied transects, our Wm estimates indicate that a strong component of pure shear was acting together with simple shear (Fossen and Tikoff 1998; 77–64% pure shear and 23–36% simple shear components, see Fig. 5). No significant variations between both methods and different lithologies were observed. In a classical pure shear dominated transpressional regime in which the extrusion component is upwards in the dip direction of the deformation zone, we should expect that the lineation should be sub-vertical or steeply plunging (Sanderson and Marchini 1984; Robin and Cruden 1994). However, in the case of a transpressive regime, models predict two end members with horizontal or vertical extrusion (Fossen and Tikoff 1998; Schulmann et al. 2003; Iacopini et al. 2008) depending on the orientation of the maximum axis of the finite strain ellipsoid. Iacopini et al. (2008) demonstrated that the orientation of the lineation is a function of time, strain rate and vorticity. Assuming constant strain rate, in the case of horizontal extrusion, Iacopini et al. (2008) demonstrated that a decrease in kinematic vorticity number increases the tendency of the lineation to develop sub-horizontally. In particular for low kinematic vorticity values, as in this case study, the lineation develops from gentle plunging to sub-horizontally and its orientation is stable in the flow during the progressive deformation (see Fig. 14 in Iacopini et al. 2008).

A possibility to explain the presence of sub-horizontal stretching lineations in a transpressional tectonic setting could be that at the beginning of the activation of the shear zone the pure shear component is predominant and a steeply plunging lineation develops and later, during progressive deformation, the (dextral) simple shear component increases which reorients the lineation to a sub-horizontal attitude.

We need also to consider that a deep seated shear zone such as the MGSZ developed under P conditions of 0.4–0.6 GPa and T = 650 °C, suggesting a crustal depth of nearly 12–18 km. In this case the expected vertical extrusion is not easy since it is counteracted by the lithostatic load. The sheared ductile material needs to escape but if the vertical movement is obstructed by the lithostatic pressure it will flow in another direction. A non planar dextral vertical strike slip shear zone, with dextral releasing bends could easily accommodate horizontal extrusion induced by the pure shear component. In addition, according to Iacopini et al. (2008) horizontal extrusion in a sub-vertical, ductile transpressional shear zone is theoretically possible and the horizontally extruded material can easily follow the space created by progressively opening releasing bends. This can also aid in the emplacement of the syn-kinematic leucogranite and tonalite magmas.

Another possibility to explain the structural setting could be the presence of overprinting tectonic events that in the present study could have involved thrusting followed by strike slip tectonics.

Nevertheless, the subvertical attitude of the mylonitic foliation in the MGSZ is compatible with a transpressive regime associated with a dextral shear deformation with a shortening component perpendicular to the shear zone boundaries. In the case of transtensional deformation, as previously suggested by Musumeci (1992) and Cruciani et al. (2016), the attitude of the mylonitic foliation is expected to be sub-horizontal due to the main sub-vertical shortening direction (Fossen et al. 1994; Schulmann et al. 2003).

Fp and Fp + 1 fold axes show the same trend but not the same plunge angle. This could be associated with the ongoing deformation with a sub-horizontal or slightly inclined shortening up to the final stages of collisional events. Subsequent post-collision and post-transpression gravitational instability led to the development of open folds with shallowly dipping axial planes (Fp+2). This geometry suggests the gravitational collapse of a thickened orogen (Carmignani et al. 1994).

A NE to SW increase in metamorphic grade is observed, in agreement with Musumeci et al. (2015) and Cruciani et al. (2016). The syn-kinematic Dp mineral assemblage (sillimanite + biotite + white mica) parallel to the Sp mylonitic foliation is indicative of medium- to high-temperature amphibolite-facies conditions. Phase equilibrium modelling suggests peak P–T conditions at ~ 0.4–0.6 GPa and ~ 625 °C, pointing to a high-temperature and low-pressure (HT/LP) thermal regime. Taking into account the uncertainties in our P–T estimates and those of previous studies (Cruciani et al. 2016), the observed non-coaxial deformation could be associated with P–T conditions of ~ 625 ± 25 °C and ~ 0.4 ± 0.1 GPa. The investigated mylonitic sample clearly shows sillimanite oriented parallel to Sp, suggesting that ductile deformation was still active under high-temperature conditions when sillimanite was stable. The results obtained from the thermodynamic modelling are also supported by quartz microstructures and Ti-in-biotite temperatures (625 ± 25 °C). The growth of fibrolitic sillimanite at the expense of the prismatic grains, and the presence of post-Sp biotite, may represent growth on a retrograde path during the late stages of the transpression. These conditions are consistent with the retrograde path observed by Cruciani et al. (2016).

The timing of the Dp event has been constrained by in situ U–(Th)–Pb monazite dating. Even though some monazite compositional features differ between the samples, both record a similar and comparable timing on the Sp both inside and outside the high-strain zone. This is in agreement with deformation partitioning, where contemporaneous low- and high-strain zones occurred during Dp transpression. The obtained ages of ca. 315 Ma are associated with high-Y and low-Th inner rims and in monazites that grew along Sp. In addition, the monazite crystal with sillimanite inclusions (Sample GR19, Mnz 11), compatible with domain II of the monazite chemical group, indicates similar ages at ca. 315–310 Ma, constraining the age of non-coaxial deformation. Enhanced strain partitioning characterized by low- and high-strain zones could have favoured the emplacement of igneous intrusions along weak zones during the late stages of the non-coaxial deformation (Fig. 9a). This is consistent with the syn-tectonic emplacement age of the IC at ca. 305–295 Ma (Del Moro et al. 1991) within the MGSZ and the presence of sheared granites, which highlights that deformation linked to dextral transpression was still active until ca. 300 Ma. These data indicate that the MGSZ was active over a time span of ca. 15 Ma.

Fig. 9
figure 9

a Simplified scheme of the tectonic evolution of MGSZ deduced from structural observations and the P–T–t results. The late syn-Dp intrusions have been provided; b Sketch maps of the Southern European Variscan belt during the late Carboniferous (modified from Corsini and Rolland 2009; SA Sardinia, MTM Maures–Tanneron Massif, CO Corsica, ARG Argentera Massif, AIG Aiguilles Rouge Massif); c Inferred lateral relationships between the branches of EVSZ during the late Carboniferous (modified after Simonetti et al. 2020a, b)

Full size image

The MGSZ: implications for late-Carboniferous transpressive deformation

Late Variscan transpressive shear zones played a fundamental role in the architecture of the Sardinian Variscan belt (325–305 Ma, Di Vincenzo et al. 2004; Carosi et al. 2012, 2020; Cruciani et al. 2022a, b). Similar architecture to that documented here for the MGSZ has also been described in the northern sector of Sardinia, where the amphibolite-facies transpressive Posada-Asinara shear zone is exposed (PASZ; Carosi and Oggiano 2002; Carosi and Palmeri 2002; Iacopini et al. 2008; Frassi et al. 2009; Carosi et al. 2012, 2020, 2022; Graziani et al. 2020; Petroccia 2023). The amphibolite-facies metamorphic conditions recorded by both shear zones are highlighted by the presence of syn-kinematic sillimanite + biotite or biotite + white mica parallel to the mylonitic foliation. The PASZ developed under decreasing temperature and pressure, starting at ca. 325 Ma and was active for ca. 25 Ma. Carosi et al. (2020) constrained the timing of the activity of the PASZ using the same in situ monazite dating approach used in this work. The MGSZ and the PASZ record a similar percentage of pure shear deformation (Carosi et al. 2020; Petroccia 2023). Our new data enhances a possible correlation of the MGSZ to the PASZ in the Sardinian Variscan belt framework, already proposed by Elter et al. (1990).

Geochronological data indicate that similar ages for the onset of transpression in the MGSZ have been obtained in different sectors of the Southern European Variscan belt (Simonetti 2021; Carosi et al. 2022; Fig. 9b). In particular, similar features and ages of transpressive tectonics have been observed in Sardinia (Carosi et al. 2020), as well as in the Maures–Tanneron Massif (MTM, France; Simonetti et al. 2020a; Bolle et al. 2023) and in the External Crystalline Massif (Italy and France; Simonetti et al. 2018, 2020b, 2021; Jacob et al. 2021; Fréville et al. 2022; Vanardois et al. 2022a, b). All these have been associated with the East Variscan Shear Zone framework (EVSZ; Matte 2001; Corsini and Rolland 2009; Padovano et al. 2012, 2014; Simonetti 2021; Fig. 9b). The EVSZ is a network of interconnected transpressive shear zones displaying a similar evolution (Simonetti 2021). The oldest ages (ca. 340 Ma; Simonetti et al. 2018, 2021) of the transpressive deformation are found in the External Crystalline Massif, whereas within the MTM (ca. 323 Ma) and the island of Sardinia (ca. 325–300 Ma), ages are younger. The MGSZ is slightly younger (ca. 315–300 Ma) than the PASZ in Sardina (Fig. 8c). According to Simonetti et al. (2020b), it is therefore possible that transpressional deformation within the EVSZ preferentially started to be accommodated in the lower, migmatitic crust (External Crystalline Massif; Simonetti et al. 2021; Bühler et al. 2022; Vanardois et al. 2022a, b) and later shifted into the medium- and high-grade metamorphic complex, as in northern Sardinia and the MTM (Carosi et al. 2020, 2022; Simonetti et al. 2020a). Until now, transpressive shear linked to the EVSZ has only been recognised at the boundary between the medium- and the high-grade rocks or within the migmatitic complex. However, transpression in the MGSZ started later than in other, more internal, shear zones (e.g., the PASZ in Sardinia). This is possibly caused by the progressive migration and rejuvenation of deformation from the core or the hinterland to the external sectors of the collisional belt. Integrating our results with the existing findings, the tectonic framework of EVSZ represents a network of interconnected transpressive shear zones that, due to the progressive migration of the deformation over time, localized initially in the migmatitic crust, and later affected the medium- and high-grade metamorphic complex and finally the nappe zone located in the hinterland–foreland transition zone of the Variscan belt.

Conclusions

We carried out a geological investigation to elucidate the tectono-metamorphic evolution of the non-coaxial deformation linked to the MGSZ. This study has both local and regional implications for the interpretation of this shear zone within the Sardinian Variscan belt and its role in the late-Carboniferous Variscan orogeny. We have demonstrated the following:

  1. 1.

    Meso- and microstructural data highlight that the principal structures associated with the Dp formed during deformation in which strain was partitioned into low-strain zones mostly dominated by folding and high-strain zones dominated by LS tectonites and kinematic indicators. Kinematic analysis of ductile flow structures within the high-strain zone indicates non-coaxial deformation under a pure shear-dominated transpressive regime. Phase equilibrium modelling indicates that the formation of mylonitic fabrics within the MGSZ occurred under HT-LP amphibolite-facies conditions at ~ 625 °C and ~ 0.4–0.6 GPa.

  2. 2.

    In situ U–(Th)–Pb geochronology on monazite highlights the same age of the deformation within the low- and high-strain zones. The onset and the progressive evolution of the MGSZ with the associated syn-kinematic intrusions lasted from ca. 315 up to ca. 300 Ma, over a time span activity of ca. 15 Ma.

  3. 3.

    The MGSZ shows striking similarities with other dextral ductile transpressive shear zones within both the Sardinian Variscan chain (e.g., the PASZ) and other Variscan basements in Southern Europe. Owing to its position within the chain (i.e., hinterland–foreland transition zone or Nappe Zone) and the obtained ages, the MGSZ was one of the youngest and most external transpressive shear zones active in the EVSZ framework. Our data highlight that the network of interconnected transpressive shear zones related to the EVSZ also deformed, as in the MGSZ, the nappe zone of the Variscan belt.

Software

The map has been drawn using QGis3.16 Hannover, and its final assemblage has been realized with Adobe Illustrator® CC 2020. Structural data have been plotted with the software Stereonet© 10. The kinematic vorticity analysis with the stable porphyroclasts method and the finite strain analysis were performed using the software EllipseFit 3.2 by Vollmer (2015). Geochronological data were treated with Isoplot 3.70 (Ludwig 2008).