Advertisement

International Journal of Earth Sciences

, Volume 101, Issue 5, pp 1211–1228 | Cite as

Lithosphere thermal structure at the eastern margin of the Bohemian Massif: a case petrological and geophysical study of the Niedźwiedź amphibolite massif (SW Poland)

  • J. Puziewicz
  • L. Czechowski
  • L. Krysiński
  • J. Majorowicz
  • M. Matusiak-Małek
  • M. Wróblewska
Open Access
Original Paper
First Online:

Abstract

The crustal section beneath amphibolite Niedźwiedź Massif (Fore-Sudetic Block in NE Bohemian Massif), modelled on the basis of geological and seismic data, is dominated by gneisses with subordinate granites (upper and middle crust) and melagabbros (lower crust). The geotherm was calculated based on the chemical analyses of the heat-producing elements in the rocks forming the crust and the measurements of their density and heat conductivity. The results were verified by heat flow calculations based on temperature measurements from 1,600 m deep well in the Niedźwiedź Massif and by temperature–depth estimates in mantle xenoliths coming from the nearby ca. 4.5 My basanite plug in Lutynia. The paleoclimate-corrected heat flow in the Niedźwiedź Massif is 69.5 mW m−2, and the mantle heat flow is 28 mW m−2. The mantle beneath the Massif was located marginally relative to the areas of intense Cenozoic thermal rejuvenation connected with alkaline volcanism. This results in geotherm which is representative for lithosphere parts located at the margins of zones of continental alkaline volcanism and at its waning stages. The lithosphere–asthenosphere boundary (LAB) beneath Niedźwiedź is located between 90 and 100 km depth and supposedly the rheological change at LAB is not related to the appearance of melt.

Keywords

Crust Upper mantle Lithology Geotherm Sudetes 

Introduction

The subcontinental lithospheric mantle is inhomogeneous in terms of mineral and chemical composition (e.g. Griffin et al. 1999). The variation occurs both at the regional and local scale, and it is due to modification of protolith by melting events, typically followed by later multiple infiltration of silicate melts and volatiles (“mantle metasomatism”; Downes 2001).

The lithospheric mantle beneath the European Variscan Orogen was affected by Cenozoic metasomatism related to the formation of the Central European Volcanic Province (e.g. Wilson and Downes 1991). Volcanic activity has brought to the surface mantle xenoliths in some places. The xenoliths are the source of information on the mantle composition and its evolution.

The metasomatic agents (silicate melts, volatiles) as well as the volcanism itself transfer not only the mass, but also heat. Thus, the question arises, if there exists a local and regional variability in upper mantle temperatures occurring in the recently active areas such as the Central European Volcanic Province. This question could be answered by geologic thermometry on the mantle xenoliths. The recent heat flow data coupled with the calculations of crustal geotherms enable the assessment of temperature of the crust and the upper mantle and can serve as a reference for geotherms based on mantle xenoliths. However, the xenolith thermometry suffers from numerous factors affecting calibrations, and its results show the thermal state of the mantle at the moment of xenolith entrainment, which usually is separated by time span of some millions of years from recent. The geotherm calculations are based on some assumptions which cannot be verified, such as lithology of the crustal sections involved.

In this paper, we present the case study of lithosphere temperature in the area of the amphibolite Niedźwiedź Massif in NE Bohemian Massif. We use the temperature log from ca. 1,700 m deep Niedźwiedź IG-2 well to calculate the surface heat flow, the geotherm calculations based on geological model of the crust in the area and the thermometric calculations in mantle xenoliths from the nearby Lutynia 4.5 My basanite. Our results allow the discussion of subrecent lithosphere temperature and the location of lithosphere–asthenosphere boundary.

Geological background

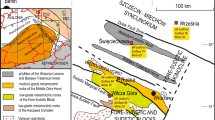
The Bohemian Massif forms the eastern part of the European Variscan Orogen. The north-eastern part of the Bohemian Massif consists of the Sudetes and Fore-Sudetic Block, which are the mosaic of crystalline basement units and sedimantary/volcanic units (e.g. Kryza et al. 2004). The eastern part of the Bohemian Massif contacts with the (located to the east) Moravo-Silesian Zone (Żelaźniewicz and Aleksandrowski 2008). The Moldanubian thrust, separating the Moravo-Silesian Zone and the Bohemian Massif, continues to the north in the Sudetes and Fore-Sudetic Block. The thrust separates the West Sudetes (the hanging wall, part of the Bohemian Massif) from the east Sudetes, belonging to the Moravo-Silesian Zone (e.g. Franke and Żelaźniewicz 2000, 2002; Żelaźniewicz and Aleksandrowski 2008). The thrust is readily recognisable in the Sudetes, whereas its location in the Fore-Sudetic Block is debatable (Fig. 1; Oberc-Dziedzic and Madej 2002; Mazur et al. 2010 and references therein).
Fig. 1

a Location of the Niedźwiedź Amphibolite Massif in the Bohemian Massif (small rectangle shows the area of map b). Granites and metamorphic rocks are marked with crosses and horizontal lines, respectively. b The contour of the Niedźwiedź Massif gravimetric anomaly (cf. Fig. 3) relative to other geological units of the eastern part of the Fore-Sudetic Block. Dashed line is the location of the Nýznerov Dislocation Zone (the prolongation of the Moldanubian Thrust) in the Fore-Sudetic Block after Skácel (1989). IG-1, IG-2—drillings of the Polish Geological Institute

The Niedźwiedź Massif is an occurrence of amphibolites located supposedly immediately above the Fore-Sudetic prolongation of the Moldanubian Thrust in the Fore-Sudetic Block (Fig. 1). The surface exposures of the amphibolites are not numerous and small. The early geological and geophysical studies suggested that the Massif is ca. 20 km long, 5–6 km wide and up to 3,800 m thick (Jerzmański 1991). More recently, Awdankiewicz (2003, 2008) suggested that the thickness of amphibolites does not exceed 3,300 m. The drillings of Polish Geological Institute showed that the Massif is covered by approximately 100 m of tertiary/quaternary sediments (Jerzmański 1992).

The surface exposures as well as cores from the two boreholes show that the Niedźwiedź Massif is dominated by garnet-hornblende granofelses, amphibolites, garnet amphibolites and zoisite amphibolites. Puziewicz and Koepke (2001) interpreted the garnet granofelses as the product of peak metamorphism, which took place under 1.2–1.3 GPa and 790°C; under these conditions, the incipient partial melting took place, resulting in leucocratic, igneous epidote-bearing tonalitic schlieren and clinopyroxene restite. The melting might have been enhanced by decompression. The further decompression and cooling, combined with deformation, led to the foliation development and converted the primary assemblage of garnet + hornblende I into the plagioclase + hornblende II, and low-grade assemblage zoisite + pumpellyite + albite + actinolite was produced in the zones of high strain (Puziewicz 2006).

Geochemical study of Awdankiewicz (2003, 2008) revealed dominating N-MORB tholeiitic geochemical characteristics of amphibolites, with some high-Mg and transitional within-plate varieties and subordinate andesites, geochemically similar to within-plate tholeiites. This led Awdankiewicz (2003, 2008) to the conclusion that the metabasic rocks of the Niedźwiedź Massif originated in a narrow intracontinental oceanic basin, probably of early Palaeozoic age. The high-Mg metabasic rocks were interpreted by the cited author as plagioclase-pyroxene cumulates, and the Massif was suggested to be the differentiated basic pluton, with upper parts of subvolcanic nature.

Sampling, analytical methods and terminology

The samples representing the rocks of the Niedźwiedź Massif and its surrounding come from surface exposures. Some of them have been petrologically described in various papers (Table 1). The samples were analysed for bulk-rock chemical compositions and their density and heat conductivity were measured.
Table 1

Summary of the petrological and geophysical data on the representative rocks of the Niedźwiedź Amphibolite Massif and its surrounding

No.

Rock name, location

Sample no and reference for petrological data

K2O (wt%)

U (ppm)

Th (ppm)

Density (kg m−3)

Radiogenic heat production per mass unit (W kg−1)

Radiogenic heat production per volume unit (W m−3)

Thermal conductivity (W K−1 m−1)

1

Garnet amphibolite Niedźwiedź Massif

C1501 (Puziewicz 2006)

0.09

<0.1

<0.2

3,213

1.72 × 10−11

5.54 × 10−8

2.518

2

Garnet amphibolite Niedźwiedź Massif

K1620 (Puziewicz 2006)

0.09

<0.1

<0.2

3,117

1.72 × 10−11

5.37 × 10−8

2.640

3

Garnet amphibolite Niedźwiedź Massif

E00

0.12

<0.1

0.3

3,084

2.07 × 10−11

6.37 × 10−8

2.235

4

Zoisite amphibolite Niedźwiedź Massif

K1636

0.04

<0.1

<0.2

3,079

1.58 × 10−11

4.86 × 10−8

2.082

5

Epidote-zoisite amphibolite Niedźwiedź Massif

C1503 (Puziewicz 2006)

0.16

0.1

<0.2

3,078

1.93 × 10−11

5.93 × 10−8

2.289

6

Amphibolite Lipniki

1526

0.22

<0.1

0.4

3,017

2.61 × 10−11

7.88 × 10−8

2.370

7

Orthogneiss Lipniki

1520

5.19

3.3

29.0

2,641

121 × 10−11

319 × 10−8

2.551

10

Amphibolite Chałupki

2202

0.92

0.4

1.4

3,050

10 × 10−11

30.7 × 10−8

2.035

11

Paragneiss Chałupki

701 (Puziewicz et al. 1999)

4.16

2.6

13.9

2,733

72.4 × 10−11

198 × 10−8

2.474

15

Granite Maciejowice

K1301

5.21

1.7

18.7

2,634

79.1 × 10−11

208 × 10−8

2.973

16

Leucocratic gneiss Maciejowice

K1307

4.47

1.5

9.0

2,806

50.2 × 10−11

141 × 10−8

1.997

17

Melagabbro Księginki

2825

0.06

0.4

0.6

2,903

5.52 × 10−11

16.0 × 10−8

2.000

18

Peridotite

Assumed

   

3,200

0.23 × 10−11

0.736 × 10−8

Eq. 2

Whole-rock chemical analyses were acquired in ACME Analytical Laboratories, Vancouver, Canada (200 mg sample, LiBO2–LiB4O7 fusion, protocol 4A for major elements, ICP-ES, protocol 4B for trace elements, ICP-MS). The details are available at http://acmelab.com. The contents of potassium, thorium and uranium were used for the calculation of radiogenic heat by the formula of Rybach (1988).

The density of rocks was determined at the laboratory of the Institute of Oil and Gas in Cracow (Poland) by means of gas picnometer AccuPuyc 1330 using helium.

Thermal conductivity was measured in the laboratory of Polish Geological Institute in Warsaw (Poland) by thermal conductivity scanner developed by Y. Popov (model of Lippman and Rauen, Germany).

The crustal structure beneath the Niedźwiedź Massif

The rock sequences are dipping to the west in the area of contact of the East and West Sudetes (e.g. Mazur and Józefiak 1999; Mazur et al. 2010), and thus, the rocks cropping out to the east of the Niedźwiedź Massif are good candidates to occur beneath the Niedźwiedź Massif.

The Niedźwiedź Massif is situated in the part of the Fore-Sudetic Block which is extremely poor in exposures of basement rocks, which are covered by Cenozoic sediments of thickness reaching a few hundred metres. Immediately above the Niedźwiedź Massif (i.e. to the west), the Chałupki paragneisses with subordinate amphibole gneisses and amphibolites occur (Puziewicz et al. 1999). The Massif is underlain by the orthogneisses with subordinate inliers of amphibolites, occurring to the east and forming small outcrop near to the village Lipniki (Mazur et al. 1997). Further to the east, in large abandoned quarry near Maciejowice granites and peraluminous leucocratic gneisses with subordinate diorites, mica schists and limestones occur (Korzekwa 1995). The Maciejowice gneisses are usually considered to be a part of the Moravo-Silesian Zone (e.g. Mazur et al. 2010), although Oberc-Dziedzic and Madej (2002) propose that they may be thrust sheet of Western Sudetic origin.

Other outcrops of the basement are located significantly more to the north (the Strzelin Crystalline Massif) or to the south (the Žulova granitic pluton with its cover rocks).

The rock assemblages exposed in Lipniki and Maciejowice are thus representative for upper crust underlying the Niedźwiedź Massif. Analogous rocks might occur also in the middle crust, although this assumption is speculative. However, for further modelling, we use the data of granites and orthogneisses occurring in Lipniki and Maciejowice. Since the paragneisses occur commonly within the basement sequences of Moravian part of the Bohemian Massif, we assume the participation of paragneissic rocks as well. They are represented by the Chałupki paragneiss in our models. This paragneiss protolith was a typical greywacke with significant participation of the pelitic material (Puziewicz et al. 1999).

The volume of granites occurring in the upper and middle crustal levels has significant bearing for heat flow modelling. We do not have observations which would be suggestive of the real volume of granites in the crust in the area of Niedźwiedź. The orthogneisses in Lipniki are poorly deformed granites (Mazur et al. 1997), which thickness probably does not exceed first kilometres (max. ca. 3 km, Badura 1985). First hundreds of metres of bodies of granites (dikes?) occur in Maciejowice. Situated to the north, Strzelin Crystalline Massif contains volumetrically small dikes and sheets of Variscan granites, which thickness does not exceed first kilometres (Oberc-Dziedzic et al. 1996). On the other hand, the relatively large Žulova granitic pluton is occurring to the south. Thus, for modelling, we used two models of granite occurrences in the upper/middle crust. The first one assumes subordinate granites occurring within the mainly gneissic upper and middle crust. The orthogneiss from Lipniki is the representative granitic rock in this model. By analogy with the geological surface data, we propose that there is 1 km of granites in that model (Fig. 2 model A). The second upper/middle crust model assumes the occurrence of granitic pluton of thickness 5 km within the upper and middle crust (Fig. 2 model B). The granite from Maciejowice is the representative granitic rock in this model. The upper/middle crust is assumed to consist of 17 km of leucocratic peraluminous gneiss (analogous to the Maciejowice orthogneiss) and 8 km of the paragneiss (analogous to the Chałupki paragneiss) + granite.
Fig. 2

Hypothetical crust models in the area of the Niedźwiedź Massif compared with located nearby seismic profiles S03 (Majdański et al. 2006) and CEL10 (Hrubcová et al. 2008). The numbers refer to shooting points in the profiles. a Model A—the granites of small thickness within the crust; b Model B—the 5 km granite intrusion within the crust

The nature of lower crust is difficult to assess. Two competitive views on the development of the Bohemian massif are currently discussed, which lead to different lower crustal lithologies. Massone (2005) proposes extensive delamination of the European Variscan orogen at ca. 340 Ma, which involved also significant (>10 km) part of lower crust, followed by hot mantle upwelling and thinning of continental crust connected with granitic magmatism. In this model, the mafic rocks occurring at the base of thickened orogen are removed during delamination. The felsic rocks moving up after deep sinking in the mantle were probably emplaced at the base of the crust (Massone 2005). This model suggests that the lower Variscan crust might be dominated by felsic granulites. Alternative model is presented by Babuška and coworkers (e.g. Babuška et al. 2010; Babuška and Plomerová 2006) who argue that no delamination took place during the development of the Variscan Orogen. This model would imply more mafic lower crust, consisting of mafic granulites. In both models, the gabbroic rocks at the base of the crust can be formed due to basic magma underplate at Moho.

The Niedźwiedź Massif is located between the seismic profiles CEL10 (Hrubcová et al. 2008) and S03 (Majdański et al. 2006). The distance to CEL10 is ca. 50 km and that to S03 is ca. 30 km. Both the profiles show Moho at 31–32 km. The crustal structure in parts of the profiles located close to the Niedźwiedź Massif is similar (cf. Fig. 2), relatively homogeneous, and characterised by:
  1. 1.

    upper crust of thickness of ca. 18 km (V p  = 6.0–6.2 km s−1); both profiles show a reflector at ca. 10 km depth;

     
  2. 2.

    middle crust from ca. 18–27 km depth (V p  = 6.35–6.55 km s−1);

     
  3. 3.

    lower crust from ca. 27–31 km (V p  = 6.85–6.90 km s−1); located to the SE in the CEL10 profile, lower crust is the terminal part of densely layered structure with V p 6.8–7.0 km s−1, which is located more to the south in the S03 profile, and we assume the S03 profile to be representative for the Niedźwiedź crust.

     

The upper and middle crustal velocities fit well the models of crust dominated by gneisses possibly intruded with negligible granites (Fig. 2). We suggest that the reflector at 18 km (S03) is located within the essentially gneissic lithologies which differ by participation of amphibolitic inliers, more abundant in the lower crustal segment. The lowest part of middle crust is characterised by velocities of ca. 6.5 km s−1 in both seismic sections (Fig. 2), and we suggest significant participation of gabbroic and/or amphibolitic rocks in the essentially gneissic lithologies (we use the seismic velocities of Christensen and Mooney 1995, at temperatures similar to those suggested by our calculations presented in the following (260°C at 10 km and 645°C at 25 km).

The lower crust velocities suggest the plagioclase-pyroxene, hornblenditic or mafic garnet granulitic lithologies (Christensen and Mooney 1995, at 25 km and temperature from 389 to 645°C). For our models, we propose the melagabbro of lower crustal origin, coming from our collection (lower crustal xenolith from the Miocene Księginki nephelinite, clinopyroxene 85.8, plagioclase 11.7, spinel 2.5 vol.%, Puziewicz et al. 2011) for which the chemical analysis including heat-producing elements is available. The rock, dominated by clinopyroxene with subordinate amount of plagioclase, fits well the model of plagioclase-pyroxene lithology. We assume that the melagabbro is not related to the Niedźwiedź basic rocks.

The lithospheric mantle in the region of the Niedźwiedź Massif

The information on lithospheric mantle is available, thanks to the Lutynia basanitic plug (Wierzchołowski 1993), located ca. 20 km SSW from the Niedźwiedź Massif and dated at 4.56 ± 0.2 My (K–Ar age; Birkenmajer et al. 2002). The basanite carries spinel harzburgite and spinel lherzolite xenoliths up to 10 cm in diameter plus some clinopyroxene megacrysts and scarce pyroxenite xenoliths (Kozłowska-Koch 1976; Matusiak-Małek et al. 2010). Their temperatures of equilibration vary between 960 and 1,000°C (Matusiak-Małek et al. 2010; two-pyroxene Brey and Köhler 1990, thermometer, for details see the cited reference).

The pressure of equilibration of the Lutynia xenoliths cannot be precisely assessed in spinel facies peridotites. At the temperature of 1,000°C, the spinel is stable at relatively narrow pressure range between 0.90 (Presnall et al. 2002 and references therein) and 1.55 GPa (Klemme and O’Neill 2000 and references therein). The 0.90 GPa corresponds to the depth of Moho beneath Niedźwiedź (31 km, the pressure calculated for both the models using measured rock densities is ca. 0.89 GPa). The upper pressure limit of 1.55 locates the spinel–garnet mantle facies transition at 51 km (the density of lower crustal pyroxenites and mantle peridotites was assumed to be 3.30 g cm−3 after Christensen and Mooney (1995). This suggests ca. 19 km thickness of spinel facies beneath the Niedźwiedź Massif.

Matusiak-Małek et al. (2010) documented post-garnet spinel-clinopyroxene symplectites in Lutynia and showed that they originated due to pressure decrease connected with cooling. In our opinion, short-distance uplift of garnet-facies rocks into the spinel facies is more likely than the large-distance transfer within the lithospheric mantle, and we speculate that the Lutynia xenoliths come from mantle region located close to the garnet–spinel facies transition. The data presented by Matusiak-Małek et al. (2010) show that the xenoliths were in chemical equilibrium before they were entrained into the erupting lava. Thus, we assume that the temperatures 960–1,000°C recorded in the Lutynia xenoliths represent the thermal state of the mantle at the moment of eruption and that the depth of their origin was ca. 50 km.

Gravity model of the Niedźwiedź Massif

The first data regarding the gravity anomaly of the Niedźwiedź Massif were discussed by Jerzmański (1991), who reported anomaly values up to several tens of mGal and the density of prevailing part of the amphibolites to be 3.0–3.2 g cm−3 (up to 92.4% in the borehole Niedźwiedź IG-2). The map of the Niedźwiedź Massif Bouguer anomaly (Jerzmański 1992; Awdankiewicz 2003) shows oval, elongated N–S isolines with maximum at the area of surface exposures of amphibolites SE of the village Lubnów. The unpublished reports of Polish Geological Institute, which were the source of geophysical data commented by Jerzmański (1992), led him to estimate amphibolites thickness of 3,800 m.

The data on relative proportions of the amphibolite varieties presented by Awdankiewicz (2003, 2008) and our density measurements show that the amphibolites density varies from 3.078 to 3.213 g cm−3. This is due to varying proportions of minerals forming the amphibolites (cf. densities of garnet amphibolites in Table 1) and various kinds of amphibolites forming the Massif. Therefore, the exact determination of average rock density in the Massif is not possible, because it would require the detailed knowledge on the rock variation. Since the “normal” amphibolites, garnet amphibolites (locally with pyroxene), zoisite amphibolites and epidote amphibolites are dominating in the Massif (from ca. 80% in the Niedźwiedź IG-1 to practically 100% in the Niedźwiedź IG-2 borehole, Awdankiewicz 2003), we assume that the density 3.10 g cm−3 is representative (cf. Table 1).

The surface exposures show that the rocks underlying the Niedźwiedź Massif are the granitic gneisses from Lipniki, containing thin inliers of amphibolites and mica schists (Cymerman and Jerzmański 1987). The Niedźwiedź IG-2 borehole documents occurrence of ca. 63 m transition zone in the footwall of the Massif, consisting of amphibole gneisses and shists, with thin inliers of quartzo-feldspathic rocks, muscovite-chlorite rocks and limestones, followed by quartzo-feldspathic mylonitic rocks with inliers of crystalline limestones, which comprise the lowest 56 m of the hole (Cymerman and Jerzmański 1987). The borehole data clearly show the mylonitic zone at the contact of the amphibolites with its surrounding (a major thrust in the regional geological interpretation of Skácel 1989). However, only thin (total 119 m) section of rocks underlying the Massif was documented by the borehole. Therefore, based on the geological sketch of Cymerman and Jerzmański (1987), for further modelling, we assume that the immediate surroundings of the Niedźwiedź Massif consist of granitic gneisses from Lipniki (density 2.641 g cm−3, cf. Table 1) with 10% of the Lipniki amphibolites (density 3.017 g cm−3, cf. Table 1), which give average 2.679 g cm−3 (we use the rounded value of 2.68 g cm−3).

The shape of the Niedźwiedź Massif can be determined with the use of gravity modelling assuming a chosen value of the density contrast between amphibolite and its neighbourhood. We used a 3-D gravity modelling. The model consists of rectangular vertical columns extending from sea level to different depths. The whole consort of columns spreads below the area of square frame 12 per 12 km where modelling is being performed (Fig. 3a). The frame contains the circular gravity anomaly of the massif (about 10 km in diameter) in its centre. The assumed characteristic value (0.42 g cm−3) of the density contrasts between amphibolites (3.10 g cm−3) and neighbourhood (granitic gneisses from Lipniki, 2.68 g cm−3).
Fig. 3

a Bouguer anomaly (mGal) in the vicinity of the Niedziwiedź massif. Thanks to courtesy of Stanisław Wybraniec from Polish Geological Institute; b depth of the lower boundary of the Niedziwiedź massif (km) according to modelling of the gravity data (assuming 0.42 g cm−3 as the density contrast). The dots show positions of the boreholes Niedźwiedź IG-1 and Niedźwiedź IG-2

The step procedure fits model field to observed Bouguer anomaly by changing the depths of all columns. It performs also a separation of the observed field into field corresponding to modelled body and the field related to the neighbourhood outside of the frame, which has a complex relief and large variation. The resulting map of the footwall of the Niedźwiedź Massif (Fig. 3b) shows its oval shape and resulting values are in good agreement with those indicated by the borehole Niedźwiedź IG-2 which pierced amphibolite at depth about 1,575 m measured from surface along the drilling line. The depth of the footwall suggested by the resulting model (Fig. 3b) at the position of the borehole is about 1,200 m below sea level, while topographic height has value 300 m there and the line of drilling has also some curvature suggested in description of the borehole (Jerzmański 1992). So, the agreement is very good since the expected depth accuracy of the gravity modelling is ±200 m here, because of uncertainty of input data.

Heat flow in the Niedźwiedź Massif

The heat flow map of Hurtig (1995) shows that the area of Niedźwiedź Massif—within the eastern margin of the eastern part of the European Variscan Orogen—is characterised by lower values of the surface heat flow (by some 10–20 mW m−2) than the western part of the Bohemian Massif. The heat flow is also lower than that to the north, in the Variscan Foreland marginal zone which includes Fore-Sudetic Monocline, with high heat flow (80–90 mW m−2) and elevated mantle heat flow (typical external Variscan foreland values range between 35 and 40 mW m−2, e.g. Majorowicz et al. 2003).

The recent map by Szewczyk and Gientka (2009) also gives mosaic pattern of heat flow showing that heat flow in the broad Niedźwiedź region is between 60 and 70 mW m−2. Recent maps of heat flow of Europe after application of paleoclimatic corrections (Majorowicz and Wybraniec 2009, 2011) show modified pattern of heat flow in comparison with the map of Hurtig (1995). The Niedźwiedź area low heat flow zone is a northern margin of a larger domain of low heat flow at the eastern part of Bohemian Massif (Fig. 4). In these recent maps, the heat flow in the Niedźwiedź area was based on assumed thermal conductivities and thermal gradient from Niedźwiedź IG-2 thermal log.
Fig. 4

Heat flow in central Europe corrected according to paleoclimatic data. The star indicates the region of Niedźwiedź. This map is a fragment of the heat flow map of Europe by Majorowicz and Wybraniec 2009)

In contrast, in this paper, we use the data of Niedźwiedź IG-2 well to re-evaluate heat flow based on the classical method of surface heat flow density (Q s) determination. It is based on both the temperature measurements of a well in an equilibrium state and the laboratory measurements (and/or estimates) of thermal conductivity (k) from net rock components.

The Q s /k relationship for any depth along the vertical (z) axis of the well follows Fourier’s law:
$$ Q_{\text{s}} = - k\,{\text{d}}T/{\text{d}}z $$
(1)
where k [W °C−1 m−1] is the coefficient of thermal conductivity, T [°C] is the temperature, dT/dz is the temperature gradient and Q s is heat flow at the surface.
The deep linear portion of the temperature–depth profile shown in Fig. 5a (Niedźwiedź IG2 well) is used to determine thermal gradient dT/dz (Fig. 5b). That gradient for the linear deep part of the log below 1,240 m is 24.3°C m−1. The linear trend line approximates temperature versus depth measurements with correlation coefficient R = 0.999.
Fig. 5

a Niedźwiedź IG-2 well temperature log (a) and thermal gradient from the linear deep part of the temperature log (b)

Thermal conductivity averages for 54 measurements on 5 samples of amphibolites in two directions (parallel and perpendicular to foliation) are:
$$ k_{1} = 2.4766\,\left[ {{\text{W}}\,^\circ {\text{C}}^{ - 1} \,{\text{m}}^{ - 1} } \right]\quad k_{2} = 2.4728\,\left[ {{\text{W}}\,^\circ {\text{C}}^{ - 1} \,{\text{m}}^{ - 1} } \right]. $$
These values are close within the error of measurement and characteristic for isotropic rocks. The relationship between the conductivities for both directions and rock type is shown in Fig. 6.
Fig. 6

Thermal conductivity of amphibolites of the Niedźwiedź Massif

We correct temperature gradient for not equilibrated conditions in the well when the temperature log was collected (10 days after drilling termination). Temperature gradient correction is determined on the basis of comparison of two logs taken at different time after circulation in the well ceased and bottom hole temperature. It is determined to be circa 1°C m−1 (0.7°C m−1). The corrected for thermal equilibrium in the well geothermal gradient will be 24.3°C m−1 + 0.7°C m−1 = 25°C m−1.

We use Eq. 1 to calculate heat flow before applying paleoclimatic correction and round up the values to one decimal place reflecting uncertainty of thermal conductivity and geothermal gradient determinations:
$$ Q_{\text{s}} \,{\text{unc}}. = 2.5\,\left[ {{\text{W}}\,^\circ {\text{C}}^{ - 1} \,{\text{m}}^{ - 1} } \right]*25\,\left[ {^\circ {\text{C}}^{ - 1} \,{\text{m}}^{ - 1} } \right] = 62.5\,\left[ {{\text{mW}}\,{\text{m}}^{ - 2} } \right]. $$

Heat flow paleoclimatic correction

Following the Paleocene to early Eocene peak warming, the climate cooled variably towards the Pleistocene glacial environment. Climate during 3 My before present changed dramatically in response to astronomical effects (Milankovitch cycles) caused changes in surface forcing. These resulted in cycles of glacials and interglacials within a gradually deepening ice age. The growth and retreat of continental ice sheets in the northern hemisphere occurred at 2 frequencies, 41 and 100 ky. This significant amplification of the response of climate to orbital forcing began 3 My ago, resulted in drastic oscillations between ice ages. The Niedźwiedź Massif is located in the area covered by the first Scandinavian glaciation and subsequently was located in the periglacial zone and thus heat flow paleoclimatic correction is necessary.

Šafanda et al. (2004) and Majorowicz et al. (2008) simulated time changes in the subsurface solving the transient heat conduction equation gives subsurface temperature change in response to surface forcing:
$$ C_{\text{v}} \,\partial T/\partial t = \partial \left[ {k\left( {\partial T/\partial z} \right)} \right]/\partial z + A $$
(2)
where T is the temperature, k is the thermal conductivity, C v is the volumetric heat capacity, A is the rate of heat generation per unit volume, z is the depth and t is the time in a one-dimensional layered geothermal models of the individual sites.

Equation 2 was solved numerically by an implicit scheme of the finite-difference to calculate a paleoclimatic correction to heat flow based on the model of past surface temperature changes for Europe (Majorowicz and Wybraniec 2011) and for Poland (Majorowicz et al. 2008). These models are well constrained by the results of inversions of deep temperature–depth logs in several locations in Poland (Mottaghy et al. 2009) and Eurasia (Demezhko et al. 2006). Demezhko et al. (2006) show that the amplitude of recent surface temperature changes varies spatially and with depth. The amplitude of the surface temperature change (Pleistocene–Holocene) was determined from many well temperature–depth inversions and varies from 8 to 23°C. The highest amplitude is derived from inversions of the highest latitude well temperature–depth profiles in Greenland and Karelia (Russia).

For the model of recent changes, the temperature before the onset of the five glacial cycles considered was assumed to be equal to the mean temperature of −4°C according to the findings from inversions of deep >2.4 km and as deep as 7 km wells in Poland and Czech Republic (Poland-Czech Republic; Majorowicz et al. 2008; Mottaghy et al. 2009; Szewczyk and Gientka 2009; Šafanda et al. 2004; Šafanda and Rajver 2001). Based on the above published evidence, the cycles are assumed to have an amplitude 14°C (−7°C, +7°C, respectively). This model simplifies likely more complicated changes in surface temperature in the past; however, these are not known with high precision (Jessop 1990; Demezhko et al. 2006). Our model of surface forcing history is based on the approximation of such history giving the best fit to the measured temperature–depth variations in this part of Europe (Poland-Czech Republic; Majorowicz et al. 2008; Mottaghy et al. 2009; Szewczyk and Gientka 2009; Šafanda et al. 2004; Šafanda and Rajver 2001) and depicts the most important features of the high amplitude surface temperature changes. The most recent high amplitude change from recent Pleistocene glacial period to Holocene is the largest influence upon observed variations of heat flow with depth due to diffusive nature of the process. Earlier in time glacial interglacial periods of surface temperature, changes in the similar amplitude are of less influence (Majorowicz et al. 2008). The northern and central Europe area was covered by ice sheet during the last glacial maximum (LGM) 25–15 ka ago. The synthetic heat flow transient profile (Fig. 7) was calculated as a response to glacial cycles with glacial–interglacial surface temperature amplitude 14, 10 and 7°C, respectively, for a homogeneous model with diffusivity 0.9 × 10−6 m2 s−1 determined from average measured thermal conductivity and density and assumed typical values of heat capacity (Jessop 1990).
Fig. 7

Paleoclimatic heat flow correction (minimal, maximal and average) for the study area

The paleoclimatic correction for the maximum amplitude of the assumed change fitting other Polish well data best and assumed for the Niedźwiedź area is determined to be 7 mW m−2 for the interval of heat flow determination as in Fig. 5b. The surface z = 0 correction is 19 mW m−2 and it decreases with depth due to diffusive process. It is comparable to corrections proposed by Balling (1995) in northern Tornquist zone, 15–20 mW m−2, though ours is on the high side in accordance with newest findings on the amplitude of the surface changes as discussed above.

This maximum correction gives us the best fit of the geotherms calculated from such increased value of heat flow versus heat flow with lesser or no paleoclimatic correction. We discuss it further in the “Discussion” section of this paper.

Heat flow with the paleoclimatic correction will be:
$$ Q_{\text{s}} \,{\text{corrected}} = Q_{\text{s}} \,{\text{unc}}. + {\text{CORRECTION}} = 62.5\left[ {{\text{mW}}\,{\text{m}}^{ - 2} } \right] + 7\left[ {{\text{mW}}\,{\text{m}}^{ - 2} } \right] = 69.5\left[ {{\text{mW}}\,{\text{m}}^{ - 2} } \right]. $$
We will be using rounded heat flow value of 69.5 mW m−2 in further modelling. However, paleoclimatic influence upon heat flow is present in the upper few km of the heat flow–depth profile as shown in Fig. 7. The equilibrium is reached circa under 5 km where heat flow is 69.5 [mW m−2] (Fig. 8).
Fig. 8

Heat flow variation with depth due to surface temperature forcing related to glacial interglacial history of change. Measured heat flow for Niedźwiedź IG2 is shown by the dashed line. Note that measured heat flow is lower than equilibrium deep heat flow by 7 mW m−2

Numerical model of temperature distribution in the crust and lithospheric mantle

The reference

The temperatures and depth of origin of the Lutynia mantle xenoliths (960–1,000°C, 50 km, for details see The lithospheric mantle in the region of the Niedźwiedź massif) may serve as a reference point for temperature distribution modelling. The xenoliths represent the thermal state of the sampled mantle at ca. 4.5 Ma. Since the Lutynia volcano was isolated, and no intense volcanic activity occurred in the neighbouring area of eastern part of West Sudetes and Fore-Sudetic Block, we assume that the sampled mantle was not rejuvenated thermally at the time of volcanic activity and is therefore representative for the lithospheric mantle in the area. We use the 50 ± 5 km depth for the calculated temperature range, to account for the uncertainties in pressure estimates.

The equation

The numerical methods are used for the calculation of geotherms. The thermal steady state is assumed and consequently our model is based on the following equation:
$$ \frac{\text{d}}{{{\text{d}}z}}\left( {k(T,p)\frac{{{\text{d}}T}}{{{\text{d}}z}}} \right) + \rho (p)H(z) = 0, $$
(3)
where k [W °C−1 m−1] is the coefficient of thermal conductivity, T [°C] is the temperature, p [Pa] is the pressure, z [m] is the depth, ρ [kg m−3] is the density and H [W kg−1] is the rate of the radiogenic heat production per unit mass (note that A = ρ H is the rate of radiogenic heat production per unit volume, A [W m−3]). The thermal diffusivity κ is defined as κ = k/(ρ c p ).

The geotherms and position of LAB are often discussed using isotherms (e.g. the 1,300°C isotherm is chosen by Majorowicz 2004, the 1,200°C by Tesauro et al. 2009) and/or potential adiabatic temperatures of 1,300°C.

A simple parametric model

We use here a simple parametric model to present the basic thermal properties of the crust-lithosphere system. According to Whittington et al. (2009), “many thermal models of the Earth’s lithosphere assume constant values of κ (~1 mm2 s−1) and/or k (~3–5 W m−1 K−1) owing to large experimental uncertainties […]. Recent advances permit accurate (±2%) measurement […]”. Moreover, they indicate that κ strongly decreases from 1.5 to 2.5 mm2 s−1 at ambient conditions to 0.5 mm2 s−1 at mid-crustal temperatures. Their results as well as the results of Abdulagatov et al. (2006) suggest that the average k of the crust is ~2 W m−1 K−1.

In our simplified model, the crust is assumed to be a homogenous layer of thickness D, thermal conductivity k c and, heat generation rate per unit volume A. The total heat generation rate for the crust per unit surface area is AD [W m−2]. The surface heat flow density and the surface temperature are Q s [W m−2] and T S [°C], respectively. For lithosphere below the MOHO, we assume k = const and A = 0. So, the model has the following parameters: D, k c, A, k. Temperature distribution in the mantle is given by (e.g. Czechowski 1993):
$$ T(z) = \frac{1}{k}\left( {Q_{\text{s}} - hD} \right)(z - D) + G\quad {\text{for}}\quad D \le z. $$
(4)
where
$$ G = - \frac{{AD^{2} }}{{2k_{\text{c}} }} + \frac{{Q_{\text{s}} D}}{{k_{\text{c}} }} + T_{\text{s}} . $$
(5)
Let us discuss the properties of the model. The following starting parameters were chosen for calculations: D = 31,000 m, k = 3 W m−1 K−1, A = 1.3 × 10−6 W m−3, k c = 1.9 W m−1 K−1, Q s = 69.5 mW m−2, and T s = 4°C. Four panels of Fig. 9 give geotherms for different values of some chosen values of parameters. The unspecified parameters are not changed comparing to above set.
Fig. 9

Geotherms for the simple model of the lithosphere (see text). a Geotherms for different values of the mantle conductivity: k = 2.5, 3, 3.5, 4 W m−1 K−1. b Geotherms for different mean heat generation in the crust h: 1.0 × 10−6, 1.1 × 10−6, 1.2 × 10−6, 1.3 × 10−6 W m−3. c Geotherms for different pairs of h and k. Lines are labelled by values of h: 1.1 × 10−6, 1.2 × 10−6, 1.3 × 10−6, 1.4 × 10−6 W m−3. The values of k are: 5.06, 3.91, 3.06, 2.42 W m−1 K−1, respectively. Each pair gives geotherms crossing the centre of the petrologic constrain. For this panel k c = 2 W m−1 K−1. d Geotherms for different values of the crust conductivity k c: 1.8, 1.9, 2, 2.1 W m−1 K−1. The values of unspecified parameters are: D = 31,000 m, k = 3 W m−1 K−1, h = 1.3 × 10−6 W m−3, k c = 1.9 W m−1 K−1

Figure 9a gives geotherms for the following values of the mantle conductivity: k = 2.5, 3, 3.5, 4 W m−1 K−1. One can see that most of them fulfil the Lutynia xenoliths p–T range. The depth of the 1,300°C isotherm varies from 74 to 98 km.

The mean heat generation in the crust A is changed in the Fig. 9b. It is the least known parameter of the models depending mainly on the effective granite participation (or other rocks with high content of radioactive isotopes) and its composition. Note that lower values of A in the crust result in higher mantle temperature and smaller depth of the 1,300°C isotherm. Note also that for the model A of the crust (Fig. 2), the value A = 1.3 × 10−6 W m−3. The geotherm for this value is also the best fit of the Lutynia xenoliths p–T range.

Figure 9c presents results of special manipulation of the mean heat generation in the crust h and thermal conductivity of the mantle k. For four values of A: 1.1 × 10−6, 1.2 × 10−6, 1.3 × 10−6, 1.4 × 10−6 W m−3), the four values of k are chosen: 5.06, 3.91, 3.06, 2.42 W m−1 K−1, respectively. Such pairs of A and k give geotherms crossing the centre of the Lutynia xenoliths p–T range (i.e. the point: T = 950°C and z = 50,000 m). For this panel, k c = 2 W m−1 K−1. The depth of the 1,300°C isotherm varies from 83 to 100 km.

The geotherms for different values of the crust conductivity k c are given in Fig. 9d. In this case, the geotherms differ one from another for the whole range of z (in the crust as well as in the mantle). The k c = 2 W m−1 K−1 is the best fit to the Lutynia xenoliths p–T range. The 1,300°C isotherm is located in the range of depth from 75 to 90 km.

This discussion indicates that even a simple model could give realistic behaviour of the temperature distribution in the lithosphere.

An advanced thermal model

More advanced model is presented here. The heat production and the thermal conductivity for the considered crustal rock are measured and given in Table 1, Figs. 10 and 11. The layered structures of the crust and their thermal properties are adopted according to Fig. 2. The effect of temperature and pressure on the crustal rock conductivity is included in the model. According to Abdulagatov et al. (2006), a sharp increase in the conductivity is found for rocks at low pressures (i.e. between 0.1 and 100 MPa) along various isotherms (between 0 and 150°C). At higher pressures (p > 100 MPa), weak linear dependence of the conductivity with the pressure was observed. Abdulagatov et al. (2006) used the following function to describe their experimental results:
$$ k(T,p) = k_{0} (T,p = \infty )\frac{(1 - 0.661\,\Upphi (p))}{(1 + 41.3\Upphi (p))} $$
(6)
where k 0(T, p = ∞) is the thermal conductivity of the rock at high pressure (i.e. for p → ∞), when all of the internal cracks are assumed to be closed. The function Φ(p) is:
$$ \Upphi \left( p \right) = \Upphi_{0} \exp \left( { - p/p_{0} } \right), $$
(7)
where Φ0 and p 0 are some constants determined by the experiments (see Table 1).
Fig. 10

Thermal conductivity for model A and k = 3.5 W m−1 K−1

Fig. 11

Heat production for the two considered models of crust

To describe the temperature dependence of k(T), we follow the paper of Clauser and Huenges (1995) and Zoth and Hänel (1988). They express the conductivity of the typical rocks by the function:
$$ k(T) = \left( {E + \frac{B}{350 + T}} \right) $$
(8)
where the coefficients E and B are given in Table 2. Note, however, that the absolute value of the thermal conductivity of the rocks considered here is measured independently (at ambient condition, see Table 1). Therefore, we use the above formula to determine the temperature dependence only (not the values). Eventually, combining formulas (6) and (8), we get:
$$ k(T,p) = k_{0} \left( {\frac{{1 + 41.3\,\Upphi_{0} }}{{1 - 0.661\,\Upphi_{0} }}} \right)\left( {\frac{1 - 0.661\,\Upphi (p)}{1 + 41.3\,\Upphi (p)}} \right)\left( {\frac{{E + \frac{B}{350 + T}}}{{E + \frac{B}{350 + 20}}}} \right), $$
(9)
where k 0 is the coefficient of thermal conductivity of a given rock at ambient conditions (given in Table 1) and T is expressed in [°C]. We believe that the above formula describes well T–p dependence of k in the crust (see also Seipold 1998).
Table 2

Constants: E, B, k 0 ,Φ 0, p 0 used in formulas (7) and (9)

Rock no (see Table 1)

E

B

Φ 0

p 0

1

0.75

705

0.0063

1.25E+08

2

0.75

705

0.0063

1.25E+08

3

0.75

705

0.0063

1.25E+08

4

0.75

705

0.0063

1.25E+08

5

0.75

705

0.0063

1.25E+08

6

0.75

705

0.0063

1.25E+08

7

0.64

807

0.0055

7.00E+07

8

0.75

705

0.0055

7.00E+07

9

0.75

705

0.0055

7.00E+07

10

0.75

705

0.0063

1.25E+08

11

0.75

705

0.0055

7.00E+07

12

0.64

807

0.0055

7.00E+07

13

0.75

705

0.0055

7.00E+07

14

0.75

705

0.0055

7.00E+07

15

0.64

807

0.0055

7.00E+07

16

0.75

705

0.0055

7.00E+07

17

1.18

474

0.0015

9.00E+07

After Clauser and Huenges (1995), Zoth and Hänel (1988) and Abdulagatov et al. (2006)

Let us now discuss the thermal properties of the rocks below the MOHO. Most of the results (e.g. Clauser and Huenges 1995; Seipold 1998; Tommasi et al. 2001; Abdulagatov et al. 2006; Katsur 2007; Whittington et al. 2009) indicate that thermal conductivity and thermal diffusivity stabilize for the p–T range of upper lithospheric mantle (i.e. for: 1–4 GPa, and 700–1,500°C). The same behaviour of k results from Eq. 9. Moreover, Katsur (2007) states: “thermal diffusivity in the upper mantle has almost constant values of 7–8 × 10−7 m2 s−1”. Therefore, we assume in the model that k is constant below the MOHO. Eventually, the calculations are performed for k = 2.5, 3, 3.5 W m−1 K−1. Note that Hofmeister (1999) results for forsterite give 4.5 W m−1 K−1 for 100°C, but 2.2 W m−1 K−1 only for 1,300°C. Other data suggest that k in the upper mantle is in the range 2–3 W m−1 K−1.

The radiogenic heat production chosen for the mantle (2.3 × 10−12 W kg−1) corresponds to depleted peridotite. The compressibility of the rocks is described by:
$$ \rho (p) = \rho (0)\left( {1 + \frac{p}{K}} \right), $$
(10)
where ρ(0) is the density for zero pressure given in Table 1. The bulk modulus K is calculated from seismic velocity of longitudinal waves V p from the formula:
$$ K = \frac{5}{9}\frac{{V_{p}^{2} }}{\rho (0)}, $$
(11)
It is assumed here that both Lame’s modules are equal, i.e., V s  = (1/3)1/2 V p . We used this approximate formula because density is not a critical factor for our model.
The following boundary conditions are used:
  1. 1.

    Heat flow at the surface, i.e., Q s(z = 0) = 69.5 or 62.5 mW m−2.

     
  2. 2.

    Temperature at the surface, i.e., T(0) = −4°C for z = 0 m.

     

The Eq. 3 with k(T, p) given by (9) is nonlinear. To solve it, we used the software developed by Czechowski (1993).

Results of the model

The calculations were performed for two models of the crustal structure: model A and model B (Fig. 2). The discrepancy of the results is negligible, so model A was used for the rest of the calculations. The main results are geotherms, i.e., functions T(z). The results presented in Fig. 12 indicate that:
Fig. 12

Geotherms calculated for the advanced model (see text). Two models of the crust are assumed (cf. Fig. 2, models A and B). The red rectangle gives the Lutynia xenoliths p–T range. The potential adiabatic temperature 1,300°C is for olivine

  1. 1.

    Correction of the heat flow in the Niedźwiedź borehole based on the paleoclimatic data (see the previous chapter) results in considerable increase in temperature in the lower crust and in the upper mantle (compare model A for Q s = 69.5 mW m−2 and model A for Q s = 62.5 mW m−2 and the appropriate lines in Fig. 12).

     
  2. 2.

    The critical test is a comparison with the Lutynia xenoliths data. The Lutynia xenoliths p–T range is given by the rectangle on the Fig. 12. The geotherms calculated for model A and B fit well this constraint if k = 3 W m−1 K−1 is used as the mantle conductivity. Lower and higher values of k in the range from 2.5 to 3.5 W m−1 K−1 are also possible.

     
  3. 3.

    The models A and B correspond to essentially the same mantle heat flow, i.e., 27.6 mW m−2.

     

Depth of the 1,300°C isotherm for paleoclimatically corrected heat flow is less than 100 km (Fig. 12) For uncorrected heat flow, the isotherm would be considerably deeper (130–140 km). Note that this isotherm is used often as the lithosphere–asthenosphere boundary. The same conclusion holds for LAB defined by the potential adiabatic temperature.

Discussion

Crustal and mantle heat flow

The crustal geotherms presented by us is strongly affected by the amount of granites assumed to occur in the crust and their geochemical characteristics. The crustal segment of Erzgebirge (NW Bohemian Massif) described by Förster and Förster (2000) contains significant granites enriched in heat-producing elements, resulting in high surface heat flow reaching locally 112 mW m−2. The crustal segment beneath the Niedźwiedź Massif is poor in granites, which contain smaller amounts of heat-producing elements, resulting in smaller heat flow of 70 mW m−2. The Niedźwiedź Massif, consisting of amphibolites of MORB affinity, is the “cold” element in the crust due to its very low content of heat-producing elements. Thus, the crustal geotherms in crystalline areas will be dependent on the amount of “warm” (granitic) and “cold” (metabasaltic) elements, typically embedded in the gneissic matrix (as in the described by us part of the Bohemian Massif). The area of the Niedźwiedź Massif is representative for the crust poor in granites, containing significant metabasalts. Moreover, the granites contain relatively low amounts of heat-producing elements.

We found that the mantle heat flow is low (ca. 28 mW m−2) beneath the Niedźwiedź Massif. Our result is close to conclusions Förster and Förster (2000), who indicate that the mantle heat flow is 20–30 mW m−2 in Erzgebirge on the basis of a study of the correlation between heat flow and upper crustal heat production. In the area of Sudetes, Christensen et al. (2001) suggest the mantle heat flow of 42 mW m−2 beneath the Kozákov, which is used for their modelling, assuming surface heat flow of 70 mW m−2. However, their model assumes not thermally equilibrated crust affected by Cenozoic volcanism. Typical external Variscan values found for Polish and German part of the Fore-Sudetic Monocline and beyond are 35–40 mW m−2 (e.g. Majorowicz et al. 2003). The discrepancies among the reported values of mantle heat flow may be due to different methods of its estimate employed, and clearly, more data are necessary to allow the discussion on the mantle heat flow beneath the Bohemian Massif.

The depth of asthenosphere

The lithosphere is defined as a thermal boundary layer whose temperature is lower than that defined by mantle adiabat (e.g. Fischer et al. 2010; Artemieva 2009). For characterisation of the mean depth of this layer, a formal conventional surface between lithosphere and asthenosphere is defined and termed lithosphere–asthenosphere boundary (LAB). The LAB can be defined on the basis elastic, thermal, electrical and seismic data (e.g. Artemieva 2009). The seismic studies suggest that the contrast in chemical composition (including water content) or presence of melt is necessary in addition to temperature increase to explain the velocity gradients in many Phanerozoic areas (Fischer et al. 2010). The useful convention is to define LAB at adiabat of potential temperature of 1,300°C (the lower temperature limit for mantle adiabats).

In the areas of Cenozoic basaltic volcanism, the LAB (asthenosphere defined as a convecting layer where the thermal gradient is adiabatic) is usually located at depth 90–100 km (O’Reilly and Griffin 1996). When similar definition of asthenosphere is assumed, the geotherm calculated for the Niedźwiedź area also locates the LAB at depth between 90 and 100 km (Fig. 13).
Fig. 13

The Niedźwiedź geotherms (depicted as in Fig. 12) and their relationship to geotherms: representative for culmination of alkaline volcanism (SE Australia, O’Reilly and Griffin 1996), waning alkaline volcanism (EMAC, Eastern Margin of Australian Craton, Pearson et al. 1991 b), subcontinental lithospheric mantle located at the margin of rifted area (Catalonia, Galán et al. 2011)

The thickness of lithosphere exceeding 100 km beneath the Sudetic part of the Bohemian Massif was suggested by Babuška and Plomerová (2006) on the basis of seismic study. Babuška et al. (2010) show the lithosphere–asthenosphere boundary (LAB) to be located at ca. 140 km beneath the Moldanubian core of the Bohemian Massif, shallowing to 80 km beneath Ohře Rift (Eger Graben) and to 80–100 beneath Saxothuringian Zone. Christensen et al. (2001), based on the petrological constraints, locate the LAB beneath Kozákov (western part of Sudetes) at 90 km. The petrological constraints in Christensen et al. and in this study are based on mantle xenoliths brought to the surface at similar time of ca. 4.5 My and probably are representative for the stage of waning volcanic activity in the area.

To assess the nature of LAB, we compared our geotherm with the location of dry lherzolite solidus in the T-depth diagram. We have chosen the anhydrous solidus because most of the mantle xenoliths brought to the surface by Cenozoic alkaline rocks in SW Poland have the composition of anhydrous harzburgite or lherzolite (Puziewicz et al. 2011); this is also the case for the Lutynia harzburgites/lherzolites (Matusiak-Małek et al. 2010), occurring close to the Niedźwiedź Massif and assumed by us to be representative for the lithospheric mantle beneath. The lithospheric mantle beneath SW Poland was affected by dry metasomatism which did not produce amphibole with exception of two locations (Wilcza Góra, Smulikowski and Kozłowska-Koch 1984; Wołek Hill, Nowak et al. 2010). The absence of amphibole suggests very low water activity during metasomatic event (Lamb and Popp 2009) implying water contents in olivine in the range of first tens of ppm, thus much too low to affect significantly the solidus temperatures (Liu et al. 2006 and references therein).

The lithospheric mantle beneath SW Poland belongs to the spinel mantle facies and practically all of the mantle xenoliths from SW Poland contain clinopyroxene, even if its volume is low enough for the host rock to be classified as harzburgite. Thus, the mantle solidus is well described by melting in the system olivine + orthopyroxene + clinopyroxene ± spinel. The enriched anhydrous peridotite solidus (Hirschmann 2000), probably representative for the asthenosphere, locates the beginning of melting below Niedźwiedź at ca. 113 km (Fig. 13). The solidus of model lherzolite containing from 0 to ca. 8 wt% of FeO (Gudfinnsson and Presnall 2000) is probably representative for melting of lithospheric mantle beneath the Sudetes (almost all of the xenoliths studied by Matusiak-Małek et al. (2010) and Puziewicz et al. (2011) contain <8 wt% of FeO). This solidus indicates the beginning of melting at depth of ca. 130 km. This suggests that the melt-induced softening of the asthenospheric mantle occurs at depth greater by ca. 20 or more km than that of LAB (defined as above).

Geological considerations

The geological scenario describing the recent evolution of lithosphere in the area of Bohemian Massif is very crude. The intense Cenozoic alkaline volcanic activity in the western part of the Bohemian Massif, culminating during Oligocene/Miocene, was probably connected with thermal erosion (due to partial melting) of the base of lithosphere and intense veining and metasomatism of overlying lithospheric segment (cf. Soustelle et al. 2009 and references therein) and must led to thermal rejuvenation of upper mantle. This rejuvenation is recorded in mantle xenoliths brought to the surface by some lavas in the area of the Ohře Rift (Puziewicz et al. 2011).

The Cenozoic volcanic activity in the eastern part of the Bohemian Massif and in the adjoining part of the Moravo-Silesian Zone was of low intensity. In the Sudetes and Fore-Sudetic Block, it is restricted to few volcanic centres. Supposedly, the lithosphere located outside the volcanic centres in Ohře Rift was not disturbed thermally by scarce and volumetrically small lava extrusions.

The Niedźwiedź geotherms were constructed based on the current surface heat flow calculation and the rate of heat generation for the assumed geological model of the crust. The geotherms fall in the temperature–depth range suggested by xenoliths from nearby 4.5 Ma Lutynia volcano (Fig. 13), suggesting that the cooling of mantle during last few millions of years was not significant and that the sampled mantle was not much disturbed thermally at the time of volcanism. The Niedźwiedź geotherm is probably representative for the eastern part of the Bohemian Massif which was located outside of the zone of intense volcanism (Ohře Rift and its close surrounding) and shows recent temperatures.

The xenolith-based geotherms of Cenozoic alkaline volcanic areas located within the Paleozoic crystalline basement have been presented for numerous locations in the world. The mantle—and sporadically lower rust—parts of these geotherms are based on temperature–depths data yielded by the xenoliths (e.g. Pearson et al. 1991a, b; O’Reilly and Griffin 1996; Werling and Altherr 1997; Foley et al. 2006). Thus, they show the real mantle temperatures at the time of sampling by volcanic eruptions.

The geotherm for Southeastern Australia, considered to be representative for alkaline volcanic provinces (Pearson et al. 1991a; O’Reilly and Griffin 1996), is parallel but shifted to higher temperatures relative to the Niedźwiedź geotherm (Fig. 13). The Niedźwiedź geotherm is identical to one of the eastern margin of Australian Craton, which is based on lower crustal and mantle xenoliths bearing the record of cooling (O’Reilly and Griffin 1996; Pearson et al. 1991a, b).

Conclusions

The north-eastern part of the Bohemian Massif and adjoining part of the Moravo-Silesian Zone are poor in Cenozoic alkaline lavas relative to the located to the west Ohře Rift and its surrounding. We modelled the crustal structure in the area of the amphibolite Niedźwiedź Massif in order to estimate the relative proportions of heat produced by crust and mantle. Our model is based on the local geological structure and neighbouring seismic profiles (located 30–50 km from the Niedźwiedź Massif). The crust in the region is assumed to be dominated by gneisses with subordinate granites (1 km of the latter was assumed in the model). The amphibolites of the Niedźwiedź Massif occur close to the surface. The occurrence of some melagabbros (not related to the Niedźwiedź amphibolites) was assumed at the base of the crust.

The temperature log from the ca. 1,600 m “Niedźwiedź IG2” well in Niedźwiedź Massif enabled the calculation of surface heat flow, which was found to be 69.5 mW m−2 after the correction for paleoclimatic effect was applied. The heat budget modelling suggested the geotherm, which cross-cuts the temperature–depth range suggested by petrological study of the peridotite xenoliths occurring in the ca. 4.5 Ma Lutynia basanite, occurring ca. 20 km from the Niedźwiedź Massif. Our calculations yield the mantle heat flow of 28 mW m−2. The geotherm is supposedly representative for parts of lithosphere affected by continental alkaline volcanism, but distant from the volcanic centres and not rejuvenated thermally.

The lithosphere-asthenosphere boundary is located between 90 and 100 km depth if the adiabat of the potential temperature of 1,300°C is considered as the upper asthenosphere limit. The lithospheric mantle in the NE Bohemian Massif contains no hydrous phases, and its melting requires relatively high temperatures. In consequence, the melt appears ca. 20 km or even more beneath the LAB defined by the 1,300°C adiabat.

Notes

Acknowledgments

This study originated thanks to the project MNiSW N N307 100634. The comments of Dr. Andrea Förster (GFZ Potsdam) and Prof. Andrzej Żelaźniewicz (Institute of Geological Sciences of Polish Academy of Sciences) to the earlier versions of the text enabled its improvements and are gratefully acknowledged.

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

References

  1. Abdulagatov IM, Emirov SN, Abdulagatova ZZ, Askerov SY (2006) Effect of pressure and temperature on the thermal conductivity of rocks. J Chem Eng Data 51:22–33CrossRefGoogle Scholar
  2. Artemieva IM (2009) The continental lithosphere: reconciling thermal, seismic, and petrologic data. Lithos 109:23–46CrossRefGoogle Scholar
  3. Awdankiewicz H (2003) Petrology and geochemistry of metabasites of the Niedźwiedź Massif in the Fore-Sudetic Block. PhD thesis, Polish Geological Institute (in Polish)Google Scholar
  4. Awdankiewicz H (2008) Petrology and geochemistry of the metabasites of the Niedźwiedź Massif in the Fore-Sudetic Block. Prace Państwowego Instytut Geologicznego 189:5–53 (in Polish, English summary)Google Scholar
  5. Babuška V, Plomerová J (2006) European mantle lithosphere assembled from rigid microplates with inherited seismic anisotropy. Phys Earth Planet Interiors 158:264–280CrossRefGoogle Scholar
  6. Babuška V, Fiala J, Plomerova J (2010) Bottom to top lithosphere and evolution of western Eger Rift (Central Europe). Int J Earth Sci 99:891–907Google Scholar
  7. Badura J (1985) Detailed geological map of the Sudetes 1:25000. Sheet Lipniki. Polish Geological InstituteGoogle Scholar
  8. Balling N (1995) Heat flow and thermal structure of the lithosphere across the Baltic Shield and northern Tornquist Zone. Tectonophysics 244:13–50CrossRefGoogle Scholar
  9. Birkenmajer K, Pécskay Z, Grabowski J, Lorenc MW, Zagożdżon PP (2002) Radiometric dating of the Tertiary volcanics in Lower Silesia, Poland. II. K–Ar and paleomagnetic data from Neogene basanites near Lądek Zdrój, Sudetes Mts. Ann Soc Geol Pol 72:119–121Google Scholar
  10. Brey GP, Köhler T (1990) Geothermobarometry in four-phase Lherzolites II. New thermobarometers, and practical assessment of existing thermobarometers. J Petrol 31:1353–1378Google Scholar
  11. Christensen NI, Mooney WD (1995) Seismic velocity structure and composition of the continental crust: a global view. J Geophys Res 100(B7):9761–9788CrossRefGoogle Scholar
  12. Christensen NI, Medaris LG Jr, Wang HF, Jélínek E (2001) Depth variation of seismic anisotropy and petrology in central European lithosphere: a tectonothermal synthesis from spinel lherzolite. J Geophys Res 106B1:645–664CrossRefGoogle Scholar
  13. Clauser C, Huenges E (1995) Thermal conductivity of rocks and minerals. In rock physics and phase relations. A handbook of physical constants. AGU Ref Shelf 3:105–126CrossRefGoogle Scholar
  14. Cymerman Z, Jerzmański J (1987) Metamorphic rocks of eastern part of the Fore-Sudetic Block in the region of Niedźwiedź near Ziębice. Kwartalnik Geologiczny 31:239–262 (in Polish, English summary)Google Scholar
  15. Czechowski L (1993) Theoretical approach to mantle convection. In: Teisseyre R, Czechowski L, Leliwa-Kopystyński J (eds) Dynamics of the Earth’s evolution. Elsevier, Amsterdam, pp 161–271Google Scholar
  16. Demezhko DY, Utkin VI, Duchkov AD, Ryvkin DG (2006) Geothermic estimates of the amplitudes of Holocene warming in Europe. Doklady Earth Sci 407:259–261CrossRefGoogle Scholar
  17. Downes H (2001) Formation and modification of the shallow sub-continental lithospheric mantle: a review of geochemical evidence from ultramafic xenolith suites and tectonically emplaced ultarmafic massifs of Western and Central Europe. J Petrol 42:233–250CrossRefGoogle Scholar
  18. Fischer KM, Ford HA, Abt DL, Rychert CA (2010) The lithosphere-asthenosphere boundary. Annu Rev Earth Planet Sci 38:551–575CrossRefGoogle Scholar
  19. Foley SF, Andronikov AV, Jacob DE, Melzer S (2006) Evidence from Antarctic mantle peridotite xenoliths for changes in mineralogy, geochemistry and geothermal gradients beneath a developing rift. Geochim Cosmochim Acta 70:3096–3120CrossRefGoogle Scholar
  20. Förster A, Förster HJ (2000) Crustal composition and mantle heat flow: implications from surface heat flow and radiogenic heat production in the Variscan Erzgebirge (Germany). J Geophys Res 105(B12):27917–27938CrossRefGoogle Scholar
  21. Franke W, Żelaźniewicz A (2000) The eastern termination of the Variscides: terrane correlation and kinematic evolution. In: Franke W, Haak V, Oncken O, Tanner D (eds) Orogenic processes: quantification and modelling in the variscan belt. Geological Society London Special Publication 179:63–86Google Scholar
  22. Franke W, Żelaźniewicz A (2002) Structure and the evolution of the Bohemian Arc. In: Winchester JA, Pharaorah TC, Verniers J (eds) Palaeozoic amalgamation of Central Europe. Geological Society London Special Publication 201:279–293Google Scholar
  23. Galán G, Oliveras V, Paterson BA (2011) Thermal and redox state of the subcontinental lithospheric mantle of NE Spain from thermobarometric data on mantle xenoliths. Int J Earth Sci 100:81–106Google Scholar
  24. Griffin WL, O’Reilly SY, Ryan CG (1999) The composition and origin of sub-continental lithospheric mantle. In: Fei Y, Bertka CM, Mysen B (eds) Mantle petrology: field observations and high pressure experimentation: a tribute to Francis (Joe) Boyd. The Geochemical Society Special Publication 6:13–45Google Scholar
  25. Gudfinnsson GH, Presnall DC (2000) Melting behaviour of model lherzolite in the system CaO-MgO-Al2O3-SiO2-FeO at 0.7–2.8 GPa. J Petrol 41:1241–1269CrossRefGoogle Scholar
  26. Hirschmann MM (2000) Mantle solidus: experimental constraints and the effects of peridotite composition. Geochem Geophys Geosyst 1:2000GC000070CrossRefGoogle Scholar
  27. Hofmeister AM (1999) Mantle values of thermal conductivity and the geotherm from phonon lifetimes. Science 283:1699–1706CrossRefGoogle Scholar
  28. Hrubcová P, Środa P, CELEBRATION 2000 Working Group (2008) Crustal structure at the easternmost termination of the Variscan belt based on CELEBRATION 2000 and ALP 2002 data. Tectonophysics 460:55–75CrossRefGoogle Scholar
  29. Hurtig E (1995) Temperature and heat-flow density along European transcontinental profiles. Tectonophysics 244:75–83CrossRefGoogle Scholar
  30. Jerzmański J (1991) New basite and ultrabasite bodies in the Ślęza Massif vicinity on the Fore-Sudetic Block. Biuletyn Państwowego Instytutu Geologicznego 367:87–103 (in Polish, English summary)Google Scholar
  31. Jerzmański J (1992) Niedźwiedź IG-1, Niedźwiedź IG-2. Profile głębokich otworów wiertniczych Państwowego Instytutu Geologicznego 75:1–109 (in Polish)Google Scholar
  32. Jessop AM (1990) Thermal geophysics. Elsevier, Amsterdam, p 306Google Scholar
  33. Katsur T (2007) Thermal diffusivity of olivine under upper mantle conditions. Geophys J Int 122:63–69CrossRefGoogle Scholar
  34. Klemme S, O’Neill HStC (2000) The near-solidus transition from garnet lherzolite to spinel lherzolite. Contrib Mineral Petrol 138:237–248CrossRefGoogle Scholar
  35. Korzekwa W (1995) Petrography of granitoids and associated crystalline rocks from the vicinity of Otmuchów. Unpublished M.Sc. thesis, University of Wrocław, pp 1–55Google Scholar
  36. Kozłowska-Koch M (1976) Petrography of ultramafic nodules in basaltoids from the environs of Lądek (Sudetes). Bull Acad Pol Sci 24(2):67–76Google Scholar
  37. Kryza R, Mazur S, Oberc-Dziedzic T (2004) The sudetic mosaic: insights into the root of the Variscan orogen. Przegląd Geologiczny 52:761–773Google Scholar
  38. Lamb WM, Popp RK (2009) Amphibole equilibria in mantle rocks: determining values of mantle a H2O and implications for mantle H2O contents. Am Mineral 94:41–52CrossRefGoogle Scholar
  39. Liu X, O’Neill HStC, Berry AJ (2006) The effects of small amounts of H2O, CO2 and Na2O on partial melting of spinel lherzolite in the system CaO-MgO-Al2O3-SiO2 ± H2O ± CO2 ± Na2O at 1.1 GPa. J Petrol 47:409–434CrossRefGoogle Scholar
  40. Majdański M, Grad M, Guterch A, SUDETES 2003 Working Group (2006) 2-D seismic tompographic and ray-tracing modelling of the crustal structure across the Sudetes Mountains basing on SUDETES 2003 experiment data. Tectonophysics 413:249–269CrossRefGoogle Scholar
  41. Majorowicz JA (2004) Thermal lithosphere across the Trans-European Suture Zone in Poland. Geol Q 48:1–14Google Scholar
  42. Majorowicz J, Wybraniec S (2009) Variscan geotherms in the context of the new heat flow map of Central Europe corrected for the paleoclimatic glacial-hiolocene change. Schiftenreihe der Deutschen Gesselschaft für Geowissenschaften 63:168Google Scholar
  43. Majorowicz J, Wybraniec S (2011) New terrestrial heat flow map of Europe after regional paleoclimatic correction application. Int J Earth Sci 100:881–887Google Scholar
  44. Majorowicz JA, Čermak V, Šafanda J, Krzywiec P, Wróblewska M, Guterch A, Grad M (2003) Heat flow models across the Trans-European Suture Zone in the area of the POLONAISE’97 seismic experiment. Phys Chem Earth 28:375–391CrossRefGoogle Scholar
  45. Majorowicz J, Šafanda J, Toruń-1 Working Group (2008) Heat flow variation with depth in Poland: evidence from equlibrium temperature logs in 2.9-km-deep well Torun-1. Int J Earth Sci 97:307–315CrossRefGoogle Scholar
  46. Massone HJ (2005) Involvement of crustal material in delamination of the lithosphere after continent-continent collision. Int Geol Rev 47:792–804CrossRefGoogle Scholar
  47. Matusiak-Małek M, Puziewicz J, Ntaflos T, Grégoire M, Downes H (2010) Metasomatic effects in the lithospheric mantle beneath NE part of Bohemian Massif: a case study of Lutynia (SW Poland) peridotite xenoliths. Lithos 117:49–60CrossRefGoogle Scholar
  48. Mazur S, Józefiak D (1999) Structural record of Variscan thrusting and subsequent extensional collapse in the mica schists from vicinities of Kamieniec Ząbkowicki, Sudetic Foreland, Poland. Ann Soc Geol Pol 69:1–26Google Scholar
  49. Mazur S, Puziewicz J, Szczepański J (1997) Deformed granites from Lipniki (Fore-Sudetic Block) record of Variscan extension in the West/East Sudetes boundary zone (SW Poland). Przegląd Geologiczny 45:290–294 (in Polish, English abstract)Google Scholar
  50. Mazur S, Kröner A, Szczepański J, Turniak K, Hanžl P, Melichar R, Rodionov NV, Paderin Y, Sergeev SA (2010) Single zircon U-Pb ages and geochemistry of granitoid gneisses from SW Poland: evidence for an Avalonian affinity of the Brunian microcontinent. Geol Mag 147:508–526Google Scholar
  51. Mottaghy D, Majorowicz J, Rath V (2009) Ground surface temperature histories reconstructed from boreholes in Poland: implications for spatial variability. In: Przybylak R, Majorowicz J, Brázdil R, Kejna M (eds) The Polish climate in the European context: an historical overview. Springer, Berlin, pp 375–387Google Scholar
  52. Nowak M, Puziewicz J, Muszyński A (2010) Amphibole from peridotite xenoliths, Wołek Hill, north-eastern part of Central European Volcanic Province (SW Poland). Geophys Res Abstr 12:EGU2010-9299Google Scholar
  53. O’Reilly SY, Griffin WL (1996) 4-D lithosphere mapping: methodology and examples. Tectonophysics 262:3–18CrossRefGoogle Scholar
  54. Oberc-Dziedzic T, Madej S (2002) The Variscan overthrust of the Lower Palaeozoic gneiss unit on the Cadomian basement in the Strzelin and Lipowe Hills massifs, Fore-Sudetic Block, SW Poland: is this part of the East-West Sudetes boundary? Geologia Sudetica 34:39–58Google Scholar
  55. Oberc-Dziedzic T, Pin C, Duthou JL, Couturie JP (1996) Age and origin of the Strzelin granitoids (Fore-Sudetic Block, Poland): 87Rb/86Sr data. Neues Jahrbuch für Mineralogie Abhandlungen 171:187–198Google Scholar
  56. Pearson NJ, O’Reilly SY, Griffin WL (1991a) Heterogeneity in the thermal state of the lower crust and upper mantle beneath Eastern Australia. Explor Geophys 22:295–298CrossRefGoogle Scholar
  57. Pearson NJ, O’Reilly SY, Griffin WL (1991b) The granulite to eclogite transition beneath the eastern margin of the Australian craton. Eur J Mineral 3:293–322Google Scholar
  58. Presnall DC, Gudfinnsson GH, Walter MJ (2002) Generation of mid-ocean ridge basalts at pressures from 1 to 7 GPa. Geochim Cosmochim Acta 66:2073–2090CrossRefGoogle Scholar
  59. Puziewicz J (2006) The retrograde metamorphism in the Niedźwiedź Amphibolite Massif (SW Poland): from incipient melting to pumpellyite crystallization. Neues Jahrbuch für Mineralogie Abhandlungen 183:1–11CrossRefGoogle Scholar
  60. Puziewicz J, Koepke J (2001) Partial meltuing of garnet-hornblende granofels and the crystallisation of igneous epidote in the Niedźwiedź Amphibolite Massif (Fore-Sudetic Block, SW Poland). Neues Jahrbuch für Mineralogie Montashefte 2001:529–547Google Scholar
  61. Puziewicz J, Mazur S, Papiewska C (1999) Petrography and origin of two-mica paragneisses and amphibolites of the Doboszowice metamorphic unit (Sudetes, SW Poland). Archiwum Mineralogiczne 52:35–65 (in Polish, English abstract)Google Scholar
  62. Puziewicz J, Koepke J, Grégoire M, Ntaflos T, Matusiak-Małek M (2011) Lithospheric mantle modification during Cenozoic rifting in Central Europe: evidence from the Księginki nephelinite xenolith suite. J Petrol (in press) Google Scholar
  63. Rybach L (1988) Determination of heat production rate. In: Haenel R, Rybach L, Stegena L (eds) Handbook of terrestial heat-flow density determination. Kluwer, Dordrecht, pp 125–142Google Scholar
  64. Šafanda J, Rajver D (2001) Signature of the last ice age in the present subsurface temperatures in the Czech Republic and Slovenia. Global Planet Change 29:241–257CrossRefGoogle Scholar
  65. Šafanda J, Szewczyk J, Majorowicz J (2004) Geothermal evidence of very low glacial temperatures on a rim of the Fennoscandian ice sheet. Geophys Res Lett 31:L07211. doi: 10.1029/2004GL019547 CrossRefGoogle Scholar
  66. Seipold U (1998) Temperature dependence of thermal transport properties of crystalline rocks—a general law. Tectonophysics 291:161–171CrossRefGoogle Scholar
  67. Skácel J (1989) Crossing of the marginal fault of the Lugicum and the dislocation zone of Nýznerov between Vápenná and Javorník in Silesia (Czechoslovakia). Acta Universitatis Palackianae Olomucensis Geographica-Geologica 28:31–45 (in Czech, English abstract)Google Scholar
  68. Smulikowski K, Kozłowska-Koch M (1984) Basaltoids of Wilcza Góra near Złotoryja (Lower Silesia) and their enclosures. Archiwum Mineralogiczne 40:53–94 (in Polish, English summary)Google Scholar
  69. Soustelle V, Tommassi A, Bodinier JL, Garrido CJ, Vauchez A (2009) Deformation and reactive melt transport in the mantle lithosphere above a large-scale partial melting domain: the Ronda Peridotite Massif, Southern Spain. J Petrol 50:1235–1266CrossRefGoogle Scholar
  70. Szewczyk J, Gientka D (2009) Terrestrial heat flow density in Poland—a new approach. Geol Q 53:125–140Google Scholar
  71. Tesauro M, Kaban MK, Cloeting SAPL (2009) A new thermal and rheological model of the European lithosphere. Tectonophysics 476:478–495CrossRefGoogle Scholar
  72. Tommasi A, Gibert B, Seipold U, Mainprice D (2001) Anisotropy of thermal diffusivity in the upper mantle. Nature 411:783–786CrossRefGoogle Scholar
  73. Werling F, Altherr R (1997) Thermal evolution of the lithosphere beneath the French Massif Central as deduced from geothermobarometry on mantle xenoliths. Tectonophysics 275:119–141CrossRefGoogle Scholar
  74. Whittington AG, Hofmeister AM, Nabelek PI (2009) Temperature-dependent thermal diffusivity of the Earth’s crust and implications for magmatism. Nature 458:319–321CrossRefGoogle Scholar
  75. Wierzchołowski B (1993) Systematic position and genesis of the Sudetic volcanic rocks. Archiwum Mineralogiczne 49:199–235 (in Polish, English summary)Google Scholar
  76. Wilson M, Downes H (1991) Tertiary-Quaternary extensional-related alkaline magmatism in Western and Central Europe. J Petrol 32:811–849Google Scholar
  77. Żelaźniewicz A, Aleksandrowski P (2008) Tectonic subdivision of Poland: Southwestern Poland. Przegląd Geologiczny 56:904–911 (in Polish, English abstract)Google Scholar
  78. Zoth G, Hänel R (1988) Appendix, in handbook of terrestrial heat flow density determination. In: Haenel R, Rybach L, Stegena L (eds) Handbook of terrestial heat-flow density determination. Kluwer, Dordrecht, pp 449–466CrossRefGoogle Scholar

Copyright information

© The Author(s) 2011

Authors and Affiliations

  • J. Puziewicz
    • 1
  • L. Czechowski
    • 2
  • L. Krysiński
    • 2
  • J. Majorowicz
    • 3
  • M. Matusiak-Małek
    • 1
  • M. Wróblewska
    • 4
  1. 1.Institute of Geological SciencesUniversity of WrocławWrocławPoland
  2. 2.Institute of GeophysicsUniversity of WarsawWarszawaPoland
  3. 3.Department of PhysicsUniversity of AlbertaEdmontonCanada
  4. 4.Polish Geological InstituteWarszawaPoland

Personalised recommendations