Abstract
We compute the indicial roots of the Lichnerowicz Laplacian on Ricci-flat cones and give a detailed description of the corresponding radially homogeneous tensor fields in its kernel. For a Ricci-flat conifold (M, g) which may have asymptotically conical as well as conically singular ends, we compute at each end a lower bound for the order with which the metric converges to the tangent cone. As a special subcase of our result, we show that any Ricci-flat ALE manifold \((M^n,g)\) is of order n and thereby close a small gap in a paper by Cheeger and Tian.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and main results
Ricci-flat metrics belong perhaps to the most interesting class of Riemannian metrics studied in differential geometry and theoretical physics. Compact Ricci-flat manifolds are particularly hard to find. For a long time, any known compact Ricci-flat manifold was actually flat until the resolution of the Calabi conjecture by Yau provided the existence of other examples [29].
It is easier to construct Ricci-flat metrics on noncompact manifolds where a lot of recent work has been focusing on. The Ricci-flat manifolds we are considering in this paper are allowed to have a finite number of ends which are either asymptotically conical or conically singular. We will refer to these with the unifying notion of conifolds.
Various examples of asymptotically conical Ricci-flat manifolds have been discovered so far. In the subclass of Ricci-flat asymptotically locally Euclidean (ALE for short) manifolds, many examples are provided by Kronheimer’s classification [17]. Asymptotically conical Ricci-flat manifolds which are not ALE were found in [6, 8]. Various additional examples were found over the last decade, see e.g. [11, 12, 16]. On the other hand, many examples of Ricci-flat orbifolds are known (e.g. noncollapsed limits of compact Ricci-flat 4-manifolds [1]) and conically singular (nonorbifold) Ricci-flat metrics were constructed in [15].
The goal of this paper lies in computing for each end of an arbitrary Ricci-flat conifold the precise order. We compute a formula for the optimal decay, given entirely in terms of spectral data on the link of the cone. This extends previous work of [2, 10, 12], who focus on the ALE situation or the Kähler case.
A necessary step in order to compute this order lies in computing possible growth and decay rates for solutions of the linearization of the equation \(\textrm{Ric}=0\) on the tangent cone. The linearization is up to a gauge term given by the Lichnerowicz Laplacian and the growth and decay rates are known as indicial roots. We give a complete computation of all indicial roots, based on the idea of commuting operators and the formulas we get are surprisingly simple.
1.1 Indicial roots of the Lichnerowicz Laplacian on Ricci-flat cones
Let \(\widehat{M}^{n-1}\) be a closed manifold and let \(\overline{P}\) be a self-adjoint Laplace type operator on \(\overline{M}=(0,\infty )\times \widehat{M}\), which is of the form
for some Laplace type operator \(\widehat{P}\) on \(\widehat{M}\). The Laplace–Beltrami operator with respect to the cone metric on \(\overline{M}\) is the simplest operator of this type, but we also allow more general Laplace type operators on vector bundles. The Hodge Laplacian acting on the exterior algebra and the aforementioned Lichnerowicz Laplacian on symmetric 2-tensors are typical examples. If \(\overline{P}\) is of such a form and \(\nu \in \mathbb {R}\) is an eigenvalue of \(\widehat{P}\), we call the (possibly complex) values
indicial roots of \(\overline{P}\) (here, we use the convention \(\sqrt{x}:=\sqrt{|x|}\cdot i\) for \(x<0\)). Their union is called indicial set of \(\overline{P}\). The real parts of the indicial roots correspond to possible growth and decay rates of radially homogeneous solutions of the equation
For the Laplace–Beltrami operator on the cone \(\overline{M}\), the indicial roots are just calculated from the Laplace eigenvalues on \(\widehat{M}\). For more general operators on vector bundles which are of this form, these are in general much harder to compute.
For an operator like the Lichnerowicz Laplacians, it seems to be particularly difficult, since the Lichnerowicz Laplacians on \(\widehat{M}\) and \(\overline{M}\) are in a very complicated relation to each other, see the formulas in [14, Lemma 7.4] and [13, Lemma 4.3] which are lenghty and not very practical for our purposes. This comes from the fact that one has to split up the symmetric (0, 2)-tensors on \(\overline{M}\) in radial, tangential and mixed components and the covariant derivative does not preserve this splitting. Our first main result overcomes these problems in the case of Ricci-flat cones.
Theorem 1.1
Let \((\overline{M}^n,\overline{g})\) be a Ricci-flat cone over a closed manifold \((\widehat{M}^{n-1},g)\) with \(\widehat{\textrm{Ric}}=(n-2)\widehat{g}\).
Let \(0=\lambda _0<\lambda _1\ldots \) be the eigenvalues of the Laplace–Beltrami operator on \(\widehat{M}\), \(\mu _1<\mu _2<\ldots \) be the eigenvalues of the connection Laplacian on divergence-free 1-forms on \(\widehat{M}\) and \(\kappa _1<\kappa _2<\ldots \) be the eigenvalues of the Einstein operator on transverse and traceless tensors on \(\widehat{M}\).
-
(i)
The indicial set of the Lichnerowicz Laplacian \(\overline{\Delta }_L\) on \(\overline{M}\) is given by

-
(ii)
The indicial set of \(\overline{\Delta }_L\) on tensors satisfying the linearized Bianchi gauge is given by
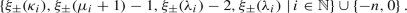
-
(iii)
The indicial set of \(\overline{\Delta }_L\) on tensors satisfying the linearized Bianchi gauge, but which are not Lie derivatives, is given by

The main result follows from Theorem 3.15 and Proposition 3.20 below. We find the indicial roots by writing down all possible growth and decay rates of radially homogeneous tensors in \(\textrm{ker}(\overline{\Delta }_L)\). Let us briefly outline how we get all these tensors (recall that a tensor with vanishing trace and divergence is called a TT-tensor):
-
If h is a TT-tensor on \(\widehat{M}\), any \(r^{\alpha }h\) is a TT-tensor on \(\overline{M}\). It is quite straightforward to show that if \(\widehat{\Delta }_Eh=\kappa h\) (where \(\widehat{\Delta }_E\) is the Einstein operator on \(\widehat{M}\)), then \(r^{\xi _{\pm }(\kappa )}h\in \textrm{ker}(\overline{\Delta }_L)\).
-
If \(v\in C^{\infty }(\widehat{M})\) satisfies \(\widehat{\Delta } v=\lambda v\), then \(r^{\xi _{\pm }(\lambda )}v\) is harmonic on \(\overline{M}\) and therefore, we also have that \(r^{\xi _{\pm }(\lambda )}v\cdot \overline{g}\in \textrm{ker}(\overline{\Delta }_L)\).
In these two cases, the TT and the conformality condition simplify the calculations to a great extent. It would be however far too complicated to work out the general formulas after relaxing these conditions. Instead, in order to get all other r-homogeneous tensors in \(\textrm{ker}(\overline{\Delta }_L)\), we exploit commutation formulas involving \(\overline{\Delta }_L\) and other operators to a great extent:
-
If \(\omega \) is a divergence-free 1-form on \(\widehat{M}\) such that \(\widehat{\Delta }_1\omega :=\widehat{\nabla }^*\widehat{\nabla }\omega =\mu \cdot \omega \), then a short calculation shows that \(r^{\xi _{\pm }(\mu +1)}\omega \) is again divergence free and \(\overline{\Delta }_1(r^{\xi _{\pm }(\mu +1)}\omega )=0\). If we now apply the symmetric part \(\overline{\delta }^*\) of the covariant derivative, we get \(\overline{\Delta }_L(\overline{\delta }^*(r^{\xi _{\pm }(\mu +1)}\omega ))=0\) due to a commutation formula for Ricci-flat manifolds. In addition, we have \(\overline{\delta }^*(r^{\xi _{\pm }(\mu +1)}\omega )={\mathcal {O}}(r^{\xi _{\pm }(\mu +1)-1})\) and so, \(\xi _{\pm }(\mu +1)-1\) are both indicial roots. Because \(\overline{\Delta }_L\) is also of the form (1.1) all indicial roots must be of the form (1.2). Thus, there are further indicial roots which are dual to those two. More precisely, \(\xi _{+}(\mu +1)+1\) appears as the weight dual to \(\xi _{-}(\mu +1)-1\) and \(\xi _{+}(\mu +1)+1\) appears as the weight dual to \(\xi _{-}(\mu +1)-1\).
-
We extend this kind of argumentation when we discuss further indicial roots coming from eigenfunctions of the Laplace–Beltrami operator. If \(v\in C^{\infty }(\widehat{M})\) satisfies \(\widehat{\Delta } v=\lambda v\), then \(v_{\pm }:=r^{\xi _{\pm }(\lambda )}v\) are harmonic on \(\overline{M}\). By commutation, \(d v_{\pm }\in \textrm{ker}(\overline{\Delta }_1)\), with \(d v_{\pm }={\mathcal {O}}(r^{\xi _{\pm }(\lambda )-1})\). Thus, \(\xi _{\pm }(\lambda )-1\) are both indicial roots of \(\overline{\Delta }_1\) and as in the previous duality argument, there are also the dual weights \(\xi _{\mp }(\lambda )+1\), with corresponding harmonic forms \(\omega _+=r^{\xi _{+}(\lambda )-\xi _{-}(\lambda )+2}d v_{-}\) and \(\omega _-=r^{\xi _{-}(\lambda )-\xi _{+}(\lambda )+2}d v_{+}\). Applying \(\overline{\delta }^*\) to \(dv_{\pm }\) and \(\omega _{\pm }\) yields four elements in \(\ker (\overline{\Delta }_L)\) with decay rates

Again, duality implies that \(\xi _{\pm }(\lambda )+2\) is also an indicial root as it is dual to \(\xi _{\mp }(\lambda )-2\). Finally, if \(\lambda =0\) (and hence v is constant), some of the constructed tensors vanish, which is why we need to deal only with the four values

To conclude the proof, one of course needs to show that the above arguments have, in fact, constructed all the indicial roots. The method explained here not only allows us to compute the indicial roots in an efficient way, but also enables us to read of almost directly which of the corresponding tensors are geometrically essential (cf. Theorem 1.1 (ii) and (iii)).
As a byproduct of our result, we get a new proof of the following theorem (cf. page 22):
Theorem 1.2
([19, Theorem 1.2]) With the notation of Theorem 1.1, we have \(\overline{\Delta }_L\ge 0\) in the \(L^2\)-sense if and only if the TT-eigenvalues of the Einstein operator satisfy
The condition \(\overline{\Delta }_L\ge 0\) is referred in the literature as the condition of linear stability, which appears in the study of the Einstein–Hilbert action (see e.g. [5, Chapter 4 G]) and in the study of dynamical stability of fixed points of the Ricci flow (see e.g. [27]).
The proof in [19] is based on a suitable decomposition of the space of symmetric (0, 2)-tensors on \(\overline{M}\) and many tedious \(L^2\)-estimates. The new proof presented in this paper is much more stringent and due to Theorem 1.1, the structure of \(\overline{\Delta }_L\) on the cone is now understood in much greater detail.
Besides its importance for the computation of the order of Ricci-flat AC/CS ends (cf. Definition 1.3), we think that Theorem 1.1 is also of great independent interest. Moreover, there are further potential applications, for example the desingularization of Einstein conifolds by smooth Einstein metrics. In addition, the method of using commuting operators to compute indicial roots can also be used for other operators, in particular the Hodge Laplacian for the exterior algebra, for which the exterior derivative and its adjoint would serve as commuting operators. This could in turn be used to compute convergence rates of other geometric structures at infinity.
1.2 The order of Ricci-flat conifolds
Let us start this subsection by making the notion of conifolds precise.
Definition 1.3
A manifold \(M^n\) is called a manifold with ends if there exists a compact subset \(K\subset M\), called the core of M, such that
-
(i)
\(M\setminus K\) consists of a disjoint union of connected manifolds \(M_i\), \(i=1,\ldots N\), called the ends of M, and
-
(ii)
for each \(i=1,\ldots N\), there exists a closed manifold \(\widehat{M}_i\) such that \(M_i\) is diffeomorphic to the manifold \((0,\infty )\times \widehat{M}_i\).
In the following, we use the convention \(\nabla ^0:=\textrm{id}\).
Definition 1.4
Let \(M^n\) be a manifold with ends \(M_i\), \(i=1,\ldots , N\), endowed with a Riemannian metric g.
-
(i)
We say that an end \(M_i\) is called asymptotically conical if there exist constants \(\tau _i,R_i>0\), a Riemannian metric \(\widehat{g}_i\) on \(\widehat{M}_i\) and a diffeomorphism \(\varphi _i: M_i\rightarrow (R_i,\infty )\times \widehat{M}_i\) such that for all \(k\in \mathbb {N}_0\), we have
$$\begin{aligned} |\overline{\nabla }^k((\varphi _i)_*g-\overline{g_i})|_{\overline{g_i}}={\mathcal {O}}(r^{-\tau _i-k}),\qquad r \rightarrow \infty , \end{aligned}$$where \(\overline{g}_i=dr^2+r^2\widehat{g}_i\) denotes the cone metric on \((0,\infty )\times \widehat{M}_i\) and \(\overline{\nabla }\) denotes its Levi-Civita connection.
-
(ii)
We say that an end \(M_i\) is called conically singular if there exist constants \(\tau _i,R_i>0\), a Riemannian metric \(\widehat{g}_i\) on \(\widehat{M}_i\) and a diffeomorphism \(\varphi _i: M_i\rightarrow (0,R_i)\times \widehat{M}_i\) such that for all \(k\in \mathbb {N}_0\), we have
$$\begin{aligned} |\overline{\nabla }^k((\varphi _i)_*g-\overline{g_i})|_{\overline{g_i}}={\mathcal {O}}(r^{+\tau _i-k}),\qquad r \rightarrow 0, \end{aligned}$$where, again, \(\overline{g}_i=dr^2+r^2\widehat{g}_i\) denotes the cone metric on \((0,\infty )\times \widehat{M}_i\) and \(\overline{\nabla }\) denotes its Levi-Civita connection.
In both cases, \(\varphi _i\) is called an asymptotic chart and \(\tau _i\) is called an order of the end \(M_i\). We call the manifold \(((0,\infty )\times \widehat{M}_i,\overline{g}_i)\) the tangent cone of the end \(M_i\), and we say that \(M_i\) is tangent to its tangent cones. Furthermore, we call (M, g)
-
(iii)
asymptotically conical (AC for short) if all ends are asymptotically conical;
-
(iv)
conically singular (CS for short) if all ends are conically singular and
-
(v)
conifold (AC/CS for short) if each end is either asymptotically conical or conically singular.
Evidently, the order of an end is not unique: if an end is of order \(\tau \), then it is also of order \(\tau '\) for any \(\tau '<\tau \). Our goal in this paper is to find a lower bound for the order which is as large as possible.
To cover a special situation, which we later call the resonance-dominated case, we introduce a slightly refined notion of asymptotic order:
Definition 1.5
With the notation of Definition 1.3, an asymptotically conical end \((M_i,g_i)\) of a conifold is called asymptotically conical weakly of order \(\tau _i\) if there exists an asymptotic chart \(\phi _i\) in which we have for all \(k\in \mathbb {N}\) that
Note that if and AC end is weakly of order \(\tau \), then it is of order \(\tau -\epsilon \) for all \(\epsilon >0\).
Schematic picture of a conifold, cf. Definitions 1.3 and 1.4
Remark 1.6
If (M, g) is Ricci-flat and AC, it can at only have one end: If it had at least two ends, it would contain a line. Because (M, g) has in particular nonegative Ricci curvature, it would split isometrically as \((M,g)=(\mathbb {R}\times N,dr^2+h)\) by the Cheeger-Gromoll splitting theorem [9]. However, because (M, g) is AC, this can only happen if it is isometric to Euclidean space (which has only one end).
Now let \((\overline{M},\overline{g})\) be a Ricci-flat cone and \(\lambda _i,\mu _i,\kappa _i\) and E as in Theorem 1.1. Denote by \({\textrm{Re}}(E)\subset \mathbb {R}\) the set of real parts of elements in E and define

and

see also Fig. 2 on page 14. Furthermore, we define
Note that both numbers are positive and depend entirely on spectral data on the link \((\widehat{M},\widehat{g})\) of the cone. Note also that there are no a priori positive lower or upper bounds for \(\xi _+\) and \(\xi _-\). We write \(\xi _+(\widehat{M},\widehat{g})\), resp. \(\xi _-(\widehat{M},\widehat{g})\) if we wish to emphasize the dependence of these values on \((\widehat{M},\widehat{g})\).
Definition 1.7
We call a Ricci-flat cone resonance-dominated if

An end of a conifold is called resonance-dominated if its tangent cone is resonance-dominated.
Now we are able to formulate the second main result of this paper.
Theorem 1.8
Let \((M^n,g)\) be a Ricci-flat conifold with ends \(M_i\), \(i=1,\ldots ,N\), which are modeled by Ricci-flat cones over Einstein manifolds \((\widehat{M}_i,\widehat{g}_i)\). Then the following assertions hold:
-
(i)
If \(M_i\),
 , is an asymptotically conical end, then it is of order \(\xi _-(\widehat{M}_i,\widehat{g}_i)\) if it is not resonance-dominated and weakly of order \(\frac{n-2}{2}\) otherwise.
, is an asymptotically conical end, then it is of order \(\xi _-(\widehat{M}_i,\widehat{g}_i)\) if it is not resonance-dominated and weakly of order \(\frac{n-2}{2}\) otherwise. -
(ii)
If \(M_i\),
 , is a conically singular end, then it is of order \(\xi _+(\widehat{M}_i,\widehat{g}_i)\).
, is a conically singular end, then it is of order \(\xi _+(\widehat{M}_i,\widehat{g}_i)\).
Remark 1.9
We do not claim here that the largest possible order of each end is exactly \(\xi _{\pm }(\widehat{M}_i,\widehat{g}_i)\). For some conifolds, the order could be a priori larger. However one would need to study this with methods adjusted to these specific situations and can not be treated in this general framework. In this paper, we will use the adjective “optimal” in this sense.
The construction of the asymptotic chart is based on a global slice theorem for the action of the diffeomorphism group on the space of metrics. We impose the Bianchi gauge, which is made precise in Definition 4.5 below.
We will prove that given a conifold metric g on a manifold M, there exists for any metric \({\tilde{g}}\) sufficiently close to g in a suitable topology (with respect to weighted Sobolev spaces) a diffeomorphism \(\psi \) on M such that up to an arbitrarily small open subset U (which we are free to choose), g is in Bianchi gauge with respect to \(\psi ^*{\tilde{g}}\). Given a Ricci-flat conifold (M, g), we may choose now \({\tilde{g}}\) such that it agrees with g in the core of M and (with respect to given asymptotic charts \(\varphi _i\)) agrees with the exact cone metrics \(\overline{g}_i\) at the ends. With the help of Theorem 1.1, we then compute the order of \(g-\psi ^*{\tilde{g}}\). As a consequence, the new asymptotic charts \(\varphi _i\circ \psi \) will give us the desired orders.
In contrast to [2, 10] who construct the gauge locally at the (single) end, our gauge is constructed globally on all of the manifold and gives us the “optimal” asymptotic charts for all ends at once.
Remark 1.10
Intuitively, one may think of an asymptotic order \(\tau \) at infinity to be “small” if \(\tau <n-2\), since \(n-2\) is the decay rate of the fundamental solution of the Laplace equation. By Theorem 1.8, an AC end has small order if \(E_-\cap (2-n,0)\ne \emptyset \). By definition of \(E_-\), this is the case if some \(\kappa _i\) are negative (this means that the link of the cone is unstable with respect to the Einstein–Hilbert action, cf. [5, Definition 4.63]).
The notion of ADM mass of an asymptotically Euclidean manifold can be generalized to asymptotically conical manifolds.
Definition 1.11
The ADM mass of an asymptotically conical manifold (M, g) with a single end tangent to \(((0,\infty )\times \widehat{M},dr^2+r^2 \widehat{g})\) is

where \(\varphi \) is an asymptotic chart.
In view of Remark 1.10, we obtain the following result:
Corollary 1.12
Let \((\overline{M},\overline{g})\) be a Ricci-flat cone over an Einstein manifold which is linearly stable with respect to the Einstein–Hilbert action. Then any Ricci-flat AC manifold with tangent cone \((\overline{M},\overline{g})\) has vanishing ADM mass.
Example 1.13
For some AC manifolds, the optimal order is known from the construction. Using our main result, we can deduce the existence of certain eigenvalues on the link and make assertions about the stability of the link. For the order \(\tau \), we have \(\tau \in E_-\). By the definition of \(E_-\), we have \(\tau \in (0,\frac{n-2}{2})\) if and only if it is of the form \(-\tau =\xi _{+}(\kappa )\) and \(\tau \in (\frac{n-2}{2},n-2)\) if and only if it is of the form \(-\tau =\xi _{-}(\kappa )\) for some TT-eigenvalue \(\kappa \). In both cases \(\kappa \in (-\frac{(n-2)^2}{4},0)\) and thus, the link is unstable with respect to the Einstein–Hilbert action.
-
(i)
In [12], it is shown that the AC Stenzel metric on \(T^*S^m\) has order \(2\frac{m}{m-1}\) and this is the optimal order. For \(m>2\), \(2\frac{m}{m-1}\in (0,2m-2)\) and thus, the link of the tangent cone of the Stenzel metric is unstable.
-
(ii)
Bryant and Salomon [8] constructed the first examples of AC Ricci-flat manifolds of holonomy \(G_2\) on the manifolds \(\Lambda ^2_-S^4\), \(\Lambda ^2_-\mathbb {C}P^2\) and \(S^3\times \mathbb {R}^4\). The examples on the first two manifolds are of order 4, while the other are of order 3. Because the examples are seven-dimensional and both orders are less than 5, the links are unstable.
Example 1.14
Any 9-dimensional product Einstein manifold \(\widehat{M}_1\times \widehat{M}_2\) with positive Ricci curvature satisfies \(\kappa _1=-2(m-2)=-\frac{(m-2)^2}{4}\) (with \(m=10\)), see e.g. [18, Section 4]. Moreover, if the products are Einstein–Hilbert stable (for example, if both \(\widehat{M}_1\) and \(\widehat{M}_2\) are spheres), all other \(\kappa _i\) are nonnegative. The 10-dimensional cones over such products are resonance-dominated. Ricci-flat AC manifolds tangent to such cones were constructed in [6] and these examples are by definition resonance-dominated as well.
In more specific geometric situations, where the tangent cones are quotients of Euclidean space, we derive the following from Theorem 1.8
Theorem 1.15
Every Ricci-flat orbifold is of order 2.
Theorem 1.16
Every n-dimensional Ricci-flat ALE manifold is ALE of order n.
A classical result by Bando, Kasue and Nakajima (see [2, Theorem 1.5]) states that every ALE manifold is of order \(n-1\) and of order n if the manifold is Kähler or if \(n=4\). Theorem 1.16 shows that we always have order n without additional assumptions. This was already claimed by Cheeger and Tian in [10, Theorem 5.103]. However, their proof contains a tiny gap which seems to have been overlooked so far in the literature.
Let us explain this gap for completeness. The central argument in [10, p. 538] is that any harmonic function f on \(\mathbb {R}^n/\Gamma \) with \(f={\mathcal {O}}(r^{1-n})\) satisfies \(f={\mathcal {O}}(r^{-n})\) if  . This is because the leading order term is exactly of the form \(x\mapsto \langle x,a\rangle r^{-1}\) for some \(a\in \mathbb {R}^n\) and this is not invariant under any nontrivial \(\Gamma \). For this reason, it was argued that the same decay rate should also hold for a harmonic TT-tensor. However, if h is a harmonic tensor on \(\mathbb {R}^n/\Gamma \), expanded in flat coordinates as
. This is because the leading order term is exactly of the form \(x\mapsto \langle x,a\rangle r^{-1}\) for some \(a\in \mathbb {R}^n\) and this is not invariant under any nontrivial \(\Gamma \). For this reason, it was argued that the same decay rate should also hold for a harmonic TT-tensor. However, if h is a harmonic tensor on \(\mathbb {R}^n/\Gamma \), expanded in flat coordinates as
then the functions \(h_{ij}\) are not necessarily \(\Gamma \)-invariant, so the above argument for functions cannot be applied. Consider the following example: Equip \(\mathbb {R}^4\cong \mathbb {C}^2\) with complex coordinates \((z_1,{\bar{z}}_1,z_2,{\bar{z}}_2)\), where \(z_i=x_i+iy_i\) and \(\overline{z}_i=x_i-iy_i\), \(i=1,2\). Recall that
where \(\partial _{z_i}=1/2(\partial _{x_i}-i\partial _{y_i})\) and \(\partial _{{\bar{z}}_i}=1/2(\partial _{x_i}+i\partial _{y_i})\). The function \(f:z\mapsto (z_1)^3\) is harmonic and invariant under the multiplicative action of the group  and so is its real part, which is given by the function \(g={\textrm{Re}}(f):(x_1,y_1,x_2,y_2)\mapsto (x_1)^3-4(x_1)(y_1)^2\). The tensor \(\nabla ^2g\) is now harmonic and \(\Gamma \)-invariant and its component functions are linear. Therefore, \(h=r^{-4}\nabla ^2g\) is another harmonic \(\Gamma \)-invariant tensor which is of order \({\mathcal {O}}(r^{-3})\).
and so is its real part, which is given by the function \(g={\textrm{Re}}(f):(x_1,y_1,x_2,y_2)\mapsto (x_1)^3-4(x_1)(y_1)^2\). The tensor \(\nabla ^2g\) is now harmonic and \(\Gamma \)-invariant and its component functions are linear. Therefore, \(h=r^{-4}\nabla ^2g\) is another harmonic \(\Gamma \)-invariant tensor which is of order \({\mathcal {O}}(r^{-3})\).
On the other hand, \(h=r^{-4}\nabla ^2g\) is not a TT-tensor and even its trace-free part is not TT. Thus it does not contradict our results which imply that any harmonic \(\Gamma \)-invariant TT-tensor decaying at infinity decays of order n. But as the example of the function g shows, this cannot be directly concluded from the fact that linear functions are not \(\Gamma \)-invariant for any nontrivial \(\Gamma \).
1.3 Structure of the paper
In Sect. 2, we introduce some notations, conventions and commutation formulas which we use throughout the paper. In Sect. 3, Laplace type operators on cones are discussed in great detail. After collecting a few general statements, we first discuss the connection Laplacian on 1-forms. Building upon this, we are able to unravel the complicated structure of the Lichnerowicz Laplacian on cones and prove Theorems 1.1 and 1.2. Section 4 is devoted to the construction of optimal coordinates on conifolds. After an introduction into weighted function spaces and a discussion of decay of Ricci-flat metrics in Bianchi gauge on cones, we prove a slice theorem for the Bianchi gauge on conifolds. These decay results and the slice theorems are then used to prove Theorem 1.8 before we conclude with an application in the orbifold and ALE cases to prove Theorems 1.15 and 1.16.
2 Notations, conventions and formulas
Some results and calculations presented here and in the next section have been previously done in [20] by the first author for different purposes. For convenience we will use the same notation as there.
For a Riemannian manifold (M, g) we define the Riemannian curvature tensor with the sign convention such that
where \(\nabla \) is the Levi-Civita connection of g. The Ricci tensor is denoted by \(\textrm{Ric}\) and the scalar curvature by \(\textrm{scal}\). The Laplace–Beltrami operator \(\Delta :C^{\infty }(M)\rightarrow C^{\infty }(M)\) with the sign convention such that \(\Delta f=-\textrm{tr}{\nabla ^2}f=-g^{ij}\nabla ^2_{ij}f\). With the same sign convention, we define the connection Laplacians
on 1-forms and symmetric (0, 2)-tensors, respectively. To distinguish between these operators and the Laplace–Beltrami operator, we sometimes also use the notation \(\Delta _0\) instead of \(\Delta \).
The symmetric tensor product of \(\omega ,\eta \in C^{\infty }(T^*M)\) is defined as \(\omega \odot \eta =\omega \otimes \eta +\eta \otimes \omega \in C^{\infty }(S^2\,M)\). The divergences of \(\omega \in C^{\infty }(T^*M)\) and \(h\in C^{\infty }(S^2M)\) are defined with the sign convention such that
respectively. The formal adjoint \(\delta ^*:C^{\infty }(T^*M)\rightarrow C^{\infty }(S^2\,M)\) of \(\delta \) is given by
Note that \(\delta ^*d f=\nabla ^2f\) for any \(f\in C^{\infty }(M)\) and that \(\delta ^*\) is related to the Lie derivative by \(2\delta ^*\omega ={\mathcal {L}}_{\omega ^{\sharp }}g\), where \(\omega ^{\sharp }\in C^{\infty }(TM)\) is the dual vector field of \(\omega \) with respect to g. Note moreover that \(\textrm{tr}\circ \delta ^* = -\delta \). We also have trace-free versions of \(\delta ^*\) and \(\nabla ^2\), given by
Furthermore, we introduce the Bianchi operator, given by
This notion comes from the fact that B arises from linearizing the Bianchi gauge condition \(V({g},{\tilde{g}})=0\), where the vector field \(V({g},{\tilde{g}})\) depending on two Riemannian metrics \(g,{\tilde{g}}\) is given in local coordinates by
More precisely, a short calculation shows

The Lichnerowicz Laplacian \(\Delta _L:C^{\infty }(S^2\,M)\rightarrow C^{\infty }(S^2\,M)\) is defined by
where \((h\circ k)_{ij}=g^{mn}k_{im}h_{jm}\), and the full curvature term is \(\mathring{R}h_{ij}=g^{km}g^{ln}R_{iklj}h_{mn}\), where \(R_{iklj}=g(R_{\partial _i,\partial _k}\partial _l,\partial _j)\). The term \(\mathring{R}\in \textrm{End}(S^2M)\) is called the curvature potential. Up to a gauge term, \(1/2\cdot \Delta _L\) is the linearization of the Ricci tensor. More precisely, we have

see [5, Theorem 1.174]. The Einstein operator \(\Delta _E:C^{\infty }(S^2M)\rightarrow C^{\infty }(S^2M)\) is defined by
Note that the two operators are related by \(\Delta _L=\Delta _E+2\lambda \) whenever \(\textrm{Ric}=\lambda \cdot g\). In this case, we additionally have

which is easily seen from (2.9). If \((M^n,g)\) is Einstein with \(\textrm{Ric}_g=\lambda \cdot g\), we furthermore have a variety of commutation identities involving these differential operators: For \(v\in C^{\infty }(M)\), \(\omega \in C^{\infty }(T^*M)\) and \(h\in C^{\infty }(S^2M)\), we have
The computations can be found in [22], see also [18, p. 8]. Note that the third line follows trivially from the first and the second line and that the formulas on the right-hand side follow from the ones on the left-hand side by taking the formal adjoints. Also, note that from (2.11), we can deduce in an obvious way other commutation formulas involving the operators \(\Delta _L\), \(\mathring{\delta }^*\), \(\mathring{\nabla }^2\) and B.
The spectrum of a differential operator P is denoted by \(\textrm{spec}(P)\) and its strictly positive part is denoted by \(\textrm{spec}_+(P)=\textrm{spec}(P)\cap (0,\infty )\). If \(\lambda \) is an eigenvalue of the operator P, we denote the corresponding eigenspace by \(E(P,\lambda )\).
For a section u of a Riemannian vector bundle with metric connection, we write \(u={\mathcal {O}}_k(r^{\alpha })\) if \(|\nabla ^lu|={\mathcal {O}}(r^{\alpha -l})\) for all \(l=0,\ldots k\) and \(u={\mathcal {O}}_{\infty }(r^{\alpha })\) if \(u={\mathcal {O}}_{k}(r^{\alpha })\) for all \(k\in \mathbb {N}\). Furthermore, we write \(u={\mathcal {O}}_k(r^{\alpha }\log r)\) if \(|\nabla ^lu|={\mathcal {O}}(r^{\alpha -l}\log (r))\) for all \(l=0,\ldots k\) and \(u={\mathcal {O}}_{\infty }(r^{\alpha }\log (r))\) if \(u={\mathcal {O}}_{k}(r^{\alpha }\log (r))\) for all \(k\in \mathbb {N}\).
For a vector bundle V, we denote by \(C^{\infty }(V)\), \(C^{2,\alpha }(V)\) etc. the space of sections with respective regularity. If P is a differential operator acting on sections of V, we denote by \(\textrm{ker}_{C^{\infty }}(P)\), \(\textrm{ker}_{C^{2,\alpha }}(P)\) etc. the elements in the kernel of P with respective regularity, cf. [26]. While \(S^2M\) denotes the bundle of all symmetric (0,2)-tensors, the subset \(S^2_+M\subset S^2\,M\) is the set of all positive definite scalar products over all points of M. Although \(S^2_+M\) is not a vector bundle, we denote for notational convenience by \(C^{\infty }(S^2_+M)\), \(C^{2,\alpha }(S^2_+M)\) etc. the set of Riemannian metrics with the respective regularity.
There are several metrics of interest in this paper, and the interplay between them is crucial. For brevity, a system of diacritical marks has been implemented in the notation. Metrics, covariant derivatives, curvatures, Laplace type operators and bundles connected to the link, a Riemannian cone and a generic metric are denoted by hats (\(\widehat{g}\), \(\widehat{\nabla }\) etc.), overlines (\(\overline{g}\), \(\overline{\nabla }\) etc.) and tildes (\({\tilde{g}}\), \({\tilde{\nabla }}\) etc.), respectively. Moreover, geometric objects connected to the conifold metric under consideration carry no diacritical marks. This convention is not applied to tangential operators.
3 Ricci-flat cones and their tangential operators
Throughout this section, we fix a smooth closed Riemannian manifold \((\widehat{M},\widehat{g})\) of dimension \(n-1\) (with \(n>2\)) and its n-dimensional cone, denoted by
where r is the canonical coordinate on \(\mathbb {R}\). We will use the canonical projections to pull back objects on \(\widehat{M}\) to objects on \(\overline{M}\). For notational convenience, we will drop the explicit reference to the projections. We denote the indices corresponding to coordinates on \(\widehat{M}\) by \(i,j,k,\ldots \), and the index r refers to the r-coordinate in the manifold \(\overline{M}\). Let us denote the indices corresponding to coordinates on \(\overline{M}\) by \(\alpha ,\beta ,\gamma \). The Christoffel symbols on \(\overline{M}\) are related to the ones on \(\widehat{M}\) by
while the other Christoffel symbols vanish. Therefore. the curvature tensors of \(\overline{g}\) and \(\widehat{g}\) are related by
while the other components of \(\overline{R}\) vanish. Consequently, the Ricci tensors are related by
while the other components of \( \overline{\textrm{Ric}}\) vanish. In particular, \((\overline{M},\overline{g})\) is Ricci-flat if and only if \((\widehat{M},\widehat{g})\) is Einstein with \(\widehat{\textrm{Ric}}=(n-2)\widehat{g}\). Note that this latter condition can be achieved via a homothetic rescaling for any positive Einstein manifold. In this situation, we call \((\overline{M},\overline{g})\) the Ricci-flat cone over \((\widehat{M},\widehat{g})\). We will assume from now on that \((\overline{M},\overline{g})\) is Ricci-flat.
3.1 Conical and tangential operators
Let \(\overline{V}\) be a Riemannian vector bundle over \(\overline{M}\) with metric connection \(\overline{\nabla }\) and denote its restriction by  . By identifying the bundle restrictions
. By identifying the bundle restrictions  with each other via parallel transport along radial lines (i.e. curves of the form \(\gamma (r):=(r,p)\) for fixed \(p\in \widehat{M}\)), we get a natural identification
with each other via parallel transport along radial lines (i.e. curves of the form \(\gamma (r):=(r,p)\) for fixed \(p\in \widehat{M}\)), we get a natural identification
Via this parallel transport, we will sometimes consider sections in \(\widehat{V}\) as sections in \(\overline{V}\), without mentioning the extension of the domain from  to \(\overline{M}\) explicitly. Let us assume that all the induced connections \({}^{r}\nabla \) on
to \(\overline{M}\) explicitly. Let us assume that all the induced connections \({}^{r}\nabla \) on  do coincide. We denote this connection on \(\widehat{V}\) by \(\widehat{\overline{\nabla }}\).
do coincide. We denote this connection on \(\widehat{V}\) by \(\widehat{\overline{\nabla }}\).
Definition 3.1
A self-adjoint Laplace type operator \(\overline{\Delta }_{\overline{V}}\) acting on \(C^{\infty }(\overline{V})\) is called a conical operator if it is with respect to (3.4) of the form
where \({\Box }_{\widehat{V}}\) is a self-adjoint Laplace type operator acting on \(C^{\infty }({\widehat{V}})\). We we call \({\Box }_{\widehat{V}}\) the tangential operator of \(\overline{\Delta }_{\overline{V}}\).
Lemma 3.2
If \(\overline{\Delta }_{\overline{V}}=\overline{\nabla }^*\overline{\nabla }\) is the connection Laplacian of \(\overline{V}\), then it is a conical operator and its tangential operator is the connection Laplacian \(\widehat{\overline{\nabla }}^*\widehat{\overline{\nabla }}=-\widehat{g}^{ij}\left( \overline{\nabla }_{i}\overline{\nabla }_{j}-\overline{\nabla }_{\widehat{\nabla }_{\partial _{i}}\partial _{j}} \right) \) of the induced connection \(\widehat{\overline{\nabla }}\) on \(\widehat{V}\) with respect to the metric \(\widehat{g}\).
Proof
This simply follows from writing
and observing that \(\overline{\nabla }_{r}\sim \partial _r\) via (3.4). \(\square \)
Lemma 3.3
If \(\overline{\Delta }_{\overline{V}}=\overline{\nabla }^*\overline{\nabla }+\overline{A}\) with a potential \(\overline{A}\in C^{\infty }(\textrm{End}(\overline{V}))\), then \(\overline{\Delta }_{\overline{V}}\) is a conical operator if and only if \(\overline{R}=r^{-2}\widehat{A}\) for some potential \(\widehat{A}\in C^{\infty }(\textrm{End}(\widehat{V}))\).
Proof
This is obvious. \(\square \)
Example 3.4
The Laplace–Beltrami operator on \(\overline{M}\) is a conical operator and its tangential operator is the Laplace–Beltrami operator on \(\widehat{M}\).
Example 3.5
Let \(\overline{\Delta }_1\) be the connection Laplacian on \(T^*\overline{M}\), and let \(x^i\) be coordinates on \(\widehat{M}\). Because \(\overline{\nabla }_rdr=0\) and \(\overline{\nabla }_r(r dx^i)=0\) the natural identification  is given by
is given by
It is easy to see that this identification is compatible with the natural connection on \(T^*\overline{M}\). Thus by Lemma 3.2, \(\overline{\Delta }_1\) is a conical operator.
Example 3.6
Let \(\overline{\Delta }_L\) be the Lichnerowicz Laplacian on \(S^2\overline{M}\). The identification  coming from parallel transport is given by
coming from parallel transport is given by
Again, checking that this identification is compatible with the natural connection on \(S^2\overline{M}\) is straightforward. Furthermore, the curvature potential \(\mathring{\overline{R}}\in C^{\infty }(\textrm{End}(S^2\overline{M}))\) scales correctly under that identification. Thus by Lemma 3.3, \(\overline{\Delta }_L\) is a conical operator. We denote its tangential operator by \(\Box _L\).
3.2 Harmonic sections of conical operators
Recall the indicial root functions \(\xi _\pm \) from (1.2) and let us introduce
By definition,
and \(\eta \) restricts to a function \(\eta :\mathbb {R}\rightarrow \mathbb {R}\). Furthermore, it is easy to see that
The following Lemma is obvious from (3.5):
Lemma 3.7
Let \(\overline{\Delta }_{\overline{V}}\) be a conical self-adjoint Laplace type operator with tangential operator \(\Box _{\widehat{V}}\). If \(u\in C^{\infty }(\widehat{V})\) satisfies \(\Box _{\widehat{V}} u=\nu u\) for some \(\nu \in \mathbb {R}\), then
If \(\nu =-\frac{(n-2)^2}{4}\), then \(\xi _{+}(\nu )=\xi _{-}(\nu )=-\frac{n-2}{2}\) and we also have
Conversely, if \(\overline{u}\in {\textrm{ker}}(\overline{\Delta }_{\overline{V}})\) is of the form \(\overline{u}=r^{\alpha }u\) or \(\overline{u}=r^{\alpha }\log (r)u\), with \(u\in C^{\infty }(E)\), then we have
Definition 3.8
An element  is called an indicial root of \(\overline{\Delta }_{\overline{V}}\).
is called an indicial root of \(\overline{\Delta }_{\overline{V}}\).
Note that self-adjointness and ellipticity of \(\overline{\Delta }_{\overline{V}}\) get inherited to \(\Box _{\widehat{V}}\) and therefore \(\textrm{spec}(\Box _{\widehat{V}})\) consists solely of eigenvalues of finite multiplicity which tend to infinity. In particular only a finite number of eigenvalues can be negative, a fact we will use later. Let now  be the eigenvalues of \(\Box _{\widehat{V}}\), counted with multiplicity and
be the eigenvalues of \(\Box _{\widehat{V}}\), counted with multiplicity and  be an orthonormal basis of \(L^2(\widehat{V})\) such that \(\Box _{\widehat{V}}(u_i)=\nu _i\cdot u_i\). Then every \(\overline{u}\in \textrm{ker}( \overline{\Delta }_{\overline{V}})\) can be expanded as
be an orthonormal basis of \(L^2(\widehat{V})\) such that \(\Box _{\widehat{V}}(u_i)=\nu _i\cdot u_i\). Then every \(\overline{u}\in \textrm{ker}( \overline{\Delta }_{\overline{V}})\) can be expanded as
with constants \(a_i,a_j,b_i,b_j\), which may have to be complex in order to ensure that \(\overline{u}\) is real. Note that for \(\nu _i< -\frac{(n-2)^2}{4}\), we have
for some constants \(c_i,d_i\in \mathbb {R}\). Now, let

A straightforward consequence for the boundary behavior of harmonic sections is the following:
Corollary 3.9
Let \(\overline{u}\in {\textrm{ker}}(\overline{\Delta }_{\overline{V}})\), not necessarily defined on all of \(\overline{M}\).
-
(i)
If \(\overline{u}\) is defined on \((0,\epsilon )\times \widehat{M}\) and \(|\overline{u}|\rightarrow 0\) as \(r\rightarrow 0\), then \(\overline{u}=\mathcal {O}_{\infty }(r^{\xi ^{\widehat{V}}_+})\) as \(r\rightarrow 0\).
-
(ii)
If \(\overline{u}\) is defined on \((R,\infty )\times \widehat{M}\) and \(|\overline{u}|\rightarrow 0\) as \(r\rightarrow \infty \), then we divide into two subcases:
-
(iia)
If
 , then \(\overline{u}=\mathcal {O}_{\infty }(r^{-\xi ^{\widehat{V}}_-})\) as \(r\rightarrow \infty \).
, then \(\overline{u}=\mathcal {O}_{\infty }(r^{-\xi ^{\widehat{V}}_-})\) as \(r\rightarrow \infty \). -
(iib)
If
 , then \(\overline{u}=\mathcal {O}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
, then \(\overline{u}=\mathcal {O}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
-
(iia)
The decay rate of decaying harmonic fields at infinity (cf. Corollary 3.9). The figure shows the real part of the indicial roots \(\xi _\pm \) corresponding to eigenvalues, cf. (1.2). Note that the two branches \(\xi _\pm \) coincide at the critical point \(-\frac{(n-2)^2}{4}\) and here a logarithmic factor arises. However, if there is another eigenvalue in the shaded region then a slower decay rate dominates the logarithmic one at infinity
3.3 The tangential operator of the connection Laplacian \(\overline{\Delta }_1\)
We define

As it is well known from the Hodge decomposition, we have the \(L^2\)-orthogonal splitting
since \(\widehat{M}\) is compact. Due to the commutation rules (2.11), this splitting is preserved by \(\widehat{\Delta }_1\) and we have
Let \(0=\lambda _0<\lambda _1<\lambda _2\ldots \) be the eigenvalues of \(\widehat{\Delta }\) and let \(\mu _1<\mu _2<\mu _3\ldots \) be the eigenvalues of \(\widehat{\Delta }_1|_{D(\widehat{M})}\). A standard calculation shows that \(\widehat{\Delta }_1=2\widehat{\delta }\circ \widehat{\delta }^*+(n-2)\) holds on \(D(\widehat{M})\). In particular, \(\mu _i\ge (n-2)\) for all \(i\in \mathbb {N}\) and \(\widehat{\Delta }_1\omega =(n-2)\omega \) holds if and only if \(\widehat{\delta }^*\omega =0\), i.e. if \(\omega ^{\sharp }\) is a Killing vector field. To emphasize this relation to Killing vector fields, we always start to count the \(\mu _i\) from 0, whenever \((n-2)\in \textrm{spec}(\widehat{\Delta }_1|_{D(\widehat{M})})\), i.e. we set \(\mu _0=(n-2)\).
Lemma 3.10
Let \(\omega \in D(\widehat{M})\), \({\varphi }\in C^{\infty }(0,\infty )\) and \(\overline{\omega }\in C^{\infty }(T^*\overline{M})\) be given by \(\overline{\omega }=\varphi \cdot r\omega \). Then,
and
Proof
If \(\omega \) and \(\overline{\omega }\) are as in the statement, (3.2) implies
and (3.10) follows by taking the trace and the fact that \(\overline{\omega }_r=0\). By applying the covariant derivative once again, we obtain from (3.2) that
and (3.11) follows by taking the trace and using that \(\widehat{\delta } \omega =0\). \(\square \)
Proposition 3.11
The spectrum of the tangential operator \({\Box }_1\) is given by

where
The corresponding eigenspaces are

where \(i\in \mathbb {N}\).
Remark 3.12
The indicial values of \(\overline{\Delta }\) and \(\overline{\Delta }_1\) coming from an eigenfunction \(v\in E(\widehat{\Delta },\lambda _i)\) are related as follows:
Proof (Proof of Proposition 3.11)
[Proof of Proposition 3.11] Let \(\omega \in D(\widehat{M})\) be such that \(\widehat{\Delta }_1\omega =\mu \omega \). Then due to Lemma 3.10, we have
On the other hand, because \(\overline{\Delta }_1\) is a conical operator, we have
which gives the first type of eigenvalues and eigenforms. Now, take \(v\in C^{\infty }(\widehat{M})\) with \(\widehat{\Delta } v=\lambda v\). Then,
and because \(d\circ \overline{\Delta }=\overline{\Delta }_1\circ d\), we also get
because \((\overline{M},\overline{g})\) is Ricci-flat. Since \(\overline{\Delta }_1\) is a conical operator, we conclude that the section

satisfies
For \(\lambda >0\), observe that the reals \(\xi _{\pm }(\lambda )\) and the section dv are all nonvanishing. For \(\lambda =\lambda _0=0\), \(v\equiv c\in \mathbb {R}\) and \(\xi _+(0)=0\), \(\xi _-(0)=1-n\). Hence,
We have now constructed all eigenvalues and eigenspaces stated in the proposition. Since the \(L^2\)-span of the \(E(\widehat{\Delta },\lambda _i)\) is already all of \(L^2(\widehat{M})\) and the \(L^2\)-span of \(E(\widehat{\Delta }_1,\mu _i)\) is all of \(L^2(D(\widehat{M}))\), it follows with the help of (3.8) that the \(L^2\)-span of the eigenspaces for \(\Box _1\) we have constructed so far is already all of

This finishes the proof of the lemma. \(\square \)
3.4 The tangential operator of the Lichnerowicz Laplacian \(\overline{\Delta }_L\)
Let us assume in this subsection that the dimension of \(\widehat{M}\) is \(n-1\ge 3\). We have the \(L^2\)-orthogonal splitting

where  denotes the space of transverse traceless tensors on \(\widehat{M}\). The Einstein operator (2.10) has a block diagonal form with respect to this decomposition [5, p. 130] (see also [19, Section 2] for the refined version stated here).
denotes the space of transverse traceless tensors on \(\widehat{M}\). The Einstein operator (2.10) has a block diagonal form with respect to this decomposition [5, p. 130] (see also [19, Section 2] for the refined version stated here).
Lemma 3.13
Let \(h\in TT(\widehat{M})\), \(\varphi \in C^{\infty }((0,\infty ))\) and \(\overline{h}\in C^{\infty }(S^2\overline{M})\) be defined by \(\overline{h}=\varphi \cdot r^2\,h\). This tensor satisfies
and
Proof
The condition \(\overline{h}(\partial _r,.)=0\) holds as \(\overline{h}_{rr}=\overline{h}_{rj}=0\). This immediately implies \(\overline{\textrm{tr}}\overline{h}=0\) as \(\widehat{\textrm{tr}}_{\widehat{g}}h=0\). By using (3.2),
and by taking the trace with respect to \(\overline{g}\) and using \(\widehat{\textrm{tr}}h=0\), we obtain \( \overline{\delta }\overline{h}=0\). Taking the covariant derivative once again, we obtain
By taking the trace and using that \(h\in TT(\widehat{M})\), we obtain
It remains to consider the curvature term. However, the only nonvanishing term of the curvature of \(\overline{g}\) is
therefore
which by adding up finishes the proof of the lemma. \(\square \)
Lemma 3.14
Let \(\varphi ,\psi \in C^{\infty }((0,\infty ))\), \(\omega \in C^{\infty }(T^*\widehat{M})\) and \(v\in C^{\infty }(\widehat{M})\). Then, the form
satisfies
Proof
Straightforward calculations show that
and the result is immediate. \(\square \)
Theorem 3.15
The spectrum of the tangential operator \(\Box _L\) of the Lichnerowicz Laplacian is given by

where
The corresponding eigenspaces are

Here, \(\mathring{\widehat{\nabla }}^2\) denotes the trace-free part of the Hessian (2.6) and \(\mathring{\widehat{g}}=\widehat{g}-(n-1)dr\otimes dr\) denotes the trace-free part of \(\widehat{g}\) with respect to \(\overline{g}\).
Remark 3.16
If \((\widehat{M},\widehat{g})\) admits Killing fields, then we start to count the \(\mu _i\) from zero and \(\mu _0=(n-2)\), cf. the discussion at the beginning of Sect. 3.3. In this case, \(\xi _+(\mu _0+1)=1\) and the eigenvalue \(\mu _{0,+}\) drops as the corresponding eigentensor vanishes. On the other hand \(\mu ^{(1)}_{0,-}\) still exists and equals \(\mu ^{(1)}_{0,-}=\lambda ^{(2)}_{0,-}=2n\). Thus by this counting convention, we do not need to distinguish between the cases with or without Killing fields in Theorem 1.1 and always count \(\mu _i\) for \(i\in \mathbb {N}\) there.
Similarly by the Lichnerowicz–Obata eigenvalue inequality [25], we have \(\lambda _i\ge n-1\) for all \(i\in \mathbb {N}\) and equality holds only for the round sphere. In this case, we have \(\mathring{\widehat{\nabla }}^2v=0\) for the corresponding eigenfunctions. In this case \(\xi _+(\lambda _{1})=1\) and the eigenvalue \(\lambda ^{(2)}_{1,+}\) drops and the eigenvalue \(\lambda ^{(2)}_{1,-}=3(n+1)\) is still present.
Remark 3.17
The indicial values of \(\overline{\Delta }\) and \(\overline{\Delta }_L\) coming from an eigenfunction \(v\in E(\widehat{\Delta },\lambda _i)\) are related by
and indicial values of \(\overline{\Delta }_1\) and \(\overline{\Delta }_L\) coming from an eigenform \(\omega \in E(\widehat{\Delta }_1|_{D(\widehat{M})},\mu _i)\) are related by
Proof (Proof of Theorem 3.15)
[Proof of Theorem 3.15] Let \(h\in TT(\widehat{M})\) be such that \(\widehat{\Delta }_Eh=\kappa h\). Then due to Lemma 3.13, we have
Comparing (3.16) and the conical structure of \(\overline{\Delta }_L\), we however immediately get
Next let \(\omega \in D(\widehat{M})\) be such that \(\widehat{\Delta }_1\omega =\kappa \omega \). From Lemma 3.10, we know that
From Lemma 3.14 and the commutation rules (2.11),
Because the Einstein operator is conical, we get that the sections

satisfy
To conclude the discussions on eigenvalues and eigensections generated by elements in \(D(\widehat{M})\), we recall that \(\mu \ge n-2\) and \(\widehat{\Delta }_1\omega =(n-2)\omega \) if and only if \(\widehat{\delta }^*\omega =0\). In this case, \(\xi _{+}(\mu +1)-1=\xi _{+}(n-1)-1=0\), therefore \(h_+=0\) and \(\xi _{-}(\mu +1)-1=\xi _{-}(n-1)-1=-n\). This implies \(h_-\in \mathbb {R}\cdot \omega \odot dr\) and \(h_-\ne 0\) if \(\omega \ne 0\).
It remains to compute the eigenvalues and eigensections generated by smooth functions on \(\widehat{M}\). Let \(w\in C^{\infty }(\widehat{M})\) be such that \(\widehat{\Delta } w=\lambda w\). Then,
and hence
Due to the structure of the Lichnerowicz Laplacian, we get for

that
Finally, it remains to consider the \(\overline{g}\)-traceless eigensections generated by functions. For \(v\in C^{\infty }(\widehat{M})\) with \(\widehat{\Delta }_0 v = \lambda v\) and \(\alpha ,\beta \in \mathbb {R}\), we first make the ansatz
Using Lemma 3.14, we get
and we conclude the trace-free part of the symmetrized covariant derivative equals
We now want to find \(\alpha ,\beta \in \mathbb {R}\) such that \(\overline{\omega }\in \ker (\overline{\Delta }_1)\). By Proposition 3.11, we have
Since the connection Laplacian \(\widehat{\Delta }_1\) on one-forms is conical, the forms
are all harmonic on \(\overline{M}\). Due to the previous computations, the trace-free parts of their symmetrized covariant derivatives are given by the tensors
which are, by the commutation rules (2.11), all in the kernel of the Lichnerowicz Laplacian. Simple manipulations yield
and therefore,
This implies that
Furthermore, we compute
therefore
Because the Lichnerowicz Laplacian is conical, we get that the three tensors

are eigensections of \(\Box _L\) with eigenvalues
This finishes the discussion of eigenvalues \(\lambda >0\). Recall that if \(\lambda =0\), one has \(\xi _+(\lambda )=0\) and \(\xi _-(\lambda )=2-n\); moreover, v is constant and all its covariant derivatives vanish. In this case, the only nonvanishing tensor of the above is
and the corresponding eigenvalue is \(\eta (\xi _-(\lambda )-2)=\eta (-n)=(-n)(-n+n-2)=2n\). By now we have constructed all eigenvalues and eigensections that appear in the assertion of the theorem. Using the natural identification

together with the decompositions (3.8) and (3.14), we get that the \(L^2\)-span of the eigensections we have constructed equals all of  . \(\square \)
. \(\square \)
In this specific situation, Corollary 3.9 is
Corollary 3.18
Let \(\overline{h}\in {\textrm{ker}}(\overline{\Delta }_{\overline{L}})\), not necessarily defined on all of \(\overline{M}\). Let \(\nu _i\), \(i\in \mathbb {N}\) be the eigenvalues of \(\Box _L\) and define

Then we have:
-
(i)
If \(\overline{h}\) is defined on \((0,\epsilon )\times \widehat{M}\) and \(|\overline{h}|\rightarrow 0\) as \(r\rightarrow 0\), then \(\overline{h}=\mathcal {O}_{\infty }(r^{\xi ^L_+})\) as \(r\rightarrow 0\).
-
(ii)
If \(\overline{h}\) is defined on \((R,\infty )\times \widehat{M}\) and \(|\overline{h}|\rightarrow 0\) as \(r\rightarrow \infty \), then we divide into two subcases:
-
(iia)
If
 , then \(\overline{h}=\mathcal {O}_{\infty }(r^{-\xi ^L_-})\) as \(r\rightarrow \infty \).
, then \(\overline{h}=\mathcal {O}_{\infty }(r^{-\xi ^L_-})\) as \(r\rightarrow \infty \). -
(iib)
If
 , then \(\overline{h}=\mathcal {O}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
, then \(\overline{h}=\mathcal {O}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
-
(iia)
3.5 A simple proof of linear stability
Recall that the Hardy inequality states that
Lemma 3.19
Let \(\overline{\Delta }_{\overline{V}}\) be a conical self-adjoint Laplace type operator acting on sections of a vector bundle \(\overline{V}\) over \(\overline{M}\). Let \(\Box _{\widehat{V}}\) be its tangential operator. Then,
if and only if
Proof
Let \(\overline{u}\in C^{\infty }(\overline{V})\) be of the form for \(\overline{u}=\varphi (r)u\in C^{\infty }(\overline{V})\) with some \(\varphi \in C^{\infty }((0,\infty ))\) and an eigensection \(u\in E(\Box _{\widehat{V}},\nu )\) normalized such that \(\left\| u\right\| _{L^2}=1\). By using (3.5) and integrating by parts in r, we can write
Because the space of finite linear combinations of such sections is \(H^1\)-dense in \( C^{\infty }(\overline{E})\), the result now follows from the Hardy inequality. \(\square \)
Using this result, we can now give a simple proof of Theorem 1.2.
Proof of Theorem 1.2
Recall from the beginning of Subsection 3.3, that \(\mu _i\ge (n-2)\) for \(i\in \mathbb {N}\). Moreover, by the Lichnerowicz–Obata eigenvalue inequality [25], we get \(\lambda _i\ge (n-1)\) for \(i\in \mathbb {N}\). By definition of the numbers \(\mu ^{(1)}_{i,\pm }\), \(\lambda ^{(2)}_{i,\pm }\) in Theorem 3.15, we obtain
Therefore, the assertion directly follows from Lemma 3.19 and Theorem 3.15. \(\square \)
3.6 Decay of perturbations satisfying the Bianchi gauge
In the previous subsection, we have established possible growth and decay rates for homogeneous solutions of the equation \(\overline{\Delta }_L\overline{h}=0\). However, not all of them are relevant for our further considerations. Instead, we will later only need to consider the solutions which additionally satisfy the equation \(B_{\overline{g}}(\overline{h})=(\overline{\delta }+\frac{1}{2}d\circ \overline{\textrm{tr}})(\overline{h})=0\) because by (2.8) and (2.9), this implies

so Ricci-flatness and the Bianchi gauge are both preserved at a linear level. For the second main theorem, it turns out that we can also exclude the solutions which are given by Lie derivatives. Recall that for each eigenvalue \(\nu \in \textrm{spec}(\Box _L)\) with \(\nu \ne -\frac{(n-2)^2}{4}\) and each eigensection \(h\in E(\Box _L,\nu )\), we have two tensors \(\overline{h}_{\pm }:=r^{\xi _{\pm }(\nu )}h\in \textrm{ker}(\overline{\Delta }_L)\). If \(\nu =-\frac{(n-2)^2}{4}\), we use the notation \(\overline{h}_+=r^{-\frac{n-2}{2}}\log (r)h\) and \(\overline{h}_-=r^{-\frac{n-2}{2}}h\). Throughout this subsection, we also keep the notation from Theorem 3.15.
Proposition 3.20
Let \(\nu \) be an eigenvalue of \(\Box _L\), \(h\in E(\Box _L,\nu )\) and \(\overline{h}_{\pm }\) as above. Then, the equation
is satisfied by the following tensors \(\overline{h}_{\pm }\):
-
(i)
If \(\nu =\kappa _i\) for some \(i\in \mathbb {N}\), then \(\overline{h}_{\pm }\) both satisfy (3.23).
-
(ii)
If \(\nu =\mu ^{(1)}_{i,+}\) for some \(i\in \mathbb {N}\), then \(\overline{h}_{+}\) solves (3.23) but \(\overline{h}_{-}\) does not.
-
(iii)
If \(\nu =\mu ^{(1)}_{i,-}\) for some \(i\in \mathbb {N}_0\), then \(\overline{h}_{-}\) solves (3.23) but \(\overline{h}_{+}\) does not.
-
(iv)
If \(\nu =\lambda ^{(2)}_{i,+}\) for some \(i\in \mathbb {N}\), then \(\overline{h}_{+}\) solves (3.23) but \(\overline{h}_{-}\) does not.
-
(v)
If \(\nu =\lambda ^{(2)}_{i,-}\) for some \(i\in \mathbb {N}\), then \(\overline{h}_{-}\) solves (3.23) but \(\overline{h}_{+}\) does not.
-
(vi)
If \(\nu =\lambda _{i}\) for some \(i\in \mathbb {N}\), then \(\overline{h}_{+}\) solves (3.23) if and only if h is of the form
$$\begin{aligned} h=\mathring{\widehat{\nabla }}^2v +\frac{\lambda _i(n-2)}{n(n-1)}v\mathring{\widehat{g}}-\frac{1}{2}(n-2)\widehat{\nabla } v\odot dr+\frac{1}{n}(\xi _+(\lambda _i)-\xi _-(\lambda _i)-2)\xi _-(\lambda _i)v\cdot \overline{g} \end{aligned}$$and \(\overline{h}_{-}\) solves (3.23) if and only if h is of the form
$$\begin{aligned} h=\mathring{\widehat{\nabla }}^2v +\frac{\lambda _i(n-2)}{n(n-1)}v\mathring{\widehat{g}}-\frac{1}{2}(n-2)\widehat{\nabla } v\odot dr+\frac{1}{n}(\xi _-(\lambda _i)-\xi _+(\lambda _i)-2)\xi _+(\lambda _i)v\cdot \overline{g} \end{aligned}$$for some function \(v\in E(\widehat{\Delta },\lambda _i)\).
-
(vii)
If \(\nu =\lambda _{0}=0\), then \(\overline{h}_{+}\) solves (3.23) but \(\overline{h}_{-}\) does not.
-
(viii)
If \(\nu =\lambda _{0,-}^{(2)}=2n\), then \(\overline{h}_{-}\) solves (3.23) but \(\overline{h}_{+}\) does not.
Furthermore, only in the cases (i) and (vi), the tensors \(\overline{h}_{\pm }\) which solve (3.23) are not given by Lie derivatives of the metric \(\overline{g}\) along any vector fields.
Proof
The tensors \(\overline{h}_{\pm }\) were constructed in (3.22) in the proof of Theorem 3.15 by eigensections \(v\in C^{\infty }(\widehat{M})\), \(\omega \in C^{\infty }(T^*\widehat{M})\) and \(h\in C^{\infty }(TT(\widehat{M}))\). If two different tensors \(\overline{h}_{\pm }\), \(\overline{k}_{\pm }\) are constructed out of such, the 1-forms
are linearly independent unless these both tensors are constructed from the same eigensection and have the same growth rate. Therefore, we can check the main assertion in each of the cases (i)-(viii) separately. Throughout the proof, we use the formulas found in the proof of Theorem 3.15.
-
(i)
If \(h\in E(\Box _L,\kappa _i)\), then h is a TT-tensor on \(\widehat{M}\) and \(\overline{h}_{\pm }\) are both TT-tensors on \(\overline{M}\) by Lemma 3.13 and thus solve (3.23).
-
(ii)
If \(h\in E(\Box _L,\mu ^{(1)}_{+})\), then \(h=\widehat{\delta }^*\omega +\frac{1}{2}(\xi _{\pm }(\mu _i+1)-1)\omega \odot dr \), where \(\omega \in E(\widehat{\Delta }_1,\mu )=E(\Box _1,\mu +1)\). Furthermore, we have
$$\begin{aligned} \overline{h}_{+}&=r^{\xi _{+}(\mu )} (\widehat{\delta }^*\omega +\frac{1}{2}(\xi _{+}(\mu +1)-1)\omega \odot dr )=\overline{\delta }^*(r^{\xi _{+}(\mu +1)}\omega ). \end{aligned}$$Because \(\widehat{\delta }\omega =0\), \(\overline{h}_{+}\) is trace free. Because \(\omega \in E(\Box _1,\mu +1)\), we have \(r^{\xi _{+}(\mu +1)}\omega \in \ker (\overline{\Delta }_1)\). Therefore,
$$\begin{aligned} \overline{\delta }\overline{h}_{+}=\overline{\delta }(\overline{\delta }^*(r^{\xi _{+}(\mu +1)}\omega ))=\overline{\Delta }_1(r^{\xi _{+}(\mu +1)}\omega )=0, \end{aligned}$$which implies that \(\overline{\delta }\overline{h}_{+}\) is a TT-tensor. On the other hand, the tensor
$$\begin{aligned} \overline{\delta }\overline{h}_{-}=r^{\xi _{-}(\mu )}h=r^{2-n-\xi _{+}(\mu )}h=r^{2-n}\overline{\delta }\overline{h}_{+} \end{aligned}$$is still trace free, but not divergence free, as
$$\begin{aligned} \overline{\delta }\overline{h}_{-}=\overline{\delta }(r^{2-n}\overline{h}_{+})= r^{2-n}\overline{\delta }(\overline{h}_{+})+(2-n)r^{1-n}\overline{h}_{+}(dr,.) =\frac{2-n}{2}(\xi _{+}(\mu +1)-1)r^{1-n}\omega . \end{aligned}$$In particular, we have
$$\begin{aligned} (\overline{\delta }+\frac{1}{2}d\circ \overline{\textrm{tr}})(\overline{h}_{-})=\overline{\delta }(\overline{h}_{-})\ne 0. \end{aligned}$$ -
(iii)
This is completely analogous to (ii), with the positions of \(+\) and − interchanged throughout the proof.
-
(iv)
If \(h\in E(\Box _L,\lambda ^{(2)}_{+})\), then \(h=\mathring{\widehat{\nabla }}^2v-\left( \frac{\lambda }{n-1}-\xi _{+}(\lambda )\right) v\mathring{\widehat{g}}+(\xi _{+}(\lambda )-1)\widehat{\nabla } v\odot dr \), where \(v\in E(\widehat{\Delta },\lambda )\). Furthermore, we have
$$\begin{aligned} \overline{h}_{+}&=r^{\xi _{+}(\lambda ^{(2)}_{+})}\left( \mathring{\widehat{\nabla }}^2v-\left( \frac{\lambda }{n-1}-\xi _{+}(\lambda )\right) v\mathring{\widehat{g}}+(\xi _{+}(\lambda )-1)\widehat{\nabla } v\odot dr\right) \\&=\mathring{\overline{\nabla }}^2(r^{\xi _{+}(\lambda )}v)={\overline{\nabla }}^2(r^{\xi _{+}(\lambda )}v)=\overline{\delta }^*(d(r^{\xi _{+}(\lambda )}v)). \end{aligned}$$Because \(v\in E(\widehat{\Delta },\lambda )\), we have \(r^{\xi _{+}(\lambda )}v\in \ker (\overline{\Delta })\). Therefore,
$$\begin{aligned} \overline{\delta }\overline{h}_{+} = \overline{\delta }(\mathring{\overline{\nabla }^2}(r^{\xi _{+}(\lambda )}v))=\left( 1-\frac{1}{n}\right) \overline{\Delta }_1(\overline{\nabla }(r^{\xi _{+}(\lambda )}v))=0, \end{aligned}$$which implies that \(\overline{\delta }\overline{h}_{+}\) is a TT-tensor and thus solves (3.23). On the other hand, the tensor
$$\begin{aligned} \overline{\delta }\overline{h}_{-}=r^{\xi _{-}(\lambda ^{(2)}_{+})}h=r^{2-n-\xi _{+}(\lambda ^{(2)}_{+})}h=r^{2-n}\overline{\delta }\overline{h}_{+} \end{aligned}$$is still trace free, but not divergence free, as
$$\begin{aligned} \overline{\delta }\overline{h}_{-}&=\overline{\delta }(r^{2-n}\overline{h}_{+})= r^{2-n}\overline{\delta }(\overline{h}_{+})+(2-n)r^{1-n}\overline{h}_{+}(dr,.)\\&=(2-n)(\lambda -(n-1)\xi _+(\lambda ))\lambda vdr+ (2-n)(\xi _{+}(\lambda )-1)r^{1-n}\widehat{\nabla } v. \end{aligned}$$In particular, we have
$$\begin{aligned} B_{\overline{g}}(\overline{h}_{-})=\overline{\delta }(\overline{h}_{-})\ne 0. \end{aligned}$$ -
(v)
This is completely analogous to (iv), with the positions of \(+\) and − interchanged throughout the proof.
-
(vi)
If \(h\in E(\Box _L,\lambda )\), then
$$\begin{aligned} h=\mathring{\widehat{\nabla }}^2v +\frac{\lambda (n-2)}{n(n-1)}v\mathring{\widehat{g}}-\frac{1}{2}(n-2)\widehat{\nabla } v\odot dr+w\cdot \overline{g}, \end{aligned}$$with \(v,w \in E(\widehat{\Delta },\lambda ) \). Let us set \(w=0\) for the moment. Then we have
$$\begin{aligned} \overline{h}_{+}&=r^{\xi _+(\lambda )}\left( \mathring{\widehat{\nabla }}^2v +\frac{\lambda (n-2)}{n(n-1)}v\mathring{\widehat{g}}-\frac{1}{2}(n-2)\widehat{\nabla } v\odot dr\right) \\&=\mathring{\overline{\delta }^*}(r^{\xi _+(\lambda )+1}(\xi _-(\lambda )vdr+rdv)). \end{aligned}$$Observe that \(\overline{h}_{+}\) is trace free. Let us now abbreviate \(\overline{\omega }=r^{\xi _+(\lambda )+1}(\xi _-(\lambda )vdr+rdv)\) and recall that \(\overline{\Delta }_1(\overline{\omega })=0\). Then we get
$$\begin{aligned} B_{\overline{g}}\overline{\omega }=\overline{\delta }\mathring{\overline{\delta }^*}\overline{\omega } =\frac{1}{2}\overline{\Delta }_1\overline{\omega }+\left( \frac{1}{2}-\frac{1}{n}\right) \overline{\nabla }\overline{\delta }\overline{\omega }= \frac{n-2}{2n}d\overline{\delta }\overline{\omega }. \end{aligned}$$We furthermore compute
$$\begin{aligned} \overline{\delta }(\overline{\omega })&=\overline{\delta }(r^{\xi _+(\lambda )-\xi _-(\lambda )+2}r^{\xi _-(\lambda )-1}(\xi _-(\lambda )vdr+rdv)) \\&=\overline{\delta }(r^{\xi _+(\lambda )-\xi _-(\lambda )+2}d(r^{\xi _-(\lambda )}v))\\&=-\langle d(r^{\xi _+(\lambda )-\xi _-(\lambda )+2}),d(r^{\xi _-(\lambda )}v)\rangle _{\overline{g}}+r^{\xi _+(\lambda )-\xi _-(\lambda )+2}\overline{\Delta }(r^{\xi _-(\lambda )}v)\\&=(\xi _-(\lambda )-\xi _+(\lambda )+2)\xi _-(\lambda )r^{\xi _+(\lambda )}v \end{aligned}$$and consequently,
$$\begin{aligned} B_{\overline{g}}(\overline{h}_{+})&=\frac{n-2}{2n}d\overline{\delta }(\overline{\omega })=\frac{n-2}{2n}(\xi _-(\lambda )-\xi _+(\lambda )+2)\xi _-(\lambda )d(r^{\xi _+(\lambda )}v). \end{aligned}$$On the other hand, if \(v=0\), \(\overline{h}_{+}=(r^{\xi _+(\lambda )}w)\cdot \overline{g}\) and
$$\begin{aligned} B_{\overline{g}}(\overline{h}_{+})&=\left( -1+\frac{n}{2}\right) d(r^{\xi _+(\lambda )}w)=\frac{n-2}{2}d(r^{\xi _+(\lambda )}w). \end{aligned}$$Now we assume that both v and w are nonzero. From summing up the two subcases we considered before, we see that
$$\begin{aligned} B_{\overline{g}}(\overline{h}_{+})=0 \end{aligned}$$if and only if
$$\begin{aligned} nw=(\xi _+(\lambda )-\xi _-(\lambda )-2)\xi _-(\lambda )v. \end{aligned}$$The discussion for \(\overline{h}_{-}\) is completely analogous, with interchanging the positions of \(+\) and − everywhere in the calculation.
-
(vii)
If \(h\in E(\Box _L,\lambda _0=0)\), then \(\overline{h}_{+}=\alpha \cdot \overline{g}\) and \(\overline{h}_{-}=\alpha r^{2-n}\overline{g}\), where \(\alpha \in \mathbb {R}\). In the first case, \(\overline{h}_{+}\) is parallel and hence solves (3.23) whereas in the second case
$$\begin{aligned} B_{\overline{g}}(\overline{h}_{-})=\alpha \frac{n-2}{2} d(r^{2-n})=\frac{\alpha }{2}(n-2)^2r^{1-n}dr\ne 0. \end{aligned}$$ -
(viii)
If \(h\in E(\Box _L,\lambda _{0_-}=2n)\), then \(h=\alpha \cdot (n-2)\cdot ((n-1)dr\otimes dr-\widehat{g})\) for some \(\alpha \in \mathbb {R}\) and
$$\begin{aligned} \overline{h}_{-}=\alpha \mathring{\overline{\delta }^*}((2-n)r^{1-n}dr)=\alpha \mathring{\overline{\nabla }}^2r^{2-n}=\alpha {\overline{\nabla }}^2r^{2-n}=\alpha {\overline{\delta }}^*(d(r^{2-n})). \end{aligned}$$Because \(r^{2-n}\) is a harmonic function, we easily conclude
$$\begin{aligned} \overline{\delta }( \mathring{\overline{\nabla }}^2r^{2-n})=\overline{\delta }({\overline{\nabla }}^2r^{2-n})=\overline{\Delta }_1 d(r^{2-n})=0 \end{aligned}$$and so, \(\overline{h}_{-}\) solves (3.23) because it is a TT-tensor. On the other hand, \(\overline{h}_{+}\) is trace free but not divergence free, since
$$\begin{aligned} \overline{h}_{+}=r^{n+2} \overline{h}_{-}, \end{aligned}$$which implies
$$\begin{aligned} \overline{\delta }(\overline{h}_{+})=\overline{\delta }(r^{n+2} \overline{h}_{-})=(n+2)r^{n+1} \overline{h}_{-}(dr)+r^{n+2}\overline{\delta }\overline{h}_{-}=\alpha (n+2)(n-2)(n-1)rdr\ne 0. \end{aligned}$$
To finish the proof, we recall that the cases (ii)-(v) and (viii), the tensors \(\overline{h}_{\pm }\) which are in the kernel of \(B_{\overline{g}}\) are of the form \(\overline{h}_{\pm }=\overline{\delta }^*(\overline{\omega }_{\pm })=\frac{1}{2}{\mathcal {L}}_{(\overline{\omega }_{\pm })^{\sharp }}\overline{g}\). This is also the case for the metric (case (vii)), since \(\overline{g}=\overline{\delta }^*(rdr)=\frac{1}{2}{\mathcal {L}}_{r\partial _r}\overline{g}\). \(\square \)
Let us label the indicial set of \(\overline{\Delta }_L\) by

and recall from Corollary 3.18 the notation
We denote the indicial set of \(\overline{\Delta }_L\) on tensors satisfying the linearized Bianchi gauge by

and set
As in the introduction, we label the subset of \(E_B\) not corresponding to Lie derivatives by

and we set
Obviously, we have
Corollary 3.21
Let \(\overline{h}\in {\textrm{ker}}(\overline{\Delta }_{L})\cap \textrm{ker}(B_{\overline{g}})\), not necessarily defined on all of \(\overline{M}\). Then we have the following:
-
(i)
If \(\overline{h}\) is defined on \((0,\epsilon )\times \widehat{M}\) for some \(\epsilon >0\) and \(|\overline{h}|\rightarrow 0\) as \(r\rightarrow 0\), then \(\overline{h}=\mathcal {O}_{\infty }(r^{\xi ^B_+})\) as \(r\rightarrow 0\).
-
(ii)
If \(\overline{h}\) is defined on \((R,\infty )\times \widehat{M}\) for some \(R>0\) and \(|\overline{h}|\rightarrow 0\) as \(r\rightarrow \infty \), then we divide into two subcases:
-
(iia)
If
 , then \(\overline{h}=\mathcal {O}_{\infty }(r^{-\xi ^B_-})\) as \(r\rightarrow \infty \).
, then \(\overline{h}=\mathcal {O}_{\infty }(r^{-\xi ^B_-})\) as \(r\rightarrow \infty \). -
(iib)
If
 , then \(\overline{h}=\mathcal {O}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
, then \(\overline{h}=\mathcal {O}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
-
(iia)
4 Optimal coordinates for conifolds
4.1 Analysis on conifolds
In order to do analysis of partial differential equations on conifolds, one has to work with weighted function spaces. In the following we recall some well-known facts for weighted Sobolev and Hölder spaces and Laplace type operators on conifolds which can be found in many articles and textbooks, see e.g. [3, 23, 24, 26].
Definition 4.1
Let (M, g) be a conifold. A smooth positive function \(\rho :M\rightarrow (0,\infty )\) is called a radius function if at each end \(M_i\), there exists an asymptotic chart \(\varphi _i\) such that \((\varphi _i)_*\rho =r\).
For simplicity, we assume that M has only one end \(M\setminus K\) which is either asymptotically conical or conically singular. Moreover, for fixed \(R\in \mathbb {R}\), we will use the notation

and similarly with  . On a cone \(\overline{M}\), we pick the function r as radius function and use the notation \(\overline{M}_{<R}\) etc. accordingly (cf. Remark 4.2).
. On a cone \(\overline{M}\), we pick the function r as radius function and use the notation \(\overline{M}_{<R}\) etc. accordingly (cf. Remark 4.2).
For \(p\in [1,\infty )\) and a weight \(\beta \in {\mathbb {R}}\), we define the space \(L^2_{\beta }(M)\) as the closure of \(C^{\infty }_{\text {c}}(M)\) with respect to the norm
and the weighted Sobolev spaces \(H^{k}_{\beta }(M)\) as the closure of \(C^{\infty }_{\text {c}}(M)\) under
The weighted Hölder spaces are defined as the set of maps \(u\in C^{k,\alpha }_{\text {loc}}(M)\), \(\alpha \in (0,1)\) such that the norm

is finite. Here \(\tau _x^y\) denotes the parallel transport from x to y along the shortest geodesic joining x and y, and d(x, y) is the Riemannian distance between x and y. All these spaces are Banach spaces, the spaces \(H^k_{\beta }(M)\) are Hilbert spaces and their underlying topological vector space structures do not depend on the choice of the radius function \(\rho \). All these definitions extend to Riemannian vector bundles with a metric connection in an obvious manner [26]. In the literature, there are different notational conventions for weighted spaces. We follow the more standard convention used in [3, 26]. We have, for every \(\beta \in \mathbb {R}\), \(k,l\in \mathbb {N}_0\) and \(\alpha \in (0,1)\), the obvious embeddings
In the asymptotically conical case, we further have the embeddings
for any \(\beta <\beta '\), the Sobolev embedding
for \(l>n/2\) and \(\beta <\beta '\), and pointwise multiplication extends to a continuous map
for \(\beta \le 0\), provided that \(k>n/2\). Conversely, in the conically singular case, we have
for any \(\beta '<\beta \), the Sobolev embedding
for \(l>n/2\) and \(\beta '<\beta \), and pointwise multiplication extends to a continuous map
for \(\beta \ge 0\), provided that \(k>n/2\).
Remark 4.2
If M is a conifold with multiple ends which might be AC as well as CS, these function spaces are generalized as follows: We index the AC (“large”) ends by  and the CS (“small”) ends by
and the CS (“small”) ends by  . Consider the vector \(\beta =(\zeta ,\sigma )=(\zeta _1,\ldots ,\zeta _a,\sigma _1,\ldots ,\sigma _b)\in \mathbb {R}^{a+b}\), where each \(\zeta _i\) refers to an AC end and each \(\sigma _j\) refers to a CS end. We write \(\zeta \le \zeta '\) (resp. \( \ge ,<,> \)) whenever \(\zeta _i\le \zeta '_i\) (resp. \( \ge ,<,> \)) for each i, and similarly for \(\sigma \). For \(i\in \mathbb {Z}\), we write \(\beta +i:=(\zeta +i,\sigma +i):=(\zeta _1+i,\ldots ,\zeta _a+i,\sigma _1+i,\ldots ,\sigma _b+i)\). Given \(\beta =(\zeta ,\sigma )\in \mathbb {R}^{a+b}\), choose a smooth function on M (again denoted by \(\beta :M\rightarrow \mathbb {R}\)) which at each AC end \(M_i\) coincides with \(\zeta _i\) and at each CS end \(M_j\) coincides with \(\sigma _j\). Then we can define the weighted Sobolev spaces \(H^k_{\beta }=H^k_{\zeta ,\sigma }\) and the weighted Hölder spaces \(C^{k,\alpha }_{\beta }=C^{k,\alpha }_{\zeta ,\sigma }\) exactly as above. The embedding properties from above hold for \(\beta =(\zeta ,\sigma ),\beta '=(\zeta ',\sigma ')\in \mathbb {R}^{a+b}\) with \(\zeta <\zeta '\) and \(\sigma '<\sigma \) and the multiplication properties for \(\zeta \le 0\) and \(\sigma \ge 0\).
. Consider the vector \(\beta =(\zeta ,\sigma )=(\zeta _1,\ldots ,\zeta _a,\sigma _1,\ldots ,\sigma _b)\in \mathbb {R}^{a+b}\), where each \(\zeta _i\) refers to an AC end and each \(\sigma _j\) refers to a CS end. We write \(\zeta \le \zeta '\) (resp. \( \ge ,<,> \)) whenever \(\zeta _i\le \zeta '_i\) (resp. \( \ge ,<,> \)) for each i, and similarly for \(\sigma \). For \(i\in \mathbb {Z}\), we write \(\beta +i:=(\zeta +i,\sigma +i):=(\zeta _1+i,\ldots ,\zeta _a+i,\sigma _1+i,\ldots ,\sigma _b+i)\). Given \(\beta =(\zeta ,\sigma )\in \mathbb {R}^{a+b}\), choose a smooth function on M (again denoted by \(\beta :M\rightarrow \mathbb {R}\)) which at each AC end \(M_i\) coincides with \(\zeta _i\) and at each CS end \(M_j\) coincides with \(\sigma _j\). Then we can define the weighted Sobolev spaces \(H^k_{\beta }=H^k_{\zeta ,\sigma }\) and the weighted Hölder spaces \(C^{k,\alpha }_{\beta }=C^{k,\alpha }_{\zeta ,\sigma }\) exactly as above. The embedding properties from above hold for \(\beta =(\zeta ,\sigma ),\beta '=(\zeta ',\sigma ')\in \mathbb {R}^{a+b}\) with \(\zeta <\zeta '\) and \(\sigma '<\sigma \) and the multiplication properties for \(\zeta \le 0\) and \(\sigma \ge 0\).
Definition 4.3
A Laplace type operator \(\Delta _V\) on a Riemannian vector bundle V with connection over an asymptotically conical/conically singular manifold M is called asymptotically conical/conically singular of order \(\alpha \) if there exists a Riemannian vector bundle \(\overline{V}\) with connection over \((R,\infty )\times \widehat{M}\) (resp. \((0,\epsilon )\times \widehat{M}\)), a conical operator \(\overline{\Delta }_{\overline{V}}\), a vector bundle isomorphism \(\Phi :V|_{M\setminus K}\rightarrow \overline{V}\) covering an asymptotic chart \(\phi \) and a constant \(\alpha >0\), such that for any section \(u={\mathcal {O}}_{\infty }(r^{\beta })\), \(\beta \in \mathbb {R}\), we have
as \(r\rightarrow \infty \) in the AC case, and
as \(r\rightarrow 0\) in the CS case. A Laplace type operator over a conifold is called a conifold operator if it is asymptotically conical and conically singular at each asymptotically conical and conically singular end, respectively.
For any \(\beta \in \mathbb {R}\), a conifold operator \(\Delta _V\) defines a continuous map
Additionally, it is Fredholm for all \(\beta \in \mathbb {R}\) up to a discrete set, see e.g. [24, Proposition 5.64]: Let

where \(\Box _V\) is the tangential operator of the conical operator \(\overline{\Delta }_{\overline{V}}\). In other words D is the set of the real part of the indicial roots of \(\overline{\Delta }_{\overline{V}}\). We call \(\beta \) nonexceptional whenever \(\beta \in \mathbb {R}\setminus D\) and exceptional, whenever \(\beta \in D\). It is a standard fact that the operator (4.2) is Fredholm if and only if \(\beta \) is nonexceptional. An analogous statement holds for weighted Hölder spaces but we will not need it for our purposes.
To conclude this short introduction, we mention an important duality argument. Note that the \(L^2\)-scalar product induces a bounded map
consequently we can think of \(L^2_{-n-\beta }\) as being the dual space of \(L^2_{\beta }\). Motivated by this, we define
If \(\Delta _V\) is formally self-adjoint, the dual map of
is, via the \(L^2\)-pairing, again given by \(\Delta _V\), seen as a map
Recall that a Fredholm map is surjective if its dual map is injective. Therefore,
is surjective if and only if
However, by elliptic regularity for weighted spaces,
for every \(l\in \mathbb {N}\). This gives us a useful criterion for checking isomorphism properties for \(\Delta _V\).
For example, consider the conical operator \(\overline{\Delta }_{\overline{V}}\) over a Riemannian cone \((\overline{M},\overline{g})\). In view of Remark 4.2, we may think of \(\overline{M}\) as a conifold with one AC and one CS end and choose the same weight \(\beta \) on both ends. We may choose \(\rho =r\) as the radius function. By (3.6), an element \(u\in \textrm{ker}(\overline{\Delta }_{\overline{V}})\) defined on all of \(\overline{M}\) can not satisfy \(u\in o(r^{\alpha })\) both as \(r\rightarrow 0\) and \(r\rightarrow \infty \) for any \(\alpha \in \mathbb {R}\). For this reason,
is injective for all weights \(\beta \). By the duality argument above, \(\overline{\Delta }_{\overline{V}}\) is also surjective for all nonexceptional weights \(\beta \). Summing up, we conclude:
Proposition 4.4
A conical operator \(\overline{\Delta }_{\overline{V}}\) over a Riemannian cone \((\overline{M},\overline{g})\), seen as an operator
is an isomorphism for every nonexceptional weight \(\beta \).
4.2 Decay of Ricci-flat metrics on the cone
Recall that for two different Riemannian metrics \(g,{\tilde{g}}\) the vector field \(V({g},{\tilde{g}})\) is given in local coordinates by
Definition 4.5
We say that a metric g is in Bianchi gauge with respect to \({\tilde{g}}\) if \(V(g,{\tilde{g}})=0\).
Theorem 4.6
Let \((\overline{M},\overline{g})\) be a Ricci-flat cone and let g be a Ricci-flat metric defined on an open set \(U\subset \overline{M}\) which is in Bianchi gauge with respect to \(\overline{g}\). Then the following assertions hold:
-
(i)
If U is an open neighborhood of 0 (i.e. if U contains \(\overline{M}_{<R}\) for some \(R\in \mathbb {R}\)) and \(g-\overline{g}= {\mathcal {O}}_2(r^{\alpha })\) for some \(\alpha >0\) as \(r\rightarrow 0\), then we have \(g-\overline{g}= {\mathcal {O}}_{\infty }(r^{\xi ^B_+})\) as \(r\rightarrow 0\).
-
(ii)
If U is an open neighborhood of \(\infty \) (i.e. if \(M\setminus U\) is compact) and \(g-\overline{g}\in {\mathcal {O}}_2(r^{-\alpha })\) for some \(\alpha >0\) as \(r\rightarrow \infty \), then we divide into two subcases:
-
(iia)
If
 , then \(g-\overline{g}=\mathcal {O}_{\infty }(r^{-\xi ^B_-})\) as \(r\rightarrow \infty \).
, then \(g-\overline{g}=\mathcal {O}_{\infty }(r^{-\xi ^B_-})\) as \(r\rightarrow \infty \). -
(iib)
If
 , then \(g-\overline{g}=\mathcal {O}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
, then \(g-\overline{g}=\mathcal {O}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
-
(iia)
Proof
In this proof, all norms and tensor products are taken with respect to \(\overline{g}\). By the assumptions of the theorem, we have the equation
on U, which can be written with respect to the difference \(h=g-\overline{g}\) as
where, as usual, \(*\) denotes finite linear combinations of tensor contractions with covariantly constant coefficients. This follows essentially from [28, Lemma 2.1], but is carried out in more detail in [21, Lemma 3.1]. From here on, the proof is a standard iteration procedure in weighted function spaces, but we decided to present it here for completeness. We focus on case (i), the other one is completely analogous. Without loss of generality, we assume that h is defined on \(\overline{M}_{< R}\) for some \(R>0\). We extend h smoothly to a tensor \(\overline{h}\) on \(\overline{M}\) such that
At first, by elliptic regularity, \(\overline{h}={\mathcal {O}}_{\infty }(r^{\alpha })\) as \(r\rightarrow 0\) (and for trivial reasons also as \(r\rightarrow \infty \)). Thus by (4.3),
in both the cases \(r\rightarrow \infty \) and \(r\rightarrow 0\). Therefore,
for any \(k\in \mathbb {N}_0\) and for any \(\epsilon >0\) and by Proposition 4.4, we find a unique tensor \(h_1\in H^{k+2}_{2\alpha -\epsilon }(S^2\overline{M})\) such that
provided that \(2\alpha -\epsilon \) is a nonexceptional weight. Note that \(h_1\) is independent of the choice of k (but not of the choice of \(\epsilon \)) as \(H^{k+2}_{2\alpha -\epsilon }\subset H^{k'+2}_{2\alpha -\epsilon }\) if \(k\le k'\). In particular, \(h_1\in H^{k}_{2\alpha -\epsilon }\) for all \(k\in \mathbb {N}\) and \(\epsilon >0\) so by Sobolev embedding, \(h_1\in {\mathcal {O}}_{\infty }(r^{2\alpha -2\epsilon })\) as \(r\rightarrow 0\).
Because \(h_0:={\bar{h}}-h_1\in \ker (\Delta _L)\) and \(h_0\in {\mathcal {O}}_{\infty }(r^{\beta })\) for some \(\beta >0\) as \(r\rightarrow 0\), we know by Corollary 3.9 that \(h_1\in {\mathcal {O}}_{\infty }(r^{\xi ^L_+})\). We obtain on the set \(\overline{M}_{< R}\) that
as \(r\rightarrow 0\). If \(2\alpha -2\epsilon >\xi ^L_+\) for some \(\epsilon >0\), we are done. Otherwise we repeat the same procedure again, starting with the new decay rate \(\alpha ':=2\alpha -2\epsilon \). After iterating this procedure at most a finite number of times, we will be in the situation where \(2\alpha -2\epsilon >\xi ^L_+\). In this case, we can now conclude
where \(\overline{\Delta }_Lh_0=0\) and \(h_1\in {\mathcal {O}}_{\infty }(r^{\xi ^L_++\epsilon })\) for some \(\epsilon >0\). By expanding \(h_0\) as in (3.6) and subsuming all terms of faster decay under \(h_1\), we may furthermore assume that \(h_0\) is of the form \(h_0=r^{\xi ^L_+}{\hat{h}}_0\) for some radially parallel tensor \({\hat{h}}_0\).
The equation \(V(g,\overline{g})=0\) is equivalent to
Consequently \(B_{\overline{g}}(h_0)\in {\mathcal {O}}_{\infty }(r^{\xi ^L_+-1+\epsilon })\). On the other hand, because \(h_0=r^{\xi ^L_+}{\hat{h}}_0\), we get \(B_{\overline{g}}(h_0)=r^{\xi ^L_+-1}{\hat{\omega }}\) for some r-parallel 1-form \({\hat{\omega }}\). We conclude \(B_{\overline{g}}(h_0)=0\). Thus, if \(\xi ^L_+<\xi ^B_+\), we get \(h_0=0\) by Corollary 3.21. Therefore \(h\in {\mathcal {O}}_{\infty }(r^{\xi _+^L+\epsilon })\). We then continue with the same procedure as above till we arrive at a decomposition \(h=h_0+h_1\) with \(\overline{\Delta }_Lh_0=0\) and \(B_{\overline{g}}(h_0)=0\), where by Corollary 3.21, \(h_0\) is of the form \(h_0=r^{\xi ^B_+}{\hat{h}}_0\) for some radially parallel tensor \({\hat{h}}_0\) and \(h_1\) decays faster than \(h_0\). This implies the desired result. \(\square \)
4.3 The Bianchi gauge
In this subsection, we want to find out under which conditions the Bianchi gauge condition actually defines a reasonable gauge. For simplicity, we assume again that our manifold has only one end which is either asymptotically conical or conically singular. We start with the following observation:
Lemma 4.7
The set

is an open subset of a vector space. In particular, it is a submanifold of \(H^k_{\beta }(S^2_+M)\).
Proof
Choose a point \(p\in M\), and \(h={\tilde{g}}-g\). In g-normal coordinates around p, we compute at p that
Therefore,

since \(B_g(g)=0\). Hence, we have redefined \({\mathcal {G}}_{\beta }^k\) by a linear equation, which proves the lemma. \(\square \)
Remark 4.8
The fact that the above gauge condition is linear is the reason why we prefer it over the condition \(V({\tilde{g}},g)=0\) for fixed g. In fact, if g has nontrivial Killing fields, the differential of the linearization is not surjective and the set of metrics satisfying this condition may fail to form a manifold.
Lemma 4.9
Pick \(\beta \in \mathbb {R}\) such that the two operators
and
are both Fredholm. Then, we have \(Bh\in \Delta _1(H^{k+1}_{\beta +1}(T^*M))\) if and only if
for every \(\eta \in H^k_{1-n-\beta }(T^*M)\) with \(\Delta _1\eta =0\). Here, \(B^*\omega =\delta ^*\omega +\frac{1}{2}\delta \omega \cdot g\) is the formal adjoint of B.
Proof
By duality, \(Bh=\Delta _1\omega \) for some \(\omega \in H^{k+1}_{\beta +1}(T^*M)\) if and only if
for all \(\eta \in H^{1-k}_{1-n-\beta }(T^*M)\) with \(\Delta _1\eta =0\). The criterion (4.5) now follows from integration by parts. By elliptic regularity, \(\eta \in H^{k}_{1-n-\beta }(T^*M)\). \(\square \)
Lemma 4.10
Let \(\beta \in \mathbb {R}\) be as in Lemma 4.9. Then there exist a number \(N\in \mathbb {N}\) and for any open precompact subset \(U\subset M\) a set of tensors \(h_i\), \(i=1,\ldots N\), with support in \(\overline{U}\) such that

Proof
Note that on a Ricci-flat manifold, \(2\delta \circ B^* = \Delta _1\), therefore \(\textrm{ker}_{H^{k+1}_{\beta +1}}(B^*)\subset \textrm{ker}_{H^{k+1}_{\beta +1}}(\Delta _1).\) Since \(\textrm{ker}_{H^{k+1}_{\beta +1}}\Delta _1\) is finite dimensional, we can find a finite-dimensional vector space V such that
By the commutation formulas (2.11), \(B^*\eta \in \textrm{ker}(\Delta _L)\) for \(\eta \in V\). By assumption, \(B^*\eta \ne 0\) if \(\eta \ne 0\). In particular, \(B^*\eta \) does not vanish identically on any open subset of M by elliptic theory. For a given open and precompact set \(U\subset M\), we choose a bump function \(\chi :M\rightarrow [0,1]\) which is strictly positive in U and vanishes identically on \(M\setminus U\). Then the bilinear form
is an inner product because the tensors \(B^*\eta _i\) do not vanish identically on any open subset of U. Therefore, we may choose a basis  of V which is orthonormal with respect to the inner product A. Define \(h_i:=\chi B^*\eta _i\) for
of V which is orthonormal with respect to the inner product A. Define \(h_i:=\chi B^*\eta _i\) for  . Now let \(h\in H^k_{\beta }(S^2\,M)\) be arbitrary and make the ansatz
. Now let \(h\in H^k_{\beta }(S^2\,M)\) be arbitrary and make the ansatz
By Lemma 4.9, we have
if and only if \(({\hat{h}},B^*\eta )_{L^2}=0\) for all \(\eta \in V\), or equivalently, if and only if \(({\hat{h}},B^*\eta _j)_{L^2}=0\) for all  . By construction of the \(h_i\),
. By construction of the \(h_i\),
Because \(A(\eta _i,\eta _j)=\delta _{ij}\) by construction, (4.6) is satisfied if and only if \(\alpha _i=({\hat{h}},B^*\eta _i)_{L^2}\) for all  . This proves the lemma. \(\square \)
. This proves the lemma. \(\square \)
Lemma 4.11
We have
Furthermore, for any subspace \(Z^k_{\beta }\subset \textrm{ker}_{H^k_{\beta }}(B)\) with
we also have
Proof
The first assertion is immediate from the formula
which follows from a straightforward calculation. Since \(\textrm{ker}_{H^{k+1}_{\beta +1}}(\Delta _1)\) is finite dimensional we can choose a subspace \(Z^k_{\beta }\subset \textrm{ker}_{H^k_{\beta }}(B)\) such that
For the second assertion, consider the sum \(Z^k_\beta + \delta ^*(H^{k+1}_{\beta +1}(T^*M))\). Due to the first assertion, we have
so the sum is direct. It remains to show that the sum is equal to \(B^{-1}(\Delta _1(H^{k+1}_{\beta +1}(T^*M)))\). For an arbitrary \(h\in B^{-1}(\Delta _1(H^{k+1}_{\beta +1}(T^*M)))\), we choose a form \(\omega _0\in H^{k+1}_{\beta +1}(T^*M)\) such that \(Bh=\Delta _1\omega _0\) so that \(h-\delta ^*\omega _0\in \textrm{ker}_{H^k_{\beta }}(B)\). Now by the first assertion, we can write \(h-\delta ^*\omega _0=\delta ^*\omega _1+h_1\), with some \(h_1\in Z^k_{\beta }\) and \(h=\delta ^*(\omega _0+\omega _1)+h_1\) is the desired decomposition. \(\square \)
Let us now focus for a moment on the AC case.
Lemma 4.12
Let (M, g) be an AC manifold. Then the connection Laplacian
is injective for nonexceptional \(\beta <0\) and surjective for every nonexceptional \(\beta >2-n\).
Proof
If \(\omega \in H^{k+2}_{\beta }(T^*M)\) satisfies \(\Delta _1 \omega =0\), then
By the maximum principle and because \(|\omega |^2\rightarrow 0\) as \(r\rightarrow \infty \), we conclude that \(\omega \equiv 0\). Thus,
is an injective Fredholm operator for every nonexceptional \(\beta <0\). The surjectivity for \(\beta >2-n\) follows from duality via the \(L^2\)-pairing, as explained in Subsection 4.1. \(\square \)
The following proposition asserts that the Bianchi gauge is a very reasonable one for any asymptotically conical Ricci-flat manifold (M, g): Any metric \({\tilde{g}}\) sufficiently close to g can be brought by a diffeomorphism into Bianchi gauge, possibly up to an open subset we are free to choose.
Theorem 4.13
Let \((M^n,g)\) be an AC Ricci-flat manifold and let \(k>n/2+1\) and \(\beta <0\) be such that \(\beta +1\) is a nonexceptional value for \(\Delta _1\) and \(\beta \) is a nonexceptional value for B. Pick an open and precompact subset \(U\subset M\) and a complement \(Z^k_{\beta }\) as (4.7). Set

Then there exists an \(H^k_{\beta }\)-neighborhood \({\mathcal {U}}^k_{\beta }\) of g in the space of metrics such that for any \({\tilde{g}}\in {\mathcal {U}}_{\beta }^k\), there exists a diffeomorphism \(\varphi \) which is \(H^{k+1}_{\beta +1}\)-close to the identity and a tensor \({\tilde{h}}\) with \(\textrm{supp}({\tilde{h}})\subset \overline{U}\) such that \(\varphi ^*({\tilde{g}}+{\tilde{h}})\in {\mathcal {H}}_{\beta }^k\).
Remark 4.14
If \(\beta <-1\), we get \(Z^k_{\beta }=\textrm{ker}_{H^k_{\beta }}(B)\) and hence \({\mathcal {H}}_{\beta }^k={\mathcal {G}}_{\beta }^k\) because \(\Delta _1\) is injective on \(H^{k+1}_{\beta +1}(T^*M)\), see Lemma 4.12. On the other hand, if \(\beta >1-n\), the assertion holds without adding the tensor \({\tilde{h}}\), because \(\Delta _1\) is then surjective on \(H^{k+1}_{\beta +1}(T^*M)\), see again Lemma 4.12.
Remark 4.15
A completely analogous statement holds in the case of one conically singular end, with the only difference that \(\beta \) is chosen positive. In case of multiple ends, we also have an analogous assertion. In this case one would work with function spaces with multiple weights which were briefly introduced in Remark 4.2. One would then choose a tuple \(\beta =(\zeta ,\sigma )\) with \(\zeta <0\) and \(\sigma >0\).
Proof
Clearly, we have
Choose tensors \(h_i\),  with support in \(\overline{U}\) as in Lemma 4.10 and let \(\widetilde{V}=\textrm{span}_{\mathbb {R}}(h_i)_{1\le i\le N}\). Then, Lemma 4.11 implies that
with support in \(\overline{U}\) as in Lemma 4.10 and let \(\widetilde{V}=\textrm{span}_{\mathbb {R}}(h_i)_{1\le i\le N}\). Then, Lemma 4.11 implies that
Here, we used that \(2\delta ^*={\mathcal {L}}\circ \sharp \), where \({\mathcal {L}}:X\rightarrow {\mathcal {L}}_Xg\) is the Lie derivative and \(\sharp :\omega \mapsto \omega ^{\sharp }\) is the sharp operator with respect to g. Note that because \(\beta +1<1\), the vector fields in \(H^{k+1}_{\beta +1}(TM)\) are all complete, because they grow slower than linearly. Therefore, we have a well-defined map
where \(\psi _X\) is the flow of X, evaluated at time \(t=1\). Now we consider the smooth map
Its differential at (g, 0, 0) corresponds to the decomposition (4.8). Therefore, \(\Psi \) is a local diffeomorphism from a neighborhood of (g, 0, 0) onto a neighborhood of g by the implicit function theorem. This proves the proposition. \(\square \)
Remark 4.16
Note that the essential reason for the assumption \(\beta <0\) is to guarantee completeness for the vector fields in \(H^{k+1}_{\beta +1}\). In the conically singular case, completeness is guaranteed by assuming \(\beta >0\) as this implies that the vector fields decay at the singularity like \({\mathcal {O}}(r^{1+\epsilon })\).
4.4 Proof of the main results
This section is devoted to the proof of Theorem 1.8 and essentially builds up on the slice theorem 4.13. We prove only for the case of one AC end. The case of one conically singular end is completely analogous. The proof for multiple ends of both types is also analogous and based on a slice theorem for multiple ends, see Remark 4.15. The details are left to the reader. Recall the notation \(\overline{M}_{<R}\) and \(\overline{M}_{>R}\) from (4.1).
Theorem 4.17
Let (M, g) be an asymptotically conical Ricci-flat manifold. Then there exist compact set \(K\subset M\) and an asymptotic chart \(\varphi :M\setminus K\rightarrow \overline{M}_{>R}\) such that
-
(i)
if \((\overline{M},\overline{g})\) is not resonance-dominated, we have \(\varphi _*g-\overline{g}\in {\mathcal {O}}_{\infty }(r^{-\xi _-})\) as \(r\rightarrow \infty \) where \(\xi _-\) has been defined in (1.2),
-
(ii)
if \((\overline{M},\overline{g})\) is resonance-dominated, we have \(\varphi _*g-\overline{g}\in {\mathcal {O}}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
Construction of the new asymptotic chart in the proof of Theorem 4.17. The picture takes place in the set of metrics on M. The dash-dotted line represents metrics that are (up to a precompact set) in Bianchi gauge w.r.t. g. The shaded region represents the neighborhood \({\mathcal {U}}^k_\beta \) of metrics gaugeable by pullbacks, cf. Theorem 4.13. The family of metrics \(g_R\) converges to g, therefore it will eventually enter the neighborhood \({\mathcal {U}}^k_\beta \)
Proof
Because (M, g) is asymptotically conical, we find a compact set \(K_0\subset M\) and a diffeomorphism \(\varphi _0:M{\setminus } K_0\rightarrow \overline{M}_{>R}\) such that \((\varphi _0)^*g-\overline{g}\in {\mathcal {O}}_{\infty }(r^{-\tau })\) for some \(\tau >0\) as \(r\rightarrow \infty \). Let \(f_R:\mathbb {R}_{\ge 0}\rightarrow [0,1]\) be a smooth cutoff function such that
for some constants \(C_i\in \mathbb {R}\). Choose a radius function \(\rho \) on M such that \((\varphi _0)_*\rho =r\) and let \(F_R=f_R\circ \rho \). Let \(R_0:=\max _K \rho \), and for \(R\ge R_0\), define a metric \(g_R\) on M by
Inside \(M_{<R}\), the metric \(g_R\) agrees with g and on \(M_{>2R}\), the metric \(g_R\) agrees with \((\varphi _0)^*\overline{g}\). Moreover, by the choice of \(F_R\), we have \(g_R\rightarrow g\) in \( C^{k}_{-\tau }(S^2M)\) for any \(k\in \mathbb {N}\) as \(R\rightarrow \infty \). Thus for any \(\beta >-\tau \), we also get \(g_R\rightarrow g\) in \(H^k_{\beta }(S^2M)\) for any \(k\in \mathbb {N}\). Choose \(k>n/2+2\) pick an open set \(U\subset K_0\subset M\). Then by Theorem 4.13, there exists for a sufficiently large value for R (which we denote again by R), a diffeomorphism \(\psi _{R}\) and a tensor \(h_R\) with compact support in \(\overline{U}\subset K_0\) such that such that
Consider now the compact set \(K:=(\varphi _{R})^{-1}(K_0)\) and the diffeomorphism
By construction, the function \(F_{R}\) vanishes on the set \(M_{>2R} \subset M\). Furthermore, \(h_R\) vanishes on the domain of \(\varphi _0\). Therefore we have on the set \(\overline{M}_{>2R}\) that \(\varphi _*(\psi _R)^*g_{R}=\varphi _*(\psi _R)^*(\varphi _0)^*\overline{g}=\overline{g}\) and consequently by (4.9)
Because k was chosen to satisfy \(k>n/2+2\), we have \(\varphi _*g- \overline{g}={\mathcal {O}}_{2}(r^{-\beta /2}) \). From Theorem 4.6, we obtain that
By the proof of Theorem 4.6, we can write \(\varphi _*g- \overline{g}=h_0+h_1\) in a neighborhood of infinity, where \(h_0\in \ker (\overline{\Delta }_L)\cap \ker (B_{\overline{g}})\) is of the form \(h_0=r^{-\xi ^B_-}{\hat{h}}_0\) for some radially parallel tensor \({\hat{h}}_0\), and \(h_1\) decays faster than \(h_0\). If \(\xi ^B_-=\xi _-\), we are done. If \(\xi ^B_-<\xi _-\), we know by Proposition 3.20 that \(h_0\) is a Lie derivative. In other words, we can decompose
for some \(\epsilon >0\) and a one-form \(\overline{\omega }\) defined in a neighborhood of infinity. In the following, we are going to show that the leading gauge term \(\overline{\delta }^*\overline{\omega }\) indeed vanishes. Consider the difference
Consider the 1-form \(\overline{\omega }\) in (4.10) and extend the form \(\varphi ^*\overline{\omega }\) on \(M\setminus K\) to a smooth 1-form \(\omega _1\) on all of M. Then, we have that
for some \(\epsilon >0\). Recall that from the proof of Proposition 4.13, we have \(h_0\in Z^k_{\beta }\), where \(Z^k_{\beta }\) is a space such that
Let us proceed with the tensor \(h_1\). At first we know
Now choose \(\beta '\in (\xi ^B_--\epsilon ,\xi ^B_-)\) and choose a subspace \(Z^k_{\beta '}\) with
which additionally satisfies
Due to (4.8), we can write
with \(\omega _2\in H^{k+1}_{\beta '+1}\) and \(k_2\) is a tensor with support in a small region. Rearranging yields
where we also have taken into account that the sums on the right-hand side are all direct by (4.8). But because \(h_0\in Z^k_{\beta }\), this actually implies that \(\delta ^*(\omega _1+\omega _2)=0\). Thus,
and therefore,
for some \(\epsilon '>0\). Pulling back to the cone \(\overline{M}\), this implies (by using elliptic regularity) that
By successively improving the decay rate as in the proof of Theorem 4.17 and repeating the above procedure a finite number of times, we obtain
as desired. \(\square \)
With a combination of the analysis done in Theorem 4.6 and Theorem 4.17, one also obtains the following result:
Theorem 4.18
Let (M, g) be a Ricci-flat AC manifold and \({\tilde{g}}\) be another Ricci-flat metric which is in Bianchi gauge with respect to g. Assume that \(g-{\tilde{g}}={\mathcal {O}}(r^{-\alpha })\) for some \(\alpha >0\), as \(r\rightarrow \infty \). Then,
-
(i)
if (M, g) is not resonance-dominated, we have \(g-{\tilde{g}}\in {\mathcal {O}}_{\infty }(r^{-\xi _-})\) as \(r\rightarrow \infty \) where \(\xi _-\) has been defined in (1.2),
-
(ii)
if (M, g) is resonance-dominated, we have \(g-{\tilde{g}}\in {\mathcal {O}}_{\infty }(r^{-\frac{n-2}{2}}\log (r))\) as \(r\rightarrow \infty \).
In view of Theorem 4.17 this means the following: For both metrics \(g,{\tilde{g}}\), we can pick one common asymptotic chart for which we have the optimal decay rate from Theorem 4.17.
Another consequence of Theorem 1.8 is a criterion for AC manifolds having vanishing mass.
Proof of Corollary 1.12
If the link of the cone is linearly stable with respect to the Einstein-Hilbert action, we have \(\kappa _i\ge 0\) for all \(i\in \mathbb {N}\) by definition. This implies that \(\xi _-(\kappa _i)\ge n-2\) with equality if and only if \(\kappa _i=0\). Since \(\lambda _i>0\) for \(i>0\), we have \(\xi (\lambda _i)>n-2\). By definition of \(\xi _-\) in (1.3), we have \(\xi _-\ge n-2\) and equality holds if and only if the smallest of the \(\kappa _i\) (which is \(\kappa _1\)) satisfies \(\kappa _1=0\). Now if (M, g) is Ricci flat AC with tangent cone \((\overline{M},\overline{g})\), it is by Theorem 1.8 AC of order \(\xi _-\ge n-2\). Let \(\varphi \) be an asymptotic chart in which \(\varphi _*g-{\hat{g}}={\mathcal {O}}_{\infty }(r^{-\xi _-})\). Suppose for the moment that all \(\kappa _i>0\), that is, \(\xi _->n-2\). Then,

Suppose now \(\xi _i=n-2\), that is, \(\kappa _1=0\). Then by the proof of Theorem 4.6, we can near infinity split the tensor \( \varphi _*g-{\hat{g}}\) as
where \(h_0\in \ker (\overline{\Delta }_L)\) and \(h_0=r^{n-2}{\hat{h}}_0\) for a radially parallel tensor field. Furthermore \(h_1\in {\mathcal {O}}_{\infty }(r^{-\alpha })\) with \(\alpha >n-2\). By Theorem 3.15, \({\hat{h}}_0\) is a TT-tensor on M with \({\hat{h}}_0\in \ker ({\hat{\Delta }}_E)\). By Lemma 3.13, \(h_0\) is a TT-tensor on \(\overline{M}\). Therefore,
and because \(\alpha >n-2\), the same argument as above shows that \( m_{ADM}(M,g)=0\). This finishes the proof. \(\square \)
We conclude this paper with computing the order of orbifolds and ALE manifolds, by direct application of Theorem 4.17.
Proof of Theorems 1.15 and 1.16
We first have to consider the eigenvalue data \(\lambda _i\), \(\mu _i\) and \(\kappa _i\) for quotients \(S^{n-1}/\Gamma \). At first, we have

see e.g. [4], and by the equality case in the Lichnerowicz–Obata eigenvalue inequality, we have

whenever  . In [7, Theorem 3.2], Boucetta computed the spectrum of the Lichnerowicz Laplacian on \(S^n\). We conclude
. In [7, Theorem 3.2], Boucetta computed the spectrum of the Lichnerowicz Laplacian on \(S^n\). We conclude

Note that the differences between (4.14) and the values in [7, Theorem 3.2] come from shifting the dimension and the eigenvalue index by one, and by switching from \(\Delta _L\) to \(\Delta _E\). Recalling the notation from Sect. 1.2 (see (1.3)) we get in this case that

The results now follow from Theorem 1.8. \(\square \)
Data availibility
No data associate for the submission.
References
Anderson, Michael T.: Convergence and rigidity of manifolds under Ricci curvature bounds. Invent. Math. 102(1), 429–445 (1990)
Bando, Shigetoshi, Kazue, Atsushi, Nakajima, Hiraku: On a construction of coordinates at infinity on manifolds with fast curvature decay and maximal volume growth. Invent. Math. 97(2), 313–349 (1989)
Bartnik, Robert: The mass of an asymptotically flat manifold. Commun. Pure Appl. Math. 39(5), 661–693 (1986)
Berger, Marcel, Gauduchon, Paul, Mazet, Edmond: Le spectre d’une variété riemannienne. Lecture Notes in Mathematics, 194, Springer-Verlag, Berlin-Heidelberg, (1971)
Besse, A.L.: Einstein manifolds. Reprint of the: edition, p. 2008. Springer, Berlin (1987)
Böhm, Christoph: Non-compact cohomogeneity one Einstein manifolds. Bull. Soc. Math. France 127(1), 135–177 (1999)
Boucetta, Mohamed: Spectre des laplaciens de Lichnerowicz sur les sphères et les projectifs réels. Publ. Math. 43(2), 451–483 (1999)
Bryant, Robert L., Salomon, Simon M.: On the construction of some complete metrics with exceptional holonomy. Duke Math. J. 58(3), 829–850 (1989)
Cheeger, Jeff: Gromoll, Detlef The splitting theorem for manifolds of nonnegative Ricci curvature. J. Differ. Geom. 6(1), 119–128 (1971)
Cheeger, Jeff: Tian, Gang On the cone structure at infinity of Ricci flat manifolds with Euclidean volume growth and quadratic curvature decay. Invent. Math. 118(1), 493–571 (1994)
Chi, Hanci: Invariant Ricci-flat metrics of cohomogeneity one with Wallach spaces as principal orbits. Ann. Glob. Anal. Geom. 56(2), 361–401 (2019)
Conlon, Ronan J., Hein, Hans-Joachim.: Asymptotically conical Calabi–Yau manifolds. I. Duke Math. J. 162(15), 2855–2902 (2013)
Delay, Erwan: \(TT\)-eigentensors of the Lichnerowicz Laplacian on some asymptotically hyperbolic manifolds with warped product metrics Man. Math. 123(2), 147–165 (2007)
Guillarmou, Colin, Moroianu, Sergiu, Schlenker, Jean-Marc.: The renormalized volume and uniformization of conformal structures. J. Inst. Math. Jussieu 17(4), 853–912 (2018)
Hein, Hans-Joachim.: Sun, Song Compact Calabi–Yau manifolds with isolated conical singularities. Publ. Math. IHES 126, 73–130 (2017)
Foscolo, Lorenzo, Haskins, Mark: Nordström, Johannes Infinitely many new families of complete cohomogeneity one \(G_2\)-manifolds: \(G_2\) analogues of the Taub-NUT and Eguchi-Hanson spaces. J. Eur. Math. Soc. 23(7), 2153–2220 (2021)
Kronheimer, Peter B.: The construction of ALE spaces as hyper-Kähler quotients. J. Differ. Geom. 89(3), 665–683 (1989)
Kröncke, Klaus: On infinitesimal Einstein deformations Diff. Geom. Appl. 38(1–2), 41–57 (2015)
Kröncke, Klaus: Stable and unstable Einstein warped products. Trans. Amer. Math. Soc. 369(9), 6537–6563 (2017)
Kröncke, Klaus: Spectra, stability and rigidity of sine–cones. J. Funct. Anal. 281(8), 109115 (2021)
Kröncke, K., Lindblad Petersen, O.: \( L^ p \)-stability and positive scalar curvature rigidity of Ricci-flat ALE manifolds. arXiv:2009.11854 (2020)
Lichnerowicz, André: Propagateurs et commutateurs en relativité générale. Publ. Mathématiques de l’IHÉS 10(1), 5–56 (1961)
Lockhart, Robert B., McOwen, Robert C.: Elliptic differential operators on noncompact manifolds. Ann. Sc. Norm. Super. Pisa Cl. Sci. 12(3), 409–447 (1985)
Melrose, Richard: The Atiyah-Patodi-Singer index theorem Research Notes in Mathematics, 4. A K Peters Ltd, Wellesley, MA (1993)
Obata, Morio: Certain conditions for a Riemannian manifold to be isometric with a sphere. J. Math. Soc. Jpn. 14, 333–340 (1962)
Pacini, Tommaso: Desingularizing isolated conical singularities: uniform estimates via weighted Sobolev spaces. Commun. Anal. Geom. 21(1), 105–170 (2013)
Sesum, Natasa: Linear and dynamical stability of Ricci-flat metrics. Duke Math. J. 133(1), 1–26 (2006)
Shi, Wan-Xiong.: Deforming the metric on complete Riemannian manifolds. J. Differ. Geom. 30(1), 223–301 (1989)
Yau, Shing-Tung.: On the Ricci curvature of a compact Kähler manifold and the complex Monge-Ampère equation. I. Comm. Pure App. Math. 31(3), 339–411 (1978)
Acknowledgements
The authors want to thank Daniel Grieser, Uwe Semmelmann and Boris Vertman for helpful discussions. The work of the first author is supported by the DFG through the priority program 2026 Geometry at Infinity. The second author was partially funded by the DFG through the Research Training Group 1670 Mathematics Inspired by String Theory and Quantum Field Theory, and the National Science Center (NCN), Poland under grant number OPUS 2021/41/B/ST9/00757. A part of this paper is based on the PhD thesis of the second author.
Funding
Open access funding provided by Royal Institute of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by P. Topping.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kröncke, K., Szabó, Á. Optimal coordinates for Ricci-flat conifolds. Calc. Var. 63, 188 (2024). https://doi.org/10.1007/s00526-024-02780-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-024-02780-y




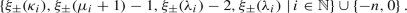




 , is an asymptotically conical end, then it is of order
, is an asymptotically conical end, then it is of order  , is a conically singular end, then it is of order
, is a conically singular end, then it is of order  , then
, then  , then
, then 
 , then
, then  , then
, then  , then
, then  , then
, then  , then
, then  , then
, then 