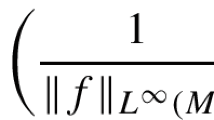Abstract
On a closed Riemannian surface \((M,{\bar{g}})\) with negative Euler characteristic, we study the problem of finding conformal metrics with prescribed volume \(A>0\) and the property that their Gauss curvatures \(f_\lambda = f + \lambda \) are given as the sum of a prescribed function \(f \in C^\infty (M)\) and an additive constant \(\lambda \). Our main tool in this study is a new variant of the prescribed Gauss curvature flow, for which we establish local well-posedness and global compactness results. In contrast to previous work, our approach does not require any sign conditions on f. Moreover, we exhibit conditions under which the function \(f_\lambda \) is sign changing and the standard prescribed Gauss curvature flow is not applicable.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \((M,{\bar{g}})\) be a two-dimensional, smooth, closed, connected, oriented Riemann manifold endowed with a smooth background metric \({\bar{g}}\). A classical problem raised by Kazdan and Warner in [11] and [10] is the question which smooth functions \(f :M \rightarrow \mathbb {R}\) arise as the Gauss curvature \(K_g\) of a conformal metric \(g(x)=\textrm{e}^{2u(x)}{\bar{g}}(x)\) on M and to characterise the set of all such metrics.
For a constant function f, this prescribed Gauss curvature problem is exactly the statement of the Uniformisation Theorem (see e.g. [12, 16]):
There exists a metric g which is pointwise conformal to \({\bar{g}}\) and has constant Gauss curvature \(K_{g}\equiv {\bar{K}}\in \mathbb {R}\).
We now use this statement to assume in the following without loss of generality that the background metric \({\bar{g}}\) itself has constant Gauss curvature \(K_{{\bar{g}}}\equiv {\bar{K}}\in \mathbb {R}\). Furthermore we can normalise the volume of \((M,{\bar{g}})\) to one. We recall that the Gauss curvature of a conformal metric \(g(x)=\textrm{e}^{2u(x)}{\bar{g}}(x)\) on M is given by the Gauss equation
Therefore the problem reduces to the question for which functions f there exists a conformal factor u solving the equation
Given a solution u, we may integrate (1.2) with respect to the measure \(\mu _{{\bar{g}}}\) on M induced by the Riemannian volume form. Using the Gauss–Bonnet Theorem, we then obtain the identity
where \(d\mu _g(x) = \textrm{e}^{2u(x)}d\mu _{{\bar{g}}}(x)\) is the element of area in the metric \(g(x)=\textrm{e}^{2u(x)}{\bar{g}}(x)\). We note that (1.3) immediately yields necessary conditions on f for the solvability of the prescribed Gauss curvature problem. In particular, if \(\pm \chi (M)>0\), then \(\pm f\) must be positive somewhere. Moreover, if \(\chi (M)=0\), then f must change sign or must be identically zero.
In the present paper we focus on the case \(\chi (M)<0\), so M is a surface of genus greater than one and \({\bar{K}} < 0\). The complementary cases \(\chi (M) \ge 0\)—i.e., the cases where \(M = S^2\) or \(M=T\), the 2-torus—will be discussed briefly at the end of this introduction, and we also refer the reader to [2, 8, 18, 19] and the references therein. Multiplying Eq. (1.2) with the factor \(\textrm{e}^{-2u}\) and integrating over M with respect to the measure \(\mu _{{\bar{g}}}\), we get the following necessary condition—already mentioned by Kazdan and Warner in [11]—for the average \({\bar{f}}:=\frac{1}{{\text {vol}}_{{\bar{g}}}}\int _M f(x)d\mu _{{\bar{g}}}(x)\), with \({\text {vol}}_{{\bar{g}}}:=\int _Md\mu _{{\bar{g}}}(x)\):
This condition is not sufficient. Indeed, it has already been pointed out in [11, Theorem 10.5] that in the case \(\chi (M)<0\) there always exist functions \(f \in C^\infty (M)\) with \({\bar{f}}< 0\) and the property that (1.2) has no solution.
We recall that solutions of (1.2) can be characterised as critical points of the functional
Under the assumption \(\chi (M)<0\), i.e., \({\bar{K}} < 0\), the functional \(E_f\) is strictly convex and coercive on \(H^1(M,{\bar{g}})\) if \(f\le 0\) and f does not vanish identically. Hence, as noted in [7], the functional \(E_f\) admits a unique critical point \(u_f \in H^1(M,{\bar{g}})\) in this case, which is a strict absolute minimiser of \(E_f\) and a (weak) solution of (1.2). The situation is more delicate in the case where \(f_\lambda =f_0+\lambda \), where \(f_0\le 0\) is a smooth, nonconstant function on M with \(\max _{x\in M}f_0(x)=0\), and \(\lambda >0\). In the case where \(\lambda >0\) sufficiently small (depending on \(f_0\)), it was shown in [7] and [1] that the corresponding functional \(E_{f_\lambda }\) admits a local minimiser \(u_\lambda \) and a further critical point \(u^\lambda \ne u_\lambda \) of mountain pass type.
These results motivate our present work, where we suggest a new flow approach to the prescribed Gausss curvature problem in the case \(\chi (M)<0\). It is important to note here that there is an intrinsic motivation to formulate the static problem in a flow context. Typically, elliptic theories are regarded as the static case of the corresponding parabolic problem; in that sense, many times the better-understood elliptic theory has been a source of intuition to generalise the corresponding results in the parabolic case. Examples of this feedback are minimal surfaces/mean curvature flow, harmonic maps/solutions of the heat equation, and the Uniformisation Theorem/the two-dimensional normalised Ricci flow.
In this spirit, a flow approach to (1.2), the so-called prescribed Gauss curvature flow, was first introduced by Struwe in [19] (and [2]) for the case \(M=S^2\) with the standard background metric and a positive function \(f \in C^2(M)\). More precisely, he considers a family of metrics \((g(t,\cdot ))_{t\ge 0}\) which fulfils the initial value problem
with
This choice of \(\alpha (t)\) ensures that the volume of \((M,g(t,\cdot ))\) remains constant throughout the deformation, i.e.,
where \(g_0\) denotes the initial metric on M. Equivalently one may consider the evolution equation for the associated conformal factor u given by \(g(t,x)=\textrm{e}^{2u(t,x)}{\bar{g}}(x)\):
Here the initial value \(u_0\) is given by \(g_0(x)=\textrm{e}^{2u_0(x)}{\bar{g}}(x)\). The flow associated to this parabolic equation is usually called the prescribed Gauss curvature flow. With the help of this flow, Struwe [19] provided a new proof of a result by Chang and Yang [6] on sufficient criteria for a function f to be the Gauss curvature of a metric \(g(x)=\textrm{e}^{2u(x)}g_{S^2}(x)\) on \(S^2\). He also proved the sharpness of these criteria.
In the case of surfaces with genus greater than one, i.e., with negative Euler characteristic, the prescribed Gauss curvature flow was used by Ho in [9] to prove that any smooth, strictly negative function on a surface with negative Euler characteristic can be realised as the Gaussian curvature of some metric. More precisely, assuming that \(\chi (M)< 0\) and that \(f \in C^\infty (M)\) is a strictly negative function, he proves that Eq. (1.9) has a solution which is defined for all times and converges to a metric \(g_\infty \) with Gaussian curvature \(K_{g_\infty }\) satisfying
for some constant \(\alpha _\infty \).
While the prescribed Gauss curvature flow is a higly useful tool in the cases where f is of fixed sign, it cannot be used in the case where f is sign-changing. Indeed, in this case we may have \(\int _Mf(x)d\mu _{g(t,\cdot )}(x)=0\) along the flow and then the normalising factor \(\alpha (t)\) is not well-defined by (1.8). As a consequence, a long-time solution of (1.9) might not exist. In particular, the static existence results of [7] and [1] can not be recovered and reinterpreted with the standard prescribed Gauss curvature flow.
In this paper we develop a new flow approach to (1.2) in the case \(\chi (M)<0\) for general \(f \in C^\infty (M)\), which sheds new light on the results in [1, 7] and [9]. The main idea is to replace the multiplicative normalisation in (1.9) by an additive normalisation, as will be described in details in the next chapter.
At this point, it should be noted that the normalisation factor \(\alpha (t)\) in the prescribed Gauss curvature flow given by (1.8) is also not the appropriate choice in the case of the torus, where, as noted before, f has to change sign or be identically zero in order to arise as the Gauss curvature of a conformal metric. The case of the torus was considered by Struwe in [18], where, in particular, he used to a flow approach to reprove and partially improve a result by Galimberti [8] on the static problem. In this approach, the normalisation in (1.8) is replaced by
With this choice, Struwe shows that for any smooth
there exists a unique, global smooth solution u of (1.9) satisfying \(u(t,\cdot )\in C^*\) for all \(t>0\). Moreover, \(u(t,\cdot )\rightarrow u_\infty (\cdot )\) in \(H^2(M,{\bar{g}})\) (and smoothly) as \(t\rightarrow \infty \) suitably, where \(u_\infty +c_\infty \) is a smooth solution of (1.2) for some \(c_\infty \in \mathbb {R}\).
In principle, the normalisation (1.11) could also be considered in the case \(\chi (M)<0\), but then the flow is not volume-preserving anymore, which results in a failure of uniform estimates for solutions of (1.9). Consequently, we were not able to make use of the associated flow in this case.
The paper is organised as follows. In Sect. 2 we set up the framework for the new variant of the prescribed Gauss curvature flow with additive normalisation, and we collect basic properties of it. In Sect. 3, we then present our main result on the long-time existence and convergence of the flow (for suitable times \(t_k \rightarrow \infty \)) to solutions of the corresponding static problem. In particular, our results show how sign changing functions of the form \(f_\lambda = f_0 + \lambda \) arise depending on various assumptions on the shape of \(f_0\) and on the fixed volume A of M with respect to the metric g(t). Before proving our results on the time-dependent problem, we first derive, in Sect. 4, some results on the static problem with volume constraint. Most of these results will then be used in Sect. 5, where the parabolic problem is studied in detail and the main results of the paper are proved. In the appendix, we provide some regularity estimates and a variant of a maximum principle for a class of linear evolution problems with Hölder continuous coefficients.
In the remainder of the paper, we will use the short form f, g(t), u(t), \(K_{g(t)}\), \({\text {vol}}_{g(t)}:=\int _M d\mu _{g(t)}=\int _M\textrm{e}^{2u(t)}d\mu _{{\bar{g}}}\), and so on instead of f(x), g(t, x), u(t, x), \(K_{g(t,\cdot )}(x)\), \(\int _M d\mu _{g(t,\cdot )}(x)=\int _M\textrm{e}^{2u(t,x)}d\mu _{{\bar{g}}}(x)\), et cetera.
2 A new flow approach and some of its properties
Before introducing the additively rescaled prescribed Gauss curvature flow, we recall an important and highly useful estimate. The following lemma (see e.g. [5, Corollary 1.7]) is a consequence of the Trudinger’s inequality [20] which was improved by Moser in [15] (for more details see e.g. [18, Theorem 2.1 and Theorem 2.2]):
Lemma 2.1
For a two-dimensional, closed Riemannian manifold \((M,{\bar{g}})\) there are constants \(\eta >0\) and \(C_{\text {MT}}>0\) such that
for all \(u\in H^1(M,{\bar{g}})\) where
in view of our assumption that \({\text {vol}}_{{\bar{g}}}=1\).
As a consequence of Lemma 2.1, we have
for every \(u \in H^1(M,{\bar{g}})\) and \(p>0\). Therefore, for a given \(A>0\), the set
is well defined. We also note that
since by Jensen’s inequality and our assumption that \({\text {vol}}_{{\bar{g}}}=1\) we have

Next, we let \(f\in C^\infty (M)\) be a fixed smooth function. As a consequence of (2.2), the energy functional \(E_f\) given in (1.5) is then well defined and of class \(C^1\) on \(H^1(M,{\bar{g}})\). Moreover, we have
We now consider the additively rescaled prescribed Gauss curvature flow given by the evolution equation
where \(\alpha (t)\) is chosen such that the volume \({\text {vol}}_{g(t)}\) of M with respect to the metric \(g(t)=\textrm{e}^{2u(t)}{\bar{g}}\) remains constant along the flow. The latter condition requires that
vanishes for \(t >0\) and therefore suggest the definition of \(\alpha (t)\) given in (2.11) below. We first note the following observations.
Proposition 2.2
Let \(T>0\), \(f \in C^\infty (M)\), \(A>0\), let \(u_0 \in {\mathcal {C}}_{A}\), and let \(u \in C([0,T), H^1(M,{\bar{g}}))\cap C^1((0,T),H^2(M,{\bar{g}}))\) be a solution of the initial value problem
where
Then
-
1.
the volume \({\text {vol}}_{g(t)}\) of (M, g(t)) is preserved along the flow, i.e., \({\text {vol}}_{g(t)}\equiv {\text {vol}}_{g_0}=A\) and therefore \(u(t) \in {\mathcal {C}}_{A}\) for \(t \in [0,T)\);
-
2.
along this trajectory, we have a uniform bound for \(\alpha \) given by
$$\begin{aligned} |\alpha (t)| \le \alpha _0\quad \text {for }t \in [0,T)\;\text { with}\quad \alpha _0:=\Vert f\Vert _{L^\infty (M,{\bar{g}})} +\frac{|{\bar{K}}|}{A}; \end{aligned}$$(2.12) -
3.
the Eq. (2.9) remains invariant under adding a constant \(c \in \mathbb {R}\) to the function f;
-
4.
the function \(t \mapsto E_f(u(t))\) is decreasing on [0, T), so in particular \(E_f(u(t))\le E_f(u_0)\) for \(t \in [0,T)\);
-
5.
there exist constants \(c_0=c_0(u_0)>0\), \(c_1=c_1(u_0)>0\) depending only on \(u_0\) with the property that
$$\begin{aligned} \Vert \nabla _{{\bar{g}}}u(t)\Vert ^2_{L^2(M,{\bar{g}})}\le c_0 + c_1 \Vert f\Vert _{L^\infty (M,{\bar{g}})} \qquad \text {for }t \in [0,T); \end{aligned}$$(2.13) -
6.
there exist constants \(m_0=m_0(u_0) \in \mathbb {R}\), \(m_1=m_1(u_0)>0\) depending only on \(u_0\) with the property that
$$\begin{aligned} m_0- m_1 \Vert f\Vert _{L^\infty (M,{\bar{g}})} \le {\bar{u}}(t)\le \frac{1}{2}\log (A) \qquad \text {for }t \in [0,T); \end{aligned}$$(2.14) -
7.
for every \(p \in \mathbb {R}\) there exist constants \(\nu _0= \nu _0(u_0,p),\,\nu _1 = \nu _1(u_0,p)>0\) with
$$\begin{aligned} \int _M \textrm{e}^{2pu(t)}d\mu _{{\bar{g}}}\le \nu _0 \textrm{e}^{\nu _1 \Vert f\Vert _{L^\infty (M,{\bar{g}})}} \qquad \text {for }t \in [0,T). \end{aligned}$$(2.15)
Proof
1. Let \(h(t)=\frac{1}{2}\bigl ({\text {vol}}_{g(t)}-A\bigr )\). Then by (2.8) we have
Since h is continuous in 0 and \(h(0)=0\), Gronwall’s inequality (see e.g. [3]) implies that \(h(t)=0\) and therefore \({\text {vol}}_{g(t)} = A\) for \(t \in [0,T)\).
2. follows directly from (2.11).
To show 3., we note that replacing f by \(f+ c\) in (2.9) gives
so the equation remains unchanged.
To see 4., we use (2.8) and get
Therefore, we have
5. Since \(u(t)\in {\mathcal {C}}_A\) for \(t \in [0,T)\) by 1., we may use 4., (2.5) and (2.6) to observe that
with constants \(c_0,c_1>0\) depending only on \(u_0\) (recall here that \(A = \int _M \textrm{e}^{2u_0(t)}d\mu _{{\bar{g}}}\)).
6. With (2.13) and Lemma 2.1 we can estimate
and therefore
with constants \(m_0 \in \mathbb {R}\), \(m_1 >0\) depending only on \(u_0\). Combining this lower bound with the upper bound given by (2.4), we obtain (2.14).
7. With Lemma 2.1, (2.5), and (2.18) we directly get for any \(p\in \mathbb {R}\) that
with constants \(\nu _i=\nu _i(u_0,p)>0\), \(i\in \{0,1\}\). \(\square \)
3 Main results
In the following, we put
The following is our first main result.
Theorem 3.1
Let \(f\in C^\infty (M)\), \(p>2\), and \(u_0\in {\mathcal {C}}_{p,A}\) for a given \(A>0\).
Then the initial value problem (2.9), (2.10) admits a unique global solution
satisfying the energy bound \(E_{f}(u(t))\le E_{f}(u_0)\) for all \(t \ge 0\).
Moreover, u is uniformly bounded in the sense that
Furthermore, if \((t_l)_l \subset (0,\infty )\) is a sequence with \(t_l \rightarrow \infty \) as \(l \rightarrow \infty \), then, after passing to a subsequence, \(u(t_l)\) converges in \(H^2(M,{\bar{g}})\) to a function \(u_\infty \in H^2(M,{\bar{g}}) \cap {\mathcal {C}}_{A}\) solving the equation
where \(f_\lambda := f +\lambda \) with
In other words, \(u_\infty \) induces a metric \(g_\infty \) with \({\text {vol}}_{g_\infty }= A\) and Gauss curvature \(K_{g_\infty }\) satisfying
Some remarks are in order.
Remark 3.2
It follows in a standard way that, under the assumptions of Theorem 3.1, the \(\omega \)-limit set
is a compact connected subset of \(H^2(M,{\bar{g}}) \cap {\mathcal {C}}_{A}\) (with respect to the \(H^2\)-topology) consisting of solutions of (3.2), (3.3), which are precisely the critical points of the restriction of the energy functional \(E_f\) to \({\mathcal {C}}_{A}\).
In particular, the connectedness implies that, if \(u_\infty \) in Theorem 3.1 is an isolated critical point in \({\mathcal {C}}_{A}\), then \(\omega (u_0)= \{u_\infty \}\) and therefore we have the full convergence of the flow line
In particular, (3.5) holds if \(u_\infty \) is a strict local minimum of the restriction of \(E_f\) to \({\mathcal {C}}_{A}\).
Remark 3.3
For functions \(f<0\), the convergence of the flow (1.9) is shown in [9]. For the additively rescaled flow (2.9) with initial data (2.10) we get convergence for arbitrary functions \(f\in C^\infty (M)\). In general we do not have any information about \(\lambda \) and therefore no information about the sign of \(f_{\lambda }\) in Theorem 3.1. On the other hand, more information can be derived for certain functions \(f \in C^\infty (M)\) and certain values of \(A>0\).
-
(i)
In the case where \(A \le - \frac{{\bar{K}}}{\Vert f\Vert _{L^\infty (M,{\bar{g}})}}\), it follows that
$$\begin{aligned} \lambda= & {} \frac{1}{A}\left( {\bar{K}}- \int _M f \textrm{e}^{2u}d\mu _{{\bar{g}}}\right) \le \frac{{\bar{K}}}{A} + \frac{\Vert f\Vert _{L^\infty (M,{\bar{g}})}}{A} \int _M \textrm{e}^{2u}d\mu _{{\bar{g}}} \\= & {} \frac{{\bar{K}}}{A} + \Vert f\Vert _{L^\infty (M,{\bar{g}})} \le 0 \end{aligned}$$for every solution \(u \in {\mathcal {C}}_{2,A}:=\left\{ v\in H^2(M,{\bar{g}})\mid \int _M\textrm{e}^{2v}d\mu _{{\bar{g}}}=0\right\} \) of the static problem (3.2), and therefore this also applies to \(\lambda \) in Theorem 3.1 in this case.
-
(ii)
The following theorems show that \(f_{\lambda }\) in Theorem 3.1 may change sign if \(A > - \frac{{\bar{K}}}{\Vert f\Vert _{L^\infty (M,{\bar{g}})}}\), so in this case we get a solution of the static problem (1.2) for sign-changing functions \(f\in C^\infty (M)\) by using the additively rescaled prescribed Gauss curvature flow (2.9).
Theorem 3.4
Let \(p>2\). For every \(A>0\) and \(c> - \frac{{\bar{K}}}{A}\) there exists \(\varepsilon = \varepsilon (c,A,{\bar{K}})>0\) with the following property.
If \(u_0 \equiv \frac{1}{2}\log (A) \in {\mathcal {C}}_{p,A}\) and \(f\in C^\infty (M)\) with \(-c \le f \le 0\) and \(\Vert f+c\Vert _{L^1(M,{\bar{g}})} < \varepsilon \) are chosen in Theorem 3.1, then the value \(\lambda \) defined in (3.3) is positive.
In particular, if f has zeros on M, then \(f_\lambda \) in (3.4) is sign changing.
Under fairly general assumptions on f, we can prove that \(\lambda >0\) if A is sufficiently large and \(u_0 \in {\mathcal {C}}_{p,A}\) is chosen suitably.
Theorem 3.5
Let \(f \in C^\infty (M)\) be nonconstant with \(\max _{x\in M} f(x) = 0\). Then there exists \(\kappa >0\) with the property that for every \(A \ge \kappa \) there exists \(u_0 \in {\mathcal {C}}_{p,A}\) such that the value \(\lambda \) defined in (3.3) is positive.
In fact we have even more information on the associated limit \(u_\infty \) in this case, see Corollary 4.7 below.
It remains open how large \(\lambda \) can be depending on A and f. The only upper bound we have is
since we must have
so that \(f_\lambda \) fulfills the necessary condition (1.4) provided by Kazdan and Warner in [11].
4 The static minimisation problem with volume constraint
To obtain additional information on the limiting function \(u_\infty \) and the value \(\lambda \in \mathbb {R}\) associated to it by (3.3) and (3.4), we need to consider the associated static setting for the prescribed Gauss curvature problem with the additional condition of prescribed volume. In this setting, we wish to find, for given \(f \in C^\infty (M)\) and \(A>0\), critical points of the restriction of the functional \(E_{f}\) defined in (1.5) to the set \({\mathcal {C}}_{A}\) defined in (2.3). A critical point \(u \in {\mathcal {C}}_{A}\) of this restriction is a solution of (3.2) for some \(\lambda \in \mathbb {R}\), where, here and in the following, we put again \(f_\lambda := f + \lambda \in C^\infty (M)\). In other words, such a critical point induces, similarly as the limit \(u_\infty \) in Theorem 3.1, a metric \(g^u\) with Gauss curvature \(K_{g^u}\) satisfying \(K_{g^u}(x)= f_{\lambda }(x)=f(x)+\lambda .\) The unknown \(\lambda \in \mathbb {R}\) arises in this context as a Lagrange multiplier and is a posteriori characterised again by
In the study of critical points of the restriction of \(E_{f}\) to \({\mathcal {C}}_{A}\), it is natural to consider the minimisation problem first. For this we set
We have the following estimates for \(m_{f,A}\):
Lemma 4.1
Let \(f \in C^\infty (M)\), \(A>0\). Then we have
Moreover, if \(\max f \ge 0\), then we have
Proof
Let \(u_0(A)\equiv \frac{1}{2}\log (A)\), so that \(\int _M\textrm{e}^{2u_0(A)}d\mu _{{\bar{g}}}=A\). Hence \(u_0(A)\) is the (unique) constant function in \({\mathcal {C}}_{A}\), and
This shows (4.1). To show (4.2), we let \(\varepsilon >0\). Since \(f \in C^\infty (M)\) and \(\max f \ge 0\) by assumption, there exists an open set \(\Omega \subset M\) with \(f \ge -\varepsilon \) on \(\Omega \). Next, let \(\psi \in C^\infty (M)\), \(\psi \ge 0\), be a function supported in \(\Omega \) and with \(\Vert \psi \Vert _{L^\infty (M,{\bar{g}})} = 2\). Consequently, the set \(\Omega ':= \{x \in M\mid \psi >1\}\) is a nonempty open subset of \(\Omega \), and therefore \(\mu _{{\bar{g}}}(\Omega ')>0\).
Next we consider the continuous function
and we note that \(h(0)= \int _M d\mu _{{\bar{g}}}=1\), and that
Hence for every \(A \ge 1\) there exists
with \(h(\tau _A)=A\) and therefore \(\tau _A \psi \in {\mathcal {C}}_{A}\). Consequently,
with
Since \(f \ge -\varepsilon \) on \(\Omega \), we thus deduce that
Since \(\frac{\tau _A}{A} \rightarrow 0\) as \(A \rightarrow \infty \) by (4.3), we conclude that
Since \(\varepsilon >0\) was chosen arbitrarily, (4.2) follows. \(\square \)
Lemma 4.2
Let \(f \in C^\infty (M)\) nonconstant with \(\max _{x\in M} f(x) = 0\). For every \(\varepsilon >0\) there exists \(\kappa _0>0\) with the following property. If \(A \ge \kappa _0\) and \(u \in {\mathcal {C}}_{A}\) is a solution of
for some \(\lambda \in \mathbb {R}\) with \(E_f(u)< \frac{\varepsilon A}{2}\), then we have \(\lambda <\varepsilon \).
Proof
For given \(\varepsilon >0\), we may choose \(\kappa _0>0\) sufficiently large so that \(\frac{|{\bar{K}}|}{2} \frac{\log (A)}{|A|}< \frac{\varepsilon }{2}\) for \(A \ge \kappa _0\).
Now, let \(A \ge \kappa _0\), and let \(u \in {\mathcal {C}}_{A}\) be a solution of (4.4) satisfying \(E_f(u)< \frac{\varepsilon A}{2}\). Integrating (4.4) over M with respect to \(\mu _{{\bar{g}}}\) and using that \({\text {vol}}_{{\bar{g}}}(M)=1\) and \(\int _{M} \textrm{e}^{2u}d\mu _{{\bar{g}}}=A\), we obtain
as claimed. Here we used (2.4) to estimate \({\bar{u}}\). \(\square \)
Proposition 4.3
Let \(f \in C^\infty (M)\) be a nonconstant function with \(\max _{x\in M} f(x) =0\). Moreover, let \(\lambda _n \rightarrow 0^+\) for \(n\rightarrow \infty \), and let \((u_n)_{n\in \mathbb {N}}\) be a sequence of solutions of
which are weakly stable in the sense that
Then \(u_n \rightarrow u_0\) in \(C^2(M)\), where \(u_0\) is the unique solution of
Proof
We only need to show that
Indeed, assuming this for the moment, we may complete the argument as follows. Suppose by contradiction that there exists \(\varepsilon >0\) and a subsequence, also denoted by \((u_n)_{n\in \mathbb {N}}\), with the property that
By (4.8) and the compactness of the embedding \(C^{2,\alpha }(M) \hookrightarrow C^2(M)\), we may then pass to a subsequence, still denoted by \((u_n)_{n\in \mathbb {N}}\), with \(u_n \rightarrow u_*\) in \(C^2(M)\) for some \(u_* \in C^2(M)\). Passing to the limit in (4.5), we then see that \(u_*\) is a solution of (4.7), which by uniqueness implies that \(u_* = u_0\). This contradicts (4.9), and thus the claim follows.
The proof of (4.8) follows by similar arguments as in [7, p. 1063 f.]. Since the framework is slightly different, we sketch the main steps here for the convenience of the reader. We first note that, by the same argument as in [7, p. 1063 f.], there exists a constant \(C_0>0\) with
Since \(\{f < 0\}\) is a nonempty open subset of M by assumption, we may fix a nonempty open subdomain \(\Omega \subset \subset \{f < 0\}\). By [1, Appendix], there exists a constant \(C_1>0\) with
and therefore
for some \(C_2>0\) by the Moser–Trudinger inequality. Next, we consider a nontrivial, nonpositive function \(h \in C^\infty _c(\Omega ) \subset C^\infty (M)\) and the unique solution \(w \in C^\infty (M)\) of the equation
Moreover, we let \(w_n:= u_n - w\), and we note that \(w_n\) satisfies
Multiplying this equation by \(\textrm{e}^{2w_n}\) and integrating by parts, we obtain
Moreover, applying (4.6) to \(h= \textrm{e}^{w_n}\) gives
Combining (4.11), (4.12) and (4.13) yields
Next we claim that also \(\Vert \textrm{e}^{w_n}\Vert _{L^2(M,{\bar{g}})}\) remains uniformly bounded. Suppose by contradiction that
We then set \(v_n:= \frac{\textrm{e}^{w_n}}{\Vert \textrm{e}^{w_n}\Vert _{L^2(M,{\bar{g}})}}\), and we note that
by (4.14). Consequently, we may pass to a subsequence satisfying \(v_n \rightharpoonup v\) in \(H^1(M,{\bar{g}})\), where v is a constant function with
However, since
by (4.11) and therefore
by (4.15), we conclude that the constant function v must vanish identically, contradicting (4.17).
Consequently, \(\Vert \textrm{e}^{w_n}\Vert _{L^2(M,{\bar{g}})}\) remains uniformly bounded, which by (4.14) implies that \(\textrm{e}^{w_n}\) remains bounded in \(H^1(M,{\bar{g}})\) and therefore in \(L^p(M,{\bar{g}})\) for any \(p < \infty \). Since \(\textrm{e}^{u_n} \le \Vert \textrm{e}^{w}\Vert _{L^\infty (M,{\bar{g}})} \textrm{e}^{w_n}\) on M for all \(n \in \mathbb {N}\), it thus follows that also \(\textrm{e}^{u_n}\) remains bounded in \(L^p(M,{\bar{g}})\) for any \(p< \infty \). Moreover, by (4.10), the same applies to the sequence \(u_n\) itself. Therefore, applying successively elliptic \(L^p\) and Schauder estimates to (4.5), we deduce (4.8), as required. \(\square \)
In the proof of the next proposition, we need the following classical interpolation inequality, see e.g. [4].
Lemma 4.4
(Gagliardo–Nirenberg–Ladyžhenskaya inequality) For every \(r>2\), there exists a constant \(C_{\text {GNL}}=C_{\text {GNL}}(r)>0\) with
Proposition 4.5
Let \(f \in C^\infty (M)\) be a nonconstant function with \(\max _{x\in M} f(x) =0\). Then there exists \(\lambda _\sharp \) and a \(C^1\)-curve \((-\infty ,\lambda _{\sharp }] \rightarrow C^2(M); \quad \lambda \mapsto u_\lambda \) with the following properties.
-
(i)
If \(\lambda \le 0\), then \(u_\lambda \) is the unique solution of
$$\begin{aligned} -\Delta _{{\bar{g}}} u + {\bar{K}} = f_\lambda \textrm{e}^{2 u} \quad \text {in }M \end{aligned}$$(4.18)and a global minimum of \(E_{f_\lambda }\).
-
(ii)
If \(\lambda \in (0,\lambda _\sharp ]\), then \(u_\lambda \) is the unique weakly stable solution of (4.18) in the sense of (4.6), and it is a local minimum of \(E_{f_\lambda }\).
-
(iii)
The curve of functions \(\lambda \mapsto u_\lambda \) is pointwisely strictly increasing on M, and so the volume function
$$\begin{aligned} (-\infty ,\lambda _\sharp ] \rightarrow [0,\infty );\quad \lambda \mapsto V(\lambda ):= \int _{M}\textrm{e}^{2u_\lambda } d\mu _{{\bar{g}}} \end{aligned}$$(4.19)is continuous and strictly increasing.
Proof
We already know that, for \(\lambda \le 0\), the energy \(E_{f_\lambda }\) admits a strict global minimiser \(u_\lambda \) which depends smoothly on \(\lambda \). Moreover, by [1, Proposition 2.4], the curve \(\lambda \mapsto u_\lambda \) can be extended as a \(C^1\)-curve to an interval \((-\infty ,\lambda _{\sharp }]\) for some \(\lambda _{\sharp }>0\). We also know from [1, Proposition 2.4] that, for \(\lambda \in (-\infty ,\lambda _{\sharp }]\), the solution \(u_\lambda \) is strongly stable in the sense that
Here we note that the function \(\lambda \mapsto C_\lambda \) is continuous since \(u_\lambda \) depends continuously on \(\lambda \) with respect to the \(C^2\)-norm. Next we prove that, after making \(\lambda _\sharp >0\) smaller if necessary, the function \(u_\lambda \) is the unique weakly stable solution of (4.18) for \(\lambda \in (0,\lambda _{\sharp }]\). Arguing by contradiction, we assume that there exists a sequence \(\lambda _n \rightarrow 0^+\) and corresponding weakly stable solutions \((u_n)_{n\in \mathbb {N}}\) of
with the property that \(u_n \not = u_{\lambda _n}\) for every \(n \in \mathbb {N}\). By Proposition 4.3, we know that \(u_n \rightarrow u_0\) in \(C^2(M)\). Consequently, \(v_n:= u_n - u_{\lambda _n} \rightarrow 0\) in \(C^2(M)\) as \(n \rightarrow \infty \), whereas the functions \(v_n\) solve
Combining this fact with (4.20), we deduce that
Since \(v_n \rightarrow 0\) in \(C^2(M)\), there exists a constant \(C>0\) with \(|(\textrm{e}^{2v_n}-1- 2v_n)v_n| \le C |v_n|^3\) on M for all \(n \in \mathbb {N}\), which then implies with Hölder’s inequality and Lemma 4.4 that
with a constant \(C>0\) independent on M. This contradicts the fact that \(v_n \rightarrow 0\) in \(H^1(M)\) as \(n \rightarrow \infty \). The claim thus follows.
It remains to prove that the curve of functions \(\lambda \mapsto u_\lambda \) is pointwisely strictly increasing on M. This is a consequence of the uniqueness of weakly stable solutions stated in (ii) and the fact that, as noted in [7], if \(u_{\lambda _0}\) is a solution for some \(\lambda _0 \in (-\infty ,\lambda _{\sharp }]\), it is possible to construct, via the method of sub- and supersolutions, for every \(\lambda < \lambda _0\), a weakly stable solution \(u_\lambda \) with \(u_\lambda < u_{\lambda _0}\) everywhere in M. \(\square \)
Corollary 4.6
Let \(f \in C^\infty (M)\) be nonconstant with \(\max _{x\in M} f (x)= 0\), and let \(\lambda _\sharp >0\) be given as in Proposition 4.5. Then there exists \(\kappa _1>0\) with the following property.
If \(A \ge \kappa _1\) and \(u \in {\mathcal {C}}_{A}\) is a solution of
for some \(\lambda \in \mathbb {R}\) with \(E_f(u)< \frac{\lambda _\sharp A}{2}\), then \(0< \lambda < \lambda _\sharp \), and u is not a weakly stable solution of (4.23), so \(u \not = u_\lambda \).
Proof
Let \(\kappa _0>0\) be given as in Lemma 4.2 for \(\varepsilon = \lambda _\sharp >0\). Moreover, let
with V defined in (4.19). Next, let \(u \in {\mathcal {C}}_{A}\) be a solution of (4.23) for some \(\lambda \in \mathbb {R}\) with \(E_f(u)< \frac{\lambda _\sharp A}{2}\). From Lemma 4.2, we then deduce that \(0< \lambda < \lambda _\sharp \), and by Proposition 4.5 (iii) we have \(u \not = u_\lambda \). Since \(u_\lambda \) is the unique weakly stable solution of (4.23), it follows that u is not weakly stable. \(\square \)
Corollary 4.7
Let \(p>2\), \(f \in C^\infty (M)\) be nonconstant with \(\max _{x\in M} f (x)= 0\), and let \(\lambda _\sharp >0\) be given as in Proposition 4.5. Then there exists \(\kappa >0\) with the property that for every \(A \ge \kappa \) the set
is nonempty, and for every \(u_0\in \tilde{{\mathcal {C}}}\) the global solution \(u \in C([0,\infty )\times M)\cap C([0,\infty );H^1(M,{\bar{g}}))\cap C^\infty ((0,\infty )\times M)\) of the initial value problem (2.9), (2.10) converges, as \(t \rightarrow \infty \) suitably, to a solution \(u_\infty \) of the static problem (4.23) for some \(\lambda \in (0,\lambda _\sharp )\) which is not weakly stable and hence no local minimiser of \(E_{f_\lambda }\).
Proof
Let \(\kappa _1>0\) be given by Corollary 4.6. By (4.2), there exists \(\kappa \ge \kappa _1>0\) with \(m_{f,A}<\frac{\lambda _\sharp A}{4}\) for fixed \(A>\kappa \). Consequently, there exists \(u_0 \in {\mathcal {C}}_{A}\cap W^{2,p}(M,{\bar{g}})\) with \(E_f(u_0)< \frac{\lambda _\sharp A}{2}\). By Theorem 3.1, the global solution \(u \in C([0,\infty )\times M)\cap C([0,\infty );H^1(M,{\bar{g}}))\cap C^\infty ((0,\infty )\times M)\) of the initial value problem (2.9), (2.10) converges, as \(t \rightarrow \infty \) suitably, to a solution \(u_\infty \in {\mathcal {C}}_{A}\) of the static problem (4.23) for some \(\lambda \in \mathbb {R}\), whereas \(E_f(u_\infty ) \le E_f(u_0) < \frac{\lambda _\sharp A}{2}\). Consequently, \(\lambda \in (0,\lambda _\sharp )\) by Corollary 4.6, and \(u_\infty \) is not weakly stable. \(\square \)
5 Proof of the main results
5.1 Preliminaries
In the following, we consider, for fixed \(T>0\), the spaces
We stress that, although these spaces depend on T, we prefer to use a T-independent notation. We also note that, since \(T<\infty \) and \({\text {vol}}_{{\bar{g}}}=1\), we have \(L^q_tL^r_x\subset L^s_tL^p_x\) for \(p,q,r,s\in [1,\infty ]\) with \(q\ge s\), \(r\ge p\).
Lemma 5.1
(Sobolev inequality) There exists a constant \(C_S>0\) such that for every \(T \le 1\) and every \(\rho \in L^\infty _t H^1_x\) we have
Proof
By Lemma 4.4, applied with \(r=4\), there exists a constant \(C_{\text {GNL}}=C_{\text {GNL}}(4)>0\) with the property that, for all \(T\le 1\),
Hence the first inequality in (5.1) holds with \(C_S = \Bigl (\frac{3 C_{\text {GNL}}}{2}\Bigr )^{\frac{1}{2}}\). Moreover, since T is finite, \(\rho \in L^\infty _tH^1_x\) implies that \(\rho \in L^p_tH^1_x\) for all \(p\in [1,\infty ]\) which shows that the RHS in (5.1) is finite. \(\square \)
Now we can turn to the proofs of the main results.
5.2 Short-time existence
Let \(A>0\) and \(p>2\) be fixed. We are looking for a short-time solution of (2.9), (2.10) with initial value \(u_0 \in {\mathcal {C}}_{p,A}\), where \({\mathcal {C}}_{p,A}\) is defined in (3.1). Using the Gauss Eq. (1.1) we can rewrite (2.9), (2.10) in the following way:
where
To find a solution of (5.2), (5.3) on a short time interval, we consider the linear equation
and use a fixed point argument in the Banach space
For this we first observe that Eq. (5.4) is strongly parabolic for \(v \in X\). Furthermore, since \(p>2\) and M is compact, we have \(u_0\in {\mathcal {C}}_{p,A} \subset H^2(M,{\bar{g}})\), and therefore \(u_0\in C(M)\).
For the fixed point argument we fix \(u_0\in {\mathcal {C}}_{p,A}\) and set
For fixed \(T>0\) and \(v\in X\), we then get, by Proposition 6.2 in the appendix, a unique solution \(u_v\in W^{2,1}_p((0,T)\times M)\) of (5.4) which satisfies (5.5) in the initial trace sense. Here \(W^{2,1}_p((0,T)\times M)\) denotes the space of functions \(u \in L^p((0,T)\times M)\) which have weak derivatives \(Du, D^2u\) and \(\partial _t u\) in \(L^p((0,T)\times M)\), so this space is compactly embedded in C(X) by Lemma 6.1 in the appendix. On \(X_R=\{ U\in X\mid \Vert U\Vert _X\le R\}\), we now define the function \(\Phi \) as follows: for \(v\in X_R\), let \(\Phi (v)=:u_v\) be the unique solution of (5.4), (5.5). First, we show that \(\Phi :X_R\rightarrow X_R\) if \(T>0\) is chosen small enough.
Lemma 5.2
If \(T>0\) is fixed with
and \(v\in X_R\), then \(\Phi (v)\in X_R\).
Proof
With Proposition 6.4 (ii) we directly get
where
hence
by (5.7) and since \(R=\Vert u_0\Vert _{L^\infty (M,{\bar{g}})}+1\), which shows the claim. \(\square \)
We now use Schauder’s fixed point Theorem [17] to show the following proposition.
Proposition 5.3
If \(u_0 \in {\mathcal {C}}_{p,A}\subset W^{2,p}(M,{\bar{g}})\) and \(T>0\) is fixed with (5.7), then there exists a short-time solution \(u \in X \cap C^{\infty }((0,T)\times M)\) of (5.2), (5.3).
Moreover, any such solution satisfies \(u \in C([0,T), H^1(M,{\bar{g}}))\).
Proof
Step 1: First we recall Schauder’s Theorem: If H is a nonempty, convex, and closed subset of a Banach space B and F is a continuous mapping of H into itself such that F(H) is a relatively compact subset of H, then F has a fixed point.
In our case, \(B\hat{=}X=C([0,T] \times M)\), \(H\hat{=}X_R=\{u\in X\mid \Vert u\Vert _X=\Vert u\Vert _{C_tC_x}\le R\}\), and \(F\hat{=}\Phi \). So to show the existence of a fixed point of \(\Phi \) in \(X_R\), it remains to show that
-
1.
\(\Phi : X_R\rightarrow X_R\) is continuous and
-
2.
\(\Phi (X_R)\subset X_R\) is relatively compact.
First, we show that \(\Phi :X_R\rightarrow X_R\) is continuous. For this, let \(v\in X_R\), and let \((v_n)_{n}\subset X_R\) be a sequence with \(\Vert v_n-v\Vert _X\rightarrow 0\). Moreover, let \(u= \Phi (v)\) and \(u_n= \Phi (v_n)\) for \(n \in \mathbb {N}\). By Proposition 6.2, we know that
for \(n \in \mathbb {N}\) with
Since \(v_n\rightarrow v\) in X, we have \(\textrm{e}^{\pm 2v_n}\rightarrow \textrm{e}^{\pm 2v}\) and therefore also \(d_n\rightarrow d\) in X, which also implies that \(d_n\rightarrow d\) in \(L^p_tL^p_x\) for all p. Moreover, the difference \(u_n-u= \Phi (v_n)-\Phi (v)\) fulfils the equation
Since also \([u_n-u](0)=0\), we have, again by Proposition 6.2,
Since \(\Vert \Delta _{{\bar{g}}}u\Vert _{L^p_tL^p_x}\) is finite, it thus follows that \(\Phi (v_n)-\Phi (v)= u_n-u \rightarrow 0\) in \(W^{2,1}_p\) and therefore also \(\Phi (v_n)-\Phi (v) \rightarrow 0\) in X, since \(W^{2,1}_p\) is embedded in X by Lemma 6.1. Together with 5.2, this shows the continuity of \(\Phi :X_R\rightarrow X_R\).
Next, we show that \(\Phi (X_R)\) is relatively compact. For this let \((u_n)_{n\in \mathbb {N}}\subset \Phi (X_R)\) be an arbitrary sequence in \(\Phi (X_R)\), and let \(v_n\in X_R\) with \(\Phi (v_n)=u_n\) for \(n \in \mathbb {N}\). So, by definition of \(\Phi \) and by Proposition 6.2, we see that
for \(n \in \mathbb {N}\). Hence \((u_n)_{n\in \mathbb {N}}\) is uniformly bounded in \(W^{2,1}_p((0,T)\times M)\). Using now that \(W^{2,1}_p((0,T)\times M)\) is compactly embedded in X by Lemma 6.1, we conclude the claim.
We have thus proved that \(\Phi \) has a fixed point u in \(X_R\), which then is a (strong) solution \(u \in W^{2,1}_p((0,T)\times M)\) of (5.2), (5.3).
Step 2: We now show that \(u \in C^\infty ((0,T)\times M)\). To see this, we first note the trivial fact that \(u \in W^{2,1}_p((0,T)\times M)\) is a strong solution of (5.4), (5.5) with \(v = u\). Since then \(v \in W^{2,1}_p((0,T)\times M) \subset C^\alpha ([0,T]\times M)\), [14, Theorems 5.9 and 5.10] imply the existence of a classical solution \({{\tilde{u}}} \in X \cap C^{2+\alpha ',1+\alpha '}_{loc}((0,T)\times M)\) of (5.4), (5.5) with \(v = u\) for some \(\alpha '>0\). Here \(C^{2+\alpha ',1+\alpha '}_{loc}((0,T)\times M)\) denotes the space of functions \(f \in C^{2,1}((0,T)\times M)\) with the property that \(\partial _t f\) and all derivatives up to second order of f with respect to \(x \in M\) are locally \(\alpha '\)-Hölder continuous. In particular, \({{\tilde{u}}} \in W^{2,1}_p((\varepsilon ,T-\varepsilon )\times M)\) for \(\varepsilon \in (0,T)\). The function \(w:= u- {{\tilde{u}}} \in W^{2,1}_p((\varepsilon ,T-\varepsilon )\times M)\) is then a strong solution of the initial value problem
By Proposition 6.4 (ii) we then have \(|w| \le \Vert u(\varepsilon ,\cdot )-{{\tilde{u}}}(\varepsilon ,\cdot )\Vert _{L^\infty (M,{\bar{g}})}\) on \((\varepsilon ,T-\varepsilon )\times M\), whereas \(\Vert u(\varepsilon ,\cdot )-{{\tilde{u}}}(\varepsilon ,\cdot )\Vert _{L^\infty (M,{\bar{g}})} \rightarrow 0\) as \(\varepsilon \rightarrow 0\) by the continuity of u and \({{\tilde{u}}}\). It thus follows that \(u \equiv {{\tilde{u}}}\) on \((0,T)\times M)\), and therefore \(u \in C^{2+\alpha ',1+\alpha '}_{loc}((0,T)\times M)\). Since u solves (5.4), (5.5) with \(v = u \in C^{2+\alpha ',1+\alpha '}_{loc}((0,T)\times M)\), we can apply [14, Theorems 5.9] and the above argument again to get \(u \in C^{4+\alpha '',2+\alpha ''}_{loc}((0,T)\times M)\) for some \(\alpha ''>0\). Repeating this argument inductively, we get \(u \in C^{k,\frac{k}{2}}_{loc}((0,T)\times M)\) for every \(k>0\), and hence \(u \in C^\infty ((0,T)\times M)\).
Step 3: It remains to show that any solution \(u \in X \cap C^{\infty }((0,T)\times M)\) of (5.2), (5.3) also satisfies \(u \in C([0,T), H^1(M,{\bar{g}}))\). Since \(u \in C^{\infty }((0,T)\times M)\), only the continuity in \(t=0\) needs to be proved. Setting \(\phi (t)= \Vert u(t)\Vert _{H^1(M,{\bar{g}})}^2\) for \(t \in (0,T)\), we see that
and therefore, by Hölder’s inequality,
for \(0<t_1<t_2<T\) with some \(\beta >0\) depending on \(p>2\), which implies that the function \(\phi \) is uniformly continuous and therefore bounded on (0, T).
We now assume by contradiction that u is not continuous at \(t=0\) with respect to the \(H^1(M,{\bar{g}})\)-norm. Then there exists a sequence \((t_n)_{n\in \mathbb {N}}\) in (0, T) and \(\varepsilon >0\) with \(t_n \rightarrow 0^+\) as \(n \rightarrow \infty \) and
Since \(\Vert u(t_n)\Vert _{H^1(M,{\bar{g}})}^2 = \phi (t_n)\) remains bounded as \(n \rightarrow \infty \), we conclude that, passing to a subsequence, the sequence \(u(t_n)\) converges weakly in \(H^1(M,{\bar{g}})\) and therefore strongly in \(L^2(M, {\bar{g}})\). Since the strong \(L^2\)-limit of \(u(t_n)\) must be \(u_0=u(0)\) as a consequence of the fact that \(u \in X\), we deduce that \(u(t_n) \rightharpoonup u_0\) weakly in \({H^1(M,{\bar{g}})}\) as \(n \rightarrow \infty \). Combining this information with Proposition 6.2 from the appendix, we deduce that
and therefore \(\Vert u(t_n)\Vert _{H^1(M,{\bar{g}})} \rightarrow \Vert u_0\Vert _{H^1(M,{\bar{g}})}\). Note here that this part of Proposition 6.2 applies since u solves (5.4), (5.5) with \(v = u \in W^{2,1}_p((0,T)\times M) \subset C^\alpha ([0,T]\times M)\) for some \(\alpha >0\). From (5.10) and the uniform convexity of the Hilbert space \({H^1(M,{\bar{g}})}\), we conclude that \(u(t_n) \rightarrow u_0\) strongly in \(H^1(M,{\bar{g}})\), contrary to (5.9). \(\square \)
5.3 Uniqueness
We now show that the solution from Proposition 5.3 is unique.
Lemma 5.4
Let \(u_0 \in W^{2,p}(M,{\bar{g}})\), \(p>2\), and \(T>0\) be fixed with (5.7). Then the short-time solution of \(u \in X \cap C^{\infty }((0,T)\times M)\) of (5.2), (5.3) given by Proposition 5.3 is unique.
Proof
Let \(u_1, u_2 \in X \cap C^{\infty }((0,T)\times M)\) be two solutions of (5.2), (5.3). The difference \(u:= u_1-u_2 \in X \cap C^{\infty }((0,T)\times M)\) then fulfils
In the following, the letter C denotes different positive constants. Multiplying (5.11) with 2u and integrating over M gives
with functions \(V \in L^p((0,T) \times M) \cap C^\infty ((0,T) \times M)\) and \(\rho \in L^\infty (0,T)\). Here we used the Sobolev embeddings \(H^1(M,{\bar{g}}) \hookrightarrow L^\rho (M)\) for \(\rho \in [1,\infty )\). Multiplying (5.11) with \(-2\Delta u\) and integrating over M yields
where we used first Hölder’s inequality with \(\alpha = \frac{2p}{p-2}\), then Young’s inequality and finally Sobolev embeddings again. Here we note that, by making \(C>0\) larger if necessary, we may assume that the constants are the same in (5.13) and (5.14). Combining these estimates gives
with the function \(g \in L^1(0,T)\) given by \(g(t)= C \Bigl (\Vert u_1(t)\Vert _{H^2(M,{\bar{g}})} + 3\Vert V(t,\cdot )\Vert _{L^p(M,{\bar{g}})}+1\Bigr )\). Integrating and using the fact that \(u \in C([0,T), H^1(M,{\bar{g}}))\) by Proposition 5.3 with \(u(0)=u_1(0)-u_2(0)=0\), we see that
It then follows from Gronwall’s inequality [3] that \(\Vert u(t)\Vert _{H^1(M,{\bar{g}})}^2 \equiv 0\) on [0, T), hence \(u_1 \equiv u_2\). \(\square \)
5.4 Global existence
Let \(f \in C^\infty (M)\), \(A>0\), \(p>2\) and \(u_0 \in {\mathcal {C}}_{p,A}\). In this section, we wish to show that the (unique) local solution
of the initial value problem (5.2), (5.3) for small \(T>0\) can be extended to a global und uniformly bounded solution defined for all positive times.
We first need the following local boundedness property on open time intervals.
Lemma 5.5
Let, for some \(T>0\), \(u\in C([0,T)\times M)\cap C([0,T),H^1(M,{\bar{g}}))\cap C^\infty ((0,T)\times M)\) be a solution of (5.2), (5.3) on [0, T). Then we have
with some \({\mathcal {M}}={\mathcal {M}}(\Vert u_0\Vert _{L^\infty (M,{\bar{g}})},\Vert f\Vert _{L^\infty (M,{\bar{g}})},T)>0\) which is increasing in all of its variables.
Proof
Since \({\bar{K}} <0\), we have
by (5.2), where
by (2.12). Hence the function \(v=-u\) satisfies
with \(c = \Vert f\Vert _{L^\infty (M,{\bar{g}})}+ \alpha _0\). Next, let \((T_k)_k \subset (0,T)\) be a sequence with \(T_k\rightarrow T\) for \(k\rightarrow \infty \). For fixed \(k \in \mathbb {N}\) the continuous function \(\textrm{e}^{2v}\) is then bounded from below by a positive constant on the compact set \([0,T_k]\times M\). Therefore Proposition 6.4 (ii) from the appendix implies that
Letting \(k \rightarrow \infty \), we deduce that
In order to derive an upper bound for u, we now observe that
on M for \(t \in [0,T)\). Applying Proposition 6.4 (ii) in the same way as above therefore gives
Combining (5.17) and (5.18) yields
as claimed in (5.18). \(\square \)
Corollary 5.6
The initial value problem (5.2), (5.3) admits a unique global solution \(u\in C([0,\infty )\times M)\cap C([0,\infty ),H^1(M,{\bar{g}}))\cap C^\infty ((0,\infty )\times M)\).
Proof
This follows from Proposition 5.3, Lemma 5.4 and Lemma 5.5 by a standard continuation argument using condition (5.7). \(\square \)
In the next lemma, with the help of (2.17), we turn (5.16) into a uniform estimate for all time.
Lemma 5.7
Let u be the global, smooth solution of the initial value problem (5.2), (5.3). Then we have
with some \({\mathcal {N}}={\mathcal {N}}(u_0,\Vert f\Vert _{L^\infty (M,{\bar{g}})})>0\) which is increasing in its second variable.
Proof
We argue similarly as in the proof of [18, Lemma 2.5].
By using the fact that u(t) is a volume preserving solution of (5.2) with \(u(0)=u_0\in {\mathcal {C}}_{p,A}\) and therefore \(\int _M\textrm{e}^{2u(t)}d\mu _{{\bar{g}}}\equiv A\), we get with (2.4) and the fact that \({\bar{K}}<0\) that
For the function
we then obtain, by combining (5.20) with (2.17), the estimate
Hence, for any \(T>0\) we find \(t_T\in [T,T+1]\) such that
with constants \(d_i = d_i(u_0)>0\). Here we used (2.6).
So, at time \(t_T\) we get with (2.7), Hölders inequality, Young’s inequality, (2.15), and (5.23) that
with constants \(d_i=d_i(u_0)\), \(i\in \{3,4\}\). Here the constants \(\nu _i(u_0,3)\), \(i\in \{0,1\}\) are given in (2.15).
Furthermore, with Sobolev’s embedding theorem we have \(W^{2,\frac{3}{2}}(M)\subset C^{0,\frac{2}{3}} \subset L^\infty (M,{\bar{g}})\). Therefore we get with Poincaré’s inequality, the Calderón–Zygmund inequality for closed surfaces, and with (5.24) that
with constants \(d_i>0\), \(i\in \{5,6,7\}\) and \(d_i=d_i(u_0)>0\), \(i\in \{8,9\}\). With (2.14) we therefore obtain the uniform bound
Upon shifting time by \(t_T\), we therefore get from Lemma 5.5
Since \({\mathcal {M}}\) is increasing in its first and second variables by Lemma 5.5, we see that \({\mathcal {N}}\) is increasing in \(\Vert f\Vert _{L^\infty (M,{\bar{g}})}\), as claimed. Since \(T>0\) was arbitrary, the claim follows. \(\square \)
5.5 Convergence of the flow
Let \(f \in C^\infty (M)\), \(A>0\), \(p>2\) and \(u_0 \in {\mathcal {C}}_{p,A}\) as before, and let u denote the global, smooth solution of the initial value problem (5.2), (5.3). In this section we shall show that for a suitable sequence \(t_l\rightarrow \infty \), \(l\rightarrow \infty \), the associated sequence of metrics \(g(t_l)\) tends to a limit metric \(g_\infty =\textrm{e}^{2u_\infty }{\bar{g}}\) with Gauss curvature \(K_{g_\infty }\), which then implies that \(K_{g_\infty }=f-\alpha ^\infty \) with a constant \(\alpha ^\infty \). Afterwards, we shall have a closer look at this constant \(\alpha ^\infty \).
By (5.22), we know that, for a suitable sequence \(t_l\rightarrow \infty \), \(l\rightarrow \infty \) we have
We can strengthen this observation as follows.
Lemma 5.8
For \(F(t)=\int _M|\partial _tu(t)|^2d\mu _{g(t)}\) as above, we have \(F(t)\rightarrow 0\) for \(t\rightarrow \infty \).
Proof
First we consider the evolution equation of the curvature \(K_{g(t)}\) and of \(\alpha (t)\). By the Gauss Eq. (1.1) and (5.2) we have
for \(t>0\). Moreover, by (2.11) we have
Combining (5.2), (5.29) and (5.30), we arrive at
We therefore get, using (2.12), that
with
With Lemma 4.4, applied with \(r=3\), \(C_{\text {GNL}}= C_{\text {GNL}}(3)>0\), (5.2) and Lemma 5.7 we can furthermore estimate
where we used Young’s inequality and the fact that
Combining (5.32) and (5.33) and using that \(G(t) \ge 0\) gives
By integrating (5.34) over \((t_l,t)\subset (t_l,T)\) and taking the supremum over \(t \in (t_l,T)\) we get
With (5.22) we also have \(\int _{t_l}^\infty F(t)dt\rightarrow 0\) for \(l\rightarrow \infty \) and thus \(1-{{\tilde{C}}}_2\int _{t_l}^\infty F(t) dt>0\) for l sufficiently large. For these l and \(T > t_l\) we thus have
Letting \(T\rightarrow \infty \) yields
which shows the claim. \(\square \)
To prove now the convergence of the flow, we first note u(t) is uniformly (in \(t \in (0,\infty )\)) bounded in \(H^1(M,{\bar{g}})\) by Proposition 2.25. and Lemma 5.8. We now consider a sequence \(t_l\rightarrow \infty \), \(l\rightarrow \infty \) and the associated sequence of functions \(u_l:=u(t_l)\). This sequence is bounded in \(H^1(M,{\bar{g}})\), hence there exists a subsequence, again denoted by \((u_l)_l\), with \(u_l\rightarrow u_\infty \) weakly in \(H^1(M,{\bar{g}})\) and therefore strongly in \(L^2(M,{\bar{g}})\). Furthermore with (2.12) we know that \(\alpha _l:=\alpha (t_l)\rightarrow \alpha _\infty \) as \(l\rightarrow \infty \) after passing again to a subsequence. Moreover we claim that \(\textrm{e}^{\pm u_l}\rightarrow \textrm{e}^{\pm u_\infty }\) (as \(l\rightarrow \infty \)) in \(L^p(M,{\bar{g}})\) for any \(2\le p<\infty \). Indeed, using Lemma 5.7 and the elementary estimate
we find that
Replacing \(u_l\) by \(-u_l\) we get also \(\textrm{e}^{-u_l}\rightarrow \textrm{e}^{-u_\infty }\) in \(L^p(M,{\bar{g}})\) as \(l\rightarrow \infty \) for any \(p<\infty \). Furthermore, we have
Since moreover \(\textrm{e}^{2u_l}\partial _tu_l\rightarrow 0\) in \(L^2(M,{\bar{g}})\) as \(l\rightarrow \infty \) with Lemma 5.7 and Lemma 5.8, the evolution Eq. (5.2) yields
Since the Laplace operator \(\Delta _{{\bar{g}}}\) is closed in \(L^2(M,{\bar{g}})\) with domain \(H^2(M,{\bar{g}})\), we deduce that \(u_\infty \) in \(H^2(M,{\bar{g}})\) with
and thus
So, we even have strong convergence \(u_l\rightarrow u_\infty \) in \(H^2(M,{\bar{g}})\) and uniformly, which implies that \(u_\infty \in {\mathcal {C}}_A\) and therefore
by integrating (5.36) over M. Consequently, for the Gauss curvature \(K_{g_\infty }\) of the limit metric \(g_\infty =\textrm{e}^{2u_\infty }{\bar{g}}\) we get from (1.1) and (5.36) that
which shows the convergence of the flow.
5.6 The Sign of the Constant \(\alpha _\infty \)
In this subsection we complete the proofs of Theorem 3.4 and Theorem 3.5. For this we show, under certain assumptions, that the expression
is positive. The proof of Theorem 3.5 is already completed by the statement of Corollary 4.7. So we can turn to Theorem 3.4.
Proof of Theorem 3.4 (completed)
We have seen in Lemma 5.7 that in the case where \(u_0 \equiv \frac{1}{2}\log (A) \in {\mathcal {C}}_{p,A}\), the uniform \(L^\infty \)-bound on the global solution of the initial value problem (5.2), (5.3) only depends on A and an upper bound on \(\Vert f\Vert _{L^\infty (M,{\bar{g}})}\). In other words, if \(A>0\) and \(c>0\) are fixed, then there exists \(\tau >0\) with the property that
for every \(f \in C^\infty (M)\) with \(\Vert f\Vert _{L^\infty (M,{\bar{g}})} \le c\) and the corresponding solution u of the initial value problem (5.2), (5.3) with \(u_0 \equiv \frac{1}{2}\log (A) \in {\mathcal {C}}_{p,A}\). Consequently, we also have \(\Vert u_\infty \Vert _{L^\infty (M,{\bar{g}})} \le \tau \) under the current assumptions on f, which implies that
Hence, if \(\Vert f+c\Vert _{L^1(M,{\bar{g}})} <\varepsilon :=\frac{c + \frac{{\bar{K}}}{A}}{\textrm{e}^{2\tau }}\), we have \(\lambda >0\). \(\square \)
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Borer, F., Galimberti, L., Struwe, M.: “Large’’ conformal metrics of prescribed gauss curvature on surfaces of higher genus. CommentariiMathematici Helvetici 90(2), 407–428 (2015). https://doi.org/10.4171/CMH/358
Buzano, R., Schulz, M., Struwe, M.: Variational Methods in Geometric Analysis. (to appear)
Cazenave, T., Haraux, A., Martel, Y.: An Introduction to Semilinear Evolution Equations. Oxford Lecture Series in Mathematics and its Application 13. The Clarendon Press, Oxford University Press, 1999
Ceccon, J., Montenegro, M.: Optimal \(L^p\)-Riemannian Gagliardo-Nirenberg inequalities. Mathematische Zeitschrift 258(4), 851–873 (2008). ISSN: 0025-5874. https://doi.org/10.1007/s00209-007-0202-8
Chang, S.-Y.A.: Non-linear elliptic equations in conformal geometry. Zurich Lectures in Advanced Mathematics 2. European Mathematical Society, (2004)
Chang, S.-Y.A., Yang, P.C.: Prescribing Gaussian curvature on S2. Acta Mathematica 159(1), 215–259 (1987). https://doi.org/10.1007/BF02392560
Ding, W.-Y., Liu, J.-Q.: A note on the problem of prescribing gaussian curvature on surfaces. Trans. Am. Math. Soc. 347(3), 1059–1066 (1995)
Galimberti, L.: Compactness issues and bubbling phenomena for the prescribed Gaussian curvature equation on the torus. Calculus of Variations and Partial Differ. Equs. 54(3), 2483–2501 (2015). https://doi.org/10.1007/s00526-015-0872-8
Ho, P.T.: Prescribed curvature flow on surfaces. Indiana Univ. Math. J. 60(5), 1517–1541 (2011)
Kazdan, J.L., Warner, F.W.: Curvature functions for open 2-manifolds. Ann. Math. 99(2), 203–219 (1974)
Kazdan, J.L., Warner, F.W.: Curvature functions for compact 2-manifolds. Ann. Math. 99(1), 14–47 (1974)
Koebe, P.: Über die Uniformisierung beliebiger analytischer Kurven (Dritte Mitteilung). Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1, 337–358 (1908)
Ladyženskaja, O., Solonnikov, V., Ural’ceva, N.: Linear and quasilinear equations of parabolic type. Vol. 23. Translations of mathematical monographs. Providence, RI: American Mathematical Society, (1968)
Lieberman, G.M.: Second order parabolic differential equations. World Sci. (1996). https://doi.org/10.1142/3302
Moser, J.: A sharp form of an inequality by N Trudinger. Indiana Univ. Math. J. 20(11), 1077–1092 (1971)
Poincaré, H.: Sur l’uniformisation des fonctions analytiques. Acta Mathematica 31, 1–64 (1908)
Schauder, J.: Der Fixpunktsatz in Funktionalraümen. Studia Mathematica 2(1), 171–180 (1930)
Struwe, M.: “Bubbling’’ of the prescribed curvature flow on the torus. Journal of the EuropeanMathematical Society 22(10), 3223–3262 (2020)
Struwe, M.: A flow approach to Nirenberg’s problem. DukeMath. J. 128(1), 19–64 (2005). https://doi.org/10.1215/S0012-7094-04-12812-X
Trudinger, N.S.: On embeddings into Orlicz spaces and some applications. J. Math. Mech. 17, 473–484 (1967)
Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), project 408275461 (Smoothing and Non-Smoothing via Ricci Flow). We would like to thank Esther Cabezas–Rivas for helpful discussions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andrea Mondino.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In this section, we collect some helpful estimates and well-posedness results for a class of linear second order parabolic equations in non-divergence form with continuous second order coefficient. Most of these results should be known to experts but seem hard to find in the required form in the literature.
As before, let \((M,{\bar{g}})\) be a two-dimensional, smooth, closed, connected, oriented Riemann manifold endowed with a smooth background metric \({\bar{g}}\). For a domain \(\Omega \subset \mathbb {R}\times M\) and \(p \ge 1\), we let \(W^{2,1}_p(\Omega )\) denote the space of functions \(u \in L^p(\Omega )\) which have weak derivatives Du, \(D^2u\) and \(\partial _tu\) in \(L^p(\Omega )\). In the following, we fix \(p>2\), and we recall the following embedding, see e.g. [13, Lemma 3.3].
Lemma 6.1
If the domain \(\Omega \subset \mathbb {R}\times M\) is bounded, then \(W^{2,1}_p(\Omega )\) is continuously embedded in \(C^\alpha ({\overline{\Omega }})\) for some \(\alpha = \alpha (p)>0\) and therefore compactly embedded in \(C({\overline{\Omega }})\).
We consider the linear parabolic problem
with \(a,c,d \in C({\overline{\Omega }})\) and \(d \in L^p(\Omega )\). We say that a function \(u \in W^{2,1}_p(\Omega )\) is a (strong) solution of (6.1) in \(\Omega \) if (6.1) holds almost everywhere in \(\Omega \). Specifically, we consider (6.1) on the cylindrical domains \(\Omega _T= (0,T)\times M\) and \({\widetilde{\Omega }}_T= (-\infty ,T)\times M\) in the following.
In particular, we consider strong solutions of (6.1) together with the initial condition
with \(u_0 \in W^{2,p}(M,{\bar{g}})\), which is supposed to hold in the (initial) trace sense.
Proposition 6.2
Let \(T>0\), \(a,c \in C({\overline{\Omega }}_T)\) with \(a_T:= \min \limits _{(t,x)\in {\overline{\Omega }}_T}a(t,x) >0\), let \(d \in L^p(\Omega _T)\) for some \(p>2\), and let \(u_0 \in W^{2,p}(M,{\bar{g}})\).
Then the initial value problem (6.1), (6.2) has a unique strong solution \(u \in W^{2,1}_p(\Omega _T)\). Moreover, u satisfies the estimate
with a constant \(C>0\) depending only on \(\Vert a\Vert _{L^\infty (\Omega _T)}\), \(\Vert c\Vert _{L^\infty (\Omega _T)}\) and \(a_T\). Moreover, C does not increase after making T smaller.
If, moreover, \(a,c,d \in C^\alpha (\Omega _T)\) for some \(\alpha >0\), then \(u \in C({\overline{\Omega }}_T) \cap C^{2,1}(\Omega _T)\) is a classical solution of (6.1), (6.2), and we have the inequality
Proof
In the following, the letter C stands for various positive constants depending only on \(\Vert a\Vert _{L^\infty (\Omega _T)}\), \(\Vert c\Vert _{L^\infty (\Omega _T)}\), and \(a_T\), and which do not increase after making T smaller.
Step 1: We first assume that we are given a strong solution \(u \in W^{2,1}_p(\Omega _T)\) of (6.1), (6.2) with \(u_0\equiv 0 \in W^{2,p}(M,{\bar{g}})\). We then define \(v: {\widetilde{\Omega }}_T \rightarrow \mathbb {R}\) by
Then \(v \in W^{2,1}_p({\widetilde{\Omega }}_T)\) solves (6.1) with a, c, d replaced by suitable extensions \({{\tilde{a}}},{{\tilde{c}}}, \in L^\infty ({\widetilde{\Omega }}_T)\), \({{\tilde{d}}}\in L^p({\widetilde{\Omega }}_T)\) satisfying \({{\tilde{a}}}(t,x)=a(x,0)\), \({{\tilde{c}}}(t,x)=c(x,0)\) and \({{\tilde{d}}}(t,x)= 0\) for \(t\le 0\), \(x \in M\).
Therefore, [14, Theorem 7.22] gives rise to the uniform bound
This translates into the estimate
Moreover, setting \(V(t):=\Vert u(t)\Vert _{L^p(M,{\bar{g}})}^p\) for \(t \in \mathbb {R}\), we have \(V(0)=0\) and
for \(t \in (0,T)\), therefore
By Gronwall’s inequality we get \(V(t) \le C \Vert d\Vert _{L^p(\Omega _t)}^p\) and thus
This already implies the uniqueness of strong solutions of (6.1), (6.2), since the difference u of two solutions \(u_1,u_2 \in W^{2,1}_p(\Omega _T)\) of (6.1), (6.2) satisfies (6.1), (6.2) with \(u_0=0\) and \(d=0\). Moreover, if \(u \in W^{2,1}_p(\Omega _T)\) is a strong solution of (6.1), (6.2), then the function \({{\hat{u}}} \in W^{2,1}_p(\Omega _T)\) given by \({{\hat{u}}}(t,x):= u(t,x)- u_0(x)\) safisfies (6.1), (6.2) with \(u_0=0\) and d replaced by \({{\hat{d}}}\) given by
Consequently, combining (6.6) and (6.7), and using an interpolation estimate for Du, we find that
as claimed in (6.3).
Step 2 (Existence): In the case where \(a,c,d \in C^\alpha (\Omega _T)\) and \(u_0\in C^{2+\alpha }(M)\), the existence of a classical solution \(u \in C({\overline{\Omega }}_T) \cap C^{2,1}(\Omega _T)\) of (6.1), (6.2) follows as in [14, Theorem 5.14].
In the general case we consider (6.1), (6.2) with coefficients \(a_n, c_n, d_n \in C^\alpha ({\overline{\Omega }}_T)\), \(u_{0,n}\in C^{2+\alpha }(M)\), in place of \(a,c,d, u_0\) with the property that \(a_n \rightarrow a\), \(c_n \rightarrow c\) in \(L^\infty (\Omega _T)\), \(d_n \rightarrow d \in L^p(\Omega _T)\) as well as \(u_{0,n}\rightarrow u_0\) in \(W^{2,p}\). The associated unique solutions \(u_n \in C({\overline{\Omega }}_T) \cap C^{2,1}(\Omega _T)\) are uniformly bounded in \(W^{2,1}_p(\Omega _T)\) by (6.3), and therefore we have \(u_n \rightharpoonup u\) in \(W^{2,1}_p(\Omega _T)\) after passing to a subsequence. For every \(\phi \in C^\infty _c(\Omega _T)\), we then have
and from this we deduce that \(\partial _tu(t,x) - a(t,x)\Delta _{{\bar{g}}} u(t,x) - c(t,x)u(t,x) - d(t,x)= 0\) almost everywhere in \(\Omega _T\), so u is a strong solution of (6.1).
Step 3: It remains to show the inequality (6.4) in the case where \(a,c,d \in C^\alpha (\Omega _T)\) for some \(\alpha >0\). Since \(u \in C(\overline{\Omega _T}) \cap C^{2,1}(\Omega _T)\) in this case and therefore
it suffices to show that
If \(u_0 \in C^{2+\alpha }(M)\) for some \(\alpha >0\), this follows by [14, Theorem 5.14] with \(\lim \) in place of \(\limsup \), since the function \(t \mapsto u(t)\) is continuous from \([0,T) \rightarrow C^{2+\alpha }(M)\) in this case. Moreover, in this case we have, by Hölder’s and Young’s inequality,
and therefore
In the general case, we consider (6.1), (6.2) with a sequence of initial conditions \(u_{n,0}\) in place of \(u_0\), where \(u_{n,0} \rightarrow u_0\) in \(H^2(M)\). The associated unique solutions \(u_n \in C({\overline{\Omega }}_T) \cap C^{2,1}(\Omega _T)\) are uniformly bounded in \(W^{2,1}_p(\Omega _T)\) by (6.3), and they are also uniformly bounded in \(C^{2,1}([\varepsilon ,T]\times M)\) by [14, Theorem 5.15] for every \(\varepsilon \in (0,T)\). Fix \(t \in (0,T)\). Passing to a subsequence, we may assume that \(u_n \rightharpoonup u\) in \(W^{2,1}_p(\Omega _T)\), \(u_n \rightarrow u\) strongly in \(C^{0}(\overline{\Omega _T})\) and \(u_n(t) \rightarrow u(t)\) strongly in \(C^1(M)\). As in Step 2, we see, by testing with \(\phi \in C^\infty _c(\Omega _T)\), that \(\partial _tu(t,x) -a(t,x)\Delta _{{\bar{g}}} u(t,x) - c(t,x)u(t,x) - d(t,x)= 0\) almost everywhere in \(\Omega _T\), so u is the unique strong solution of (6.1), (6.2). Moreover, by (6.9) we have
It thus follows that
and therefore
as claimed in (6.8). \(\square \)
Next we prove a maximum principle for solutions of (6.1), (6.2). We need the following preliminary lemma.
Lemma 6.3
Let \(T>0\).
-
(i)
For any function \(u \in C^2(M)\) we have
$$\begin{aligned} \int _{\{x\in M\mid u(x)>0\}}\Delta _{{\bar{g}}} u d\mu _{{\bar{g}}}\le 0. \end{aligned}$$ -
(ii)
Let \(u,\rho \in C^{1}([0,T])\) be functions with \(u(0) \le 0\) and \(\rho (T) \ge 0\). Then
$$\begin{aligned} \int _{\{t\in [0,T]\mid u(t)>0\}}\bigl (\rho (t) \partial _tu(t) + \kappa u(t)\bigr ) \,dt \ge 0 \qquad \text {with}\quad \kappa := \sup _{s \in (0,T)}\partial _t\rho (s). \end{aligned}$$(6.10) -
(iii)
Let \(u \in C^{2,1}(\Omega _T) \cap C^{0,1}({\overline{\Omega }}_T)\), \(\rho \in C^{0,1}({\overline{\Omega }}_T)\) be functions with \(u \le 0\) on \(\{0\}\times M\) and \(\rho \ge 0\) on \(\{T\}\times M\). Then we have
$$\begin{aligned} \begin{aligned}&\int _{\{(t,x)\in [0,T]\times M\mid u(t,x)>0\}}(\rho (t,x)\partial _t u(t,x) + \kappa u(t,x) - \Delta _{{\bar{g}}} u(t,x))d\mu _{{\bar{g}}}(x)dt \ge 0 \\&\text {with}\quad \kappa := \sup _{(s,x)\in (0,T)\times M}\partial _t\rho (s,x). \end{aligned} \end{aligned}$$(6.11)
Proof
-
(i)
By Lebesgue’s theorem, it suffices to prove
$$\begin{aligned} \int _{\{x\in M\mid u(x)>\varepsilon _n\}}\Delta _{{\bar{g}}} ud\mu _{{\bar{g}}}\le 0 \end{aligned}$$(6.12)for a sequence \(\varepsilon _n \rightarrow 0^+\). By Sard’s Lemma, we may choose this sequence such that \(\Omega _\varepsilon := \{x\in M\mid u(x)>\varepsilon _n\}\) is an open set of class \(C^1\), whereas the outer unit vector field of \(\Omega _\varepsilon \) is given by \((t,x)\mapsto - \frac{\nabla _{{\bar{g}}} u(t,x)}{|\nabla _{{\bar{g}}} u(t,x)|_{{\bar{g}}}}\). Hence (6.12) follows from the divergence theorem.
-
(ii)
The set \(\{t\in [0,T]\mid u(t)>0\}\) is a union of at most countably many open intervals \(I_j\), \(j \in \mathbb {N}\). For any such interval, partial integration gives
$$\begin{aligned} \int _{I_j }\Bigl (\rho (t) \partial _tu(t)+ \partial _t\rho (t) u(t)\Bigr ) \,dt = \left\{ \begin{aligned}&0,{} & {} \qquad \text {if }T \not \in {{\overline{I}}}_j;\\&\rho (T) u(T) \ge 0,{} & {} \qquad \text {if }T \in {{\overline{I}}}_j. \end{aligned} \right. \end{aligned}$$Consequently,
$$\begin{aligned} \int _{\{t\in [0,T]\mid u(t)>0\}}\rho (t) \partial _tu(t)\,dt&\ge - \displaystyle \int _{\{t\in [0,T]\mid u(t)>0\}}\partial _t\rho (t) u(t) \,dt \\&\ge - \displaystyle \int _{\{t\in [0,T]\mid u(t)>0\}}\kappa u(t) \,dt \end{aligned}$$with \(\kappa \) given in (6.10). This shows the claim. (iii) This is a direct consequence of (i), (ii) and Fubini’s theorem.
\(\square \)
Proposition 6.4
(Maximum principle) Let \(T>0\), \(a, c \in C({\overline{\Omega }}_T)\) with \(a_T:= \min \limits _{(t,x)\in {\overline{\Omega }}_T}a(t,x) >0\), let \(d \in L^p(\Omega _T)\) for some \(p>2\) with \(d_T:= \sup _{(t,x)\in \Omega _T}d(t,x)< \infty \), and let \(u_0 \in W^{2,p}(M,{\bar{g}})\). Moreover, let \(u \in W^{2,1}_p(\Omega _T)\) be the unique solution of (6.1), (6.2).
-
(i)
If \(u_0 \le 0\) on M and \(d_T \le 0\), then \(u \le 0\) on \(\Omega _T\).
-
(ii)
If \(c \equiv 0\) on \(\Omega _T\), then
$$\begin{aligned} u(t,x) \le \Vert u_0^+\Vert _{L^\infty (M,{\bar{g}})} + t d_T \qquad \text {for }t \in [0,T],\, x \in M. \end{aligned}$$(6.13)
Proof
(i) Step 1: We consider the special case \(a \in C^{0,1}({\overline{\Omega }}_T)\), \(u_0\le 0\) and \(d_T\le -\varepsilon \) for some \(\varepsilon >0\). We put \(\rho := \frac{1}{a} \in C^{0,1}({\overline{\Omega }}_T)\) and \(\kappa := \sup \limits _{(s,x)\in (0,T)\times M}\partial _t\rho (s,x)\) as in (6.11). Moreover, we consider the function
with \(\breve{\kappa } = \frac{|\kappa |}{\min _{(t,x)\in {\overline{\Omega }}_T}\rho (t,x)} + \Vert c\Vert _{L^\infty (\Omega _T)}\), noting that \(\breve{u}\) satisfies
We now let \((u_n)_{n\in \mathbb {N}}\) be a sequence in \(C^{2,1}(\Omega _T) \cap C^{0,1}({\overline{\Omega }}_T)\) with \(u_n(x,0)\le 0\) and \(u_n \rightarrow \breve{u}\) in \(W^{2,1}_p(\Omega _T)\). Since the functions \(g_n:= 1_{\{(t,x)\in [0,T]\times M\mid u_n(t,x)>0\}}\) are bounded in \(L^{p'}(\Omega _T)\), we may pass to a subsequence such that \(g_n \rightharpoonup g\) in \(L^{p'}(\Omega _T)\), where \(g \ge 0\) and \(g \equiv 1\) in \(\{(t,x)\in [0,T]\times M\mid \breve{u}(t,x) >0\}\), since \(u_n \rightarrow \breve{u}\) uniformly as a consequence of Lemma 6.1 and therefore \(g_n \rightarrow 1\) pointwisely on \(\{(t,x)\in [0,T]\times M\mid \breve{u}(t,x)>0\}\). Applying Lemma 6.3 (iii) to \(u_n\), we find that
for all \(n \in \mathbb {N}\) and therefore
We thus conclude that \(\{(t,x)\in (0,T)\times M\mid \breve{u}(t,x)>0\} = \{(t,x)\in (0,T)\times M\mid u(t,x) >0\} = \varnothing \) and therefore \(u \le 0\) in \((0,T)\times M\).
Step 2: In the special case where \(a \in C^{0,1}({\overline{\Omega }}_T)\), \(u_0\le 0\) and \(d_T\le 0\), we may apply Step 1 to the functions \(u_\varepsilon \in W^{2,1}_p(\Omega _T)\) defined by \(u_\varepsilon (t,x)= u(t,x)- \varepsilon t\), which yields that \(u_\varepsilon \le 0\) for every \(\varepsilon >0\) and therefore \(u \le 0\) in \(\Omega _T\).
Step 3: In the general case, we consider a sequence \(a_n \in C^{0,1}({\overline{\Omega }}_T)\) with \(a_n \rightarrow a\) in \(C({\overline{\Omega }}_T)\), and we let \(u_n\) denote the associated solutions of (6.1), (6.2) with a replaced by \(a_n\). As in the end of the proof of Proposition 6.2, we then find that, after passing to a subsequence, \(u_n \rightharpoonup {{\tilde{u}}}\) in \(W^{2,1}_p(\Omega _T)\), where \({{\tilde{u}}}\) is a solution of (6.1), (6.2). By uniqueness, we have \(u= {{\tilde{u}}}\). Moreover, since \(u_n \le 0\) for all n by Step 3, we have \(u = {{\tilde{u}}} \le 0\), as required.
(ii) We consider the function \(v \in W^{2,1}_p(\Omega _T)\) given by \(v(t,x)= u(t,x)- \Vert u_0^+\Vert _{L^\infty (M,{\bar{g}})}- t d_T\), which, by assumption, satisfies (6.1), (6.2) with \(c \equiv 0\), \(d- d_T\) in place of d and \(u_0 - \Vert u_0^+\Vert _{L^\infty (M,{\bar{g}})}\) in place of \(u_0\). Then (i) yields \(v \le 0\) in \(\Omega _T\), and therefore u satisfies (6.13). \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Borer, F., Elbau, P. & Weth, T. A variant prescribed curvature flow on closed surfaces with negative Euler characteristic. Calc. Var. 62, 262 (2023). https://doi.org/10.1007/s00526-023-02600-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-023-02600-9